Основы теории погрешностей

1. Численные методы

Тема 1.Основы теории
погрешностей
Курс лекций
Голиков Руслан Юрьевич,
к.т.н., доцент
1

2. Основные понятия

2

3. Приближённые вычисления в жизни

Прийти на остановку автобуса в заданный интервал времени
Купить товары в пределах определённой суммы
УК РФ: Статья 213. Хулиганство
Наказывается штрафом в размере от 500 000 до 1 000 000 рублей
или в размере заработной платы за период от 3 до 4 лет,
либо принудительными работами на срок до 5 лет,
либо лишением свободы на срок до 7 лет.

4. Точность вычислений

Точность вычислений определяют последствия, которые вычисления могут за собой повлечь
УК РФ: Статья 293
Халатность

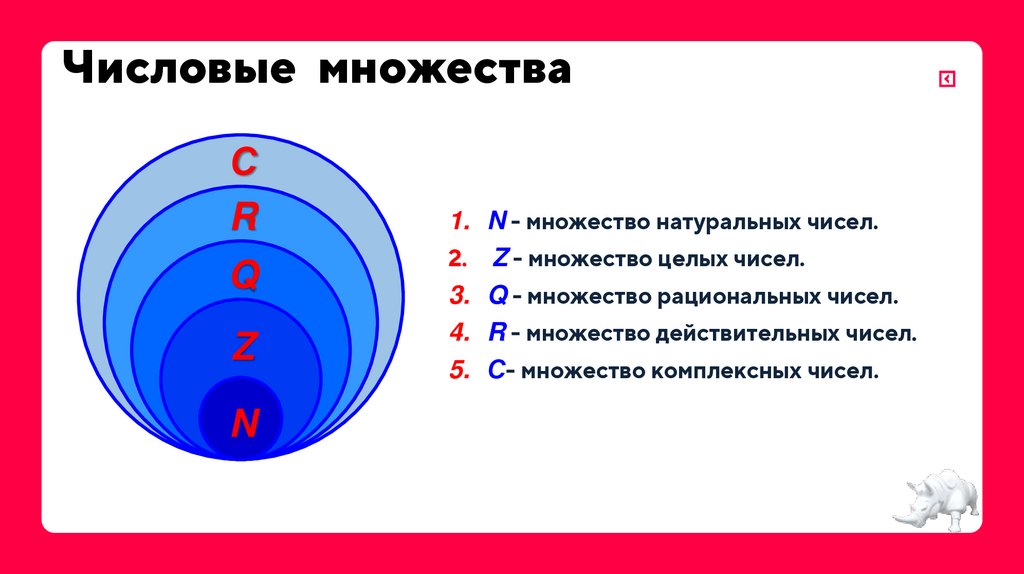
5. Числовые множества

С
R
Q
Z
N
1. N - множество натуральных чисел.
2. Z - множество целых чисел.
3. Q - множество рациональных чисел.
4. R - множество действительных чисел.
5. С- множество комплексных чисел.

6. Множество натуральных чисел

Натуральные числа {N} – это числа, используемые для счета. Они образуют
множество натуральных чисел: {N}=1, 2, 3, … , n
Для множества {N} вводятся две математические операции: сложение и умножение.
При сложении каждой паре натуральных чисел (n, p) ставится в соответствие натуральное
число s, называемое их суммой: s=n+p, n и р называют слагаемыми.
При умножении каждой паре натуральных чисел (n, p) ставится в соответствие
натуральное число s, называемое их произведением: s=n∙p, n и р называют сомножителями.
СВОЙСТВА ОПЕРАЦИЙ СЛОЖЕНИЯ И УМНОЖЕНИЯ
1. Коммутативность: (переместительный закон) n∙p=p∙n
2. Ассоциативность (сочетательный закон) (n∙p)∙k=n∙(p∙k)
3. Дистрибутивность (распределительный закон) умножения относительно сложения:
(n+p)∙k=n∙k+p∙k
* Сумма и произведение натуральных чисел опять будут натуральными числами. Поэтому
говорят, что множество {N} замкнуто относительно операций сложения и умножения.

7. Множество натуральных чисел

Также для множества {N} определены операции вычитания и деления.
Вычитание натуральных чисел есть операция, обратная сложению, т.е. соответствие,
которое паре натуральных чисел n и р относит такое натуральное число r, что r+p=n.
О числе r говорят, что оно получено в результате вычитания числа р из числа n : r = n-p.
Число r называют разностью чисел n и p, где n - уменьшаемое, р - вычитаемое.
Деление натуральных чисел есть операция, обратная умножению, т.е. соответствие, которое
упорядоченной паре натуральных чисел n и р относит такое натуральное число q, что n=p∙q.
О числе q говорят, что оно получено в результате деления числа n на число р: q=n/p. Число q
называют частным натуральных чисел n и p, где n - делимое, р - делитель.
ВАЖНО! В множестве {N} разность двух натуральных чисел определена тогда и только
тогда, когда n>p (уменьшаемое больше вычитаемого). Частное определено тогда и
только тогда, когда q ϵ {N}.
* Разность и частное натуральных чисел не всегда могут быть натуральными числами.
Поэтому множество {N} не замкнуто относительно операций вычитания и деления.
ПРИМЕР: 5-2=3; 2-5=?
4/2=2; 2/4=?

8. Множество целых чисел

Множество целых чисел {Z} есть множество, полученное в результате
добавления к множеству натуральных чисел {N} новых объектов – числа ноль и
отрицательных целых чисел.
Эти новые объекты вводятся следующим образом:
n+0=n – сумма любого натурального числа n и числа 0 есть натуральное число n.
n+(-n)=0 – любому натуральному n соответствует единственное отрицательное число
–n такое, что их сумма равна нулю.
Число –n называют противоположным числу n.
Число, противоположное числу –n есть число n: -(-n)=n. Поэтому минус на минус дает
плюс, что следует из противоположности положительных и отрицательных чисел.
Натуральные числа, входящие в множество целых чисел {Z} называют положительными
целыми числами.
* Сумма, разность и произведение целых чисел опять будут целыми числами. Поэтому говорят,
что множество {Z} замкнуто относительно этих операций.

9. Операции с целыми числами

1.
Сложение и умножение натуральных чисел в {Z} совпадает со сложением и
умножением натуральных чисел в {N}.
2. Вычитание в {Z} возможно всегда, т.е. разность двух любых целых чисел
есть число целое.
3. Абсолютным значением (или модулем) числа n называют число |n|,
вычисляемое по правилу:
• |n|=n, если n>0
• |n|=0, если n=0
• |n|=-n, если n<0
4. Деление на ноль запрещено.
Частное целых чисел не всегда может быть целым числом. Поэтому множество {Z} замкнуто
относительно операций сложения, умножения и вычитания, но не замкнуто относительно
операции деления.

10. Множество рациональных чисел

Множество рациональных чисел {Q} есть множество, полученное в результате
добавления к множеству целых чисел {Z} новых объектов – рациональных дробей.
Рациональное дробью называют пару чисел m и n , обозначаемую символом m/n, где
m – целое число ( m ϵ {Z} ) , а n – натуральное ( n ϵ {N} ) . Число m называется
числителем дроби, а число n - её знаменателем.
Рациональная дробь называется положительной, если m>0, и называется отрицательной,
|m|
если m<0. Отрицательную рациональная дробь обычно записывают в виде:
n
m1
m2
Две рациональные дроби
и
называются эквивалентными, если m1n2=n1m2.
n1
n2
Рациональное число – это такое число, которое может быть представлено в
виде m/n, где |m| и n – взаимно простые (несократимые) натуральные числа.
* Простым числом называется натуральное число, единственным делителем которого является
оно само и единица. При этом единица не считается простым числом. Все остальные числа
называются составными.

11. Множество рациональных чисел

Рациональное число n называется целым, если в множестве всех
n
эквивалентных дробей, задающих это число, содержится дробь вида: .
1
Таким образом, для вычисления суммы, произведения, разности и частного
рационального числа и целого числа n достаточно записать число n в виде
дроби, знаменатель которой равен единице.
Поэтому для рациональных чисел выполнимы все арифметические операции,
кроме деления на ноль, т.е. множество рациональных чисел замкнуто
относительно операций сложения, вычитания, умножения и деления (кроме
деления на ноль), а результат их выполнения есть число рациональное.

12. Множество действительных чисел

Множество действительных чисел {R} получается естественным (но более сложным)
расширением множества рациональных чисел {Q} путем добавления к нему
иррациональных чисел.
Иррациональным называют число, которое нельзя представить в виде рациональной дроби.
ЗАДАЧИ, НЕ ИМЕЮЩИЕ РЕШЕНИЯ НА МНОЖЕСТВЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:
l
=
...
d
c
b=1
а=1
с = а 2 b2 = 12 +12 = 2

13. Множество действительных чисел

В противоположность множеству рациональных чисел, которое замкнуто
относительно операций сложения, вычитания, умножения и деления (кроме
деления на ноль), множество иррациональных чисел не обладает свойством
замкнутости ни для одной из этих операций.
2 2 2
ПРИМЕРЫ:
0,303003000300003...
1
0,333333333333333...
0,030330333033330...
3
Суммой, разностью, произведением и частным иррационального числа и
рационального числа являются иррациональные числа. Поэтому, имея лишь
одно иррациональное число, с помощью рациональных чисел можно
построить бесконечное множество иррациональных чисел.

14. Понятие комплексного числа

Комплексным числом называется выражение a+bi, где a и b - действительные
числа, i - мнимая единица, определяемая равенствами:
i 2 = -1 или i = -1.
a - называется действительной частью, а bi - мнимой частью комплексного числа.
Если a=0, то число 0+bi=bi называется чисто мнимым, а если b=0, то получается
действительное число: a+0∙i=a.
*Слово комплекс означает связь, сочетание, совокупность понятий, предметов,
явлений образующих единое целое.

15. Десятичная позиционная система счисления

В десятичной позиционной системе счисления используются натуральные
числа от одного до девяти, которые обозначаются символами: 0 1 2 3 4 5 6 7 8 9
Эти десять символов называются цифрами десятичной позиционной системы
счисления. Используя различные комбинации цифр, мы можем для целого
числа указать количество единиц, десятков сотен, тысяч и т.д.
ЦИФРЫ ДЕСЯТИЧНОЙ ПОЗИЦИОННОЙ СИСТЕМЫ СЧИСЛЕНИЯ
1
2
3
4
5
6
7
8
Натуральные числа
ПРИМЕР:
9
0
Символ нуля
Тысячи
Сотни
Десятки
Единицы
2
0
2
5

16. Десятичная позиционная система счисления

Десятичной дробью называется число, записанное в виде: N,n1n2n3…nk… ,
где N это целое число, а n1n2n3…nk… - последовательность цифр десятичной
системы счисления. Целое число отделяют запятой от цифр десятичной
системы счисления. Такая десятичная дробь представляет собой условную
запись рационального числа:
n
n
n
n
N
k
k
.
Целое число N называется целой частью десятичной дроби. n1 - стоит в разряде
десятых долей единицы; n2 - сотых долей единицы; n3 - тысячных долей и т.д.
ПРИМЕР.
17,685 - десятичная дробь
6
8
5
600 + 80 + 5
685
137
+
+
= 17 +
= 17
= 17
- рациональная дробь (смешанная)
10 100 1000
1000
1000
200
* Записывать такие числа и выполнять с ними различные вычисления неудобно, поэтому
их представление в форме десятичной дроби является предпочтительным и привычным.
17 +

17. Десятичная позиционная система счисления

ПРЕДСТАВЛЕНИЕ РАЦИОНАЛЬНОГО ЧИСЛА В ВИДЕ ДЕСЯТИЧНОЙ ДРОБИ
1/2=0,5; 1/4=0,25; 1/8=0,125; 1/16=0,0625 …
процедура деления заканчивается через конечное число шагов. Такое число
называют конечной десятичной дробью.
1/3=0,3333333333
…
1/9=0,1111111111…
;
1/7=0,142857142857142857142857
…
;
процедура деления не заканчивается и остаток периодически повторяется.
Такое число можно представить в виде бесконечной периодической
десятичной дроби. Пишут: 0,(3) ; 0,(142857) ; 0,(1).
1/6=0,1666666666 … - остаток периодически повторяется после 1.
1/12=0,0833333333 … - остаток периодически повторяется после 8.
Такое число называют смешанной периодической десятичной дробью.
Пишут: 0,1(6) ; 0,08(3).
* Этими тремя случаями исчерпываются все варианты
рационального числа в форме десятичной дроби.
представления

18. Точные и приближенные вычисления

Арифметические действия сложения, вычитания и умножения над целыми
числами и числами, записанными в форме конечной десятичной дроби, можно
выполнять точно и получить результат, который также может быть выражен
целым числом или в форме конечной десятичной дроби.
ПРИМЕР.
Действия над числами, записанными в форме конечной десятичной дроби,
аналогичны действиям над целыми числами.
ПРИМЕР.

19. Точные и приближенные вычисления

Частное двух чисел, записанных в форме конечной десятичной дроби, не всегда
выражается целым числом или конечной десятичной дробью, поэтому если при
выполнении операции деления мы хотим сохранить точный результат, то его
следует представить в виде обыкновенной дроби.
ПРИМЕР.
Иррациональное число не выражается в виде отношения двух целых чисел и в
десятичной позиционной системе счисления записывается в форме бесконечной
непериодической десятичной дроби.

20. Точные и приближенные числа

Чтобы оперировать с конечной десятичной дробью бесконечную десятичную
дробь (периодическую или непериодическую) приходится обрывать на какой-либо
цифре после запятой.
1
= 0,142857
7
2 = 1,141
142857142857142857142857142857142857...
2135623730950488016887242097...
Число, представляемое конечной десятичной дробью, полученной в результате
обрывания бесконечной десятичной дроби, называется приближенным значением
данного числа.

21. Точные и приближенные числа

Приближенные значения чисел также возникают вследствие
различных измерений. В результате искомые величины не
могут иметь точных значений по причине появления ошибок,
связанных с несовершенством измерительных приборов,
методов измерений и геометрической неправильностью самого
измеряемого объекта.
Приближенное значение величины или конечную десятичную дробь, полученную
в результате обрывания записи, называют приближенным числом.
Истинное значение величины называют точным числом.
Разновидностью обрывания десятичной дроби (конечной или бесконечной),
является округление. Округление или просто обрывание конечной десятичной
дроби превращает точное число в приближенное.

22. Погрешность приближенного числа

22

23. Истинная и абсолютная погрешность

Приближенное число лишь тогда имеет практическую ценность, когда станет
известно, с какой точностью оно получено или, другими словами, можно оценить его
погрешность – отличие от точного числа.
ОПРЕДЕЛЕНИЕ 1. Истинной погрешностью (погрешностью) приближенного
числа называется разность между числом х и его приближенным значением а: x-a
ОПРЕДЕЛЕНИЕ 2. Абсолютной погрешностью приближенного числа
называется абсолютная величина (модуль) разности между числом х и его
приближенным значением а: Δ=|x-a|.
Точное число х чаще всего оказывается неизвестно, поэтому найти истинную и
абсолютную погрешность не представляется возможным. Но можно указать
число, которого абсолютная погрешность не превысит, т.е. границу, за
которую абсолютная погрешность выйти не может. Эту границу называют
предельной абсолютной погрешностью.

24. Предельная абсолютная погрешность

ОПРЕДЕЛЕНИЕ 3. Предельной абсолютной погрешностью приближенного
числа а называется положительное число Δа такое, что Δ≤ Δа , т.е. |x-a|≤Δа
Следствие: a-Δа ≤ x ≤ a+Δа
Запись приближенного числа: a±Δа
ПРИМЕР: 28,75±0,02 (Δа =0,02)
* По Определению 3 предельная абсолютная погрешность вводится неоднозначно.
Если некоторое число Δа1 есть предельная абсолютная погрешность, то любое
большее число также есть предельная абсолютная погрешность (Δа1<Δа2<Δа3<…<Δаn),
поскольку каждое из них удовлетворяет неравенству |x-a|≤Δа . На практике стараются
выбирать возможно меньшее и простое по записи число Δа , удовлетворяющее этому
неравенству (с 1-2 значащими цифрами) .

25. Предельная абсолютная погрешность

ПРИМЕР: Измерить линейкой длину предмета.
ММ
0
0,5
ГОСТ 427-56
0,5
1
Цена деления линейки составляет 1 мм. Длина предмета заключена где-то между её
метками 12 и 13 мм, причём ближе к 13 мм. Если разделить расстояние между этими
метками, получится 0,5 мм. Тогда можно считать длину предмета приближённо равной
13 мм и гарантировать, что абсолютная погрешность Δ не превысит 0,5 мм. Эту
величину удобно принять за значение предельной абсолютной погрешности Δа . Таким
образом, длина предмета равна: 13±0,5 мм.

26. Предельная абсолютная погрешность

ПРИМЕР 1. Определить истинную, абсолютную и предельную абсолютную
x
.
погрешность числа а=0,17, принятого в качестве приближенного значения числа
Истинная погрешность равна: х а
.
Абсолютная погрешность равна: х а
Предельная абсолютная погрешность: а
.
Примем: а

27. Предельная абсолютная погрешность

ПРИМЕР 2. Определить предельную абсолютную погрешность числа а=3,14,
принятого в качестве приближенного значения числа π
Известно, что 3,14<π<3,15. Следовательно:
Примем: а
Если учесть, что 3,14<π<3,142, то получим лучшую оценку:
Примем: а

28. Относительная погрешность

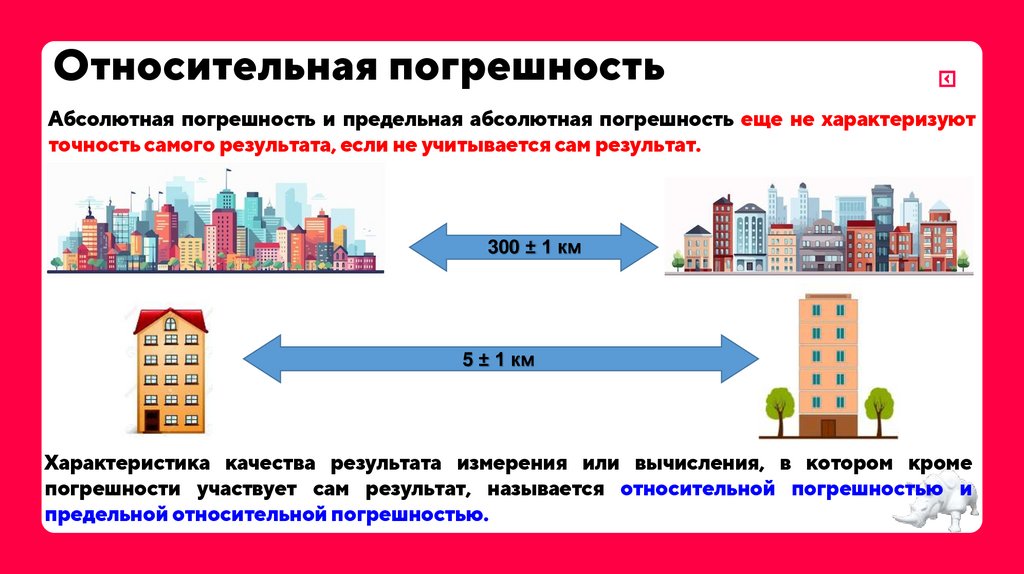
Абсолютная погрешность и предельная абсолютная погрешность еще не характеризуют
точность самого результата, если не учитывается сам результат.
300 ± 1 км
5 ± 1 км
Характеристика качества результата измерения или вычисления, в котором кроме
погрешности участвует сам результат, называется относительной погрешностью и
предельной относительной погрешностью.

29. Относительная погрешность

ОПРЕДЕЛЕНИЕ 4. Относительной погрешностью δ приближенного значения а
числа х называется отношение абсолютной погрешности Δ числа а к
абсолютной величине (модулю) числа х:
х
.
Так как точное число х обычно бывает неизвестно, его заменяют приближенным числом а:
а
.

30. Предельная относительная погрешность

ОПРЕДЕЛЕНИЕ 5. Предельной относительной погрешностью приближенного
числа а называется положительное число δа такое, что δ≤δа, т.е.
а
а
а
.
Предельную относительную погрешность часто выражают в процентах:
а
а
.
а
Также это выражение можно переписать относительно предельной абсолютной
погрешности:
а а
а
* Для краткости, когда это не вызывает недоразумений, вместо слов «предельная
относительная погрешность» говорят просто «относительная погрешность».

31. Предельная относительная погрешность

ПРИМЕР 1. Определить в процентах предельную относительную погрешность
числа а=3,14, принятого в качестве приближенного значения числа π
а .
Примем: а Тогда: а

32. Значащие цифры

Приближенное число может быть целым или записываться в форме конечной
десятичной дроби. При этом устанавливается такой способ его записи, по которому
можно узнать его погрешность. Для записи числа в арифметике существует понятие
значащей цифры.
Значащими цифрами числа называются все цифры его десятичной записи,
кроме нулей, стоящих перед первой отличной от нуля цифрой.
ПРИМЕР:
25000 – пять значащих цифр;
13,2 – три значащие цифры;
23,100 – пять значащих цифр;
0,04050 – четыре значащие цифры.

33. Верные цифры

ОПРЕДЕЛЕНИЕ 6. Цифра α называется верной (в строгом смысле),
если абсолютная погрешность приближенного числа не превосходит
половины единицы того разряда, в котором записана цифра α.
* В десятичной форме записи приближенного числа принято указывать только верные цифры.
ПРИМЕР 1. Приближенное число а=3,14 содержит верную цифру 4 в разряде сотых
долей единицы. Следовательно, абсолютная погрешность приближенного числа а не
превосходит половины единицы этого разряда (Δ≤0,005), т.е. его предельная
абсолютная погрешность Δа=0,005.
Приближенное число b=3,1415 содержит верную цифру 5 в разряде десятитысячных
долей единицы: (Δ≤0,00005). Для него предельная абсолютная погрешность Δb=0,00005.
ВАЖНО! Если приближенное число записано с некоторым количеством цифр после запятой,
причем последние цифры – нули, являющиеся верными цифрами, то их нельзя отбрасывать.
Например: если приближенное число а=2,7±0,0005 (Δа=0,0005), то его следует записывать а=2,700.
Если b=27±0,005 (Δb=0,005), то b=27,00.

34. Оценка погрешности

По количеству верных цифр в записи числа можно судить о его абсолютной погрешности,
а по количеству значащих цифр можно судить о его относительной погрешности.
Правило. Пусть в записи приближенного числа все цифры верные. Тогда
предельную относительную погрешность можно принять равной дроби, числитель
которой равен единице, а знаменатель есть удвоенное целое число, записанное при
помощи всех значащих цифр данного числа и в таком же порядке их следования.
ПРИМЕР 1. У приближенного числа а=235 все цифры верные. Его абсолютная
погрешность не превосходит половины разряда единиц (Δ≤0,5), поэтому предельная
абсолютная погрешность Δа=0,5. Относительная погрешность приближенного числа а
равна:
а
а .

35. Оценка погрешности

ПРИМЕР 2. У приближенного числа b=0,235 все цифры верные. Его абсолютная
погрешность не превосходит половины разряда тысячных (Δ≤0,0005), поэтому
предельная абсолютная погрешность Δb=0,0005. Относительная погрешность
приближенного числа b равна:
b
b
ПРИМЕР 3. У приближенного числа c=2,35 все цифры верные. Его абсолютная
погрешность не превосходит половины разряда сотых (Δ≤0,005), поэтому предельная
абсолютная погрешность Δс=0,005. Относительная погрешность приближенного числа
с равна:
с
с
ПРИМЕР 4. Для приближенного числа а=7,62±0,005 относительная погрешность равна:
а
Для удобства можно принять: а
а

36. Формы записи приближенного числа

Десятичную форму записи числа, которую мы использовали до этого, называют
естественной или формой с фиксированной запятой:
Также любое число а, записанное в десятичной позиционной системе счисления,
различными способами можно представить в виде: a=a0∙10p, где p - целое число.
ПРИМЕР:
Такой вид записи числа называют записью в форме с плавающей запятой.
Предельная абсолютная погрешность числа, записанного в форме с плавающей
запятой, равна: Δa =Δa0∙10p .
ПРИМЕР: а=0,35 ∙10-3 → а0=0,35; Δa0 =0,005; Δa=0,005 ∙10-3 =0,000005.

37. Формы записи приближенного числа

В том случае, если |а0|<1, число а0 называют мантиссой, а показатель степени p –
порядком числа а. Если при этом у мантиссы первая цифра после запятой
отлична от нуля, то такую форму записи числа называют нормализованной.
Представление числа в нормализованной форме является единственным.
ПРИМЕР 1. Число 36,6 записано в форме с фиксированной запятой.
То же число в нормализованной форме: 0,366 ∙102.
0,366 - мантисса, 2 - порядок числа.
ПРИМЕР 2. Число а=5,45 ∙10-2 записано в форме с плавающей запятой. Записать
это число в нормализованной форме и в форме с фиксированной запятой.
Число в нормализованной форме: 0,545 ∙10-1.
Число в форме с фиксированной запятой: 0,0545.

38. Округление чисел

Округление выполняют в случаях, когда точное или приближенное
число в своей записи содержит больше цифр, чем это необходимо.
ПРАВИЛО ОКРУГЛЕНИЯ:
Чтобы округлить число до n значащих цифр, отбрасывают все цифры, стоящие
после n-й значащей, или, если это требуется для сохранения разрядов числа,
заменяют их нулями. Если первая из отброшенных цифр больше или равна 5, то
последнюю оставшуюся цифру увеличивают на единицу.
Применяя это правило, мы можем быть уверены, что абсолютная погрешность
числа не превышает половины единицы разряда, определяемого последней
оставленной значащей цифрой. Поэтому если округленное число было точным,
то после округления мы получим число приближенное, а все его оставшиеся
цифры будут верными.

39. Округление приближённых чисел

ПРИМЕР 1. Округлить число π=3,141592… до трёх и до пяти значащих цифр.
Определить абсолютную погрешность округления.
При округлении до трёх значащих цифр: π=3,14
Абсолютная погрешность: Δ=|3,141-3,14|=0,001<0,005 - не превышает
половины разряда тысячных, поэтому предельная абсолютная погрешность
округления Δπ=0,005.
При округлении до пяти значащих цифр: π=3,1416
Абсолютная погрешность: Δ=|3,14159-3,1416|=0,00001<0,00005 - не превышает
половины разряда десятитысячных, поэтому предельная абсолютная
погрешность округления Δπ=0,00005.

40. Округление приближённых чисел

Операцию округления можно выполнить и над приближенным числом а с
известной предельной абсолютной погрешностью Δа. В этом случае мы получим
новое приближенное число а1. Полная погрешность числа а1 будет равна сумме
предельной абсолютной погрешности самого числа а и абсолютной погрешности
его округления.
ПРИМЕР 2. Определить абсолютную погрешность приближенного числа
а=6,52±0,01 при его округлении до двух значащих цифр.
Предельная абсолютная погрешность числа a равна: Δа =0,01.
Абсолютная погрешность округления равна: Δ=|6,52-6,5|=0,02.
Полная погрешность приближенного числа a1 равна: 0,01+0,02=0,03.
В записи приближенного числа a1 последняя значащая цифра стоит в
разряде десятых долей единицы, а суммарная погрешность числа a1 не
превосходит половины единицы этого разряда: 0,03<0,05. В соответствии с
Определением 6 в записи числа a1=6,5 все цифры верные.

41. Округление приближённых чисел

ПРИМЕР 3. Определить абсолютную погрешность приближенного числа
а=5,35, в котором все значащие цифры верные, при его округлении до двух
значащих цифр.
Предельная абсолютная погрешность числа a равна: Δа =0,005.
Абсолютная погрешность округления равна: Δ=|5,35-5,4|=0,05.
Полная погрешность приближенного числа a1 равна: 0,005+0,05=0,055.
В записи приближенного числа a1 последняя значащая цифра стоит в
разряде десятых долей единицы, но суммарная погрешность числа a1
превосходит половину единицы этого разряда: 0,055>0,05. В соответствии с
Определением 6 в записи числа a1=5,4 верной будет только первая
значащая цифра.
Округляем до одной значащей цифры. Тогда: a1≈5 и Δ=|5,35-5|=0,35.
Полная погрешность приближенного числа a1 равна: 0,005+0,35=0,355.
0,355<0,5 и значащая цифра верная.

42. Действия над приближенными числами

42

43. Теоремы о погрешностях

При выполнении арифметических действий над приближенными числами
получаемый результат также будет приближенным числом.
ТЕОРЕМА 1. Предельная абсолютная погрешность суммы нескольких приближенных
чисел равна сумме предельных абсолютных погрешностей слагаемых.
Следствие. Предельная относительная погрешность суммы положительных
приближенных чисел вычисляется как:
a+b a b a a b b
а b
a+b
a+b
a+b
ТЕОРЕМА 2. Предельная абсолютная погрешность разности нескольких приближенных
чисел равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.
Следствие. Предельная относительная погрешность разности положительных
приближенных чисел вычисляется как:
a+b a b a a b b
а b
a b
a b
a b

44. Теоремы о погрешностях

ПРИМЕР 1. Сложить приближенные числа a1=6,72±0,01 и a2=4,35±0,005.
a1+a2=6,72+4,35±(0,01+0,005)=11,07±0,015.
ПРИМЕР 2. Разность двух приближенных чисел a=2,712 и b=2,131 равна: u=a-b=2,712-2,131=0,581.
Предельные абсолютные погрешности уменьшаемого и вычитаемого определяем по виду их
записи: Δu=0,0005+0,0005=0,001.
Так как предельная абсолютная погрешность разности меньше половины единицы
разряда сотых долей единицы (0,001>0,0005), то в записи числа u верными будут только
две значащие цифры.
Оставляя в записи числа только верные цифры, округлим его до сотых долей единицы.
Погрешность округления составит Δ=|0,581-0,58|=0,001.
С добавлением ошибки округления Δu=0,001+0,001=0,002 запишем: u=0,58±0,002.

45. Теоремы о погрешностях

ТЕОРЕМА 3. Предельная относительная погрешность произведения нескольких
приближенных чисел равна сумме предельных относительных погрешностей
сомножителей.
ТЕОРЕМА 4. Предельная относительная погрешность частного от деления двух
приближенных чисел равна сумме предельных относительных погрешностей
делимого и делителя.
Замечание 1. Произведение приближенного числа на точное содержит столько
верных значащих цифр, сколько их содержит приближенное число.
ПРИМЕР 1. В произведении приближенного числа 3,14 на точное число 0,75 будет
три верных значащих цифры: u=3,14∙0,75=2,355.
Результат округлим до трех значащих цифр (т.е. до сотых долей единицы).
Погрешность округления составит Δ=|2,355-2,36|=0,005, поэтому u=2,36 и тогда все
значащие цифры будут верными.

46. Теоремы о погрешностях

ПРИМЕР 2. Найти предельную относительную погрешность произведения
приближенных чисел а=3,14 и b=0,738.
Предельные относительные погрешности определяем по виду записи множителей:
а
b
b
а
δab=δa+δb=0,0027.
Определим количество верных цифр в десятичной записи числа u=а∙b. Чтобы не производить
лишних вычислений, предварительно выполним грубую оценку величины:
u=3,14∙0,738≈3∙0,5≈1,5.
По Определению 5: u u u u
Предельная абсолютная погрешность не превышает половины разряда cотых долей единицы
(Δu≤0,005), поэтому в записи числа u верными будут 3 значащие цифры. Выполняя
умножение с использованием полной записи приближённых чисел, окончательно получим:
u=3,14∙0,738=2,32.

47. Теоремы о погрешностях

ТЕОРЕМА 5. Предельная относительная погрешность степени приближенного числа
равна произведению показателя степени на предельную относительную
погрешность основания: δan=n∙δa
ТЕОРЕМА 6. Предельная относительная погрешность корня n-й степени из
приближенного числа равна предельной относительной погрешности
приближенного подкоренного числа, деленной на показатель корня n: n a a
n
ПРИМЕР 1. Определить погрешность вычисления объема V куба, если длина
его ребра a измерена с погрешностью не более 1%.
Объем куба вычисляется по формуле V=a3. Предельная относительная
погрешность измерения длины его ребра δа=1%. Тогда предельная
погрешность вычисления объема куба δV=3∙1%=3%.

48. Теоремы о погрешностях

ПРИМЕР 2. Найти объем куба, если длина его ребра a=1,25 и все значащие цифры верные.
Объем куба вычисляется как V=a3. Предельная относительная погрешность длины ребра равна:
a
По Теореме 5: δV = δa3 =3∙0,004=0,012.
Определим количество верных цифр в десятичной записи объема куба. Чтобы не производить
лишних вычислений, предварительно выполним грубую оценку величины:
V
По Определению 5: V V V V
Предельная абсолютная погрешность не превышает половины разряда десятых долей единицы
(ΔV ≤0,05), поэтому в записи числа u верными будут 2 значащие цифры. Таким образом, после
округления до двух значащих цифр:
V
.

49. Вычисления по формуле

49

50. Оценка погрешности вычислений по формуле

В практике вычислений возникает потребность в оценке погрешности результата,
полученного при последовательном выполнении нескольких действий, например,
при вычислениях по заданной формуле. Действия, предписанные формулой,
могут выполняться как с точными, так и с приближенными числами, но в любом
случае требуется оценить погрешность итогового результата. В теории
приближенных вычислений эта задача называется ПРЯМОЙ ЗАДАЧЕЙ.
Рассмотрим ее на примере.
ПРИМЕР 1. Найти объем конуса, если радиус
основания r=1,65, высота h=3,9 и π=3,142.
С какой точностью по этим данным можно вычислить
объем и сколько значащих цифр будут верными?

51. Оценка погрешности вычислений по формуле

r
h
Объем конуса вычисляется по формуле: V
Сначала выполним грубую оценку величины объема, принимая r≈2, h≈4, π≈3.
r h
Получим: V
Число 3, стоящее в знаменателе, является точным (δ3=0).
Предельные относительные погрешности исходных данных определяем по виду записи чисел:
r
r
h
h
На основании Теоремы 5 запишем:
r 2 r
На основании Теоремы 3 запишем:
δV=δπ+δr2+δh=0,0002+0,008+0,015=0,0232.
На основании Определения 5 и с учетом грубой
оценки величины объема конуса получим его
предельную абсолютную погрешность:
V V V V
Так как ΔV<0,5, в записи числа будут две верные
значащие
цифры.
Теперь
произведём
вычисления,
используя
полную
запись
исходных данных, результат округлим до двух
значащих цифр:
V

52. Потеря точности

В ходе вычислений по заданной формуле может возникнуть ситуация, при
которой вычитаются числа, близкие по значению. Если оба числа
приближенные, то возникает эффект, который называется потерей точности.
ПРИМЕР. Найти разность приближённых чисел а=15,385, b=15,362.
Их разность равна u=a-b=15,385-15,362=0,023. По виду записи чисел определим их
предельные относительные и абсолютные погрешности:
а
b
b
а
Δa=Δb=0,0005.
С учетом Следствия к Теореме 2:
u
a b
a b
u
Предельная относительная погрешность
разности двух близких по значению чисел
в 1000 раз больше, чем уменьшаемого и
вычитаемого, поэтому при вычислениях
подобных ситуаций следует избегать.

53. Оценка погрешности вычислений по формуле

ОБРАТНУЮ ЗАДАЧУ теории приближенных вычислений можно сформулировать
следующим образом. Указаны действия, которые необходимо выполнить над
приближенными числами (например, произвести вычисления по заданной
формуле). Требуется установить допустимые погрешности приближенных чисел,
чтобы полученный результат имел наперед заданную предельную погрешность.
Рассмотрим эту задачу на следующем примере.
ПРИМЕР 1. Требуется вычислить объем конуса по
формуле так, чтобы относительная погрешность не
превышала 0,1%. С какой точностью следует
измерить радиус основания и высоту, чтобы
обеспечить заданную точность результата?

54. Оценка погрешности вычислений по формуле

r h
Объем конуса вычисляется по формуле: V
Для решения задачи необходимо знать грубые приближенные значения r и h.
Примем r≈2, h ≈ 4.
На основании Теорем 3 и 5 составим неравенство:
δπ +2δr + δh < 0,001
(относительную погрешность берём в долях единицы).
Число π мы можем брать с любой точностью, т.е. задавать δπ сколь угодно малым.
Примем π=3,142. Тогда:
В результате исходное неравенство примет вид:
2δr + δh < 0,001 - δπ → 2δr + δh < 0,0008.

55. Оценка погрешности вычислений по формуле

Неравенство 2δr + δh < 0,0008 содержит две неизвестные величины δr и δh , поэтому имеет
бесчисленное множество решений и задача становится неопределенной.
Но на δr и δh мы можем наложить некоторые дополнительные условия. Например, считать,
что измерения высоты конуса и радиуса его основания проведены инструментами с
одинаковой точностью. В этом случае предельные абсолютные погрешности этих
измерений можно считать равными (Δr=Δh), а предельные относительные погрешности
записать как:
h h
r r
r
h
r
h
2 r r
0, 0008 откуда:
2
4
4
r 0, 0008 r 0, 00064.
5
Подставляя δr и δh в неравенство, получим
Таким образом, Δr=Δh<0,00064 м; Δr=Δh<0,064 см; Δr=Δh<0,64 мм.

56. Оценка погрешности вычислений по формуле

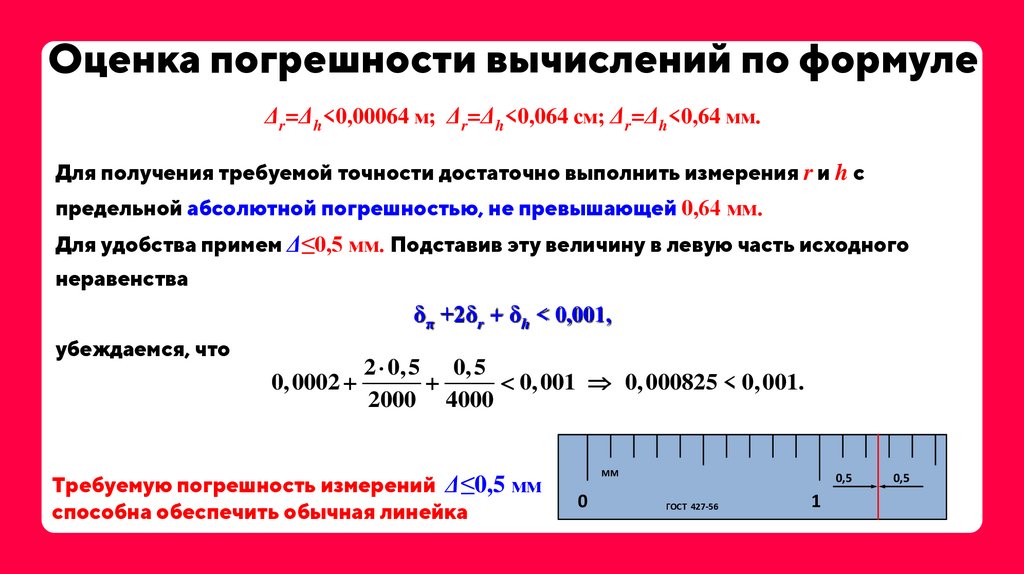
Δr=Δh<0,00064 м; Δr=Δh<0,064 см; Δr=Δh<0,64 мм.
Для получения требуемой точности достаточно выполнить измерения r и h с
предельной абсолютной погрешностью, не превышающей 0,64 мм.
Для удобства примем Δ≤0,5 мм. Подставив эту величину в левую часть исходного
неравенства
δπ +2δr + δh < 0,001,
убеждаемся, что
2 0, 5 0, 5
0, 0002
0, 001 0, 000825 < 0, 001.
2000 4000
Требуемую погрешность измерений Δ≤0,5 мм
способна обеспечить обычная линейка
ММ
0
0,5
ГОСТ 427-56
1
0,5

57. Вычисления значений функции

57

58. Оценка погрешности вычисления функции

Дифференциальное исчисление дает возможность получить общие формулы для оценки
погрешностей, применимые и для алгебраических, и для трансцендентных функций.
Пусть величина у=f(х) есть функция величины х и эта функция имеет производную
на интервале вычислений. Требуется вычислить значение функции при
некотором значении ее аргумента х, при этом истинное значение х мы не знаем и
берем его приближенное значение а, т.е. вычисляем f(а).
Абсолютная погрешность, допускаемая при вычислении функции Δу=f(х)-f(а) есть
приращение функции, а Δа=х-а есть приращение аргумента. Если приращение
аргумента мало, то приращение функции можно приближенно заменить ее
дифференциалом и принять:
Δу=|f´(а)|∙Δа.
Таким образом, предельная абсолютная погрешность функции равна произведению
модуля производной функции на предельную абсолютную погрешность аргумента.

59. Оценка погрешности вычисления функции

На основании Определения 5 можно получить выражение предельной относительной
погрешности функции:
у
Множитель
у
у
f а а
f а
f а а
f а
а
а а .
f а а
f а
f а
можно рассматривать как производную сложной функции, а
f а
именно натурального логарифма функции f(х) и переписать выражение в
следующем виде:
f а
у
а а ln f (а ) а а .
f а

60. Оценка погрешности вычисления функции

ПРИМЕР 1. Пусть у=х3.
По Теореме 5 предельная относительная погрешность вычисления функции для
приближенного значения а ее аргумента будет равна: y а3 3 а .
Предельная абсолютная погрешность с учетом Определения 5 будет иметь вид:
у у у 3 а а 3 .
С использованием производной можно получить аналогичные выражения для
предельной абсолютной и относительной погрешности вычисления функции у=х3:
у f а а 3 а 2 а а 3 а а 3 ;
f а
3а 2
у
а а 3 а а 3 а .
f а
а
Обобщим эти формулы для степенной функции на случай любого показателя степени:
у nа n 1 а ;
у n а .

61. Оценка погрешности вычисления функции

Если функция помимо аргумента содержит коэффициенты, которые также
являются приближенными числами, то ее можно рассматривать как функцию
нескольких переменных, а для вычисления погрешностей использовать понятие
полного дифференциала.
ПРИМЕР 1. Пусть у=сх3, где с= 3,23 - приближенное число. Значение функции
требуется вычислить, считая ее аргумент х приближенным числом а=2,15.
Для заданных исходных данных значение функции составляет:
у=са3=3,23∙2,153≈3,23∙9,93≈32,1.
Полный дифференциал функции вычислим, считая приближенные числа независимыми
переменными, а их предельные абсолютные погрешности – дифференциалами
независимых переменных:
у
у
са 3
са 3
у с + а
с +
а =а 3 с +3са 2 а .
с
а
с
а

62. Оценка погрешности вычисления функции

Предельные абсолютные погрешности с и а, входящих в это выражение, определим
по виду записи каждого числа:
Δс=0,005; Δа=0,005.
Тогда предельная абсолютная погрешность значения функции, вычисленная через
ее полный дифференциал, составит:
у а 3 с +3са 2 а 3 2
Примем: Δу=0,3.
Поскольку 0,3<0,5, т.е. не превышает половины разряда единиц, то в записи числа,
выражающего значение функции, верными будут только две значащие цифры.
Таким образом, при заданной точности исходных данных значение функции у=32.

63.

THE END