Похожие презентации:
Математический анализ. Лекция 1. Числовые множества. Действительные числа
1. Математический анализ
Что «анализируем»?Поведение функций
В окрестности
На всем множестве
точки (локальное)
(глобальное)
Пределы
на бесконечности
в точке
Операции над функциями:
дифференцирование, интегрирование.
2. Математический анализ
Введение в анализ (Действительные числа.Теория пределов. Непрерывность функций)
Дифференциальное Дифференциальные
исчисление
уравнения
Интегральное
Уравнения
исчисление
Теория рядов
ТФДП
ТФКП
математической
физики
Функциональный
анализ
3. Введение в анализ
1. Числовыемножества.
Действительные
числа
4. Множество
- совокупность (собрание) однородных объектов(элементов множества).
Каждое отдельное множество задается правилом или
законом, позволяющим судить относительно любого
объекта принадлежит он данному множеству или нет.
Конечное
Пустое
Бесконечное множество
характеризуется тем, что после
каждого извлечения любого
элемента этого множества оно
остается непустым Георг Кантор
Бесконечное
(1845-1918,
нем. математик)
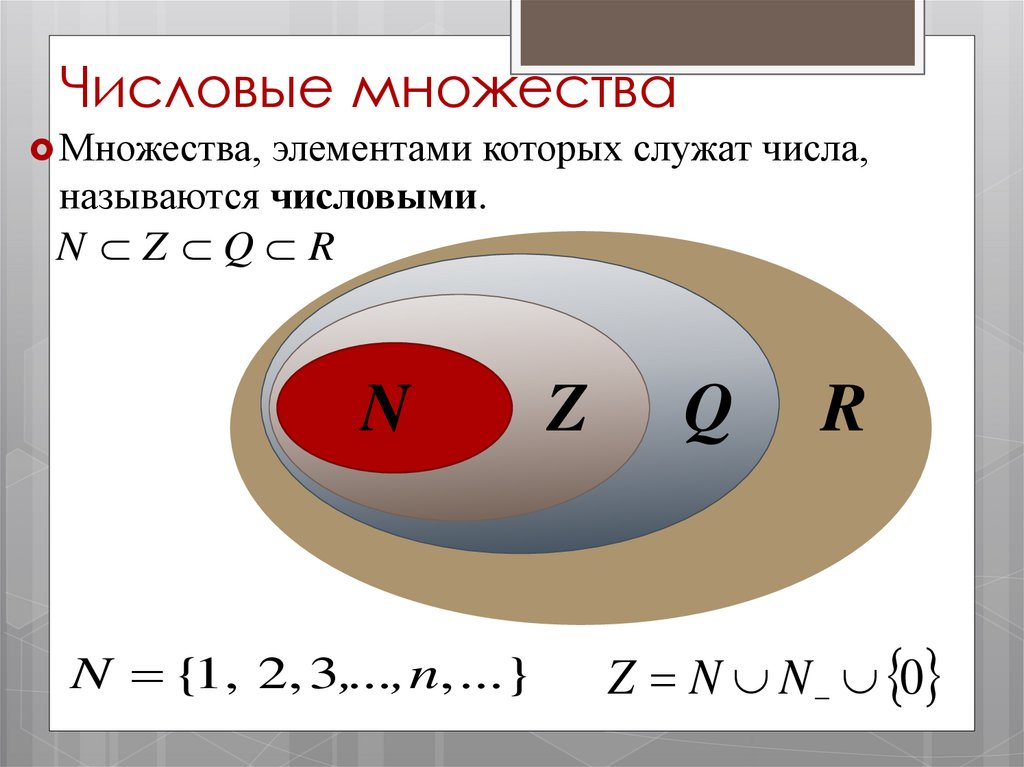
5. Числовые множества
Множества, элементами которых служат числа,называются числовыми.
N Z Q R
N
N {1, 2, 3,..., n, ...}
Z
Q
R
Z N N 0
6. Рациональные числа
от лат. quotient,«частное»
p
Q p Z, q N, НОД ( p, q ) 1
q
бесконечные периодические десятичные
дроби (в частности с нулем в периоде).
Множество Q обладает свойством плотности
a Q, b Q, с Q : a с b
Каждому рациональному числу соответствует
определенная точка на числовой оси, но не
наоборот.
7. Аксиома Архимеда
c Q, c 0, n N : n cЕсли на прямой даны любые два отрезка А и В, то
можно А повторить столько раз, чтобы сумма
была больше В.
A A ... A n A B
А
В
8. Иррациональные числа
ИррациональныеСечением множества Х
числа
I
называется такое разбиение
Метод сечений
этого множества на два
(нем. математика
непустых множества А и В,
Юлиус Вильгельм
которое удовлетворяет
Рихард Дедекинда
условиям:
(1831 – 1916))
1) каждое число попадает в
одно и только одно множество
А или В, A B Ø ;
2) каждое число а из А меньше
каждого числа b из В.
А – нижний класс, В – верхний
класс.
– число производящее
А|В=а сечение (пограничное)
9. Иррациональные числа
IВиды сечений Q
A
B
A
B
A
B
A a Q : a 0 a 2
2
B b Q : b 2
2
A| B 2
I – числа, производящие сечения множества Q, в
которых в нижнем классе нет наибольшего числа,
а в верхнем – наименьшего.
10. Действительные (вещественные) числа
RR=Q I
ТЕОРЕМА (Дедекинда). Для всякого сечения A|B
множества действительных чисел существует
действительное число а, производящее это сечение:
А|B=a. Это число будет либо наибольшим в А, либо
наименьшим в В.
A
A
B
B
Каждому действительному числу соответствует
единственная точка числовой оси (координатной
прямой), и каждой точке числовой оси соответствует
единственное действительное число.
11.
A | B ,X |Y
A X B Y
X A X A
x X : x B a A a x
12.
Свойства множества R (характерные):Упорядоченность
a R, b R, a b (a b) (a b)
Плотность
a R, b R, a b с R : a с b
Непрерывность (полнота)
A R, B R, A , B , A B ;
a A, b B, a b !c R : a c b.
13. Действительные (вещественные) числа
Rбесконечные десятичные дроби.
a R a a0 , a1a2 a3 ...
a0 Z , i ai {0,1, 2, ..., 8, 9}
- числа, которое на числовой прямой лежит
между рациональными точками вида
a0 , a1a2 ...an
и
n
a0 , a1a2 ...an 10
n N
14.
[ a ] a0Целая часть числа а (антье, пол)
– округление числа а до
ближайшего целого в меньшую
сторону.
[a] a
{a} a [a]
Дробная часть числа а
0 {a} 1
15. Модуль или абсолютная величина числа
x, x 0,| x |
x , x 0
Модуль |x| выражает расстояние от нуля до точки х
на числовой оси
|a|=|–a|
|a+b|≤|a|+|b|
|a–b|≤|a|+|b|
|a+b| |a|–|b|
| a – b | | a | – | b |.
16. Подмножества R
[ a, b ] = {x R: a ≤ x ≤ b} – отрезок или сегмент.(a, b) = ] a, b [ ={x R: a < x < b} – интервал или открытый
отрезок.
(a, b]={x R: a < x ≤ b}, [a, b)={x R: a ≤ x < b} –
полуинтервалы, или полусегмент, полуоткрытый отрезок.
Конечные числа a, b – граничные точки или концы
промежутков.
[ a, + )={x R: a ≤ x} , (– , а]= {x R: x ≤ а} – замкнутая
полупрямая или замкнутый луч.
( a, + ), (– , а ) – открытая полупрямая или открытый луч
а – вершина луча (бесконечного полуинтервала)
R= (– , + ) – числовая прямая
17. Окрестность точки
a Ra a a
0
центр
радиус
U(a, ε)=(a – ε , a + ε )={x R: | x – a | < ε } –
ε-окрестность точки а.
Любые две точки a и b имеют непересекающиеся
окрестности.
a
b
18. Проколотая окрестность точки
a Ra a a
0
центр
радиус
U ( a, )
(a – ε , a) (a, a + ε) ={x R: 0 < | x – a | < ε }
– проколотая ε-окрестность точки а.
19. Окрестность бесконечной точки
01
1
U ( , ) ,
0
1
1
U ( , ) ,
20. Ограниченные числовые множества
Множество Х называется ограниченным сверху(снизу), если существует такое число М(m) , что для
всех х из Х выполняется неравенство х≤М (х≥m ).
Числа М(m) называются верхней гранью (нижней
гранью) множества Х.
Если множество имеет верхнюю и нижнюю грани,
оно называется ограниченным (ограниченным по
модулю), т.е.
x X C 0 : | x | C
В противном случае множество называется
неограниченным.
21. Точные грани множества
Пусть множество Х ограниченно сверху.Наименьшая из всех его верхних граней называется
точной верхней гранью или супремумом.
Supremum – самый верхний, наибольший
sup Х M 0
sup x M 0
x X
Число M0 называют супремумом множества Х,
если:
1) x Х x M 0 ;
2) 0 x X : x M 0
22. Точные грани множества
Пусть множество Х ограниченно снизу.Наибольшая из всех его нижних граней называется
точной нижней гранью или инфимумом.
infimum – самый нижний, наинизшее, наименьший.
inf Х m0
inf x m0
x X
Число т0 называют инфимумом множества Х, если:
1) x Х
x m0 ;
2) 0 x X : x m0
Для неограниченных supХ=+∞ , infХ=- ∞.
23.
Каждое непустое ограниченное сверху(снизу) множество имеет бесконечно много
верхних (нижних) граней.
Всякое непустое ограничено сверху (снизу)
множество Х имеет точную верхнюю
(нижнюю) грань.
24. Система вложенных отрезков
Система числовых отрезков с действительнымиконцами называется системой вложенных отрезков,
если
a1 ... an ... bn ... b1
Принцип вложенных отрезков: всякая система
вложенных числовых отрезков имеет непустое
пересечение
c R : k N ak c bk
a1 a2
an
bn
b2 b1
25. Стягивающая система отрезков
Система вложенных отрезков называетсястягивающейся, если среди отрезков, в нее
входящих, имеются отрезки сколь угодно малой
длины, т.е.
0 N n , n N bn an
Для всякой системы стягивающихся отрезков
существует единственная точка с,
принадлежащая всем отрезкам данной
системы, при этом с=sup{an}=inf{bn}.
26.
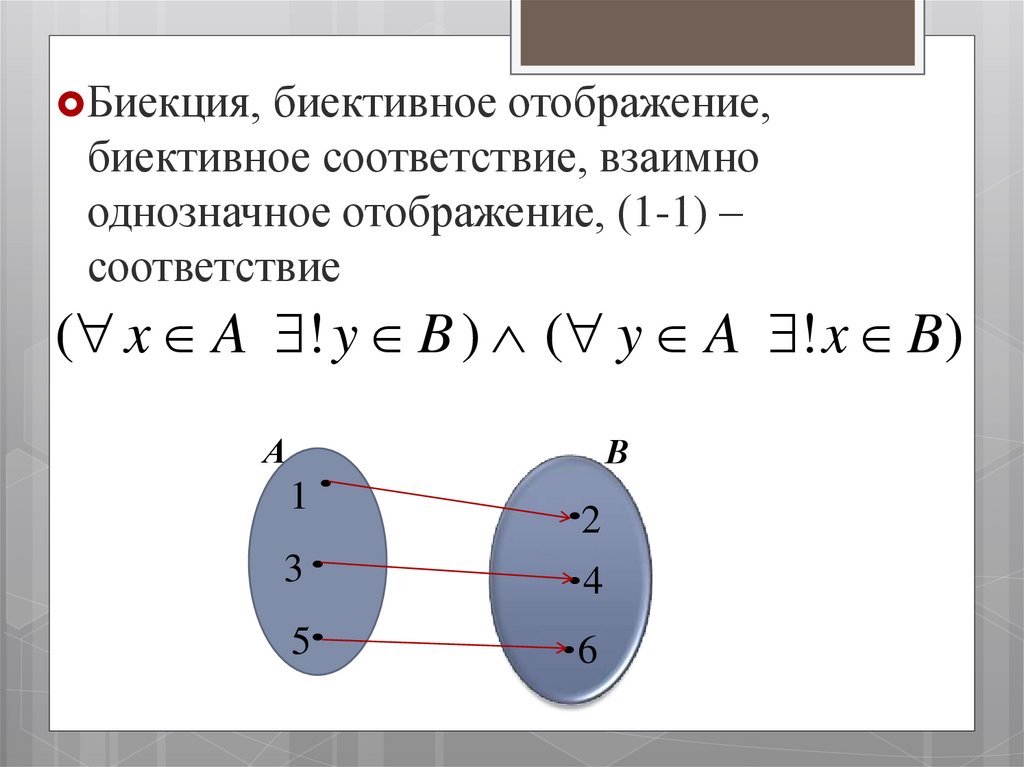
Биекция, биективное отображение,биективное соответствие, взаимно
однозначное отображение, (1-1) –
соответствие
( x A ! y B ) ( y A ! x B)
А
В
1
2
3
4
5
6
27.
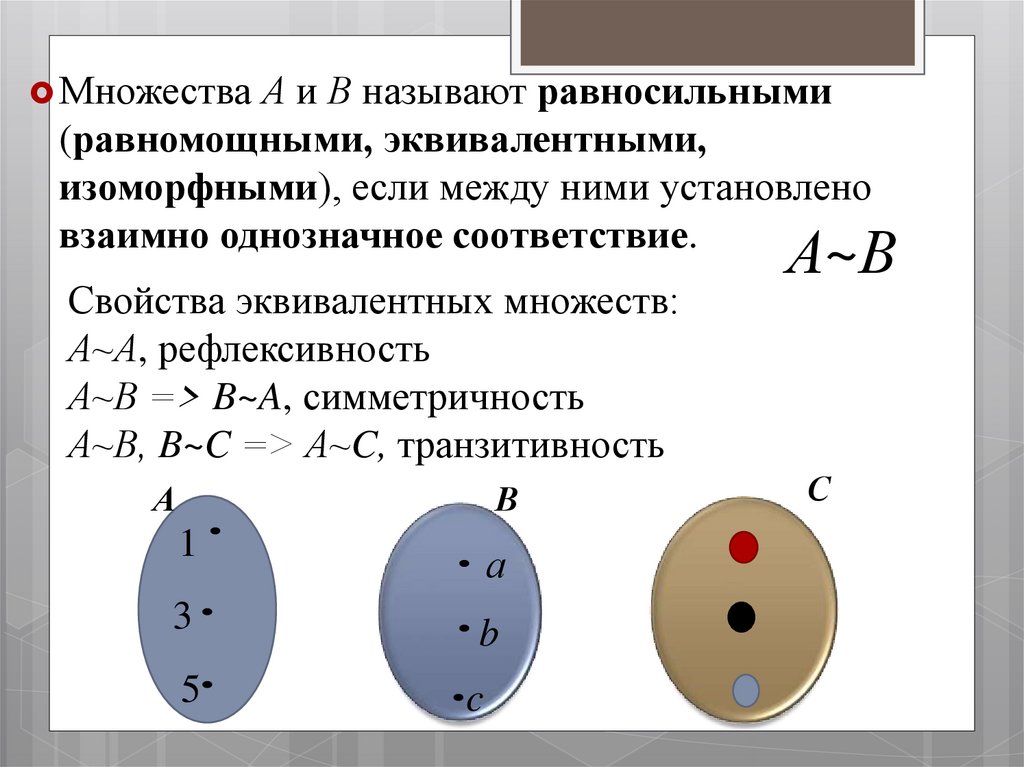
Множества А и В называют равносильными(равномощными, эквивалентными,
изоморфными), если между ними установлено
взаимно однозначное соответствие.
Свойства эквивалентных множеств:
А~А, рефлексивность
А~В => B~A, симметричность
А~В, B~C => А~C, транзитивность
А
В
1
а
3
b
5
c
А~В
С
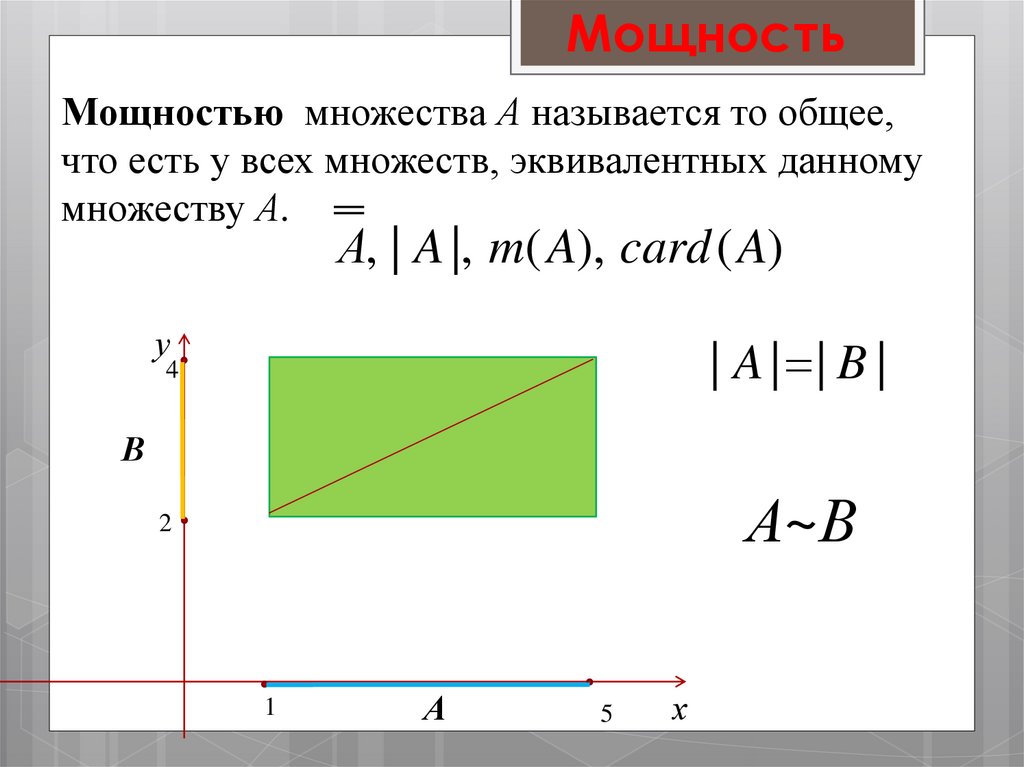
28. Мощность
Мощностью множества А называется то общее,что есть у всех множеств, эквивалентных данному
множеству А.
А, | A |, m( A), card ( A)
у
4
| A | | B |
2
А~В
В
1
А
5
х
29. Признаки равномощности множеств:
Если некоторое множество являетсяпромежуточным для двух равномощных
множеств, то все три множества
равномощны:
A B C А~С → А~В и В~С
А
B
C
30. Признаки равномощности множеств:
(Признак Кантора – Бернштейна). Есликаждое из двух данных множеств равномощно
части другого, то данные множества
равномощны:
A1 A, B1 B , А~В1, В~А1 → А~В
А
B
А1
B1
31. Счетные множества
Счетное множество – это множество, эквивалентноемножеству натуральных чисел, т.е. все его элементы
можно представить в виде бесконечной
последовательности (можно занумеровать)
А= {a1, a2, ..., an, ...}.
| N | a а – обозначение мощности счетного множества
Z : ..., 3, 2, 1, 0, 1, 2, 3, ... | R | a
7
5
3
1 2
| Z | a
4 6
| Q | a









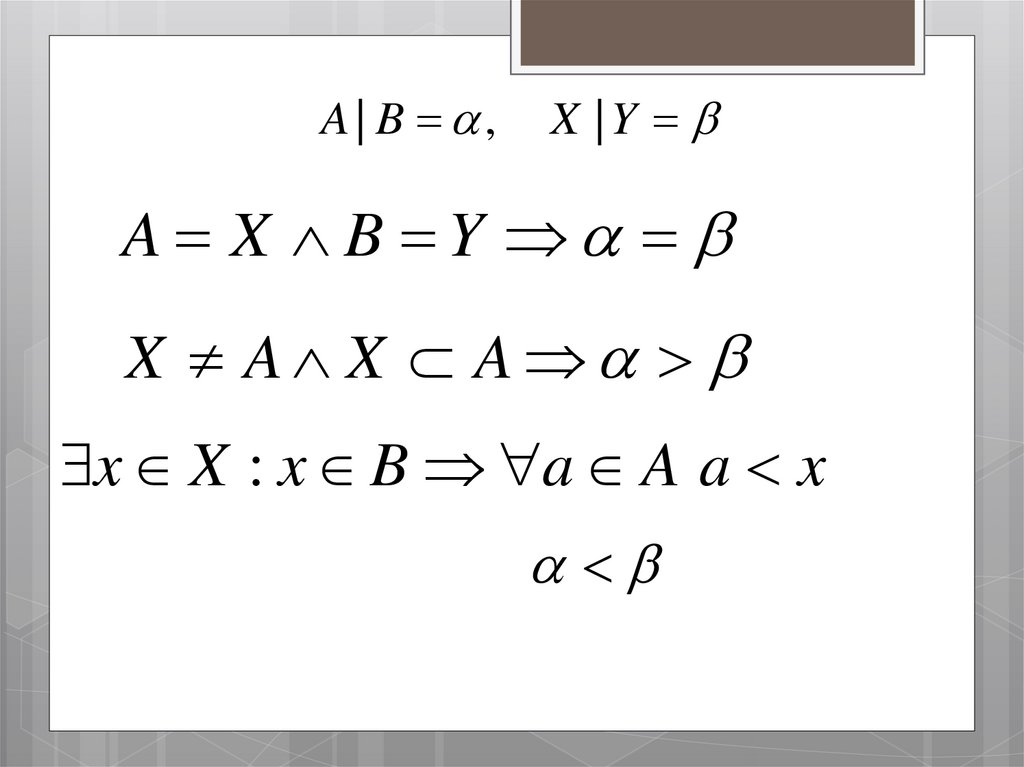

















 Математика
Математика








