Понятие действительного числа

1.

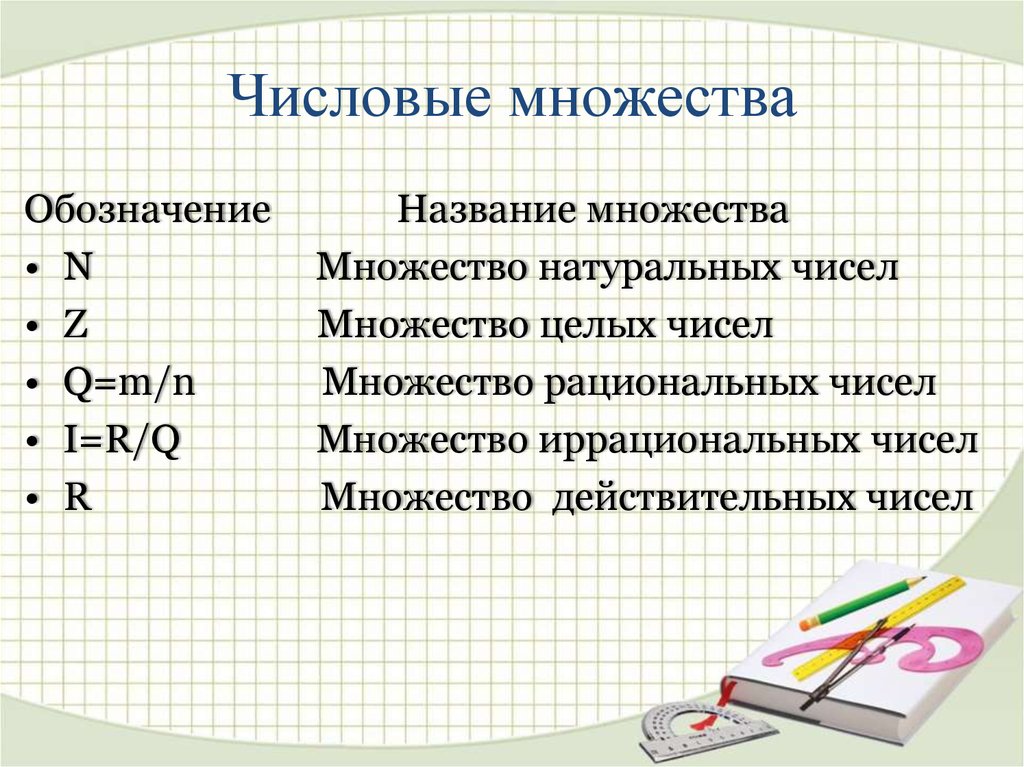
Тема урока:

2. Числовые множества

Обозначение
• N
• Z
• Q=m/n
• I=R/Q
• R
Название множества
Множество натуральных чисел
Множество целых чисел
Множество рациональных чисел
Множество иррациональных чисел
Множество действительных чисел

3. Множество натуральных чисел

• Натуральные числа - это числа счета.
• N={1,2,…n,…}.
• Заметим, что множество натуральных
чисел замкнуто относительно
сложения и умножения, т.е. сложение
и умножение выполняются всегда, а
вычитание и деление в общем случае
не выполняются

4. Множество целых чисел.

• Введем в рассмотрение новые числа:
1) число 0 (ноль),
2) число (-n), противоположное натуральному n.
При этом полагаем: n+(-n)=(-n)+n=0,
-(-n)=n.
Тогда множество целых чисел можно записать так:
Z ={…,-n,…-2,-1,0,1,2,…,n,…}.
Заметим также, что:
Это множество замкнуто относительно сложения,
вычитания и умножения, т.е.
Из множества целых чисел выделим два подмножества:
1) множество четных чисел 2k , k Z
2) множество нечетных чисел 2k 1, k Z

5. Множество рациональных чисел.

• Множество рациональных чисел можно представить
в виде: Q { m , m Z , n Z }
n
m
В частности, 1 m Z Таким образом, Z Q
Множество рациональных чисел замкнуто относительно
сложения, вычитания, умножения и деления (кроме случая
p q,
деления на 0).
p q,
p, q Q p q, Q
p
,q 0
q

6.

• Но в множестве рациональных чисел нельзя, например,
измерить гипотенузу прямоугольного треугольника с
катетам a 1, b 1 .
2
2
c
a
b
2 .
По теореме Пифагора гипотенуза будет равна
т
Но число не будет рациональным, так как 2 n ни для
каких m и n.
2
x
2 0 .
• Нельзя решить уравнение
• Нельзя измерить длину окружности и т.д.
Заметим, что всякое рациональное число можно
представить в виде конечной или бесконечной
периодической десятичной дроби.
3
1
5
2
1
3 3 0,125; 0, (285714); 0, (3)
8 2 5
7
3

7. Множество иррациональных чисел.

Числа, которые представляются бесконечной
непериодической дробью, будем называть
иррациональными.
Множество иррациональных чисел обозначим I.
Для иррациональных чисел нет единой формы
обозначения. Отметим два иррациональных числа,
которые обозначаются буквами – это числа и е.

8.

Модулем (абсолютной величиной)
действительного числа а, называется
неотрицательное действительное число:
а =
Примеры.
а, если а≥0
– а, если а<0
|5|=5
|– 5 | = 5
5 2 5 2, т.к. 5 2
5 3 3 5 , т.к. 5 3
8

9.

Заполнить таблицу:
Данное число
7
–3
Число противоположное
данному
–7
–(– 3) = 3
– 2,1
–(– 2,1) = 2,1
а+3
–а– 3
2а – 7
7 – 2а

10.

Заполнить таблицу:
Данное число
Модуль данного числа
4
4
–4
4
0
0
– 8,7
а²
8,7
а²

11.

Заполнить пропуски:
а, если ______,
а≥0
1) а
а, если а_____;
<0
____,
m
если m 0,
2) m
____,
– m если m 0.
Вычислить устно и записать ответ:
10
1) | 5 | + | – 5 | = ___
2) | – 6 | + | 6 | = 12
__
18
3) 9 ∙ | 5 – 7 | = ___
4) | 10 – 10 | ∙ 7 = __
0
–12
5) – 3 ∙ | – 4 | = ___
6
5) | – 18 | : | – 3 | = _

12.

Основные свойства модуля
№
1
свойство
|a|≥ 0
2
|a·b|=|a|·|b|
3
a
а
b
b
4
|a|2=а2
5
|a| = | – a|
6
|a|≥ а
7
|a + b|≤ |a| + |b|
8
а2 а
пример

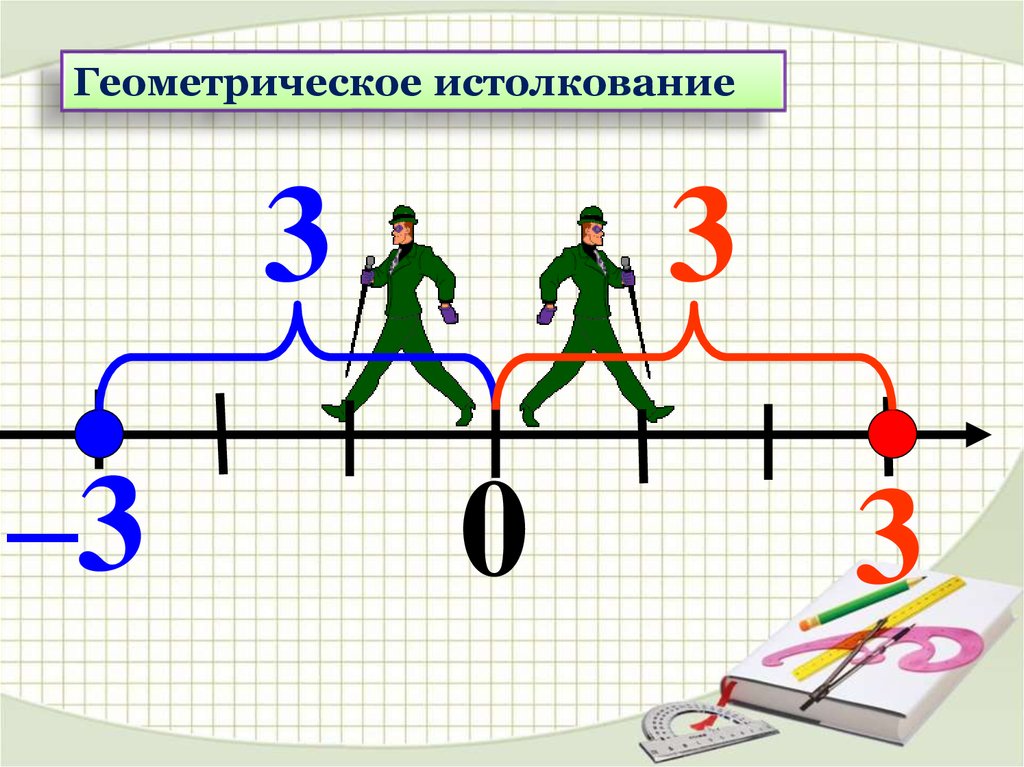
13.

Геометрическое истолкование
3
–3
3
0
3

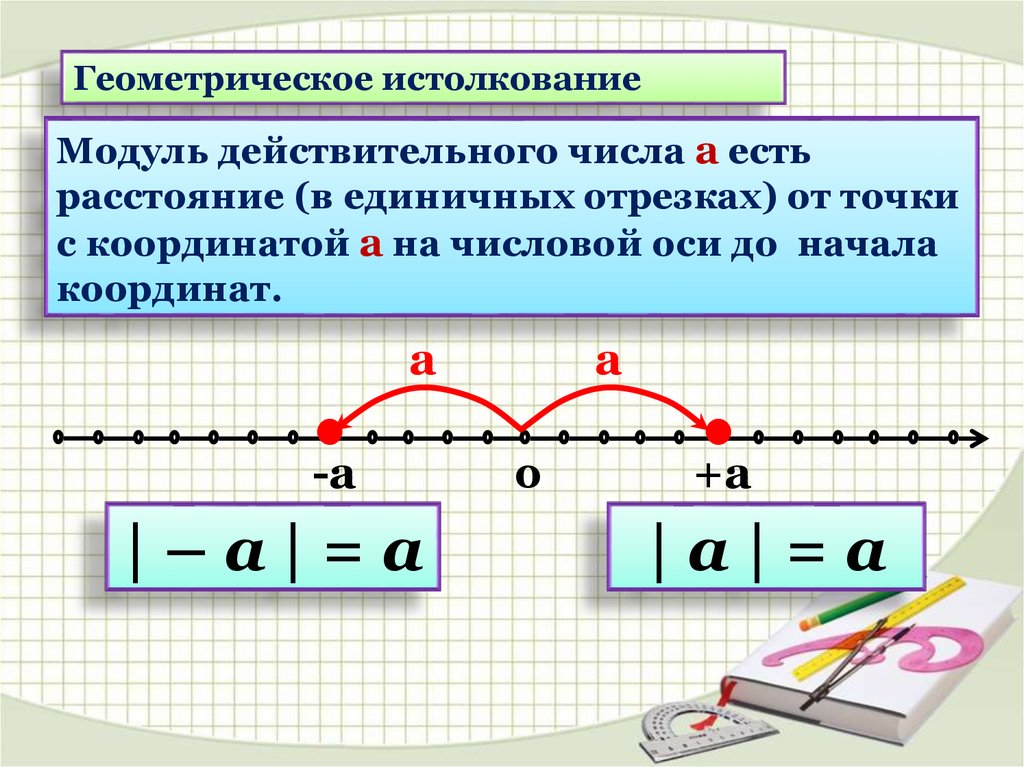
14.

Геометрическое истолкование
Модуль действительного числа а есть
расстояние (в единичных отрезках) от точки
с координатой а на числовой оси до начала
координат.
а
-а
|–а|=а
а
0
+а
|а|=а

15.

Пример №1
51 7
1)
51 5 3
75 11
8 16
2
2)
2
3)
4)
Упростить выражение
4
2
5
5
2
3
4
6
5
5
2
5
6

16.

Пример №2
1)
2)
3)
4)
Упростить выражение

17.

Пример №4
Упростить выражение
Пример №3
Упростить выражение
| х – 5| + |х – 8,5|,
если 5,6≤ х ≤8,2

18.

Пример №5
2
6
Упростить выражение
х 1 х 4
2
4
6
х 4 х 1
если х 3х 3
2
Ответ: 1
2
4
,

19.

Пример №6
Упростить выражение
Ответ: 0,25

20.

Пример №7
Упростить выражение
Ответ: 7

21.

Пример №8
Упростить выражение
Ответ: -7

22.

Пример №9
Упростить выражение
Ответ: -2

23.

Пример №10 Упростить выражение
Ответ: 2

24.

Пример №11
Упростить выражение
Ответ: -1,9

25.

Пример №12 Упростить выражение
2
х 4
4 4
4 1 2
х
х
2х
,
х 2
2
если 7 x 2,5
Ответ: -0,5