Числовые множества

1. ЧИСЛОВЫЕ МНОЖЕСТВА

1.
2.
N, Z, Q, I, R, R R, C.
Подмножества вещественных чисел:
Пусть а, в R, а в .
а, в x R | а; x в
а, в x R | a ; x в
Интервал:
Полуинтервал: a, b x R | а x , в a, b x R | а x ;в
Замкнутый луч: a, x R | x a,
, a x R | x ;a
Открытый луч: a, x R | x a , , a x R | x a
Отрезок, сегмент:
.
Определение. Пусть a R, > 0. Интервал (a – , a + ) будем называть
-окрестностью точки a .
Обозначение: U(a, )= (a – , a+ )= {x R | |x – a|< }.
1
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

2. ЧИСЛОВЫЕ МНОЖЕСТВА

R + , – = R
Пусть > 0. Тогда
U(+ , ) = (1/ ; + ) + = x R : x > 1/ ;
U(– , ) = (– ; –1/ ) – = x
R
: x < – 1/ ;
U( , ) = (– ; –1/ ) (1/ ; + ) = x
2
R
: |x|> 1/ .
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

3. АБСОЛЮТНАЯ ВЕЛИЧИНА ЧИСЛА

Для любого числа x R неотрицательное число
называется абсолютной величиной или модулем числа x (
).
1.
2.
3.
4.
|x| ≥ 0.
|x| = |– x|.
– |x| ≤ x ≤ |x|.
Пусть R, > 0. Тогда неравенства |x| ≤ и – ≤ x ≤ –
равносильны.
5. |x + y| ≤ |x| + |y|.
6. |x – y| ≥ |x| – |y|.
7. |x y| = |x| |y| и , если y 0.
3
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

4. ГРАНИ ЧИСЛОВЫХ МНОЖЕСТВ

Определение. Множество А называется ограниченным сверху
(снизу), если существует такое действительное число М (число m), что
каждый элемент x A удовлетворяет неравенству x M (x m). При этом
число М (число m) называют верхней (нижней) гранью множества А.
Определение. Множество, ограниченное сверху и снизу называется
ограниченным.
Определение. Наименьшая из всех верхних граней ограниченного
сверху множества называется точной верхней гранью.
Обозначение:
M sup x
М=sup A или
.
x A
Наибольшая из всех нижних граней ограниченного снизу множества
называется точной нижней гранью.
Обозначение: m=inf A или
m inf x .
x A
Теорема (Больцано). Любое ограниченное сверху (снизу), непустое
числовое множество имеет точную верхнюю (нижнюю) грань.
4
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

5. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Определение. Числовой последовательностью {xn}
называется упорядоченное
{x1,x2,x3,x4,...}.
Определение.
счетное
Числовой
множество
чисел
последовательностью
{xn}
называют отображение, действующее из N в R т.е. xn = f (n).
Числа
{xn},
где
последовательности,
n=1,2,3,…
символ
–
xn
элементы
–
общий
(члены)
член
последовательности, а число n – его номер.
5
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

6. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ

Пусть даны две последовательности {xn} и {yn}.
Произведением последовательности {xn} на число c называется
последовательность вида:
.
Суммой последовательности {xn} и {yn} называется последовательность вида: {xn} + {yn} = {x1 + y1; x2 + y2; …; xn + yn; …}
Разностью – последовательность вида:
{xn} – {yn} = {x1 – y1; x2 – y2; x3 – y3; …; xn – yn; …}.
Произведением – последовательность вида:
{xn} {yn} = {x1 y1; x2 y2; x3 y3; …; xn yn; …}.
Частным – последовательность вида
6
.
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

7. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Определение. Последовательность называется
ограниченной сверху, если M n xn M ;
ограниченной снизу, если m n x m ;
n
ограниченной, если m, M n m x M ;
n
неограниченной, если A 0 n | n n x A ;
возрастающей, если
неубывающей, если
убывающей, если
0
n xn xn 1
xn xn 1 ;
;
0
n
n xn xn 1 ;
невозрастающей, если
xn xn 1 .
7
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

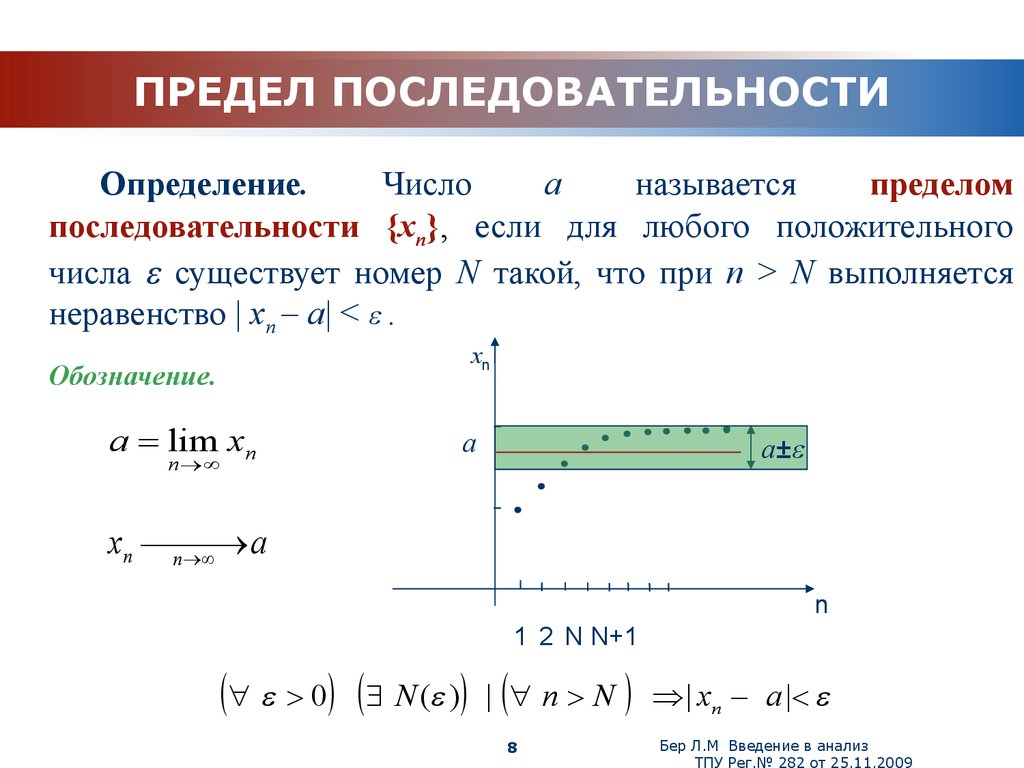
8. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ

Определение.
Число
а
называется
пределом
последовательности {xn}, если для любого положительного
числа существует номер N такой, что при n > N выполняется
неравенство | xn a| < .
xn
Обозначение.
a lim xn
n
a
a
a±
xn n
a
n
1 2 N N+1
0 N ( ) | n N
8
| xn a |
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

9. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ

Геометрическая интерпретация того,
xn
что a lim
состоит в следующем:
n
«Какого бы ни было положительное число
, все элементы последовательности,
начиная с некоторого номера
N+1,
находятся внутри -окрестности точки а».
9
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

10. Бесконечно малые и бесконечно большие последовательности

Определение.
Последовательность
{xn}
называется
бесконечно малой последовательностью (б.м.п.), если для
любого положительного числа существует номер N такой, что
при n > N выполняется неравенство |x n | < .
Определение.
Последовательность {xn}
называется
бесконечно большой последовательностью (б.б.п.), если для
любого положительного числа A существует номер N такой,
что при n > N выполняется неравенство |x n | > A.
Теорема. Если {xn} – б.м.п. и все ее члены отличны от нуля, то
{1/xn} – б.б.п., и обратно, если {xn} б.б.п., тогда {1/xn} – есть
б.м.п.
Бер Л.М Введение в анализ
10
ТПУ Рег.№ 282 от 25.11.2009

11. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ

Определение. Говорят, что при n , последовательность {xn}
сходится к пределу, равному + если
C 0 N | n N xn C
Обозначение.
lim xn
n
xn n
xn
C=100
100
Пример.
50
lim n 2
n
C=9
11
1
3
5
7
11
n
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

12. ОСНОВНЫЕ СВОЙСТВА Б.М.П.

1. Сумма и разность бесконечно малых последовательностей
есть также бесконечно малая последовательность.
Следствие. Сумма и разность любого конечного числа
б.м.п. есть также б.м.п.
2. Произведение двух б.м.п. есть б.м.п.
Следствие. Произведение любого конечного числа б.м.п.
есть также б.м.п.
3. Произведение б.м.п. на ограниченную последовательность
есть б.м.п.
Следствие. Произведение б.м.п. на число есть б.м.п.
4. Б.м.п. ограничена.
12
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

13. ОСНОВНЫЕ СВОЙСТВА Б.Б.П.

1. Если xn - ограничена, а yn такая, что lim y n , то
n
lim ( xn y n ) ;
( xn y n ) ;
б) lim
n
n
x
в) lim n 0 , если yn 0 для любого n.
n y
n
2. Если lim xn , lim y n , то
а)
n
а)
n
lim( xn y n ) ; б)
n
3. Если lim x
n
n
lim( xn y n ) .
n
, lim y , то
n
n
( xn y n ) .
а) lim( x y ) ; б) lim
n
n
n
n
4. Если lim x a , a R, a 0, lim y , то
5. Если lim x a
n
n
n
n
n
n
, a 0, lim y n 0 , то
n
13
, a 0
lim ( x n y n )
n
, a 0.
xn
, a 0
lim
n y
n
, a 0.
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

14. СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ

Теорема 1. (о единственности предела). Если последовательность имеет предел, то он единственный.
Теорема 2. Для того, чтобы последовательность {xn} была
сходящейся , необходимо и достаточно, чтобы ее можно было
представить в виде x n = a + n , где , а , а { n} б.м.п.
Теорема 3. Сходящаяся последовательность ограничена.
Теорема 4. Сумма (разность) двух сходящихся последовательностей {xn} и {yn} есть сходящаяся последовательность,
предел которой равен сумме (разности) пределов
последовательностей
lim
( x n y n ) lim
x n lim
yn
n
n
n
.
14
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

15. СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ

Теорема 5. Произведение двух сходящихся последовательностей {xn} и {yn} есть сходящаяся последовательность,
предел
которой
равен
произведению
пределов
последовательностей
lim
( xn y n ) lim
x n lim
yn .
n
n
n
Теорема 6. Частное двух сходящихся последовательностей
{xn} и {yn} при условии, что для всех n выполняется
неравенство yn 0 и предел {yn} отличен от нуля, есть
сходящаяся последовательность, предел которой равен
частному пределов последовательностей {xn} и {yn}
xn
x n lim
n
lim
n
yn
y n lim
n
15
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

16. СВОЙСТВА СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ

Теорема 7. Пусть {xn} сходящаяся последовательность и
xn b
n xn b
. Тогда lim
.
n
Следствие. Если {xn} и {yn} сходящиеся последовательности и
n xn y n
lim
xn lim
y,n то
.
n
n
Теорема 8. Пусть {xn}, {yn} и {zn} – последовательности, и 1.
{xn} и {zn} и сходящиеся последовательности;
n xn yn zn
2.
;
lim
x n lim
zn a
n
n
3.
.
Тогда {yn} также сходящаяся последовательность и
lim
yn a
n
Бер Л.М Введение в анализ
16 .
ТПУ Рег.№ 282 от 25.11.2009

17. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Числовая последовательность называется {xn} называется
xn xn 1 ;
строго возрастающей, если n xn xn 1 ;
возрастающей, если
убывающей, если
xn xn 1
строго убывающей, если
;
n xn xn 1 .
Убывающие и возрастающие последовательности
называются монотонными, а строго убывающие и строго
возрастающие последовательности называются строго
монотонными.
17
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

18. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Теорема 9. (Вейерштрасса)
Всякая возрастающая числовая последовательность {xn}
имеет предел: конечный, если она ограниченна сверху, и
бесконечный, если она неограниченна сверху, причем
lim
x sup{ x }.
n n
n
Аналогично, если {xn} – убывающая последовательность, то
существует (конечный или бесконечный) предел
lim
x inf{x },
n n
n
и, следовательно, этот предел конечен,
если
последовательность ограниченна снизу, и бесконечный, если
она неограниченна снизу.
18
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

19. КРИТЕРИЙ КОШИ

Теорема 10 (Критерий Коши).
Для того чтобы последовательность {xn} сходилась
к конечному пределу, необходимо и достаточно, чтобы
N . m, n N xm xn
Последовательность,
удовлетворяющая
этому
условию
называется
«фундаментальной
последовательностью» или последовательностью,
«сходящейся в себе».
19
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009

20. Спасибо за внимание

LOGO
Спасибо за внимание
Бер Л.М Введение в анализ
ТПУ Рег.№ 282 от 25.11.2009
20