Похожие презентации:
Транспорт в мембранах. Биопотенциалы
1. ТРАНСПОРТ В МЕМБРАНАХ. БИОПОТЕНЦИАЛЫ
1. Строение, функции и физические свойствабиологических мембран.
2. Пассивный транспорт в мембранных системах.
Виды пассивного транспорта. Уравнение Фика.
Уравнение Нернста –Планка.
3. Активный транспорт веществ в мембранных
системах. Натрий-калиевый насос.
4. Потенциал покоя.
5. Стационарный потенциал ГольдманаХоджкина–Каатца.
6. Потенциал действия.
2. 1. Строение, функции и физические свойства биологических мембран.
• Основу структуры объёма мембраныпредставляет двойной липидный слой.
3.
• Мембрана выглядит так• Гидрофобные хвосты направлены внутрь
(при этом обеспечивается наименьший
контакт с водой)
• Однако такое представление мембраны не
дает ответов на вопросы:
4. 1 вопрос.
• О расположении белка(в некоторых их больше половины
от их массы)
5. 2 вопрос.
• Как (вода) гидрофильные частицыпопадают внутрь?
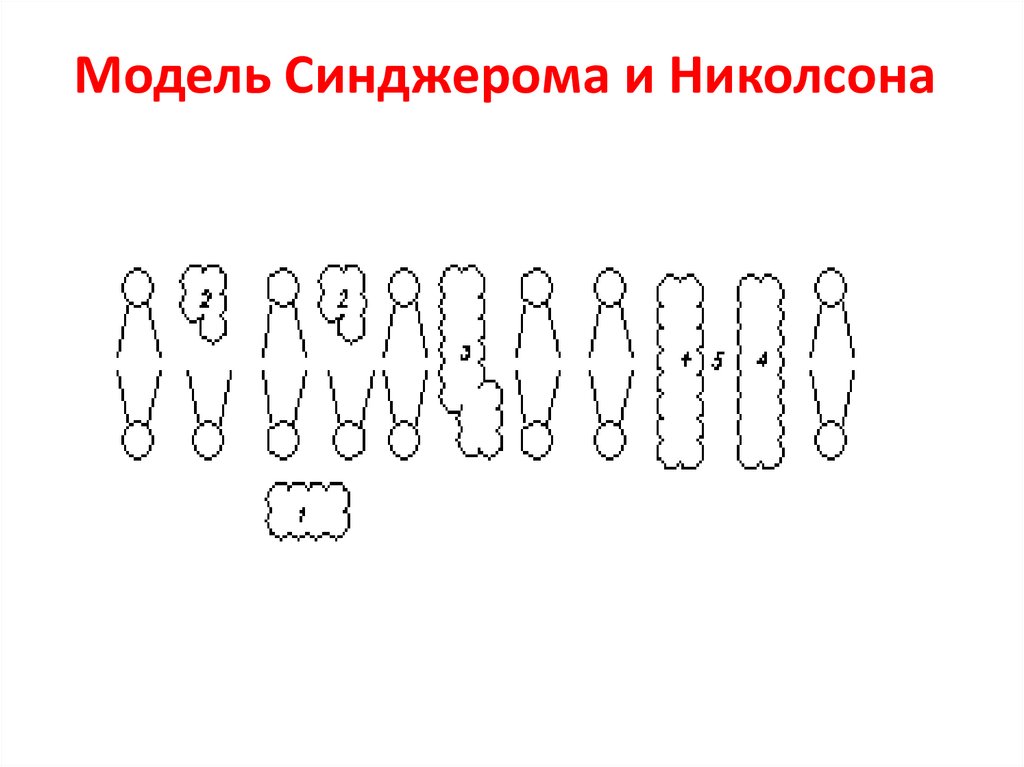
6. Модель Синджерома и Николсона
7.
• 1, 2, 3, 4 – белки, за счёт которыхосуществляется (полностью или частично)
функции мембраны – проницаемость,
активный перенос, генерация
электрического потенциала и так далее.
• 1 – поверхностные белки;
• 2 – полупогруженные белки;
• 3 – полностью погруженные белки;
• 4.-. белки, формирующие «ионный канал»
8. Мембрана – подвижная структура.
• Липиды и белки меняются местами иперемещаются как вдоль плоскости
мембраны – латеральная диффузия, так и
поперёк её – так называемый «флип –
флоп».
• Латеральной диффузии соответствует
высокая подвижность липидов, а «флип –
флоп» - низкая. То есть обмен местами
липидов находящихся по разные стороны
мембраны является редким процессом.
9. Мембраны выполняют две функции:
• Матричную, то есть являются матрицей поудержанию белков, выполняющих разные
функции.
• Барьерная – защищает клетку и отдельные
компоненты от проникновения
нежелательных частиц.
• Если эти функции 1 и 2 нарушены, то
нормальное функционирование клетки
прекращается. То есть ведёт к
заболеваниям.
10.
• Изменение подвижности молекулмембраны и диффузии частиц через
мембрану свидетельствует о том, что
билипидный слой ведёт себя подобно
жидкости. С другой стороны,
мембрана есть упорядоченная
структура. Эти два фактора позволяют
думать, что в мембране при её
естественном функционировании
бислой находится в
жидкокристаллическом состоянии.
11. Двойной фосфолипидный слой уподобляет мембрану конденсатору
• Проводниковые пластиныконденсатора образуют
электролиты наружного и
внутреннего растворов
(внеклеточного и цитоплазмы).
Проводники разделены липидным
бислоем. Липиды – диэлектрики
12. Пассивный транспорт в мембранных системах. Виды пассивного транспорта.
Мембраны способны
пропускать или не пропускать
молекулы и ионы. Вероятность
проникновения частиц в мембрану
зависит как от направления их
перемещения, так и от
разновидности молекул и ионов.
13. Явлением переноса:
называют необратимыепроцессы, в результате которых в
физической системе происходят
пространственные перемещения
(перенос) массы, импульса,
энергии, заряда или какой – либо
другой физической величины.
14.
• К явлению переноса относитсядиффузия (перенос массы
вещества), теплопроводность
(перенос энергии),
электропроводность (перенос
заряда).
• Перенос ещё называется
транспортом частиц.
15.
• Пусть через некоторую S во всехнаправлениях перемещаются молекулы
жидкости, то есть молекулы пересекают S ,
перескакивая из одного положения
равновесия в другое.
16.
• На расстоянии - равном расстояниюсреднего перемещения молекул (среднее
расстояние между молекулами жидкости)
построим прямоугольные
параллелепипеды небольшой толщины l
( l ).
• Объём каждого параллелепипеда равен
S l
17.
.Если n - концентрация молекул, то внутри
каждого параллелепипеда имеется S l n
молекул, S l n1 S l n2
Выберем одно направление перемещения
молекул из n1 и n2 , следовательно от 1
параллелепипеда перескакивает
1 / 6 S l n1 от 2 1 / 6 S l n2
Время t пролёта этой площадки S
найдём следующим образом.
18.
• Пусть все молекулы из n2 и n1 движутся содинаковыми скоростями ~ . Тогда все
молекулы из данных объёмов, дошедшие
до площади S , пересекут её в течении
~
• t l /
(1)
• Средняя скорость пробега равна:
• /
(2)
• Подставим (2) в (1)
• t l
(3)
• где среднее время «осёдлой жизни»
молекулы (среднее время перескока).
19.
• «Баланс» переноса молекул черезплощадку S за t равен
• 1 / 6 S l n1 1 / 6 S l n2
(4)
• Умножая (4) на массу и деля на t , находим
поток вещества через S :
1 S l m
n1 n2
6
t
• где t - время пролёта.
(5)
20.
• Изменение концентрации n1 n2 можноdn
представить как
на расстоянии 2
dх
между выделенными объёмами:
dn
n1 n2
2
d
(6)
21.
• Преобразуем уравнение (5), подставивзначение (3) и (6) получим:
1 S l m dn
1
dn
2 S
m
•
(7)
6 l
d
3
d
2
• Отношение потока к площади площадки
через которую он проходит, называется
плотностью потока:
1
dn
J
m
S 3
dx
2
(8)
22.
•C m n -массовая концентрация
dn dC
m
dx dx
(9)
• Учитывая это из (7) имеем
1 dС
J
3 dx
2
- уравнение диффузии
23.
• Обычно записывается в виде:dC
• J D
dx
- уравнение Фика (10)
• «-» - показывает, что суммарная плотность
потока направлена в сторону меньшей
концентрации.
1 2
• D
- коэффициент диффузии.
3
(11)
24.
• Изменение концентрации молекул впространстве означает неодинаковость
химического потенциала в разных местах
системы, следовательно, плотность потока
можно связать с градиентом химического
потенциала.
N 2i
C 2i
R T ln
R T ln
N1i
C1i
(12)
25.
• где• N1i , 2i числа частиц i го компонента;
• C1i , 2 i молярная концентрация;
• T - температура;
• R - постоянная.
C2i
R T ln
K T ln C2 ln C1 (13)
C1i
• (13)- химический потенциал
26.
• Для малых изменений концентраций:dC
d R T ln C R T
C
(14)
или для произвольной по координате:
d R T dC
dx
C
dx
(15)
Следовательно градиент концентрации равен:
dC
C d
dx R T dx
(16)
27.
• Используя (10) к (16), получаем:C d
J D
R T dx
(17)
• Эйнштейн показал, что коэффициент
диффузии пропорционален температуре:
D Um R T
(18)
• учитывая (18) выражение (17) примет вид:
28.
dJ U m C
dx
где U m подвижность частиц.
(19)
29. Уравнение Нернста Планка:
dCd
J P
U m Z FC 0
dx
dx
(20)
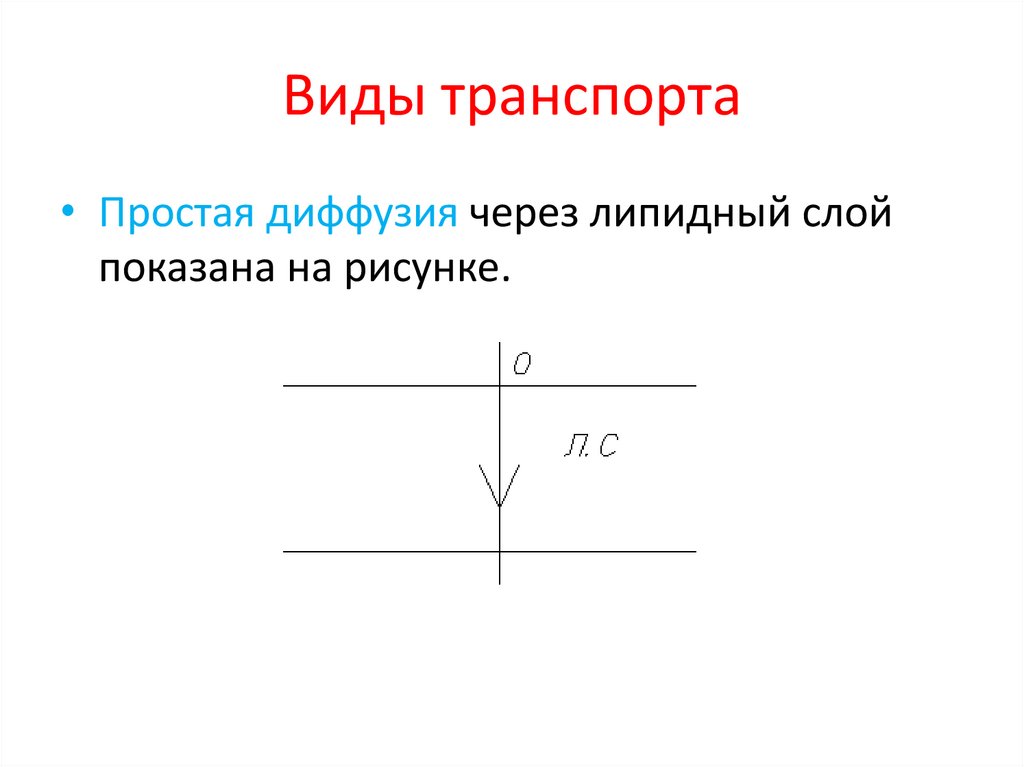
30. Виды транспорта
• Простая диффузия через липидный слойпоказана на рисунке.
31.
• В живой клетке такая диффузияосуществляет перенос кислорода и
углекислого газа.
• Ряд лекарственных веществ и ядов
также проникают через мембрану
по той же схеме.
32.
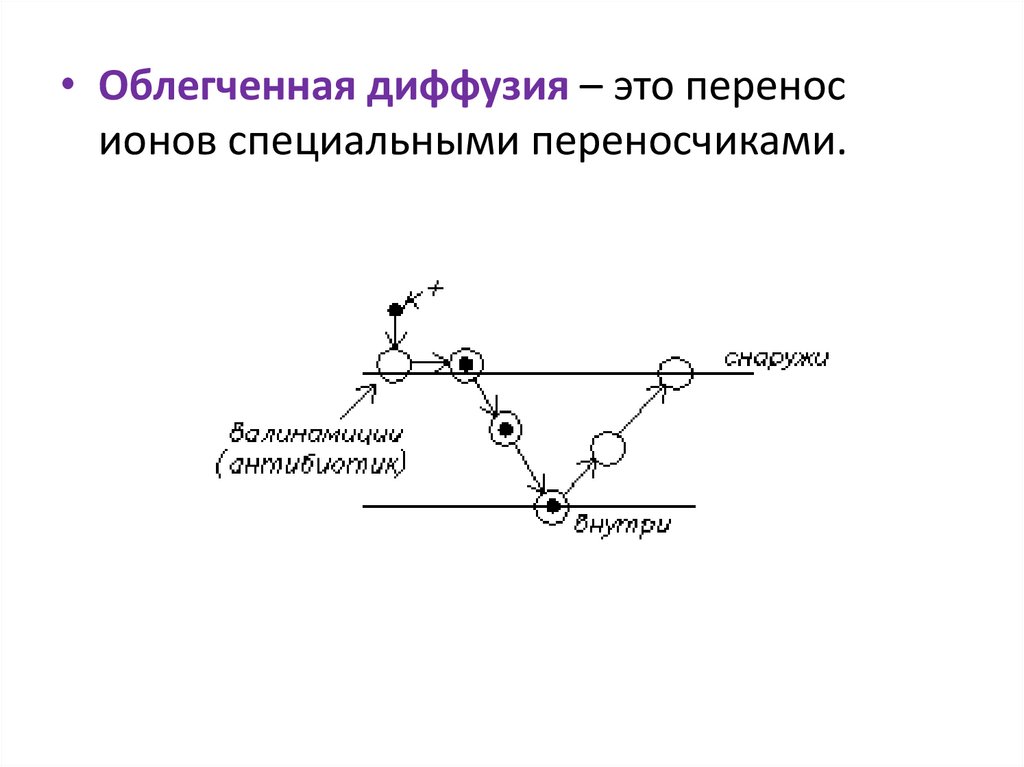
• Облегченная диффузия – это переносионов специальными переносчиками.
33.
• Активный транспорт веществ вмембранных системах.
Натрий-калиевый насос
34.
САМОСТОЯТЕЛЬНО35. Потенциал покоя.
• Поверхностная мембрана клетки не одинаковопроницаема для разных ионов. Концентрация
каких-либо ионов по разные стороны мембраны
различна. Это говорит о том, что при
нормальном функционировании возникает
разность потенциалов, между цитоплазмой и
окружающей средой (потенциал покоя).
Основной вклад в создание и поддержание
потенциала покоя вносят ионы калия, натрия и
хлора.
• Суммарная плотность потока этих ионов с
учётом их знаков равна J j Na j K jCl (21)
36. Стационарный потенциал Гольдмана-Ходжкина–Катца.
• В стационарном состояниисуммарная плотность потока равна
0, то есть число различных ионов,
проходящих в единицу времени
через мембрану внутрь клетки,
равно числу выходящих из клетки.
37.
• Запишем (21) через плотность потоков вследующем виде:
Na e Na
P
i
Na
0
e 1
K e K
P
i
0
e 1
K
Cl e Cl
P
0 (22)
i
Cl
e 1
0
38.
• Сократим (23) наи преобразуем:
e 1
• [ ] – концентрация.
PNa Na
P K P Cl
i
K
Cl
i
0
P
Cl
e PNa Na 0 PK K 0 Cl
i
Где i внутри;
0 -снаружи.
39.
• ИлиPNa Na i PK K i PCl Cl 0
е
PNa Na 0 PK K 0 PCl Cl j
• Логарифмируем:
PNa Na i PK K i PCl Cl 0
ln
PNa Na 0 PK K 0 PCl Cl j
40.
Z Fm
R T
• Если от безразмерного потенциала
вернутся к электрическому потенциалу, то
(
имеем:
R T
PNa Na i PK K i PCl Cl 0
m
ln (
)
PNa Na 0 PK K 0 PCl Cl j
F
– уравнение Гольдмана – Ходткина – Катца.
41.
• Различные концентрации ионов внутри созданыионными насосами – системами активного
транспорта.
• То есть потенциал покоя обязан активному
транспорту.
• Проницаемость ионов зависит от состояния
организма.
• В состоянии покоя при физиологических условиях
соотношение коэффициента проницаемости равно
PK : РNa : РСl 1 : 0,04 : 0,45
• Следовательно, в потенциал покоя основной вклад
вносят только ионы калия и хлора.
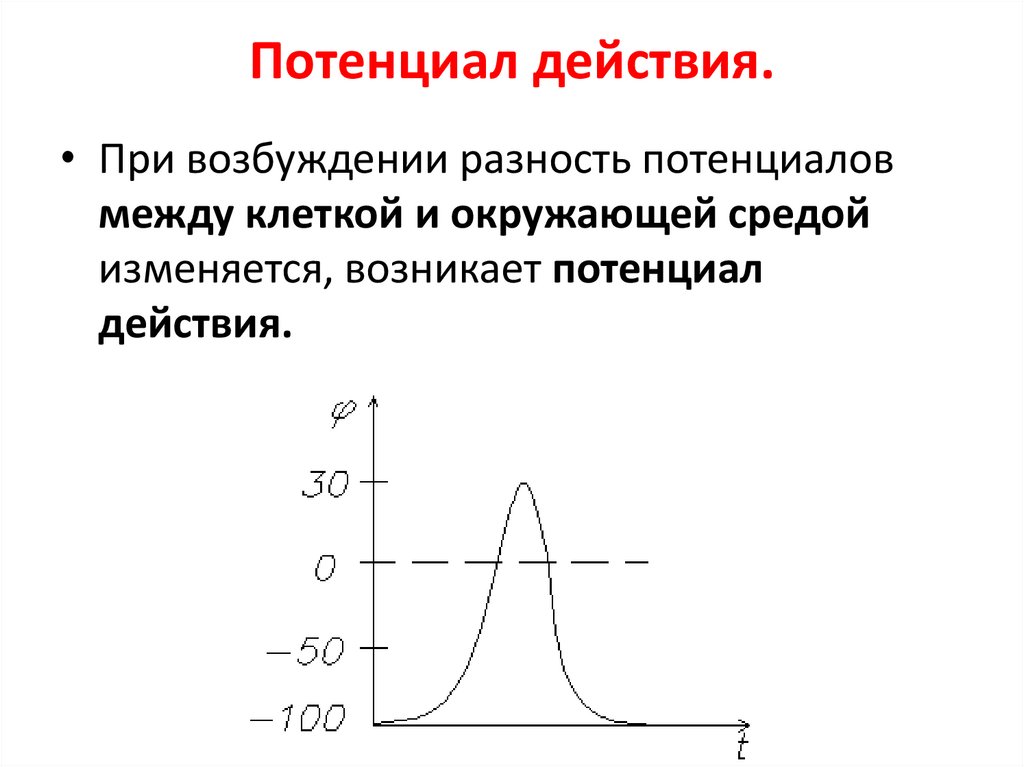
42. Потенциал действия.
• При возбуждении разность потенциаловмежду клеткой и окружающей средой
изменяется, возникает потенциал
действия.
43.
• Потенциал действия напоминаетапериодические процессы, происходящие
при зарядке и разрядке конденсатора
• В нервных волокнах происходит
распространение потенциала действия.
• Изменение сопротивления мембраны во
время возникновения потенциала действия
показал, что оно изменяется, повторяя по
формуле временную зависимость
потенциала действия.
44.
• Что бы выяснить для каких ионовизменяется проницаемость мембраны,
следует обратить внимание, что потенциал
действия приводит к кратковременному
возрастанию потенциала внутри клетки.
45.
• Отрицательный относительно внешней средыпотенциал становится положительным.
• Так как при изменении проницаемости
мембраны, для какого-либо иона, этот ион
будет проникать через неё, стремясь создать
равновесное состояние, то числовые данные
показывают, что внутрь клетки проникают
ионы натрия, создавая там положительный
потенциал, следовательно, при возбуждении в
начальный период увеличивается
проницаемость мембран именно для ионов
натрия.
46.
• Измерить проницаемость мембран длякакого–либо иона (иначе говоря,
электропроводимость или сопротивление
мембраны для этого иона) можно, если на
основании закона Ома найти отношение тока к
напряжению, или наоборот. Это сложно, так
как проницаемость (электрическое
сопротивление) мембраны при возбуждении
изменяется со временем. Это приводит к
перераспределению электрического
напряжения в цепи, и разность потенциалов
на мембране изменяется.
47.
• Ходжкин и Хаксли смогли получитьвыражение для плотности суммарного
потока через мембрану:
d
4
j C ( к )g к n ( na )g na ( у )g у
dt
48.
• где• С – электроемкость мембраны (на единицу
площади);
• - потенциал действия (между наружной и
внутренней поверхностями мембраны);
• к, na, у - равновесные потенциалы
для K+, N+,Na+ и всех остальных ионов;
• g к - удельная проводимость при полностью
открытых каналах;
• N – доля активных (открытых) каналов для К+;
• M – для Na+;
• h - доля неинактивированных, т.е. не
закрывающихся натриевых каналов.



































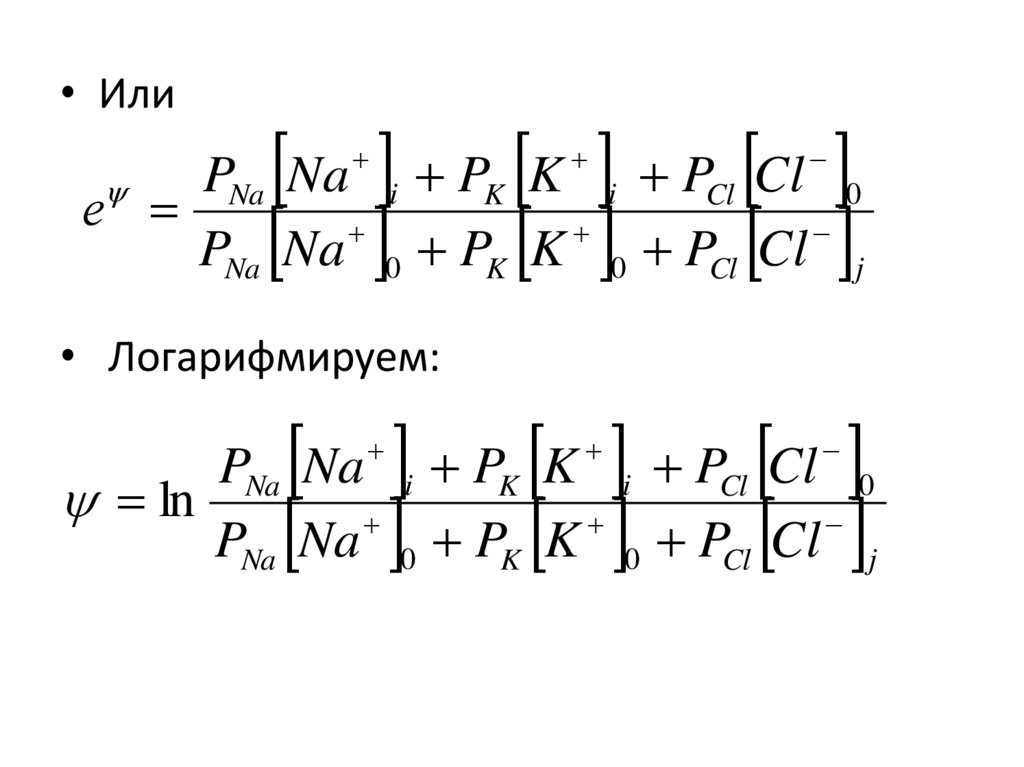








 Биология
Биология