Похожие презентации:
Дифференциал функции. Производные и дифференциалы высших порядков
1.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы Екатерины II
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
ЛЕКЦИЯ 3
Дифференциал функции.
Производные и дифференциалы высших порядков.
22.05.2025
г. Санкт-Петербург
2025
1/14
2.
Содержание лекции•Понятие дифференциала
•Геометрический смысл дифференциала.
•Свойства дифференциала
•Приложения к приближенным вычислениям.
•Производные и дифференциалы высших порядков
2|14
3.
Дифференциал функцииПусть функция
Линейная часть
Дифференциал функции
это линейная относительно
этой точке
дифференцируема в точке тогда
Нелинейная часть
в точке
часть приращения функции в
-дифференциал независимой переменной:
3|14
4.
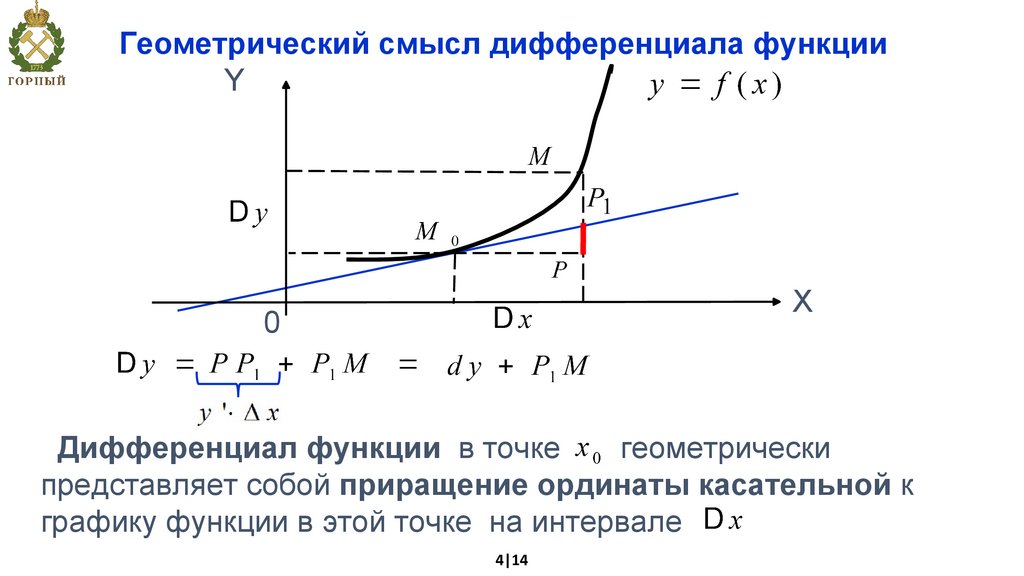
Геометрический смысл дифференциала функцииY
X
0
Дифференциал функции в точке
геометрически
представляет собой приращение ординаты касательной к
графику функции в этой точке на интервале
4|14
5.
,Свойства дифференциала
.
Если функции u=u(x) и v=v(x) дифференцируемы в точке x
и С=const, то дифференциал обладает следующими свойствами :
.
(«де игрек по де икс»)
Производная функции f в точке х равна отношению дифференциала
функции в этой точке к дифференциалу независимой переменной х.
5|14
6.
, т.е.Инвариантность формы дифференциала
Если х- независимая переменная, а у=f(x) – дифференцируемая
функция, то
Пусть
переменной и
дифференцируемая функция одной
Для сложной
. функции y=y(x(t)) :
Свойство инвариантности (независимости) формы 1-го
дифференциала по отношению к аргументу:
дифференциал функции не зависит от того, является ли
аргумент функцией или независимой переменной
6|14
7.
Пример.Решение.
7|14
8.
Пример.Решение.
8|14
9.
Применение дифференциалав приближенных вычислениях
Пример.
Рассмотрим функцию
=
9|14
10.
Производные высших порядковПусть функция f(x) имеет производную
во всех точках интервала (a,b)
задана функция
Производной от функции f порядка n называется 1–я
производная от производной (n-1)-го порядка от функции f
Функция f(x) называется n раз дифференцируемой на интервале
(a,b), если существуют ее производные до порядка n
10|14
11.
Дифференциалы высших порядковПусть функция y=f(x) дифференцируема на интервале (a;b).
Тогда ее дифференциал
функция только х
Дифференциал 2 -го порядка от функции y=f(x) в точке х – это дифференциал от 1–го
дифференциала:
Для сложной функции y=y( (t)), х= (t):
Вывод:
дифференциалы высших порядков сложной
функции не обладают свойством инвариантности формы.
11|14
Если x=at+b, a,b – постоянные,
то вид 2-го дифференциала не
меняется, т.к.
12.
Пример.Пример.
12|14
13.
Пример. Найти13|14
14.
Спасибо за вниманиеСанкт-Петербургский горный
университет
императрицы Екатерины II,
199106, г. Санкт-Петербург,
Малый пр. В.О., д. 83
Тел.: +7(812) 328-82-98;
14|14





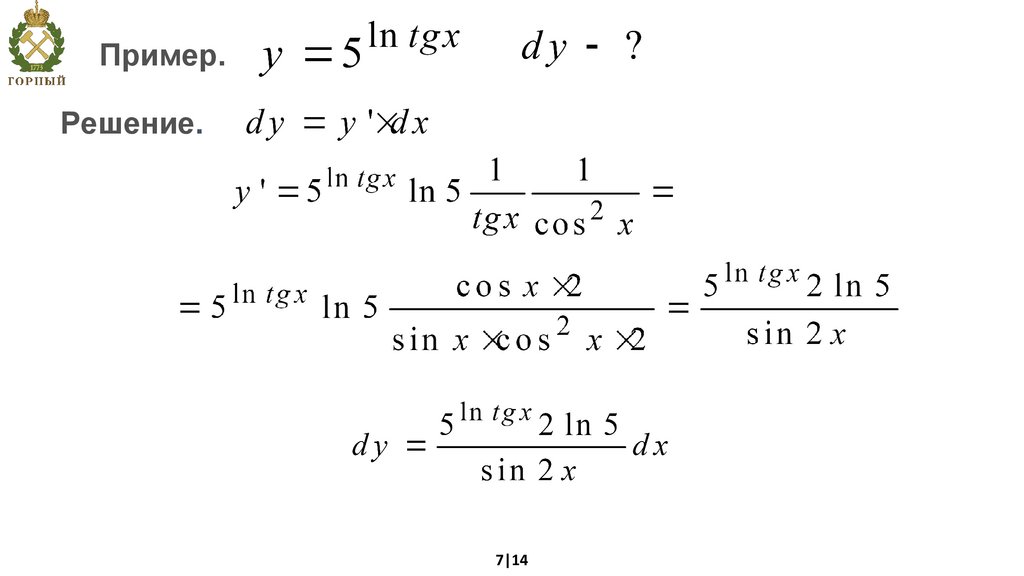
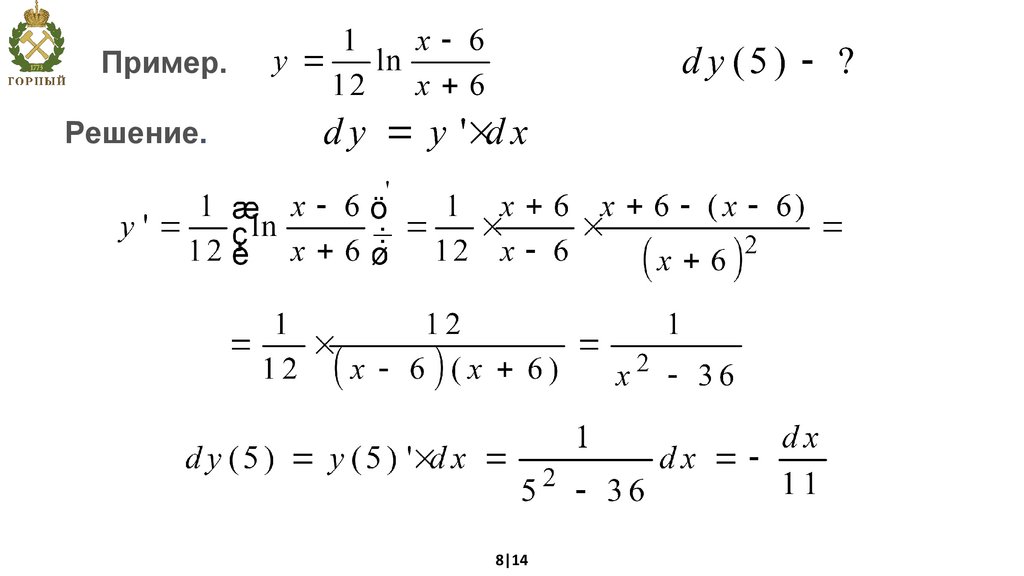



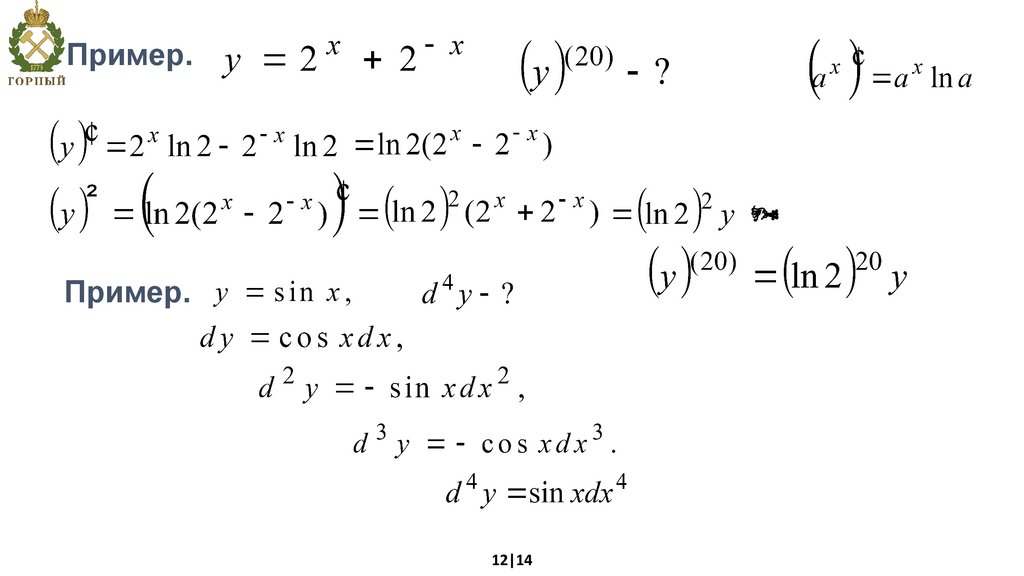


 Математика
Математика








