Дифференциал функции

1. Дифференциал функции

Определение 1.
Пусть приращение функции
можно представить в виде
y
y A x o( x)
где A не зависит от x ,
o( x)- бесконечно малая более высокого порядка
малости, чем x при x 0
Тогда главная линейная часть
приращения функции называется дифференциалом
функции в точке 0 :
Определение 2.
Дифференциалом независимой переменной
называется приращение переменной:
x
dy A x
dy A dx
dx x

2. Пусть y = f(x) определена и непрерывна в точке

x x 0 ,
Если полное приращение функции в этой точке можно представить в виде
y A x o( x),
то функция y = f(x) называется дифференцируемой при x x 0 ,
а выражение
A x dy.
Здесь o( x ) - бесконечно малая величина при x 0 более высокого
порядка, чем x.

3. Необходимое и достаточное условие дифференцируемости функции

Для того, чтобы функция
y f ( x ) в точке x 0 была дифференцируемой
необходимо и достаточно, чтобы для нее в этой точке существовала конечная
производная y ' f ( x 0 ). При выполнении этого условия равенство
y A x o( x) имеет место при значении постоянной
A y' f ' ( x 0 ) :
y y' x o( x).
Доказательство.
Необходимость. Выполняется
y A x o( x).
y
o ( x )
A
.
x
x
y
o( x )
A lim
,
x 0 x
x 0 x
lim
x 0
y
y'.
x 0 x
A lim
Разделим на x :

4. Достаточность.

По условию существует производная
Тогда
y
y' o( x )
x
y' f ' ( x 0 ) :
y
y' ,
x 0 x
lim
и
y y' x o( x).
Приращение функции записано в таком виде, следовательно, функция
дифференцируема.

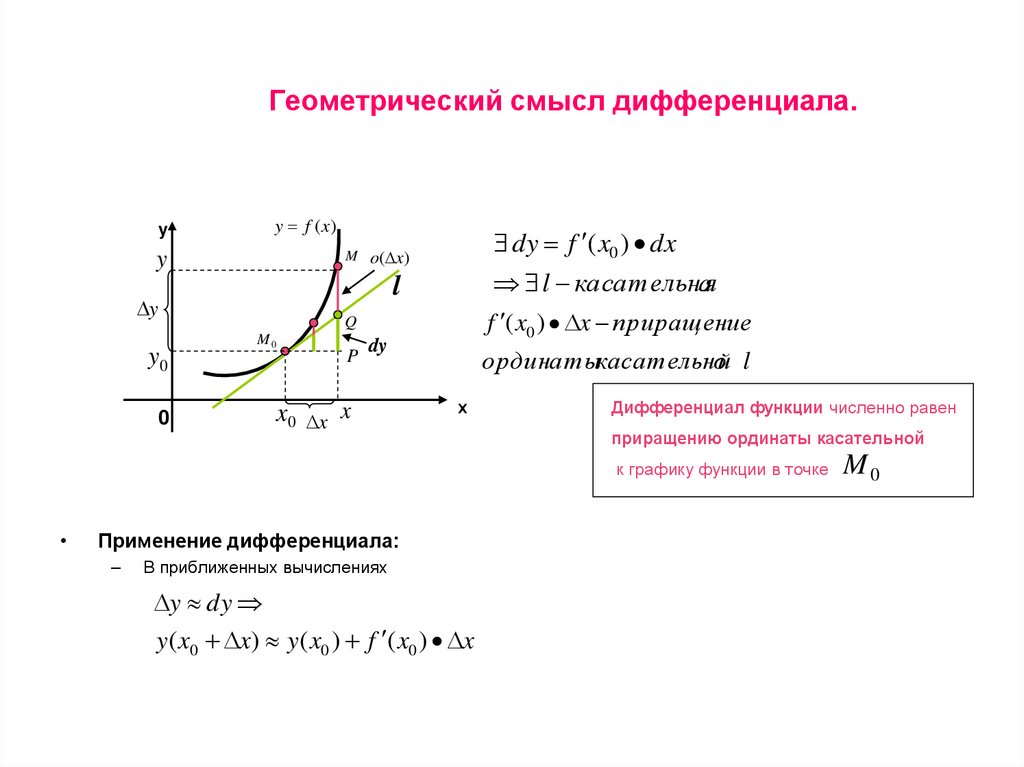
5. Геометрический смысл дифференциала.

y f (x)
y
dy f ( x0 ) dx
M o( x)
y
l касательная
l
y
f ( x0 ) x приращение
Q
y0
M0
0
P
x0
x
dy
x
ординатыкасательной l
х
Дифференциал функции численно равен
приращению ординаты касательной
к графику функции в точке
Применение дифференциала:
–
В приближенных вычислениях
y dy
y ( x0 x) y ( x0 ) f ( x0 ) x
M0

6. Свойства дифференциала.

y f ( x) и y g ( x)
Пусть функции
дифференцируемые.
Тогда:
1.
d ( f g ) df dg ;
2. d ( f g ) (df ) g f (dg) ;
3.
4. Инвариантность формы дифференциала.
Пусть функция
Функция
Тогда
f
(df ) g f (dg)
d( )
;
2
g
g
y f (u )
u g (x)
дифференцируемая;
дифференцируемая.
dy f (u ) du f ( g ( x)) dx
du g ( x) dx
f (u) g ( x)
Форма дифференциала функции
не зависит от того, является ли ее
аргумент независимой переменной или
функцией от новой переменной.

7. Таблица дифференциалов основных элементарных функций.

1.
2.
3.
4.
5.
6.
7.
d (C ) 0
d ( x n ) nxn 1dx
d (a x ) a x ln a dx
d (e x ) e x dx
1
d (loga x)
dx
1 x ln a
d (ln x) dx
x
d (sin x) cos x dx
8.
d (cosx) sin x dx
9.
1
d (tgx)
dx
2
cos x
10.
1
d (ctgx) 2 dx
sin x
11.
12.
13.
14.
d (arcsin x)
1
dx
1 x
1
d (arccosx)
dx
2
1 x
1
d (arctgx)
dx
1 x2
1
d (arcctgx)
dx
2
1 x
2

8. Функции двух переменных

• Функцией двух переменных называется
закон, по которому каждой паре
значений независимых переменных
(аргументов) из области определения
соответствует значение зависимой
переменной (функции).

9. Данную функцию обозначают следующим образом: Z = f(x; y)

• Поскольку упорядоченная пара
значений «икс» и «игрек» определяет
точку на плоскости, то функцию также
записывают через z = f(M), где M –
точка плоскости с координатами x,y.
Такое обозначение широко
используется в некоторых практических
заданиях.

10. Область определения

• Областью определения функции двух
переменных называется множество
всех пар (x;y), для которых существует
значение z.
• Графически область определения
представляет собой всю плоскость
либо её часть.

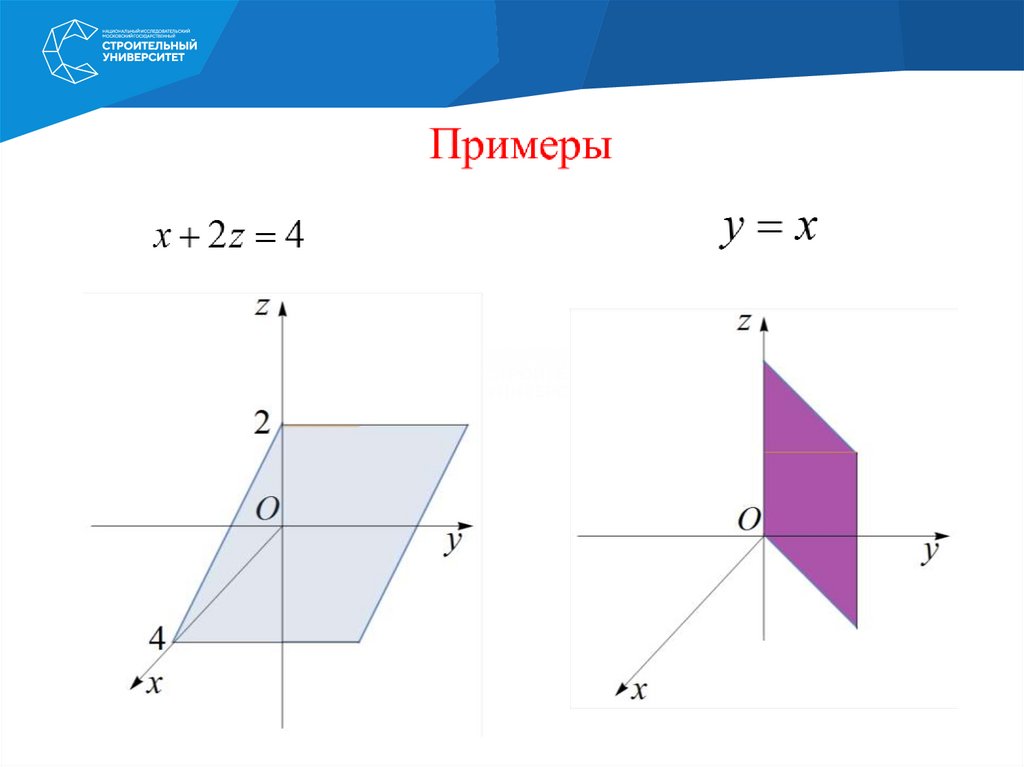
11. Пример

• Найти область определения функции
z
x y 1
x
• Решение: подкоренное выражение должно быть
неотрицательным: x y 1 0
• и знаменатель не может равняться нулю: x 0 .
• Таким образом, область определения задаётся
системой x y 1 0
.
x 0
• Со вторым условием системы тоже всё просто:
уравнение задаёт ось ординат, и коль скоро , то её
следует исключить из области определения.

12. Построение области определения

• Строим прямую x + y - 1 = 0 и определяем
полуплоскость, которая соответствует
неравенству x y 1 0 .
• Поскольку неравенство нестрогое, то сама
прямая также будет являться решением.
• Второе условие системы: уравнение x = 0
задаёт ось ординат, и так как x 0
• , то эту ось следует исключить из области
определения.
x 0

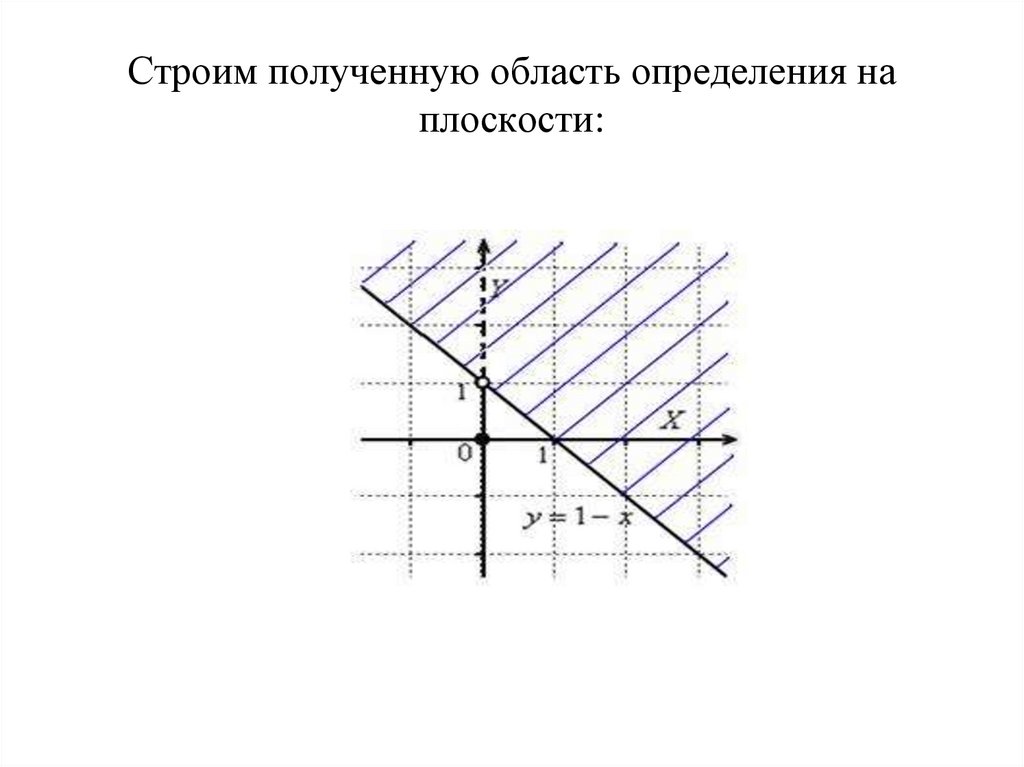
13. Строим полученную область определения на плоскости:

14. Пример

Найти область определения функции
z 3 x2 y 2
Решение:
Подкоренное выражение должно быть
неотрицательным: 3 x2 y 2 0
или x 2 y 2 3
Это круг радиуса 3 с центром в начале координат.
Изобразим область определения на чертеже:

15. Изобразим область определения на чертеже:

16.

17. Имеем дело с областями , ограниченными линиями.

Линия, ограничивающая данную область,
называется границей области.
Точки области, не лежащие на границе,
называются внутренними точками области.
Область, состоящая из одних внутренних
точек, называется открытой.

18. Если же к области относятся и точки границы, то область называется замкнутой.

• Связной называется область, любые две точки
которой можно соединить линией, целиком
лежащей в этой области.

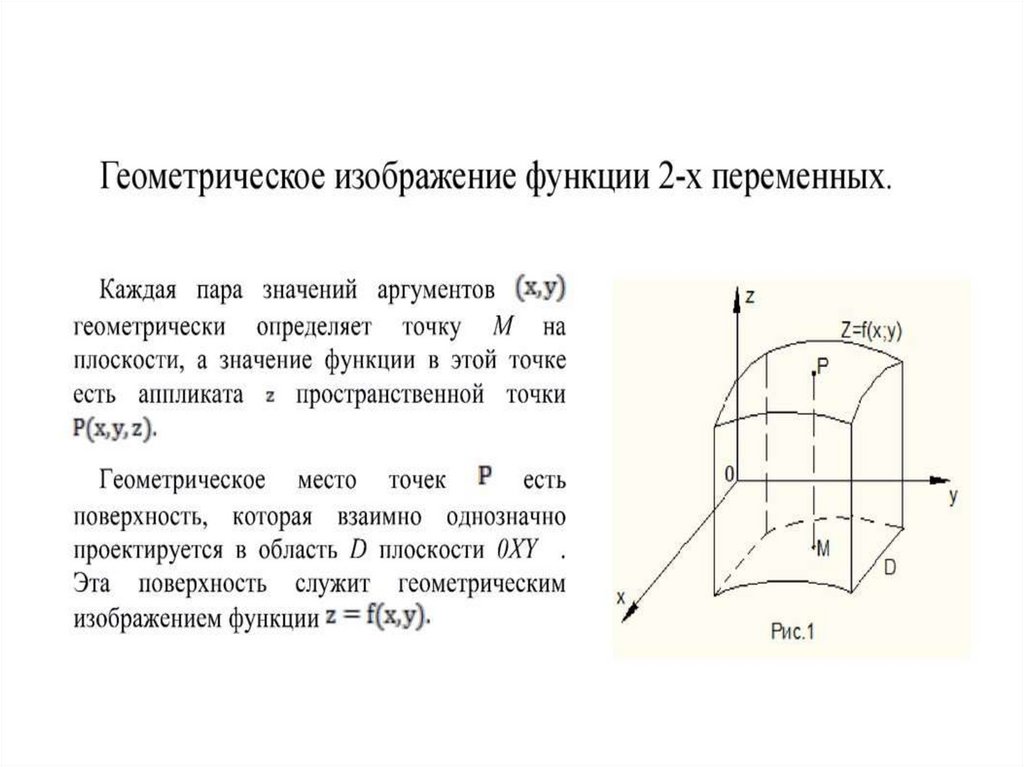
19. Геометрическое изображение функции двух переменных.

• Графиком функции z = f(x; y) является
поверхность с уравнением z = f(x; y).

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30. Пример

31.

32. Построить самостоятельно:

Плоскость: z = 1 – x
Полусфера:
z 4 x2 y2

33. Ограниченность функции двух переменных

• Функция z = f(x;y) называется
ограниченной в области D, если
существуют такие числа M и N, что
M f ( x; y) N
для всех (х,у) из области D.
2
z
sin(
x
2 y)
Например,

34.

35.

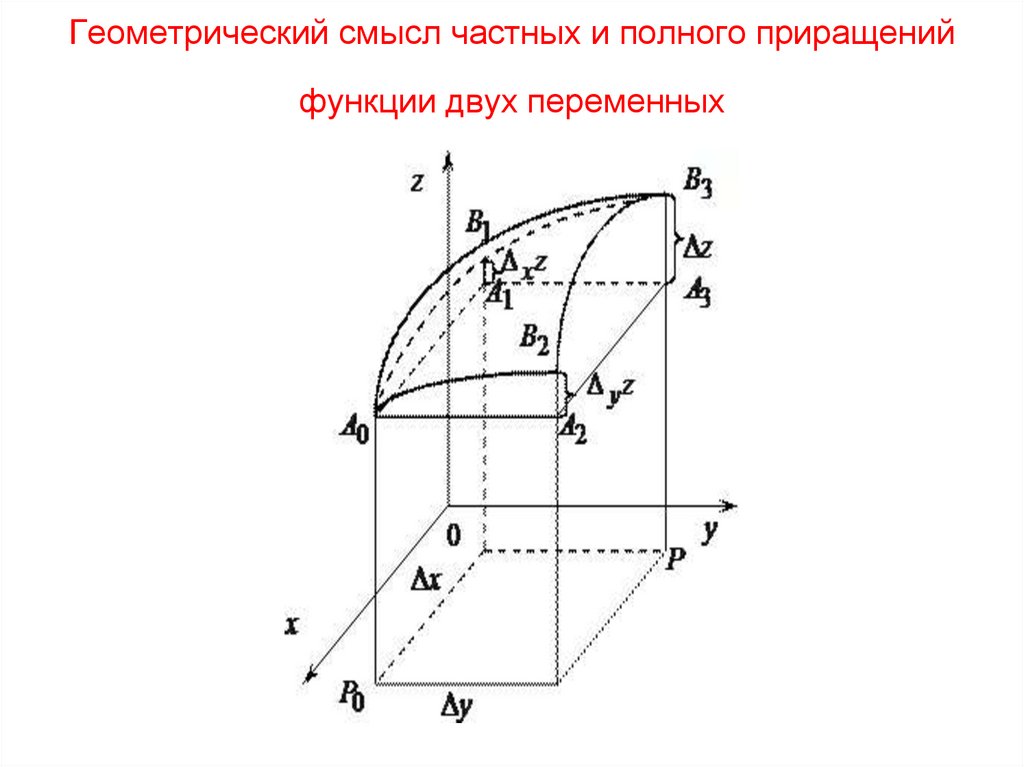
36. Частные приращения функции двух переменных

• Частным приращением по x функции z = f(x; y) в
точке ( x0 ; y0 ) называется разность
x z f ( x0 x; y0 ) f ( x0 ; y0 ) ,
• то есть приращение функции, полученное за счет
приращения x при y - const.

37.

Частным приращением по y функции
z = f(x; y) в точке ( x0 ; y0 ) называется разность
y z f ( x0 ; y0 y ) f ( x0 ; y0 ),
то есть приращение функции, полученное за
счет приращения y при x - const.

38. Полное приращение функции z = f(x;y)

Полным приращением функции z = f(x;y) в
точке ( x0 ; y0 ) называется разность
z f ( x0 x; y0 y ) f ( x0 ; y0 )

39. Геометрический смысл частных и полного приращений функции двух переменных

40.

41. Непрерывность функции в точке.

• Функция z f (M ) называется непрерывной в точке M 0 ,
если
1). функция определена в точке
и некоторой ее
окрестности;
2). существует lim f (M ) ;
M M 0
3). lim f (M ) f (M 0 ) .
M M 0

42. Второе определение непрерывности функции z =f(x; y) в точке

Пусть функция z = f(x; y) непрерывна в точке
M 0 ( x0 ; y0 )
(по первому определению).
lim f ( x0 x; y0 y ) f ( x0 ; y0 )
Тогда x x0 x, y y0 y ,
x 0
y 0
или
lim [f ( x0 x; y0 y ) f ( x0 ; y0 )]=0 .
x 0
y 0
Но f ( x0 x; y0 y ) f ( x0 ; y0 ) z - полное приращение
функции.
Пусть
( x )2 ( y )2
, при x 0 и y 0, 0 , тогда получим
lim z = 0
0

43.

44. Частные производные функции двух переменных z = f (x; y)

Частной производной функции z = f(x; y) по x
называется
x z
f ( x0 x; y0 ) f ( x0 ; y0 )
lim
x 0 x
x 0
x
z x lim
(y - const)
z
Другое обозначение: x
Частной производной функции z = f(x; y) по y
называется
z y lim
y 0
( x - const)
yz
y
lim
z
Другое обозначение: y
y 0
f ( x0 ; y0 y ) f ( x0 ; y0 )
y

45. Пример

Найти частные производные:
z 3x 2 y 5x y 2 xy 4 x y 5
4
3
2
z
12 x3 10 xy 2 y 2 4
x
(y = const)
z
6 y 2 5 x 2 4 xy 1
y
(x = const)
2

46. Пример

Найти частные производные:
z e2 x 5 ysin (4 - 2 x+5y2 )
2 x 5 y
2
2 x 5 y
2
zx e
2 sin(4 - 2 x+5y ) e
cos(4 - 2 x+5y ) ( 2)
(y = const)
2 x 5 y
2
2 x 5 y
2
zy e
5 sin(4 - 2 x+5y ) e
cos(4 - 2 x+5y ) (10y)
(x = const)

47. Геометрический смысл частных производных

Пусть y y0 const . Это плоскость, параллельная
координатной плоскости Oxz. В пересечении с
поверхностью z = f(x; y) получим линию.
Угол - угол, образованной касательной к этой
линии и положительным направлением оси Ox.
Касательная проведена в точке P0 ( x0 ; y0 ;z0 ), где
z0 f ( x0 ; y0 ).

48. Аналогично,

Пусть x x0 const . Это плоскость,
параллельная координатной плоскости Oyz. В
пересечении с поверхностью z = f(x; y)
получим линию.
Угол - угол, образованной касательной к
этой линии и положительным направлением
оси Oy.
Касательная проведена в той же точке.

49.

50. Физический смысл частных производных

Частная производная
- это скорость
изменения z относительно переменной x в точке
P0 ( x0 ; y0 ).
Частная производная z y ( x0 ; y0 ) - это скорость
изменения z относительно переменной y в той же
точке.

51.

52.

53. Или: функция называется дифференцируемой в точке, если

ее полное приращение можно представить в виде
z A x B y 1 x 2 y ,
где
1 0 и 2 0 при x 0, y 0

54. Полный дифференциал:

dz A x B y
Что представляют собой A и B ?

55. Связь между дифференцируемостью и существованием частных производных функции двух переменных

Если функция z = f(x; y) имеет в точке M(x; y) дифференциал
, то в этой точке существуют и обе
частные производные z и z , причем
x
y
z
z
A
, B
.
x
y

56. Доказательство

Дадим приращение x величине x, а y оставляем
постоянным ( y 0 ),
Тогда dz A x ,
x z dz o( ) A x o( | x| ) ,
так как | x|.
x z
o( | x | )
lim
lim A
A
x 0 x
x 0
x
Это значит, существует
z
A.
x
Аналогично,
z
B.
y

57.

58. Теорема

z z
и
Если в точке (x; y) частные производные
x y
существуют и непрерывны, то в этой точке
функция имеет дифференциал.

59. Теорема. Связь между дифференцируемостью и непрерывностью функции в точке.

Если функция z = f(x; y) дифференцируема в точке (x; y), то она
непрерывна в этой точке.
Доказательство.
По условию функция дифференцируема, это значит ее полное
приращение можно представить в виде:
z z x x z y y 1 x 2 y
тогда
lim z 0
x 0
y 0

60. Частные производные высших порядков

Частными производными второго порядка функции z = f (x,y)
называются частные производные от частных производных
первого порядка.
2 z z
z xx ( z x ) x
2
x
x x
z xy ( z x ) y
2 z
z
x y y x
z yx ( z y ) x
2 z
z
y x x y
z yy ( z y ) y
2 z
z
y 2 y y

61. Теорема

Пусть функция z = f(x; y) в некоторой окрестности
точки (x; y) имеет смешанные производные z xy и z yx ,
причем они непрерывны в этой точке. Тогда в этой
точке смешанные производные равны между собой:
z xy z yx

62. Пример

Найти частные производные второго порядка
z 3x4 y3 xy x2 y5 4x 7 y 10
z x 12x3 y 2xy5 4, z y 3 y 2 x 5x2 y 4 7
z xx ( z x )x 36 x 2 2 y 5 , z xy ( z x ) y 1 10 xy 4 ,
z yx ( z y )x 1 10 xy 4 , z yy ( z y ) y 6 y 20 x 2 y 3

63.

64. Геометрическое изображение точек экстремума:

65.

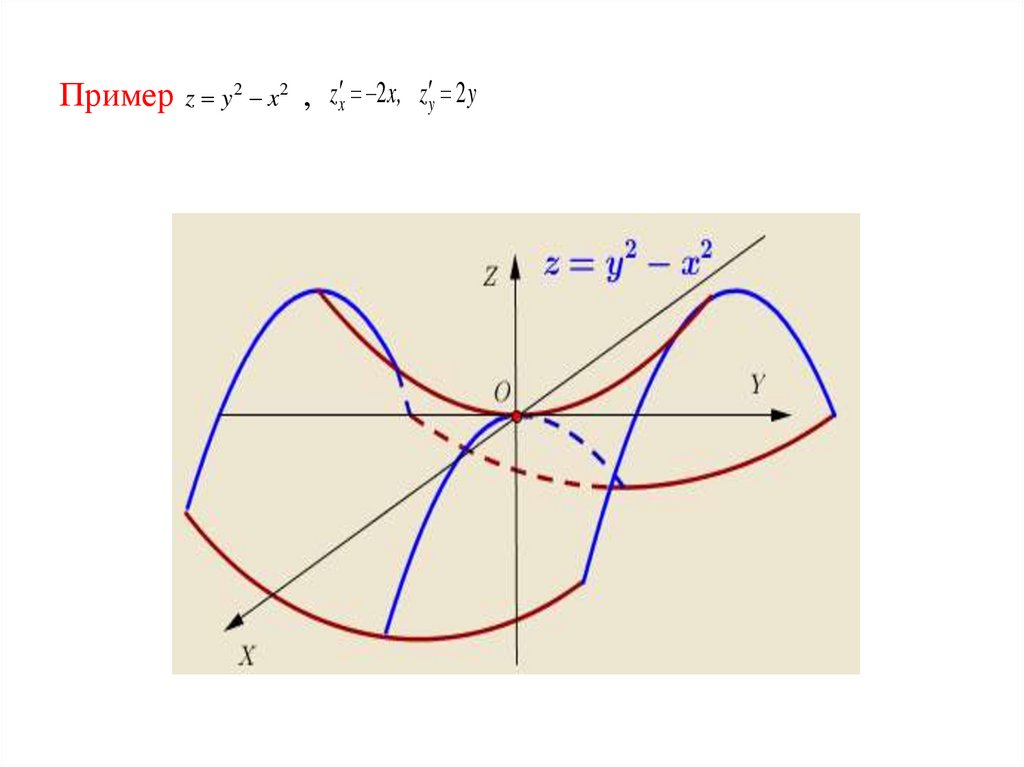
66. Пример ,

Пример
z y 2 x2
, z x 2x, z y 2 y

67.

68. Пример

Исследовать на экстремум функцию
z x3 8 y3 6 xy 1