Основные понятия и аксиомы. Связи и их реакции. Система сходящихся сил. Тема 1.1

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра менеджмента в строительстве
Теоретическая механика
Тема 1.1
Основные понятия и аксиомы.
Связи и их реакции.
Система сходящихся сил.
Нестерова Ольга Павловна
к.т.н., доцент кафедры строительной механики

2.

«Миллионы людей видели, как падают яблоки,
но только Ньютон спросил почему»
Бернард Барух

3. Введение

• Теоретическая механика – это наука, в которой изучаются
общие законы механического движения и механического
взаимодействия материальных тел.
• Механическим движением называется изменение с
течением времени взаимного положения материальных
точек в пространстве.
• Механическим взаимодействием называется такое
взаимодействие материальных тел, которое изменяет или
стремится изменить характер механического движения.
• Кинематическое состояние тела – это состояние покоя или
движения какого-либо определенного характера.
3

4. Введение

• Статика – это раздел теоретической механики, в котором
изучаются правила сложения сил, приложенных к телу, и
устанавливаются условия равновесия сил.
• Кинематика – раздел теоретической механики, в
котором изучается механическое движение тел без учета
их массы и взаимодействия с другими телами (геометрия
движения).
• Динамика - раздел теоретической механики, в котором
изучаются общие законы механического движения тела с
учетом его массы и взаимодействия с другими телами.
4

5. Введение

• Абсолютно твердое тело – это тело, расстояния между
любыми точками которого всегда остаются постоянными.
• Материальная точка – материальное тело, размеры
которого в условиях рассматриваемой задачи можно не
учитывать.
• Механическая система – такая совокупность материальных
тел, в которой положение и движение каждого тела зависит
от положения и движения других тел данной системы.
• Свободное тело – это тело, которое может из данного
положения совершать любые перемещения в пространстве.
• Несвободное тело – это тело, на перемещения которого в
пространстве наложены какие-либо ограничения.
5

6. Основные понятия и определения статики

• Сила – это мера механического взаимодействия тел,
определяющая интенсивность и направления этого
взаимодействия. Сила – это векторная величина. Она
характеризуется модулем, направлением и точкой
приложения.
• Линия действия силы – прямая, вдоль которой направлена
сила.
Линия действия силы
P
Точка приложения силы
6

7. Основные понятия и определения статики

• Система сил – совокупность нескольких сил, действующих
на данное тело.
• Эквивалентными называются системы сил, под действием
каждой из которых тело находится в одинаковом
кинематическом состоянии.
• Равнодействующей называется сила, эквивалентная
данной системе сил.
• Уравновешивающей называется сила, равная по модулю
равнодействующей и направленная по линии её действия в
противоположную сторону.
• Уравновешенная система сил – система сил,
эквивалентная нулю, под действием которой тело может
находиться в равновесии.
7

8. Основные понятия и определения статикиa

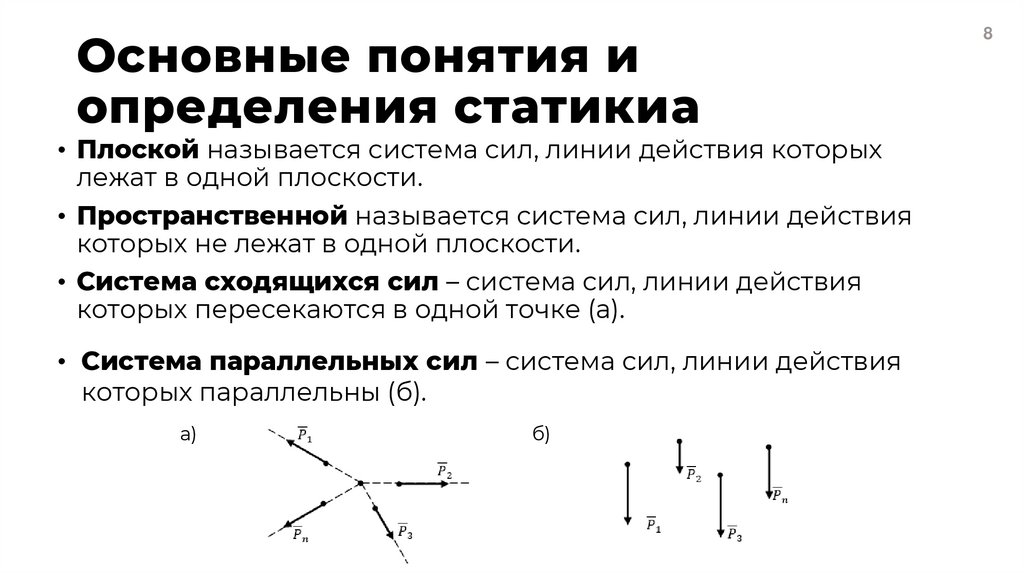
• Плоской называется система сил, линии действия которых
лежат в одной плоскости.
• Пространственной называется система сил, линии действия
которых не лежат в одной плоскости.
• Система сходящихся сил – система сил, линии действия
которых пересекаются в одной точке (а).
• Система параллельных сил – система сил, линии действия
которых параллельны (б).
а)
б)
8

9. Основные понятия и определения статики

• Внешними называются силы, действующие на тела данной
механической системы со стороны тел, не входящих в данную
механическую систему.
• Внутренними называются силы взаимодействия между
телами данной механической системы.
Две основные задачи статики:
1. Упрощение системы сил, т.е. приведение системы сил к
эквивалентной системе более простого вида.
2. Исследование условий равновесия системы сил.
9

10. Аксиомы статики

1. Аксиома инерции: если к свободному твердому телу
приложена уравновешенная система сил, тело будет
сохранять состояние покоя или равномерного
прямолинейного движения.
2. Аксиома равновесия тела под действием двух сил:
свободное твердое тело находится в равновесии под
действием двух сил тогда и только тогда, когда эти
силы равны по модулю и направлены по одной
прямой в противоположные стороны.
10

11. Аксиомы статики

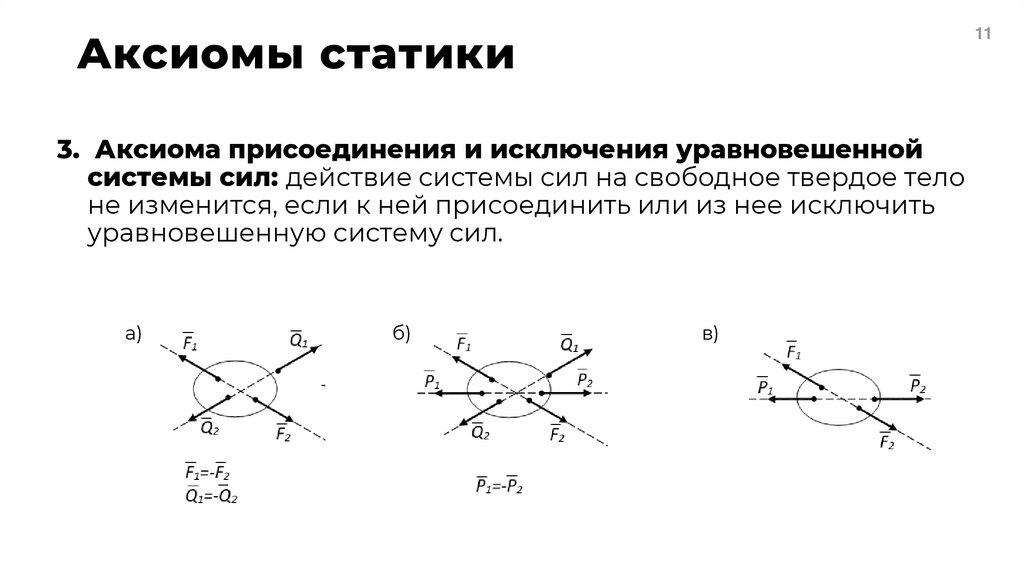
11
3. Аксиома присоединения и исключения уравновешенной
системы сил: действие системы сил на свободное твердое тело
не изменится, если к ней присоединить или из нее исключить
уравновешенную систему сил.
а)
б)
в)

12. Аксиомы статики

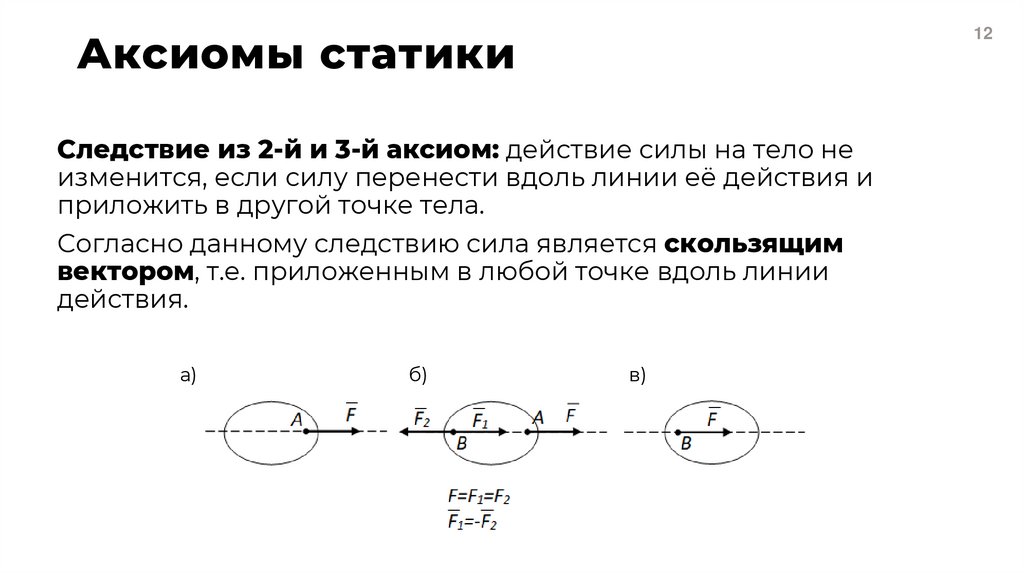
12
Следствие из 2-й и 3-й аксиом: действие силы на тело не
изменится, если силу перенести вдоль линии её действия и
приложить в другой точке тела.
Согласно данному следствию сила является скользящим
вектором, т.е. приложенным в любой точке вдоль линии
действия.
а)
б)
в)

13. Аксиомы статики

4. Аксиома параллелограмма сил: равнодействующая двух сил,
приложенных в одной точке, равна их геометрической сумме,
т.е. определяется как диагональ параллелограмма,
построенного на этих силах.
13

14. Аксиомы статики

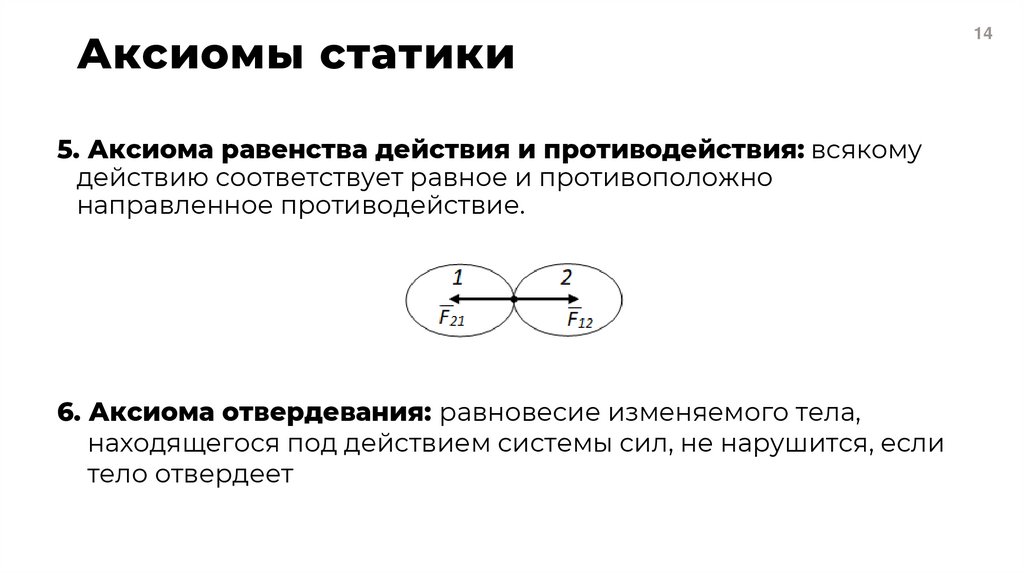
5. Аксиома равенства действия и противодействия: всякому
действию соответствует равное и противоположно
направленное противодействие.
6. Аксиома отвердевания: равновесие изменяемого тела,
находящегося под действием системы сил, не нарушится, если
тело отвердеет
14

15. Связи. Реакции связей

• Связи – это тела, ограничивающие перемещение данного тела в
пространстве.
• Реакция связи – это сила, с которой данная связь действует на
тело.
• Все методы решения задач статики справедливы только для
свободных тел, находящихся под действием сил.
• Принцип освобождаемости от связей: несвободное тело
можно считать свободным, если отбросить связи и заменить их
действие соответствующими реакциями.
15

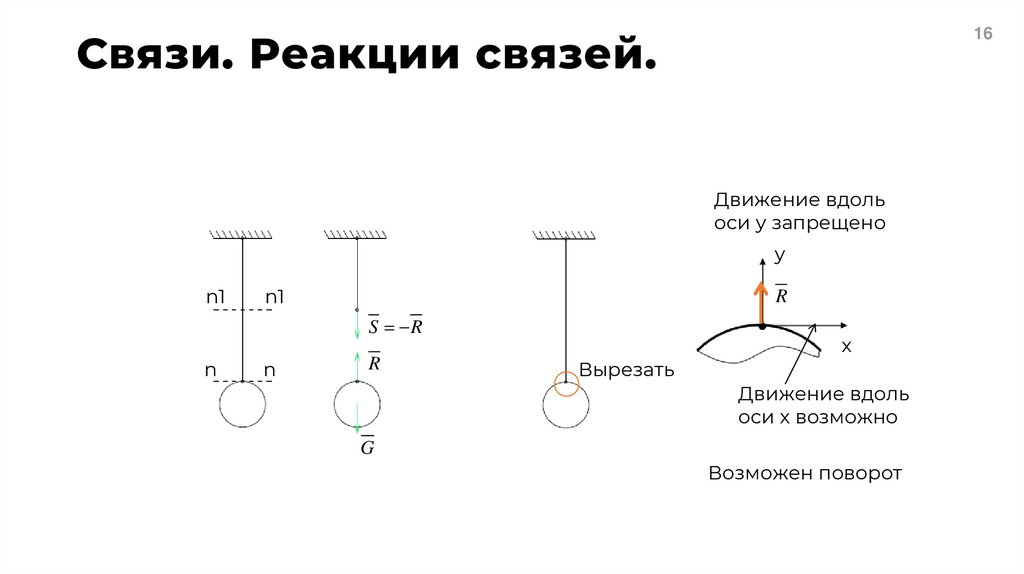
16. Связи. Реакции связей.

16
Движение вдоль
оси у запрещено
y
n1
n1
R
S R
n
n
R
x
Вырезать
Движение вдоль
оси х возможно
G
Возможен поворот

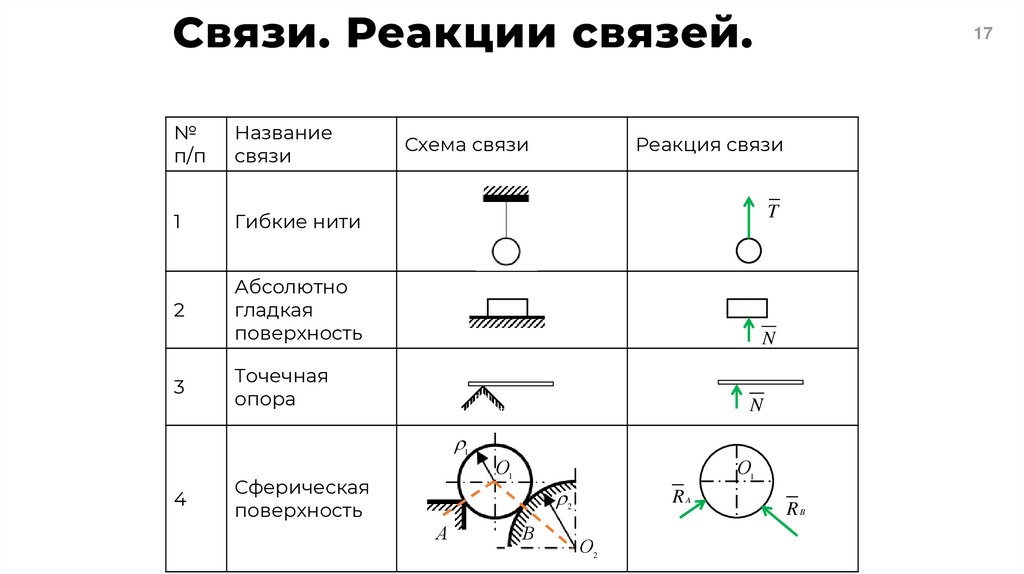
17. Связи. Реакции связей.

17
№
п/п
Название
связи
1
Гибкие нити
2
Абсолютно
гладкая
поверхность
N
Точечная
опора
N
3
Схема связи
Реакция связи
T
1
4
О1
Сферическая
поверхность
О1
2
А
В
RA
О2
RB

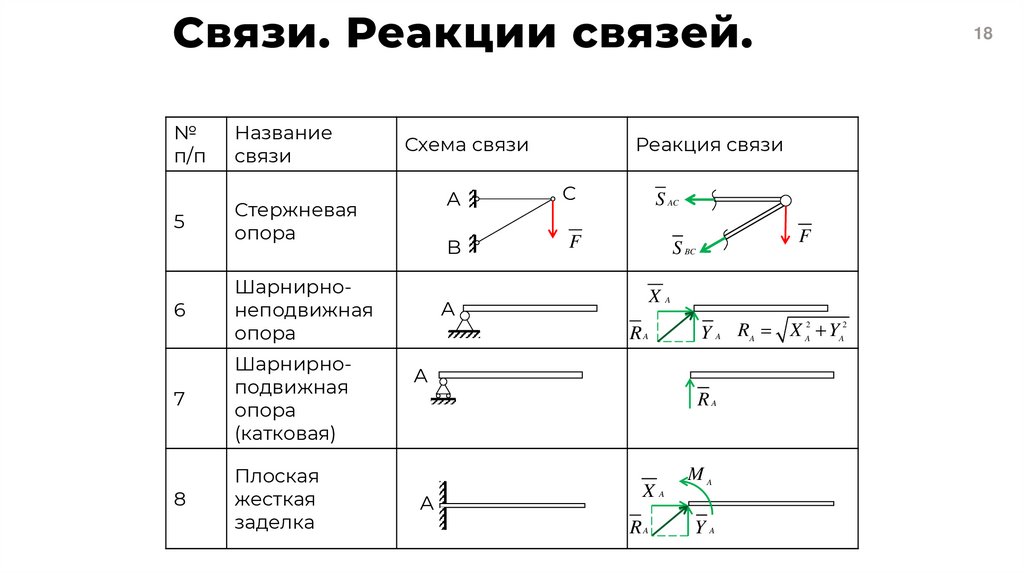
18. Связи. Реакции связей.

№
п/п
5
6
Название
связи
Схема связи
Стержневая
опора
Шарнирнонеподвижная
опора
7
Шарнирноподвижная
опора
(катковая)
8
Плоская
жесткая
заделка
Реакция связи
A
C
B
F
S AC
F
S BC
XA
A
RA
2
2
Y A RA X A YA
A
RA
A
18
XA
RA
MA
YA

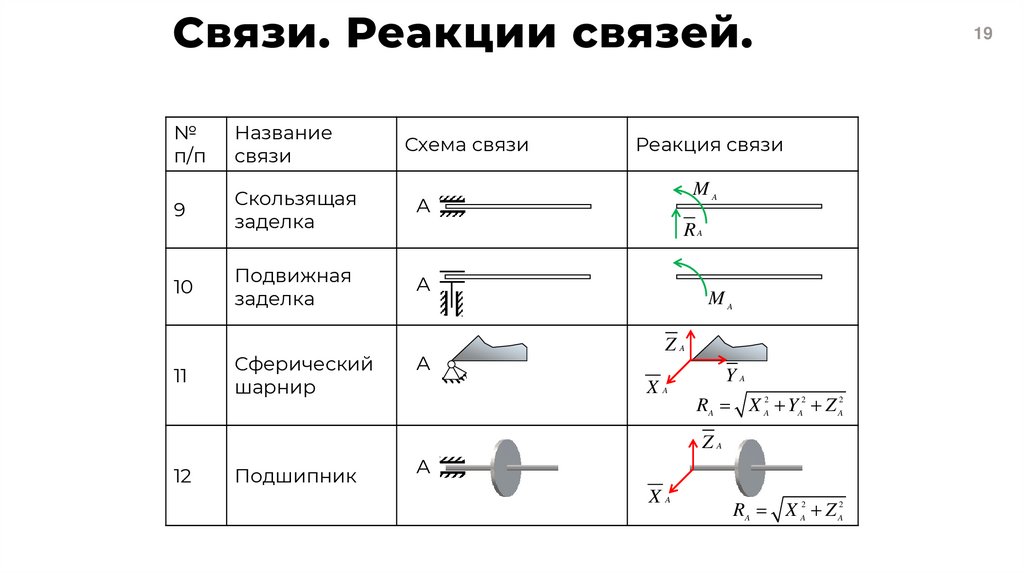
19. Связи. Реакции связей.

№
п/п
Название
связи
9
Скользящая
заделка
A
Подвижная
заделка
A
10
11
Сферический
шарнир
Схема связи
Реакция связи
MA
RA
A
MA
ZA
XA
YA
RA X A2 YA2 Z A2
ZA
12
Подшипник
A
XA
RA X A2 Z A2
19

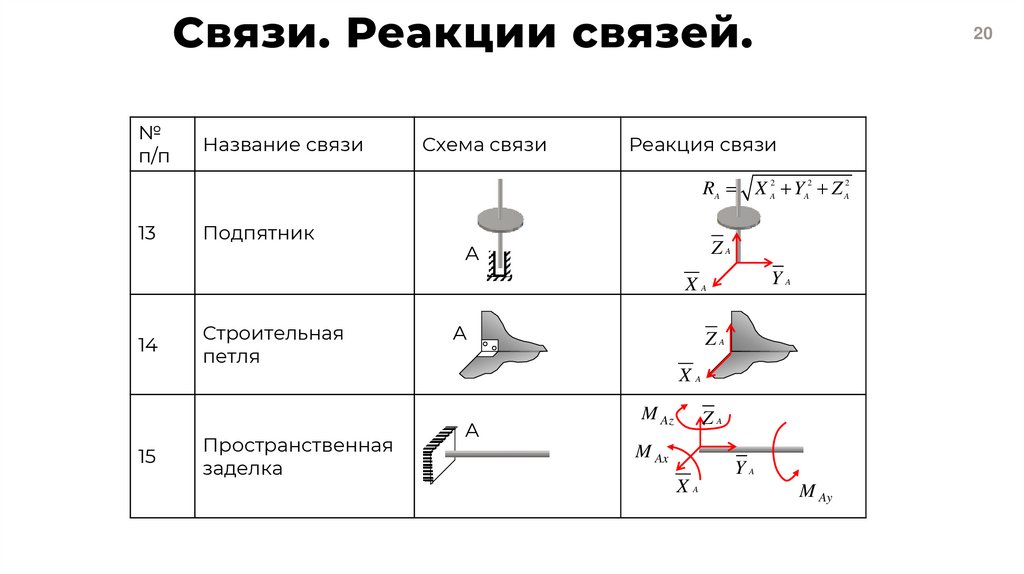
20. Связи. Реакции связей.

№
п/п
Название связи
Схема связи
20
Реакция связи
RA X A2 YA2 Z A2
13
Подпятник
ZA
A
YA
XA
14
Строительная
петля
A
ZA
XA
15
Пространственная
заделка
A
M Az
ZA
M Ax
YA
XA
M Ay

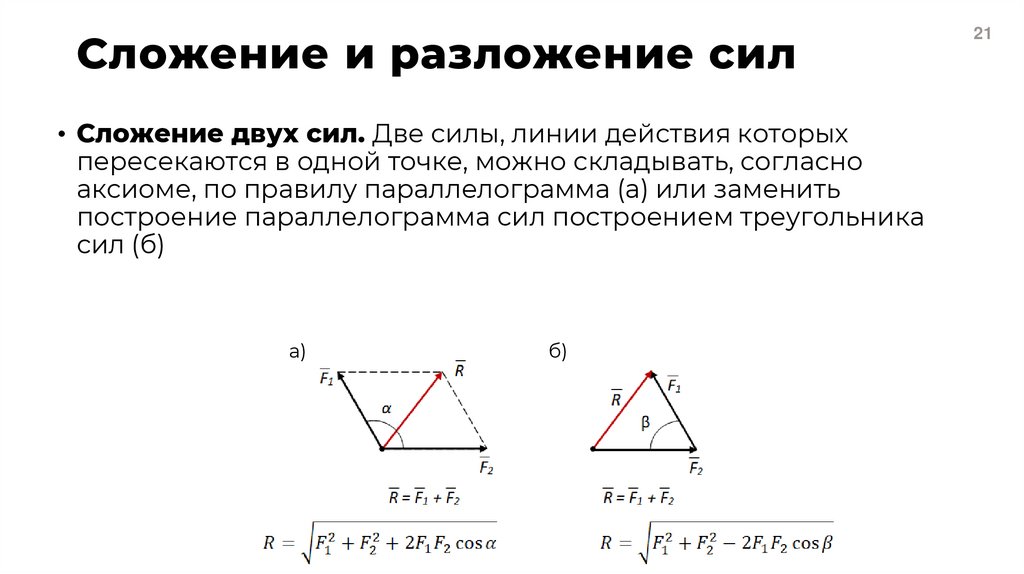
21. Сложение и разложение сил

• Сложение двух сил. Две силы, линии действия которых
пересекаются в одной точке, можно складывать, согласно
аксиоме, по правилу параллелограмма (а) или заменить
построение параллелограмма сил построением треугольника
сил (б)
а)
б)
21

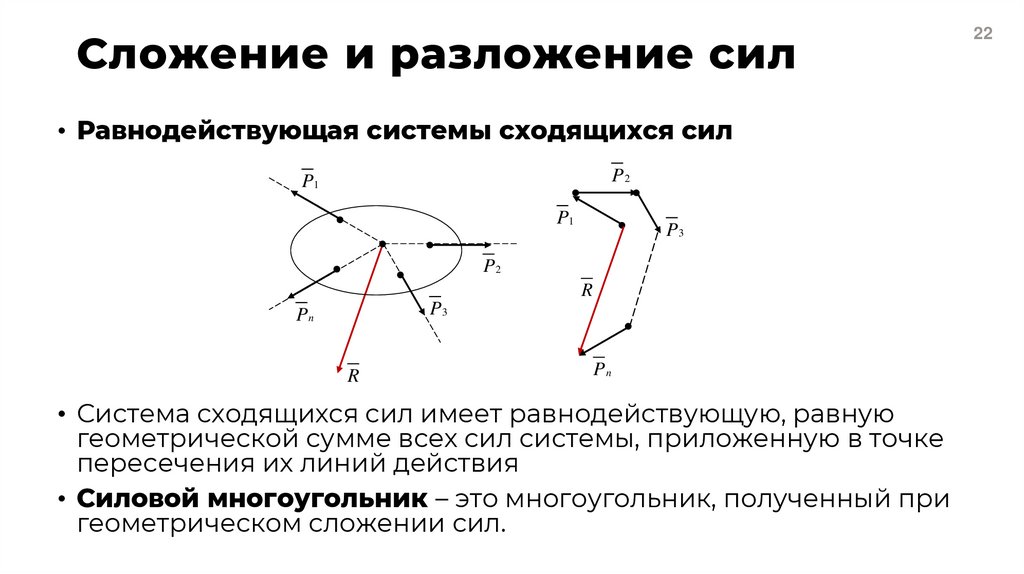
22. Сложение и разложение сил

• Равнодействующая системы сходящихся сил
P2
P1
P1
P3
P2
R
P3
Pn
R
Pn
• Система сходящихся сил имеет равнодействующую, равную
геометрической сумме всех сил системы, приложенную в точке
пересечения их линий действия
• Силовой многоугольник – это многоугольник, полученный при
геометрическом сложении сил.
22

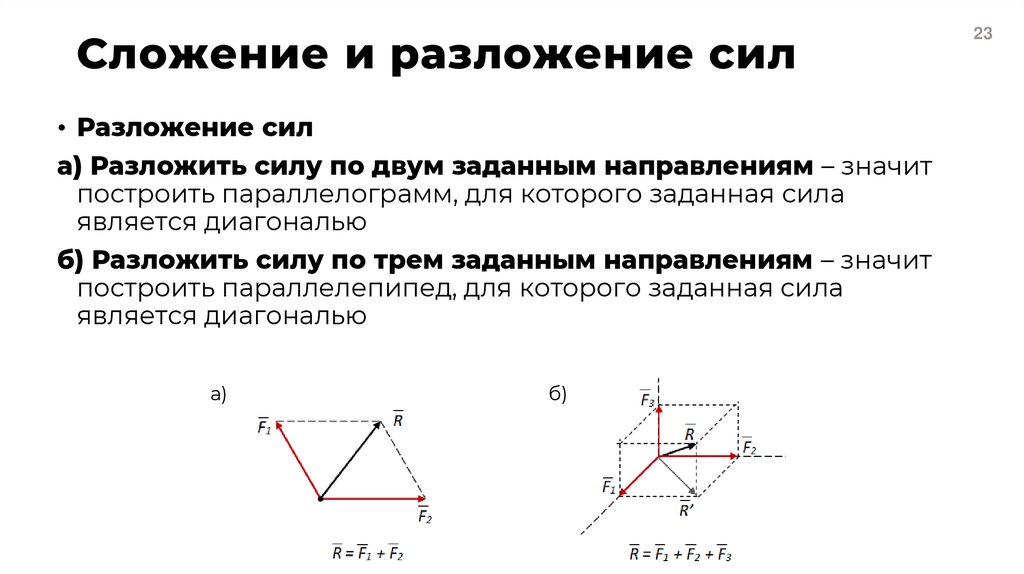
23. Сложение и разложение сил

• Разложение сил
а) Разложить силу по двум заданным направлениям – значит
построить параллелограмм, для которого заданная сила
является диагональю
б) Разложить силу по трем заданным направлениям – значит
построить параллелепипед, для которого заданная сила
является диагональю
а)
б)
23

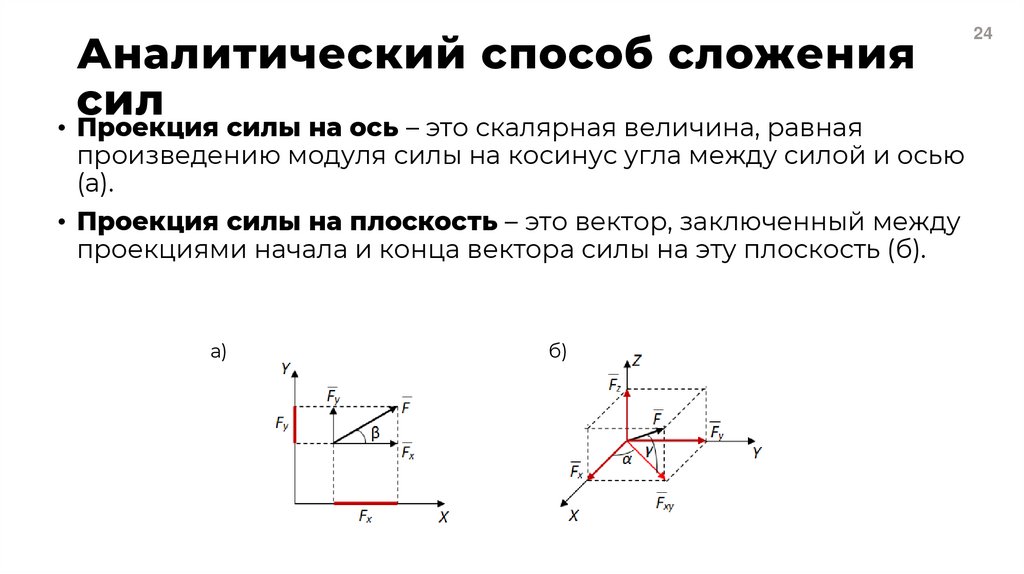
24. Аналитический способ сложения сил

• Проекция силы на ось – это скалярная величина, равная
произведению модуля силы на косинус угла между силой и осью
(а).
• Проекция силы на плоскость – это вектор, заключенный между
проекциями начала и конца вектора силы на эту плоскость (б).
а)
б)
24

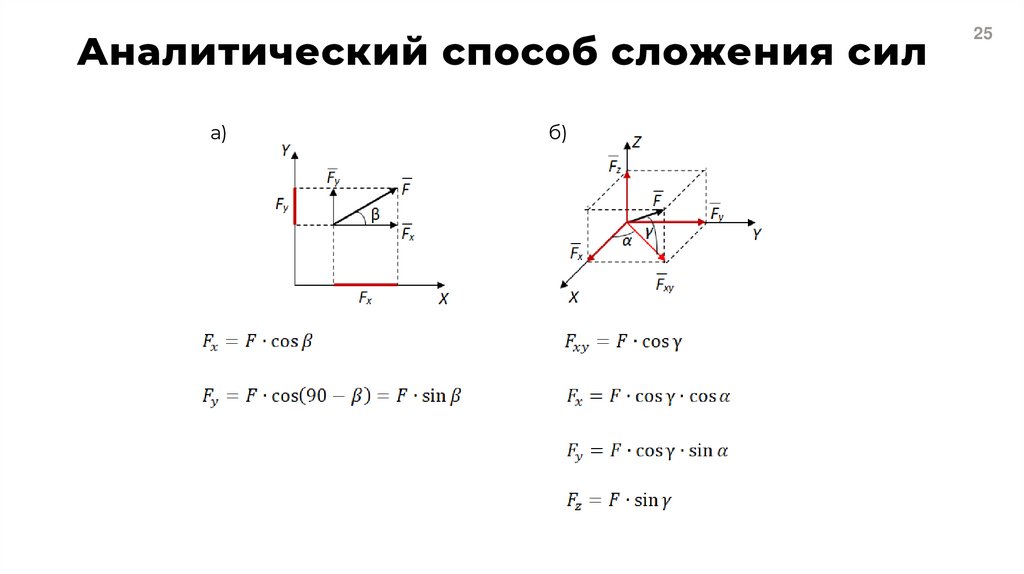
25. Аналитический способ сложения сил

а)
б)
25

26. Аналитический способ сложения сил

• Определение равнодействующей системы сил
Проекция равнодействующей на какую-либо ось равна
алгебраической сумме проекций всех сил системы на эту ось:
Модуль равнодействующей:
Направление равнодействующей задается направляющими
косинусами:
26

27. Равновесие системы сходящихся сил

• Для равновесия системы сходящихся сил необходимо и
достаточно, чтобы их равнодействующая была равна нулю
• Геометрическое условие равновесия
Для равновесия системы сходящихся сил необходимо и
достаточно, чтобы силовой многоугольник, построенный на
этих силах,
был замкнут.
27

28. Равновесие системы сходящихся сил

• Аналитические условия равновесия
Модуль равнодействующей определяется через её проекции:
Это условие выполняется, если:
Для равновесия системы сходящихся сил необходимо и
достаточно, чтобы суммы проекций всех сил системы на каждую
из трёх координатных осей были равны нулю
28

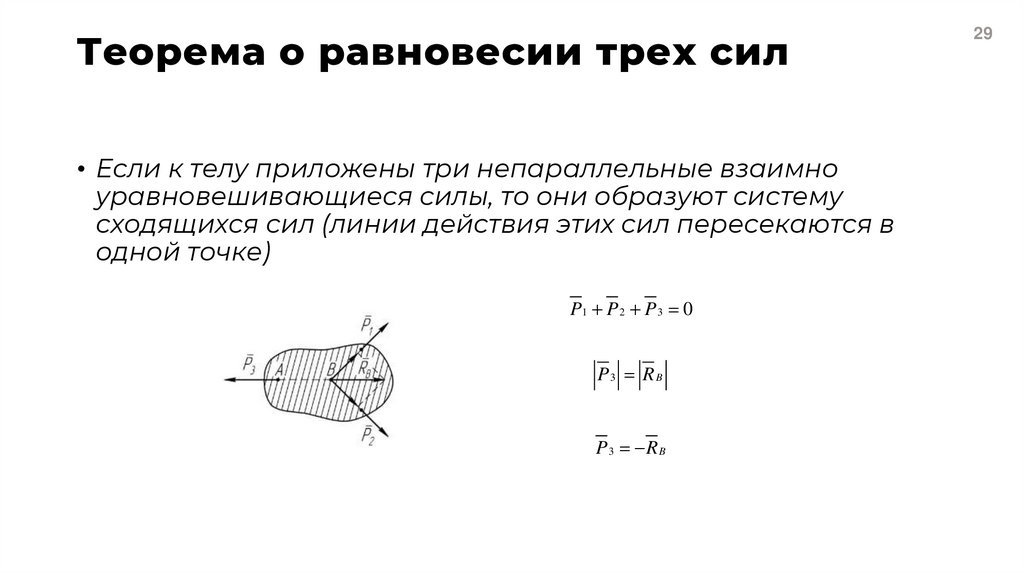
29. Теорема о равновесии трех сил

• Если к телу приложены три непараллельные взаимно
уравновешивающиеся силы, то они образуют систему
сходящихся сил (линии действия этих сил пересекаются в
одной точке)
P1 P 2 P 3 0
P3 R B
P3 R B
29

30. Пример.

Пример .
30
Определить реакцию в опоре балки
(точке A) весом G и натяжение нити BC.
С
Т
В
Т
RA
RA
G
А
G

31. Алгоритм решения задач на тему: «Равновесие системы сходящихся сил»

Задачи на равновесие твердого тела, находящегося под
действием системы сходящихся сил, рекомендуется решать в
следующем порядке:
1) Выделить тело, равновесие которого необходимо рассмотреть.
2) Изобразить активные (заданные) силы
3) Освободить тело от связей, приложив соответствующие
реакции.
4) Направить оси координат, указать необходимые углы, которые
силы составляют с осями.
5) Составить уравнения равновесия системы сходящихся сил.
6) Решить систему полученных уравнений относительно
неизвестных величин.
31

32.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра менеджмента в строительстве
Автор:
Нестерова Ольга Павловна
tehmeh@spbgasu.ru