Автоматизация конструкторско-технологического проектирования. Лекция 10

1. Автоматизация конструкторско-технологического проектирования

Автоматизация конструкторскотехнологического проектирования
Лекция 10
Размещение: постановка задачи
01

2.

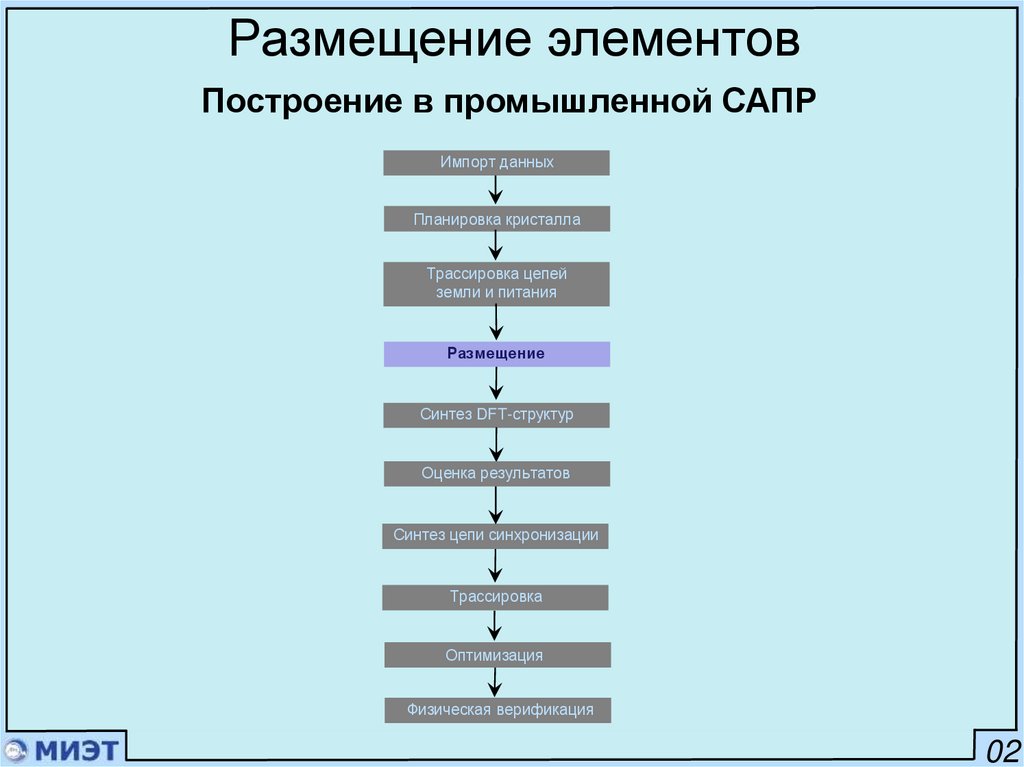
Размещение элементов
Построение в промышленной САПР
Импорт данных
Планировка кристалла
Трассировка цепей
земли и питания
Размещение
Синтез DFT-структур
Оценка результатов
Синтез цепи синхронизации
Трассировка
Оптимизация
Физическая верификация
02

3.

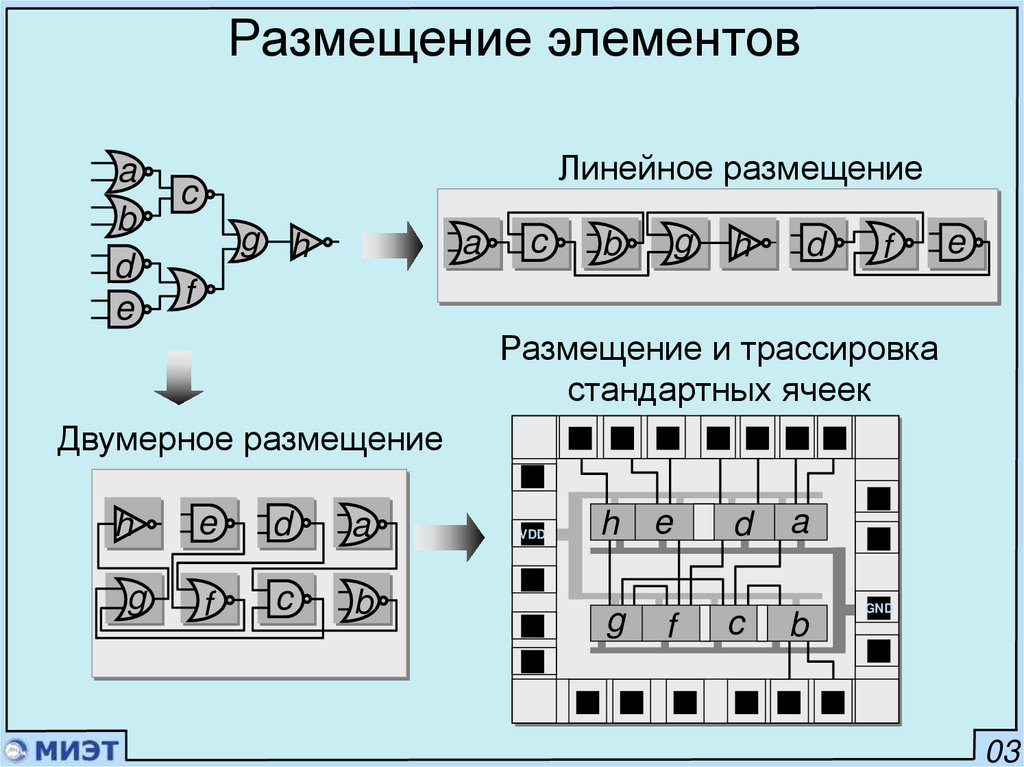
Размещение элементов
a
b
d
e
Линейное размещение
c
g h
a
c
g
b
h
d
f
e
f
Размещение и трассировка
стандартных ячеек
Двумерное размещение
h
e
d
a
g
f
c
b
VDD
h e
g
f
d
c
a
b
GND
03

4.

Актуальность задачи
Размещение – фундаментальная проблема физического
проектирования
Служит связующим звеном при топологическом
проектировании
Определяет структуру микросхемы
Проблемы с межсоединениями на глубоком субмикроне
– межсоединения в первую очередь определяются при
размещении → больше возможностей
Информация о размещении необходима и для планировки и
логического синтеза
Размерность задач размещения сильно возросла
Качество решений у существующих алгоритмов далеко от
оптимального (от 150% до 200% глобального оптимума)
04

5. Постановка задачи

Входная информация:
множество блоков (макро или стандартных ячеек) В: B1, ... , Bn
B=FB U MB, FB – фиксированные блоки, MB - неразмещенные
библиотека с формой элементов и положением терминалов
список цепей (гиперграф): N: N1, ... , Nm
Выходная информация:
Координаты (xi ,yi ) для каждого блока Bi.
Нет наложений между блоками
координаты терминалов или I/O (если не были назначены)
Необходимо:
Получить трассируемую схему с учетом функциональных и технических
ограничений (задержки, мощность, шумы)
Трудности:
Количество ячеек очень велико (>> 1 миллиона)
Временные ограничения крайне строгие
05

6.

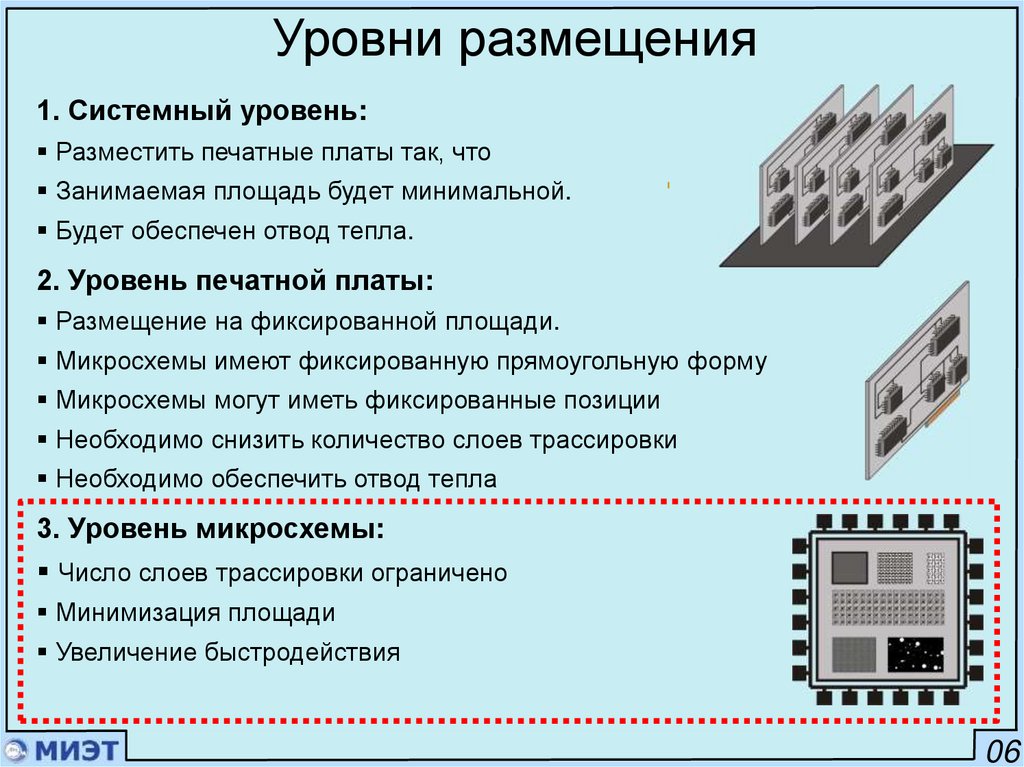
Уровни размещения
1. Системный уровень:
Разместить печатные платы так, что
Занимаемая площадь будет минимальной.
Будет обеспечен отвод тепла.
2. Уровень печатной платы:
Размещение на фиксированной площади.
Микросхемы имеют фиксированную прямоугольную форму
Микросхемы могут иметь фиксированные позиции
Необходимо снизить количество слоев трассировки
Необходимо обеспечить отвод тепла
3. Уровень микросхемы:
Число слоев трассировки ограничено
Минимизация площади
Увеличение быстродействия
06

7. Этапы размещения

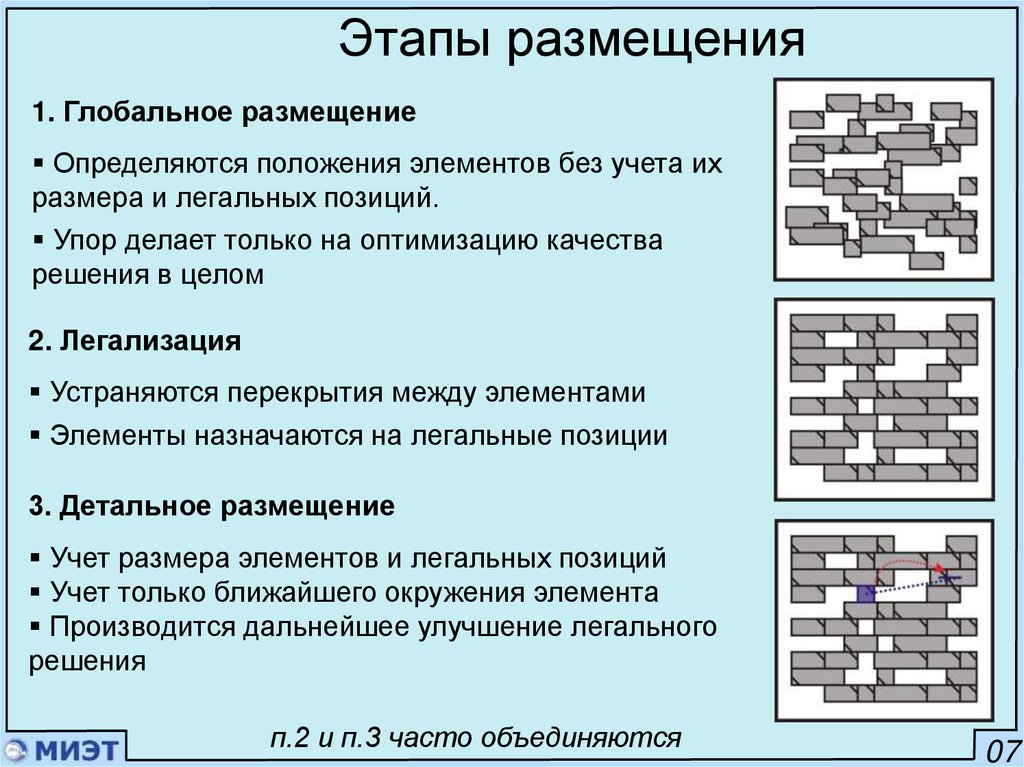
1. Глобальное размещение
Определяются положения элементов без учета их
размера и легальных позиций.
Упор делает только на оптимизацию качества
решения в целом
2. Легализация
Устраняются перекрытия между элементами
Элементы назначаются на легальные позиции
3. Детальное размещение
Учет размера элементов и легальных позиций
Учет только ближайшего окружения элемента
Производится дальнейшее улучшение легального
решения
п.2 и п.3 часто объединяются
07

8.

Стили проектирования
Заказное проектирование
Никаких ограничений на расположение
блоков
Минимизируется общая площадь
Минимизация площади мертвых областей
– Нерегулярность формы блоков –
основная причина мертвых областей
Для схем с высоким быстродействием
накладываются дополнительные ограничения
на длину цепи.
Минимизация общей площади иногда
конфликтует с критерием минимизации
максимальной длины цепи.
08

9.

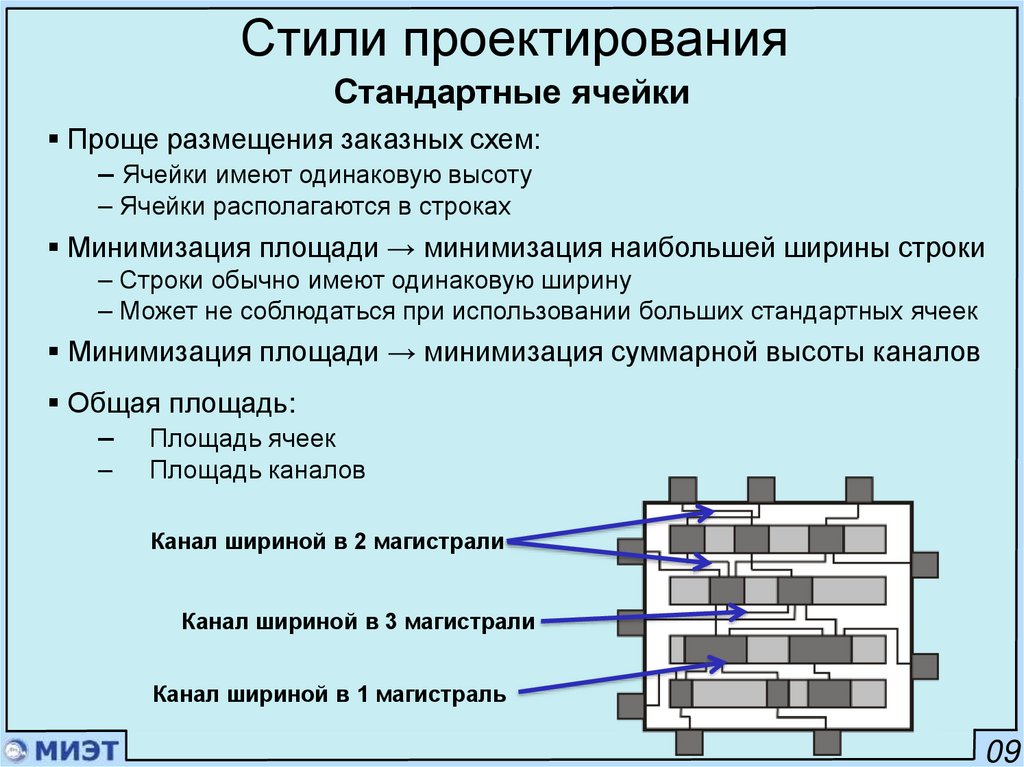
Стили проектирования
Стандартные ячейки
Проще размещения заказных схем:
– Ячейки имеют одинаковую высоту
– Ячейки располагаются в строках
Минимизация площади → минимизация наибольшей ширины строки
– Строки обычно имеют одинаковую ширину
– Может не соблюдаться при использовании больших стандартных ячеек
Минимизация площади → минимизация суммарной высоты каналов
Общая площадь:
– Площадь ячеек
–
Площадь каналов
Канал шириной в 2 магистрали
Канал шириной в 3 магистрали
Канал шириной в 1 магистраль
09

10.

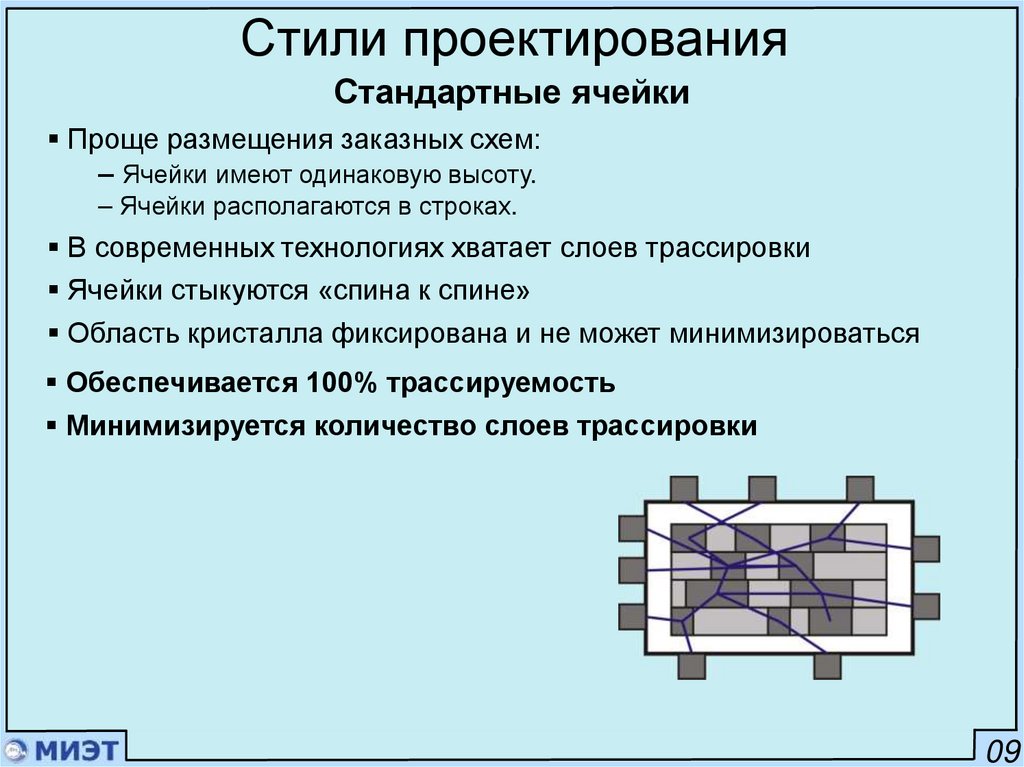
Стили проектирования
Стандартные ячейки
Проще размещения заказных схем:
– Ячейки имеют одинаковую высоту.
– Ячейки располагаются в строках.
В современных технологиях хватает слоев трассировки
Ячейки стыкуются «спина к спине»
Область кристалла фиксирована и не может минимизироваться
09

11.

Стили проектирования
Стандартные ячейки
Проще размещения заказных схем:
– Ячейки имеют одинаковую высоту.
– Ячейки располагаются в строках.
В современных технологиях хватает слоев трассировки
Ячейки стыкуются «спина к спине»
Область кристалла фиксирована и не может минимизироваться
Обеспечивается 100% трассируемость
Минимизируется количество слоев трассировки
09

12.

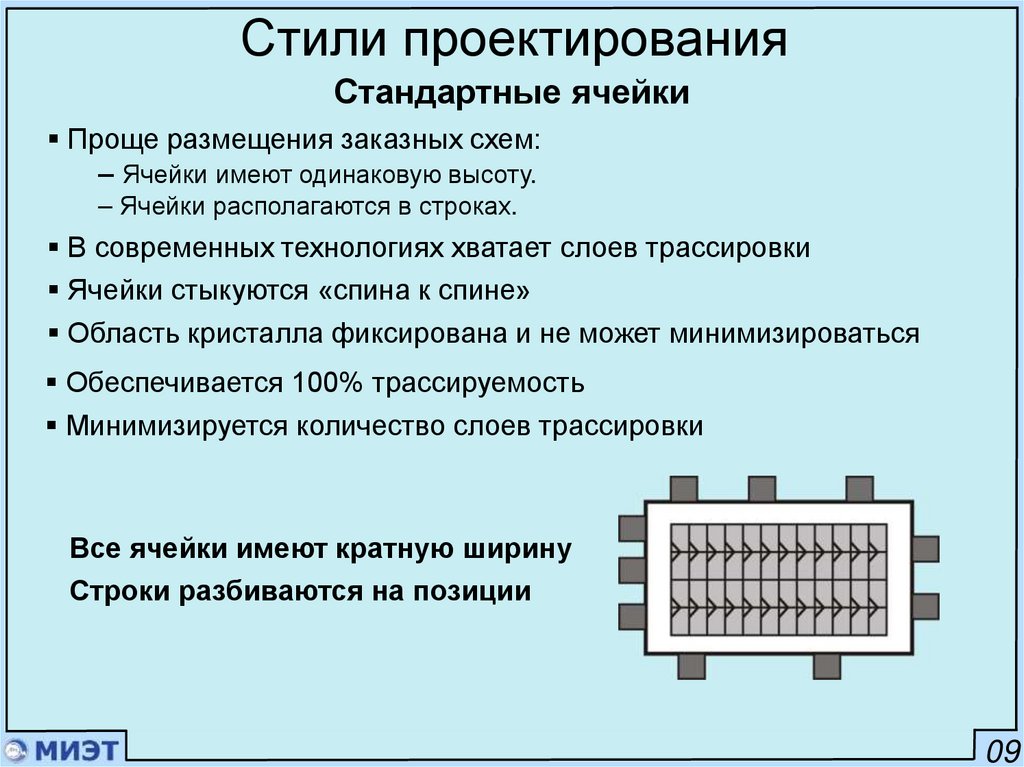
Стили проектирования
Стандартные ячейки
Проще размещения заказных схем:
– Ячейки имеют одинаковую высоту.
– Ячейки располагаются в строках.
В современных технологиях хватает слоев трассировки
Ячейки стыкуются «спина к спине»
Область кристалла фиксирована и не может минимизироваться
Обеспечивается 100% трассируемость
Минимизируется количество слоев трассировки
Все ячейки имеют кратную ширину
Строки разбиваются на позиции
09

13.

Стили проектирования
Вентильная матрица, БМК
Уже имеется произведенная логика:
A
C
Ограниченная площадь трассировки
B
Необходимо обеспечить трассируемость в
ограниченном пространстве
Минимизация площади трассировки не
важна
C
A
B
10

14.

Размещение элементов
Без предварительной планировки
+ Хорошее качество оптимизации
+ Не требовательно к методологии
САПР
– Занимает много памяти
– Долго проектировать
– Небольшие изменения
затрагивают всю схему
11

15.

Размещение элементов
С планировкой кристалла
Схема нарезается на меньшие части
+ Блоки могут работать параллельно:
улучшенная производительность
+ Свобода для контроля размещения
+ Предоставляет сведения о
критических цепях
+ Проще перепроектировать
+ Поздние изменения меньше влияют
на всю схему
12

16.

Размещение элементов
С планировкой кристалла
Схема нарезается на меньшие части
– Результат зависит от иерархии
– Дополнительные требования к
методологии
– Затрудняет работу САПР
– Поздние изменения могут затронуть
много компонент
12

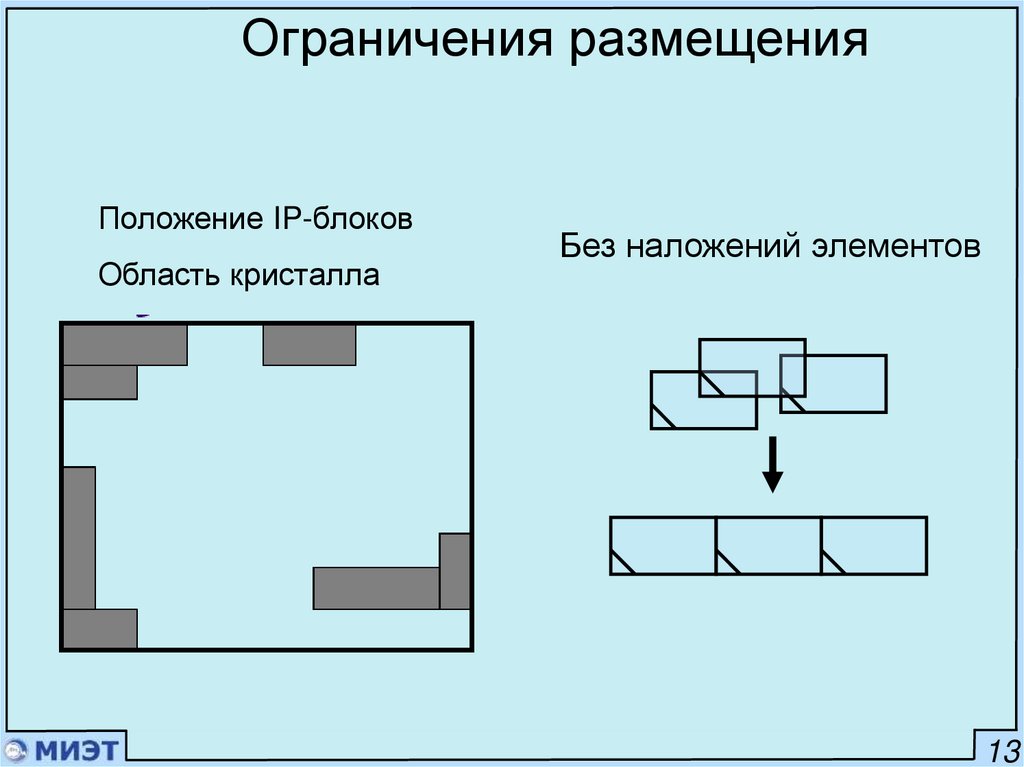
17. Ограничения размещения

Положение IP-блоков
Область кристалла
Без наложений элементов
13

18.

Строение алгоритмов размещения
Четыре составляющих алгоритма
1. Используемый алгоритм
FM, квадратичное, моделирование отжига, ….
2. Используемая целевая функция
Разрез, длина цепей, перегруженность, число пересечений …
3. Гранулярность списка цепей (кластеризация)
4. Детализация топологической модели
2x2, 4x4, ….
Выбирается удачное соотношение вышеперечисленного
Надо вовремя переключаться с одного на другое.
14

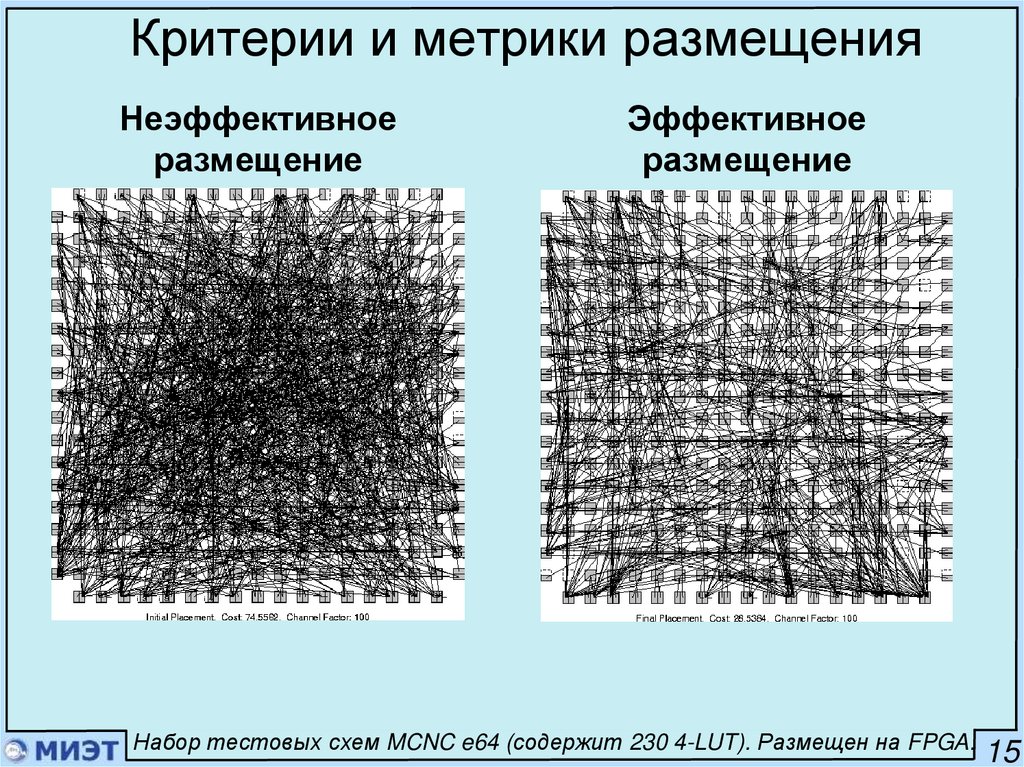
19. Критерии и метрики размещения

Неэффективное
размещение
Эффективное
размещение
Набор тестовых схем MCNC e64 (содержит 230 4-LUT). Размещен на FPGA.
15

20. Критерии и метрики размещения

Критерии размещения
Неэффективное размещение
– Занимает большую площадь
– Приводит к проблемам
трассировки
– Приводит к ухудшению
производительности
– Плохо размещенная схема не
может быть улучшена
высококлассным
трассировщиком
Эффективное размещение
+ Минимизирована площадь
(суммарная площадь трассировки)
+ Обеспечена трассируемость
+ Целостность сигналов
+ Решены проблемы
тепловыделения
+ Максимальная
производительность
16

21. Критерии и метрики размещения

Предсказание характеристик схемы
Имеются критические целевые функции:
– площадь,
– длина цепей,
– перегруженность,
– задержки, …
Предсказание стремится оценить значения целевых
функций без полного проектирования системы.
Позволяет быстро обходить область решений, локализует
поиск
Пример:
– Статистические wire-load модели
– Длина цепей при размещении
17

22. Критерии и метрики размещения

Предсказание характеристик схемы
Две фундаментальных парадигмы:
Статистическое предсказание
# 2-терминальных цепей в любой схеме
# 2-терминальных цепей с длиной больше 10 в любой схеме
Конструктивное предсказание
# 2-терминальных цепей с длиной больше 10 в текущей схеме
# критических 2-терминальных цепей в текущей схеме, на
основе статистических данных и быстрого анализа структуры
схемы.
“Абсолютное знание характеристик”
или
“Мне нужно просто улучшить решение”
18

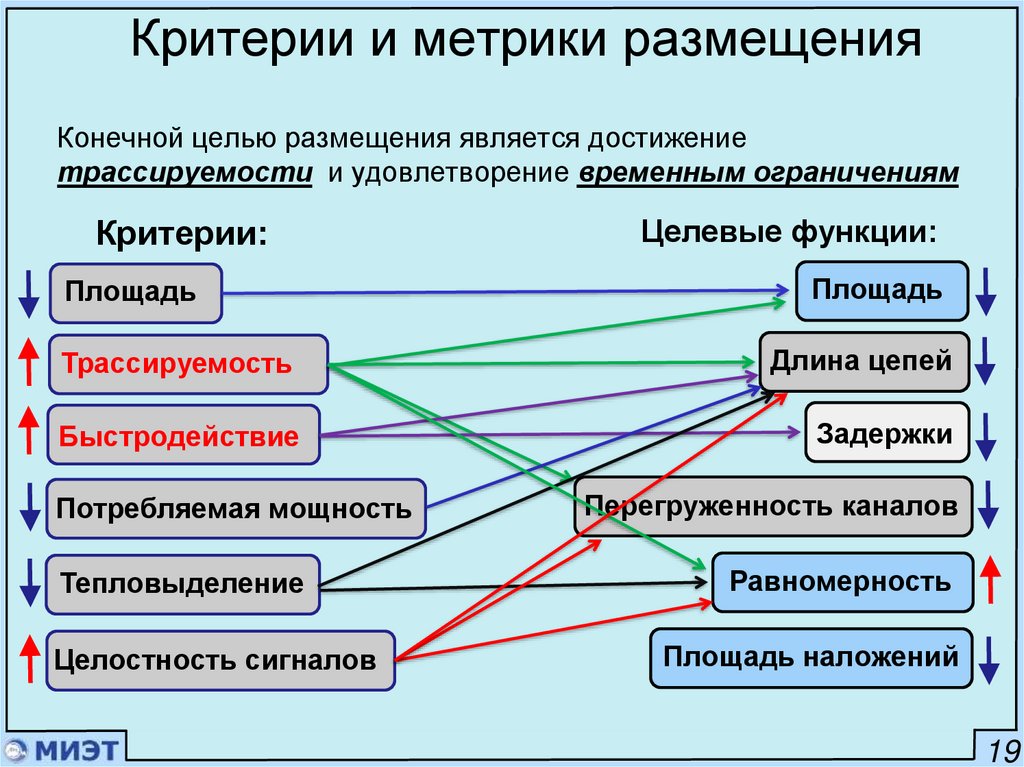
23. Критерии и метрики размещения

Конечной целью размещения является достижение
трассируемости и удовлетворение временным ограничениям
Критерии:
Площадь
Целевые функции:
Площадь
Трассируемость
Длина цепей
Быстродействие
Задержки
Потребляемая мощность
Тепловыделение
Целостность сигналов
Перегруженность каналов
Равномерность
Площадь наложений
19

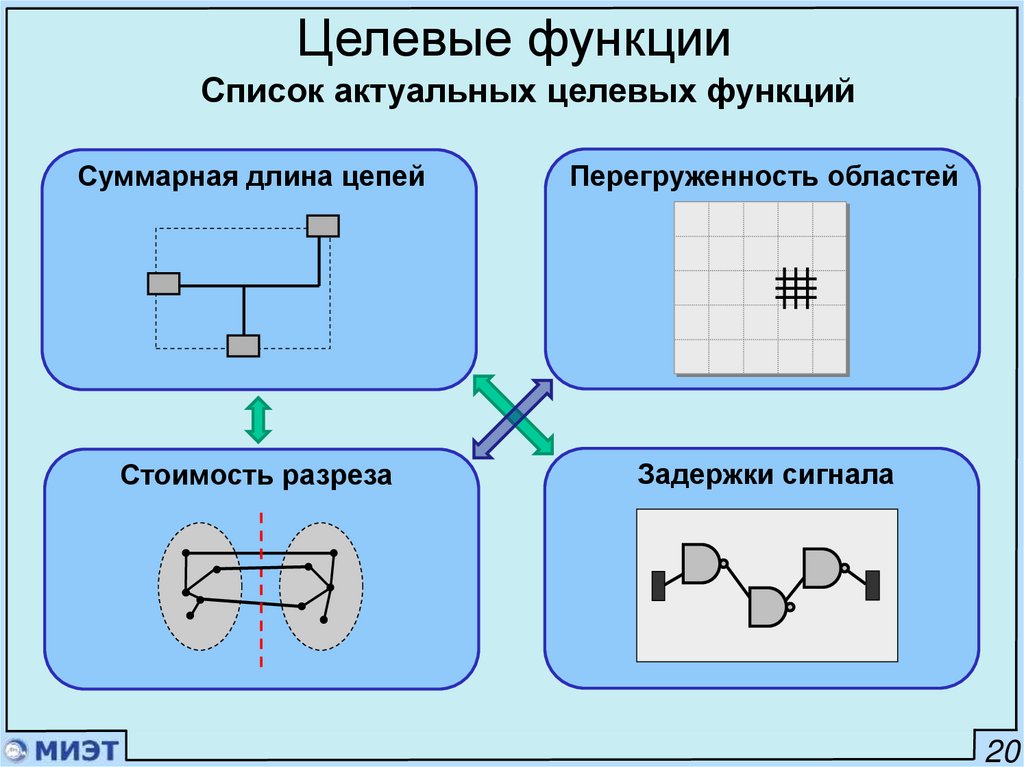
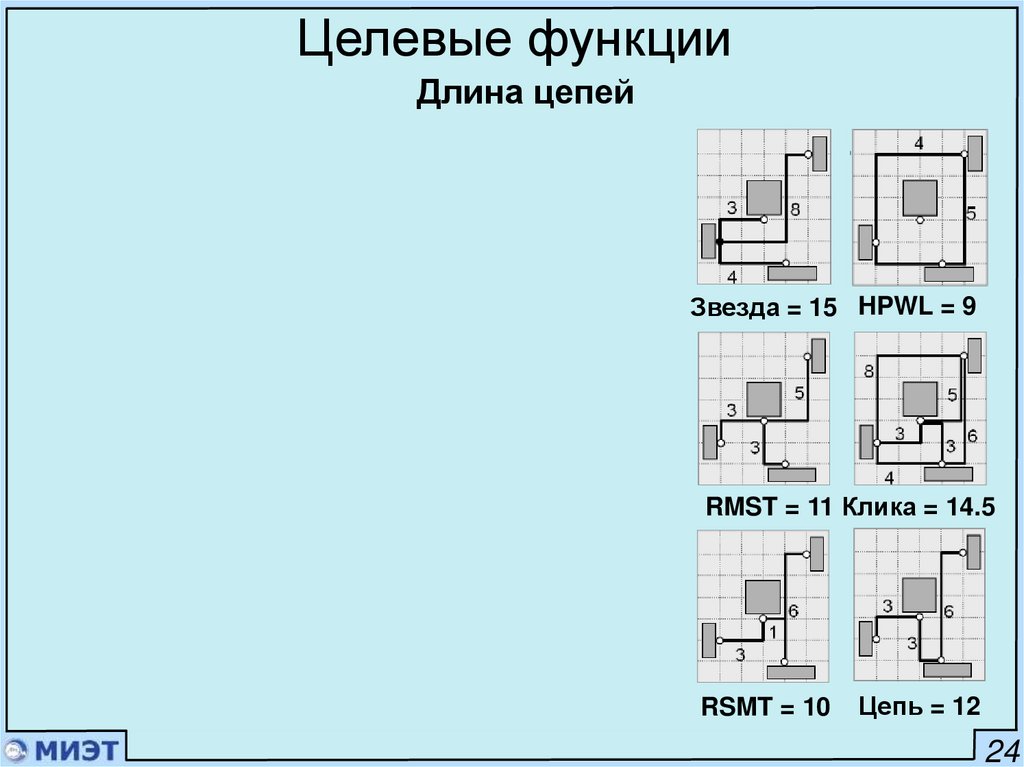
24.

Целевые функции
Список актуальных целевых функций
Суммарная длина цепей
Перегруженность областей
Стоимость разреза
Задержки сигнала
20

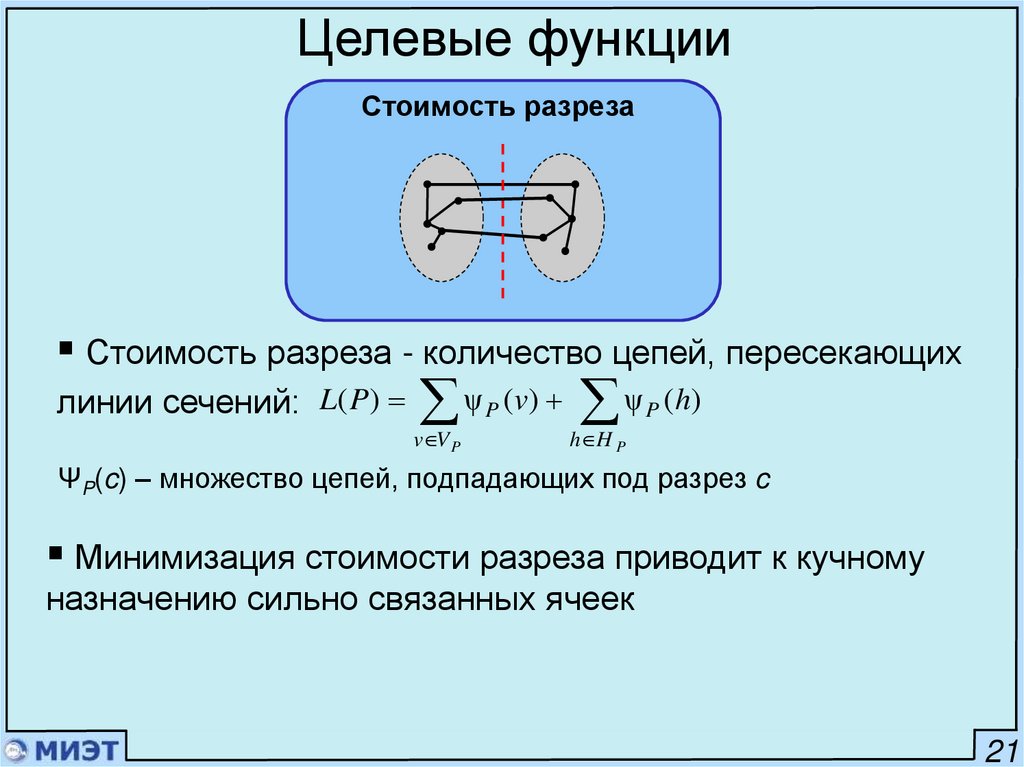
25.

Целевые функции
Стоимость разреза
Стоимость разреза - количество цепей, пересекающих
линии сечений: L( P)
ψ (v ) ψ ( h )
P
v V P
P
h H P
ΨP(c) – множество цепей, подпадающих под разрез c
Минимизация стоимости разреза приводит к кучному
назначению сильно связанных ячеек
21

26.

Целевые функции
Стоимость разреза
Пример расчета:
Цепи
N1 = (a1, b1, d2)
N2 = (c1, d1, f1)
N3 = (e1, f2)
Стоимость разрезов
ψP(v1) = 1 ψP(v2) = 2
ψP(h1) = 3 ψP(h2) = 2
Общее число пересечений в P
ψP(v1) + ψP(v2) + ψP(h1) + ψP(h2) =
=1+2+3+2=8
Стоимости разреза
X(P) = max(ψP(v1),ψP(v2)) = max(1,2) = 2
Y(P) = max(ψP(h1),ψP(h2)) = max(3,2) = 3
22

27.

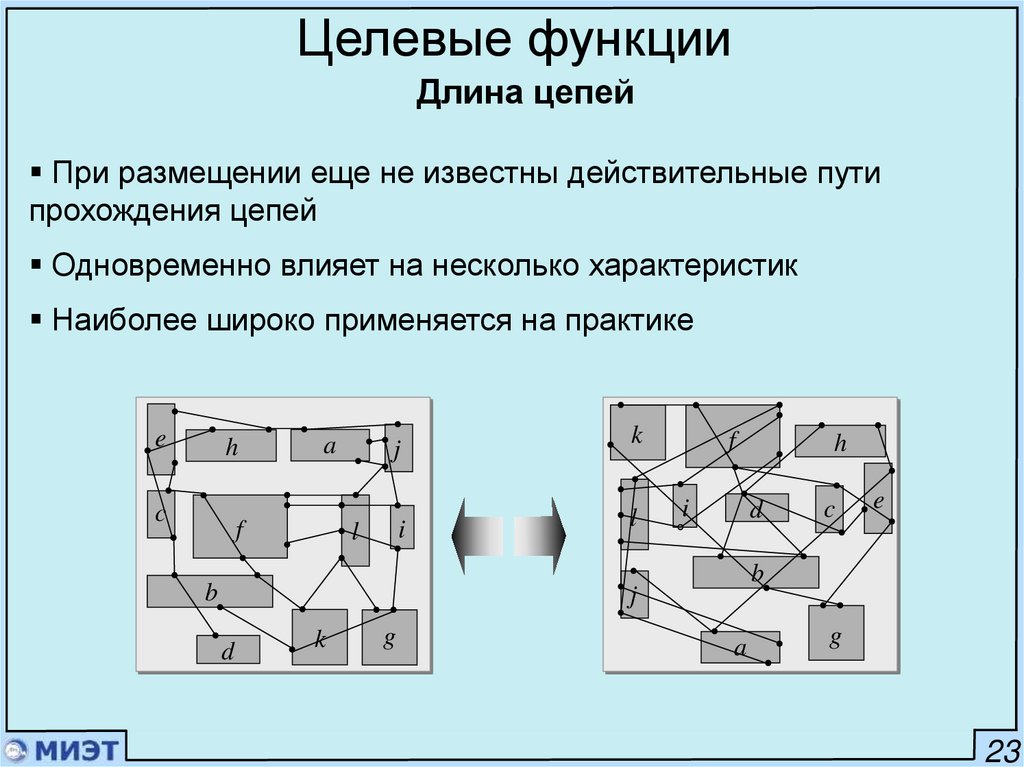
Целевые функции
Длина цепей
При размещении еще не известны действительные пути
прохождения цепей
Одновременно влияет на несколько характеристик
Наиболее широко применяется на практике
e
h
c
a
f
j
i
l
b
k
l
f
i
d
k
g
c
e
b
j
d
h
a
g
23

28.

Целевые функции
Длина цепей
Способы оценки:
1. Полупериметр охватывающего прямоугольника (HPWL – Half
Perimeter Wire Length)
Самый быстрый способ оценки
Суммарная ошибка ~8%
HPWL = 9
24

29.

Целевые функции
Длина цепей
Способы оценки:
2. Полный граф (клика)
Среднее быстродействие
Сокращает максимальную длину
Клика = (2/p) e Cl dM(e) = 14.5
HPWL = 9
24

30.

Целевые функции
Длина цепей
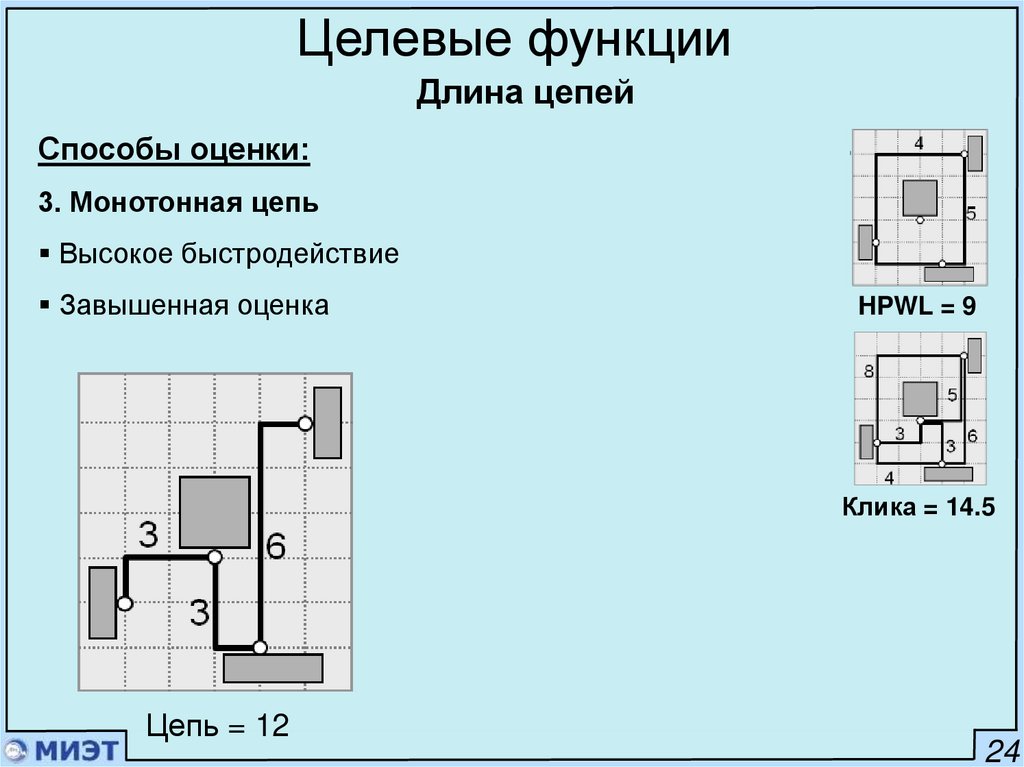
Способы оценки:
3. Монотонная цепь
Высокое быстродействие
Завышенная оценка
HPWL = 9
Клика = 14.5
Цепь = 12
24

31.

Целевые функции
Длина цепей
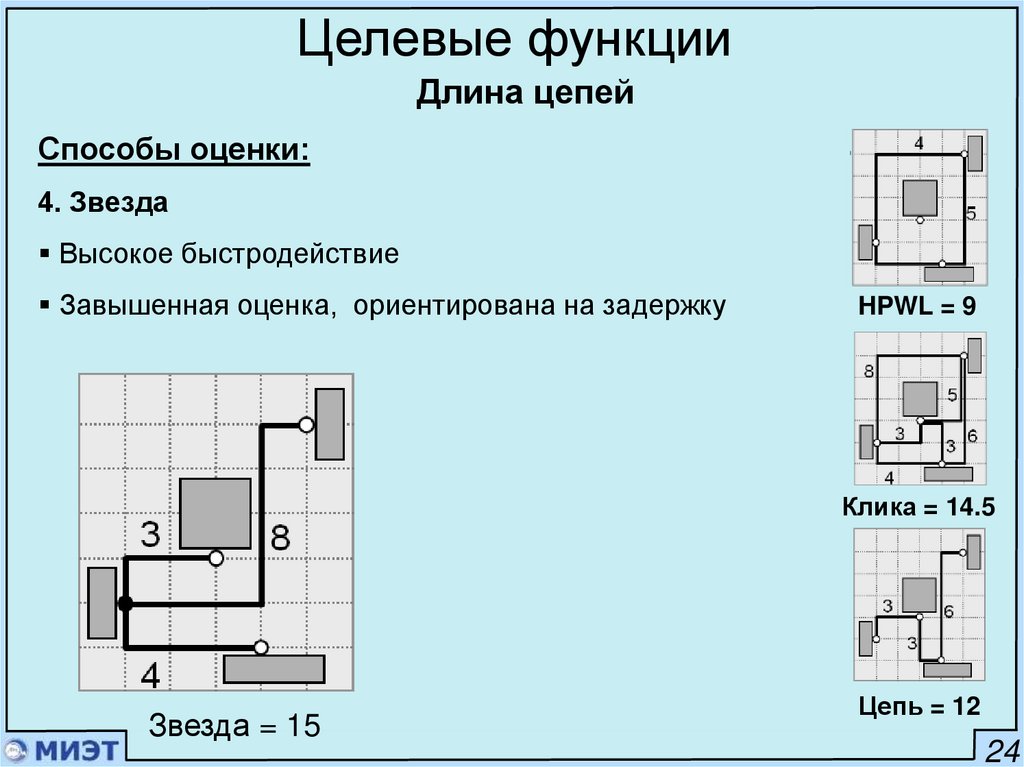
Способы оценки:
4. Звезда
Высокое быстродействие
Завышенная оценка, ориентирована на задержку
HPWL = 9
Клика = 14.5
Звезда = 15
Цепь = 12
24

32.

Целевые функции
Длина цепей
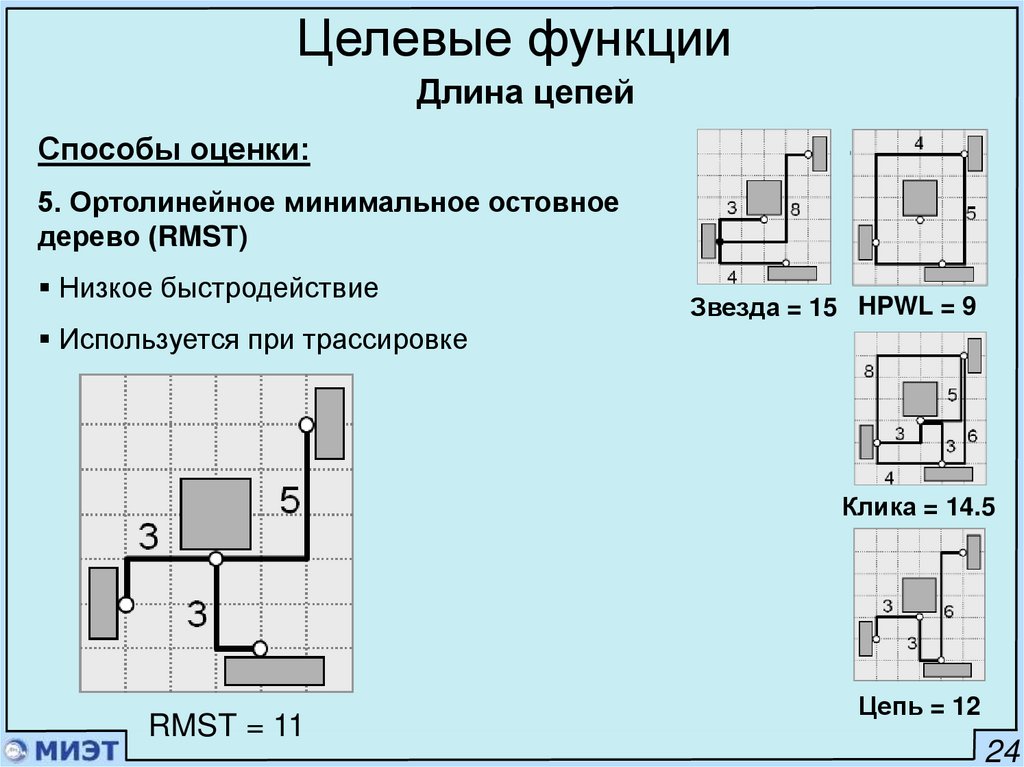
Способы оценки:
5. Ортолинейное минимальное остовное
дерево (RMST)
Низкое быстродействие
Звезда = 15 HPWL = 9
Используется при трассировке
Клика = 14.5
RMST = 11
Цепь = 12
24

33.

Целевые функции
Длина цепей
Способы оценки:
6. Ортолинейное минимальное дерево
Штейнера(RSMT)
Низкое – очень низкое быстродействие
Звезда = 15 HPWL = 9
Используется при трассировке (очень точное)
RMST = 11 Клика = 14.5
RSMT = 10
Цепь = 12
24

34.

Целевые функции
Длина цепей
Звезда = 15 HPWL = 9
RMST = 11 Клика = 14.5
RSMT = 10
Цепь = 12
24

35.

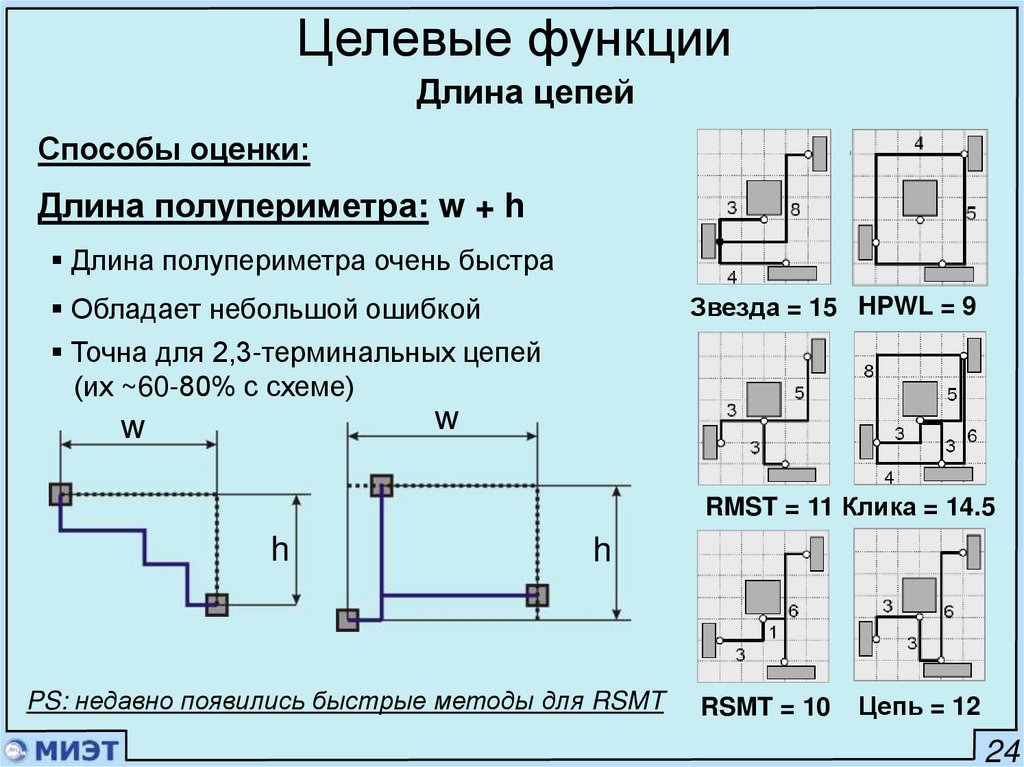
Целевые функции
Длина цепей
Способы оценки:
Длина полупериметра: w + h
Длина полупериметра очень быстра
Звезда = 15 HPWL = 9
Обладает небольшой ошибкой
Точна для 2,3-терминальных цепей
(их ~60-80% с схеме)
w
w
RMST = 11 Клика = 14.5
h
h
PS: недавно появились быстрые методы для RSMT
RSMT = 10
Цепь = 12
24

36.

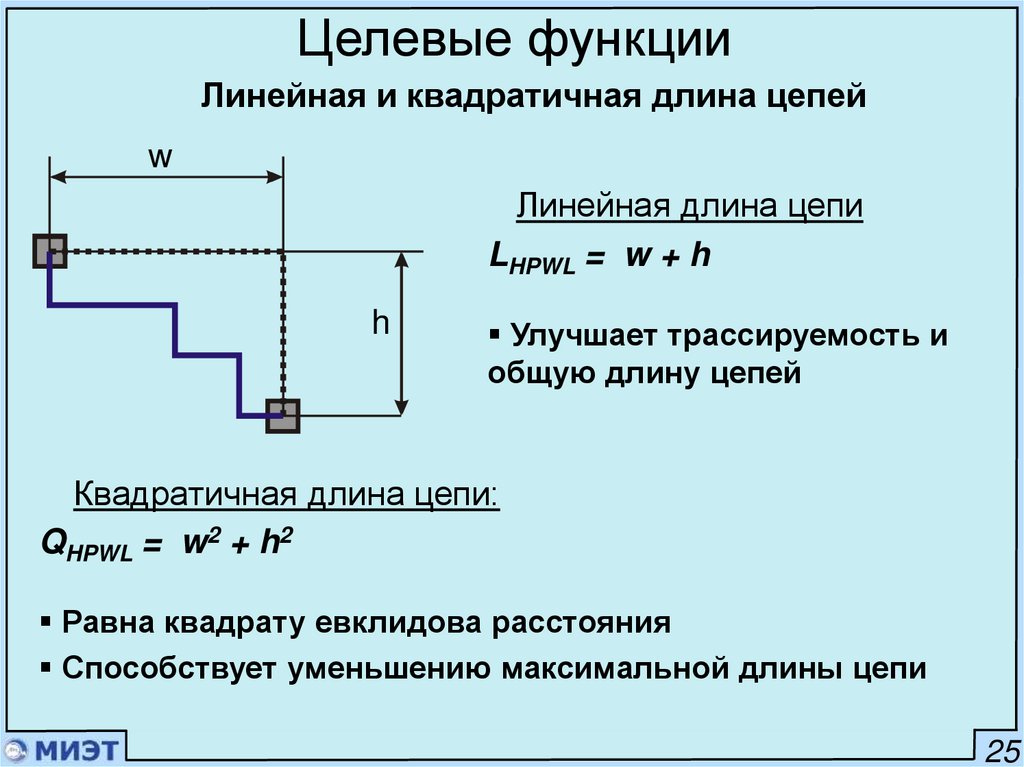
Целевые функции
Линейная и квадратичная длина цепей
w
Линейная длина цепи
LHPWL = w + h
h
Улучшает трассируемость и
общую длину цепей
Квадратичная длина цепи:
QHPWL = w2 + h2
Равна квадрату евклидова расстояния
Способствует уменьшению максимальной длины цепи
25

37.

Целевые функции
Суммарная взвешенная длина цепей
Для заданного размещения P оценкой суммарной
взвешенной длины цепей будет
L( P) w(n) L(n)
n P
w(n) – вес цепи n, L(n) – оценка длины цепи n
Пример:
a
Цепи
Веса
N1 = (a1, b1, d2)
w(N1) = 2
N2 = (c1, d1, f1)
w(N2) = 4
N3 = (e1, f2)
w(N3) = 1
L( P )
b
a1
c
c1
d1
d
d2
b1
f1 f
f2
e1
e
w(net) L(net) 2 7 4 4 1 3 33
net P
26

38.

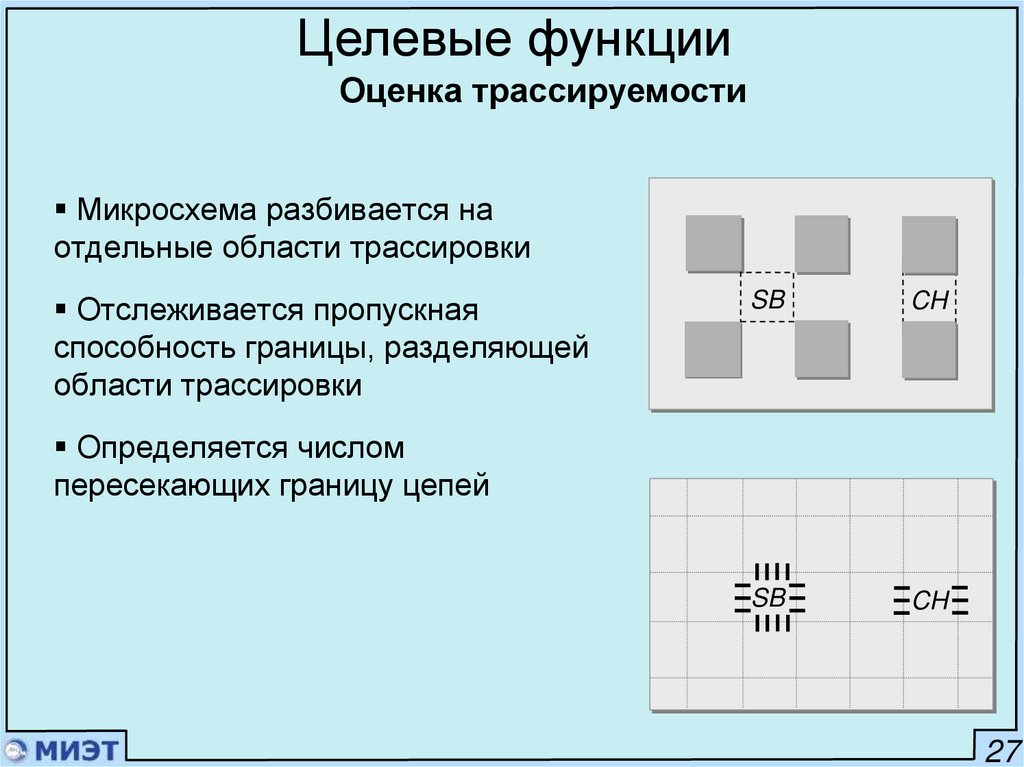
Целевые функции
Оценка трассируемости
Микросхема разбивается на
отдельные области трассировки
Отслеживается пропускная
способность границы, разделяющей
области трассировки
SB
CH
SB
CH
Определяется числом
пересекающих границу цепей
27

39.

Целевые функции
Оценка трассируемости
Микросхема разбивается на
отдельные области трассировки
Отслеживается пропускная
способность границы, разделяющей
области трассировки
Определяется числом
пересекающих границу цепей
Составляется модель областей в
виде графа
глобальная ячейка
1/2
1/2
0/2
0/2
2/2
2/2
0/2
0/2
Ребрам назначается емкость и
число проходящих цепей
28

40.

Целевые функции
Оценка трассируемости
1. Плотность цепей
Локальная плотность φP(e) ребра e между глобальными ячейками:
φ P (e)
η P (e)
σ P (e)
ηP(e) – количество пересекающих e цепей
σP(e) – емкость e (максимальное число цепей)
Если φP(e) > 1, то размещение P считается нетрассируемым
29

41.

Целевые функции
Оценка трассируемости
1. Плотность цепей
Локальная плотность φP(e) ребра e между глобальными ячейками:
φ P (e)
η P (e)
σ P (e)
ηP(e) – количество пересекающих e цепей
σP(e) – емкость e (максимальное число цепей)
Если φP(e) > 1, то размещение P считается нетрассируемым
Плотность цепей у P равна ( P) max φ P (e)
e E
E – множество всех ребер
Если Φ(P) < 1, тогда схема полностью трассируема,
Иначе (Φ(P) 1) при трассировке цепям придется обходить по
менее перегруженным ребрам
30

42.

Целевые функции
Оценка трассируемости
Пример оценки плотности цепей:
v3
ηP(h1) = 1
ηP(h2) = 2
ηP(h3) = 0
ηP(h4) = 1
ηP(h5) = 1
ηP(h6) = 0
ηP(v1) = 1
ηP(v2) = 0
ηP(v3) = 0
ηP(v4) = 0
ηP(v5) = 2
ηP(v6) = 0
Максимум: ηP(e) = 2
h4
v6
h6
h5
v2
v5
h1
h3
h2
σP(e) = 3
( P)
η P ( e) 2
σ P ( e) 3
v1
v4
Трассируемо
31

43.

Целевые функции
Оценка трассируемости
1. Перегруженность областей трассировки
ηP(e) – σP(e) , если ηP(e) > σP(e)
O(e) =
0
, если ηP(e) ≤ σP(e)
ηP(e) – количество пересекающих e цепей
σP(e) – емкость e (максимальное число цепей)
Если O(e)>0, то размещение считается нетрассируемым
32

44.

Целевые функции
Оценка трассируемости
1. Перегруженность областей трассировки
ηP(e) – σP(e) , если ηP(e) > σP(e)
O(e) =
0
, если ηP(e) ≤ σP(e)
ηP(e) – количество пересекающих e цепей
σP(e) – емкость e (максимальное число цепей)
Если O(e)>0, то размещение считается нетрассируемым
Перегруженность цепей у P равна O(P)=∑ O(e)
e E
E – множество всех ребер
Если O(P) = 0, тогда схема полностью трассируема,
Иначе (O(P) > 0) при трассировке цепям придется обходить
по менее перегруженным ребрам
32

45.

Целевые функции
Оценка трассируемости
Пример оценки перегруженности цепей:
O(e) = σP(e) - ηP(h1)
v3
σP(e) = 3
ηP(h1) = 1
O(h1) = 0
ηP(v1) = 1
O(v1) = 0
ηP(h2) = 2
O(h2) = 0
ηP(v2) = 0
O(v2) = 0
ηP(h3) = 0
O(h3) = 0
ηP(v3) = 0
O(v3) = 0
ηP(h4) = 1
O(h4) = 0
ηP(v4) = 0
O(v4) = 0
ηP(h5) = 1
O(h5) = 0
ηP(v5) = 2
O(v5) = 0
ηP(h6) = 0
O(h6) = 0
ηP(v6) = 0
O(v6) = 0
h4
v6
h6
h5
v2
v5
h1
h3
h2
v1
O(P)=∑ O(e) = 0
e E
v4
Трассируемо
33

46.

Целевые функции
Перегруженность и длина цепей
Замечено, что минимизация длины позволяет сократить
перегруженность.
Вывод: не всегда утверждение верно
– Все равно придется искать баланс между величинами
Минимизирована
перегруженность
Минимизирована
длина цепей
34

47.

Целевые функции
Целевые функции для перегруженности
WL: Стандартная длина цепей.
Перегруж: Суммарное переполнение ребер (прямая оценка).
Гибрид: (1- a)∙WL + a∙Перегруж
QL: Квадратичное плюс линейная функция.
LQ: Линейная плюс квадратичная функция.
СмВпрд: Модифицированная перегруженность (с просмотром вперед).
(1- aT)∙WL + aT∙Перегруж : Изменяющийся со временем гибрид
– позволяет изменять приоритет от длины цепей к перегруженности
по мере оптимизации.
Минимизация длины цепей может глобально минимизировать перегруженность.
Пост-обработка с минимизацией перегруженности и минимизация длины цепей
работает лучше всего.
35

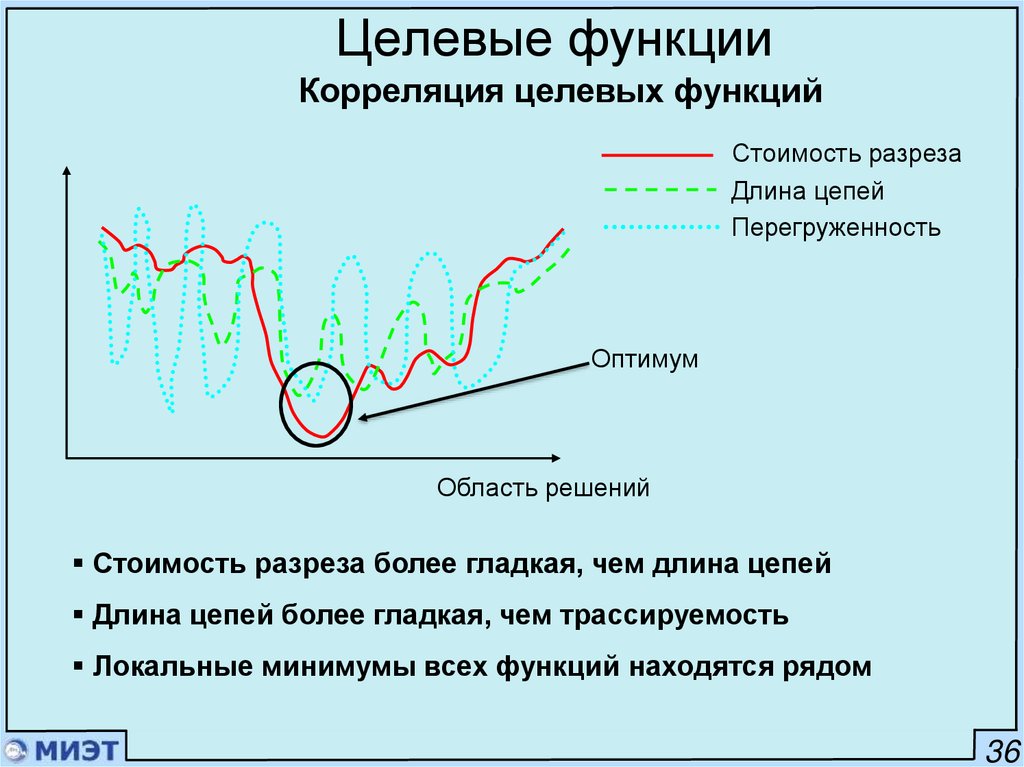
48. Целевые функции

Корреляция целевых функций
Стоимость разреза
Длина цепей
Перегруженность
Оптимум
Область решений
Стоимость разреза более гладкая, чем длина цепей
Длина цепей более гладкая, чем трассируемость
Локальные минимумы всех функций находятся рядом
36

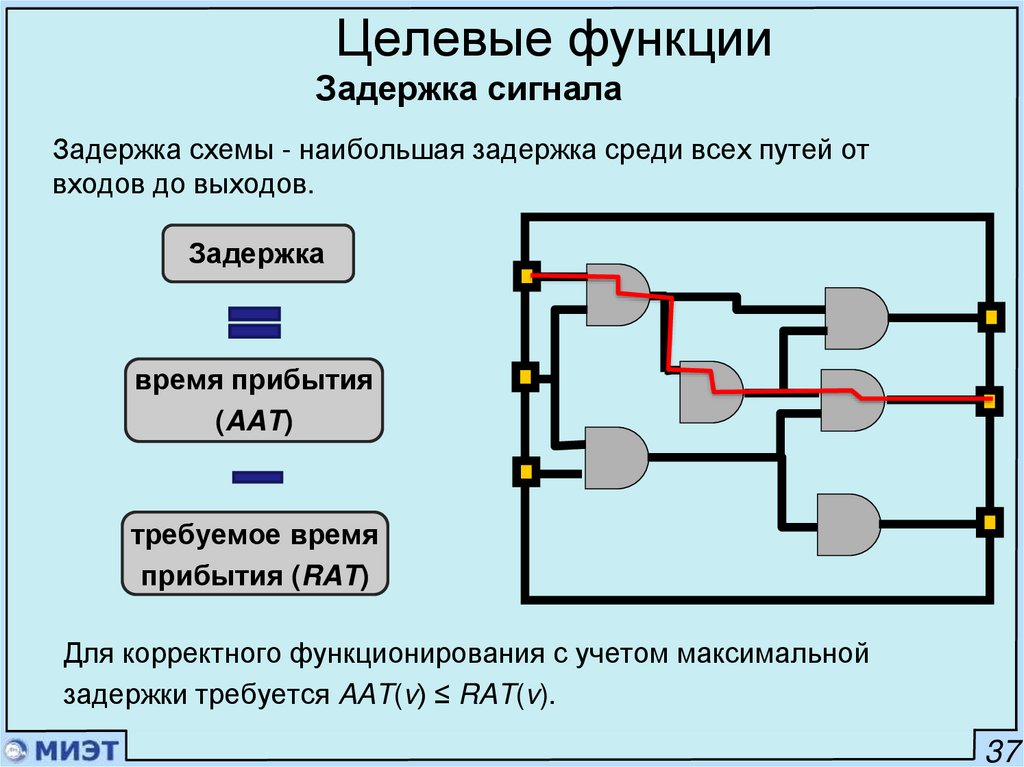
49. Целевые функции

Задержка сигнала
Задержка схемы - наибольшая задержка среди всех путей от
входов до выходов.
Задержка
время прибытия
(AAT)
требуемое время
прибытия (RAT)
Для корректного функционирования с учетом максимальной
задержки требуется AAT(v) ≤ RAT(v).
37

50.

Размещение элементов
Другие целевые функции
Используемая мощность.
– Взвешенные цепи
– Двойное напряжение (тяжелое ограничение при размещении)
Тепловыделение.
– Плотность размещения элементов
– Для точной оценки:
переключательная активность
паразитные элементы
информация из библиотеки
– Для быстрой оценки:
размер элемента ~ мощность
длина подключенных цепей
38

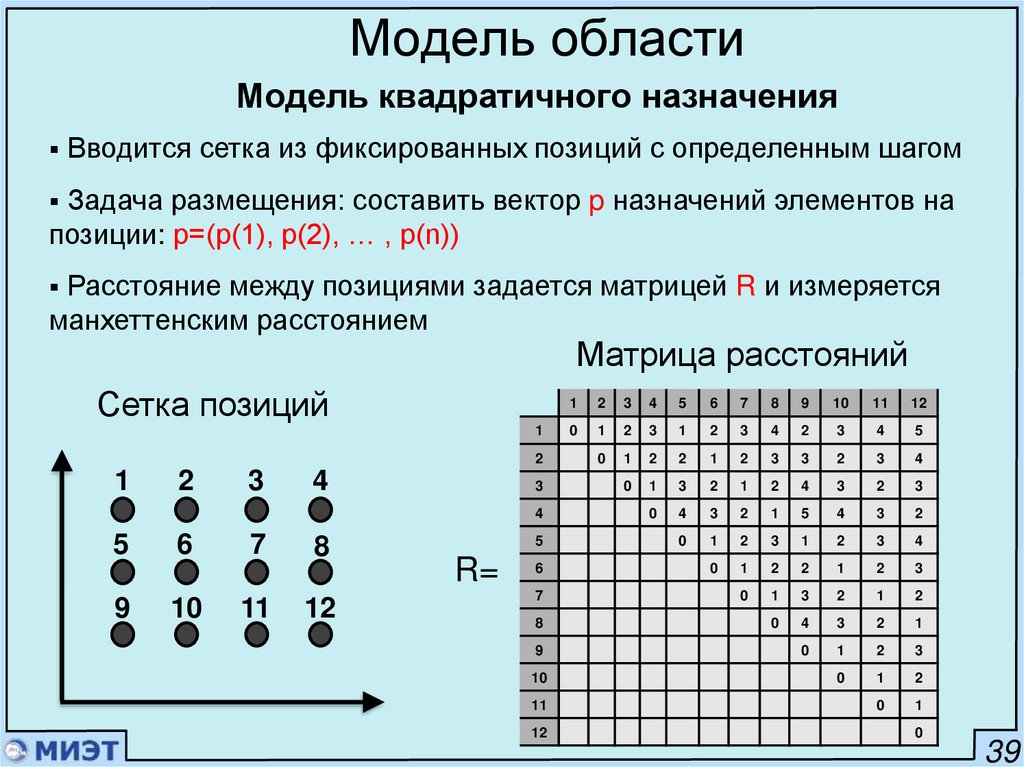
51. Модель области

Модель квадратичного назначения
Вводится сетка из фиксированных позиций с определенным шагом
Задача размещения: составить вектор p назначений элементов на
позиции: p=(p(1), p(2), … , p(n))
Расстояние между позициями задается матрицей R и измеряется
манхеттенским расстоянием
Матрица расстояний
Сетка позиций
1
2
1
2
3
4
3
4
5
9
6
10
7
11
8
12
5
R=
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
1
2
3
4
2
3
4
5
0
1
2
2
1
2
3
3
2
3
4
0
1
3
2
1
2
4
3
2
3
0
4
3
2
1
5
4
3
2
0
1
2
3
1
2
3
4
0
1
2
2
1
2
3
0
1
3
2
1
2
0
4
3
2
1
0
1
2
3
0
1
2
0
1
0
39

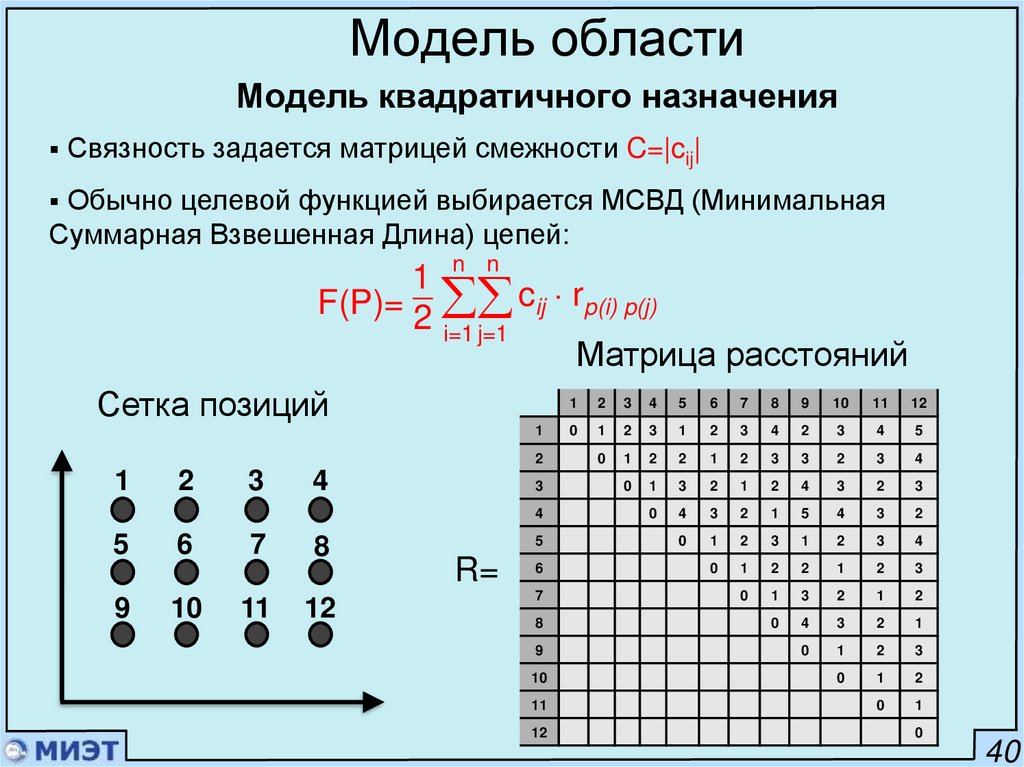
52. Модель области

Модель квадратичного назначения
Связность задается матрицей смежности C=|cij|
Обычно целевой функцией выбирается МСВД (Минимальная
Суммарная Взвешенная Длина) цепей:
n n
1
_
F(P)= 2 cij rp(i) p(j)
i=1 j=1
Матрица расстояний
1 2 3 4
5
6
7
8
9
10
11
12
Сетка позиций
1
2
1
2
3
4
3
4
5
9
6
10
7
11
8
12
5
R=
6
7
8
9
10
11
12
0
1
2
3
1
2
3
4
2
3
4
5
0
1
2
2
1
2
3
3
2
3
4
0
1
3
2
1
2
4
3
2
3
0
4
3
2
1
5
4
3
2
0
1
2
3
1
2
3
4
0
1
2
2
1
2
3
0
1
3
2
1
2
0
4
3
2
1
0
1
2
3
0
1
2
0
1
0
40

53.

Алгоритмы размещения
Алгоритмы глобального размещения
Основные классы алгоритмов:
Дихотомические алгоритмы:
Список цепей и топология разделяются на меньшие части
Процесс повторяется, пока каждая подсхема и подобласть не
будут насколько малы, чтобы быть разрешены оптимально
Аналитические алгоритмы:
Моделируют задачу размещения при помощи целевой
функции, которая может быть оптимизирована численным
анализом
Стохастические алгоритмы:
Случайные изменения помогают при движении в гору,
используются при оптимизации целевой функции
41

54.

Лекция окончена
42