Управление машинными экспериментами. Лекция №10

1. ЛЕКЦИЯ №10

Курс: Модели информационных процессов и систем
Тема: Управление машинными экспериментами.
1. Основные понятия теории планирования
2. Стратегическое планирование
3. Тактическое планирование
4. Проблема обеспечения точности и достоверности результатов
моделирования

2. 1. Основные понятия теории планирования

Эффективность машинных экспериментов существенно зависит от выбора
плана эксперимента, так как план определяет объем и порядок
проведения вычислений на ЭВМ, приемы накопления и статистической
обработки результатов моделирования искомой системы.
Основная задача планирования машинных экспериментов с имитационной
моделью заключается в том, чтобы получить необходимую информацию
об объекте моделирования, заданном в виде имитационной модели при
минимальных затратах машинных ресурсах.
Необходимо предусмотреть при разработке имитационной модели в том
числе и инструментальные средства, позволяющие планировать и
автоматически обрабатывать результаты экспериментов, сохраняя их в
базе данных.
Отметим следующие преимущества машинных экспериментов перед
натурными:
1. простота повторений условий эксперимента для альтернативных
вариантов с целью выбора более эффективного варианта,
2. возможность управления экспериментом, включая его прерывания и
возобновления,
3. возможность изменения условий воздействия внешней среды.
2

3. 1. Основные понятия теории планирования

Планирование экспериментов основано на представлении объекта как
“черного ящика”, т.е. в процессе исследования изучается влияние
входной переменной (фактора) x на выходную переменную (реакцию,
отклик) y.
x1
ОБЪЕКТ
y
“черный ящик”
xk
Имея на выходе соответствующие установившиеся значения y, полученные
из имитационной модели, формируем таблицу значений выходной
переменной y1,..., yN. Значения Х(i) и соответствующие им yi задают в
табличном виде искомую статистическую характеристику.
Для построения аналитического вида статистической характеристики могут
быть использованы соответствующие методы аппроксимации функции
нескольких переменных.
Введем ряд ключевых понятий, используемых в теории планирования.
3

4. 1. Основные понятия теории планирования

4
Факторное пространство
Факторное пространство - это множество внешних и внутренних параметров
модели, значение которых исследователь может контролировать в ходе
подготовки и проведения модельного эксперимента.
В общем случае факторы могут быть количественного и качественного вида.
Например, при оценке пользовательского интерфейса такими факторами может
быть цветовая палитра, степень подготовки пользователей и т.д.
Для факторов количественного вида числовые значения факторов называют
уровнями. Если при проведении эксперимента исследователь может изменять
уровни факторов, эксперимент называется активным, в противном случае –
пассивным.
Каждый из факторов имеет верхний и нижний уровни, расположенные симметрично
относительно некоторого нулевого уровня. Точка в факторном пространстве,
соответствующая нулевым уровням всех факторов, называется центром плана.
Интервалом варьирования фактора называется некоторое число J, прибавление
которого к нулевому уровню дает верхний уровень, а вычитание – нижний
уровень.

5. 1. Основные понятия теории планирования

Определенный вектор значений уровней варьируемых факторов задает одно из
возможных состояний рассматриваемой системы, и этому состоянию
соответствует определенная точка в многомерном факторном пространстве.
Функциональная связь между факторами и реакцией называется функцией
реакции (чаще называемой функцией реакции или функцией отклика), а
геометрический образ этой функции есть поверхность реакции (поверхность
отклика).
Как правило, план эксперимента строится относительно одного (основного)
выходного скалярного параметра Y, который называется наблюдаемой
переменной. Если моделирование используется как инструмент принятия
решений, то в роли наблюдаемой переменной выступает показатель
эффективности.
При этом предполагается, что значение наблюдаемой переменной, полученное в
ходе эксперимента, складывается из двух составляющих:
Y=f(x)+ e(x),
(5.1)
где f(x) – функция отклика
e(x) – ошибка эксперимента (случайная величина)
х – точка в факторном пространстве (определенное сочетание уровней факторов).
5

6. 1. Основные понятия теории планирования

6
1. Основные понятия теории планирования
В соответствии с формулой (5.1), имеем, что Y – случайная переменная, которая
зависит от случайной величины е. Дисперсия Dy наблюдаемой переменной,
которая характеризует точность измерений, равна дисперсии ошибки – Dy=De
Dy называют дисперсией воспроизводимости эксперимента. Она характеризует
качество эксперимента. Эксперимент называют идеальным при Dy=0.
Так как на значение величины Y оказывают влияние стохастические воздействия
разного рода, то форма связи между величинами X и Y определяется линией
регрессии, показывающей, как в среднем изменяется величина Y при изменении
входной величины X, и аппроксимирующая функция строится как функция
регрессии
f(X, B)= M[Y/X],
(6.1)
где B - неизвестные параметры уравнения регрессии,
M[Y/X]- математическое ожидание значения Y при изменении величины X.

7. 1. Основные понятия теории планирования

В общем случае к факторам предъявляются следующие требования:
1) факторами могут быть либо входные, либо режимные переменные и именно они
являются аргументами в искомой зависимости: y=f(X);
2) факторы есть количественные параметры, задаваемые численно в какой-либо
системе единиц;
3) для численных значений факторов должна быть задана допустимая область их
значений;
4) факторы должны быть линейно независимы.
Для выходных переменных необходимо соблюдение следующих условий.
1) уравнения связи между X и y должны быть разрешены относительно y и
являться однозначной функцией входных и режимных переменных, что
в свою очередь задает область определения выходных переменных;
2) выходные переменные должны быть линейно независимы между собой, в
случае если их несколько.
В дополнение к этим условиям необходимо, чтобы целевая функция
(сформированная из выходных переменных) была выражена количественно и
имела конкретный содержательный смысл.
7

8. 1. Основные понятия теории планирования

8
Существует два варианта постановки задачи планирования эксперимента:
1)из всех допустимых выбрать такой план, который позволял бы получить
наиболее достоверное значение функции отклика f(x) при
фиксированном числе опытов;
2) выбрать такой допустимый план, при котором статистическая оценка
функции отклика могла бы быть получена с заданной точностью при
минимальном объеме испытаний.
Решение задачи в первой постановке называется стратегическим
планированием, а во второй – тактическим планированием.

9. 2. Стратегическое планирование экспериментов

Цель стратегического планирования эксперимента – получение
максимального объема информации об исследуемой системе в каждом
эксперименте (наблюдении). Другими словами, при каком сочетании
уровней внутренних и внешних факторов может быть получена наиболее
полная и достоверная информация о поведении системы.
При стратегическом планировании должны быть решены следующие основные
задачи:
идентификация факторов;
выбор уровней факторов.
9

10. 2. Стратегическое планирование экспериментов

10
Под идентификацией факторов понимается их ранжирование по степени
влияния на значение наблюдаемой переменной (или показатель
эффективности).
По итогам идентификации все факторы делятся на 2 группы – первичные и
вторичные. Первичные факторы – это те, в исследовании влияния которых
заинтересован сам экспериментатор непосредственно. Вторичные факторы –
те, что не являются предметом исследования, но их влиянием нельзя
пренебречь.
Выбор уровней факторов производится с учетом двух противоречивых
требований:
уровни факторов должны перекрывать весь возможный диапазон его
изменений;
общее количество уровней по всем факторам не должно приводить к
чрезмерному объему моделирования.
Отыскание компромиссного решения – это и есть задача стратегического
планирования эксперимента.

11. 2. Стратегическое планирование экспериментов

Способы построения стратегического плана
Эксперимент, в котором реализуются все возможные сочетания уровней
факторов, называется полным факторным экспериментом (ПФЭ).
Общее число различных комбинаций уровней в ПФЭ для k факторов можно
определить как
N q1 q1...qk ,
(11.1)
где qi – число уровней i-го фактора.
Если число уровней для всех факторов одинаково, то вместо
формулы (11.1) получим:
N qk
где q – число уровней,
k – число факторов.
(11.2)
11

12. 2. Стратегическое планирование экспериментов

12
Недостаток ПФЭ – большие временные затраты на подготовку и проведение.
Например, в модели отражены 3 фактора, влияющие на значение ПЭ.
Каждый фактор имеет 4 возможных уровня (значения). План ПФЭ включает
N=43 =64 эксперимента.
Если при этом каждый эксперимент длится хотя бы одну минуту (с учетом
времени на изменение значения факторов), то на однократную реализацию
ПФЭ требуется более 1 часа.
Использование ПФЭ целесообразно, если в ходе имитационного моделирования
исследуется взаимное влияние всех факторов, фигурирующих в модели.
Если такие взаимодействия считают отсутствующими, или их эффектом
пренебрегают, проводят частичный факторный эксперимент (ЧФЭ).
Рассмотрим некоторые планы ЧФЭ.

13. 2. Стратегическое планирование экспериментов

13
Рандомизированный план
Рандомизированный план – предполагает выбор сочетания уровней факторов для
каждого прогона случайным образом. При использовании этого метода
отправной точкой в формировании плана является число экспериментов,
которое считает возможным (или необходимым) провести исследователь.

14. 2. Стратегическое планирование экспериментов

14
Латинский план
Латинский план («Латинский квадрат») – используется в том случае, когда
проводится эксперимент с одним первичным и несколькими вторичными
факторами.
Латинский квадрат – есть таблица размером n*n, в каждой строке и в каждом
столбце которой все элементы различны. Латинский квадрат широко
используется в теории кодирования, связи в секретных системах (шифровании),
теории планирования эксперимента.
Суть такого планирования с использованием латинского квадрата состоит в
следующем. Если первичный фактор A имеет q уровней, то для каждого
вторичного фактора B и C, также выбирается q уровней. Выбор комбинации
уровней факторов выбирается таким образом, чтобы для каждого первичного
фактора Ai получить равномерное распределение относительно вторичных
факторов Bj и Ck .

15. 2. Стратегическое планирование экспериментов

15
Латинский план
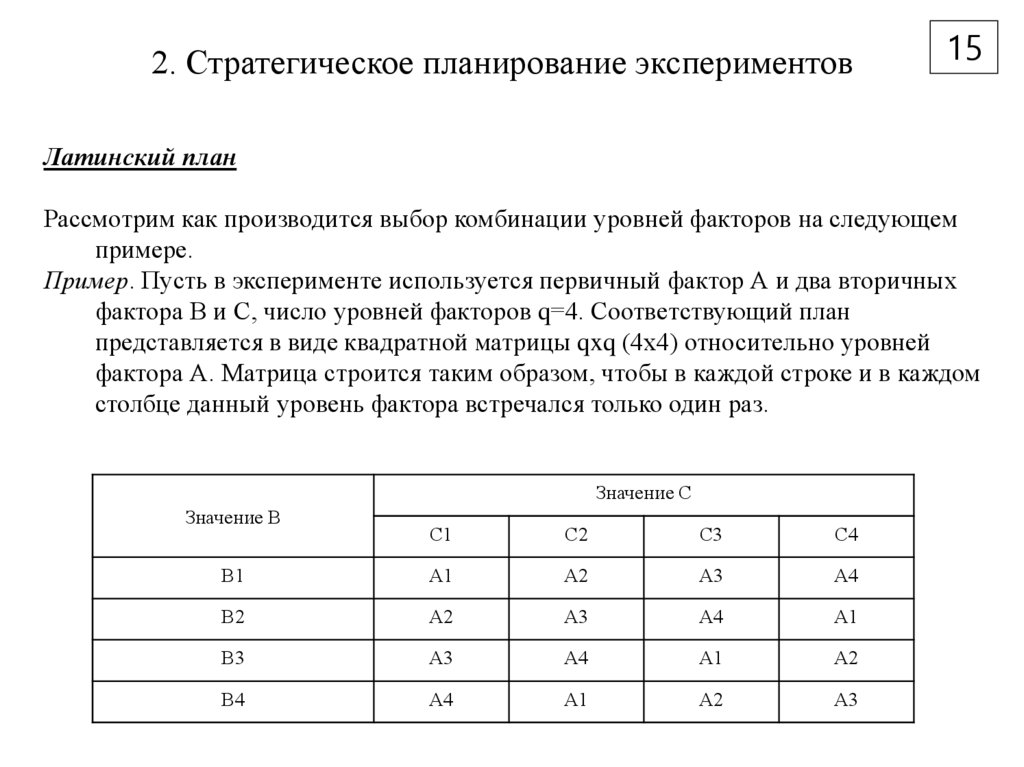
Рассмотрим как производится выбор комбинации уровней факторов на следующем
примере.
Пример. Пусть в эксперименте используется первичный фактор А и два вторичных
фактора В и С, число уровней факторов q=4. Соответствующий план
представляется в виде квадратной матрицы qxq (4х4) относительно уровней
фактора А. Матрица строится таким образом, чтобы в каждой строке и в каждом
столбце данный уровень фактора встречался только один раз.
Значение С
Значение В
С1
С2
С3
С4
В1
А1
А2
А3
А4
В2
А2
А3
А4
А1
В3
А3
А4
А1
А2
В4
А4
А1
А2
А3

16. 2. Стратегическое планирование экспериментов

16
Латинский план
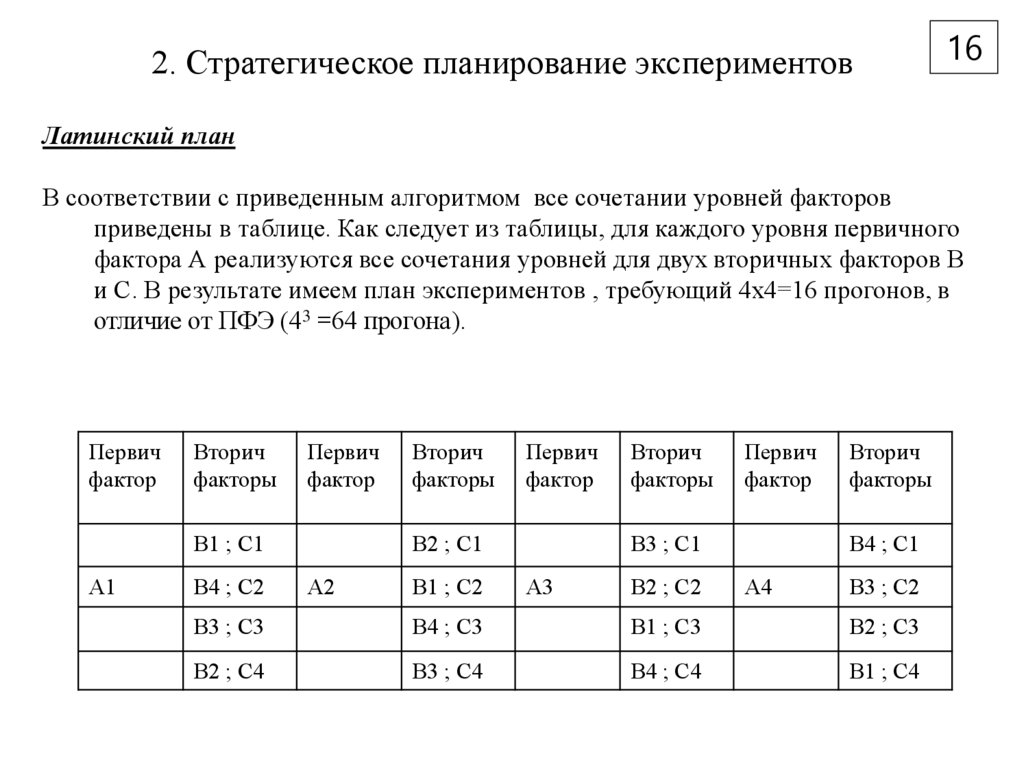
В соответствии с приведенным алгоритмом все сочетании уровней факторов
приведены в таблице. Как следует из таблицы, для каждого уровня первичного
фактора А реализуются все сочетания уровней для двух вторичных факторов В
и С. В результате имеем план экспериментов , требующий 4х4=16 прогонов, в
отличие от ПФЭ (43 =64 прогона).
Первич
фактор
Вторич
факторы
Первич
фактор
В1 ; С1
А1
В4 ; С2
Вторич
факторы
Первич
фактор
В2 ; С1
А2
В1 ; С2
Вторич
факторы
Первич
фактор
В3 ; С1
А3
В2 ; С2
Вторич
факторы
В4 ; С1
А4
В3 ; С2
В3 ; С3
В4 ; С3
В1 ; С3
В2 ; С3
В2 ; С4
В3 ; С4
В4 ; С4
В1 ; С4

17. 2. Стратегическое планирование экспериментов

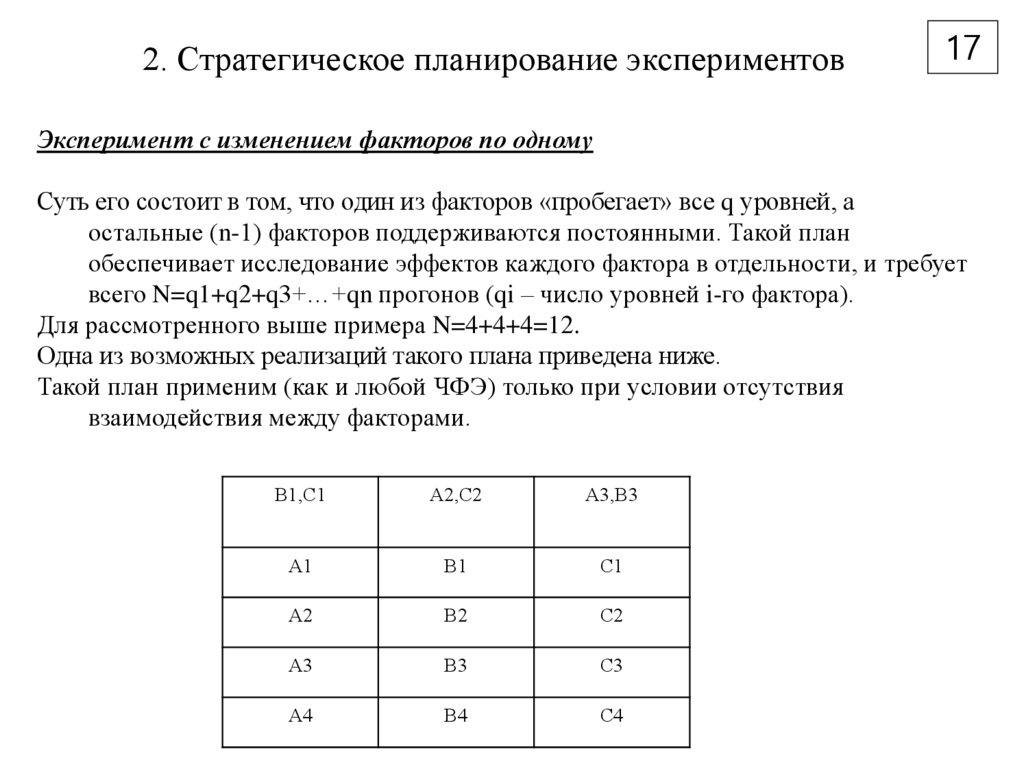
17
Эксперимент с изменением факторов по одному
Суть его состоит в том, что один из факторов «пробегает» все q уровней, а
остальные (n-1) факторов поддерживаются постоянными. Такой план
обеспечивает исследование эффектов каждого фактора в отдельности, и требует
всего N=q1+q2+q3+…+qn прогонов (qi – число уровней i-го фактора).
Для рассмотренного выше примера N=4+4+4=12.
Одна из возможных реализаций такого плана приведена ниже.
Такой план применим (как и любой ЧФЭ) только при условии отсутствия
взаимодействия между факторами.
В1,С1
А2,С2
А3,В3
А1
В1
С1
А2
В2
С2
А3
В3
С3
А4
В4
С4

18. 2. Стратегическое планирование экспериментов

Линейная модель планирования
Для линейной модели планирования связь между факторами и реакцией
исследуемой системы имеет следующий вид
yl b0 b1 x1 ... bk xk
(18.1)
где k – число факторов,
l – номер проведенного эксперимента.
Так как приведенный полином содержит (k+1) коэффициент, то число
экспериментов должно быть больше чем (k+1).
Проделав n – испытаний, получим вектор наблюдений в виде
y1
y ...
y n
(18.2)
18

19. 2. Стратегическое планирование экспериментов

19
Линейная модель планирования
Для проведения эксперимента необходимо задать значения факторов, т.е.
сформировать план проведения эксперимента. План эксперимента может быть
записан в виде следующей матрицы D:
x11
x
D 12
...
x1n
x21
x22
...
x2 n
...
...
...
...
xk 1
xk 1
...
xk 1
(19.1)
где - xim - значения, которые принимает i-ый фактор, в m-м испытании.
Приведенная матрица (19.1) называется матрицей планирования. Перед
проведением экспериментов предварительно проводят
масштабирование факторов.

20. 2. Стратегическое планирование экспериментов

20
Линейная модель планирования
Масштабирование факторов меняет минимальное значение фактора на минус
единицу (-1), а максимальное значение на плюс единицу (+1). Используя
процедуру масштабирования, может быть получено следующее значение
кодированного фактора:
xj
2 x j x j0
(20.1)
x j
где xj - натуральное значение фактора,
xj0 – нулевой уровень для натурального значения,
∆xj – интервал варьирования натуральных значений фактора,
j- номер фактора.
В соответствии с формулой (20.1) при xj = xmin получим кодирование значение = -1,
а, при xj = xmax получим кодирование значение = +1.

21. 2. Стратегическое планирование экспериментов

Линейная модель планирования
Используя формулу (20.1) для линейного планирования, для 2-х факторного
эксперимента получим следующую матрицу планирования:
План эксперимента (k=2)
Значения факторов
№ эксперимента
Х1
Х2
1
-1
-1
2
-1
+1
3
+1
-1
4
+1
+1
21

22. 2. Стратегическое планирование экспериментов

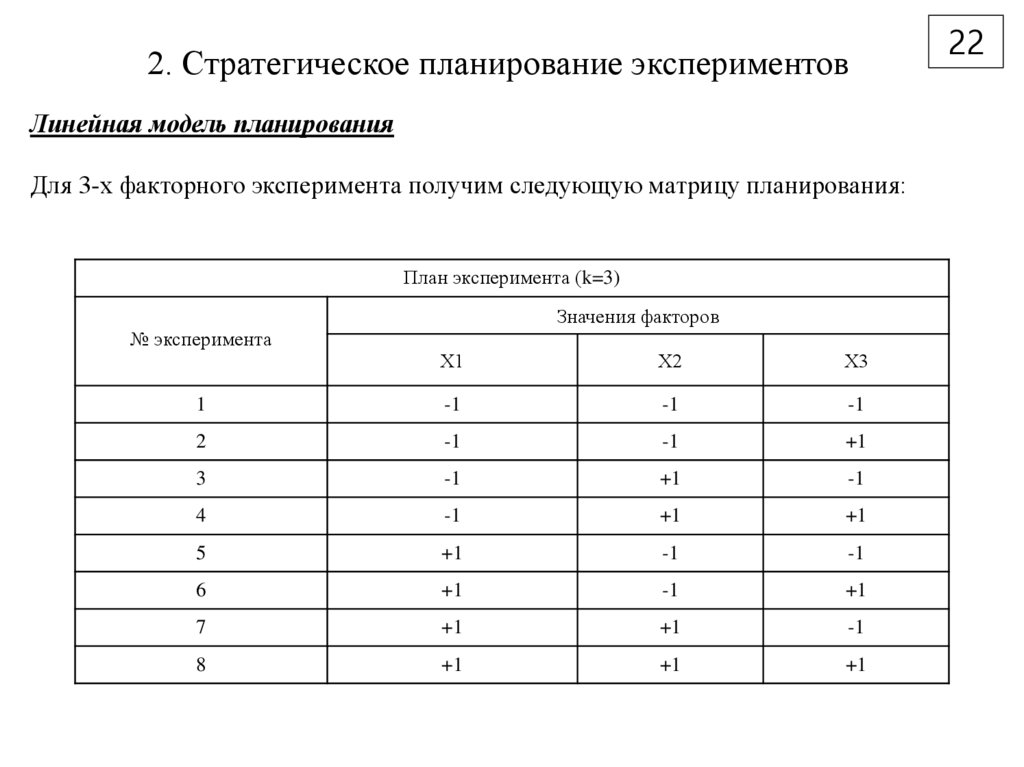
Линейная модель планирования
Для 3-х факторного эксперимента получим следующую матрицу планирования:
План эксперимента (k=3)
Значения факторов
№ эксперимента
Х1
Х2
Х3
1
-1
-1
-1
2
-1
-1
+1
3
-1
+1
-1
4
-1
+1
+1
5
+1
-1
-1
6
+1
-1
+1
7
+1
+1
-1
8
+1
+1
+1
22

23. 2. Стратегическое планирование экспериментов

23
Линейная модель планирования
Выделим важные свойства, которыми обладают приведенные матрицы планирования
для линейной модели:
1.) свойство симметричности:
x 0
1i
(23.1)
2.) свойство нормированности:
2
x
1i n
(23.2)
3.) свойство ортогональности:
x x 0
1i
2i
(23.3)

24. 3. Тактическое планирование экспериментов

24
Совокупность методов установления необходимого объема испытаний относят
к тактическому планированию экспериментов.
Поскольку имитационное моделирование (ИМ) представляет собой статистический
эксперимент, то при его проведении необходимо: получить достоверный
результат и обеспечить его «измерение» с заданной точностью.
В общем случае объем испытаний (величина выборки), необходимый для получения
оценок наблюдаемой переменной с заданной точностью, зависит от следующих
факторов:
- вида распределения наблюдаемой переменной у;
- коррелированности между собой элементов выборки;
наличия и длительности переходного режима функционирования
моделируемой системы.
Если исследователь не обладает информацией о перечисленных выше
факторах, то у него остается единственный способ повышения точности
оценок истинного значения наблюдаемой переменной – многократное
повторение прогонов модели для каждого сочетания уровней факторов,
выбранного на этапе стратегического планирования.

25. 3. Тактическое планирование экспериментов

25
3. Тактическое планирование экспериментов
Такой подход получил название – формирование простой случайной выборки
(ПСВ). Другими словами, при использовании ПСВ каждый пункт плана
повторяется определенное число раз.
При таком подходе общее число прогонов модели, необходимых для достижения
цели моделирования, равно Nsum=N*Np, где N – число сочетаний уровней
факторов по стратегическому плану, а Np – число прогонов модели для каждого
сочетания, вычисленное при тактическом планировании.
Например, если для ПФР N=64, а для обеспечения требуемой точности оценок
Np должно быть равно Np=20, то общее число прогонов Nsum=1280. Требуемое
время для проведения испытаний (по 1 мин. на каждое), более 20 часов.
Поэтому, при использовании ПСВ до начала испытаний необходимо определить
тот минимальный объем выборки, который обеспечит требуемую точность
расчета.
Нахождение необходимого объема испытаний тесно связано с вопросом обеспечения
точности и достоверности результатов моделирования.

26. 4. Проблема обеспечения точности и достоверности результатов моделирования

26
Имитационное моделирование исследуемой системы представляет собой машинный
эксперимент и поэтому результатом расчета показателя эффективности Es
исследуемой системы может быть только оценка этого показателя.
В качестве показателей эффективности могут использоваться следующие :
1. Вероятность появления некоторого события A.
2. Среднее значение некоторой случайной величины ξ.
Выбор количества реализаций для получения устойчивых значений этих показателей
зависит от того, какие требования предъявляются к результатам моделирования.
Пусть в качестве оценки некоторого параметра a , который оценивается по
результатам моделирования значений xi , выбирается величина
Xm . В силу случайности процесса величина Xm будет отличаться от параметра a .

27. 4. Проблема обеспечения точности и достоверности результатов моделирования

27
Отличие величины Xm от параметра a запишем следующим образом.
Зададим величину ε и назовем ее точностью, которая удовлетворяет неравенству:
‫׀‬a - Xm ‫ < ׀‬ε,
(27.1)
а вероятность α того, что неравенство (27.1) выполняется назовем достоверностью.
Тогда можем записать следующее соотношение:
P a Xm
(27.2)
Соотношению (27.2) можно дать наглядную частотную интерпретацию.
Если для оценки параметра a мы будем использовать величину Xm с точностью ε и
достоверностью α, то в среднем на каждые 100 случаев применения этого
правила, в 100 α случаях Xm будет отличаться от a меньше чем на ε, и только
в (1- α ) 100 случаях разница между ними может превосходить ε.

28. 4. Проблема обеспечения точности и достоверности результатов моделирования

28
Рассмотрим 1-ый способ оценки эффективности системы на основе оценки
вероятности появления p(A) случайного события A. В качестве оценки
вероятности р(А) выступает частота р=m/N, где m – число положительных
исходов.
В каждой реализации процесса с помощью имитационной модели событие А может
наступить или не наступить. Другими словами, количество наступления
события А является случайной величиной ξ, принимающей значение Х1=1 с
вероятностью Р и значение Х2=0 с вероятностью (1-Р). Легко определить
математическое ожидание и дисперсию случайной величины ξ.
M x1 p x2 (1 p) p
D x1 M p x2 M (1 p) p 1 p
2
(28.1)
2
(28.2)

29. 4. Проблема обеспечения точности и достоверности результатов моделирования

29
В качестве оценки для искомой вероятности принимается частота m/N наступления
события А при N реализациях. Но частоту m/N можно представить в
следующем виде:
m
1 N
i
N
N i 1
(29.1)
где ξi –количество наступлений события А при реализации испытания с
номером i.
Из формул (28.1), (28.2) и (29.1) можно получить:
m
M p
N
(29.2)
m
D p 1 p
N
(29.3)

30. 4. Проблема обеспечения точности и достоверности результатов моделирования

30
4. Проблема обеспечения точности и
достоверности результатов моделирования
Используя формулу (29.2), запишем соотношение (27.2) в следующем виде:
m
P p p
N
(30.1)
В силу центральной предельной теоремы теории вероятностей частоту m/N
при больших значениях N можно рассматривать как случайную величину,
описываемую нормальным законом распределения с математическим
ожиданием p и дисперсией p(1-p)/N. Учитывая это, (30.1) можно записать:
p p
p p
m
P p p 0
N 0
N
p 1 p
p 1 p
N
где Ф0(z) – функция Лапласа.
(30.2)

31. 4. Проблема обеспечения точности и достоверности результатов моделирования

31
Учитывая, что Ф0(-z)=1-Ф0(z), получим:
2 0
1
p 1 p
(31.1)
1
2
p 1 p
(31.2)
N
или
0
N
Отсюда можно получить следующее соотношение:
N
p 1 p
t
t 2 p 1 p
N
2
где tα – квантиль нормального распределения.
Окончательно число реализаций для обеспечения заданной
точности с достоверностью α найдется из следующего
соотношения:
(31.3)

32. 4. Проблема обеспечения точности и достоверности результатов моделирования

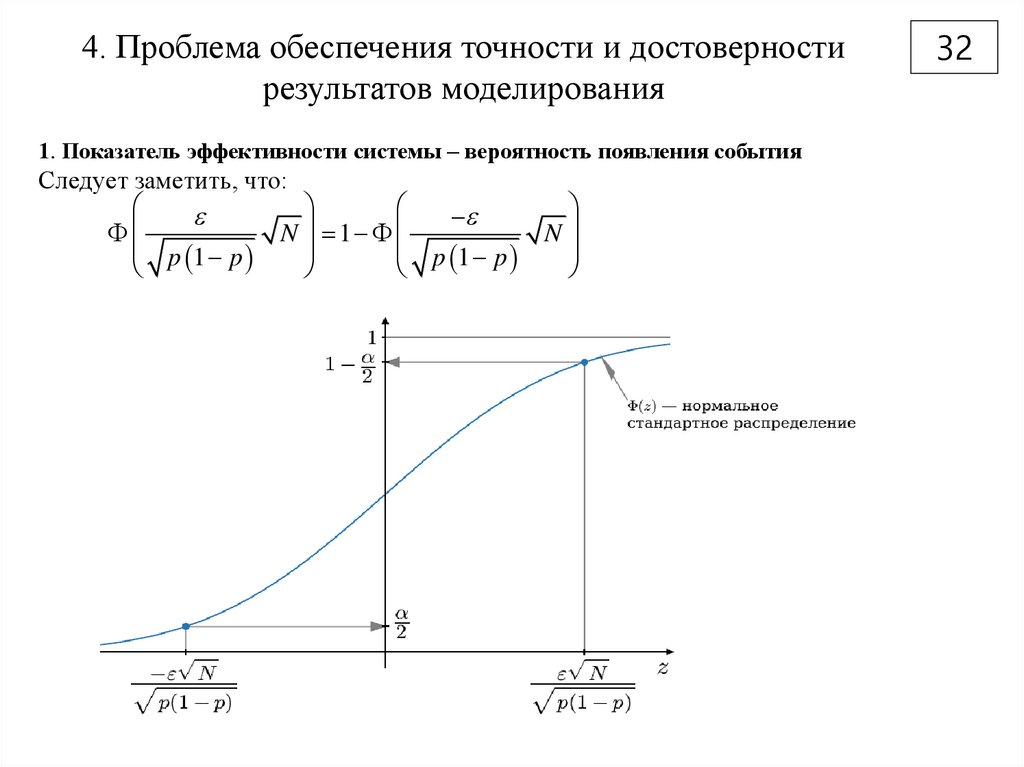
1. Показатель эффективности системы – вероятность появления события
Следует заметить, что:
N 1
p 1 p
p 1 p
N
32

33. 4. Проблема обеспечения точности и достоверности результатов моделирования

Аналогично формуле (31.3) можно получить соотношение для вычисления
количества реализаций при определении среднего значения некоторой
случайной величины ξ:
N
t 2 2
2
где σ2 – дисперсия случайной величины ξ.
(33.1)
33