Исследование динамики многозвенных колесных платформ

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
“УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ”
Институт математики, информационных технологий и физики
Кафедра теоретической и экспериментальной физики
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
ИССЛЕДОВАНИЕ ДИНАМИКИ МНОГОЗВЕННЫХ
КОЛЕСНЫХ ПЛАТФОРМ
Выполнил:
студент группы ОБ-03.03.01.01-41
В. А. КРАСНОВА
Научный руководитель:
кандидат физико-математических наук, доцент
кафедры теоретической и экспериментальной физики
Т. Б. ИВАНОВА
Ижевск — 2025

2.

Некоторые известные конструкции мобильных роботов
– Тележка с двумя закрепленными колесными парами [1]. Система эквивалентна задаче о санях
Чаплыгина [2, 3] (платформе с закрепленным лезвием и двумя гладкими ножками).
– Снейкборд (snakeboard) — колесный экипаж с двумя колесными парами [4, 5], в котором обе
колесные пары могут свободно вращаться.
– Колесные экипажи, состоящий из трех и более тележек (обзор литературы можно найти в [6, 7]).
[1]
Borisov A. V., Kilin A. A., Mamaev I. S. On the Hadamard – Hamel Problem and the Dynamics of Wheeled Vehicles // Regular
and Chaotic Dynamics, 2015, vol. 20, no. 6, pp. 752–766.
[2]
Chaplygin S. A., On the theory of motion of nonholonomic systems. The reducing-multiplier theorem // Regular and Chaotic
Dynamics, 2008, vol. 13, pp. 369–376; see also: Mat. Sb., 1912, vol. 28, no. 2, pp. 303-–314.
[3]
Caratheodory, C.: Der schlitten. Z. Angew. Math. Mech. 13(2), 71—76 (1933)
[4]
Borisov A. V., Kilin A. A., Mamaev I. S., Invariant Submanifolds of Genus 5 and a Cantor Staircase in the Nonholonomic Model
of a Snakeboard, International Journal of Bifurcation and Chaos, 2019, vol. 29, no. 3, 1930008, 19 pp.
[5]
Borisov A. V., Mamaev I. S., Kilin A. A., Bizyaev I. A. Qualitative Analysis of the Dynamics of a Wheeled Vehicle // Regular and
Chaotic Dynamics, 2015, vol. 20, no. 6, pp. 739–751.
[6]
Bravo-Doddoli A. and García – Naranjo L. C., The Dynamics of an Articulated n-Trailer Vehicle // Regular and Chaotic
Dynamics, 2015, vol. 20, no. 5, pp. 497–517.
[7]
Artemova E. M., Kilin A. A., A Nonholonomic Model and Complete Controllability of a Three-Link Wheeled Snake Robot,
Russian Journal of Nonlinear Dynamics, 2022, vol. 18, no. 4, pp. 671-697
2

3.

Целью работы является теоретическое и экспериментальное исследование управляемого движения
многозвенных колесных систем. В частности,
1
исследование динамики движения (вывод и анализ уравнений движения);
2
анализ системы в зависимости от вида управления: изучение возможных траекторий движения при
различных параметрах управляющей функции, анализ эффективности управления, поиск параметров
управляющей функции при периодическом движении системы;
3
экспериментальное исследование движения роллер рэйсера вдоль прямой и по окружности, в
зависимости от массо-геометрических характеристик;
4
экспериментальное исследование движения трехзвенного робота вдоль прямой и по окружности для
натурного образца, в зависимости от выбранных параметров управления.
3

4.

Задачами исследования движения мобильных систем является:
1
Изучение и дальнейшее использование высокоточной оптической системы захвата движения Vicon,
которая позволяет получать координаты маркеров, закрепленных на платформах мобильных роботов;
2
Определение массо-геометрических параметров и параметров управляющей функции роллер рэйсера,
при которых средняя скорость движения вдоль прямой и окружности будет оптимальной
(максимальной);
3
Экспериментальная проверка зависимости средней скорости продвижения роллер рэйсера от
параметров управляющей функции, в том числе амплитуды;
4
Изучение и апробация методики определения бокового проскальзывания (смещения колес вдоль оси
вращения колесной пары звена) во время движения трехзвенного мобильного робота;
5
Определение параметров управляющей функции, при которых скорость проскальзывания в
поперечном направлении движения будет минимальной;
6
Экспериментальный анализ траекторий движения, скоростей поступательного движения и бокового
проскальзывания трехзвенного робота с особыми конфигурациями (взаимными расположениями
звеньев);
7
Моделирование возможных типов траекторий центрального звена робота при периодических
управлениях. Определение условия прямолинейного в среднем движения.
4

5.

Роллер рэйсер
Роллер рэйсер — мобильный робот, состоящий из двух соединенных между собой (с помощью
цилиндрического шарнира) платформ, которые могут свободно вращаться в горизонтальной плоскости
относительно друг друга.
Рис. 3: 3D модель роллер рэйсера
Рис. 1: Роллер рэйсер
Рис. 2: Натурный образец роллер
рэйсера
5

6.

Некоторые известные результаты исследования динамики роллер рэйсера
– В наиболее общем случае свободная динамика роллер рэйсера исследуется в [8]. Получены уравнения
движения по плоскости и показано, что в общем случае движение относительно неподвижной
системы координат является асимптотическим: за исключением прямолинейного движения все
траектории стремятся к окружностям, движение является ограниченным.
– В [9, 10] исследуется управляемое движение роллер рэйсера. Предполагается, что угол между
платформами (управляющая функция) является заданной периодической функцией времени.
Показано, что периодическое изменение угла может привести к неограниченному ускорению.
Доказано, что в общем случае при наличии сил вязкого трения в точке контакта колес с плоскостью
постоянное ускорение отсутствует.
– Сравнение теоретических и экспериментальных результатов управляемого движения роллер рэйсера в
случае прямолинейного движения с учетом вязкого трения представлено в [11, 12].
[8]
Bizyaev I. A. The Inertial Motion of a Roller Racer // Regular and Chaotic Dynamics, 2017, vol. 22, no. 3, pp. 239–247.
[9]
Krishnaprasad, P. and Tsakiris, D. P., Oscillations, SE (2)-snakes and motion control: A study of the roller racer, Dynamical
Systems: An International Journal, 2001, vol. 16, no. 4, pp. 347–397.
[10] Bizyaev, I. A., Borisov, A. V., and Mamaev, I. S., Exotic dynamics of nonholonomic roller racer with periodic control. Regular and
Chaotic Dynamics, 2018, vol. 23, no. 7, pp. 983—994.
[11] Yefremov K. S., Ivanova T. B., Kilin A. A., Karavaev Y. L., Theoretical and experimental investigations of the controlled motion
of the Roller Racer, 2020 International Conference Nonlinearity, Information and Robotics – IEEE, 2020, pp. 1–5.
[12] Kilin A. A., Karavaev Y. L., Yefremov K. S., Experimental Investigations of the Controlled Motion of the Roller Racer Robot,
Climbing and Walking Robots Conference: Robotics for Sustainable Future, CLAWAR 2021, 2022, pp. 428-437
6

7.

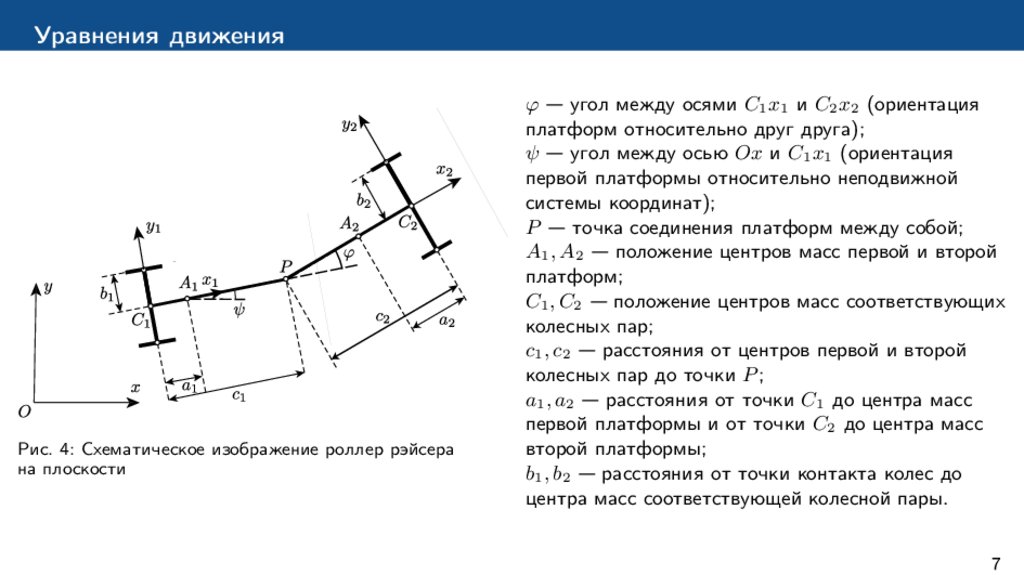
Уравнения движения
Рис. 4: Схематическое изображение роллер рэйсера
на плоскости
φ — угол между осями C1 x1 и C2 x2 (ориентация
платформ относительно друг друга);
ψ — угол между осью Ox и C1 x1 (ориентация
первой платформы относительно неподвижной
системы координат);
P — точка соединения платформ между собой;
A1 , A2 — положение центров масс первой и второй
платформ;
C1 , C2 — положение центров масс соответствующих
колесных пар;
c1 , c2 — расстояния от центров первой и второй
колесных пар до точки P ;
a1 , a2 — расстояния от точки C1 до центра масс
первой платформы и от точки C2 до центра масс
второй платформы;
b1 , b2 — расстояния от точки контакта колес до
центра масс соответствующей колесной пары.
7

8.

Уравнения движения
Для описания движения системы определим три системы координат:
– инерциальную систему координат Oxy, плоскость Oxy совпадает с плоскостью движения;
– неинерциальную систему координат C1 x1 y1 , жестко связанную с первой платформой и началом
отсчета C1 в центре масс колесной пары. Оси C1 x1 и C1 y1 направим соответственно по касательной
и нормали к плоскости колес;
– неинерциальную систему координат C2 x2 y2 , жестко связанную со второй платформой и началом
отсчета C2 в центре масс колесной пары, оси также направим по касательной и нормали к плоскости
колес.
Основные особенности конструкции и предположения, в рамках которых мы будем рассматривать
динамику роллер рейсера:
— Будем полагать, что центр масс первой и второй платформ (точки A1 и A2 ) лежат соответственно
на осях C1 x1 и C2 x2 (см. рис. 4).
— Угол φ ориентации платформ относительно друг друга является заданной периодической функцией
времени (с периодом T ).
— При качении роллер рэйсера в точках контакта колес с плоскостью отсутствует проскальзывание.
8

9.

Конфигурационное пространство
Динамику рассматриваемой системы будем описывать
квазискоростями v = (v1 , v2 ) и ω, где v — скорость точки P в
проекции на оси подвижной системы координат C1 x1 y1 , а ω —
абсолютная угловая скорость первой платформы.
Квазискорости связаны с обобщенными скоростями
соотношениями:
v1 = ẋ cos ψ + ẏ sin ψ,
v2 = −ẋ sin ψ + ẏ cos ψ,
ω = ψ̇. (1)
Рис. 5: Фото натурного образца
[1]
Borisov A. V., Kilin A. A., Mamaev I. S. On the Hadamard – Hamel Problem and the Dynamics of Wheeled Vehicles // Regular
and Chaotic Dynamics, 2015, vol. 20, no. 6, pp. 752–766.
9

10.

Неголономные связи. Уравнения движения
Неголономные связи, выражающие отсутствие проскальзывания в точках контакта колес, имеют вид [10]:
f1 = v2 − c1 ω = 0,
f2 = −v1 sin φ(t) + v2 cos φ(t) + c2 (ω + φ̇(t)) = 0.
(2)
Для исследования влияния силы трения на динамику роллер рейсера будем рассматривать простейшую
модель вязкого трения [9].
Пусть в точках контакта колес с плоскостью действуют силы вязкого трения с функцией Рэлея (κ1 , κ2 —
коэффициенты вязкого трения). С учетом соотношений (7), (8) функция Рэлея, записанная через
квазикоординаты, имеет вид:
R = k1 (b21 ω 2 + v12 ) + k2 (b22 (φ̇(t) + ω)2 + (v1 cos φ + v2 sin φ)2 ),
[9]
k1 = κ1 /h2 ,
k2 = κ2 /h2 .
(3)
Krishnaprasad, P. and Tsakiris, D. P., Oscillations, SE (2)-snakes and motion control: A study of the roller racer, Dynamical
Systems: An International Journal, 2001, vol. 16, no. 4, pp. 347–397.
[10] Bizyaev, I. A., Borisov, A. V., and Mamaev, I. S., Exotic dynamics of nonholonomic roller racer with periodic control. Regular and
Chaotic Dynamics, 2018, vol. 23, no. 7, pp. 983—994.
10

11.

Уравнения движения
Скорость v1 с учетом связяей и сил вязкого трения, описываемых функцией Рэлея, после выражения
неопреденных множителей Лагранжа имеет вид:
v̇1 = A(t) − C(t) v1 + B1 (t) + B2 (t) − D(t),
(4)
где
A(t) = −
φ̇ sin φ(J1 S2 + δS1 )
,
S1 (J1 sin2 φ + M S12 )
B2 (t) =
B1 (t) =
φ̈ sin φ(J1 c2 − J2 S1 )
(J1 sin2 φ + M S12 )
φ̇2 (J1 c1 c2 sin2 φ − S1 (c1 δ cos φ − εc2 S1 ))
S1 (J1 sin2 φ + M S12 )
C(t) = 2
(b21 k1 + b22 k2 ) sin2 φ + k1 S12 + k2 S22
,
J1 sin2 φ + M S12
φ̇ sin φ c1 k2 (b22 − c22 ) cos φ − c2 (b21 k1 + c21 k2 )
,
D(t) = 2
J1 sin2 φ + M S12
S1 = c1 cos φ + c2 ,
S2 = c1 + c2 cos φ.
Здесь для сокращения записи мы ввели следующие обозначения: δ = c1 a2 m2 + c2 a1 m1 , ε = m1 a1 + c1 m2 ,
J1 = I10 + I20 + m1 a21 + m2 (a22 + c21 − c22 ), J2 = I20 − m2 (c22 − a22 ), где I10 , I20 — моменты инерции первой и
второй платформ относительно их центров масс (точек A1 и A2 ).
11

12.

Уравнения движения
Выражая скорость v2 из первого уравнения связи (8) и подставляя ее в соотношения (7), получаем
квадратуры для конфигурационных переменных, определяющих движение точки P относительно
неподвижной системы координат Oxy:
υ1 sin φ − c2 φ̇
ẋ = υ1 cos ψ − c1
sin ψ,
c1 cos φ + c2
υ1 sin φ − c2 φ̇
ẏ = υ1 sin ψ + c1
cos ψ,
c1 + c2 cos φ,
ψ̇ = υ1 sin φ − c2 φ̇ .
c1 cos φ + c2
(5)
Полученная система уравнений (4), (5) описывает поведение роллер рейсера, в случае если угол φ(t)
между платформами является заданной функцией времени.
В данном случае из системы (4), (5) отделяется неавтономное уравнение (4), описывающее эволюцию
скорости v1 .
Таким образом, редуцированная система сводится к одному неавтономному линейному
дифференциальному уравнению (4), решение которого зависит от вида управляющей функции и
параметров роллер рейсера.
12

13.

Примеры периодических управлений
Управления могут быть промоделированы следующей непрерывной дифференцируемой функцией,
которую в данной работе мы будем рассматривать в качестве управляющей:
QN
Z
2π n=1 (2n + 1)
2πt
(2N +1)
dt + φ0 , α, T, φ0 = const.
cos
φ(t) = α
QN
T
T
n=1 2n
(6)
Множители перед интегралом в (6) определены таким
образом, чтобы максимальное отклонение функции φ(t)
от φ0 было равно α, N — целое число, определяющее
«резкость маха» (скорость смены знака функции φ(t) в
середине периода), (см. рис. 6).
Чем больше N , тем ближе к вертикали касательная к
функции φ(t) при t = T /2.
Случай управляющей функции (6) при N = 0 рассмотрен
также в [10].
Рис. 6: Графики функции φ(t) при N = 0 и N = 5,
α = 0.4, φ0 = 0.1, T = 1
[10] Bizyaev, I. A., Borisov, A. V., and Mamaev, I. S., Exotic dynamics of nonholonomic roller racer with periodic control. Regular and
Chaotic Dynamics, 2018, vol. 23, no. 7, pp. 983—994.
13

14.

Экспериментальные результаты
Для съемки траектории и восстановления взаимного углового положения платформы, на большой (I) и
малой (II) платформах расположены светоотражающие маркеры для системы захвата движения VICON.
Рис. 7: 3D модель натурного образца
роллер рэйсера
14

15.

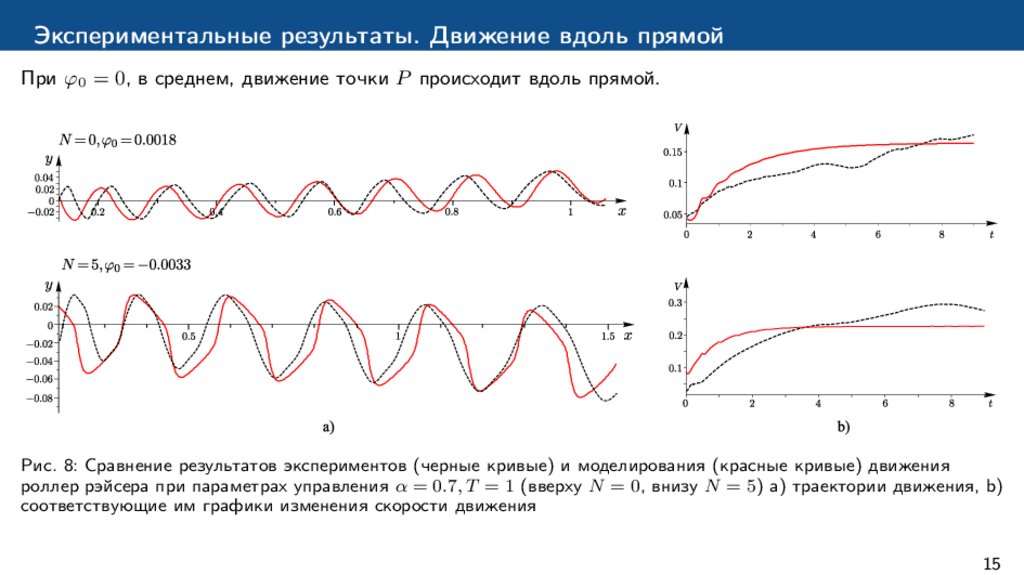
Экспериментальные результаты. Движение вдоль прямой
При φ0 = 0, в среднем, движение точки P происходит вдоль прямой.
Рис. 8: Сравнение результатов экспериментов (черные кривые) и моделирования (красные кривые) движения
роллер рэйсера при параметрах управления α = 0.7, T = 1 (вверху N = 0, внизу N = 5) a) траектории движения, b)
соответствующие им графики изменения скорости движения
15

16.

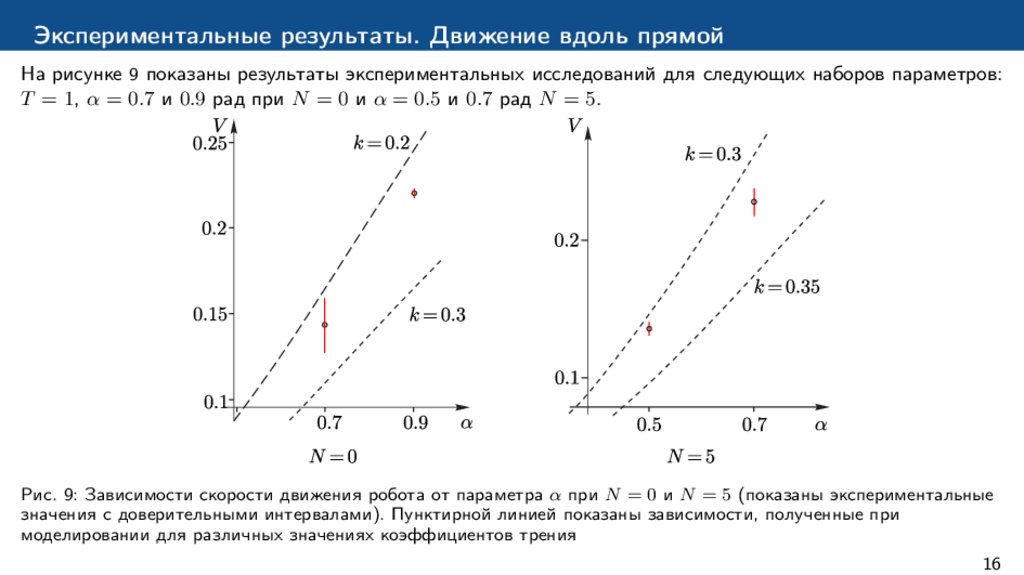
Экспериментальные результаты. Движение вдоль прямой
На рисунке 9 показаны результаты экспериментальных исследований для следующих наборов параметров:
T = 1, α = 0.7 и 0.9 рад при N = 0 и α = 0.5 и 0.7 рад N = 5.
Рис. 9: Зависимости скорости движения робота от параметра α при N = 0 и N = 5 (показаны экспериментальные
значения с доверительными интервалами). Пунктирной линией показаны зависимости, полученные при
моделировании для различных значениях коэффициентов трения
16

17.

Экспериментальные результаты. Движение вдоль окружности
При φ0 ̸= 0 в среднем движение точки P
происходит вдоль окружности.
Рис. 10: Сравнение результатов экспериментов (черные кривые) и
моделирования (красные кривые) движения роллер рейсера при
параметрах управления α = 0.7, T = 1, φ0 = 0.47 (вверху N = 0,
внизу N = 5) a) траектории движения, b) соответствующие им
графики изменения скорости движения
17

18.

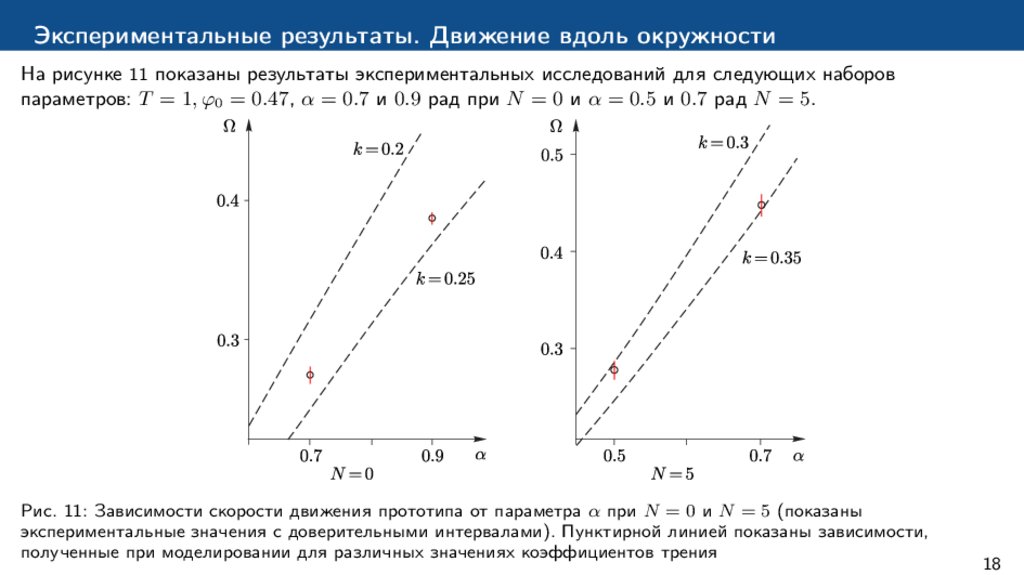
Экспериментальные результаты. Движение вдоль окружности
На рисунке 11 показаны результаты экспериментальных исследований для следующих наборов
параметров: T = 1, φ0 = 0.47, α = 0.7 и 0.9 рад при N = 0 и α = 0.5 и 0.7 рад N = 5.
Рис. 11: Зависимости скорости движения прототипа от параметра α при N = 0 и N = 5 (показаны
экспериментальные значения с доверительными интервалами). Пунктирной линией показаны зависимости,
полученные при моделировании для различных значениях коэффициентов трения
18

19.

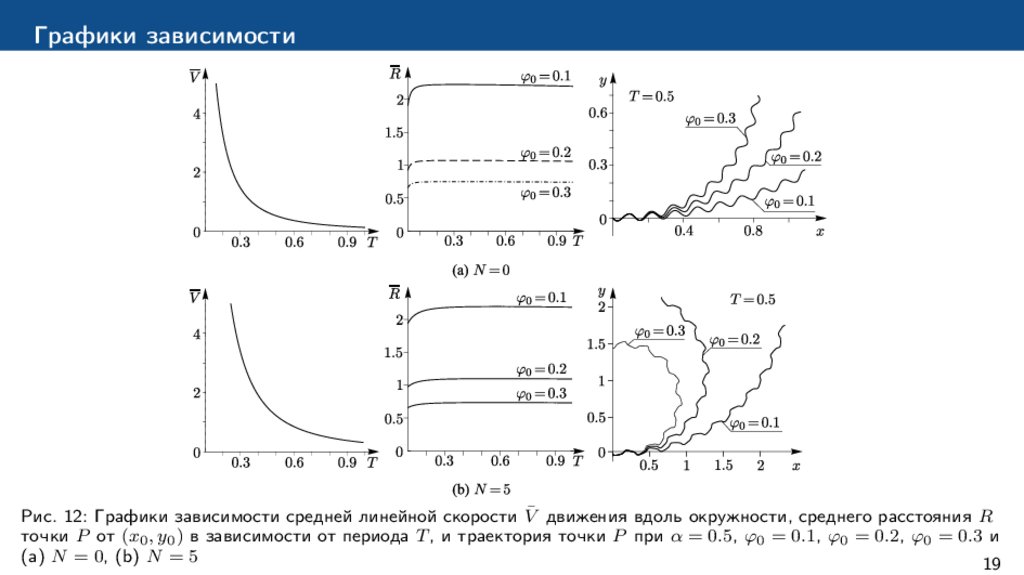
Графики зависимости
Рис. 12: Графики зависимости средней линейной скорости V̄ движения вдоль окружности, среднего расстояния R
точки P от (x0 , y0 ) в зависимости от периода T , и траектория точки P при α = 0.5, φ0 = 0.1, φ0 = 0.2, φ0 = 0.3 и
(a) N = 0, (b) N = 5
19

20.

Техзвенный колесный робот
В работе исследуется управляемое движение многозвенного мобильного робота по горизонтальной
плоскости. Фото натурного образца представлены на рис. 13.
Рис. 13: Фото натурного образца трехзвенного мобильного робота
20

21.

Некоторые известные результаты исследования многозвенных колесных систем
Управление колесными многозвенниками рассматривается, например, в работах [13, 14]. Обзор не только
аналитических исследований таких систем, но и исследований, связанных с моделированием
роботов-змей, представлен в работе [15]. В работе [16] предложен метод генерации управлений для
плоских неголономных n + 1-звенных роботов (n ≥ 3), управляемых за счет изменения углов между всеми
платформами. При этом движения, генерируемые предложенным методом, гарантированно
удовлетворяют неголономным ограничениям.
В работе [17] представлены кинематические уравнения движения, описывающие управляемое движение
многозвенника и, в частности, трехзвенника, в рамках неголономной модели. В работе [18] строится
управление, при котором трехзвенник устойчиво двигается по периодической траектории задним ходом.
[13] Tanaka M., Matsuno F., Modeling and control of head raising snake robots by using kinematic redundancy // J. of Intelligent
and Robotic Systems, 2014, vol. 75(1), pp. 53–69.
[14] Crespi A., Badertscher A., Guignard A., Ijspeert A. J., Amphibot I: an amphibious snake-like robot // Robot. Auton. Syst., 2005,
vol. 50(4), pp. 163–175.
[15] Liljeback P., Pettersen K. Y., Stavdahl O., Gravdahl J. T., A review on modelling, implementation, and control of snake
robots // Robot. and Auton. Syst., 2012, vol. 60(1), pp. 29–40.
[16] Itani O., Shammas E., Motion planning for redundant multi-bodied planar kinematic snake robots // Nonlinear Dynam., 2021,
vol. 104(4), pp. 3845–3860.
[17] Dear T., et al, Locomotion of a multi-link nonholonomic snake robot // Dynamic Systems and Control Conference, 2017, 58288,
V002T21A011.
[18] Surov M., Gusev S., Freidovich L., Constructing transverse coordinates for orbital stabilization of periodic trajectories // 2020
American Control Conference (ACC) — IEEE, 2020, pp. 836–841.
21

22.

Математическая модель трехзвенника
0
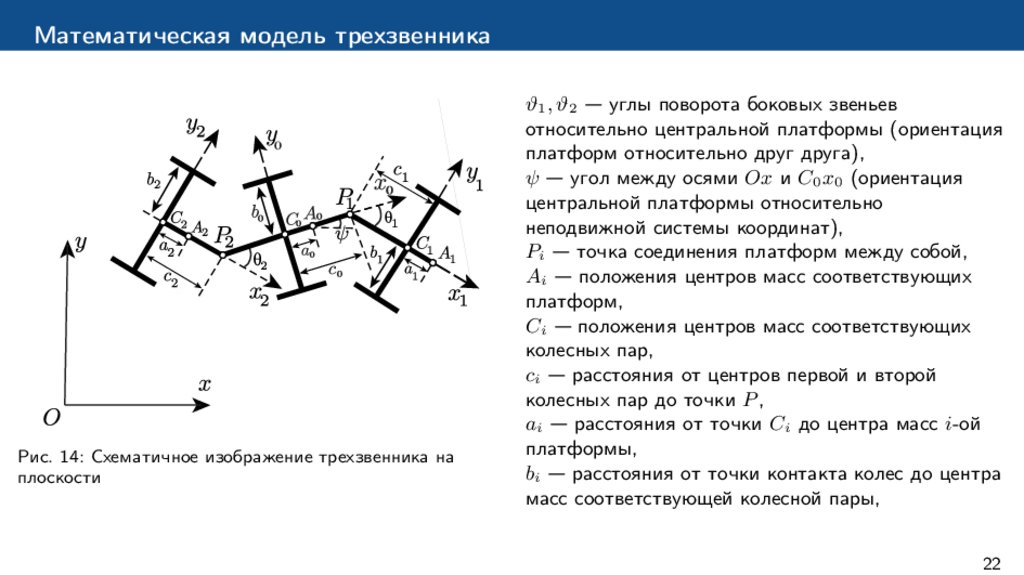
Рис. 14: Схематичное изображение трехзвенника на
плоскости
ϑ1 , ϑ2 — углы поворота боковых звеньев
относительно центральной платформы (ориентация
платформ относительно друг друга),
ψ — угол между осями Ox и C0 x0 (ориентация
центральной платформы относительно
неподвижной системы координат),
Pi — точка соединения платформ между собой,
Ai — положения центров масс соответствующих
платформ,
Ci — положения центров масс соответствующих
колесных пар,
ci — расстояния от центров первой и второй
колесных пар до точки P ,
ai — расстояния от точки Ci до центра масс i-ой
платформы,
bi — расстояния от точки контакта колес до центра
масс соответствующей колесной пары,
22

23.

Математическая модель трехзвенника
Сделаем следующие допущения относительно конструкции всего экипажа и каждой из платформ:
1
Платформы соединены цилиндрическими шарнирами и могут свободно вращаться независимо
относительно друг друга в горизонтальной плоскости (см. рис. 14).
2
Точки крепления платформ между собой лежат на прямых, проходящих через центры масс платформ
и перпендикулярных осям колесных пар.
3
Колесные пары закреплены на каждой платформе на одинаковом расстоянии от точек соединения
платформ.
4
Центр масс каждой платформы лежит на прямой, проходящей через точки соединения платформ и
крепления колесной пары.
5
Далее будем считать что углы ϑ1 , ϑ2 представляют собой заданные функции времени (управления).
Определим две системы координат:
− неподвижную систему координат Oxy;
− подвижную систему координат Cx1 x2 , жестко связанную с центральной платформой, с началом в
точке центра масс центральной платформы и с осями Cx1 и Cx2 , направленными перпендикулярно и
вдоль оси колесной пары соответственно.
23

24.

Конфигурационное пространство. Неголономные связи
Динамику рассматриваемой системы будем описывать квазискоростями v = (v1 , v2 ) и ω, где v — скорость
центра масс центральной платформы в проекции на оси подвижной системы координат Cx1 x2 , а ω — ее
абсолютная угловая скорость. Квазискорости связаны с обобщенными скоростями соотношениями:
v1 = ẋC cos ψ + ẏC sin ψ,
v2 = −ẋC sin ψ + ẏC cos ψ,
ω = ψ̇.
(7)
Неголономные связи, выражающие отсутствие проскальзывания в точках контакта колес, имеют вид
f1 = v2 − c0 ω = 0,
f2 = −v1 sin ϑ1 + v2 cos ϑ1 + a(ω + ϑ̇1 ) + (a − c0 ) cos ϑ1 ω = 0,
(8)
f3 = −v1 sin ϑ2 + v2 cos ϑ2 − a(ω + ϑ̇2 ) − (a + c0 ) cos ϑ2 ω = 0.
[1]
Borisov A. V., Kilin A. A., Mamaev I. S. On the Hadamard – Hamel Problem and the Dynamics of Wheeled Vehicles // Regular
and Chaotic Dynamics, 2015, vol. 20, no. 6, pp. 752–766.
24

25.

Уравнения движения
Кинетическая энергия всей системы представляется в форме
m(a + c )2
m(a − c2 )2
j0 2
3m 2
1
ω + (ϑ̇1 + ω)2 + (ϑ̇2 + ω)2 +
(v1 + v22 ) +
(ω + ϑ̇1 )2 +
(ω + ϑ̇2 )2 +
T =
2
2
2
2
+m(a2 + c20 )ω 2 + mω (a − c0 )(a + c1 )(ω + ϑ̇1 ) cos ϑ1 + (a + c0 )(a − c2 )(ω + ϑ̇2 ) cos ϑ2 −
−2mc0 ωv2 + m(a + c1 )(ω + ϑ̇1 ) (v2 cos ϑ1 − v1 sin ϑ1 ) − m(a − c2 )(ω + ϑ̇2 ) (v2 cos ϑ2 − v1 sin ϑ2 ) .
Уравнения движения запишем в виде уравнений Лагранжа–Эйлера в квазискоростях [1]:
3
X
d ∂T
∂T
∂fi
=
λi
= N1 ,
−ω
dt ∂v1
∂v2
∂v
1
i=1
3
X
∂T
∂fi
d ∂T
+ω
=
λi
= N2 ,
dt ∂v2
∂v1
∂v
2
i=1
3
X
∂T
∂T
∂fi
d ∂T
+ v1
− v2
=
λi
= N3 ,
dt ∂ω
∂v2
∂v1
∂ω
i=1
(9)
где λ1 , λ2 , λ3 — неопределенные множители, соответствующие силам реакции в точках контакта колес с
плоскостью, N1 , N2 , N3 — проекции общей реакции всех связей.
25

26.

Уравнения движения
Дополнив уравнения (9) кинематическими соотношениями (7) получим полную систему уравнений
описывающую динамику рассматриваемой системы.
В рассматриваемом случае размерность пространства скоростей совпадает с числом неголономных
связей. В результате уравнения Лагранжа–Эйлера (9) совпадают с производным по времени связей (8). А
зависимости скоростей (v1 , v2 , ω) от времени определяются в явном виде из уравнений связей (8):
v1 =
a(ϑ̇1 cos ϑ2 − ϑ̇2 cos ϑ1 + ϑ̇1 − ϑ̇2 )
,
sin(ϑ1 + ϑ2 ) + sin ϑ1 + sin ϑ2
v2 = −
ω=−
c0 (ϑ̇1 sin ϑ2 + ϑ̇2 sin ϑ1 )
,
sin(ϑ1 + ϑ2 ) + sin ϑ1 + sin ϑ2
(10)
ϑ̇1 sin ϑ2 + ϑ̇2 sin ϑ1
,
sin(ϑ1 + ϑ2 ) + sin ϑ1 + sin ϑ2
Замечание. Связи (8) могут быть разрешены относительно скоростей v1 , v2 и ω при условии
△ = sin(ϑ1 + ϑ2 ) + sin ϑ1 + sin ϑ2 ̸= 0.
(11)
26

27.

Уравнения движения
Подставляя эти выражения для скоростей в кинематические соотношения (7) получим уравнения для
конфигурационных переменных (xC , yC , ψ):
ẋC
−a(1 + cos ϑ1 ) cos ψ + c0 sin ϑ1 sin ψ
a(1 + cos ϑ2 ) cos ψ + c0 sin ϑ2 sin ψ
ϑ̇2
ϑ̇
1
ẏC = a(1 + cos ϑ2 ) sin ψ − c0 sin ϑ2 cos ψ
+ −a(1 + cos ϑ1 ) sin ψ − c0 sin ϑ1 cos ψ
△
△
− sin ϑ1
− sin ϑ2
ψ̇
Условие (11) соответствует особым конфигурациям многозвенника со следующими взаимными
расположениями звеньев:
1
ϑ1 = −ϑ2 — крайние звенья повернуты на один и тот же угол;
2
ϑ1 = ±π — первое звено совпадает с центральным;
3
ϑ2 = ±π — второе звено совпадает с центральным.
Особые конфигурации ϑ1,2 = ±π соответствуют физически нереализуемым в реальном эксперименте
конфигурациям трехзвенника (две или все три платформы сложены друг на друга).
Далее будем рассматривать более подробно управления ϑ1 , ϑ2 , которые в некоторый момент времени
t = tcr удовлетворяют условию вырождения связей
ϑ1 (tcr ) + ϑ2 (tcr ) = 0.
(12)
27

28.

Управляющая функция
В работе мы рассмотрим различные периодические функции управления ϑ1 (t) — угол поворота
центральной платформы относительно первой и ϑ2 (t) — угол поворота последней платформы
отностительно центральной:
2πt
2πt
ϑ1 (t) = α + A sin
, ϑ2 (t) = β + A sin
+D .
T
T
(13)
где A — амплитуда колебаний, α и β — смещения для управляющих функций, T — период колебаний, D
— задержка одного сервопривода относительно другого.
28

29.

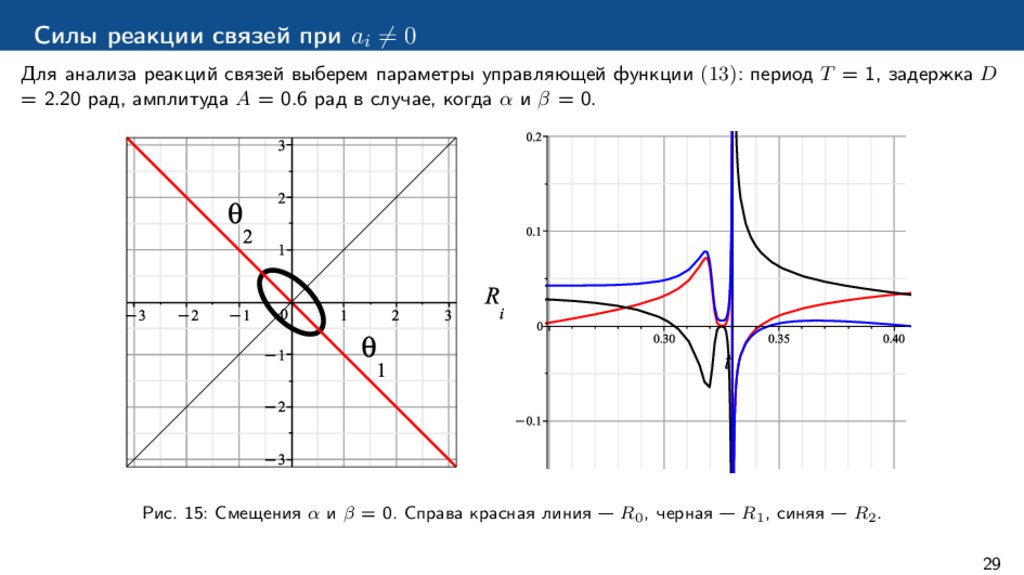
Силы реакции связей при ai ̸= 0
Для анализа реакций связей выберем параметры управляющей функции (13): период T = 1, задержка D
= 2.20 рад, амплитуда A = 0.6 рад в случае, когда α и β = 0.
Рис. 15: Смещения α и β = 0. Справа красная линия — R0 , черная — R1 , синяя — R2 .
29

30.

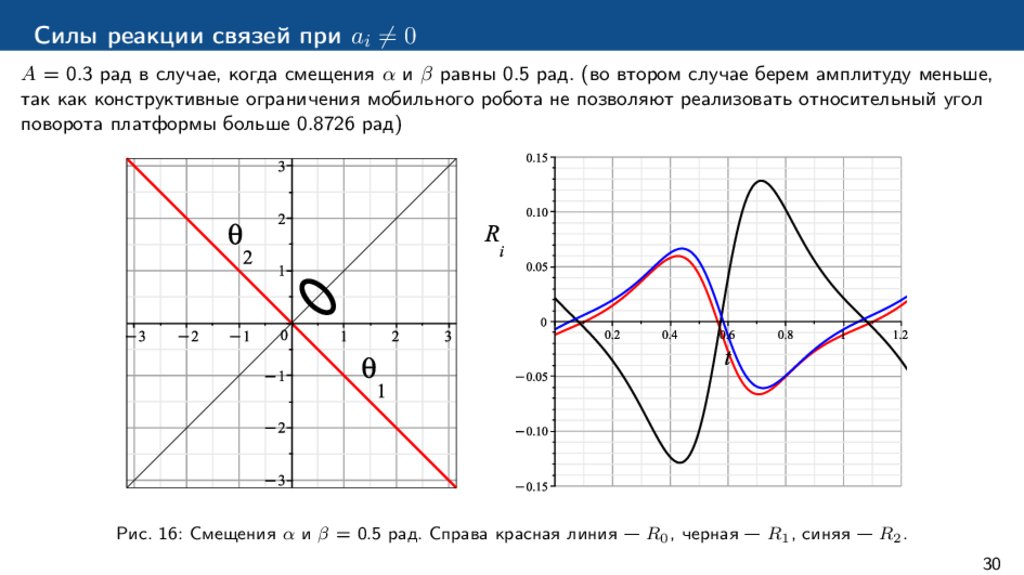
Силы реакции связей при ai ̸= 0
A = 0.3 рад в случае, когда смещения α и β равны 0.5 рад. (во втором случае берем амплитуду меньше,
так как конструктивные ограничения мобильного робота не позволяют реализовать относительный угол
поворота платформы больше 0.8726 рад)
Рис. 16: Смещения α и β = 0.5 рад. Справа красная линия — R0 , черная — R1 , синяя — R2 .
30

31.

Экспериментальные исследования движения многозвенного робота
Для оценки адекватности предложенной модели движения была проведена серия экспериментов с
различными управлениями (с пересечением особых конфигураций и без).
Рис. 17: Аксонометричекая проекция, 3D модель и фото мобильного трехзвенного робота
31

32.

Экспериментальные исследования движения многозвенного робота
Экспериментально параметры движения каждого звена определяются по маркерам системы захвата
движения Vicon, закрепленным на каждой платформе (точность определения координат до ±0.5мм и
частотой дискретизации 100 Гц).
Массо-геометрические
параметры прототипа:
m0 = 0.235 кг, m1 = 0.175 кг,
m2 = 0.204 кг, a0 = 0.011 м,
a1 = 0.012 м, a2 = 0.012 м,
c = 0.038 м,
j0 = 1.704427330 · 10−7 кг/м2 ,
j1 = 1.269254395 · 10−7 кг/м2 ,
j2 = 1.479587980 · 10−7 кг/м2 .
32

33.

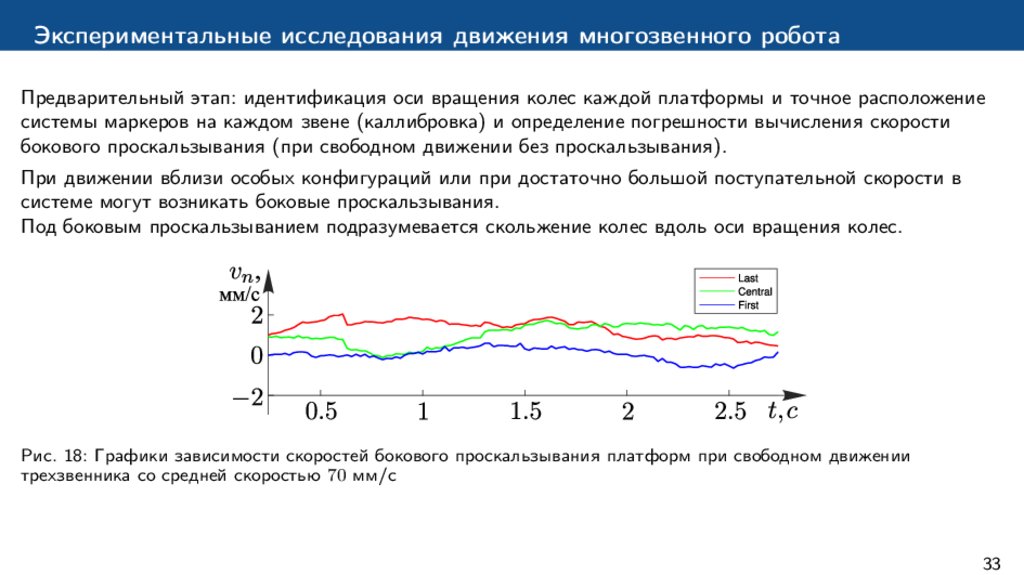
Экспериментальные исследования движения многозвенного робота
Предварительный этап: идентификация оси вращения колес каждой платформы и точное расположение
системы маркеров на каждом звене (каллибровка) и определение погрешности вычисления скорости
бокового проскальзывания (при свободном движении без проскальзывания).
При движении вблизи особых конфигураций или при достаточно большой поступательной скорости в
системе могут возникать боковые проскальзывания.
Под боковым проскальзыванием подразумевается скольжение колес вдоль оси вращения колес.
Рис. 18: Графики зависимости скоростей бокового проскальзывания платформ при свободном движении
трехзвенника со средней скоростью 70 мм/с
33

34.

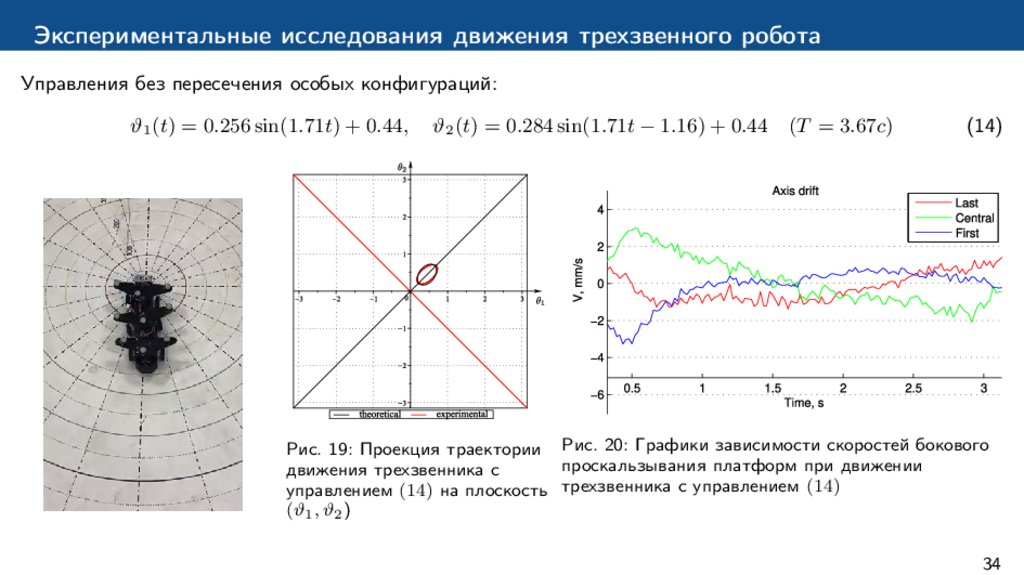
Экспериментальные исследования движения трехзвенного робота
Управления без пересечения особых конфигураций:
ϑ1 (t) = 0.256 sin(1.71t) + 0.44,
ϑ2 (t) = 0.284 sin(1.71t − 1.16) + 0.44
(T = 3.67c)
(14)
Рис. 19: Проекция траектории Рис. 20: Графики зависимости скоростей бокового
проскальзывания платформ при движении
движения трехзвенника с
управлением (14) на плоскость трехзвенника с управлением (14)
(ϑ1 , ϑ2 )
34

35.

Экспериментальные исследования движения трехзвенного робота
Рис. 22: Теоретическая и экспериментальная траектории
центра масс центральной платформы трехзвенника,
движущегося с управлением (14)
Рис. 21: Графики теоретической и экспериментальной
зависимостей скоростей поступательного движения и
проскользывания платформ при движении трехзвенника с
управлением (14)
Рис. 23: Реакции связей трехзвенника, движущегося с
управлением (14)
35

36.

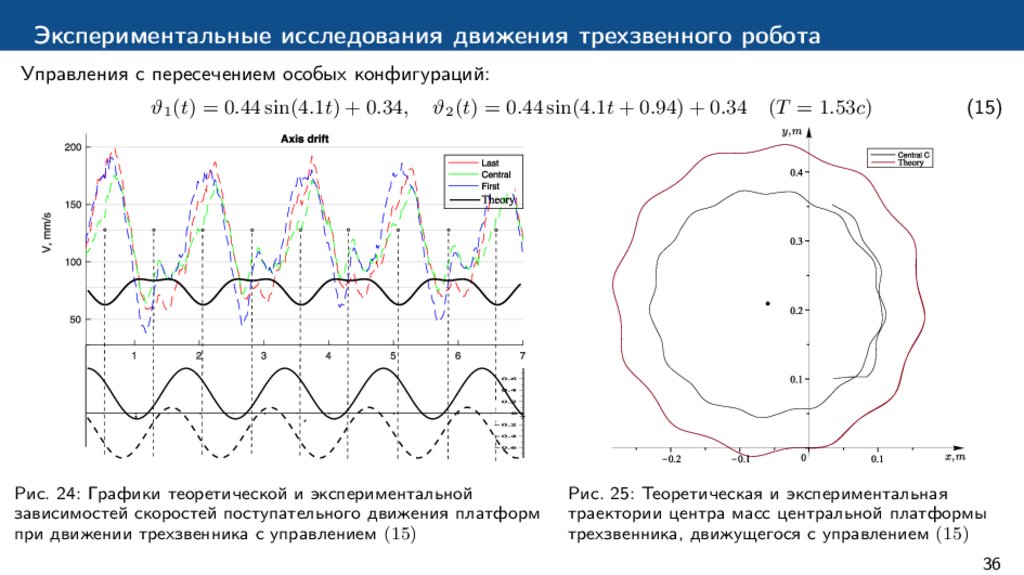
Экспериментальные исследования движения трехзвенного робота
Управления с пересечением особых конфигураций:
ϑ1 (t) = 0.44 sin(4.1t) + 0.34,
ϑ2 (t) = 0.44 sin(4.1t + 0.94) + 0.34
Рис. 24: Графики теоретической и экспериментальной
зависимостей скоростей поступательного движения платформ
при движении трехзвенника с управлением (15)
(T = 1.53c)
(15)
Рис. 25: Теоретическая и экспериментальная
траектории центра масс центральной платформы
трехзвенника, движущегося с управлением (15)
36

37.

Благодарю за внимание!