Линейные дифференциальные уравнения n-го порядка

1. Линейные дифференциальные уравнения n-го порядка

Общий вид линейного дифференциального
уравнения n-го порядка такой:
y( n ) a1( x )y( n 1 ) a2 ( x )y( n 2 )
an ( x )y f ( x )
a1( x ),a2 ( x ), ,an ( x ), f ( x ) - заданные функции от x или
числа.
Это уравнение линейно относительно неизвестной
функции y(x) и ее производных (т.е. содержит их в
первой степени).
( 1)

2. Пример линейного дифференциального уравнения второго порядка

y 5 y 6 y ( 2 x 1 )e
x

3. Теорема существования и единственности решения задачи Коши для линейного уравнения.

Если на отрезке [a;b] коэффициенты a1( x ),a2 ( x ), ,an ( x ) и
функция f ( x ) непрерывны, то существует решение
уравнения (1), удовлетворяющее начальным условиям:
y( x0 ) y0
y ( x ) y
0
1
y( n 1 ) ( x0 ) yn 1
при x0 [a;b]
y0 , y1 , , yn 1 - любые числа.
Это решение единственно.

4. Определение. Если правая часть , то линейное уравнение называется однородным.

Определение. Если правая часть f ( x ) 0 , то
линейное уравнение называется однородным.
Линейное однородное дифференциальное
уравнение (ЛОДУ):
y( n ) a1( x )y( n 1 ) a2 ( x )y( n 2 )
an ( x )y 0
Пример ЛОДУ второго порядка
y 5 y 6 y 0
( 2)

5. Определение. Если правая часть (не равна нулю тождественно), то линейное уравнение (1) называется неоднородным.

Определение. Если правая часть
f ( x ) 0 (не равна
нулю тождественно), то линейное уравнение (1)
называется неоднородным.
Пример
y 4 y 18 y (2 x 1)e 3 x

6. Линейные однородные дифференциальные уравнения (ЛОДУ)

Свойства решений
1. Сумма конечного числа решений линейного
однородного дифференциального уравнения также
является решением этого уравнения.
Дано: y1( x ), y2 ( x ) - решения уравнения (2), то есть при
подстановке в уравнение (2) превращают его в
тождество.
Доказать: y( x ) y1( x ) y2 ( x ) -также решение уравнения (2).
Доказательство. Подставим
в уравнение
(2).

7. Получим:

( y1 y2 )( n ) a1( x )( y1 y2 )( n 1 ) a2 ( x )( y1 y2 )( n 2 )
an ( x )( y1 y2 ) 0
y1( n ) y2( n ) a1( x )y1( n 1 ) a1( x )y2( n 1 ) a2 ( x )y1( n 2 ) a2 ( x )y2( n 2 )
an ( x )y1 an ( x )y2 0
y1( n ) a1( x )y1( n 1 ) a2 ( x )y1( n 2 )
an ( x )y1 y2( n ) a1( x )y2( n 1 ) a2 ( x )y2( n 2 )
0 0
Что и требовалось доказать.
an ( x )y2 0

8. 2. Произведение решения линейного однородного дифференциального уравнения на число также является решением этого уравнения.

Т.е. если y - решение уравнения (2) и С - const, то
Cy - также решение (2).

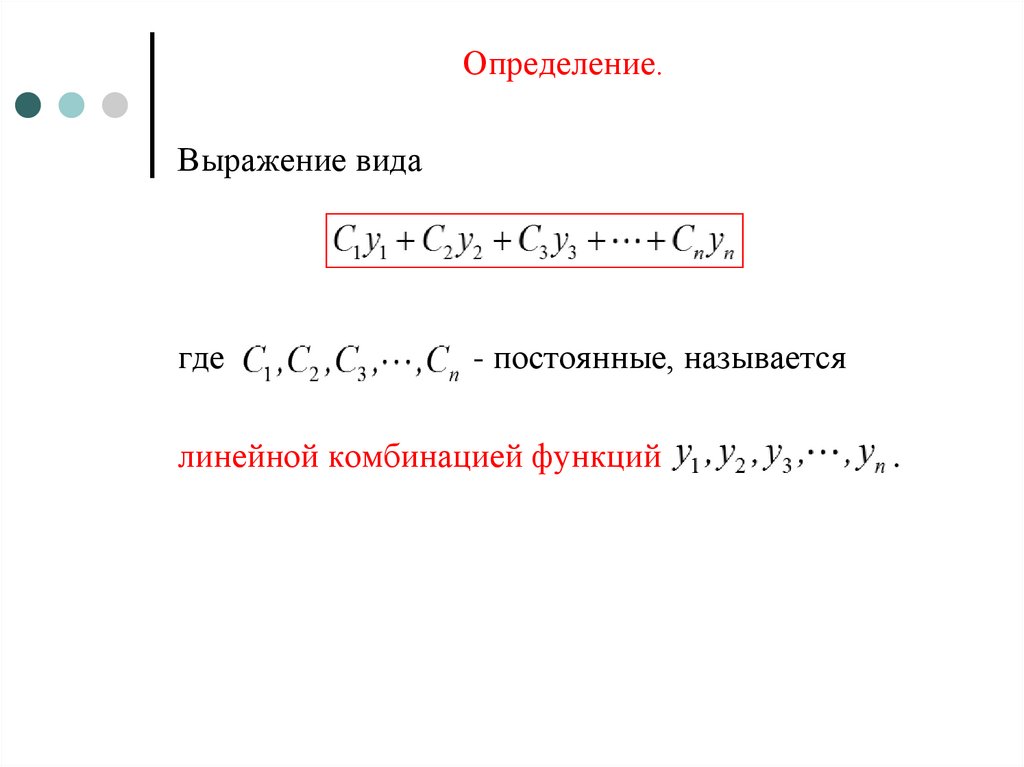
9. Определение.

Выражение вида
где
- постоянные, называется
линейной комбинацией функций
.

10. 3. Линейная комбинация решений ЛОДУ (2) является решением этого уравнения.

То есть если
- решения (2), и
- постоянные, то линейная комбинация
также будет решением этого дифференциального
уравнения.

11. Линейно зависимые и независимые системы функций на интервале.

Определение. Система функций
y1( x ), y2 ( x ), y3 ( x ), , yn ( x )
называется линейно зависимой на интервале (a;b),
если одна из этих функций может быть
представлена в виде линейной комбинации
остальных.
Т.е., например, yn C1 y1 C2 y2 C3 y3 Cn 1 yn 1
где C1 ,C2 ,C3 , ,Cn 1 - некоторые числа, x (a;b) .

12. Пример

Пусть
y1 1, y2 x, y3 x2 , y4 3 x 2 , y5 x3
Эта система функций линейно зависима, так как
3 x 2 3 1 0 x x 2 0 x3
Или
y4 3 y1 0 y2 y3 0 y5 3 y1 y3
y4 3 y1 y3

13. Определение. Система функций называется линейно независимой на интервале (a;b), если ни одна из этих функций не может быть

представлена в виде линейной комбинации
остальных.
Пример 1. y1 e x , y2 e2 x , y3 e3 x - линейно независима.
Докажем от противного.
Пусть
e3 x C1e x C2e2 x
e2 x C1 C2e x
( e2 x ) ( C1 C2e x )
2e2 x C2e x
2e x C2
( 2e x ) ( C2 )
2e x 0 - противоречие

14. Пример 2.

Система функций y1 1, y2 x, y3 x2 линейно независима.
Докажем от противного. Пусть
x2 C1 1 C2 x
x2 C2 x C1 0
это равенство выполняется не более, чем в двух
точках оси OX (квадратное уравнение имеет не более двух
решений), а если функции y1 , y2 , y3 линейно зависимы, то
оно должно выполняться при любых x.
Значит,
- линейно независимы.

15. Замечание

Две функции y1( x ), y2 ( x ) называются линейно
зависимыми, если их отношение равно const
y1( x )
const , то
y2 ( x )
- линейно зависимы.
Пример. y1 cos x, y2 3cos x - линейно зависимы.
Если y1( x ) const , то y1 , y2 - линейно независимы.
y2 ( x )
Пример. y1 e x , y2 e3 x
y1 e x
3 x e 2 x const , значит y1 , y2 - линейно независимы.
y2 e

16. Определитель Вронского

Пусть функции y1( x ), y2 ( x ), y3 ( x ), , yn ( x ) имеют
непрерывные производные до порядка n-1
включительно.
Определитель
W [ y1 , y2 , , yn ]
y1 ( x)
y1 ( x)
y2 ( x )
y2 ( x)
yn ( x )
yn ( x)
y1( n 1) ( x) y2( n 1) ( x)
yn( n 1) ( x)
называется определителем Вронского системы
функций y1 , y2 , , yn .
Другое обозначение: W( x)

17. Необходимое условие линейной зависимости

Пусть функции
имеют в
( a,b) непрерывные производные до порядка n-1
включительно. Если система
линейно зависима на (a,b), то W( y1 , y2 , , yn ) 0 для всех
x ( a,b ) .

18. Доказательство (для n = 3)

Рассмотрим систему функций y1 , y2 , y3 . По условию
она линейно зависима. Это значит, что
y3 C1 y1 C2 y2 , C1 ,C2 const
y1 y2
W( y1 , y2 , y3 ) y1 y2
y1 y2
y3 y1 y2 C1 y1 C2 y2
y3 y1 y2 C1 y1 C2 y2
y3 y1 y2 C1 y1 C2 y2
y1 y2
C1 y1 y2
y1 y2
y2
y2 0
y2
y1
y1 y2
y1 C2 y1 y2
y1
y1 y2
что и требовалось доказать.

19. Следствие

Если W( y1 , y2 , , yn ) 0 хотя бы в одной точке x0 ( a,b ) ,
то система функций y1 , y2 , , yn линейно независима на
(a,b).
То есть не обращение в 0 определителя Вронского W достаточное условие линейной независимости.

20. Необходимое условие линейной независимости системы решений линейного однородного дифференциального уравнения

Пусть функции
линейно независимы на (a,b)
и являются там решениями ЛОДУ:
Тогда определитель Вронского W( y1 , y2 , , yn ) 0
всюду в (a,b).

21. Доказательство для n = 3 (от противного)

Пусть найдется точка x0 (a, b) , такая что W ( x0 ) 0, то есть
y1 ( x0 )
W ( x0 ) y1 ( x0 )
y1 ( x0 )
y2 ( x0 )
y2 ( x0 )
y2 ( x0 )
y3 ( x0 )
y3 ( x0 ) 0 .
y3 ( x0 )
Составим систему трех линейных однородных уравнений с тремя
неизвестными C1 , C2 , C3, для которой W ( x0 ) является определителем
системы:
C1 y1 ( x0 ) C2 y2 ( x0 ) C3 y3 ( x0 ) 0
C1 y1 ( x0 ) C2 y2 ( x0 ) C3 y3 ( x0 ) 0
C y ( x ) C y ( x ) C y ( x ) 0
2 2
0
3 3
0
1 1 0
(5)
Эта система имеет нулевое решение: C1 C2 C3 0 .
Но из теории систем линейных уравнений следует, что если
определитель системы равен нулю, то существует и ненулевое
решение: C1 C1 , C2 C2 , C3 C3 , и хотя бы одно из C1 , C2 , C3 не равно
нулю.

22. Рассмотрим функцию .

Рассмотрим функцию y C1 y1 C2 y2 C3 y3 .
По свойствам решений линейного однородного
дифференциального уравнения эта функция y тоже
является решением данного уравнения, и для этой
функции система (5) означает:
y ( x0 ) 0
y ( x0 ) 0
y ( x ) 0
0
( 6) - нулевые условия Коши в точке x0 .
По теореме существования и единственности
существует единственное нулевое решение задачи
Коши:
y a1 ( x) y a2 ( x) y a3 ( x) y 0

23. То есть .

То есть y 0 .
Или C1 y1 C2 y2 C3 y3 0 , и хотя бы одно из
не
равно нулю. Пусть, для определенности C3 0 , тогда
y3
C1
C
y1 2 y2 ,
C3
C3
то есть система функций y1 , y2 , y3 - линейно зависима.
Полученное противоречие доказывает теорему.

24. Фундаментальная система решений (ФСР)

Определение. Фундаментальной системой решений
однородного линейного дифференциального
уравнения n-го порядка называется n линейно
независимых решений этого уравнения.
Порядок уравнения и количество решений в
ФСР равны!

25. Теорема о структуре линейного однородного дифференциального уравнения n-го порядка

Если функции y1( x ), y2 ( x ), , yn ( x ) образуют ФСР
линейного однородного дифференциального
уравнения (2), то общее решение этого уравнения
имеет вид:
y C1 y1( x ) C2 y2 ( x ) Cn yn ( x ) ,
где C1 ,C2 ,
,Cn - произвольные постоянные.

26. Доказательство.

Докажем, что функция y будет удовлетворять обоим
условиям определения общего решения
дифференциального уравнения n-го порядка.
1. y C1 y1 C2 y2 Cn yn содержит n произвольных
постоянных.
По третьему свойству решений линейного
однородного дифференциального уравнения эта
функция y является решением дифференциального
уравнения (2) при любых значениях этих
произвольных постоянных.

27. 2. Пусть заданы начальные условия:

y ( x0 ) y0
y ( x ) y (3)
0
1
, где y0 , y1 , , yn 1 - некоторые числа.
y ( n 1) ( x0 ) yn 1
Покажем, что из функции
можно
получить частное решение, удовлетворяющее
начальным условиям (3).
Для нахождения значений произвольных постоянных
составим систему n уравнений с n неизвестными
C1 , C2 , , Cn :

28. Получим:

C1 y1 ( x0 ) C2 y2 ( x0 ) Cn yn ( x0 ) y0
C1 y1 ( x0 ) C2 y2 ( x0 ) Cn yn ( x0 ) y1
C1 y1( n 1) ( x0 ) C2 y2( n 1) ( x0 ) Cn yn( n 1) ( x0 ) yn 1
Главный определитель этой системы:
y1 ( x0 )
y1 ( x0 )
y2 ( x0 )
y2 ( x0 )
yn ( x0 )
yn ( x0 )
y1( n 1) ( x0 )
y2( n 1) ( x0 )
yn( n 1) ( x0 )
W ( x0 )

29. - это определитель Вронского системы решений .

W ( x0 ) - это определитель Вронского
системы решений
.
По условию решения
составляют
ФСР (фундаментальную систему решений)
дифференциального уравнения (2), то есть они
линейно независимы.
Следовательно, по необходимому условию
линейной независимости W ( x0 ) 0 .
А если основной определитель системы линейных
уравнений не равен нулю, эта система имеет
единственное решение: C1 C1o , C2 C2o , , Cn Cno .
Если эти значения произвольных постоянных
подставить в функцию y , то мы получим частное
решение y C1o y1 ( x) C20 y2 ( x) Cno yn ( x)

30. Если эти значения произвольных постоянных подставить в функцию y , то мы получим частное решение ,

удовлетворяющее начальным условиям (3).
Таким образом, функция y удовлетворяет и второму
условию определения общего решения
дифференциального уравнения n - го порядка,
значит она является общим решением
дифференциального уравнения (2), что и
требовалось доказать.

31. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами

y( n ) a1 y( n 1 ) a2 y( n 2 )
an y 0 (4)
где a1 ,a2 , ,an - действительные числа.
Например,
y 4 y 5 y 0

32. Будем искать решение уравнения (4) в виде

y e
k - пока неизвестное число.
y ekx , y kekx , y k 2ekx , , y( n 1 ) k n 1ekx , y ( n ) k ne kx
Подставим в уравнение (4):
k n ekx a1k n 1ekx
anekx 0
ekx ( k n a1k n 1
an ) 0
k n a1k n 1
an 0 - это
- характеристическое уравнение
(5)
kx

33. То есть функция будет решением дифференциального уравнения (4), если k является корнем характеристического уравнения.

То есть функция e kx будет решением
дифференциального уравнения (4), если k является
корнем характеристического уравнения.
Основная теорема линейной алгебры говорит о том,
что уравнение (5) с действительными
коэффициентами всегда имеет n корней действительных или комплексных, простых или
кратных (т. е. равных).

34. ФСР в случае действительных различных корней характеристического уравнения.

Если все корни k1 ,k2 , ,kn характеристического
уравнения действительны и различны, то мы знаем n
различных решений дифференциального уравнения
(2):
y1 ek1x , y2 ek2 x ,
, yn ekn x
Эти решения линейно независимы.

35. Докажем это для случая n = 3

Для это составим определитель Вронского:
ek1x
W [ y1 , y2 , y3 ] k1e k1x
k12 ek1x
1
e( k1 k2 k3 ) x k1
k12
1
k2
k22
e k2 x
k 2 e k2 x
k22 e k2 x
e k3 x
k3e k3 x
k32 e k3 x
1
0
k3 e( k1 k2 k3 ) x k1 k3
k32
k12 k32
0
k 2 k3
k22 k32
1
k3
k32
e(k1 k2 k3 ) x (k1 k3 )(k22 k32 ) (k2 k3 )(k12 k32 ) e(k1 k2 k3 ) x (k1 k3 )(k2 k3 ) k2 k3 k1 k3
e( k1 k2 k3 ) x (k1 k3 )(k2 k3 )(k2 k1 ) 0 т.к. все корни
характеристического уравнения различны (по
условию).

36. Значит, по достаточному условию линейной независимости - линейно независимые решения, следовательно, образуют ФСР.

Значит, по достаточному условию линейной
независимости y1 , y2 , , yn - линейно независимые
решения, следовательно, образуют ФСР.
Общее решение ЛОДУ в этом случае по теореме о
структуре общего решения такого уравнения будет:
y C1e C2e
k1 x
k2 x
Cn e
kn x

37. Пример 1

Найти общее решение: y 12 y 35 y 0
Решение (подробное).
Ищем решение в виде: y ekx
Найдем производные: y kekx , y k 2ekx , y k 3ekx
Подставляем в уравнение:
k 3ekx 12k 2ekx 35kekx 0
ekx (k 3 12k 2 35k ) 0
ekx 0,
k 3 12k 2 35k 0 - характеристическое
уравнение
(т.е. при составлении характеристического уравнения третья производная
y дает k 3, вторая производная y дает k 2 , первая производная y дает k , y единицу).

38. Корни характеристического уравнения: Фундаментальная система решений (ФСР):

y1 e0 x 1, y2 e5 x , y3 e7 x
Общее решение составляется так: y C1 y1 C2 y2 C3 y3
(по теореме о структуре общего решения линейного однородного
дифференциального уравнения).
Значит
y C1 1 C2e5 x C3e7 x
Ответ: y C1 C2e5 x C3e7 x
(C1 , C2 , C3 - произвольные постоянные).

39. Пример 2

Найти общее решение: y 2 y 3 y 0
Решение:
k 2 2k 3 0 - характеристическое
уравнение
k1 3, k2 1
y1 e 3 x , y2 e x - ФСР
y C1e 3 x C2e x - общее решение

40.

41.

42.

43.

44.

45. Примеры

Решить уравнения:
1.
x2 1 0
x 2 1
x1,2 1 i
2
x
4 x 13 0
2.
4 16 52 4 36 4 ( 1) 36
x1,2
2
2
2
4 1 36 4 6i
2 3i
2
2

46.

Многие математические положения на языке комплексных
чисел формулируются очень кратко и изящно.
Доказательство многих теорем становится очень
компактным и простым. Вычисления в технике и в таких
науках, как физика, механика, астрономия, значительно
упрощаются.
Большой вклад в развитие теории функций комплексного
переменного внесли русские ученые:
Н. И. Мусхелишвили занимался ее применениями к теории
упругости,
М. В. Келдыш и М. А. Лаврентьев - к аэро- и
гидродинамике,
Н. Н. Богомолов и В. С. Владимиров - к проблемам
квантовой теории поля.
Также комплексными числами пользовался отец русской
авиации Н. Е. Жуковский при разработке теории крыла,
автором которой он является.
Комплексные числа и функции от комплексного
переменного находят применение во многих вопросах
науки и техники.

47. ФСР в случае наличия комплексных корней характеристического уравнения

Пусть ФСР:
y1 ek1x , y2 ek2 x ,
, yn ekn x
k1 , k2 , , kn различны, но среди них есть комплексные:
k1 i , k2 i
Получаем решения дифференциального уравнения:
y1 e( i ) x , y2 e( i ) x
Это комплексные функции, а мы должны найти
действительные решения.

48. Формулы Эйлера

ei x cos x i sin x
ei x e i x
cos x
2
ei x e i x
sin x
2i

49. Так как - решения ЛОДУ, то

Так как y1 e( i ) x , y2 e( i ) x - решения ЛОДУ, то
1
y1 ( y1 y2 ),
2
y2
1
( y1 y2 ) - также решения
2i
(по свойствам решений линейных однородных дифференциальных
уравнений).
Преобразуем y1 , y2 , используя формулы Эйлера.

50. Получим:

1
1
1
y1 ( y1 y2 ) (e( i ) x e( i ) x ) (e x ei x e x e i x )
2
2
2
ei x e i x
e
e x cos x
2
x
y1 e x cos x
y2 e x sin x
Это две линейно независимые функции, так
как их отношение
y1 cos x
ctg x const
y2 sin x

51. Заменим в ФСР на и на , система останется фундаментальной системой решений.

Заменим в ФСР y1 , y2 , , yn
y1 на y1 и y2 на y2 ,
система останется фундаментальной системой
решений.

52. Итак,

каждому простому действительному корню k
характеристического уравнения в ФСР
соответствует решение e kx ,
а паре комплексно сопряженных корней i два решения
e x cos x и e x sin x

53. Пример

Найти общее решение
y 4 y 29 y 0
Решение
y ekx
k 2 4k 29 0 - характеристическое уравнение
k1,2 2 4 29 2 5i
2x
y1 e2 x cos5x , y2 e sin5x - ФСР
y C1e2 x cos5x C2e2 x sin5x - общее решение

54. ФСР в случае кратных корней характеристического уравнения

Если среди корней характеристического уравнения
есть кратные (т.е. равные), то мы сможем найти
частные решения вида e 1 , но их число будет
kx
меньше n , и следовательно, они не будут
составлять ФСР.

55. Утверждение

Каждому действительному корню
характеристического уравнения k1 кратности r в
ФСР соответствуют решения:
ek1x ,xek1x ,x2ek1x , ,xr 1ek1x

56. Доказательство для уравнения второго порядка (n = 2).

Дано дифференциальное уравнение второго порядка с
постоянными коэффициентами
y a1 y a2 y 0 (7)
Его решение ищем в виде y ekx , получаем характеристическое
уравнение k 2 a1k a2 0 , которое по условию имеет два равных
корня k1 k2 .
Одно частное решение есть: y1 ek1x .
Нужно найти второе частное решение, линейно независимое с
первым. Ищем его в виде y2 u( x)ek1x , где u ( x) - неизвестная
функция, которую нужно определить.

57. Определим эту неизвестную функцию из условия, что является решением дифференциального уравнения (7), то есть при

Определим эту неизвестную функцию из условия,
что y2 u( x)ek x является решением
дифференциального уравнения (7), то есть при
1
подстановке в уравнение (7) превращает его в
тождество. Выполним эту подстановку. Для этого
сначала вычислим производные от y2 uek x :
1
y2 u ek1x uk1ek1x
y2 u ek1x u k1ek1x u k1ek1x uk12ek1x u ek1x 2u k1ek1x uk12ek1x
Подставим в уравнение (2).
u ek1x 2u k1ek1x uk12ek1x a1 (u ek1x uk1ek1x ) a2uek1x 0

58. Преобразуем последнее равенство.

Получим
u u (2k1 a1 ) u(k12 a1k1 a2 ) 0
Первая скобка равна нулю, т.к. по теореме Виета
k1 k2 a1 . В нашем случае k1 k2 , значит 2k1 a1 .
Вторая скобка равна нулю, т.к. k1 является корнем
характеристического уравнения.
То есть остается u 0 , отсюда u A, u Ax B .
Можно взять A 1, B 0 , тогда u x , и y2 xek x.
1

59. Два решения

y1 ek x , y2 xek x
1
1
линейно независимы, так как их отношение
y2 xek1x
k1x x const .
y1 e
Значит y1 e 1 , y2 xe 1 образуют фундаментальную
kx
kx
систему решений (ФСР) линейного однородного
дифференциального уравнения второго порядка (7) , и общее
решение этого уравнения имеет вид:
y C1ek1x C2 xek1x

60. Примеры

Найти общее решение
1.
y 6 y 9 y 0
y ekx
k 2 6k 9 0
( k 3 )2 0
k1,2 3
y1 e3 x , y2 xe3 x - ФСР
y C1e3 x C2 xe3 x - общее решение

61. 2.

y( 4 ) 5 y 6 y 0
Решение ищем в виде
y ekx
k 4 5k 3 6k 2 0
k 2 ( k 2 5k 6 ) 0
k1,2 0, k3 2, k4 3
y1 e0 x 1, y2 xe0 x x, y3 e2 x , y4 e3 x
y C1 C2 x C3e2 x C4e3 x
-ФСР
- общее решение

62. Таблица для n = 2

Корни характеристического
уравнения
Общее решение ЛОДУ второго
порядка с постоянными
коэффициентами
1. k1 k2
действительные и различные
y C1ek1x C2ek2 x
2. k1 k2 k
кратные (равные)
y C1ekx C2 xekx
3. k1,2 i
комплексные
y C1e x cos x C2e xsin x
3а. k1,2 i
чисто мнимые
y C1cos x C2sin x