Корреляционный анализ. Лекция №5

1.

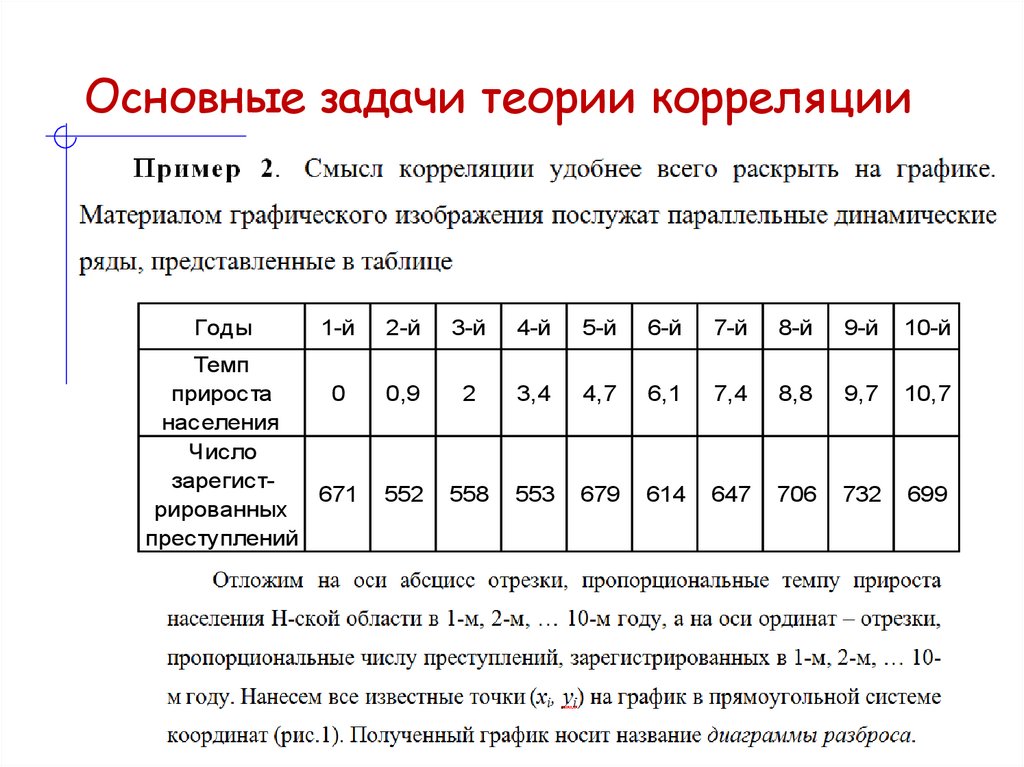
Корреляционный анализ
Основные задачи теории корреляции
Коэффициент линейной корреляции
Пирсона
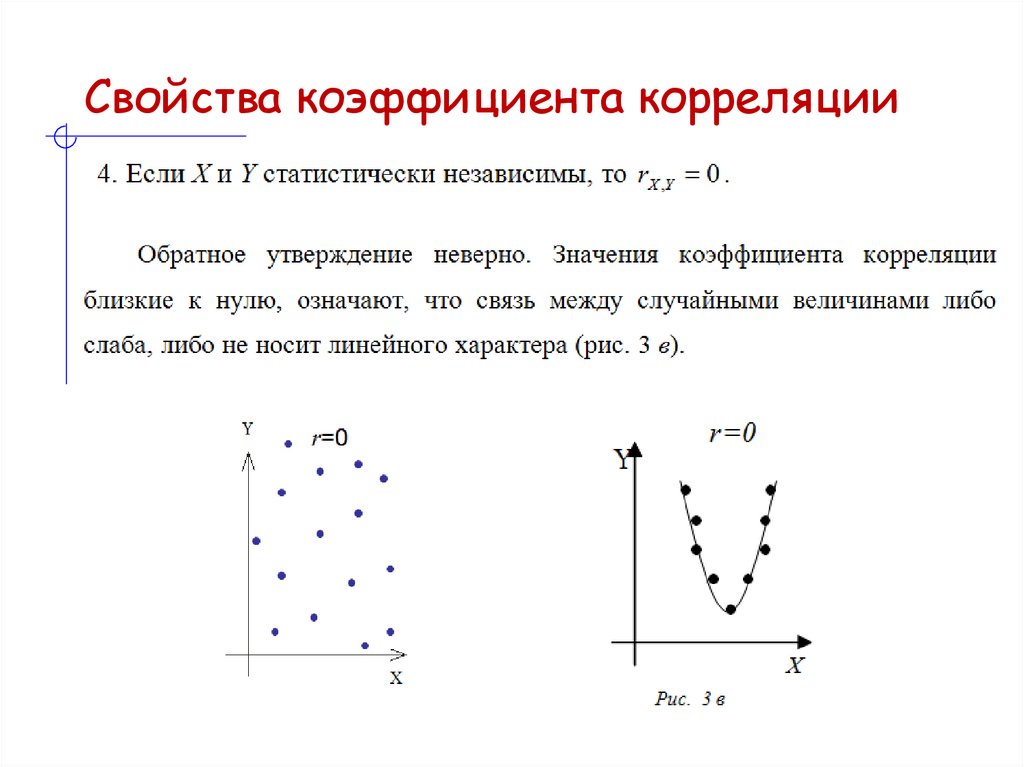
Свойства коэффициента корреляции
Проверка гипотезы о значимости
выборочного коэффициента корреляции
Оценка значения коэффициента
корреляции

2. Основные задачи теории корреляции

3. Основные задачи теории корреляции

4. Основные задачи теории корреляции

Годы
1-й
Темп
прироста
0
населения
Число
зарегист671
рированных
преступлений
2-й
3-й
4-й
5-й
6-й
7-й
8-й
9-й
10-й
0,9
2
3,4
4,7
6,1
7,4
8,8
9,7
10,7
552
558
553
679
614
647
706
732
699

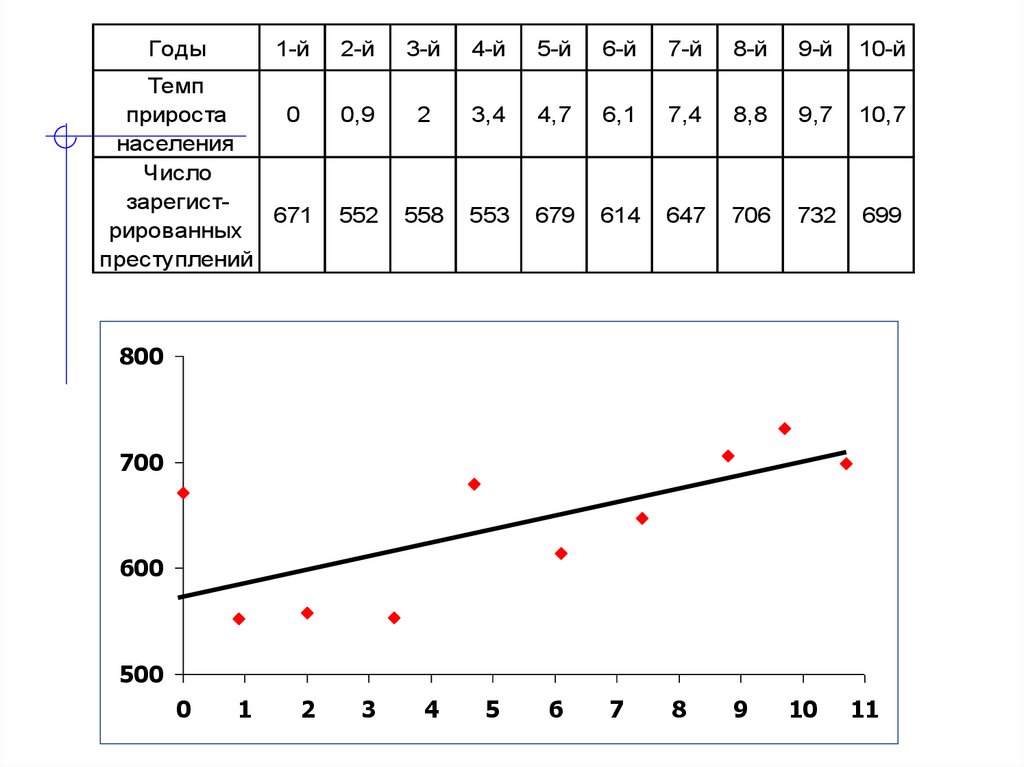
5.

Годы
1-й
Темп
прироста
0
населения
Число
зарегист671
рированных
преступлений
2-й
3-й
4-й
5-й
6-й
7-й
8-й
9-й
10-й
0,9
2
3,4
4,7
6,1
7,4
8,8
9,7
10,7
552
558
553
679
614
647
706
732
699
3
4
5
6
7
8
9
10
11
800
700
600
500
0
1
2

6. Основные задачи теории корреляции

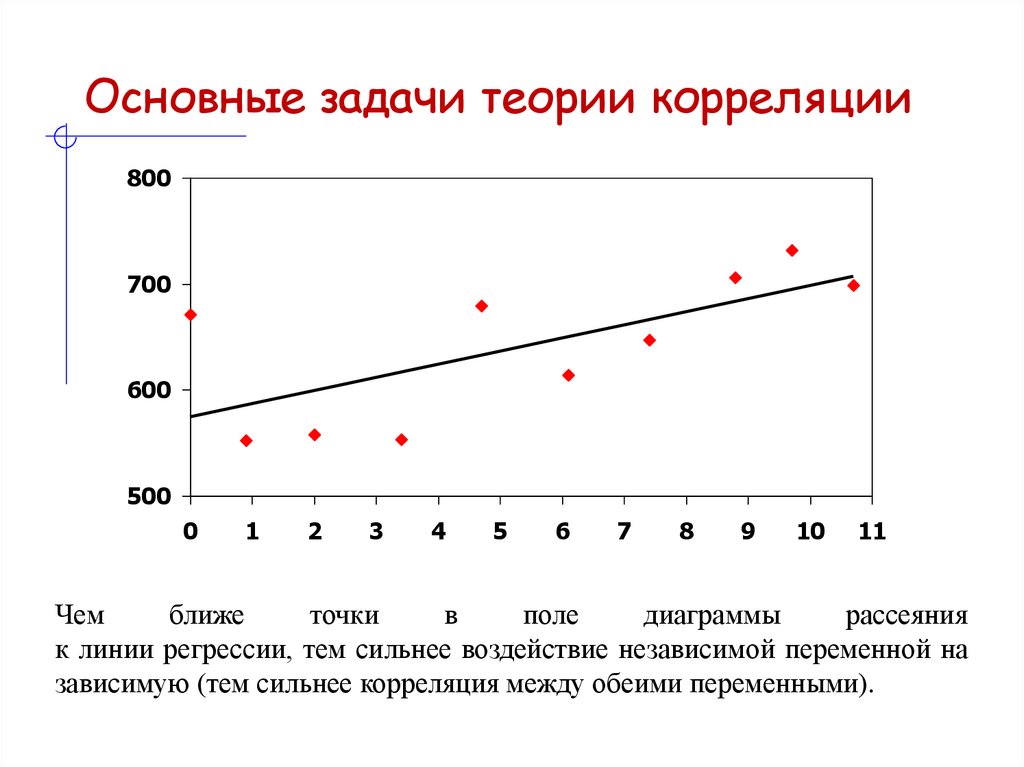
Линия регрессии – это графическое
представление ведущей тенденции связи
между количественными признаками.

7. Чем ближе точки в поле диаграммы рассеяния к линии регрессии, тем сильнее воздействие независимой переменной на зависимую (тем

Основные задачи теории корреляции
800
700
600
500
0
1
2
3
4
5
6
7
8
9
10
11
Чем
ближе
точки
в
поле
диаграммы
рассеяния
к линии регрессии, тем сильнее воздействие независимой переменной на
зависимую (тем сильнее корреляция между обеими переменными).

8. Основные задачи теории корреляции

9. Коэффициент линейной корреляции Пирсона

10. Коэффициент линейной корреляции Пирсона

11. Коэффициент линейной корреляции Пирсона

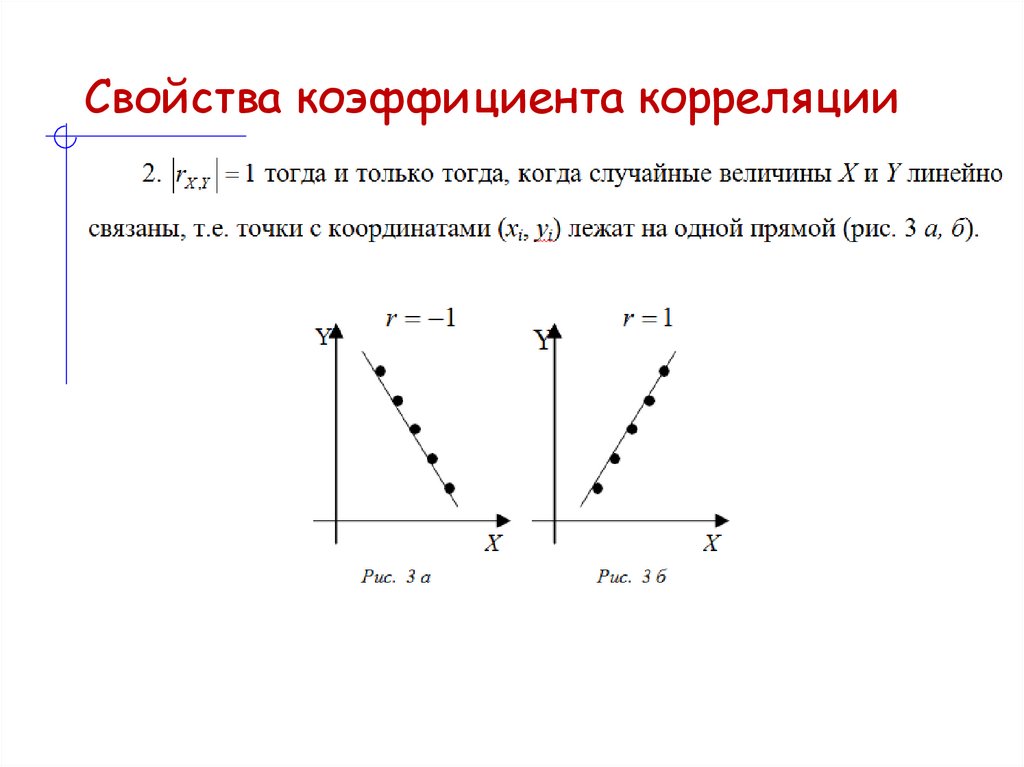
12. Свойства коэффициента корреляции

13. Свойства коэффициента корреляции

14. Свойства коэффициента корреляции

15. Свойства коэффициента корреляции

16. Свойства коэффициента корреляции

17. Проверка гипотезы о значимости выборочного коэффициента корреляции

18. Проверка гипотезы о значимости выборочного коэффициента корреляции

19. Оценка значения коэффициента корреляции

20. Оценка значения коэффициента корреляции

r 0 – связь отсутствует;
r 0,3 – связь слабая;
0,3 < r 0,5 – связь умеренная;
0,5< r 0,7 – связь значительная;
0,7 < r 0,9 – связь сильная;
0,9 < r – очень сильная;
r = 1– функциональная связь.

21. Оценка значения коэффициента корреляции

22. Оценка значения коэффициента корреляции

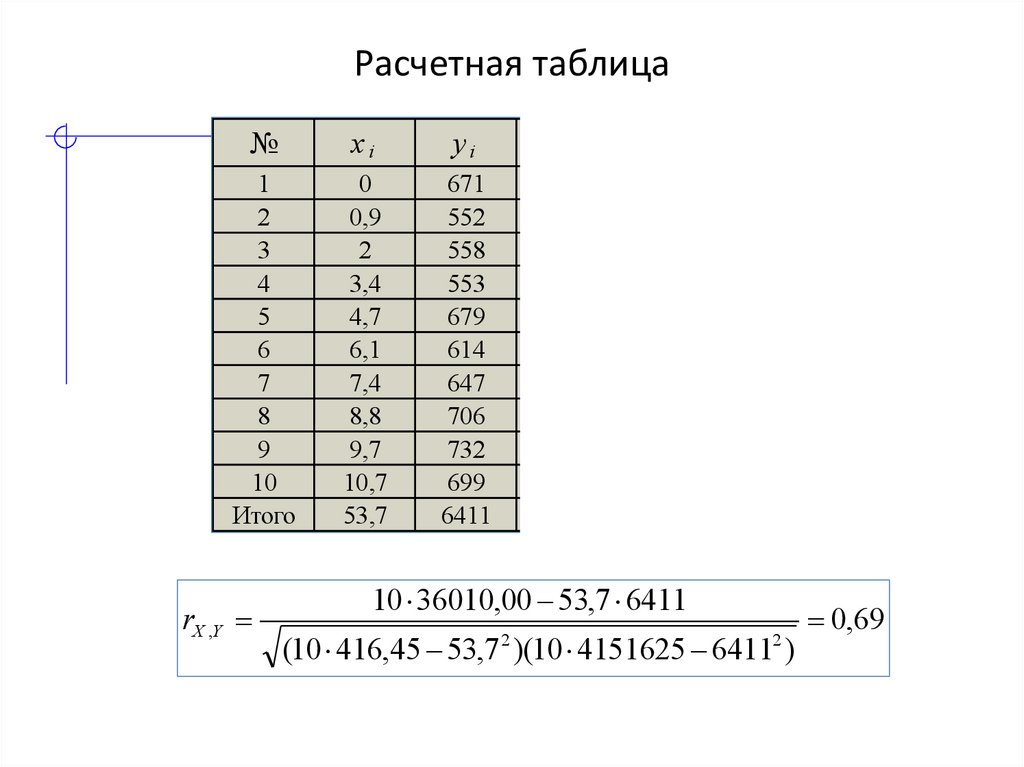
23. Расчетная таблица

№
хi
yi
хi 2
1
2
3
4
5
6
7
8
9
10
Итого
0
0,9
2
3,4
4,7
6,1
7,4
8,8
9,7
10,7
53,7
671
552
558
553
679
614
647
706
732
699
6411
0
450241
0,81
304704
4
311364
11,56 305809
22,09 461041
37,21 376996
54,76 418609
77,44 498436
94,09 535824
114,49 488601
416,45 4151625
rX ,Y
yi 2
хi yi
0
496,8
1116
1880,2
3191,3
3745,4
4787,8
6212,8
7100,4
7479,3
36010
10 36010,00 53,7 6411
(10 416,45 53,7 )(10 4151625 6411 )
2
2
0,69

24. Оценка значения коэффициента корреляции

25. Оценка значения коэффициента корреляции

26. Оценка значения коэффициента корреляции

27. Оценка значения коэффициента корреляции

28. Проверка гипотезы о значимости выборочного коэффициента корреляции

29. Проверка гипотезы о значимости выборочного коэффициента корреляции

30. Проверка гипотезы о значимости выборочного коэффициента корреляции