Похожие презентации:
Простые одномерные методы численного интегрирования
1.
Презентация к отчёту по вычислительнойпрактике на тему:
«Простые одномерные методы численного
интегрирования»
Выполнил:
Невзоров Николай Владимирович
Студент 1 курса группы 06-412
2.
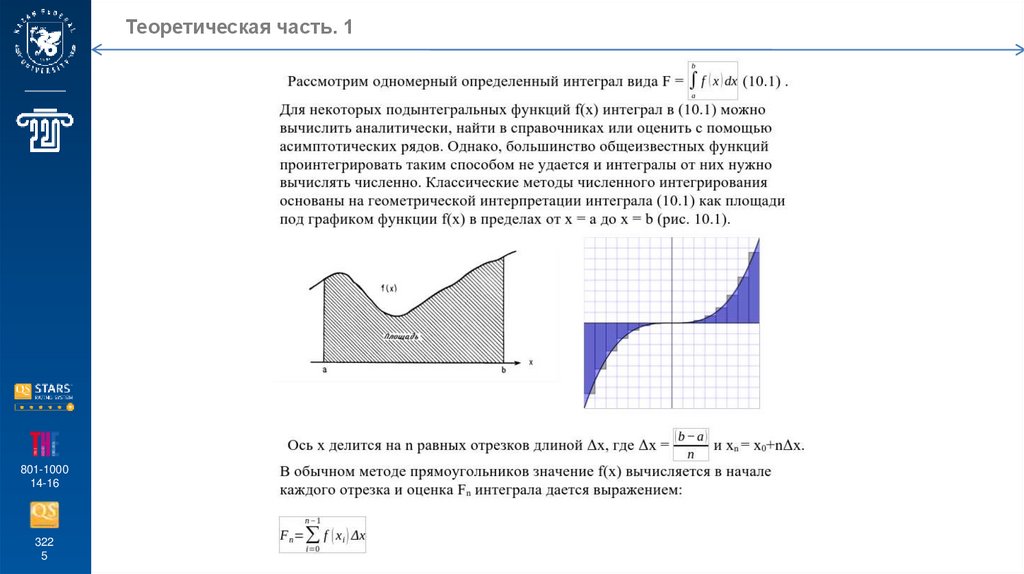
Теоретическая часть. 1801-1000
14-16
322
5
3.
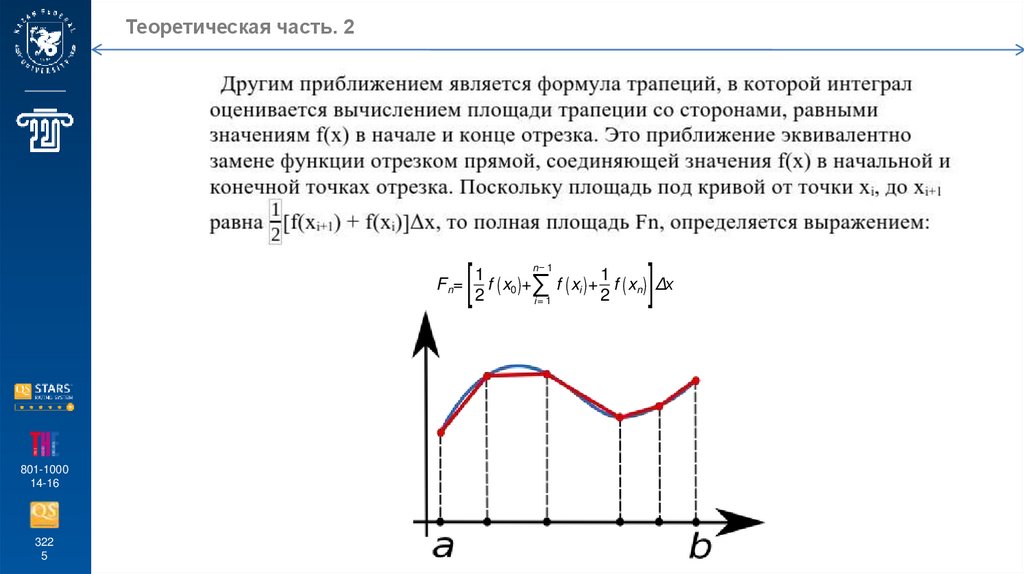
Теоретическая часть. 2[
n− 1
]
1
1
F n= f ( x0 )+ ∑ f ( xi )+ f ( xn ) Δx
2
2
i= 1
801-1000
14-16
322
5
4.
Решение задач:10.1 а)
801-1000
14-16
322
5
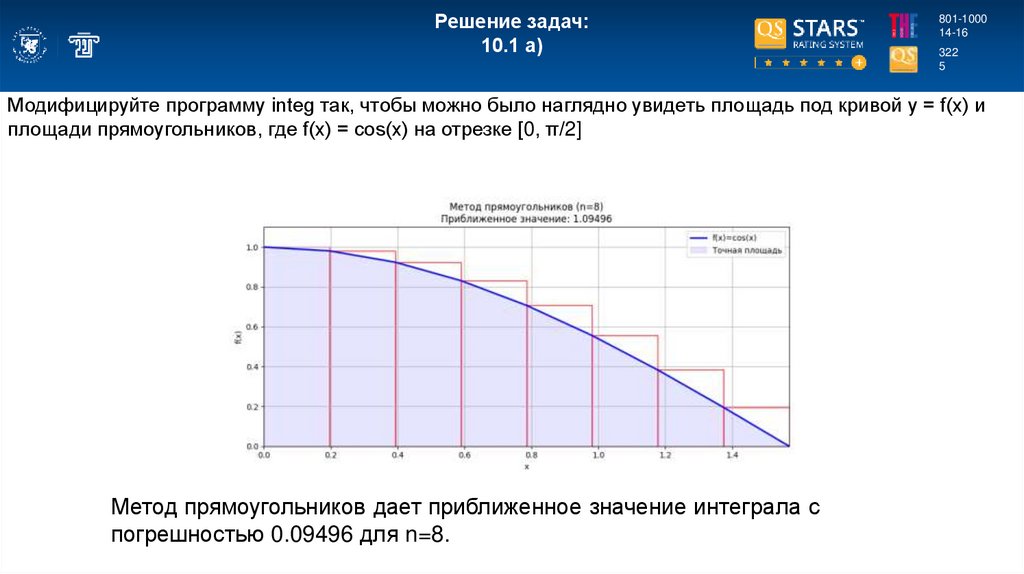
Модифицируйте программу integ так, чтобы можно было наглядно увидеть площадь под кривой у = f(х) и
площади прямоугольников, где f(x) = cos(x) на отрезке [0, π/2]
Метод прямоугольников дает приближенное значение интеграла с
погрешностью 0.09496 для n=8.
5.
Решение задач:10.1 б)
801-1000
14-16
322
5
Используя метод прямоугольников, оцените численно определенные интегралы от функций f(x) = 2x +3x2 +
4x3 и f(x) =е-x на отрезке 0 ≤ x ≤ 1. Как приблизительно зависит погрешность от n в каждом случае?
Погрешность уменьшается с ростом n. Погрешность ∆n ≈ 1/n
6.
Решение задач:10.2 а)
801-1000
14-16
322
5
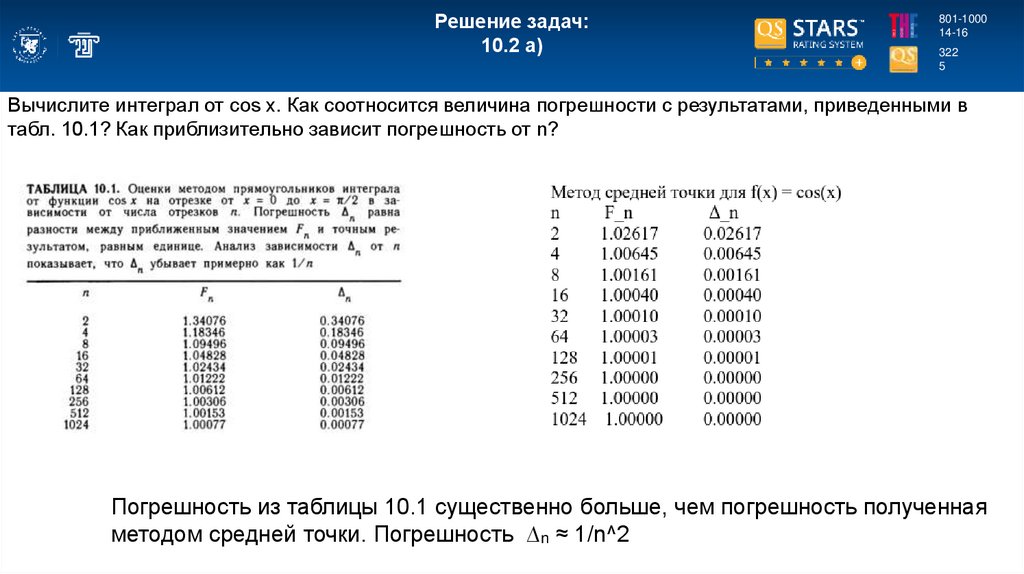
Вычислите интеграл от cos x. Как соотносится величина погрешности с результатами, приведенными в
табл. 10.1? Как приблизительно зависит погрешность от n?
Погрешность из таблицы 10.1 существенно больше, чем погрешность полученная
методом средней точки. Погрешность ∆n ≈ 1/n^2
7.
Решение задач:10.2 б)
801-1000
14-16
322
5
Используя метод средней точки, оцените определенные интегралы от функций f(x) = 2x + 3x2 + 4x3 и f(x) = ex , на отрезке 0 ≤ x ≤ 1. Как приблизительно зависит погрешность от n каждом случае?
Погрешность ∆n ≈ 1/n^2
8.
Решение задач:10.3 а)
801-1000
14-16
322
5
Каким образом можно модифицировать подпрограмму Simpson для одновременного получения оценок
интеграла от функции f(x) по формулам трапеций и Симпсона?
9.
Решение задач:10.3 б)
801-1000
14-16
322
5
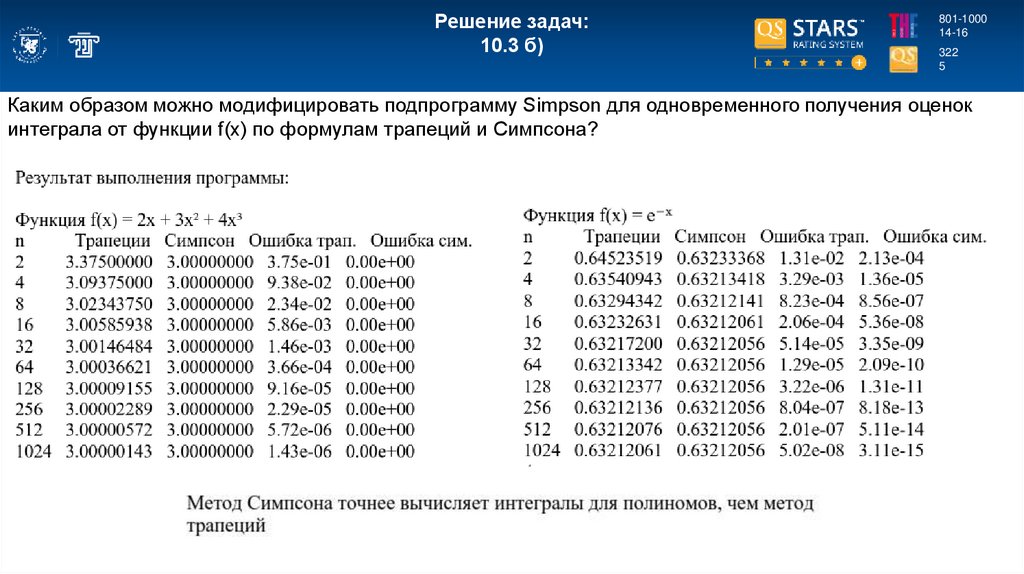
Каким образом можно модифицировать подпрограмму Simpson для одновременного получения оценок
интеграла от функции f(x) по формулам трапеций и Симпсона?
10.
Решение задач:10.3 в)
801-1000
14-16
322
5
−1
Используя формулу Симпсона, оцените значение интеграла от функции
на отрезках -1 ≤ x ≤ 1, -2 ≤ x ≤ 2 и -3 ≤ x ≤ 3
2
( 2π) 2 e− x
11.
Решение задач:10.3 г)
Используя оба метода, оцените определенный интеграл от функции (1+x^2)^-1
на отрезках 0 ≤ x ≤ 1 и 0 ≤ x ≤ 2. Какой метод приводит к лучшим результатам? Помните о
более высокого порядка не всегда дает более высокую точность.
801-1000
14-16
322
5
том, что метод
12.
Решение задач:10.3 д)
801-1000
14-16
322
5
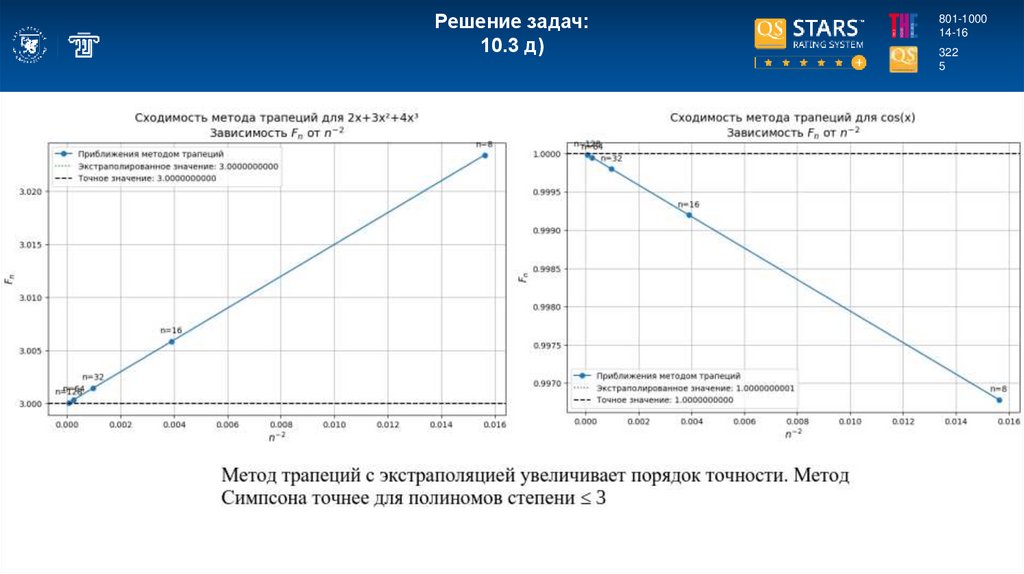
Постройте график оценки Fn , в зависимости от n2 и получите экстраполированноезначение F. Какие
предположения необходимо сделать для того, чтобы процедура экстраполяции была успешной?
Примените описанный метод к интегралам, рассмотренным в предыдущих задачах, и сравните
полученные результаты с тем, что дают один метод трапеций и
метод Симпсона.
13.
Решение задач:10.3 д)
801-1000
14-16
322
5
14.
Выводы:801-1000
14-16
322
5
15.
Спасибо за внимание!Выполнил:
Невзоров Николай Владимирович
Студент 1 курса группы 06-412









 Информатика
Информатика








