Похожие презентации:
Курсовой проект на тему: Написать программу «Приближённые методы численного интегрирования»
1. КУРСОВОЙ ПРОЕКТ по дисциплине: “Основы алгоритмизации и программирование” на тему: Написать программу «Приближённые методы
Федеральное агентство по рыболовствуФедеральное государственное бюджетное образовательное
учреждение высшего образования
«Астраханский государственный технический университет»
Система менеджмента качества в области образования, воспитания, науки и инноваций
сертифицирована
ООО «ДКС РУС» по международному стандарту ISO 9001:2015
КУРСОВОЙ ПРОЕКТ
по дисциплине:
“Основы алгоритмизации и программирование”
на тему:
Написать программу «Приближённые методы численного интегрирования
(метод прямоугольников, метод трапеций, метод парабол)»
Выполнил: обучающийся группы ДИПРб-11
Ушаков Виталий Витальевич
Руководитель: асс. Кравченкова Елена Павловна
Астрахань 2025
1
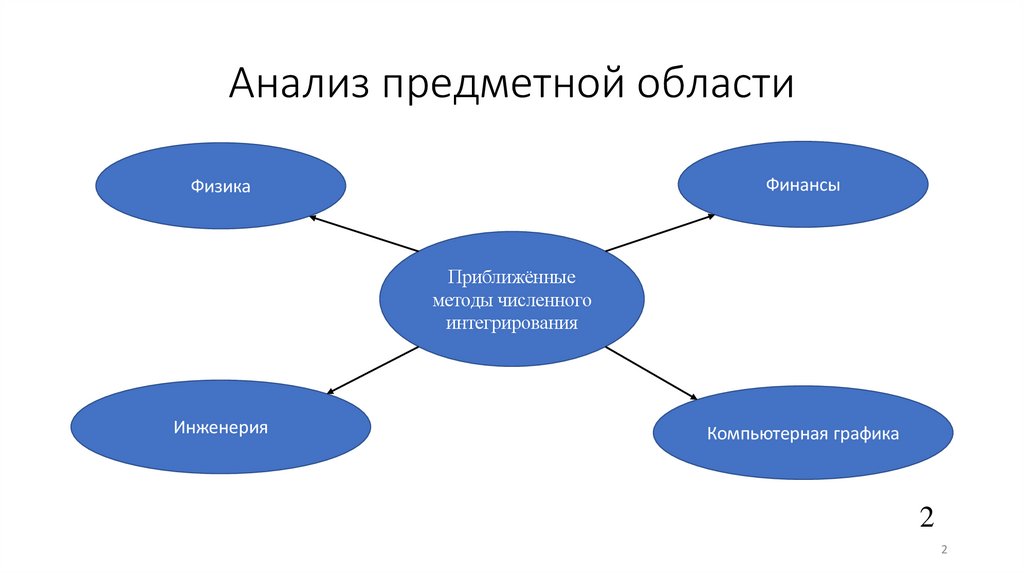
2. Анализ предметной области
ФинансыФизика
Приближённые
методы численного
интегрирования
Инженерия
Компьютерная графика
2
2
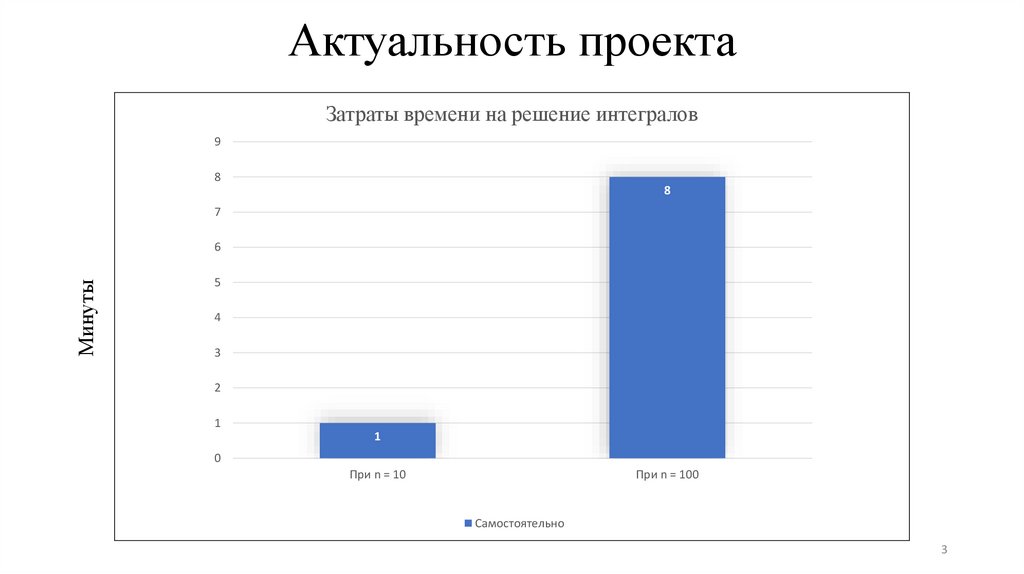
3.
Актуальность проектаЗатраты времени на решение интегралов
9
8
8
7
Минуты
6
5
4
3
2
1
1
0
При n = 10
При n = 100
Самостоятельно
3
4.
ЦЕЛЬ КУРСОВОГО ПРОЕКТАУглублённое изучение материала по дисциплинам «Основы
алгоритмизации и программирование» и «Математический анализ» по
теме «Приближённые методы численного интегрирования (метод
прямоугольников, метод трапеций, метод парабол).»
4
5.
ЗАДАЧИ КУРСОВОГО ПРОЕКТАДля реализации поставленной цели, необходимо решить следующие задачи:
1. Анализ предметной области по теме: «Приближённые методы численного
интегрирования»
2. Раскрытие основных понятий изучаемых дисциплин: «Основы
алгоритмизации и программирование» и «Математический анализ».
3. Разработка технического задания (входные, выходные данные, все, что будет
делать, разрабатываемая программа).
4. Разработка программного продукта, который предоставляет пользователю
возможность находить приближенное значение интегралов с помощью
приближенных методов числового интегрирования.
5
6.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛb
f
(
x
)
dx
a
Определенный интеграл - число,
равное площади криволинейной
трапеции – фигуры, ограниченной
графиком положительной на отрезке
[a;b] функции y = f(x), прямыми x = a и
x = b, осью OX.
Приближенные методы заменяют
вычисление интеграла суммированием
значений функции в конечном числе
точек.
6
7.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛИнтервал [a, b] делится на n частей в длину.
b a
h
n
h – шаг разбиения, то есть длина каждого
подотрезка.
Чем меньше h, тем выше точность
приближенного
интегрирования.
7
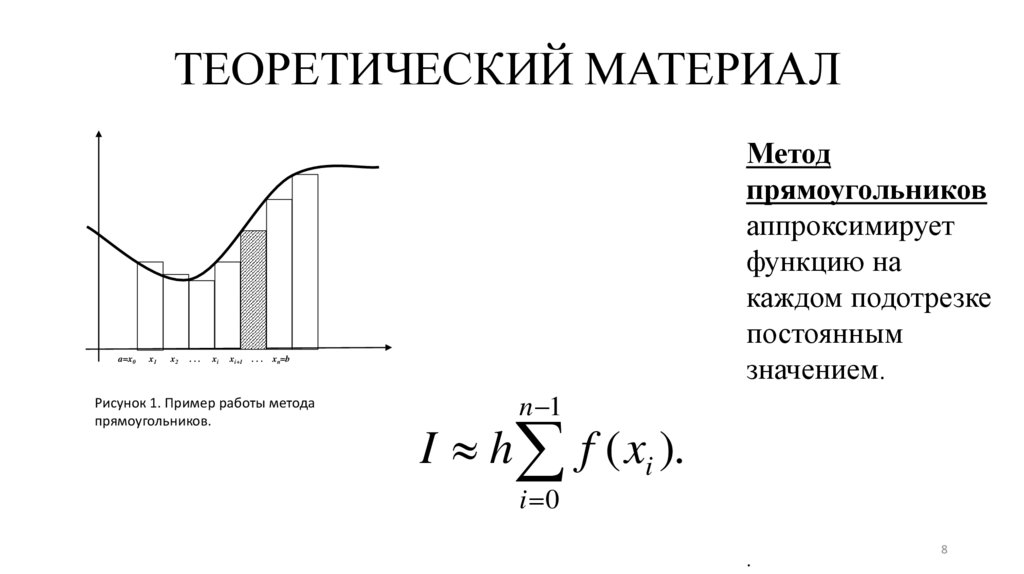
8.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛa=x0
x1
x2
...
xi
xi+1
...
Метод
прямоугольников
аппроксимирует
функцию на
каждом подотрезке
постоянным
значением.
xn=b
Рисунок 1. Пример работы метода
прямоугольников.
n 1
I h f ( xi ).
i 0
.
8
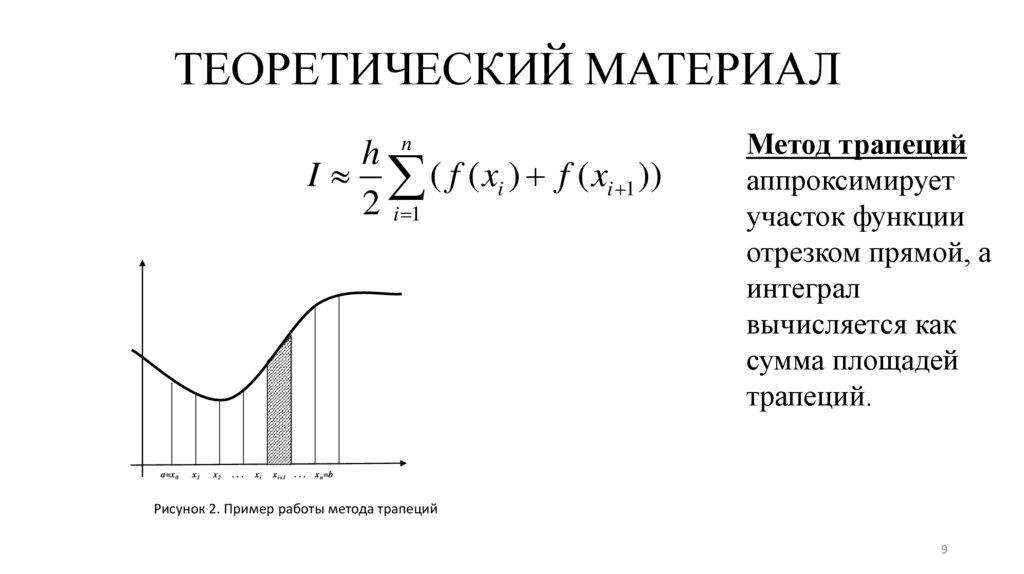
9.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛh n
I ( f ( xi ) f ( xi 1 ))
2 i 1
a=x0
x1
x2
...
xi
xi+1
...
Метод трапеций
аппроксимирует
участок функции
отрезком прямой, а
интеграл
вычисляется как
сумма площадей
трапеций.
xn=b
Рисунок 2. Пример работы метода трапеций
9
10.
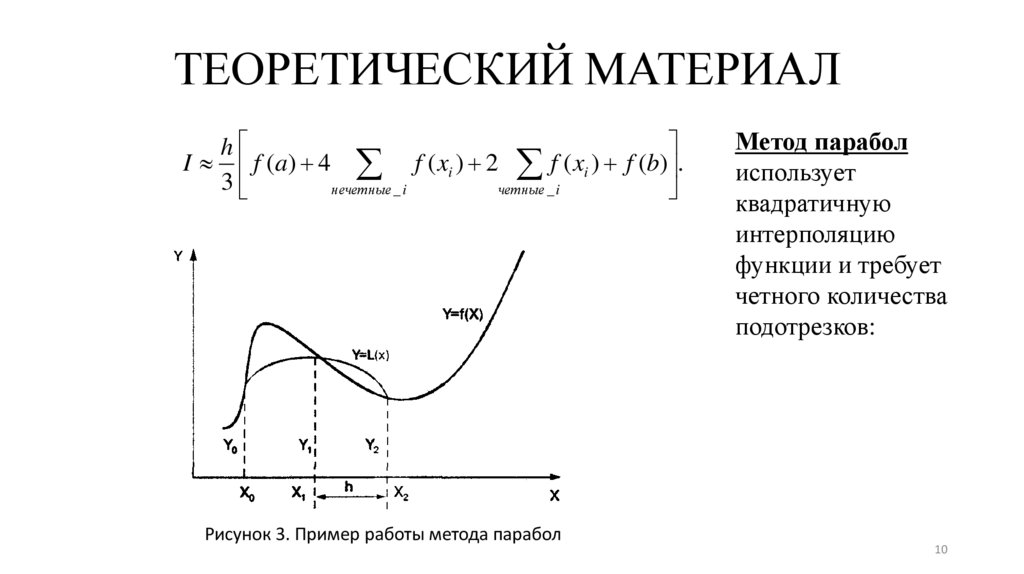
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛh
I f (a) 4 f ( xi ) 2 f ( xi ) f (b) .
3
нечетные _ i
четные _ i
Рисунок 3. Пример работы метода парабол
Метод парабол
использует
квадратичную
интерполяцию
функции и требует
четного количества
подотрезков:
10
11.
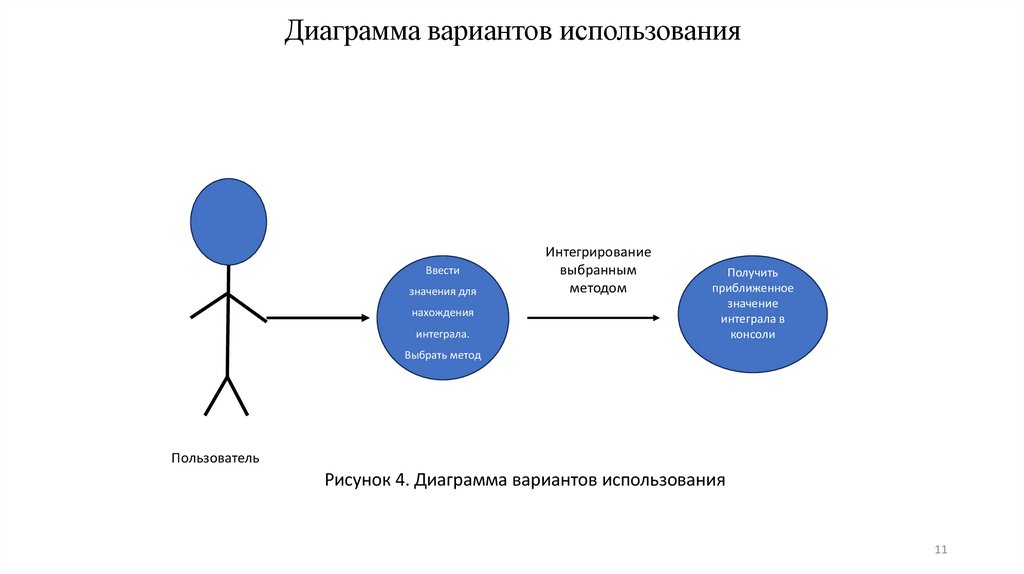
Диаграмма вариантов использованияВвести
значения для
нахождения
интеграла.
Интегрирование
выбранным
методом
Получить
приближенное
значение
интеграла в
консоли
Выбрать метод
Пользователь
Рисунок 4. Диаграмма вариантов использования
11
12.
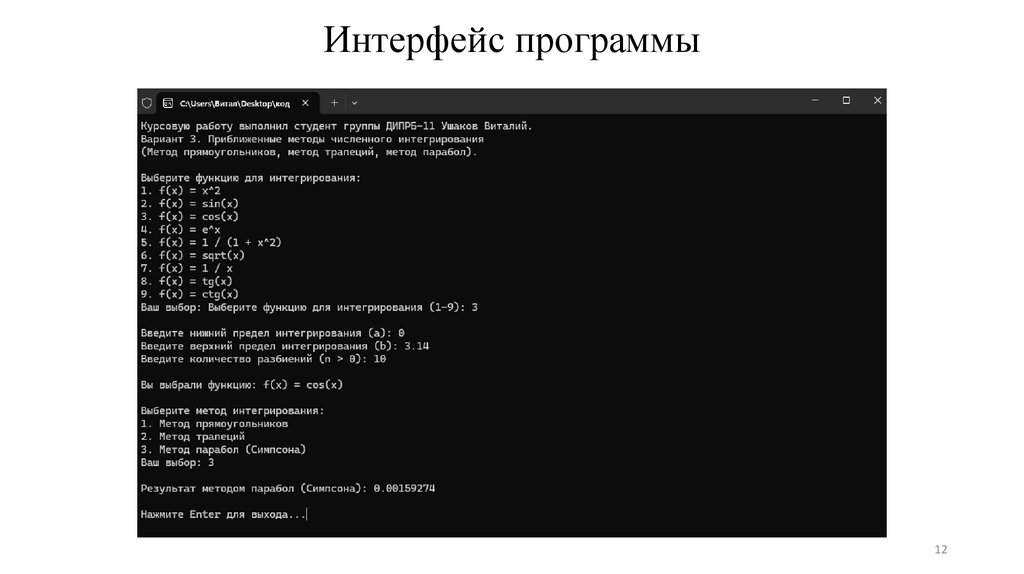
Интерфейс программы12
13.
Входные и выходные данныеВходные данные:
• Нижний предел (R – значение из
множества действительных чисел)
• Верхний предел (R – значение из
множества действительных чисел).
• Шаг разбиения (N+ – значение из
множества положительных
натуральных чисел).
• Номер функции из предложенного
списка (целое число от 1 до 9).
• Номер метода интегрирования (целое
число от 1 до 3).
Выходные данные:
• Численное значение определённого
интеграла, вычисленное выбранным
методом.
13
14.
Средства разработкиЯзык разработки: С++ (17)
Среда разработки: Visual Studio 2022 (17.14.0)
Документации: MS Word 2021
Презентация: MS Power Point 2021
14
15.
Системные требованияПроцессор: процессор с тактовой частотой не менее 1,6 ГГц;
Оперативная память: не менее 512 МБ ОЗУ;
Жесткий диск: не менее 200 МБ свободного места на жестком
диске;
ОС: Windows 10 (x64).
15
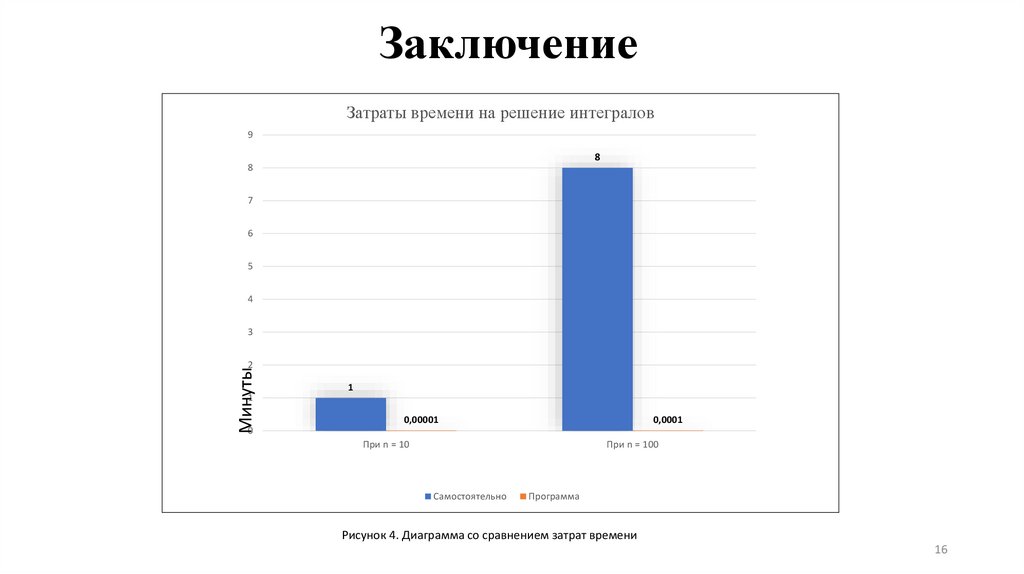
16. Заключение
Затраты времени на решение интегралов9
8
8
7
6
5
4
3
Минуты
2
1
1
0,00001
0,0001
0
При n = 10
При n = 100
Самостоятельно
Программа
Рисунок 4. Диаграмма со сравнением затрат времени
16
17.
Спасибо за внимание!17









 Программирование
Программирование Информатика
Информатика








