Теория вероятностей и математическая статистика

1. Теория вероятностей и математическая статистика

2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
Предметом теории вероятностей является изучение
вероятностных закономерностей массовых однородных
случайных событий.

2.

• Понятие вероятности вводится как мера
правдоподобия случайного события
Представление данных в виде таблиц, диаграмм, графиков,
интерпретация данных.
7 класс
Описательная статистика: среднее арифметическое,
медиана, размах, наибольшее и наименьшее значения набора
числовых данных. Примеры случайной изменчивости.
Случайный эксперимент (опыт) и случайное событие.
Вероятность и частота. Роль маловероятных и практически
достоверных событий в природе и в обществе. Монета и
игральная кость в теории вероятностей.
Графы
Описательная статистика: среднее арифметическое, медиана, размах, наибольшее и
наименьшее значения, квартили, среднее гармоническое, среднее гармоническое
числовых данных.
Примеры случайной изменчивости при измерениях, в массовом производстве,
тенденции и случайные колебания, группировка данных, представление случайной
изменчивости с помощью диаграмм, частоты значений, статистическая устойчивость.
Утверждения и высказывания. …
Случайный эксперимент (опыт) и случайное событие. Вероятность и частота случайного
события. Роль маловероятных и практически достоверных событий в природе и в
обществе.

3. 8 класс

• Множество. Операции над множествами …
• Измерение рассеивания данных. Дисперсия и стандартное
отклонение числовых наборов. Диаграмма рассеивания.
• Элементарные события случайного опыта. Случайные
события. Вероятности событий. Опыты с
равновозможными элементарными событиями.
Случайный выбор. Связь между маловероятными и
практически достоверными событиями в природе, обществе
и науке.
• Дерево. … Правило умножения. Решение задач с помощью
графов.
• Противоположные события. Диаграмма Эйлера.
Объединение и пересечение событий. Несовместные
события. Формула сложения вероятностей. Условная
вероятность. Правило умножения. Независимые события.
Представление эксперимента в виде дерева. Решение задач на
нахождение вероятностей с помощью дерева случайного
эксперимента, диаграмм Эйлера.

4. 9 класс

• Перестановки и факториал. Сочетания и число сочетаний.
Треугольник Паскаля. Решение задач с использованием
комбинаторики.
• Геометрическая вероятность. Случайный выбор точки из
фигуры на плоскости, из отрезка и из дуги окружности.
• Испытание. Успех и неудача. Серия испытаний до первого
успеха. Серия испытаний Бернулли. Вероятности событий
в серии испытаний Бернулли.
• Случайная величина и распределение вероятностей.
Математическое ожидание и дисперсия. Примеры
математического ожидания как теоретического среднего
значения величины. Математическое ожидание и дисперсия
случайной величины «число успехов в серии испытаний
Бернулли».
• Понятие о законе больших чисел. Измерение вероятностей
с помощью частот. Роль и значение закона больших чисел в
природе и обществе.

5.

• Испытание (опыт, эксперимент, наблюдение) –
это выполнение определенного комплекса
условий или действий, который может быть
воспроизведен неограниченное число раз, при
которых происходит соответствующее явление.
• Событие – возможный результат (исход) опыта
или наблюдения, т.е. любой факт, который
может наступить в условиях испытания.
A1, A2 ,
, An - события

6. Виды событий

• Достоверное
• Случайное
- событие,
которое в
данном опыте
обязательно
произойдет
- событие, которое
- событие,
в данном
которое не
испытании может
может
либо произойти, осуществиться в
либо не
эксперименте
произойти.
• Невозможное
∅

7.

• Случайное событие, наступившее в результате
испытания, которое невозможно представить в виде
суммы более простых событий, связанных с тем же
испытанием, называют элементарным событием
или элементарным исходом испытания.
• Пространство
элементарных
исходов
совокупность
всех
элементарных
исходов
испытания.
пространство элементарных событий
1, 2 ,
i
, n
- элементарные исходы
А
Все исходы, входящие в подмножество А, называются
исходами, благоприятствующими событию А.

8.

• Испытание – подбрасывание игрального кубика
• Элементарные исходы: i= {выпало число i на
игральном кубике}, i=1,2,…, 6.
• ={ 1, 2, 3, 4, 5, 6}
• A – {выпало число 2 на игральном кубике}
• А={ 2}
• B – {на игральном кубике выпало четное число}
• В={ 2, 4, 6}
• С – {на игральном кубике выпало нечетное число}
• С={ 1, 3, 6}
• D – {на игральном кубике выпало больше 4}
D={ 5, 6}

9.

• Испытание – подбрасывание игрального кубика
• Элементарные исходы: i= {выпало число i на
игральном кубике}, i=1, 2, …, 6.
• ={ 1, 2, 3, 4, 5, 6}
• Е – {выпало не больше 6}
• Е={ 1, 2, 3, 4, 5, 6} =
• F – {на игральном кубике выпало 7}
• F=∅

10.

• События называют равновозможными, если
есть основания считать, что ни одно из них не
является более возможным, чем другое.
A – {выпало число 2 на игральном кубике}
A1– {выпало число 6 на игральном кубике}
B – {на игральном кубике выпало четное число}
С – {на игральном кубике выпало нечетное число}
A и A1 – равновозможные
B и С – равновозможные

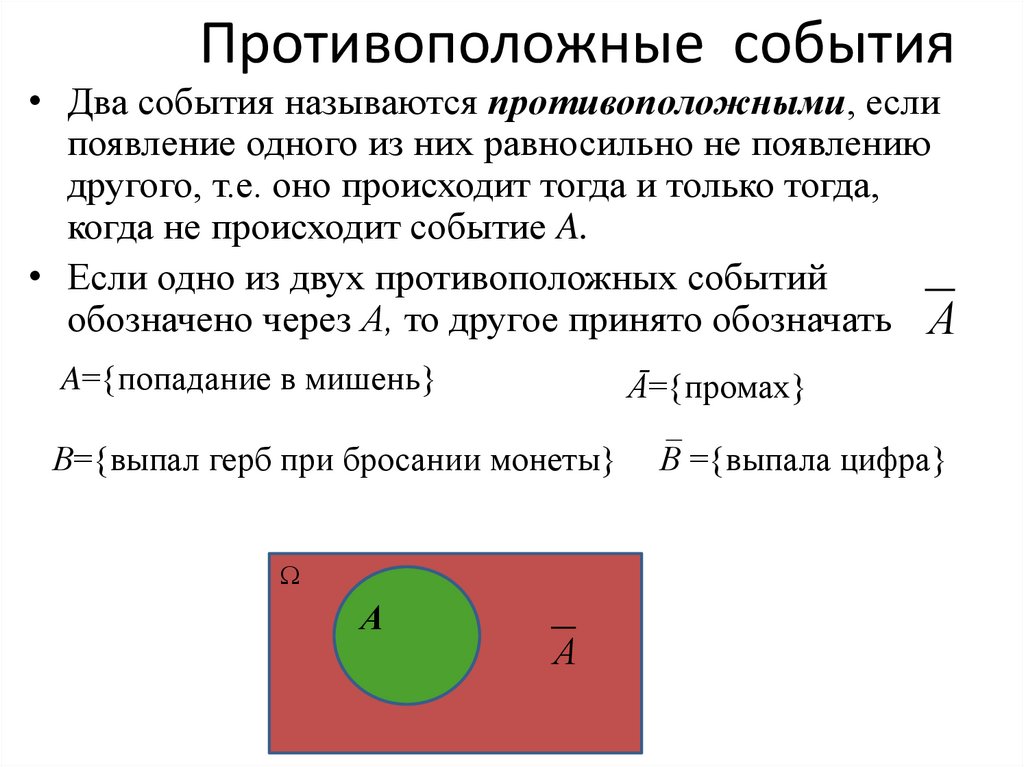
11. Противоположные события

• Два события называются противоположными, если
появление одного из них равносильно не появлению
другого, т.е. оно происходит тогда и только тогда,
когда не происходит событие A.
• Если одно из двух противоположных событий
обозначено через А, то другое принято обозначать A
A={попадание в мишень}
Ā={промах}
В={выпал герб при бросании монеты}
А
A
В ={выпала цифра}

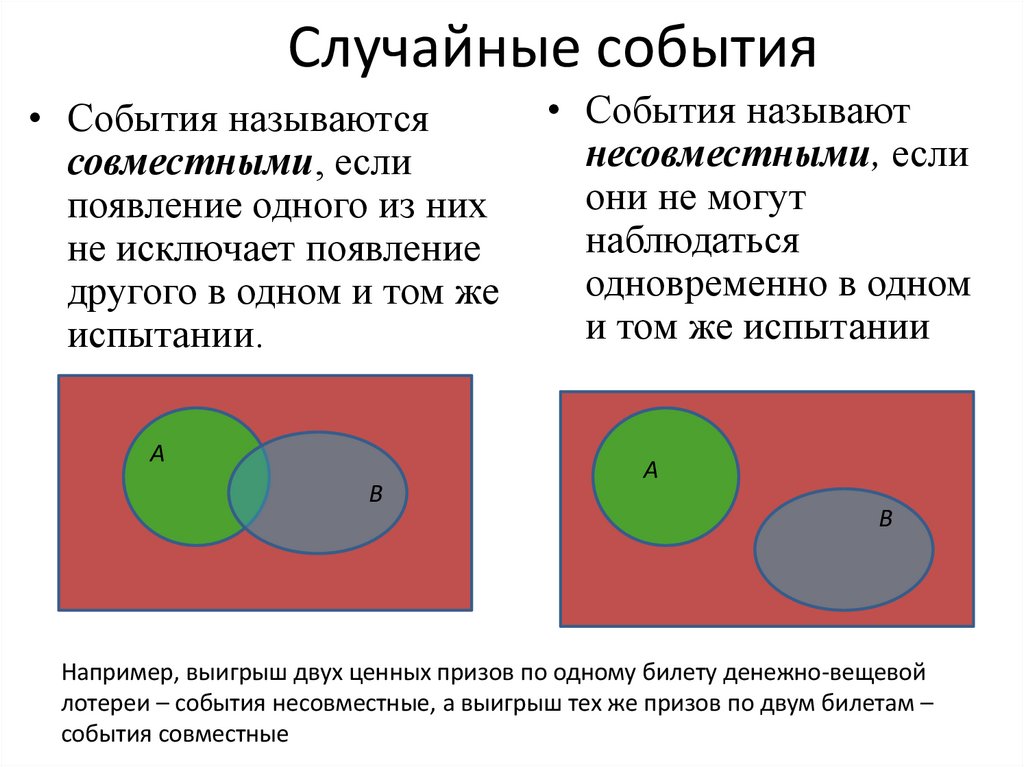
12. Случайные события

• События называются
совместными, если
появление одного из них
не исключает появление
другого в одном и том же
испытании.
А
В
• События называют
несовместными, если
они не могут
наблюдаться
одновременно в одном
и том же испытании
А
В
Например, выигрыш двух ценных призов по одному билету денежно-вещевой
лотереи – события несовместные, а выигрыш тех же призов по двум билетам –
события совместные

13.

• Какие события являются совместными, А и В D и С
DиВ
а какие несовместными? А и С С и В
• Элементарные исходы: i= {выпало число i на
игральном кубике}, i=1,2,…, 6.
• ={ 1, 2, 3, 4, 5, 6}
• A – {выпало число 2 на игральном кубике}
• А={ 2}
• B – {на игральном кубике выпало четное число}
• В={ 2, 4, 6}
• С – {на игральном кубике выпало нечетное число}
• С={ 1, 3, 5}
• D – {на игральном кубике выпало больше 4}
• D={ 5, 6}

14. Полная группа событий

• Несколько событий Н1, Н2, , Нn образуют
полную
группу,
если
они
попарно
несовместны и в каждом испытании появится
только одно из них, т.е. в результате испытания
появится хотя бы одно из них.
• События, образующие полную группу, попарно
несовместны, и в результате испытания
появится одно и только одно из этих событий.
• ={ 1, 2, 3, 4, 5, 6}
• Нi={выпало число i на игральном кубике},
i=1,2,…, 6.

15.

• З а д а ч а . Бросают две игральные кости.
Выпишите полную группу событий данного
испытания.
Р е ш е н и е.
• ωij – на первой кости выпало i очков, на второй – j.
• Все такие событий равновозможные, несовместны
и образуют полную группу, т. е. являются
элементарными исходами.
11
21
31
41
51
61
12
22
32
42
52
62
13
23
33
43
53
63
14
24
34
44
54
64
15
25
35
45
55
65
16
26
36
46
56
66

16. Сумма событий

• Суммой, или объединением двух
событий А и В называют событие,
состоящее в появлении события А, или
события В, или обоих этих событий.
A B
A B
Суммой n событий называют событие,
которое состоит в появлении хотя бы
одного из этих событий.
n
A1 A2 An Ak
k 1
n
A1 A2 An Ak
k 1

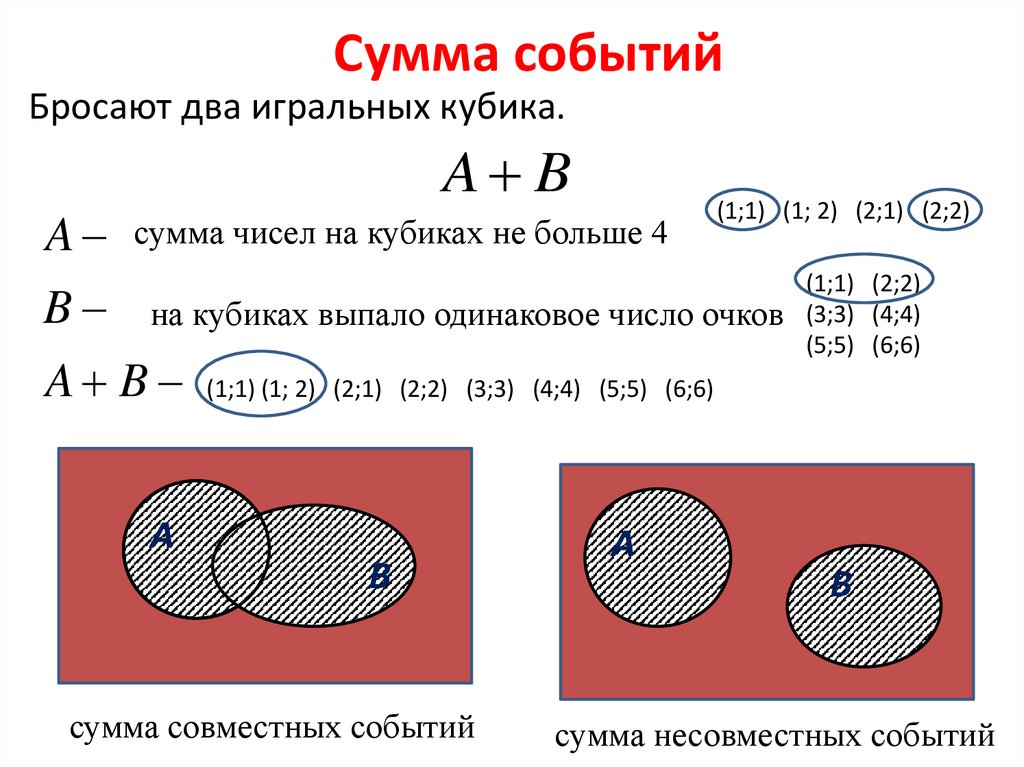
17. Сумма событий

Бросают два игральных кубика.
A B
A сумма чисел на кубиках не больше 4
(1;1) (1; 2) (2;1) (2;2)
B на кубиках выпало одинаковое число очков
A B (1;1) (1; 2) (2;1) (2;2) (3;3) (4;4) (5;5) (6;6)
А
В
сумма совместных событий
(1;1) (2;2)
(3;3) (4;4)
(5;5) (6;6)
А
В
сумма несовместных событий

18. Произведение событий

• Произведением, или пересечением двух
событий А и В, называют событие,
состоящее в одновременном появлении
этих событий.
А∙В
A B
Произведением n событий называют
событие, состоящее в совместном
появлении всех этих событий.
A1 A2 An
n
A1 A2 An Ak
k 1

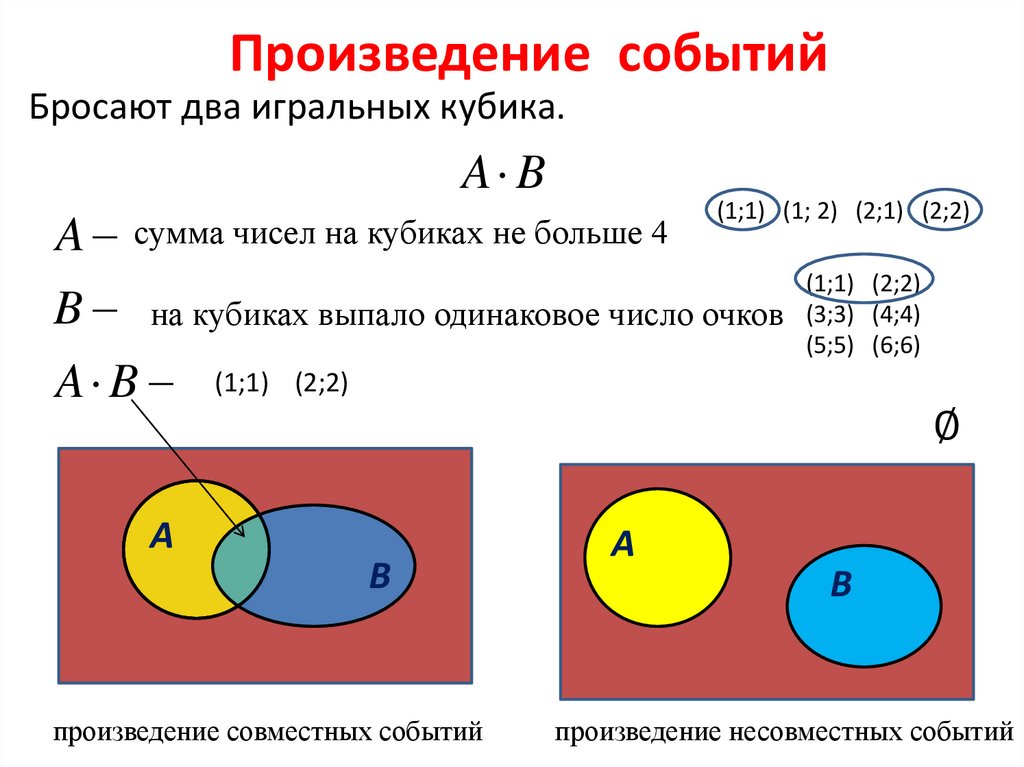
19. Произведение событий

Бросают два игральных кубика.
A B
(1;1) (1; 2) (2;1) (2;2)
A сумма чисел на кубиках не больше 4
(1;1) (2;2)
B на кубиках выпало одинаковое число очков (3;3) (4;4)
(5;5) (6;6)
A B (1;1) (2;2)
А
В
произведение совместных событий
∅
А
В
произведение несовместных событий

20. Свойства операций над событиями

1
А+В=В+А
7
А В=В А
2
(А+В)+С= А+(В+С)
8
(А В) С=А (В С)
3
А+А=А; А+Ā= ; А+ = ;
А+ =А
9
А А=А; А Ā= ; А =А; А =
4
(А+В) С=А С+В С;
10 А+В С=(А+В) (А+С)
5
A B А+В=В; А В=А
11
6
А+А В=А; А (А+В)=А
12 A B A B ;