«Математическое моделирование процессов в природных, социально-экономических средах

1. Курс «Математическое моделирование процессов в природных, социально-экономических средах»

КУРС
«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ПРОЦЕССОВ В ПРИРОДНЫХ,
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ СРЕДАХ»

2. Глава 1 ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

ГЛАВА 1
ЭТАПЫ ПОСТРОЕНИЯ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ
2

3.

Процесс создания математических моделей трудоемок, длителен и связан
с использованием труда различных специалистов достаточно высокого
уровня, обладающих хорошей подготовкой как в предметной области,
связанной с объектом моделирования, так и в области прикладной
математики, современных численных методов, программирования,
знающих возможности и особенности современной вычислительной
техники.
Отличительной
особенностью
математических
моделей,
создаваемых в настоящее время, является их комплексность, связанная
со сложностью моделируемых объектов. Например, при моделировании
процессов деформирования различных конструкций под действием
приложенной нагрузки приходится учитывать не только происходящие
при деформировании процессы массопереноса, но и теплоперенос, а
также связанные с этими процессами изменения структуры и свойств
3
материала.

4.

В некоторых случаях необходимо учитывать влияние
различных
видов
гравитационных
предыстории
и
излучения,
воздействия
электромагнитных
деформирования.
Кроме
того,
полей,
для
современных моделей характерно представление объекта
моделирования в виде более или менее сложной системы
взаимодействующих элементов.
4

5.

Все отмеченные выше особенности приводят к усложнению
модели
и
необходимости
совместного
использования
нескольких теорий (нередко из разных областей знания),
применения современных вычислительных методов и
вычислительной
техники
для
получения
и
анализа
результатов моделирования
5

6.

Необходимость массового построения моделей требует разработки
некоторой совокупности правил и подходов, которые позволили
бы снизить затраты на разработку моделей и уменьшить
вероятность появления трудно устранимых впоследствии ошибок.
Подобную
совокупность
правил
можно
было
бы
назвать
технологией создания математических моделей.
Процесс построения любой математической модели можно
представить последовательностью этапов, представленных на рис.
6

7.

7

8.

1. Обследование объекта моделирования
Математические модели, особенно использующие численные методы и
вычислительную
технику,
требуют
для
своего
построения
значительных интеллектуальных, финансовых и временных затрат.
Поэтому решение о разработке новой модели принимается лишь в
случае отсутствия иных, более простых путей решения возникших
проблем (например, модификации одной из существующих моделей).
Необходимость в новой модели может появиться в связи с проведением
научных исследований (особенно на стыке различных областей
знания),
выполнением проектных и конструкторских
производстве,
созданием
систем
автоматического
работ на
управления,
планирования и контроля.
8

9.

Человека или организацию, заинтересованных в разработке новой
математической модели, для краткости будем называть заказчиком.
После
принятия
решения
о
необходимости
построения
новой
математической модели заказчик ищет исполнителя своего заказа. В
качестве исполнителя, как правило, может выступать рабочая группа,
включающая специалистов разного профиля: прикладных математиков,
специалистов, хорошо знающих особенности объекта моделирования,
программистов.
9

10.

Итак, если решение о создании модели принято и рабочая группа
сформирована, то можно приступать к этапу обследования объекта
моделирования. Основной целью данного этапа является подготовка
содержательной постановки задачи моделирования.
Перечень сформулированных в содержательной (словесной) форме
основных вопросов об объекте моделирования, интересующих заказчика,
составляет содержательную постановку задачи моделирования.
10

11.

Подготовка списка вопросов, на которые должна ответить новая
модель, зачастую является самостоятельной проблемой, требующей для
своего
решения
специалистов
со
специфическими
знаниями
и
способностями. Они должны не только хорошо разбираться в
предметной области моделирования, знать возможности современной
вычислительной математики и техники, но и быть достаточно
коммуникабельными, т.е. уметь общаться с людьми, «разговорить»
практиков, хорошо «чувствующих» объект моделирования, нюансы его
поведения. Подобных специалистов в настоящее время называют
постановщиками задач.
11

12.

На основании анализа всей собранной информации постановщик
задачи должен сформулировать такие требования к будущей модели,
которые, с одной стороны, удовлетворяли бы заказчика, а с другой —
позволяли бы реализовать модель в заданные сроки и в рамках
выделенных материальных средств.
Этап
обследования
проводится
членами
рабочей
группы
под
руководством постановщиков задач и включает следующие работы:
12

13.

тщательное обследование собственно объекта моделирования с
целью выявления основных факторов, механизмов, влияющих на
его
поведение,
определения
соответствующих
параметров,
позволяющих описывать моделируемый объект;
сбор и проверка имеющихся экспериментальных данных об
объектах-аналогах, проведение при необходимости дополнительных
экспериментов;
аналитический обзор литературных источников, анализ и сравнение
между собой построенных ранее моделей данного объекта (или
подобных рассматриваемому объекту);
анализ и обобщение всего накопленного материала, разработка
общего плана создания математической модели.
13

14.

На
основе
собранной
информации
об
объекте
моделирования
постановщики совместно с заказчиком формулируют содержательную
постановку задачи моделирования, которая, как правило, не бывает
окончательной и может уточняться и конкретизироваться в процессе
разработки модели.
14

15.

Весь собранный в результате обследования материал о накопленных к
данному моменту знаниях об объекте, содержательная постановка задачи
моделирования, дополнительные требования к реализации модели и
представлению результатов оформляются в виде технического задания
на проектирование и разработку модели.
Техническое задание является итоговым документом, заканчивающим
этап обследования, который, как уже отмечалось, является очень
важным и ответственным.
Рассмотрим пример содержательной постановки задачи о баскетболисте.
15

16.

Пример. Содержательная постановка задачи о баскетболисте.
Разработать математическую модель, позволяющую описать полет
баскетбольного мяча, брошенного игроком в баскетбольную корзину.
Модель должна позволять:
• вычислять положение мяча в любой момент времени;
• определять точность попадания мяча в корзину после броска при
различных начальных параметрах.
Исходные данные:
• масса и радиус мяча;
• начальные координаты, начальная скорость и угол броска мяча;
• координаты центра и радиус корзины.
16

17.

2. Концептуальная постановка задачи моделирования
На основании содержательной модели разрабатывается концептуальная,
или «естественно-научная» (физическая, химическая, биологическая и
т.д.),
постановка
задачи
моделирования,
служащая
основой
для
концептуальной модели объекта.
Концептуальная
постановка
задачи
моделирования
это
сформулированный в терминах конкретных дисциплин (физики, химии,
биологии и т.д.) перечень основных вопросов, интересующих заказчика, а
также совокупность гипотез относительно свойств и поведения
17
объекта моделирования.

18.

Наибольшие трудности при формулировке концептуальной постановки
приходится преодолевать в моделях, находящихся на «стыке» различных
дисциплин. Различия традиций, понятий и языков, используемых для
описания одних и тех же объектов, являются очень серьезными
препятствиями, возникающими при создании «междисциплинарных»
моделей. Например, такие понятия как «прибыль» и «баланс»
вызывают совершенно разные ассоциации у экономиста и математика-
прикладника.
18

19.

Можно сказать, что когнитивные модели, стоящие за этими понятиями,
у этих двух специалистов совершенно различны. Если экономист, говоря
о прибыли и балансе, связывает с этими понятиями конкретное
производство, цену и себестоимость продукции, то для математика
данные понятия выглядят более формально как результаты решения
некоторых математических уравнений.
19

20.

Выше отмечалось, что концептуальная модель строится как некоторая
идеализированная модель объекта, записанная в терминах конкретных
(например, естественно-научных) дисциплин. Для этого формулируется
совокупность гипотез о поведении объекта, его взаимодействии с
окружающей средой, изменении внутренних параметров. Как правило,
эти гипотезы правдоподобны в том смысле, что для их обоснования
могут
быть
приведены
некоторые
теоретические
доводы
и
использованы экспериментальные данные, основанные на собранной
ранее информации об объекте. В выборе и обосновании принимаемых
гипотез в значительной степени проявляется искусство, опыт и знания,
накопленные членами рабочей группы. Согласно принятым гипотезам
определяется множество параметров, описывающих состояние объекта,
а также перечень законов, управляющих изменением и взаимосвязью
20
этих параметров между собой.

21.

Пример. Концептуальная постановка задачи о баскетболисте.
Движение баскетбольного мяча может быть описано в соответствии с
законами классической механики Ньютона (рис. 2).
y
v0
0
xk
L
x
21
Рис. 2. Схема к постановке задачи о баскетболисте

22.

Примем следующие гипотезы:
• объектом моделирования является баскетбольный мяч радиуса R;
• мяч будем считать материальной точкой массой m, положение
которой совпадает с центром масс мяча;
• движение происходит в поле сил тяжести с постоянным ускорением
свободного падения g и описывается уравнениями классической
механики Ньютона;
• движение мяча происходит в одной плоскости, перпендикулярной
поверхности Земли и проходящей через точку броска и центр
корзины;
• пренебрегаем сопротивлением воздуха и возмущениями, вызванными
собственным вращением мяча вокруг центра масс.
22

23.

В соответствии с изложенными гипотезами в качестве параметров движения
мяча можно использовать координаты (х и у) и скорость (ее проекции vx и vy)
центра масс мяча. Тогда для определения положения мяча в любой момент
времени достаточно найти закон движения центра масс мяча, т.е. зависимость
координат х, у и проекций вектора скорости vx и vy центра мяча от времени. В
качестве оценки точности броска можно рассматривать величину расстояния
по горизонтали (вдоль оси х) от центра корзины до центра мяча в момент, когда
последний пересекает горизонтальную плоскость, проходящую через плоскость
кольца корзины.
23

24.

С учетом вышеизложенного можно сформулировать концептуальную
постановку задачи о баскетболисте в следующем виде: определить закон
движения материальной точки массой m под действием силы тяжести,
если известны начальные координаты точки x0 и у0, ее начальная
скорость v0 и угол бросания 0. Центр корзины имеет координаты хk и
уk. Вычислить точность броска = x(tk) хk, где tk определяется из
условий: tk > 0, vy < 0, y(tk) = уk.
24

25.

Рассмотрим особенности приведенной в примере концептуальной
постановки задачи о баскетболисте. Первая из перечисленных гипотез
особенно важна, так как она выделяет объект моделирования. В данном
случае объект можно считать простым. Однако в качестве объекта
моделирования можно рассматривать систему «игрок мяч кольцо».
Требуемая для описания подобной системы модель будет уже намного
сложнее, так как игрок в свою очередь представляет сложную
биомеханическую систему и его моделирование является далеко не
тривиальной задачей. В данной ситуации выбор в качестве объекта
моделирования только мяча обоснован, поскольку именно его движение
требуется исследовать, а влияние игрока можно учесть достаточно
просто через начальные параметры броска. Для сложных систем выбор
объекта моделирования — далеко не простая и неоднозначная задача. 25

26.

Гипотеза о том, что мяч можно считать материальной точкой, широко
применяется
для
исследования
движений
тел
в
механике.
В
рассматриваемом случае она оправдана в силу симметрии формы мяча
и малости его радиуса по сравнению с характерными расстояниями
перемещения мяча. Предполагается, что последний является шаром с
одинаковой толщиной стенки.
26

27.

Гипотезу о применимости в данном случае законов классической
механики
можно
обосновать
огромным
экспериментальным
материалом, связанным с изучением движения тел вблизи поверхности
Земли со скоростями много меньше скорости света. Учитывая, что
высота полета мяча лежит в пределах 5 10 м, а дальность 5 20 м,
предположение о постоянстве ускорения свободного падения также
представляется обоснованным. Если бы моделировалось движение
баллистической ракеты при дальности и высоте полета более 100 км, то
пришлось бы учитывать изменение ускорения свободного падения в
зависимости от высоты и широты места.
27

28.

Гипотеза о движении мяча в плоскости,
перпендикулярной
ограничивает
траекторий
поверхности
класс
и
Земли,
рассматриваемых
значительно
упрощает
модель. Траектория мяча может не лежать
в одной плоскости, если при броске он
Рис. 3. Обтекание мяча потоком
воздуха
сильно
подкручивается
вокруг
вертикальной оси. В этом случае скорости
точек поверхности мяча относительно воздуха на различных сторонах мяча
будут различны. Для точек, движущихся навстречу потоку, относительная
скорость выше, а для точек противоположной стороны, движущихся по потоку,
ниже скорости центра масс мяча. В соответствии с законом Бернулли, давление
газа на поверхность больше там, где его относительная скорость меньше.
28

29.

Поэтому для ситуации, изображенной на рис. 3, на мяч будет
действовать дополнительная сила, направленная (для данной схемы)
сверху вниз. Этот эффект будет проявляться тем больше, чем больше
скорость центра масс мяча и скорость его вращения. Для баскетбола
характерны относительно низкие скорости полета мяча (до 10 м/с). При
этом довольно редко используется подкрутка мяча рукой. Поэтому
гипотеза о движении мяча в одной плоскости кажется оправданной. Ее
использование позволяет отказаться от построения значительно более
сложной трехмерной модели движения мяча.
29

30.

Гипотеза об отсутствии влияния сопротивления воздуха наименее
обоснована.
При
движении
тела
в
газе
или
жидкости
сила
сопротивления увеличивается с ростом скорости движения. Учитывая
невысокие скорости движения мяча, его правильную обтекаемую
форму и малые дальности бросков, указанная гипотеза может быть
принята в качестве первого приближения.
30

31.

Следует
отметить,
что
концептуальная
постановка
задачи
моделирования в отличие от содержательной постановки использует
терминологию конкретной дисциплины (в рассматриваемом случае —
механики). При этом моделируемый реальный объект (мяч) заменяется
его механической моделью (материальной точкой). Фактически в
приведенном примере концептуальная постановка свелась к постановке
классической задачи механики о движении материальной точки в поле
сил
тяжести.
Концептуальная
постановка
более
абстрактна
по
отношению к содержательной, так как материальной точке можно
сопоставить произвольный материальный объект, брошенный под
углом к горизонту: футбольный мяч, ядро, камень или артиллерийский
снаряд.
31

32.

3. Математическая постановка задачи моделирования
Законченная концептуальная постановка позволяет сформулировать
математическую постановку задачи моделирования, включающую
совокупность различных математических соотношений, описывающих
поведение и свойства объекта моделирования.
Математическая постановка задачи моделирования это совокупность
математических соотношений, описывающих поведение и свойства
объекта моделирования.
32

33.

Следует отметить, что во многих областях знаний (механике, физике, биологии
и т.д.) принято выделять законы, справедливые для всех объектов исследования
данной области знаний, и соотношения, описывающие поведение отдельных
объектов или их совокупностей. К числу первых в физике и механике относятся,
например, уравнения баланса массы, количества движения, энергии и т.д.,
справедливые при определенных условиях для любых материальных тел,
независимо от их конкретного строения, структуры, состояния, химического
состава. Уравнения этого класса подтверждены огромным количеством
экспериментов,
хорошо
изучены
и
в
силу
этого
применяются
в
соответствующих математических моделях как данность. Соотношения второго
класса в физике и механике называют определяющими, или физическими
уравнениями, или уравнениями состояния. Они устанавливают особенности
поведения
материальных
объектов
или
их
совокупностей
(например,
жидкостей, газов, упругих или пластических сред и т.д.) при воздействиях
различных внешних факторов.
33

34.

В качестве классических примеров определяющих соотношений можно
привести закон Гука в теории упругости или уравнение Клапейрона
для идеальных газов. Очевидно, определяющие соотношения должны
отражать
реальное
атомно-молекулярное
строение
исследуемых
материальных объектов.
Соотношения второго класса гораздо менее изучены, а в ряде случаев
их приходится устанавливать самому исследователю (особенно при
анализе объектов, состоящих из новых материалов). Необходимо
отметить, что определяющие соотношения это основной элемент,
«сердцевина» любой математической модели физико-механических
процессов. Именно ошибки в выборе или установлении определяющих
соотношений приводят к количественно (а в некоторых случаях и
качественно) неверным результатам моделирования.
34

35.

Совокупность математических соотношений указанных двух классов
определяет оператор модели. В большинстве случаев оператор модели
включает в себя систему обыкновенных дифференциальных уравнений
(ОДУ), дифференциальных уравнений в частных производных (ДУЧП)
и/или интегродифференциальных уравнений (ИДУ). Для обеспечения
корректности
постановки
задачи
к
системе
ОДУ
или
ДУЧП
добавляются начальные и/или граничные условия, которые, в свою
очередь,
могут
быть
алгебраическими
или
дифференциальными
соотношениями различного порядка.
35

36.

Можно выделить несколько наиболее распространенных типов задач для
систем ОДУ или ДУЧП:
задача Коши, или задача с начальными условиями, в которой по заданным в
начальный
момент
времени
переменным
(начальным
условиям)
определяются значения этих искомых переменных для любого момента
времени;
начально-граничная, или краевая, задача, когда условия на искомую функцию
выходного параметра задаются в начальный момент времени для всей
пространственной области и на границе последней в каждый момент
времени (на исследуемом интервале);
задачи
на
собственные
значения,
в
формулировку
которых
входят
неопределенные параметры, определяемые из условия качественного
изменения поведения системы (например, потеря устойчивости состояния
равновесия или стационарного движения, появление периодического
режима, резонанс и т.д.).
36

37.

Для контроля правильности полученной системы математических
соотношений требуется проведение ряда обязательных проверок:
Контроль размерностей, включающий правило, согласно которому
приравниваться и складываться могут только величины одинаковой
размерности.
При
переходе
к
вычислениям
данная
проверка
сочетается с контролем использования одной и той же системы единиц
для значений всех параметров.
Контроль порядков, состоящий из грубой оценки сравнительных
порядков складываемых величин и исключением малозначимых
параметров. Например, если для выражения х + у + z = 0 в результате
оценки установлено, что в рассматриваемой области значений
параметров модели z ≪ x и
≪ y то третьим слагаемым
в исходном выражении можно пренебречь.
37

38.

Контроль характера зависимостей заключается в проверке того, что
направление
и
скорость
изменения
выходных
параметров
модели,
вытекающие из выписанных математических соотношений, такие, как это
следует непосредственно из «физического» смысла изучаемой модели.
Контроль экстремальных ситуаций проверка того, какой вид принимают
математические соотношения, а также результаты моделирования, если
параметры модели или их комбинации приближаются к предельно
допустимым для них значениям, чаще всего к нулю или бесконечности. В
подобных
экстремальных
ситуациях
модель
часто
упрощается,
математические соотношения приобретают более наглядный смысл,
упрощается их проверка. Например, в задачах механики деформируемого
твердого
тела
деформация
материала
в
исследуемой
области
в
изотермических условиях возможна лишь при приложении нагрузок,
отсутствие же нагрузок должно приводить к отсутствию деформаций.
38

39.

Контроль граничных условий, включающий проверку того, что
граничные условия действительно наложены, что они использованы
в процессе построения искомого решения и что значения выходных
параметров модели на самом деле удовлетворяют данным условиям.
Контроль физического смысла проверка физического или иного, в
зависимости от характера задачи, смысла исходных и промежуточных
соотношений, появляющихся по мере конструирования модели.
39

40.

Контроль математической замкнутости, состоящий в проверке того, что
выписанная система математических соотношений дает возможность,
притом
однозначно,
решить
поставленную
математическую
задачу.
Например, если задача свелась к отысканию n неизвестных из некоторой
системы алгебраических или трансцендентных уравнений, то контроль
замкнутости состоит в проверке того факта, что число независимых
уравнений должно быть n. Если их меньше n, то надо установить
недостающие уравнения, а если их больше п, то либо уравнения зависимы,
либо при их составлении допущена ошибка. Однако если уравнения
получаются из эксперимента или в результате наблюдений, то возможна
постановка задачи, при которой число уравнений превышает n, но сами
уравнения удовлетворяются лишь приближенно, а решение ищется,
например, по методу наименьших квадратов. Неравенств среди условий
также может быть любое число, как это бывает, например, в задачах
линейного программирования.
40

41.

Свойство
математической
замкнутости
системы
математических
соотношений тесно связано с введенным Ж. Адамаром понятием
корректно поставленной математической задачи, т.е. задачи, для
которой решение существует, оно единственно и непрерывно зависит от
исходных данных. В данном случае решение считается непрерывным,
если малому изменению исходных данных соответствует достаточно
малое изменение решения.
41

42.

Понятие корректности задачи имеет большое значение в прикладной
математике.
Например,
численные
методы
решения
оправдано
применять лишь к корректно поставленным задачам. При этом далеко
не все задачи, возникающие на практике, можно считать корректными
(например,
так
называемые
обратные
задачи).
Доказательство
корректности конкретной математической задачи — достаточно
сложная проблема, она решена только для некоторого класса
математически
поставленных
задач.
Проверка
математической
замкнутости является менее сложной по сравнению с проверкой
корректности математической постановки. В настоящее время активно
исследуются свойства некорректных задач, разрабатываются методы их
решения. Аналогично понятию «корректно поставленная задача»
можно ввести понятие «корректная математическая модель».
42

43.

Математическая
модель
является
корректной,
если
для
нее
осуществлен и получен положительный результат всех контрольных
проверок:
размерности,
порядков,
характера
зависимостей,
экстремальных ситуаций, граничных условий, физического смысла и
математической замкнутости.
43

44.

Пример. Математическая постановка задачи о баскетболисте
Математическую постановку задачи о
баскетболисте можно представить как в
векторной, так и в координатной форме
(рис. 4).
O
Рис. 4. Расчетная схема
Векторная форма.
Найти зависимости векторных параметров от времени r (t ) и
v (t )
из решения системы обыкновенных дифференциальных уравнений
dv
dr
m
mg , v
(1)
dt
dt
при начальных условиях
r(0) = 0, v(0) = v0.
44
(2)

45.

Вычислить параметр по формуле
rx ( t k ) rxk ,
(3)
где tk определить из следующих условий:
t k 0, v y ( t k ) 0,
Проецируя векторные соотношения
y( t k ) y k .
(4)
на оси координат, получим
математическую постановку задачи о баскетболисте в координатной
форме.
45

46.

2. Координатная форма.
Найти зависимости x(t), y(t) и vx(t), vy(t) из решения системы
дифференциальных уравнений:
dv x
dx
0, v x
,
dt
dt
dv y
dy
m
mg , v y
dt
dt
m
(5)
при следующих начальных условиях:
x ( 0) x 0 ,
y ( 0) y 0 ,
v x (0) v 0 cos 0 , v y (0) v 0 sin 0 .
(6)
46

47.

Вычислить параметр по формуле
x( t k ) x k ,
(7)
где tk определить из условий
t k 0, v y ( t k ) 0,
y( t k ) y k .
(8)
47

48.

Как можно видеть, с математической точки зрения задача о
баскетболисте свелась к задаче Коши для системы ОДУ первого
порядка с заданными начальными условиями. Полученная система
уравнений является замкнутой, так как число независимых уравнений
(четыре дифференциальных и два алгебраических) равно числу
искомых параметров задачи (х, у, vx, vy, , tk). Выполним контроль
размерностей задачи: уравнение динамики
m
кг м кг м
dv
[м/с]
F [кг ]
[H ]
2
dt
[c]
с с2
связь скорости и перемещения
dr
[м] м
v
.
dt
[c] с
48

49.

Существование и единственность решения задачи Коши доказана
математиками. Поэтому данную математическую модель можно считать
корректной.
Математическая
постановка
задачи
еще
концептуальная,
так
сводит
исходную
как
более
абстрактна,
задачу
к
чем
чисто
математической (например, к задаче Коши), методы решения которой
достаточно хорошо разработаны. Умение свести исходную проблему к
известному классу математических задач и обосновать правомочность
такого
сведения
прикладника.
требует
высокой
квалификации
математика49

50.

4. Выбор и обоснование выбора метода решения задачи
При использовании разработанных математических моделей, как
правило, требуется найти зависимость некоторых неизвестных заранее
параметров объекта моделирования (например, координат и скорости
центра масс тела, точности броска), удовлетворяющих определенной
системе уравнений. Таким образом, поиск решения задачи сводится к
отысканию некоторых зависимостей искомых величин от исходных
параметров модели. Все методы решения задач, составляющих «ядро»
математических моделей, можно подразделить на аналитические и
алгоритмические.
50

51.

Следует отметить, что при использовании аналитических решений для
получения результатов «в числах» также часто требуется разработка
соответствующих алгоритмов, реализуемых на ЭВМ. Однако исходное
решение при этом представляет собой аналитическое выражение (или их
совокупность). Решения же, основанные на алгоритмических методах,
принципиально не сводимы к точным аналитическим решениям
рассматриваемой задачи.
Аналитические методы более удобны для последующего анализа
результатов, но применимы лишь для относительно простых моделей. В
случае, если математическая задача (хотя бы и в упрощенной
постановке) допускает аналитическое решение, последнее, без сомнения,
предпочтительнее численного.
51

52.

Алгоритмические
методы
сводятся
к
некоторому
алгоритму,
реализующему вычислительный эксперимент с использованием ЭВМ.
Точность моделирования в подобном эксперименте существенно
зависит от выбранного метода и его параметров (например, шага
интегрирования). Алгоритмические методы, как правило, более
трудоемки в реализации, требуют от членов рабочей группы хорошего
знания методов вычислительной математики, обширной библиотеки
специального программного обеспечения и мощной вычислительной
техники.
Численные методы применимы лишь для корректных математических
задач,
что
существенно
ограничивает
использование
их
в
математическом моделировании.
52

53.

Общим для всех численных методов является сведение математической
задачи к конечномерной. Это чаще всего достигается дискретизацией
исходной задачи, т.е. переходом от функции непрерывного аргумента к
функциям дискретного аргумента. Например, траектория центра
тяжести баскетбольного мяча определяется не как непрерывная
функция времени, а как табличная (дискретная) функция координат от
времени, т.е. определяющая значения координат лишь для конечного
числа моментов времени. Полученное решение дискретной задачи
принимается за приближенное решение исходной математической
задачи.
53

54.

Применение любого численного метода неминуемо приводит к
погрешности результатов решения задачи. Выделяют три основных
составляющих возникающей погрешности при численном решении
исходной задачи:
неустранимая
погрешность,
связанная
с
неточным
заданием
исходных данных (начальные и граничные условия, коэффициенты
и правые части уравнений);
погрешность метода, связанная с переходом к дискретному аналогу
исходной задачи (например, заменяя производную у'(х) разностным
аналогом
(у(х + х) у (х) ) / х,
получаем
погрешность
дискретизации, имеющую при х 0 порядок х);
ошибка округления, связанная с конечной разрядностью чисел,
представляемых в ЭВМ.
54

55.

Естественным
алгоритма
требованием
является
для
конкретного
согласованность
в
вычислительного
порядках
величин
перечисленных трех видов погрешностей.
Численный, или приближенный, метод реализуется всегда в виде
вычислительного алгоритма. Поэтому все требования, предъявляемые
к алгоритму, применимы и к вычислительному алгоритму. Прежде
всего, алгоритм должен быть реализуем обеспечивать решение задачи
за допустимое машинное время. Важной характеристикой алгоритма
является его точность, т.е. возможность получения решения исходной
задачи с заданной точностью > 0 за конечное число Q( ) действий.
55

56.

Очевидно, чем меньше , тем больше затрачиваемое машинное время.
Для очень малых значений время вычислений может быть
недопустимо большим. Поэтому на практике добиваются некоторого
компромисса между точностью и затрачиваемым машинным временем.
Очевидно, что для каждой задачи, алгоритма и типа ЭВМ имеется свое
характерное значение достигаемой точности.
56

57.

Время работы алгоритма зависит от числа действий Q( ), необходимых
для достижения заданной точности. Для любой математической задачи,
как правило, можно предложить несколько алгоритмов, позволяющих
получить решение с заданной точностью, но за разное число действий
Q( ). Алгоритмы, включающие меньшее число действий для достижения
одинаковой точности, будем называть более экономичными, или более
эффективными.
57

58.

В процессе работы вычислительного алгоритма на каждом акте
вычислений возникает некоторая погрешность. При этом от действия к
действию она может возрастать или не возрастать (а в некоторых
случаях даже уменьшаться). Если погрешность в процессе вычислений
неограниченно
возрастает,
то
такой
алгоритм
называется
неустойчивым, или расходящимся. В противном случае алгоритм
называется устойчивым, или сходящимся.
58

59.

Можно выделить следующие группы численных методов по объектам, к
которым они применяются:
интерполяция и численное дифференцирование;
численное интегрирование;
определение корней линейных и нелинейных уравнений;
решение систем линейных уравнений (подразделяют на прямые и
итерационные методы);
решение систем нелинейных уравнений;
решение задачи Коши для обыкновенных дифференциальных
уравнений;
решение краевых задач для обыкновенных дифференциальных
уравнений;
решение разностных уравнений;
решение систем разностных уравнений;
решение уравнений в частных производных;
решение интегральных уравнений.
59

60.

Следует отметить, что вычислительная математика в определенном
смысле являет собой более искусство, нежели науку (в понимании
последней как области культуры, базирующейся на формальной
логике).
Очень
часто
эффективность
применяемых
методов,
разработанных программ определяется нарабатываемыми годами и
десятками
лет
интуитивными
приемами, не обоснованными
с
математических позиций. В связи с этим эффективность одного и того
же метода может весьма существенно отличаться при его применении
различными исследователями.
60

61.

Пример. Аналитическое решение задачи о баскетболисте.
Для получения решения рассмотренной выше задачи о баскетболисте в
постановке (5) (8) можно использовать как аналитические, так и
численные методы. Проинтегрировав соотношения (5) по времени,
получим
x ( t ) C 2 C1t , y( t ) C 4 C 3 t gt 2 / 2,
v x ( t ) C1 ,
v y ( t ) C 3 gt .
(9)
Константы интегрирования найдем из начальных условий (6). Тогда
решение задачи можно записать следующим образом:
x ( t ) x 0 v 0 t cos 0 , y( t ) y0 v 0 t sin 0 gt 2 / 2,
v x ( t ) v 0 cos 0 ,
v y ( t ) v 0 sin 0 gt .
(10)
61

62.

Примем для простоты, что в момент броска мяч находится в начале
координат и на одном уровне с корзиной (т.е. х0 = y0 = yk.= 0). Под
дальностью L броска будем понимать расстояние вдоль оси Ох, которое
пролетит мяч от точки броска до пересечения с горизонтальной
плоскостью, проходящей через кольцо корзины. Из соотношений (10)
дальность броска выразится следующим образом:
v 02
L
sin 2 0 .
g
(11)
С учетом (7) точность броска
=L xk.
(12)
Например, при броске мяча со штрафной линии можно принять
следующие исходные данные: х0 = y0 = yk = 0; хk = 4,225 м; v0 = 6,44 м/с;
0 = 45 . Тогда из (11) и (12) имеем L = 4,225 м; = 0 м.
62

63.

Пример. Алгоритмическое решение задачи о баскетболисте.
В простейшем случае можно использовать метод Эйлера. Алгоритм
решения данной задачи на псевдокоде приведен ниже.
Алгоритм 1
program Задача о баскетболисте.
Данные: т, R масса и радиус мяча;
х0, у0 начальные координаты мяча;
v0, 0 начальная скорость и угол броска мяча;
хk, уk координаты центра корзины;
t текущее время;
dt шаг по времени;
fx, fy силы, действующие на мяч;
х, y, vx, vy текущие координаты и проекции скорости мяча.
63

64.

Результаты: L и дальность и точность броска.
start
g := 9,81
m := 0,6
R := 0,12
v0 := 6,44
0 := 45
x0 := 0
y0 := 0
xk := 4,225
yk := 0
vx := v0cos
vy := v0sin
dt := 0,1
t := 0
x := x0; y := y0
64

65.

while ((vy 0) or ((vy < 0) and (y yk)))
t := t + dt
fx := 0
fy := mg
силы, действующие на мяч
vx := vx + fx dt/m
vy := vy + fy dt/m
x := x + dt vx
y := y + dt vy
компоненты скорости
координаты мяча
end while
L := x x0
:= x xk
stop
65

66.

5. Реализация математической модели в виде программы для ЭВМ
При создании различных программных комплексов, используемых для
решения разнообразных исследовательских, проектно-конструкторских
и управленческих задач, в настоящее время, основой, как правило,
служат математические модели. В связи с этим возникает необходимость
реализации модели в виде программы для ЭВМ. Процесс разработки
надежного и эффективного программного обеспечения является не
менее сложным, чем все предыдущие этапы создания математической
модели. Успешное решение данной задачи возможно лишь при
уверенном владении современными алгоритмическими языками и
технологиями
программирования,
знании
возможностей
вычислительной техники, имеющегося программного обеспечения,
66
особенностей реализации на ЭВМ методов вычислительной математики,
наличии опыта решения подобных задач.

67.

Процесс создания программного обеспечения можно разбить на ряд
этапов:
составление технического задания на разработку пакета программ
программного обеспечения;
проектирование структуры программного комплекса;
кодирование алгоритма;
тестирование и отладка;
сопровождение и эксплуатация.
67

68.

Техническое
задание
на
разработку
программного
обеспечения
оформляют в виде спецификации. Примерная форма спецификации
включает следующие семь разделов:
Название задачи дается краткое определение решаемой задачи,
название
программного
программирования
для
комплекса,
его
указывается
реализации
и
система
требования
к
аппаратному обеспечению (компьютеру, внешним устройствам и
т.д.).
2. Описание подробно излагается математическая постановка задачи,
описываются применяемая математическая модель для задач
вычислительного характера, метод обработки входных данных для
задач не вычислительного (логического) характера и т.д.
3. Управление режимами работы программы - формируются основные
требования к способу взаимодействия пользователя с программой
(интерфейс «пользователь-компьютер»).
68

69.

4. Входные данные описываются входные данные, указываются пределы, в
которых они могут изменяться, значения, которые они не могут принимать,
и т.д.
5. Выходные данные описываются выходные данные, указывается, в каком
виде они должны быть представлены (в числовом, графическом или
текстовом), приводятся сведения о точности и объеме выходных данных,
способах их сохранения и т.д.
6. Ошибки перечисляются возможные ошибки пользователя при работе с
программой (например, ошибки при вводе входных данных), указываются
способы диагностики (в данном случае под диагностикой понимается
выявление, обнаружение ошибок при работе программного комплекса) и
защиты от этих ошибок на этапе проектирования, а также возможная
реакция пользователя при совершении им ошибочных действий и реакция
программного комплекса (компьютера) на эти действия.
7. Тестовые задачи приводятся один или несколько тестовых примеров, на
которых в простейших случаях проводится отладка и тестирование
программного комплекса.
69

70.

Пример. Спецификация задачи о баскетболисте.
Название задачи
Название программыBasketball
Система программирования Delphi
Компьютер IBM PC Pentium
Операционная система Windows-9x, NT
2. Описание
Приводится математическая постановка задачи и описание метода ее
решения.
3. Управление режимами работы программы
Для
управления
использовать
режимами
интерфейс
работы
Windows
с
программы
необходимо
использованием
диалоговых окон, полей ввода данных, кнопок.
меню,
70

71.

4. Входные данные
Радиус и масса мяча, его начальные координаты и скорость, угол
бросания, координаты корзины.
5. Выходные данные
Траектория центра мяча, расчетная величина дальности и точность
броска. Выходные данные представляются в табличном и графическом
виде.
71

72.

6. Ошибки
При вводе исходных данных предусмотреть контроль:
все вводимые значения должны быть положительны;
угол бросания должен быть в пределах от 5° до 85°;
начальная скорость мяча должен быть в пределах от 0 до 30 м/с;
горизонтальная координата центра корзины должна быть больше
начальной горизонтальной координаты мяча.
При диагностировании перечисленных ошибок программа должна
выдавать соответствующие сообщения, которые могут сопровождаться
звуковым сигналом, и предлагать повторить ввод.
7. Тестовые примеры
При х0 = y0 = yk = 0; хk = 4,225; v0 = 6,44; 0 = 45 получаем:
L = 4,225; = 0.
72

73.

На этапе проектирования формируется общая структура программного
комплекса. Вся программа разбивается на программные модули. Для
каждого
программного
модуля
формулируются
требования
по
реализуемым функциям и разрабатывается алгоритм, выполняющий
эти
функции.
Определяется
схема взаимодействия программных
модулей, называемая схемой потоков данных программного комплекса.
Разрабатывается план и задаются исходные данные для тестирования
отдельных модулей и программного комплекса в целом.
73

74.

Большое значение следует придавать освоению современных технологий
программирования:
структурной,
абстрактной,
объектно-
ориентированной и визуальной. Назначение любой технологии — это в
первую очередь повышение надежности программного обеспечения и
увеличение производительности труда программиста. Причем чем
серьезней и объемней программный проект, тем большее значение
приобретают
вопросы
программирования.
привести
к
использования
Пренебрежение
значительным
данными
временным
надежности программного комплекса.
современных
технологий
вопросами
издержкам
и
может
снижению
74

75.

Важнейшим фактором, определяющим надежность и малые сроки
создания программного комплекса для решения конкретного класса
задач, является наличие развитой библиотеки совместимых между собой
программных модулей. Программа получается более надежной и
создается
за
меньшие
сроки
при
максимальном
использовании
стандартных программных элементов. Для эффективной разработки
программного обеспечения в области математического моделирования
необходимо обратить внимание на создание следующих стандартных
библиотек программ:
75

76.

приближенные и численные методы (процессоры);
средства подготовки исходных данных (препроцессоры);
средства
визуализации
и
представления
результатов
(постпроцессоры).
Разработка таких общих библиотек программ возможна лишь при
стандартизации потоков передачи данных между препроцессором,
процессором и постпроцессором. В простейшем случае речь может идти
об унификации форматов передаваемых файлов.
76

77.

6. Проверка адекватности модели
Под адекватностью математической модели будет пониматься степень
соответствия результатов, полученных по разработанной модели,
данным эксперимента или тестовой задачи. Прежде чем переходить к
проверке адекватности модели, необходимо убедиться в правильном
комплексном функционировании всех алгоритмов и программ модели,
выполнить независимое тестирование и отладку всех отдельных
алгоритмов
(например,
используемых
программных
модулей,
реализующих используемый численный метод).
77

78.

Проверка адекватности модели преследует две цели:
1) убедиться
в
справедливости
совокупности
гипотез,
сформулированных на этапах концептуальной и математической
постановок. Переходить к проверке гипотез следует лишь после
проверки использованных методов решения, комплексной отладки и
устранения всех ошибок и конфликтов, связанных с программным
обеспечением;
2) установить, что точность полученных результатов соответствует
точности, оговоренной в техническом задании.
78

79.

Проверка разработанной математической модели выполняется путем
сравнения с имеющимися экспериментальными данными о реальном
объекте или с результатами других, созданных ранее и хорошо себя
зарекомендовавших моделей. В первом случае говорят о проверке путем
сравнения с экспериментом, во втором о сравнении с результатами
решения тестовой задачи.
Решение вопроса о точности моделирования зависит от требований,
предъявляемых к модели, и ее назначения. При этом должна
учитываться точность получения экспериментальных результатов или
особенности постановок тестовых задач. В моделях, предназначенных
для
выполнения
удовлетворительной
оценочных
считается
и
прикидочных
точность
10 15%.
расчетов,
В
моделях,
используемых в управляющих и контролирующих системах, требуемая
79
точность может быть 1 2% и даже более.

80.

Как правило, различают качественное и количественное совпадение
результатов сравнения. При качественном сравнении требуется лишь
совпадение некоторых характерных особенностей в распределении
исследуемых параметров (например, наличие экстремальных точек,
положительное или отрицательное значение параметра, его возрастание
или убывание и т.д.). Фактически при качественном сравнении
оценивается совпадение лишь вида функции распределения параметров
(убывающая
или
возрастающая,
с
одним
экстремумом
или
с
несколькими). Вопрос о количественном сравнении можно ставить
лишь после удовлетворительного ответа на вопрос о качественном
соответствии результатов. При количественном сравнении большое
значение
следует
моделирования
параметров.
и
придавать
точности
соответствующих
им
исходных
данных
для
значений
80
сравниваемых

81.

Неадекватность результатов моделирования возможна, по крайней мере,
по трем причинам:
а) значения
задаваемых
параметров
модели
не
соответствуют
допустимой области этих параметров, определяемой принятой системой
гипотез. Например, в задаче о баскетболисте гипотезу об отсутствии
сопротивления воздуха можно использовать лишь при относительно
малых (менее 5 м/с) скоростях движения тела. При больших значениях
начальной
скорости
мяча
влияние
силы
сопротивления
будет
существенным;
б) принятая система гипотез верна, но константы и параметры в
использованных определяющих соотношениях установлены не точно.
Например, в случае задачи о баскетболисте значение ускорения
свободного падения g может быть уточнено в зависимости от широты
местности, где находится баскетболист;
в) неверна исходная совокупность гипотез.
81

82.

Все
три
случая
требуют
дополнительного
исследования
как
моделируемого объекта (с целью накопления новой дополнительной
информации о его поведении), так и исследования самой модели (с
целью уточнения границ ее применимости).
Замечание.
В данном случае не анализируется влияние выбранного численного
метода на точность получаемого решения, а значит, и на адекватность
модели. Вопрос о сходимости алгоритма и устойчивости получаемого
выбранным численным методом решения, а также накопление
погрешностей, связанных с ошибками округления при использовании
ЭВМ, здесь не рассматривается.
82

83.

При возникновении проблем, связанных с адекватностью модели, ее
корректировку требуется начинать с последовательного анализа всех
возможных
причин,
приведших
к
расхождению
результатов
моделирования и результатов эксперимента. В первую очередь требуется
исследовать модель и оценить степень ее адекватности при различных
значениях варьируемых параметров (начальных и граничных условиях,
параметров, характеризующих свойства объектов моделирования). Если
модель неадекватна в интересующей исследователя области параметров,
то можно попытаться уточнить значения констант и исходных
параметров модели. Если же и в этом случае нет положительных
результатов, то единственной возможностью улучшения модели остается
изменение принятой системы гипотез.
83

84.

Данное решение фактически означает возвращение ко второму этапу
процесса разработки модели и может повлечь не только серьезное
изменение математической постановки задачи, но и методов ее решения
(например,
переход
от
аналитических
к
численным),
полной
переработки программного обеспечения и нового цикла проверки
модели на адекватность. Поэтому решение об изменении принятой
системы гипотез должно быть всесторонне взвешено и приниматься
только в том случае, если исчерпаны все прочие возможности по
улучшению адекватности модели.
84

85.

Примечание.
Надлежит предостеречь начинающих исследователей от попыток
«перепрыгнуть» рассмотренный этап моделирования, от желания
быстрее перейти к решению «настоящей задачи». Как показывает
собственный опыт авторов, подобный образ действий приводит к
огромным временным издержкам (не говоря уже о психологических).
Особенно опасной является ситуация, в которой при решении реальной
задачи с использованием не проверенной должным образом модели
получаются правдоподобные результаты. Для других условий модель
может дать качественно неверные результаты, но истоки ошибок
85
разработчики будут искать уже не в модели.

86.

Пример. Проверка адекватности решения задачи о баскетболисте.
Соотношения (10) являются аналитическим решением задачи о
баскетболисте и позволяют определить значения координат и скоростей
центра масс мяча в любой момент времени. Для координат х и у
соотношения (10) есть уравнения параболы в параметрической форме.
Мяч при броске движется по траектории, близкой к параболе. Поэтому в
данном случае можно говорить о качественном совпадении результатов
моделирования и экспериментальных данных. Вопрос о количественном
совпадении результатов моделирования и эксперимента скорее всего
будет решен отрицательно, так как отказ от учета силы сопротивления
воздуха является грубым предположением.
86

87.

Для удовлетворительной оценки точности попадания мяча в корзину
расхождение результатов моделирования и эксперимента не должно
превышать 1 2 см. Поэтому гипотезу об отсутствии силы сопротивления
воздуха в концептуальной постановке задачи заменим новой: сила
сопротивления воздуха прямо пропорциональна скорости мяча:
Fсопр = kсопрv,
где kсопр коэффициент сопротивления, зависящий от свойств среды и
формы тела.
87

88.

Для тела в форме шара коэффициент сопротивления определялся по
формуле Стокса:
kсопр = 6 R,
где динамическая вязкость среды (для воздуха при температуре 20°С
и давлении 1 атм = 0,0182 Н с/м2), R – радиус шара. Проверим
размерность.
Н с м
[ Fсопр ] [k ][v ]
м [Н]
2
м
с
В соответствии с принятыми в баскетболе правилами длина окружности
мяча может изменяться от 0,749 до 0,780 м, что соответствует изменению
радиуса мяча от 0,119 до 0,124 м. Масса мяча должна быть в пределах от
0,567 до 0,650 кг. Примем для определенности радиус мяча R = 0,12 м, а
массу мяча m = 0,6 кг. Тогда коэффициент сопротивления среды
составляет kсопр = 0,0412 Н с/м.
88

89.

Соотношения (5) в математической постановке задачи следует заменить
на новые:
dv x
dx
kсопр v x ,
vx ,
dt
dt
dv y
dy
m
mg kсопр v y , v y .
dt
dt
m
89

90.

Разделяя переменные и интегрируя с учетом начальных условий (6),
можно получить решение в следующем виде:
x m k v x 0 (1 exp( t / m k )),
y m k ( m k g v y 0 )(1 exp( t / m k )) m k gt ,
v x v x 0 exp( t / m k ),
(13)
v y ( m k g v y 0 ) exp( t / m k ) m k g ,
где mk = m / kсопр.
90

91.

Для определения дальности броска следует второе соотношение в (13)
записать в виде
yk mk ( mk g v0 sin 0 )(1 exp( t / mk )) mk gt ,
где ук координата центра корзины. При уk = 0 получим нелинейное
уравнение относительно времени
( mk g v0 sin 0 )(1 exp( t / mk )) gt .
(14)
Определив время из решения (14) и подставив его в первое из
соотношений (13), можно найти дальность броска. Однако в данном
случае
нет
возможности
определить
аналитическое
решение
соотношения (14), что не позволяет построить соотношение для
дальности L
броска, аналогичное (11). В этом случае можно только
сравнить результаты решения (10) и (13) для некоторых фиксированных
значений v0 и 0.
91

92.

Сила сопротивления воздуха зависит не только от kсопр, но и от
скорости
мяча.
Ниже
приведены
данные
сравнения
силы
сопротивления по отношению к силе тяжести.
v, м / с
5
10
15
20
Fсопр., Н с/м2
0,206
0,412
0,618
0,824
Fсопр. / (mg), %
3,5
7,0
10,5
14,0
92

93.

Как можно видеть, сила сопротивления воздуха при скорости движения
мяча 20 м/с не превышает 14% величины силы тяжести. Однако даже
такое
незначительное
воздействие
на
движение
мяча
может
существенно сказаться на точности попадания. Так, при броске мяча
под углом 45° с начальной скоростью 6,44 м/с дальность броска с
учетом и без учета сил сопротивления будет отличаться на 17 см. При
радиусе корзины Rk = 23,3 см разница составляет более половины Rk.
93

94.

Учет сил сопротивления приводит к изменению результатов в задаче о
попадании мяча в корзину. Так, при моделировании без учета
сопротивления среды броска мяча со штрафной линии при начальных
данных х0 = y0 = yk= 0; хk = 4,225; 0 = 45 полученный в разд. 4
результат для начальной скорости v0 составил 6,44 м/с. С учетом
сопротивления среды начальная скорость мяча должна быть равной
6,575 м/с, т.е. увеличится на 2,1%.
94

95.

Вывод формул (13).
Решаем ОДУ:
m
dv x
kсопр v x , v x (0) v0 cos 0 v x0
dt
kсопр
dv
x
vx
m
dt
v x Ce
kсопр
m
t
.
kсопр
С учетом начальных условий C v x0 , отсюда v x v x0 exp m t .
m
Обозначим mk
, тогда
kсопр
t
,
v x ( t ) v x0 exp
mk
x ( t ) v x ( t )dt v x0 e
t
mk
(13.3)
dt m k v x0 e
t
mk
C1 .
95

96.

Начальные условия (6): х(0) = х0 = 0, тогда
x (0) mk v x0 C1 0 C1 mk v x0 ,
следовательно,
x ( t ) m k v x0 e
t
mk
m k v x0 m k v x0 (1 e
x ( t ) mk v x0 (1 exp( t / mk ))
t
mk
)
(13.1)
96

97.

Решаем ОДУ:
m
dv y
dt
mg kсопрv y , v y (0) v0 sin 0 v y0
обозначим
kсопр
m
dv y
dt
g
kсопр
m
vy,
.
97

98.

Получим линейное ДУ первого порядка:
dv y
dt
v y g .
(1)
Используем метод Лагранжа.
Решаем линейное однородное уравнение
dv y
dt
v y 0
v y Ce t
полагаем
v y C ( t )e t
(2)
v y C ( t )e t C ( t )e t
(3)
98

99.

Подставляем
v y , v y
из (2), (3) в (1):
C ( t )e t C ( t )e t C ( t )e t g C ( t ) ge t
g
C ( t ) g e t dt e t C 2
g
g
v y C ( t )e t e t C 2 e t C 2e t
v y C 2e t
g
.
99

100.

Начальное условие v y (0) v y0 C 2
C 2 v y0
g
g
g
g
v y v y0 e t
kсопр t
mg m
v y v y0
e
kсопр
mg
kсопр
.
100

101.

Используем обозначение mk
v y (v y0 m k g )e
t
mk
m
kсопр
, тогда
m k g v y ( m k g v y0 ) exp( t / m k ) m k g (13.4)
y( t ) v y ( t )dt (v y0 m k g ) e
y( t ) m k ( m k g v y0 )e
t
mk
t
mk
dt m k g dt
m k gt C 3 .
101

102.

Начальное условие: у(0) = у0 = 0:
mk ( mk g v y0 ) C 3 0 C 3 mk (v y0 mk g )
y( t ) m k ( m k g v y0 )e
t
mk
m k gt m k (v y0 m k g )
Окончательно получаем
y( t ) mk ( mk g v y0 )(1 exp( t / mk )) mk gt ,
(13.2).
102

103.

7. Практическое использование построенной
модели и анализ результатов моделирования
Дескриптивная модель – модель, предназначенная для описания и
объяснения наблюдаемых фактов или прогноза поведения объектов.
Дескриптивные модели, рассмотренные выше, предназначены для
описания исследуемых параметров некоторого явления или процесса, а
также для изучения закономерностей изменения этих параметров. Эти
модели могут использоваться:
для изучения свойств и особенностей поведения исследуемого объекта
при различных сочетаниях исходных данных и разных режимах;
как моделирующие блоки в различных САПР и автоматизированных
системах управления (АСУ);
103
при построении оптимизационных моделей и моделей-имитаторов
сложных систем и комплексов.

104.

Модели, разрабатываемые для исследовательских целей, как правило,
не доводятся до уровня программных комплексов, предназначенных для
передачи сторонним пользователям. Время их существования чаще
всего ограничено временем выполнения исследовательских работ по
соответствующему направлению. Эти модели отличает поисковый
характер, применение новых вычислительных процедур и алгоритмов,
неразвитый программный интерфейс.
104

105.

Модели и построенные на их основе программные комплексы,
предназначенные для последующей передачи сторонним пользователям
или коммерческого распространения, имеют развитый дружественный
интерфейс. Данные модели обычно строятся на апробированных и
хорошо себя зарекомендовавших постановках и вычислительных
процедурах. Программные комплексы имеют подробные и качественно
составленные описания и руководства для пользователя; по всем
неясным
вопросам
Однако
следует
фирма-производитель
помнить,
что
проводит
такие
консультации.
коммерческие
модели
предназначены только для решения четко оговоренного класса задач.
Как
правило,
они
усовершенствованы.
самостоятельно
не
Так,
расширять
могут
быть
модернизированы
пользователь
не
библиотеку
используемых
методов или изменять систему исходных гипотез.
имеет
и
возможности
численных
105

106.

Независимо от области применения созданной модели группа разработчиков
обязана провести качественный и количественный анализ результатов
моделирования.
Работая с моделью, разработчики становятся специалистами в области,
связанной с объектом моделирования. Они достаточно хорошо представляют
свойства объекта, могут предсказать и объяснить его поведение. Поэтому
всесторонний анализ результатов моделирования позволяет:
выполнить
модификацию
рассматриваемого
объекта,
найти
его
оптимальные характеристики или, по крайней мере, лучшим образом учесть
его поведение и свойства;
обозначить область применения модели, что особенно важно в случае
использования моделей для систем автоматического управления;
проверить обоснованность гипотез, принятых на этапе математической
постановки, оценить возможность упрощения модели с целью повышения ее
эффективности при сохранении требуемой точности;
показать, в каком направлении следует развивать модель в дальнейшем.
106

107.

Пример. Анализ результатов решения задачи о баскетболисте.
Соотношения (10) (12) представляют аналитическое решение задачи о
баскетболисте без учета сил сопротивления среды, а соотношения
(13) (14) с учетом этих сил. Достоинством первого решения является
его простота, а к недостаткам можно отнести меньшую по сравнению с
(13), (14) точность. Невозможность получения аналитических оценок для
дальности броска следует считать недостатками решения (13) и (14). Это
обстоятельство затрудняет аналитический анализ данного решения.
Вместе с тем, как следует из приведенных в предыдущем разделе оценок
начальной скорости броска, ее изменение для решения (13) и (14)
составляет несколько процентов, что позволяет не отбрасывать решение
(10) (12) и выполнить его анализ.
107

108.

Из соотношения (11) можно заключить, что заданную величину
дальности броска можно определить при двух значениях угла бросания,
обеспечивающих настильную (при 0 < 45°) и навесную (при 0 > 45°)
траектории движения мяча. При 0 = 45° указанные траектории
совпадают. Для обеспечения одинаковой точности (при отсутствии
сопротивления) для навесной и настильной траекторий начальные
скорости мяча должны быть одинаковы.
108

109.

Для оценки точности попадания мяча в
кольцо рассмотрим ситуации, возникающие
при подлете мяча к корзине со скоростью v
под углом к плоскости корзины (рис. 5).
Отрезок АВ длиной 2d определяет ширину
коридора
так
называемого
«чистого»
попадания мяча в корзину.
Задачу определения d можно свести к чисто геометрической. Для этого
достаточно определить длину гипотенузы прямоугольного треугольника
ACD и вычесть ее из величины внутреннего радиуса корзины:
d = Rk R/sin .
(15)
109

110.

Величина d получилась зависящей от угла падения мяча. При d = 0
можно найти минимальное значение mjn, при котором еще возможно
«чистое» попадание мяча:
sin min = R/Rk
(16)
Принимая внутренний радиус кольца корзины Rk равным 0,225 м,
получаем значение минимального угла mjn = 32,2°.
Если рассматривать броски при условии уk = у0, то в отсутствии силы
сопротивления воздуха угол падения мяча равен углу его бросания 0.
В этом случае для обеспечения чистого попадания мяча в корзину угол
0 должен быть больше mjn = 32,2°.
110

111.

Проведенный анализ позволяет ввести ограничение на точность броска:
d d. В предельном случае, учитывая (12) и выражая дальность,
получим L = xk ± d. Подставив выражение для дальности (11) и определив
из полученного соотношения начальную скорость мяча, найдем
(17)
g
( xk d ) .
sin 2 0
определяет интервал начальных
v0
Соотношение
(17)
скоростей,
обеспечивающих чистое попадание мяча в корзину при заданном угле
бросания.
111

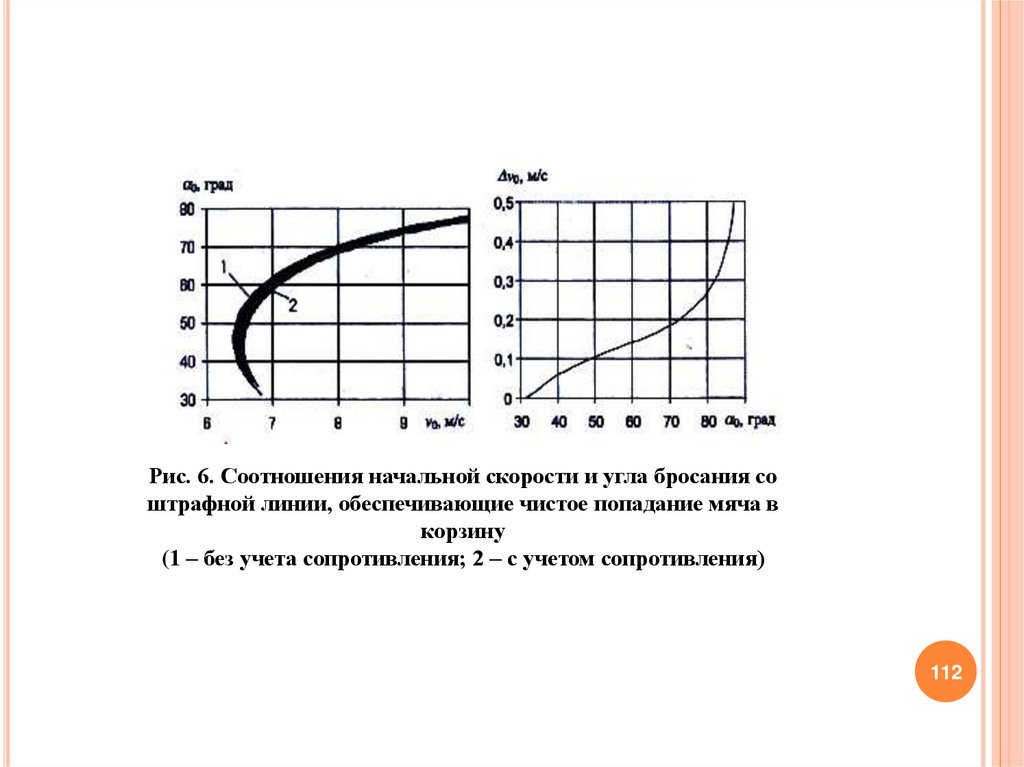
112.

Рис. 6. Соотношения начальной скорости и угла бросания со
штрафной линии, обеспечивающие чистое попадание мяча в
корзину
(1 – без учета сопротивления; 2 – с учетом сопротивления)
112

113.

На рис. 6,а приведена графическая иллюстрация соотношения (17).
Допустимые начальные скорости мяча образуют С-образную полоску.
Черная полоска соответствует чистому попаданию по модели (10) 12).
Серая полоска соответствует попаданию по модели (13). Изменение
ширины полосок в зависимости от величины угла бросания приведено
на рис. 6, б. Учет силы сопротивления приводит к незначительному
увеличению начальной скорости мяча. При этом ширина полоски при
учете сопротивления воздуха практически не изменяется.
113

114.

Особенно быстро ширина полоски допустимых скоростей увеличивается
при 0 > 80°. Однако в этом случае сильно возрастает также начальная
скорость мяча (при
0 = 89° она должна быть более 34 м/с). Можно
предположить, что чем выше начальная скорость броска, тем с большей
погрешностью
баскетболист
может
ее
сообщить
мячу.
Поэтому
штрафные броски под углом 0 > 80° надо исключить из рассмотрения.
Приведенный здесь анализ попадания мяча в корзину при броске со
штрафной линии следует считать приближенным, так как при
определении допустимых скоростей
и углов бросания мяча не
учитывалась возможность попадания за счет отскоков от щита и кольца
корзины. Более подробно эта задача будет рассмотрена далее.
114

115.

Вопросы для самопроверки
1. Кто участвует в разработке содержательной постановки задачи?
2. На
основании
какой
информации
выполняется
формулировка
концептуальной постановки задачи моделирования?
3. Какие функции выполняет постановщик задач?
4. Какая
из
постановок
задачи
(содержательная,
концептуальная
или
математическая) является самой абстрактной?
5. Что включает понятие корректности математической задачи?
6. Каким условиям должна удовлетворять корректная модель?
7. К каким математическим задачам можно применять численные методы?
8. Назовите три составляющие погрешности численных методов.
9. Какие цели преследует проверка адекватности модели?
10. Перечислите причины возможной неадекватности модели.
11. Для решения каких задач может быть использована математическая модель?
115

116.

Задания для самостоятельного выполнения
1. Используя
приведенную в данной главе «технологию», разработайте
математическую модель движения железнодорожного состава. В первом
приближении вагоны можно считать абсолютно жесткими телами, связи
между ними — линейными или нелинейно упругими.
2. Выполните содержательную, концептуальную и математическую постановки
для математической модели, описывающей взлет космического аппарата с
Луны.
3. Выполните содержательную, концептуальную и математическую постановки
для математической модели, описывающей посадку спутника в атмосфере
Земли.
4. Выполните содержательную, концептуальную и математическую постановки
для математической модели, описывающей движение шарика в сферической
ямке. Выберите и реализуйте метод решения полученной математической
116
задачи. Исследуйте траектории шарика в зависимости от начальных условий.

117.

5. Выполните содержательную, концептуальную и математическую
постановки для математической модели, описывающей движение
срубленного дерева.
6. Выполните содержательную, концептуальную и математическую
постановки для математической модели, описывающей движение
заряженной частицы в магнитном поле.
7. Космический аппарат совершает движение по орбите вокруг Земли и
может быть виден некоторым наблюдателем, находящимся на ее
поверхности в точке с заданными координатами. Выполните
содержательную, концептуальную и математическую постановки для
математической модели, описывающей движение космического
аппарата по небосводу Земли с точки зрения наблюдателя.
117

118.

8. Выполните содержательную, концептуальную и математическую постановки
для
математической
модели,
описывающей
движение
лыжника,
выполняющего прыжок с трамплина.
9.
Выполните содержательную, концептуальную и математическую
постановки для математической модели, описывающей процесс
нагревания и закипания чайника.
10. Разработайте математическую модель какого-либо процесса в
интересующей вас области знаний, опишите особенности каждого из
этапов
моделирования,
сравните
их
с
этапами
построения
математической модели предыдущего задания.
118

119.

Спасибо за внимание!
119