Запись, сравнение, действия с действительными числами, числовая прямая

1.

9 класс
АЛГЕБРА
Запись, сравнение, действия с
действительными числами, числовая прямая

2. ЗАПИСЬ

Письменное счисление есть способ изображать все возможные целые
числа немногими знаками и выговаривать написанные числа.
Эти знаки называются цифрами.
Цифра. Цифра есть условный знак, служащий для изображения
чисел. Цифр десять. Первые девять цифр изображают первые девять
чисел:
1 (один), 2 (два), 3 (три), 4 (четыре), 5 (пять), 6 (шесть), 7 (семь), 8
(восемь), 9 (девять).
Они называются значащими цифрами.
Нуль. Десятая цифра есть 0 (нуль). Знак этот не выражает никакого
числа, а указывает только на отсутствие единиц.

3. СРАВНЕНИЕ ЧИСЕЛ

Сравнить два числа — это значит определить, какое из чисел
больше другого, меньше другого или равно другому.
Записывается это с помощью знаков:
“>” — больше;
“<” — меньше;
“=” — равно.
Два целых числа называют равными, когда их запись полностью
совпадает. Иначе они считаются неравными.

4. СРАВНЕНИЕ ЧИСЕЛ

Любое целое отрицательное число меньше целого
положительного и наоборот.
Из двух отрицательных чисел меньшим является то, модуль
которого больше и наоборот.

5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

6.

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

7.

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

8.

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

9.

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

10.

11.

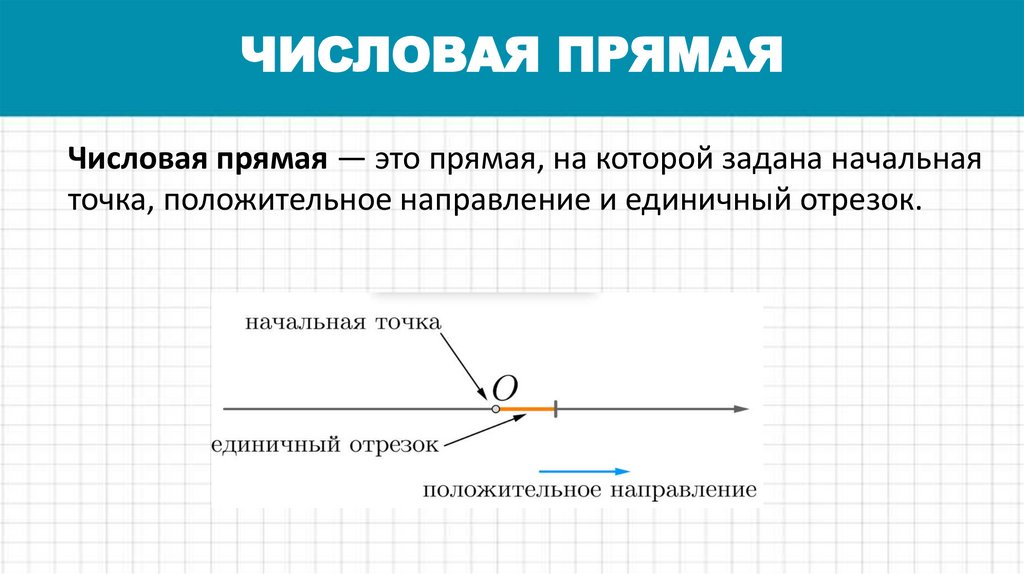
ЧИСЛОВАЯ ПРЯМАЯ
Числовая прямая — это прямая, на которой задана начальная
точка, положительное направление и единичный отрезок.

12. КВАДРАТНЫЙ КОРЕНЬ

13.

КВАДРАТНЫЙ КОРЕНЬ

14.

КВАДРАТНЫЙ КОРЕНЬ

15.

КВАДРАТНЫЙ КОРЕНЬ

16.

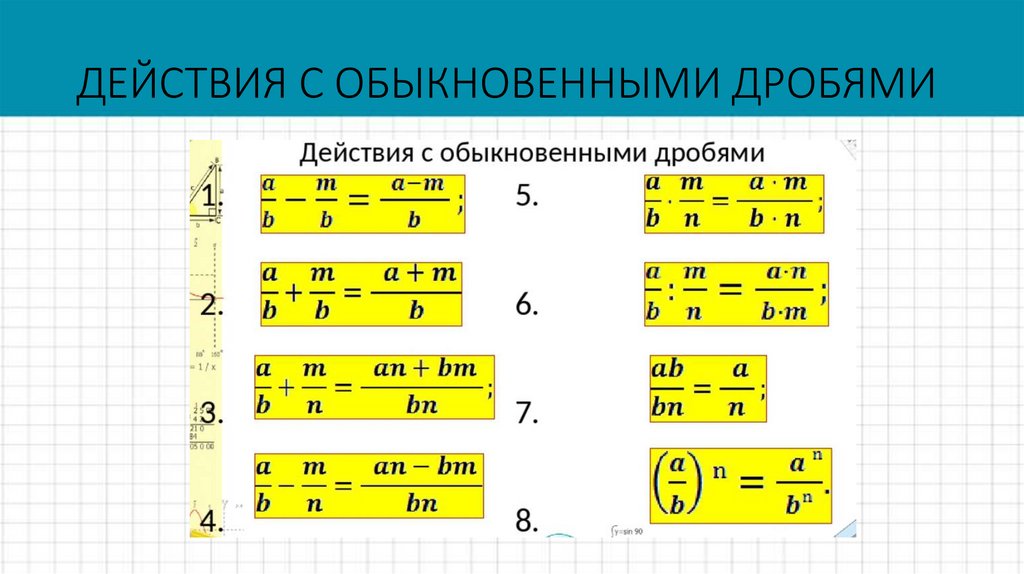
СВОЙСТВО ДЕЙСТВИТЕЛЬНЫЪ ЧИСЕЛ

17. ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ

18. Приступим к решению заданий!

19. Задание 1

Решение:
По условию a < d = c < d, поэтому d > a.
Правильный ответ указан под номером 2.
Ответ: 2.

20. Задание 2

Решение:
Заметим, что по условию a положительно и находится в интервале
от 0 до 1. Поэтому числа a2, a3 и тоже будут положительными,
тогда как число –a будет отрицательным. Таким образом, –
a является наименьшим из предложенных в качестве вариантов
ответа чисел.
Правильный ответ указан под номером 3.
Ответ: 3.

21. Задание 3

Решение:

22. Задание 4

Решение:
Ответ: 31,6.

23. Задание 5

Решение:
Ответ: 16.

24. Задание 6

Решение:
Ответ: 12.

25. Задание 7

Решение:
Ответ: 7.

26. Задание 8

Решение:
Ответ: 320.

27. Рефлексия

28. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ

29. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ

30. Домашнее задание