Повторение. Основные методы решения целых рациональных уравнений

1. Повторение. Основные методы решения целых рациональных уравнений

2.

Определение
Целым уравнением с одной переменной
называется уравнение, левая и правая части
которого – целые выражения.
Например:
х² + 2х – 6 = 0,
х⁴ + х⁶ = х² - х³,
⅓(х + 1) - ⅕(х² - х + 6) = 2х², т.п.

3.

Определение
Если уравнение с одной переменной записано
в виде Р(х) = 0, Р(х) – многочлен стандартного
вида, то степень этого многочлена называют
степенью уравнения.
Например:
х³ + 2х² - 2х – 1 = 0 – уравнение 3-ей степени;
х⁶ - 3х³ - 2 = 0 – уравнение 6-ой степени.

4. ах + b = 0 – линейное уравнение; ах² + bх + с = 0 – квадратное уравнение.

Алгоритмы решения таких уравнений
нам известны.
1) 5х - 10,5 = 0,
2) х² - 6х + 5 = 0,
5х = 10,5,
D = 4,
х = 2,1.
х = 3 ± 2,
Ответ: 2,1.
х₁ = 5, х₂ = 1.
Ответ: 1 и 5.

5.

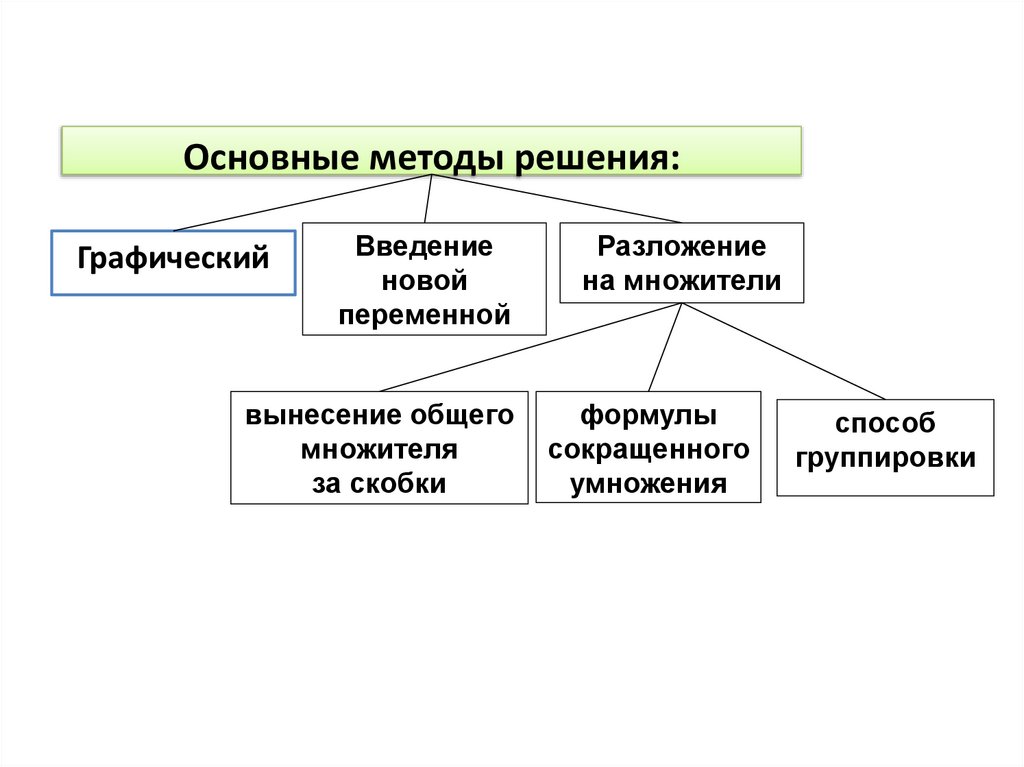
Основные методы решения:
Графический
Введение
новой
переменной
вынесение общего
множителя
за скобки
Разложение
на множители
формулы
сокращенного
умножения
способ
группировки

6. Определение. Уравнение вида ах⁴ + bх² + с = 0, являющееся квадратным относительно х², называется биквадратным. Метод решения –

введение новой переменной.
1) х⁴ - 6х² + 5 = 0,
пусть х² = t,
тогда t² - 6t + 5 = 0,
D = 16,
t = 3 ± 2,
t₁ = 5, t₂ = 1,
х² = 1, х = ±1,
х² = 5, х = ±√5.
Ответ: ±1; ±√5.
2) х⁴ + 4х² - 5 = 0;
пусть х² = t, тогда
t² + 4t – 5 = 0;
D = 36;
t = -2 ± 3;
t₁ = 1; t₂ = -5;
х² = 1; х = ±1;
х² = -5; корней нет.
Ответ: ±1.

7. Уравнения, решаемые методом введения новой переменной.

(х² - 5х + 4)(х² - 5х + 6) = 120;
пусть х² - 5х + 4 = t,
тогда t(t + 2) = 120;
t² + 2t – 120 = 0;
D = 484;
t = -1 ± 11;
t₁ = 10; t₂ = -12.
Если t = 10, то х² - 5х + 4 = 10.
Если t = - 12, то х² - 5х + 4 = -12.

8. Решение уравнений методом разложения на множители

2. 3х³ + х² + 18х + 6 = 0,
1. у³ - 4у² = 0,
х²(3х + 1) + 6(3х + 1) = 0,
у²(у - 4) = 0.
(3х + 1)(х² + 6) = 0,
у = 0 или у – 4 = 0,
3х + 1 = 0 или х² + 6 = 0,
у = 4.
х = -1/3
корней нет.
Ответ:0 и 4.
Ответ: -1/3.
Вынесение
множителя
за скобки.
Разложение
на множители
способом группировки.

9. Решение уравнений методом разложения на множители

2. 3х³ + х² + 18х + 6 = 0,
1. у³ - 4у² = 0,
х²(3х + 1) + 6(3х + 1) = 0,
у²(у - 4) = 0.
(3х + 1)(х² + 6) = 0,
у = 0 или у – 4 = 0,
3х + 1 = 0 или х² + 6 = 0,
у = 4.
х = -1/3
корней нет.
Ответ:0 и 4.
Ответ: -1/3.
Вынесение
множителя
за скобки.
Разложение
на множители
способом группировки.

10. Решение уравнений графическим способом

Алгоритм графического решения уравнений:
1. Преобразовать уравнение так, чтобы в левой и
правой части стояли известные функции.
2. В одной системе координат построить графики
этих функций.
3. Найти точки пересечения графиков.
4. Абсциссы точек пересечения являются
решением данного уравнения.
5.Записать ответ.

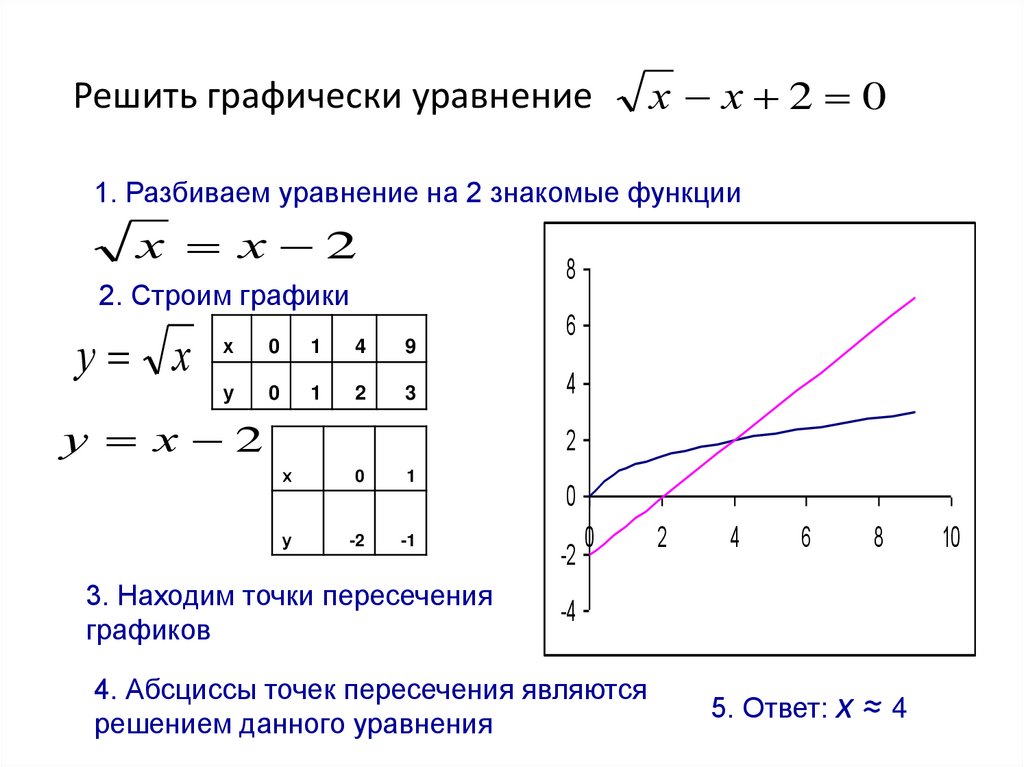
11. Решить графически уравнение

х х 2 0
1. Разбиваем уравнение на 2 знакомые функции
х х 2
8
2. Строим графики
у х
х
0
1
4
9
у
0
1
2
3
у х 2
6
4
2
х
0
1
у
-2
-1
3. Находим точки пересечения
графиков
0
-2
0
2
4
6
8
-4
4. Абсциссы точек пересечения являются
решением данного уравнения
5. Ответ: х ≈ 4
10

12.

Решите уравнения
1. х2 - 3х + 2 = 0
2. х⁴ - 6х² + 5 = 0
3. 3х³ + х² + 18х + 6 = 0
4. (х + 3)4 - 13(х + 3)2 - 14 = 0