«13-й порок мира взрослых», или Введение в теорию вероятностей (для учащихся 9-х классов )

1. "13-й порок мира взрослых", или Введение в теорию вероятностей (для учащихся 9-х классов )

"13-й порок мира взрослых", или
Введение в теорию вероятностей (для
учащихся 9-х классов )
Классическое определение
вероятности. Решение задач.

2. Москва, Болотная площадь, скульптура Михаила Шемякина “Дети в окружении пороков взрослых”.

3. 1. «Алкоголизм»

4. 2. «Война»

5. 3. «Воровство»

6. 4. «Лженауки»

7. 5. «Садизм»

8. 6. «Нищета»

9. 7. «Наркомания»

10. 8. «Проституция»

11. 9. «Пропаганда насилия»

12. 10. «Эксплуатация детского труда»

13. 11.Невежество

14. 12.Равнодушие.

15. 13-й порок. «Приобщения к азартным играм»

• Самый распространенный тип зависимости среди
молодежи – это зависимость от игровых автоматов.
Огромное количество подростков после школы, а то и
вместо нее, бегут к “одноруким бандитам” в надежде
выиграть энную сумму денег. Проигрывают, ищут
возможности их найти, порой криминальные, чтобы опять
скормить их груде металлолома”.
• Очень часто можно наткнуться на лохотронщиков, они
преграждают путь, хватают за рукава, ничего не боятся.
• И что самое ужасное, некоторые соглашаются сыграть!
• Азартные игры появились практически на заре
человечества. Сначала это были игральные кости,
сводившие с ума еще древних египтян; затем появились
карты, рулетка.

16.

• Прежде, чем соглашаться играть, советую
подумать и все просчитать- какие условия
игры вам предлагают. И чтобы в этом вы
могли разбираться мы сегодня изучаем эту
тему.

17. Игра

Кидают 6 шестигранных карандашей, на
каждой грани – числа от 1 до 6. (Почему
карандаши? К кубикам меньше доверия у
игроков.) Сумма выпавших чисел
суммируется. Если выпадет от 6 до 15 очков
или от 30 до 36 очков – большой выигрыш,
а если от 15 до 30 очков – проигрыш. Как
утверждается, вероятность выигрыша 50 на
50.

18.

Подумайте, стали бы вы играть в эту игру?
А поменяв условия выигрыша и проигрыша
наоборот? В первом случае математики
откажутся играть, а во втором – охотно
согласятся.
Не спешите давать ответ, подсчитайте, что
чаще выпадает: очки от 6 до 15 и от 30 до 36,
или очки от 15 до 30.

19. Проверка домашнего задания: №790,792

№790. Выберите 7 строк произвольного текста.
Проведя подсчет букв, найдите относительную
частоту появления буквы: а) «о»; б) «е»; в) «а»; г)
«ю».
№792. Проделайте дома такой опыт: подбросьте 50
раз монету достоинством 1 руб. и подсчитайте,
сколько раз выпадет орел. Запишите результаты в
тетрадь. В классе подсчитайте, сколько всеми
учениками было проведено опытов и каково общее
число выпадений орла. Вычислите относительную
частоту выпадения орла при бросании монеты.

20.

• Зарождение теории вероятности
произошло в поисках ответа на вопрос: как
часто наступает то или иное событие в
большой серии происходивших в
одинаковых условиях испытаний со
случайным исходом?

21. Определение вероятности события

• Если в длинной серии одинаковых опытов
со случайными исходами значения
относительных частот появления
одного и того же события близки к
некоторому определенному числу, то
это число принимают за вероятность
данного случайного события.
• Такой подход к определению вероятности
называется статистическим.

22. Определение вероятности события

•Вероятностью события
называется отношение m
благоприятствующих исходов события к
n всевозможным исходам события: р = m/n.
•Такой подход к определению вероятности
называется классическим.

23. Как найти вероятность события?

Для того, чтобы найти вероятность события
(при классическом подходе), надо
1)определить число всех исходов испытания,
2)определить число благоприятных для этого
события исходов,
3) найти отношение числа благоприятных для
этого события исходов к числу всех исходов
испытания.

24. Задача №1.

Условие
Бросаются на стол 2
игральных кубика.
Нам надо, чтобы
выпала сумма очков,
равная 5. Найдите
вероятность этого
события.
Решение
Сколько всего вариантов выпадения
очков на 2 кубиках возможно?
Подсчитаем с помощью комбинаторного
правила умножения: на первом – 6, и для
каждого из них – любой из 6 способов на
втором. Значит, всего – 36.
Сколько вариантов нам подходит?
5очков=1+4, 2+3, 3+2, 4+1, т.е. 4 варианта.
Подходит – 4 способа, всего – 36
способов. Значит, вероятность того, что
выпадет 5 очков: р = 4/36 = 1/9.

25. Задача №2

Условие
А теперь ответим на
вопрос: какая сумма
очков наиболее
вероятно выпадет
при бросании 2
игральных кубиков?
2 очка,3очка,4очка,
5очков,6очков,
7очков,8очков,
9очков, 10очков,
11очков, 12очков?
Решение
Всего исходов: 6*6=36
2очка=1+1 (1 способ); р=1/36.
3очка=1+2, 2+1 (2 способа);
р=2/36=1/18.
4очка=1+3, 2+2, 3+1 (3 способа);
р=3/36=1/12.
5очков= 1+2, 2+3, 3+2, 4+1(4 способа);
р=4/36=1/9.
6очков=1+5, 2+4, 3+3, 4+2, 5+1 (5 сп); р=5/36.
7очков= 1+6, 2+5, 3+4, 4+3, 5+2, 6+1 (6 способов);
р=6/36=1/6.
8очков=2+6, 3+5, 4+4, 5+3, 6+2
(5 способов); р=5/36.
9очков=3+6, 6+3, 4+5, 5+4 (4 способа);
р=4/36=1/9.
10очков=4+6, 5+5, 6+4 (3 способа);
р=3/36=1/12.
11очков=5+6, 6+5 (2 способа);
р=2/36=1/18.
12очков=6+6 (1 способ); р=1/36.
Чаще всего выпадает 7 очков!

26. Для повторения

Расположите в порядке возрастания числа:
1/36, 1/6, 1/12, 1/18, 1/9.
Ответ: 1/36< 1/18< 1/12< 1/9<1/6.
Правило: если числители дробей
одинаковые, то меньше та дробь, чей
знаменатель больше.

27. Проверь себя- задача №3

Антон и Игорь бросают белый и черный
игральные кубики и подсчитывают сумму
выпавших очков. Они договорились, что если
при очередном бросании в сумме выпадет 8
очков, то выигрывает Антон, а если в сумме 7
очков, то выигрывает Игорь. Можно ли
считать, что шансы выиграть в этой игре у
мальчиков одинаковые?

28. Ответ/Решение

У Игоря шансов выиграть больше, чем у Антона.
Пусть событие А означает, что при бросании кубиков
в сумме выпало 8 очков.
Пусть событие В означает, что при бросании кубиков
в сумме выпало 7 очков.
Для события А благоприятными являются 5 исходов
(2,6),(3,5),(4,4),(5,3),(6,2).
Для события В благоприятными являются 6 исходов
(1,6),(2,5),(3,4),(4,3),(5,2),(6,1).
Общее число равновозможных исходов: 6*6=36.
Вероятность наступления событий:
Р(А)=5/36, Р(В)=6/36=1/6. (5/36<6/36).

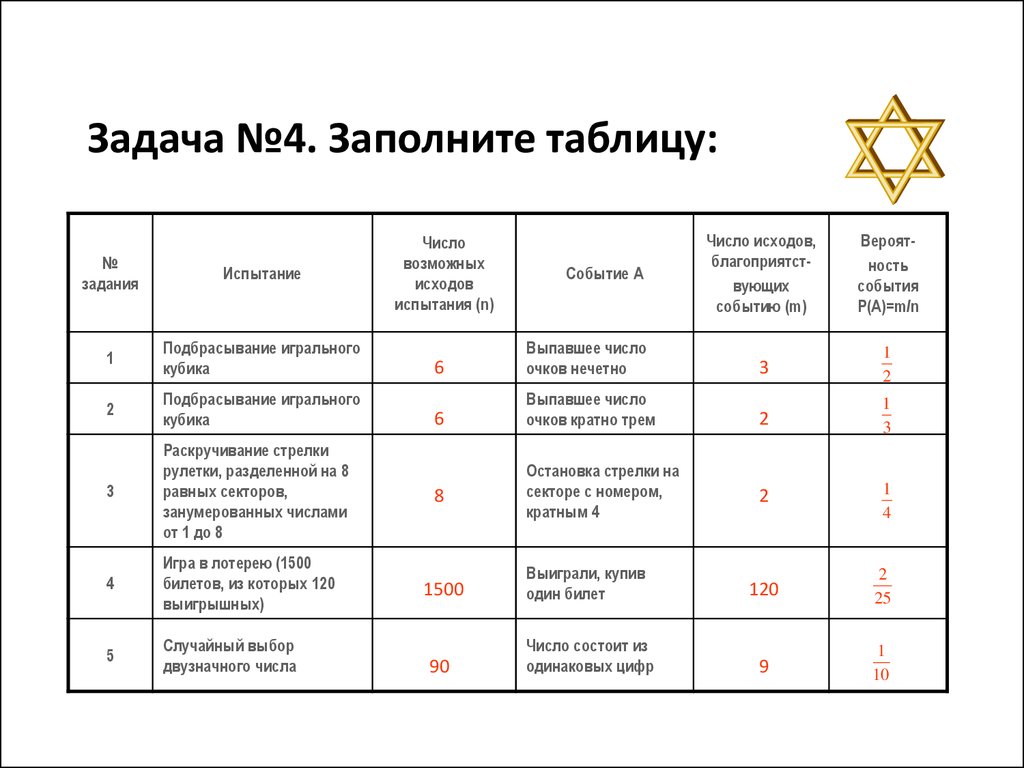
29. Задача №4. Заполните таблицу:

Число
возможных
исходов
испытания (n)
Число исходов,
благоприятствующих
событию (m)
Вероятность
события
Р(А)=m/n
№
задания
Испытание
1
Подбрасывание игрального
кубика
6
Выпавшее число
очков нечетно
3
1
2
2
Подбрасывание игрального
кубика
6
Выпавшее число
очков кратно трем
2
1
3
3
Раскручивание стрелки
рулетки, разделенной на 8
равных секторов,
занумерованных числами
от 1 до 8
2
1
4
4
Игра в лотерею (1500
билетов, из которых 120
выигрышных)
5
Случайный выбор
двузначного числа
8
Событие А
Остановка стрелки на
секторе с номером,
кратным 4
1500
Выиграли, купив
один билет
120
2
25
90
Число состоит из
одинаковых цифр
9
1
10

30. Задача №5.

Условие :
На четырех карточках написаны
буквы О, Т, К, Р. Карточки
перевернули и перемешали.
Затем открыли наугад
последовательно
эти карточки и положили в ряд.
Какова вероятность того, что
получится
слово «КРОТ»?
К Р О
Т
Решение:
Исходы – все возможные
перестановки из четырех
элементов (О, Т, К, Р); общее
число исходов: n=P₄ =4!=24
Событие А = {после открытия
карточек получится слово
«КРОТ»}: m=1
p(A)= m/n=1/24.

31. Задача №6.

Условие :
Решение:
На четырех карточках
написаны цифры 1, 2, 3, 4.
Карточки перевернули и
перемешали. Затем открыли
наугад последовательно три
карточки и положили в ряд.
Какова вероятность того, что
в результате получилось
число 123?
Исходами опыта являются все
возможные размещения
четырех карточек на трех
местах (порядок расположения
важен). Общее число исходов:
4!
n A43
2 3 4 24.
(4 3)!
1
2
3
4
Событие А- из трех карточек
образовано число 123, число
благоприятных этому событию
исходов m=1.
mA 1
P( A)
.
n
24

32. Задача №7.

Условие: в ящике лежат 1 белый и три черных шара.
Наугад вынимаются 2 шара. Какова вероятность того,
что вынуты 2 черных шара?
Решение.
Исходы – все возможные сочетания-пары шаров.
Общее число исходов
4!
3 4
C42
2! ( 4 2)!
Событие А={вынуты два черных шара};
m A C32
3!
m
3 1
3; P( A) A .
2! 1!
n
6 2
1 2
6.

33. Задача №8.

Условие:
Монету бросают три раза.
Какое событие более
вероятно: событие А- все три
раза выпала цифра, или
событие В- два раза выпала
цифра и один раз герб?
Подсчитать вероятность
каждого события.
Решение:

34. Решить дома.

• Кидают 6 шестигранных карандашей, на
каждой грани – числа от 1 до 6. Сумма
выпавших чисел суммируется. Если выпадет
от 6 до 15 очков или от 30 до 36 очков –
большой выигрыш, а если от 15 до 30 очков
– проигрыш. Как утверждается, вероятность
выигрыша 50 на 50. Найдите вероятность
этих двух событий. Верно ли утверждение,
что вероятность выигрыша 50 на 50?

35. Домашнее задание.

№ 803, 804, 805, 806, выучить определения
и формулы.

36.

• “Болен игрой” – такой диагноз в последние
годы не является редкостью.
• Азартные игры – то же самое, что
наркотическая или алкогольная
зависимости: вылечиться от этого нельзя,
можно только бросить и больше никогда не
притрагиваться.
• Так что, играть или не играть и во что играть
– решайте сами!