Векторы_1_3

1.

ГЛАВА 2. ВЕКТОРНАЯ АЛГЕБРА
Лектор: Ефремова О.Н., доцент ТПУ

2. Глава II. Векторная алгебра.

Раздел математики, в котором изучаются свойства операций над
векторами, называется векторным исчислением.
Векторное исчисление подразделяют на векторную алгебру и
векторный анализ. В векторной алгебре изучаются линейные
операции над свободными векторами (сложение векторов и
умножение вектора на число) и различные произведения
векторов (скалярное, псевдоскалярное, векторное, смешанное
и двойное векторное). В векторном анализе изучают векторы,
являющиеся функциями одного или нескольких скалярных
аргументов.

3. 1. Определение вектора. Основные отношения на множестве векторов

Определение. Вектором называется направленный отрезок, т.е.
отрезок, у которого одна из ограничивающих его точек
принимается за начало, а вторая – за конец.
Обозначают: AB (где A – начало вектора, а B – его конец),
a , b и т. д.
Изображают вектор так:
a
A
B

4.

Расстояние от начала вектора до его конца называется длиной
(или модулем) вектора. Обозначают: AB или a .
Вектор, длина которого равна единице, называется единичным
или ортом.
Вектор, начало и конец которого совпадают, называется
нулевым и обозначается
Нулевой вектор не имеет определенного направления и имеет
длину, равную нулю.
Векторы, лежащие на одной или параллельных прямых,
называются коллинеарными (параллельными).
Записывают: a
b – если векторы a и b коллинеарные, и
a b – если a и b неколлинеарные.

5.

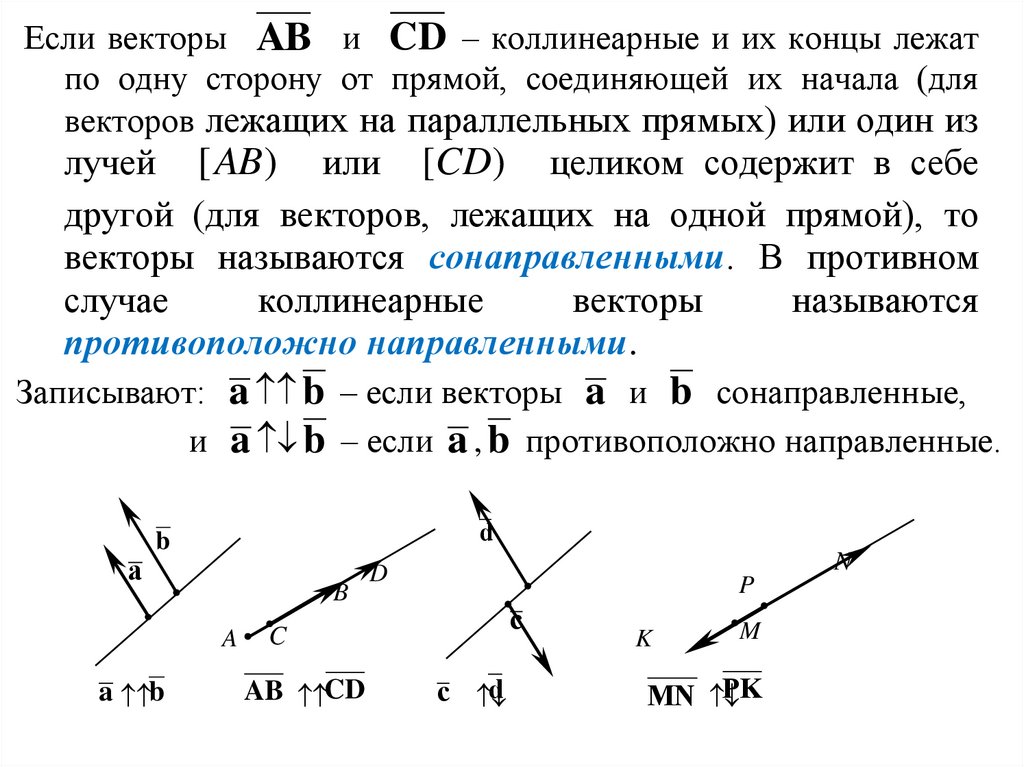
Если векторы AB и CD – коллинеарные и их концы лежат
по одну сторону от прямой, соединяющей их начала (для
векторов лежащих на параллельных прямых) или один из
лучей [AB) или [CD) целиком содержит в себе
другой (для векторов, лежащих на одной прямой), то
векторы называются сонаправленными. В противном
случае
коллинеарные
векторы
называются
противоположно направленными.
Записывают: a b – если векторы a и b сонаправленные,
и a b – если a , b противоположно направленные.
a
d
b
B
A
a b
N
D
P
c
C
AB CD
d
c
K
M
PK
MN

6.

Два вектора
a и b называются равными, если они
сонаправлены и имеют одинаковую длину.
Записывают: a b .
Все нулевые векторы считаются равными.
Векторы a и b , лежащие на перпендикулярных прямых,
называются перпендикулярными (ортогональными).
Записывают: a b .
Три вектора, лежащие в одной или в параллельных плоскостях,
называются компланарными.

7. 2. Линейные операции на множестве векторов

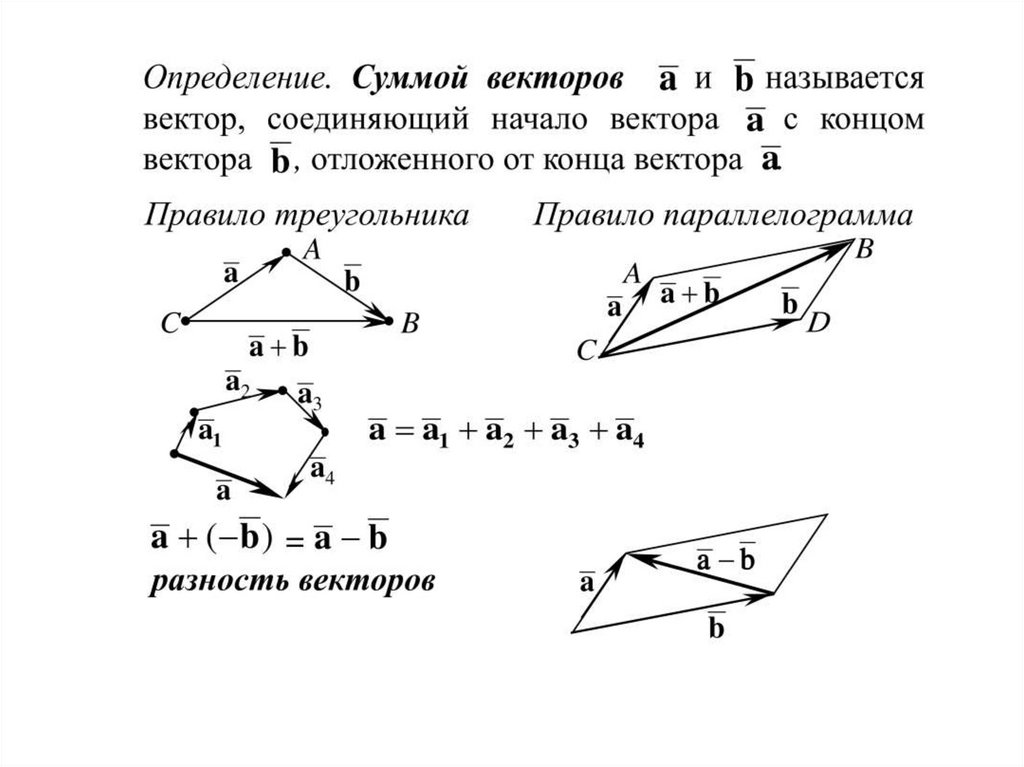
1. Умножение на число.
2. Сложение векторов
Определение. Произведением вектора
a 0 на число
0 называется вектор, длина которого равна a ,
а направление совпадает с направлением вектора a при
0 и противоположно ему при 0 .
Если a 0 или 0 , то их произведение полагают
равным 0 .
Обозначают: a .
Частный случай: произведение ( 1) a .
Вектор ( 1) a называют противоположным вектору a и
обозначают ( a ).

8.

Лемма 2.1 (критерий коллинеарности векторов).
Два вектора a и b коллинеарны тогда и только тогда,
когда a b для некоторого числа 0 .
Пропустить 0,5 страницы

9.

10.

11. 3. Понятия линейной зависимости и независимости. Базис

Определение. Говорят, что векторы ā1, ā2, …, āk линейно
зависимы, если существуют числа 1, 2, …, k , не все
равные нулю и такие, что линейная комбинация
1 · ā1+ 2 · ā2+ …+ k · āk
равна нулевому вектору ō.
Если равенство 1 · ā1+ 2 · ā2+ …+ k · āk = ō возможно только
при условии 1 = 2 = …= k = 0, то векторы ā1, ā2, …, āk
называют линейно независимыми.

12.

Лемма 3.1 (необходимое и достаточное условие линейной
зависимости векторов).
Векторы ā1, ā2, …, āk линейно зависимы хотя бы один из
них линейно выражается через оставшиеся.
Пропустить 0,5 страницы
Замечание. Часто в качестве определения линейно зависимых
векторов берут формулировку леммы 2.

13.

Лемма 3.2 (критерий линейной зависимости двух
векторов).
Два ненулевых вектора ā и
линейно зависимы они
коллинеарны.
Пропустить 0,5 страницы
Лемма 3.3 (критерий
векторов).
Три ненулевых вектора
они компланарны.
Пропустить 0,5 страницы
линейной
зависимости
трех
линейно зависимы

14.

Пусть V(3) (V(2)) – множество свободных векторов пространства
(плоскости).
Определение. Максимальное линейно независимое множество
векторов в V(3) (V(2)) называется базисом этого множества.

15.

Теорема 3.4. Любые два базиса множества на плоскости
(в пространстве) состоят из одного и того же числа векторов.
Пропустить 0,5-1 страница
Лемма 3.5.
1. Базисом на плоскости являются любые два
неколлинеарных вектора.
2. Базисом в пространстве являются любые три
некомпланарных вектора.

16.

Теорема 3.6. (о базисе).
Каждый вектор плоскости
(пространства) линейно выражается через любой его базис,
причем единственным образом.
Пропустить 0,5 страницы

17.

4. Декартова система координат

18. Правая тройка векторов

Определение. Тройка некомпланарных векторов a , b и
c называется правой, если поворот от вектора a к
вектору b на меньший угол виден из конца вектора c
против часовой стрелки. В противном случае, тройка
векторов будет левой.
c
b
a

19.

Декартова прямоугольная система координат

20. Проекция вектора на ось

Определение. Коэффициенты в разложении вектора по
базису называются координатами этого вектора в данном
базисе.
Определение. Прямую, на которой выбрано направление,
называют осью.
Пусть – ось, AB – некоторый
вектор, A 1 и B 1 – ортогональные
проекции на ось точек A и B
соответственно.
B
A
A1
Вектор A1B1 назовем векторной проекцией
вектора AB на ось .
B1

21.

Определение. Проекцией (ортогональной проекцией) вектора AB на ось называется длина его векторной
проекции A1B1 на эту ось, взятая со знаком плюс, если
вектор A1B1 и ось сонаправлены, и со знаком минус –
если вектор A1B1 и ось противоположно направлены.
Обозначают: Пр AB .
Теорема 4.1. Координаты вектора ā V(2) (V(3))
в декартовом прямоугольном базисе i, j (i, j, k) есть проекции
этого вектора на соответствующие координатные оси.

22.

Свойства проекций

23.

Свойства проекций
Пропустить 0,5-1 страница

24.

Линейные операции над векторами, заданными в
координатной форме
Теорема 4.2.
1) Если вектор a имеет в базисе e1, e2 , e3 координаты
{ 1, 2 , 3} , вектор b имеет в том же базисе координаты { 1, 2 , 3} , то вектор a b будет иметь в базисе
e1 , e2 , e3 координаты
{ 1 1, 2 2 , 3 3} .
2) Если вектор a имеет в базисе e1, e2 , e3 координаты
{ 1 , 2 , 3} , то для любого действительного числа
вектор a будет иметь в том же базисе координаты
{ 1 , 2 , 3} .
Пропустить 0,5 страницы

25.

Пропустить 1 -1,5 страницы

26.

Теорема 4.3 (критерий коллинеарности свободных
векторов в координатной форме).
Векторы a { 1; 2 ; 3 } и b { 1; 2 ; 3 } коллинеарны
тогда и только тогда, когда их координаты –
пропорциональны, т.е.
1 2 3
k.
1 2 3
Причем, если коэффициент пропорциональности k > 0 ,
то векторы a и b – сонаправлены, а если k < 0 – то
противоположно направлены
Пропустить 0,5-1 страница

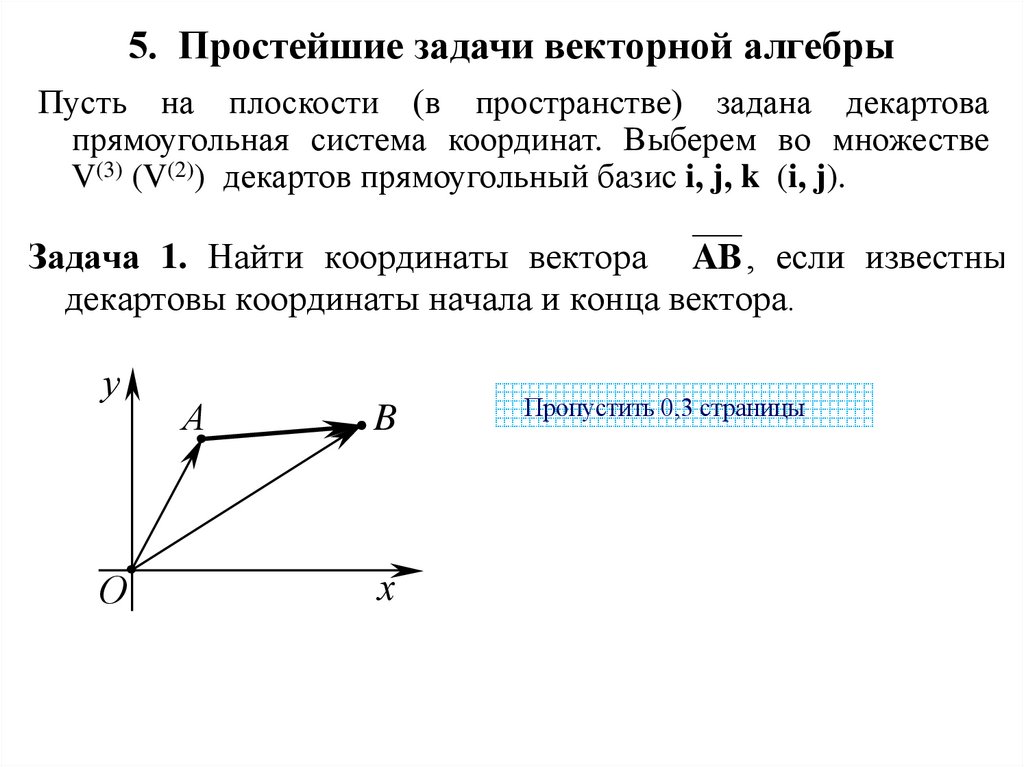
27. 5. Простейшие задачи векторной алгебры

Пусть на плоскости (в пространстве) задана декартова
прямоугольная система координат. Выберем во множестве
V(3) (V(2)) декартов прямоугольный базис i, j, k (i, j).
Задача 1. Найти координаты вектора AB , если известны
декартовы координаты начала и конца вектора.
y
O
A
B
x
Пропустить 0,3 страницы

28.

Задача 2. Найти длину вектора, если известны его координаты
в декартовом прямоугольном базисе.
y
B
ay
A
O
ax
C
x
Задача 3. Известны координаты вектора. Найти координаты
его орта.
Определение. Ортом вектора a называется вектор
a0 , сонаправленный с вектором a и имеющий единичную
длину.
Пропустить 0,3 страницы

29. Геометрический смысл координат орта вектора

Обозначим через , и углы, которые вектор a
Ox ,
Oz
Oy и
образует с координатными осями
соответственно.
cos , cos , cos называются направляющими
косинусами вектора a .
Пропустить 0,5 страницы
Координаты орта вектора a являются его
направляющими косинусами.
Замечание. Так как a0 1 и a0 cos ; cos ; cos , то
cos 2 cos 2 cos 2 1 .
Это равенство называют основным
направляющих косинусов вектора.
тождеством
для

30.

Задача 4. Известны координаты концов отрезка. Найти
координаты точки, которая делит отрезок в заданном
отношении.
Определение. Говорят, что точка
M0
делит отрезок
M 1M 2 в отношении ( 1) если M1M 0 M 0M 2 .
Если λ > 0 , то точка M0 лежит между точками M1 и M2. В этом
случае говорят, что точка M0 делит отрезок M1M2 во
внутреннем отношении.
Если λ < 0 , то точка M0 лежит на продолжении отрезка M1 M2.
В этом случае говорят, что точка M0 делит отрезок M1M2 во
внешнем отношении.
M1
Пропустить 0,5-1 страница
r1
r0
O
M0
r2
M2

31. 6. Нелинейные операции на множестве векторов

1. Скалярное произведение векторов
2. Векторное произведение векторов
3. Смешанное произведение векторов
1. Скалярное произведение векторов
Определение. Скалярным произведением
двух ненулевых векторов
и
b
a
называется число, равное произведению их
модулей на косинус угла между ними, т.е.
число a b cos .
Если a 0 или b 0 , то скалярное произведение векторов
a и b полагают равным нулю.

32.

Свойства скалярного произведения векторов
Пропустить 1 страница

33.

Определение. Проекцией вектора a на
вектор b называется проекция вектора
a на ось, определяемую вектором b .
a
b
Скалярное произведение ненулевых векторов a и b равно
произведению длины вектора a на проекцию вектора b на
вектор a (длины вектора b на проекцию a на b ).
( a , b ) a Пр a b b Пр b a

34.

Лемма 6.1. (критерий ортогональности векторов).
Два ненулевые вектора a и b ортогональны тогда и только
тогда, когда их скалярное произведение равно нулю.
Пропустить 0,5 страницы
Лемма 6.2. Если в декартовом прямоугольном базисе векторы
a и b имеют координаты: a {ax ; ay ; az }, b {bx ; by ; bz },
то
(a, b ) axbx a yby az bz .
(1)
Пропустить 0,5 страницы
Формулу (1) называют выражением скалярного произведения
через декартовы координаты векторов.

35.

Физический смысл скалярного произведения
Если под действием постоянной силы F точка перемещается по прямой из точки M 1 в M 2 , то работа силы F
будет равна A F, M1M 2 .

36. 2. Векторное произведение векторов

Определение. Тройка векторов a , b и c называется
правой, если поворот от вектора a к вектору b на
меньший угол виден из конца вектора c против часовой
стрелки.
c
b
a

37.

Определение.
Векторным
произведением
двух
ненулевых векторов a и b называется вектор c ,
удовлетворяющий следующим условиям:
1) | c | | a | | b | sin , где – угол между векторами a
и b;
2) вектор c ортогонален векторам a и b ;
3) тройка векторов a , b иc – правая.
Если хотя бы один из векторов a или b нулевой, то их
векторное произведение полагают равным нулевому
вектору.
Обозначают: [a, b] или a b .

38. Свойства векторного произведения векторов

1) При перестановке векторов a
иb
их векторное
произведение меняет знак, т.е.
[a, b] [b, a ] .
2) Числовой множитель любого из двух векторов можно
вынести за знак векторного произведения, т.е.
[ a, b] [a, b] [a, b] .
3) Если один из векторов записан в виде суммы, то
векторное произведение тоже можно записать в виде
[a1 a 2 , b] [a1, b] [a2 , b] ,
суммы.
[a, b1 b2 ] [a, b1 ] [a, b2 ] .

39.

4) Критерий коллинеарности векторов
Ненулевые векторы a и b коллинеарные тогда и
только тогда, когда их векторное произведение равно
нулевому вектору.
Пропустить 0,5-1 страница

40.

5) Геометрический смысл векторного произведения
Модуль векторного произведения неколлинеарных векторов a и b равен площади параллелограмма, построенного на этих векторах.
Пропустить 0,5 страницы

41.

6) Если в декартовом прямоугольном базисе векторы a и b
имеют координаты: a {ax ; ay ; az }, b {bx ; by ; bz }, то
i j k
a y az az ax ax a y
a x a y az .
[a, b ]
;
;
b
b
b
b
x
y
y z bz bx
bx by bz
Пропустить 0,5-1 страница

42.

7) Механический смысл векторного произведения
Если вектор F это сила, приложенная к точке M , то
векторное произведение OM, F представляет собой
момент силы F относительно точки O .

43. 3. Смешанное произведение векторов

Определение.
Смешанным
произведением
трех
векторов a , b и c называется число, равное
скалярному произведению вектора a
на векторное
произведение векторов b и c , т.е. ( a,[b, c ]) .
Обозначают: ( a, b, c ) или a bc .

44. Свойства смешанного произведения векторов

1) При циклической перестановке векторов a , b , c их
смешанное произведение не меняется, т.е.
( a, b, c ) ( b, c, a ) ( c, a, b) .
Пропустить 0,3 страницы
2) При перестановке любых двух векторов их смешанное
произведение меняет знак.
Пропустить 0,3 страницы

45.

3) Числовой множитель любого из трех векторов можно
вынести за знак смешанного произведения, т.е.
( a, b, c ) ( a, b, c ) ( a, b, c ) ( a, b, c ) .
Пропустить 0,5 страницы
4) Если один из векторов записан в виде суммы, то смешанное произведение тоже можно записать в виде суммы.
( a1 a2 , b, c ) ( a1, b, c ) ( a 2 , b, c ) ,
( a, b1 b2 , c ) ( a, b1, c ) ( a, b2 , c ) ,
( a, b, c1 c2 ) ( a, b, c1 ) ( a, b, c2 ) .

46.

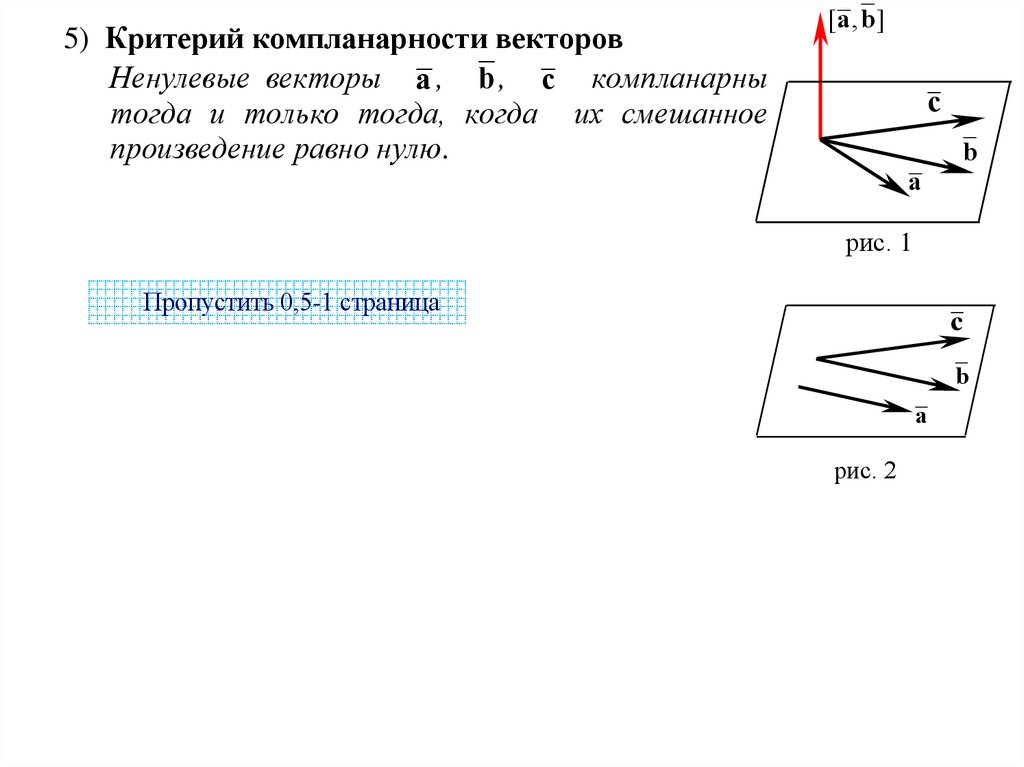
5) Критерий компланарности векторов
Ненулевые векторы a , b , c компланарны
тогда и только тогда, когда их смешанное
произведение равно нулю.
[a , b]
c
b
a
рис. 1
Пропустить 0,5-1 страница
c
b
a
рис. 2

47.

6) Если ( a, b, c ) 0 , то векторы a , b , c
образуют
правую тройку. Если ( a, b, c ) 0 , то тройка векторов
a , b , c – левая.

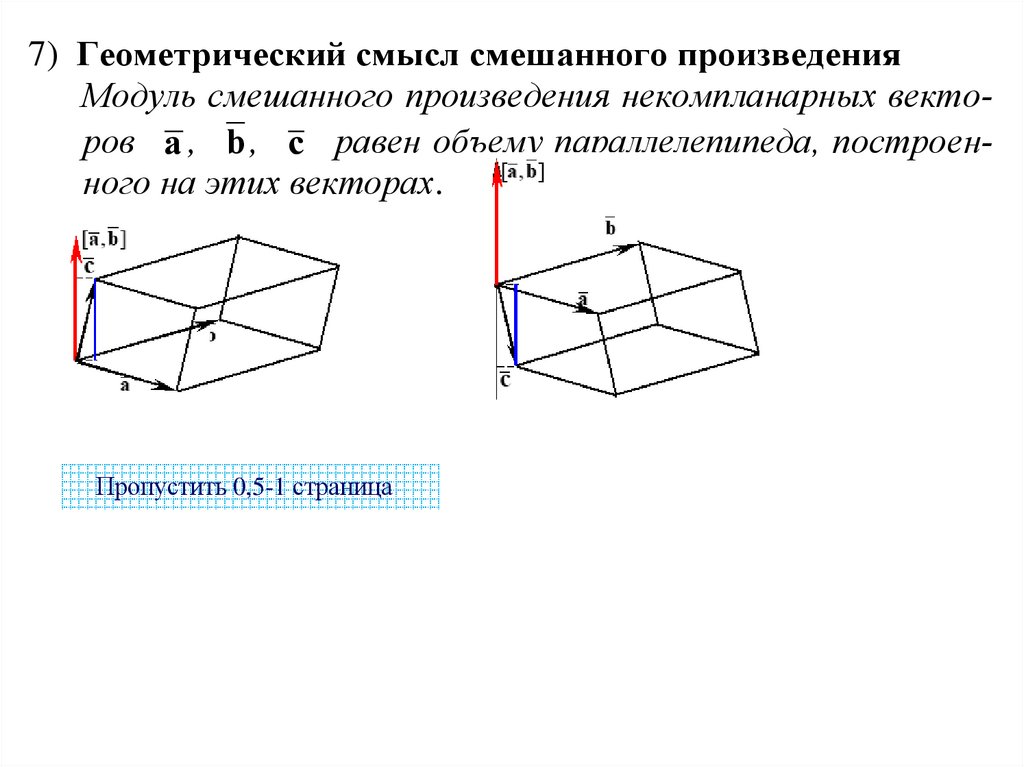
48.

7) Геометрический смысл смешанного произведения
Модуль смешанного произведения некомпланарных векторов a , b , c равен объему параллелепипеда, построенного на этих векторах.
Пропустить 0,5-1 страница

49.

8) (Следствие свойства 7). Объем пирамиды, построенной на
1
векторах a , b , c , равен
модуля их смешанного
6
произведения.
9) Если в декартовом прямоугольном базисе векторы a , b ,
b {bx ; by ; bz },
c имеют координаты a {ax ; ay ; az },
c {cx ;cy ;cz } , то
a x a y az
( a, b, c ) bx by bz .
cx c y cz
Пропустить 0,5 страницы