4.Лек.4. ОТЦ. Цепи гарм.тока

1. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ В УСТАНОВИВШЕМСЯ РЕЖИМЕ

Гармоническое колебание и способы его описания
• В электротехнике простейшим переменным сигналом считают гармонический: ЭДС - е(t), напряжение - (u(t), ток - i(t)
• Способы представления гармонического сигнала
1.Аналитически гармонический сигнал (например,
напряжение) записывается выражением:
u(t) = Umsin(ω0t+φ0) ,
(1.1)
где u(t) – мгновенное значение напряжения – напряжение в
момент времени t.
u(t) = Umcos(ω0t+φ0)
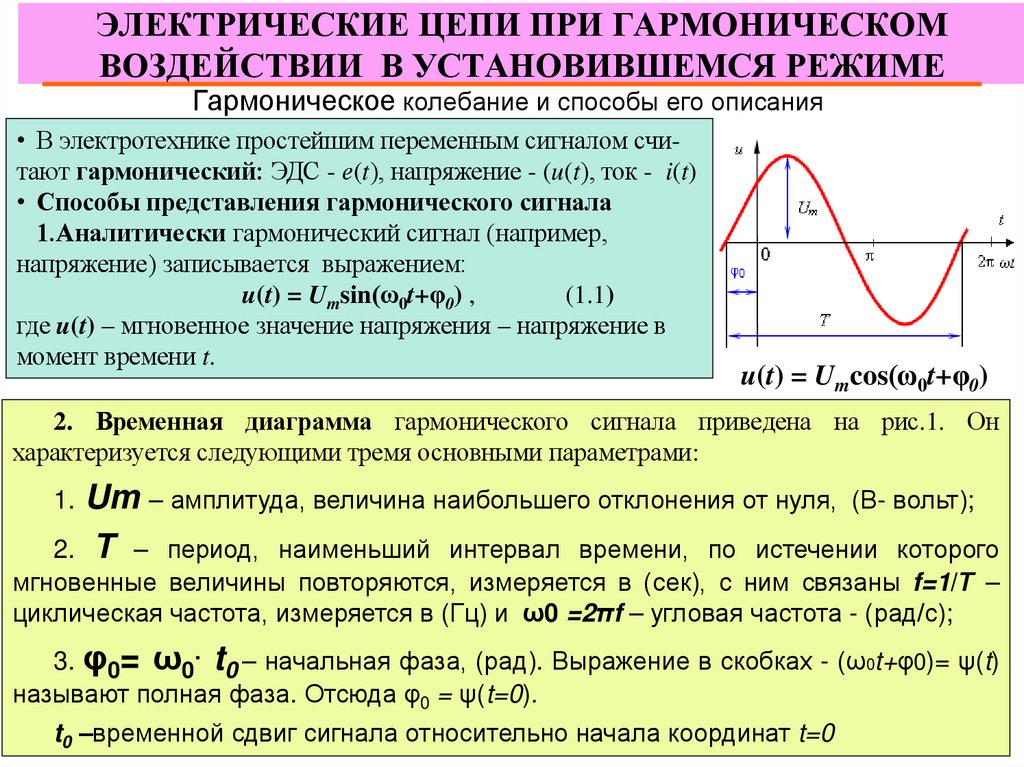
2. Временная диаграмма гармонического сигнала приведена на рис.1. Он
характеризуется следующими тремя основными параметрами:
1. Um – амплитуда, величина наибольшего отклонения от нуля, (В- вольт);
2. Т – период, наименьший интервал времени, по истечении которого
мгновенные величины повторяются, измеряется в (сек), с ним связаны f=1/Т –
циклическая частота, измеряется в (Гц) и ω0 =2πf – угловая частота - (рад/с);
3. φ0= ω0. t0 – начальная фаза, (рад). Выражение в скобках - (ω0t+φ0)= ψ(t)
называют полная фаза. Отсюда φ0 = ψ(t=0).
t0 –временной сдвиг сигнала относительно начала координат t=0
1

2. Генерирование синусоидальной э.д.с.

• В современной технике используются переменные
токи с частотой от долей герца до миллиардов герц.
В
российских
промышленных
энергосистемах
применяется частота f=50 Гц. В зависимости от
частоты
источниками
синусоидальной
э.д.с.
являются генераторы того или иного типа:
• Вращающиеся электрические машины генерируют
э.д.с. промышленной частоты (50Гц); Ионные или
полупроводниковые инверторы - промышленные и
повышенные частоты.
• Рассмотрим принцип действия генератора –
электромагнитной машины.
• В обмотке (витке), по закону Фарадея (правило
правой руки), наводится э.д.с.,:
,
N
_
B
S
e Blv
где В – магнитная индукция поля, Вб; l – длина
провода; v – линейная скорость перемещения
проводника.
2

3. Величины гармонического сигнала

Кроме амплитуд о величине периодических сигналов судят по их:
1. Среднеквадратическим (действующие) значениям за период, I, U, E
T
T
1 2
U
u dt
T 0
1 2
I
i dt
T 0
T
1 2
E
e dt
T 0
• Например, действующее значение периодического тока равно такому
значению постоянного тока, который, проходя через сопротивление r, за
период Т выделяет то же количество тепла, что и данный переменный ток i.
Связь между амплитудным и действующим значениями синусоидального
тока равна
Im
1 2 2
1 1 cos 2 t
I
I
sin
tdt
I
dt
0,707 I m
m
m
T0
T0
2
2
T
T
E
Em
U
; U m
2
2
2. Среднее значение. Среднее значение синусоидальной величины за
период равно нулю, поэтому за среднее значением
гармонического тока принимают среднее значение
за положительный полупериод:
Т
2
T
2I
2
2 2
T
2
I ср i t dt I m sin tdt m [ cos t ]0 2 I m 0,637 I m
T 0
T 0
T
3

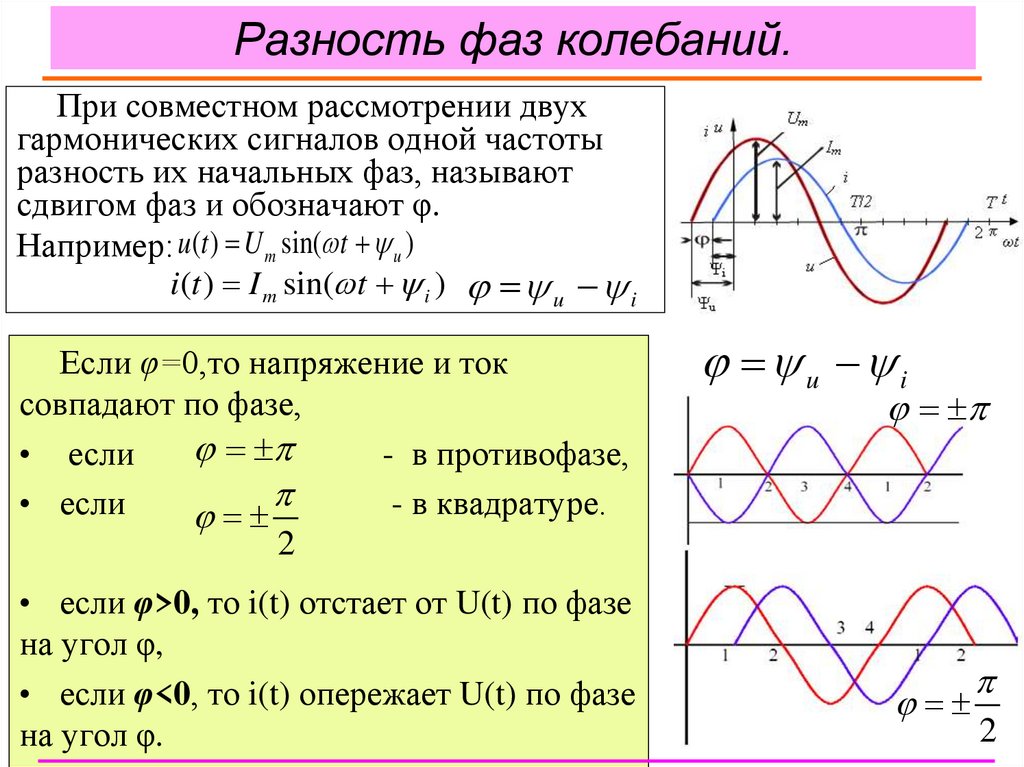
4. Разность фаз колебаний.

При совместном рассмотрении двух
гармонических сигналов одной частоты
разность их начальных фаз, называют
сдвигом фаз и обозначают φ.
Например: u (t ) U m sin( t u )
i (t ) I m sin( t i ) u i
Если φ=0,то напряжение и ток
совпадают по фазе,
• если
- в противофазе,
• если
- в квадратуре.
2
• если φ>0, то i(t) отстает от U(t) по фазе
на угол φ,
• если φ<0, то i(t) опережает U(t) по фазе
на угол φ.
u i
4
2

5. Пример сложения :

Законы Кирхгофа для мгновенных значений
Если
i t I m sin t i
u t U m sin t u
То в узле
i t 0
u
в контуре
Пример сложения :
i2 Im sin( t i )
i1 Im sin( t i )
1
t e t
2
1
2
i3 t i1 t i2 t Im sin( t i )
3
3
Im Im2 Im2 2Im Im cos( i i )
3
1
i arctg
3
2
1
2
1
Im sin i Im sin i
1
1
2
2
2
Im cos i Im cos i
1
Недостаток: громозкость вычислений.
1
2
2

6. Векторное представление гармонического сигнала

,
• При векторном представлении гармонический
сигнал, как комплексное число, изображают вектором
на комплексной плоскости.
Комплексную
амплитуду
Ím=Imejφ можно представить на
комплексной плоскости:
1. вектором длины Im и углом
поворота ψ относительно оси Re.
2.
вектором
проекции
которого на Re и Im оси равны:
Re[Ím ]= Imcos φ и Im[Ím] =Imsin
φ
Комплексный гармонический сигнал:
s(t) = Аm e j(ωt+φ) =Ȧm e jωt называют гармонический
комплекс, где e jωt – множитель вращения.
На комплексной плоскости гармонический комплекс
представляется вектором Аm c начальной фазой φ0,
вращающимся против часовой стрелки с частотой ω.
Вспомним
комплексные числа и
их графическое
представление
A a jb Ae j
A cos j sin
где A a 2 b 2
arctg
b
a
a A cos
b Asin

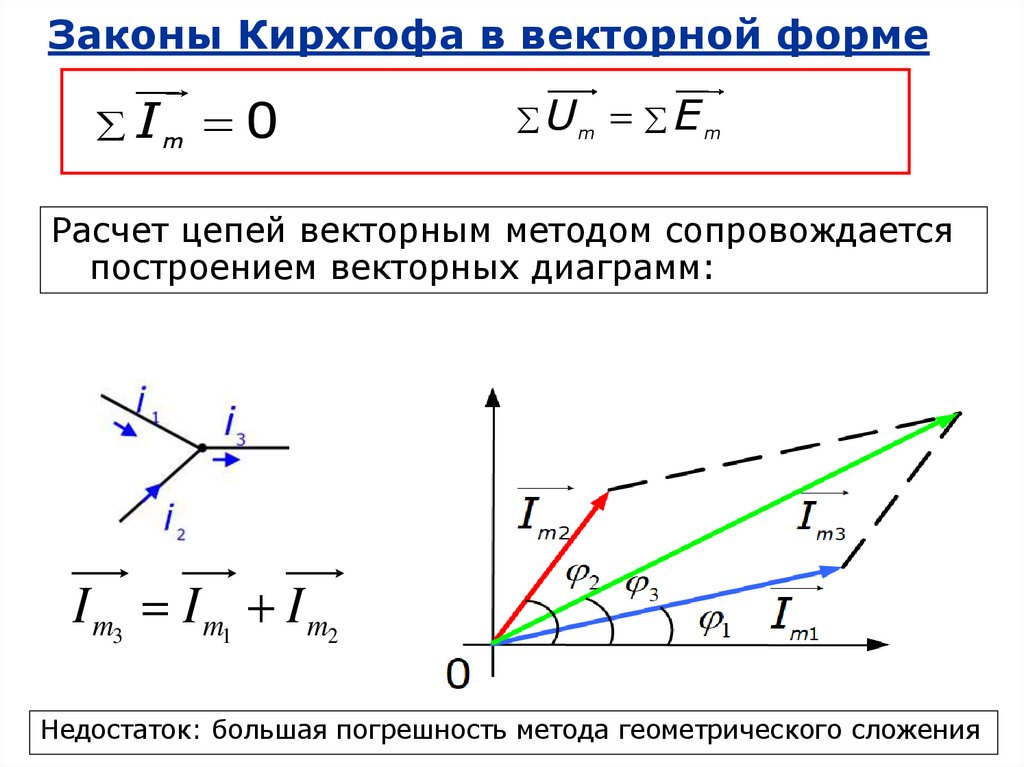
7. Законы Кирхгофа в векторной форме

Im 0
Um E m
Расчет цепей векторным методом сопровождается
построением векторных диаграмм:
I m3 I m1 I m2
Недостаток: большая погрешность метода геометрического сложения

8. Представление гармонического сигнала комплексной амплитудой

При комплексном представлении гармонический сигнал заменяется комплексным числом.
2
•Вспомним комплексные числа: Z - комплексное число. Его можно записать
в одной из трех форм: алгебраической, показательной и тригонометрической:
Z a jb Z e j Z Z sin Z j Z cos Z
, где
1 мнимая единица
где а=Re(Z), b=Im(Z) – реальная и мнимая составляющие комплексного числа Z .
Z a 2 b2 - модуль и Z arctg (b a) - аргумент комплексного числа .
• При комплексном представлении гармоническое колебание i(t) = Im sin(ωt + ψ) , как
функция времени, заменяется комплексной амплитудой Ím = Imejφт , т. е. комплексным
числом независящим от времени.
• Между комплексной амплитудой и гармоническим сигналом есть взаимнооднозначное
соответствие: i(t) = Im sin(ωt + φ )↔ Ím= Imejφ, т.е. зная одно можно записать другое.
Комплексная амплитуда как и комплексное число, имеет три формы записи:
Ím = Re[Ím ]+jIm[Ím ]
= Imejφ
= Imcos φ + jImsin φ,
алгебраическая,
показательная и тригонометрическая
где
1. Re[Ím] = Imcos φ и Im[Ím ] =Imsin φ - реальная и мнимая части комплексной
амплитуды;
2. Im=((Re[Ím]2+(Im[Ím]2)1/2 и φ=arctg(Im/Re)-модуль и аргумент комплексной
амплитуды.
Использование комплексной амплитуды позволяет: 1. заменить операции над функциями времени на операциями над комплексными числами,
2. применять для анализу цепей переменного тока все методы анализа цепей постоянного тока.

9. 3. Представление гармонического сигнала комплексной амплитудой

При комплексном представлении гармонический сигнал заменяется комплексным числом.
Комплексной амплитудой гармонического тока i(t)= Im sin(ωt + ψ) называют
комплексное число Ím= Imejφ, где Im–амплитуда, φ - начальная фаза тока. j 1
Между i(t) и Ím существует взаимнооднозначное соответствие:
i(t) = Im sin(ωt + φ )↔ Ím= Imejφ, зная одно можно записать другое.
Комплексная амплитуда, как комплексное число имеет три формы записи:
Ím = Re[Ím ]+jIm[Ím ]
= Imejφ
= Imcos φ + jImsin φ,
алгебраическая,
показательная и тригонометрическая
где
1. Re[Ím] = Imcos φ и Im[Ím ] =Imsin φ - реальная и мнимая части комплексной
амплитуды (числа);
2. Im=((Re[Ím]2+(Im[Ím]2)1/2 и φ=arctg(Im/Re)-модуль и аргумент комплексной
амплитуды (числа).
Во многих случаях пользуются понятием
комплекса действующего значения тока:
Í=Iеjφ где Í=Ím/ 2
Это комплексное числа с модулем в виде
действующего
значения
амплитуды
гармонического сигнала и аргументом в
виде начальной фазы.
Использование комплексной амплитуды
позволяет:
1. заменить операции над функциями
времени
на
операциями
над
комплексными числами,
2. применять
для анализу цепей
переменного тока все методы анализа
9
цепей постоянного тока.

10. Операции над комплексными числами

1.
Операции над комплексными числами в алгебраической формой записи:
A1 A2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j (b1 b2 )
A1 A2 (a1 jb1 ) (a2 jb2 ) (a1a2 b1b2 ) j (a1b2 a2b1 )
(b1a2 a1b2 )
A1 (a1 jb1 ) (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 )
j
2
2
A2 (a2 jb2 ) (a2 jb2 )(a2 jb2 )
a2 b2
a22 b22
2.
При умножении, делении, возведении в степень удобно пользоваться
показательной формой
A1 A2 A1e j 1 A2e j 2 A1 A2e j ( 1 2 )
A1e j 1
A1 j ( 1 2 )
A1
e
j 2
A2
A2
A2e
3. Если A a jb Ae j комплексного число, то число A a jb Ae j
- называется комплексно-сопряженным, причем:
A A a 2 b2

11. Простейшие математические операции с комплексными числами

Формула Эйлера:
e
j a
cos a j sin a
Единичные комплексы
e 1
e 1
e j
j0
j180
e
Действия с j
jj 1
j ( j ) 1
j 90
1
j
j
j 90
1
j
j
j

12.

Правила перехода из одной формы в другую
Из алгебраической в показательную
Из показательной в алгебраическую
а jb A Ae
A
а b
2
2
b
a arctg
a
j a
A Ae
j a
a jb
а A cos a
b A sin a
12

13.

Основные операции над комплексными изображениями гармонических
функций
1. Сложение гармонических функций одной частоты ω.
Определим комплексное изображение суммы гармонических функций.
Следовательно, суммированию гармонических функций времени одной
частоты соответствует
суммирование комплексных амплитуд
2. Дифференцирование гармонической функции времени a(t):
соответствует умножение их комплексных амплитуд на (jω):
3. Интегрирование гармонической функции времени a(t):
соответствует деление комплексных амплитуд на (jω):
13

14. 1.3. Комплексное сопротивление элемента (участка цепи)

Под комплексным сопротивлением элемента
отношения комплексной амплитуды напряжения
к комплексной амплитуде тока на элементе
Z
понимают
U1 m
j ( )
R jX Z e z Z cos jZ sin .
I1 m
R – активное (резистивное) сопротивление, Х– реактивное сопротивление,
Z=(R2+X2)1/2 - полное сопротивление элемента или модуль комплексного
сопротивления,
φ=ψu-ψi=arctg(X/R) – аргумент или начальная фаза комплексного
сопротивления, характеризует фазовый сдвиг между током и напряжением.
Взаимосвязь между полным,
активным и реактивным
сопротивлением
графически
представляется
векторной
диаграммой в виде «треугольника сопротивления».
По виду записи комплексного сопротивления можно судить о
характере участка цепи, если:
Z=R – активное (резистивное) сопротивление;
Z=R+jX — активно-индуктивное сопротивление;
Z=R – j X — активно-емкостное.
Z
X
R
14

15. Изображение точки комплексного числа на комплексной плоскости

Комплексное сопротивление Z может быть представлено в одной из
трех форм:
U1 m
j ( )
Z
R jX Z e z Z cos jZ sin .
I1 m
Модуль комплексного сопротивления:
Z=(R2+X2)1/2 всегда больше нуля.
Аргумент φZ комплексного сопротивления
зависит от знака r и x ( Z = ± r ± jx ), т.е. от
положения точки комплексного
сопротивления на комплексной плоскости
(рис. I.19). Угол φ отсчитывают от
действительной оси против часовой
стрелки, если точка расположена в первой
или второй четверти плоскости (Z1 и Z2). Для
точек Z3 и Z4, расположенных в третьей и
четвертой четвертях, угол отрицательный,
так как определяется от действительной оси
по часовой стрелке (рис. I.19):
15

16. Комплексная проводимость пассивного участка цепи

Комплексной проводимостью Y(jω) по определению величина, обратная
комплексному сопротивлению. Аналогично комплексному сопротивлению
(2.12) комплексная проводимость может быть записана в показательной (2.13),
тригонометрической и алгебраической (2.14) формах:
j I
I
Ie
j Y
m
Y ( j )
j U Y e
Y cos Y j sin Y g jb,
U
U Ue
I
m
где Y
Im
I
g 2 b 2 модуль, Y I U аргумент проводимости,
Um U
g резистивная часть, b реактивная часть проводимости.
Аргумент φY проводимости определяется на комплексной плоскости
проводимости так же, как показано на рис. 2.5 для сопротивления
Полезно отметить, что
φY = – φZ .
16

17. Схемы замещения комплексного сопротивления и проводимости

При анализе различных цепей часто возникает необходимость представить
комплексные сопротивления и проводимости электрическими моделями –
схемами замещения.
1. Участок цепи с сопротивлением Z = r + jx можно представить моделью в виде
последовательной схемы из двух элементов r и x (рис.а). Этот же участок цепи
можно представить параллельной схемой (рис. б),
Y = g + jb (проводимости складываются
при параллельном соединении элементов).
2. Если считать, что Z и Y – параметры одного и того же участка цепи, то можно
утверждать, что схемы на рис. а и б эквивалентные. Следовательно,
для этих схем должно выполняться
условие эквивалентности:
т.е.
I.38
I.39
3. Из выражений (I.38) можно определить связь
между резистивными и реактивными
составляющими комплексного сопротивления и
комплексной проводимости участка цепи (I.39):
17

18. 1.4. Законы Ома и Кирхгофа в комплексной форме

• Они имеют такой же вид, как и соответствующие уравнения для
цепей постоянного тока. Только токи, ЭДС, напряжения и
сопротивления входят в уравнения в виде комплексных амплитуд и
комплексных сопротивлений.
1. Закон Ома. Он устанавливает связь между комплексными
.
.
.
амплитудами тока и напряжения на участке цепи. 1.8.
1 2 U m12
I
m
Закон Ома для участка цепи, не содержащего источника ЭДС
Z
Z
где
комплексные
амплитуды
потенциалов
на
данном
участке
цепи,
.
I m и U m12 - комплексные амплитуды тока и напряжения
на участке цепи; Z – комплексное сопротивление участка цепи, –
.
2. Первый закон Кирхгофа: Алгебраическая сумма комплексных
амплитуд (действующих значений) токов в узле равна нулю
In 0
n
3. Второй закон Кирхгофа: В замкнутом контуре электрической
цепи алгебраическая сумма комплексных амплитуд (действующих
значений, ЭДС) равна алгебраической сумме комплексных падений
напряжений на элементах в нём
n
m
E U
k 1
k
k 1
k

19. Эквивалентные преобразования в цепях переменного тока

Все правила эквивалентных преобразований
в цепях переменного тока имеют такой же вид,
как и соответствующие правила для цепей
постоянного тока. При этом все пассивные
элементы схем заменяются их комплексными
сопротивлениями, а источники гармонического
сигнала заменяются на источниками
создающими комплексные амплитуды.
19

20. 1.5 Мощность в цепях синусоидального тока.

• Для характеристики мощности в цепи синусоидального тока используются следующие понятия :
1. Мгновенная мощность, характеризует скорость изменения энергии в цепи в момент времени t
p(t)=u(t)i(t)=UmSin (ωt+ψu) ImSin(ωt+ψ i)= UICos(ψu- ψi)- UICos(2ωt+ψu+ψi).
Мгновенная мощность содержит постоянную составляющую и переменную составляющую c
частотой 2 ω,
2. Активная мощность –средняя мощность за период «Т» : Р=UICosφ → [Вт].
Она характеризует энергию, которая совершает полезную работу. Активная мощность всегда
положительна и равна постоянной составляющей мгновенной мощности.
3. Реактивная мощность Q, вычисляется по формуле:
Q = UISinφ → [ВАр].
Эта мощность не совершает полезной работы, а характеризует интенсивность обмена энергией
между генератором и реактивными элементами цепи L и С, что приводит к дополнит. потерям
энергии. Поэтому она должна быть минимальной.
Реактивная мощность может быть:
положительной, если φ >0 в цепи с индуктивной нагрузкой
и отрицательной, если φ<0. в цепи с емкостной нагрузкой
4. Полная или кажущаяся мощность
S =Um.Im/2= UI →[ВА].
Между полной, активной и реактивной
мощностью существует связь
S P2 Q2
• Графически эту связь между мощностями можно представить в виде
«треугольника мощностей»
Коэффициент к=Р/S=cosφ называется «коэффициентом
мощности» (К→1).
20

21. Условия согласования источника сигнала с нагрузкой

Zi
Рассмотрим передачу сигнала от источника сигнала в нагрузку.
Источник: Е с Zi = Ri + jXi, и нагрузка Zн = Rн + jXн.
Em
Обычно рассматривают два условия (режима) согласования:
Zн
İ1m
1) согласование по напряжению - на нагрузке создается максимальное
напряжения Uн.max при этом к.п.д. цепи (кпд = Uн/U1=1);
2) согласования по мощности - на нагрузке выделяется максимальная мощностьРис. 7.5
Uн
Установим условие согласования по напряжению:
Zн
Запишем выражение для выходного напряжения
Uн
U1
Из него следует, что | U | → max, когда |Zн| >> |Zi|.
Z
Z
н
i
н
Такой режим согласования
используют в энергетических установках, Кпд=1.
Установим условие согласования по мощности:
Pн
Мощность выделяется на резистивной составляющей Rн нагрузки Zн
Найдем комп. амплитуду тока Im
Im
Em
Em
Z i Z н Ri Rн j X i X н
найдем модуль комплексной амплитуды
Активная мощность, выделяемая в нагрузке равна
Найдем условия, когда : Pн f ( Rн , X н ) max
Во-первых, потребуем Хн = –Хi.
Во-вторых, найдем максимум по второй переменной (по Rн)
Возьмем производную и приравняем ее к нулю.
Получим Rн = Ri.
Условие согласования по мощности
Im
1 2
I m Rн
2
Em
Ri Rн 2 X i X н 2
2
Rн Em
1
Pн
2 Ri Rн 2 X i X н 2
Pн max X X
н
i
Rн Em2
2 Ri Rн 2
Ri Rн ;
xi xн или Z i Z н ,

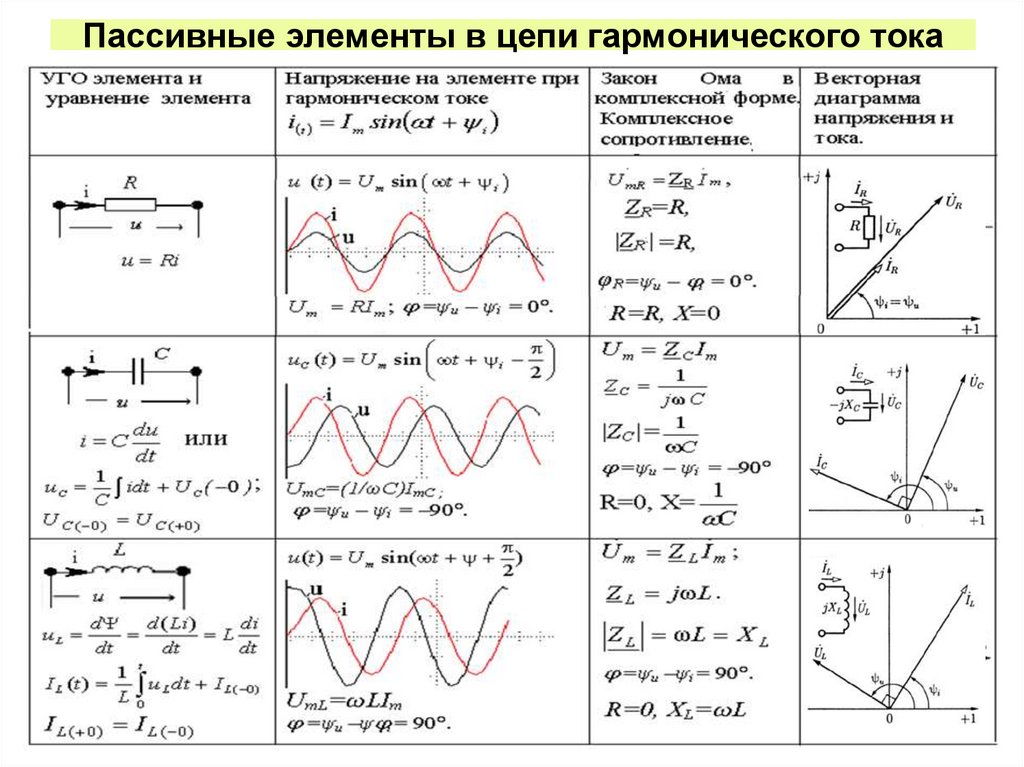
22. Пассивные элементы в цепи гармонического тока

В цепях переменного тока свойства элементов характеризуют комплексным сопротивлением. Закон Ома в комплексной форме U m , Z I m , где Z– комплексное сопротивление
U
Рассчитаем комплексное сопротивление, резистивного элемента:
ZR m R
.
I
Если i t I m cos t - i
, I m I me- j . По закону Ома найдем напряжение наm R
.
, где Um=RIm, φu=φi
u(t)=RImcos(ωt-φi )=Umcos(ωt-φu ) Um =Ume jφ
i
u
Отсюда
ZR
Um
R j0 R
Im
а) ZR =Rеj0
т.е.:
б) φ= φи - φi = 0
|ZR|=R;
Рассчитаем комплексное сопротивление, индуктивного элемента ZL
.
-jφ
Если i (t )= I mcos (ωt - φi )« I m = I me
, то по закону Ома для индуктивности запишем
u(t)= L di
i
j +
2 = j LI e j
= L I m sin t - i +
↔U m = U me
m
dt
2
π
где Um=ωLIm, e j 2 = j
.
i
ZL
Отсюда
i
Um
0 j L j L
Im
а) |ZL|=ωL; б) φ=φи - φi=π/2
Рассчитаем комплексное сопротивление
емкостного элемента Zc
.
-jφ
Если i t = I mcos ωt - φi
, I m = I me
то по закону Ома для емкостного элемента ,
i
.
j -φi -π
1
1
1
2 =
π
u t =
i(t)
dt
=
I
sin
ωt
φ
↔U
=U
e
Ime -jφi
m
m
i
m
2
C
ωC
jωC
T
гдеUm=Im/ωС, e
-j π 2
1
= -j
j
U
1
1
Отсюда Z C I m j C 0 j C
m
а) |Zс|=1/(ωС); б) φ=φи -φi =-π/2

23. Пассивные элементы в цепи гармонического тока

Закон Ома в комплексной форме U m Z I m . В цепях переменного тока свойства
элементов характеризуют комплексным сопротивлением Z U m I m . Рассчитаем:
,
Комплексное сопротивление, резистивного элемента ZR:
.
Если i t = I mcos ωt +φi I m = I me jφ, то по закону Ома ,
.
u( t) = Ri = RI mcos( ωt+φi ) =U mcos( ωt+φu ) U m U me jφ RI me jφ , где Um=RIm, φu=φi
Отсюда Z R U m R j 0 R Здесь: а) |ZR|=R – модуль сопротивления.
Im
.
б) φ= φи - φi = 0 – аргумент сопротивления.
Комплексное сопротивление, индуктивного элемента ZL :
.
Если i t = I mcos ωt +φi I m = I me jφi , то по закону Ома
i
u
u( t)=L di
dt
=LωImcos ωt+φi +π
2
.
↔Um =Ume
j φi +π
2
=LωI e jφ e jπ 2 = jLωI e jφ
i
m
i
m
φи= φi + π/2 , e
где Um=ωLIm,
Отсюда Z L
u
jπ 2
=j
Um
0 j L j L , . а) |ZL|=ωL модуль сопротивления;
Im
б) φ=φи - φi =π/2 - аргумент сопротивления.
Комплексное сопротивление емкостного элемента Zc:
.
jφ
i
t
=
I
cos
ωt
+
φ
I
m = I me
m
Если
то по закону Ома,
i ,
T
.
j φ -π
j -π
1
1
2 = 1 I e jφ e 2 = 1 I e jφ
u t =
i(t)dt =
I sin ωt+φ - π ↔U =U e
i
C
ωC
m
i
2
m
m
i
ωC
m
i
jωC
m
i
где Um=Im/ωС, φи= φi - π/2 , e -j π 2 1 = -j
U
1
1
1
j
Отсюда Z C m 0 j j
а) |Zс|=1/(ωС) –модуль сопротивления;
I m j C
C
C
б) φ=φи - φi =- π/2- аргумент сопротивления;

24. Пассивные элементы в цепи гармонического тока

24

25. Пассивные элементы в цепи гармонического тока

25

26. Анализ цепи при последовательном соединение RLC-элементов

Задача: рассчитать напряжение u(t) в цепи на рис.
• 1. Временным методом. Для мгновенных значений по
второму закону Кирхгофа запишем в уравнение:
Пусть i (t ) I m sin t , тогда:
di
1
(1.7)
u (t ) u r u L uC ir L
idt
dt C
π
1
π
u t =ImRsinωt+ωLImsin ωt+ +
Imsin ωt - =Umsin ωt±
2 ωC
2
Аналитически решать не целесообразно.
• 2. Методом векторных диаграмм. Строим векторную диаграмму.
Вектор тока и векторная диаграмма напряжений приведены на рис. 1.10.
Векторы напряжений на активном и реактивном элементах ортогональны,
а векторы напряжений на L и C смещены на +-900.
По векторной диаграмме можно рассчитать Uм и Ψ
2
2
2
2
U U a2 U X2 IR IX L IX C I R 2 ( X L X C )2 I Z где Z R ( X L X C )
arctg
U Xm
U U Cm
arctg Lm
U Rm
U Rm
• 3. Комплексным методом. В комплексной форме уравнение (1.7)
.
.
.
примет вид:
U =UR +UL +UC = I( R +jωL - j1 ωC)=(I(1.9)
R +jX)= I Z
jφ
• Здесь: Z=R+j(XL-XC)=Ze - комплексное сопротивление,
Z-модуль комплексного сопротивления; φ- фаза комплексного сопротивления; R и X=(XL-XC)–резистивное и реактивное сопротивления цепи.
• На комплексной плоскости сопротивления R, jXL, -jXC, Z - образуют
треугольник сопротивления, рис. 1.11. Если сопротивления умножить на ,
получим диаграмму напряжений, рис. 2.12 – треугольник напряжений.
26

27. Анализ цепи при параллельном соединении элементов RLC

Задача: рассчитать напряжение i(t) в цепи на рис
I
Рассмотрим параллельное соединение R, L,C элементов при
синусоидальном воздействии
u U m sin t u .
Согласно, первому закону Кирхгофа ток в неразветвленной части цепи
u 1
du
i iR iL iC udt C
.
Напряжение на всех элементах u uR uL uC .
R L
dt
I1
u
I2
R1
R2
L1
C2
мгновенные значения токов:
i I m sin t i , iR I Rm sin t R , iL I Lm sin t L , iC ICm sin t c
.
27

28.

• Согласно I закону Кирхгофа: ( ) ( ) ( ) ( )
GLCit=it+it+it
• Напряжение на входе цепи: ( ) ( ) m u u t
=U sin wt + j
• Поскольку: (
28

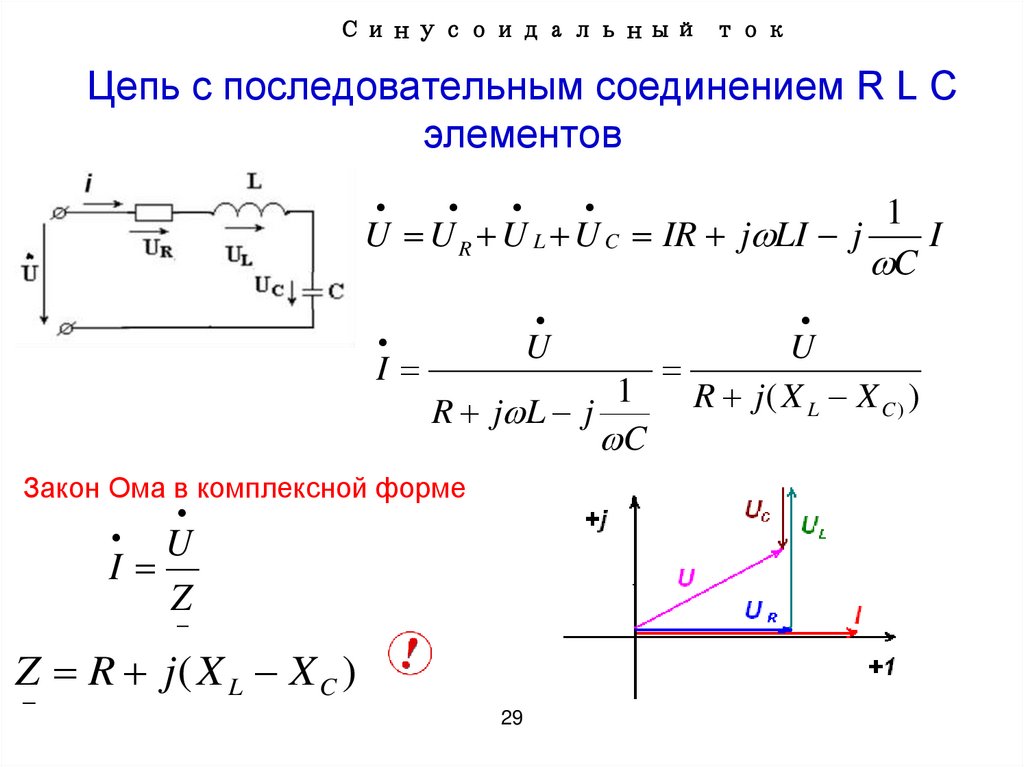
29. Цепь с последовательным соединением R L C элементов

Синусоидальный ток
Цепь с последовательным соединением R L C
элементов
1
U U R U L U C IR j LI j
I
C
I
U
1
R j L j
C
Закон Ома в комплексной форме
U
I
Z
Z R j( X L X C )
29
U
R j( X L X C ) )

30.

Пример 6.1. Рассчитать мгновенное значение тока в контуре (рис. 6.1 , если включен
источник гармонического напряжения e(t) = Ecos(ωt+φ0).
Решение. Комплексная амплитуда ЭДС E(jω) = Eejφo.
i(t)
L
Комплексное сопротивление контура Z(jω) = R + jωL.
e(t)
Комплексная амплитуда тока в контуре по закону Ома равна I(jω) = E(jω)/(R + jωL).
R
Рис.6.1
В показательной форме это выражение принимает вид:
I jω
E e
0
R j(ω L)
где
I (ω)
m
j 0
E
E e
0
2
2 j
R (ω L) e z
R (ω L)
E
0
2
2
R (ω L)
e
j( о z )
I (ω) e
m
j i
,
L
L
,
arctg
.
i
0
R
R
0
2
j 0
z arctg
2
Пропуская промежуточную запись (6.2), запишем мгновенное значение тока по формуле 6.3
i(t) I cos ( t )
m
i
E
ωL
cos (ω t arctg
).
0
2
2
R
R (ω L)
6.4
0
30

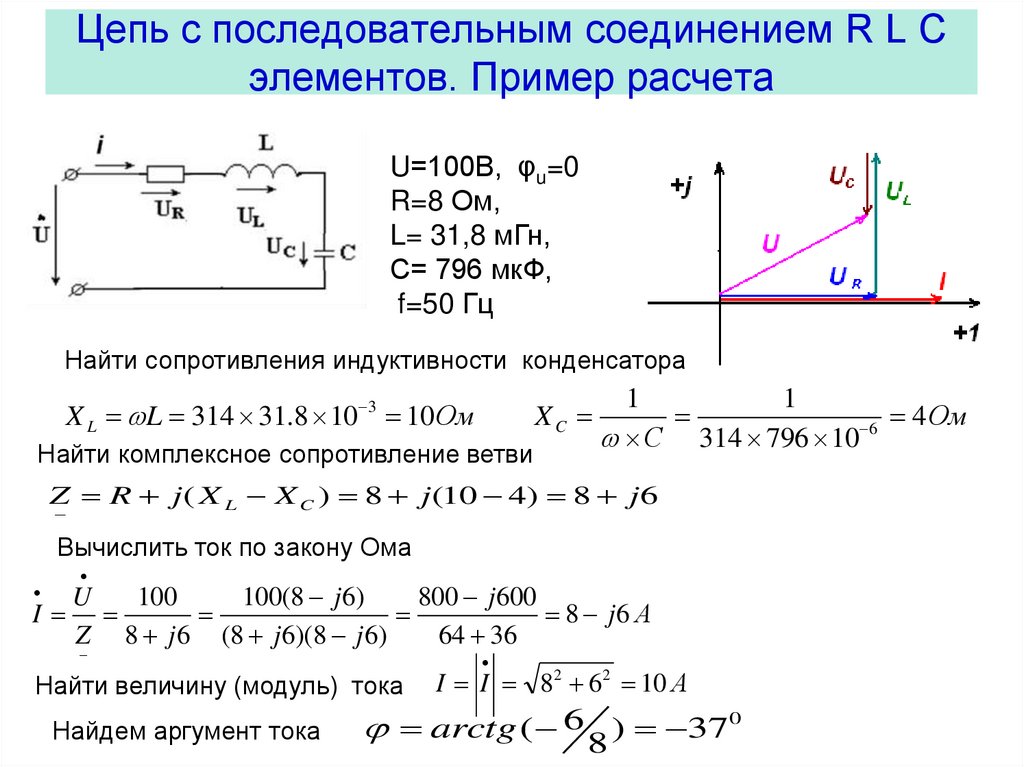
31. Цепь с последовательным соединением R L C элементов. Пример расчета

U=100В, φu=0
R=8 Ом,
L= 31,8 мГн,
С= 796 мкФ,
f=50 Гц
Найти сопротивления индуктивности конденсатора
X L L 314 31.8 10 3 10 Ом
XC
Найти комплексное сопротивление ветви
1
1
4 Ом
6
С 314 796 10
Z R j ( X L X C ) 8 j (10 4) 8 j 6
Вычислить ток по закону Ома
I
U
100
100(8 j 6)
800 j 600
8 j6 А
Z 8 j 6 (8 j 6)(8 j 6)
64 36
Найти величину (модуль) тока
Найдем аргумент тока
I I 82 62 10 А
arctg ( 6 8 ) 370

32. Цепь со смешанным соединением R L C элементов. Пример расчета

Синусоидальный ток
Цепь со смешанным соединением R L C элементов. Пример расчета
U=100В
R1=8 Ом R2=R3=10 Ом
XL=10 Ом XC=20 Ом
I=?
_______________________________________
1. Найти комплексное сопротивление ветви
Z 2 R2 jX C 10 j 20 Z 3 R3 jX L 10 j10
2. Найти комплексное сопротивление параллельного соединения Z2 и Z3
Z2 Z3
(10 j 20)(10 j10)
100 j100 j 200 j 2 200 300 j100 (300 j100)( 20 j10)
Z 23
Z 2 Z 3 (10 j 20) (10 j10)
20 j10
20 j10
(20 j10)( 20 j10)
7000 j1000
14 j 2 Ом
202 102
3. Найти комплексное сопротивление последовательного соединения
Z123 R1 Z 23 8 (14 j 2) 22 j 2 Ом
Z23 и R1
3. Найти ток
I1
U
100
100(22 j 2)
2200 j 200 2200 j 200
4,5 j 0,4 А
Z123 22 j 2 (22 j 2)( 22 j 2) 22 * 22 2 * 2
488 32
I I
4,52 0,4 2 4,52 А

33.

1.2. Расчет цепей при гармоническом воздействии
методом комплексных амплитуд (МКА)
Метод комплексных амплитуд состоит в следующем:
1) Исходная схема электрической цепи заменяется комплексной схемой замещения, в
которой:
а) все пассивные элементы заменяют их комплексными сопротивлениями, как показано
на рис.
б) все токи и напряжения в схеме заменяются их комплексными амплитудами, т.е.
х(t) = Xm cos( 0t – x) Xm = Xm e–j x и Ym cos( 0t – y) Ym = Ym e–j y. .
Рис. 1.3. Замена пассивных элементов цепей их комплексными сопротивлениями
2) Расчет электрической цепи сводится к составлению уравнений на основе законов Ома
и Кирхгофа в комплексной форме и нахождению комплексных амплитуд токов или
напряжений на интересующих нас участках цепи, т.е. Ym = Ym e–j y. методами анализа
линейных цепей по постоянному току
3) Запись окончательного решения состоит в замене рассчитанных комплексных
амплитуд на гармонические функции времени, т.е. Ym = Ym e–j y y(t) = Ym cos( 0t – y).
4) определить комплексную частотную характеристику по формуле (1).
На рис.1.4 приведены схемы замещения реактивных элементов, когда частота входного
сигнала стремится к 0 или ∞. Ими удобно пользоваться при расчете входных и
передаточных параметров цепи на этих частотах.
33

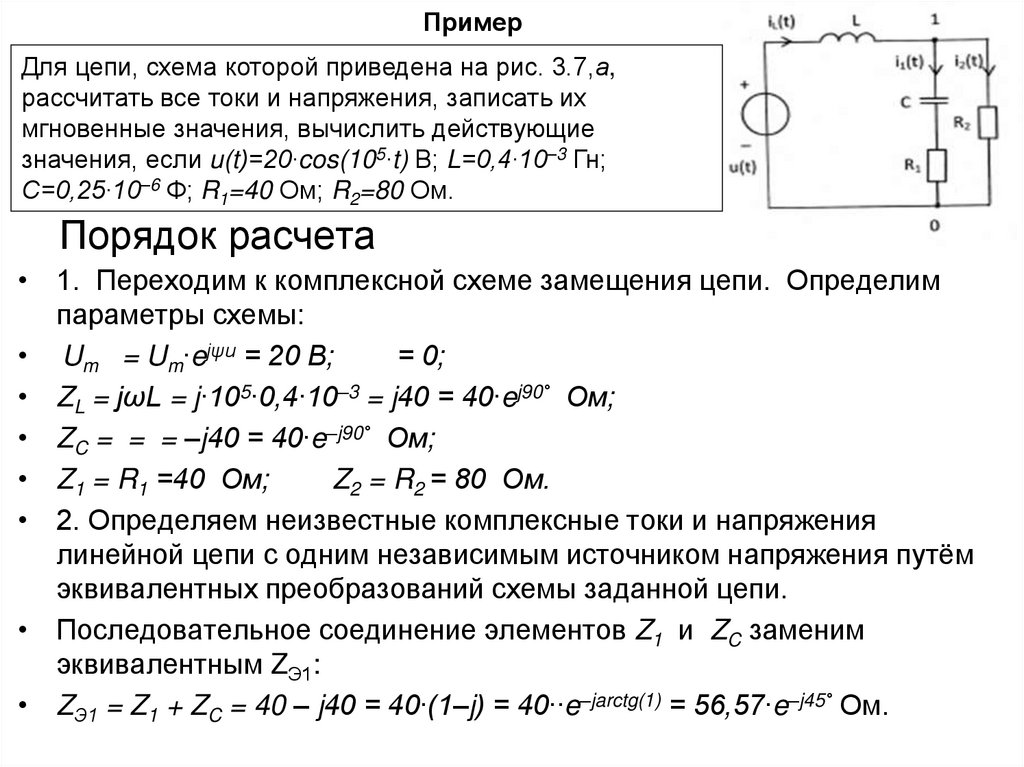
34. Пример

Для цепи, схема которой приведена на рис. 3.7,а,
рассчитать все токи и напряжения, записать их
мгновенные значения, вычислить действующие
значения, если u(t)=20∙cos(105∙t) В; L=0,4∙10–3 Гн;
С=0,25∙10–6 Ф; R1=40 Ом; R2=80 Ом.
Порядок расчета
• 1. Переходим к комплексной схеме замещения цепи. Определим
параметры схемы:
• Um = Um∙ejψu = 20 В;
= 0;
• ZL = jωL = j∙105∙0,4∙10–3 = j40 = 40∙ej90° Ом;
• ZC = = = –j40 = 40∙e–j90° Ом;
• Z1 = R1 =40 Ом;
Z2 = R2 = 80 Ом.
• 2. Определяем неизвестные комплексные токи и напряжения
линейной цепи с одним независимым источником напряжения путём
эквивалентных преобразований схемы заданной цепи.
• Последовательное соединение элементов Z1 и ZC заменим
эквивалентным ZЭ1:
• ZЭ1 = Z1 + ZC = 40 – j40 = 40∙(1–j) = 40∙∙e–jarctg(1) = 56,57∙e–j45° Ом.

35.

• Параллельное соединение элементов Z2 и ZЭ1 заменим
эквивалентным ZЭ2:
• ZЭ2 = Z2∙ZЭ1/(Z2+ZЭ1) = 80∙40∙(1–j)/(120–j40) = 16∙(2–j) = 16∙∙e–j26,57° Ом.
• Вычислим комплексную амплитуду тока
mL:
–j36,87°∙40∙ej90° = 20∙ej53,13° В, –jarctg(0,75)
= )0,5∙e
• • mLmL= = m/(Z
mLL∙Z
+Z
L Э2
=20/(32+j24)
=0,1∙(4–j3) =0,1∙∙e
=0,5∙e–j36,87° А.
• mC = m1∙ZC = 0,3162∙e–j18,44°∙40∙e–j90° = 12,648∙e–j108,44° В,
–j18,44°∙40 = 12,648∙e–j18,44° В,
∙Z1 = 0,3162∙eнапряжение
• •Вычислим
m1 =
m1комплексное
10 между узлами 1 и 0 схемы:
–j63,44°∙80 =
–j63,44°–j63,44°
–j36,87°
–j26,57°
∙Z
=
0,2236∙e
17,888∙e
В. В.
• • 10
∙Z
=
0,5∙e
∙
16∙∙e
=
17,89∙e
m2 ==
m2
2
mL Э2
• Вычислим комплексные амплитуды токов
m1 и
m2:
–j45° ) = 0,3162∙e
–j18,44° А,
переход –j63,44°
от найденных
амплитуд
• • 3. Осуществляем
/ (56,57∙eкомплексных
m1 =
10/ZЭ1 = 17,89∙e
токов и= напряжений
к косинусоидальным
функциям
–j63,44° / 80 = 0,2236∙e
–j63,44° Апо
m2
10/Z2 = 17,89∙e
формулам
• Вычислим комплексные амплитуды напряжений
mL,
mC,
m1,
m2:

36.

mL =
mL∙ZL = 0,5∙e
mC =
–j18,44°∙40∙e–j90° = 12,648∙e–j108,44° В,
m1∙ZC = 0,3162∙e
–j18,44°∙40 = 12,648∙e–j18,44° В,
m1∙Z1 = 0,3162∙e
–j63,44°∙80 = 17,888∙e–j63,44° В.
m2∙Z2 = 0,2236∙e
m1 =
m2 =
–j36,87°∙40∙ej90° = 20∙ej53,13° В,
• 3. Осуществляем переход от найденных комплексных амплитуд
токов и напряжений к косинусоидальным функциям по
формулам
Получим для ω=105 рад/с реальные токи и напряжения
iL(t) = 0,5∙cos(ωt – 36,87°) A; i1(t) = 0,3162∙cos(ωt – 18,44°) A;
i2(t) = 0,2236∙cos(ωt – 63,44°) A; uL(t) = 20∙cos(ωt + 53,13°) B;
uC(t) = 12,648∙cos(ωt – 108,44°) B; u1(t) = 12,648∙cos(ωt – 18,44°) B;
u2(t) = 17,888∙cos(ωt – 63,44°) B.

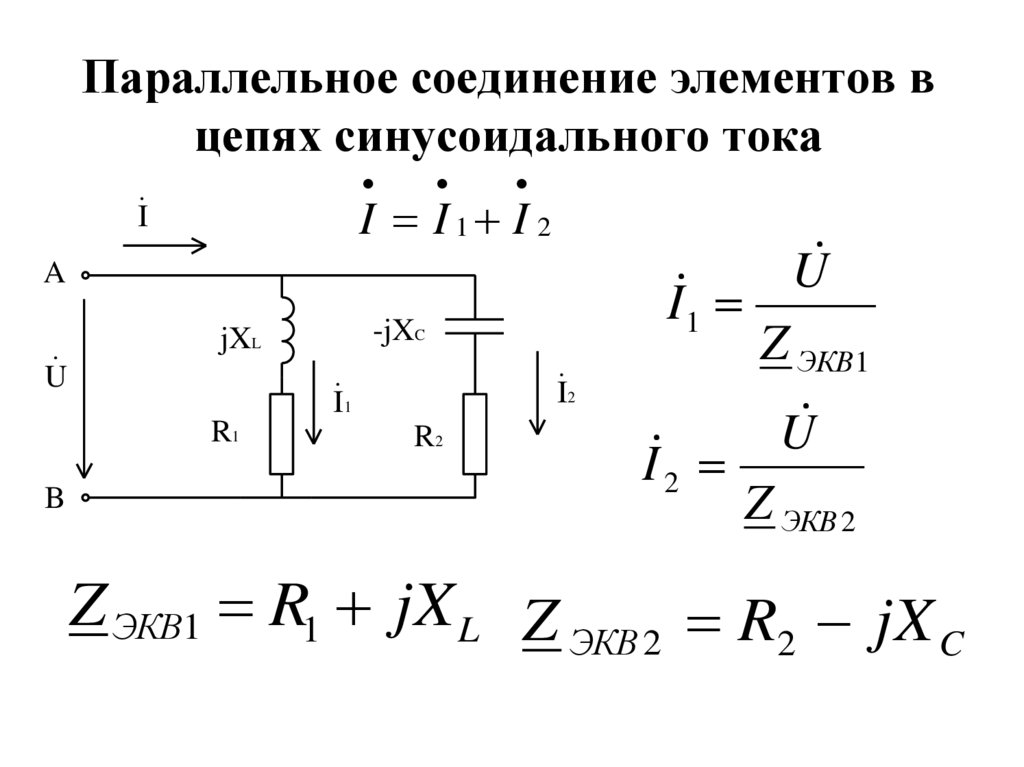
37. Параллельное соединение элементов в цепях синусоидального тока

I I1 I 2
I
A
-jXC
jXL
U
B
I2
I1
R1
I 1
R2
I 2
U
Z ЭКВ1
U
Z ЭКВ 2
Z ЭКВ1 R1 jX L Z ЭКВ 2 R2 jX C

38. Треугольники проводимостей

1
Y G jB
Z
B
G – действительная часть, активная составляющая
B – мнимая часть, реактивная составляющая
Y
jB
G Y cos
B Y sin
Y G B
2
G
R
G 2
R X2
R
G 2
Z
X
B 2
R X2
2
X
B 2
Z

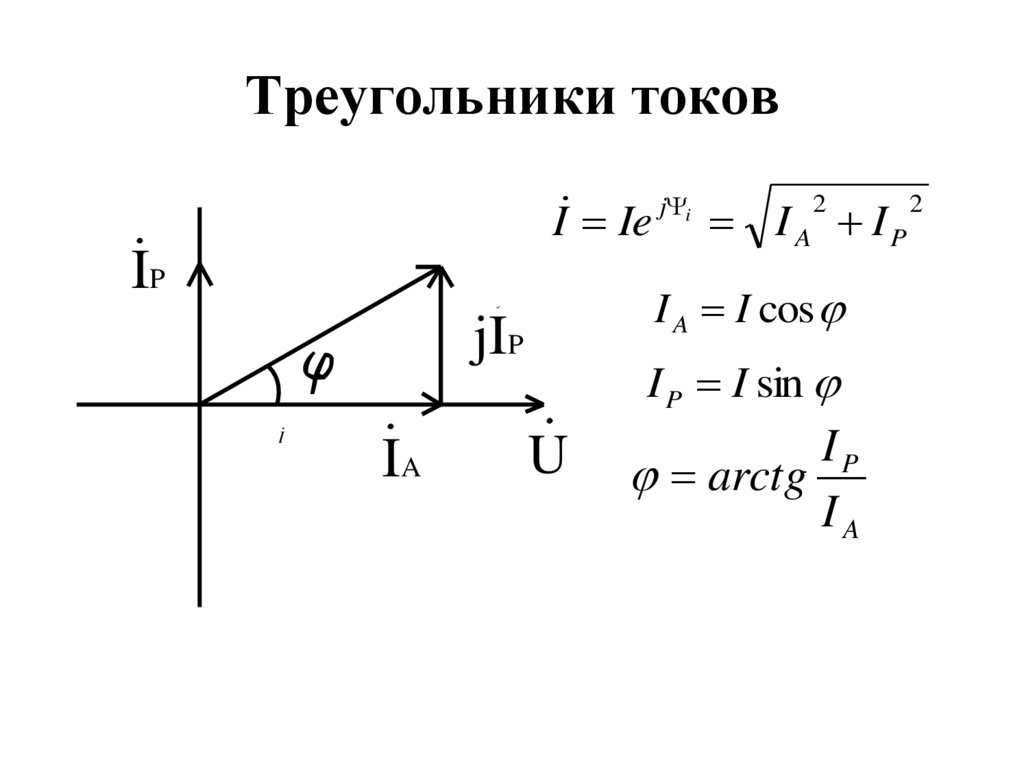
39. Треугольники токов

I Ie j i I 2 I 2
A
P
IP
I A I cos
jIP
I
IA
I P I sin
U
IP
arctg
IA

40. Магнитосвязанные цепи при гармоническом воздействии.

В данной теме рассмотрены следующие вопросы:
1. Понятие о собственной и взаимной индуктивностях.
2. Компонентные уравнения связанных индуктивных элементов;
согласное и встречное включения.
3. Понятие об одноименных зажимах связанных индуктивных
элементов.
4. Применение метода комплексных амплитуд для анализа
магнитосвязанных цепей.
5. Схема замещения связанных индуктивных элементов.
Последовательное и параллельное включение связанных индуктивных
элементов.
Линейный трансформатор.
Понятие об идеальном трансформаторе.
40

41.

Индуктивная связь. ЭДС взаимной индукции. Взаимная
индуктивность. Коэффициент связи.
Электрические цепи называются связанными, если процессы в них влияют друг на друга. Это влияние
может осуществляться посредством общего электрического или магнитного поля. В последствии случая цепи
называются индуктивно связанными.
Рассмотрим две катушки, расположенные рядом (рис. 5.1.а)
Протекающий в первой катушке с числом витков W1 и индуктивности L1 ток i1 вызывает
магнитный поток Ф11. Часть потока Ф12 охватывает находящуюся вторую катушку с числом витков
W2 и индуктивностью L2.
d 11
d
di
e1
W1 11 L1 ;
ЭДС, находящаяся в первой катушке под воздействием Ф11
dt
dt
dt
11 W1 11 L1i1
называется ЭДС самоиндукции, где
вт
d 12
d 12
dW1
W2
M 12
dt
dt
dt
12 W2 12 M 12 i1 -потокосцепления взаимной индукции,
e12
m12
e2
d 22
d 22
di
W2
L 2
dt
dt
dt
22 W2 22 L2i2
e21
d 21
d 21,
di
W1
M 21 2
dt
dt
dt
41
-ЭДС взаимной индукции, находящаяся в первой катушке под в
потока Ф .

42.

Одноименные зажимы индуктивно связанных катушек.
Рассмотрим две катушки, расположенные на одном основании (рис 5.2)
Направление тока и вызванного им магнитного потока связаны по правилу правого винта. Следовательно ток i1
будет вызывать поток Ф1,направленный влево. Ток i2 будет вызывать магнитный поток Ф2,также направленный влево.
Т.е. зажимы индуктивно связанных катушек, одинаковое направление токов относительно которых, вызывает
одинаковое направление потоков –называются одноименными. На электрических схемах цепей одноименные зажимы
катушек принято обозначать жирными точками или звездочками.
42

43.

Последовательное
согласном включении.
соединение
индуктивно связанных катушек
при
Рассмотрим две индуктивно связанные катушки, соединенные последовательно (рис 5.3). Каждая
из катушек обладает индуктивностью L1 и L2 и активным сопротивлением проводника из которого
катушка изготовлена r1 и r2.
Индуктивная связь на электрической схеме указана
двусторонней стрелкой и взаимной индуктивностью М. Рис 5.3.
Одноименные зажимы катушек обозначены жирными точками и расположены так, что протекающий под воздействием
напряжения U ток I вызывает в катушках одинаковое направление потоков.
включение
согласным.
di Поэтому
di
di называется
di
r
i
L
M
r
i
L
M
U
Запишем уравнение представленное на рис 5.3 цепи
1
1
2
2
dt
dt
dt
dt
.
для мгновенных значениях токов и напряжений.
Для комплексов действующих значений токов и напряжений r I j L I j MI r I j L I j MI U
1
1
2
2
последнее уравнение примет вид:
Перепишем это уравнение следующим образом:
r1 r2 j L1 L2 2M I U Выражение в квадратных скобках называется сопротивлением двух последова
тельно соединенных индуктивно связанных катушек при согласном включении
Z согл r1 r2 j L1 L2 2M
Выражение в круглых скобках называется полной индуктивностью двух последовательно соединенных
индуктивно связанных катушек при согласном включении
Lсогл L1 L2 2M
Очевидно Zсогл >Z, где Z-полное сопротивление двух последовательно соединенных
катушек без индуктивной связи:
Z r1 r2 j L1 L2
Увеличение сопротивления Zсогл происходит за счет
увеличения полной индуктивности Lсо
Построим векторную диаграмму двух последовательно
I
соединенных индуктивно связанных катушек при согласном
включении. Для этого задаемся вектором тока
43

44. Дисциплина: Электротехника и электроника

Лектор: Погодин Дмитрий Вадимович
Кандидат технических наук,
доцент кафедры РИИТ
(кафедра Радиоэлектроники и
информационно-измерительной
техники)
Электротехника и электроника
44