03 урок Числов характеристики (1)

1.

Вероятность и статистика
10 класс
Шубина О.В.
КОГОБУ СШ г.Орлов

2.

«Статистика может быть
охарактеризована
как наука о сокращении и анализе
материала, полученного в
наблюдениях»
Р. Фишер

3.

Среднее значение (Хср) выборки
Средним значением выборки называют
среднее арифметическое всех чисел ряда
данных выборки.
Если в ряду данных записаны n значений
х1, х2,…, хn, то

4.

Размах выборки (R)
Размах выборки – это разность между
наибольшим и наименьшим значениями
величины в выборке.
Решение: xнаим = ___; хнаиб = ___
R = ___

5.

Мода (Mo)
Мода – значение элемента выборки,
встречающееся чаще остальных.
М = ____

6.

Медиана (m)
«серединное» значение упорядоченного
ряда значений:
если количество чисел в ряду нечётное, то
медиана – число, записанное по середине;
если количество чисел в ряду чётное, то
медиана – это среднее арифметическое
двух чисел, стоящих по середине.

7.

Задание
Пример 1. При выборочном исследовании уровня
зарплаты врачей была получена следующая выборка:
18000, 23500, 15600, 45000, 36800, 21000, 31400,
48800, 22000, 45000.
Пример 2. При выборочном исследовании суммы очков,
выпадающей на двух игральных кубиках, была
получена следующая выборка:
7, 6, 5, 6, 5, 7, 6, 8, 6, 2, 10, 10, 8, 10, 8, 7, 5, 9, 6, 7.
Определите среднее арифметическое, размах, моду,
медиану, каждого ряда. Что характеризует каждый из этих
показателей?

8.

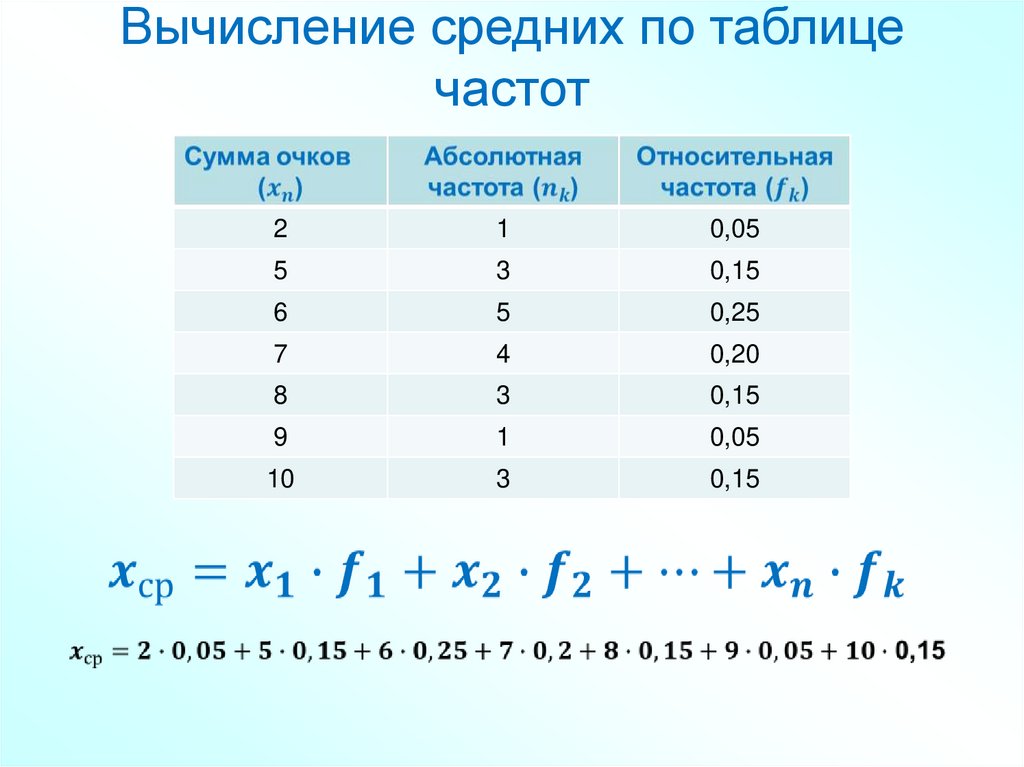
Вычисление средних по таблице
частот
По примеру 2
2
1
0,05
5
3
0,15
6
5
0,25
7
4
0,20
8
3
0,15
9
1
0,05
10
3
0,15

9.

Вычисление средних по таблице
частот
2
1
0,05
5
3
0,15
6
5
0,25
7
4
0,20
8
3
0,15
9
1
0,05
10
3
0,15

10.

Вычисление средних по таблице
частот
2
1
0,05
5
3
0,15
6
5
0,25
7
4
0,20
8
3
0,15
9
1
0,05
10
3
0,15

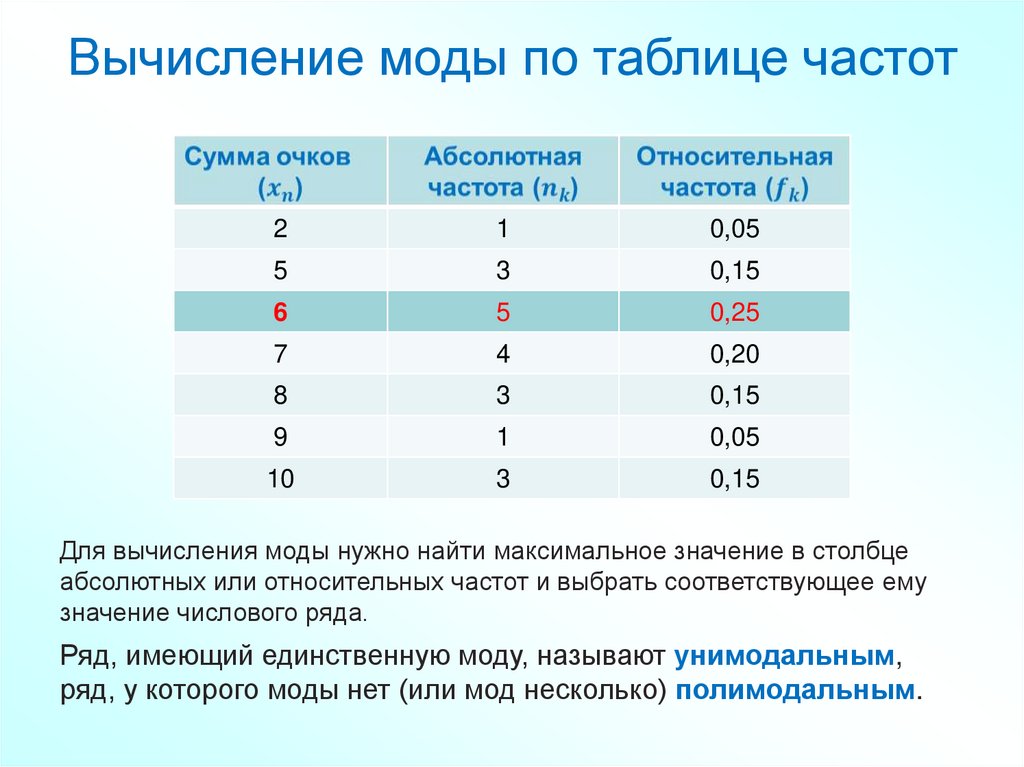
11.

Вычисление моды по таблице частот
2
1
0,05
5
3
0,15
6
5
0,25
7
4
0,20
8
3
0,15
9
1
0,05
10
3
0,15
Для вычисления моды нужно найти максимальное значение в столбце
абсолютных или относительных частот и выбрать соответствующее ему
значение числового ряда.
Ряд, имеющий единственную моду, называют унимодальным,
ряд, у которого моды нет (или мод несколько) полимодальным.

12.

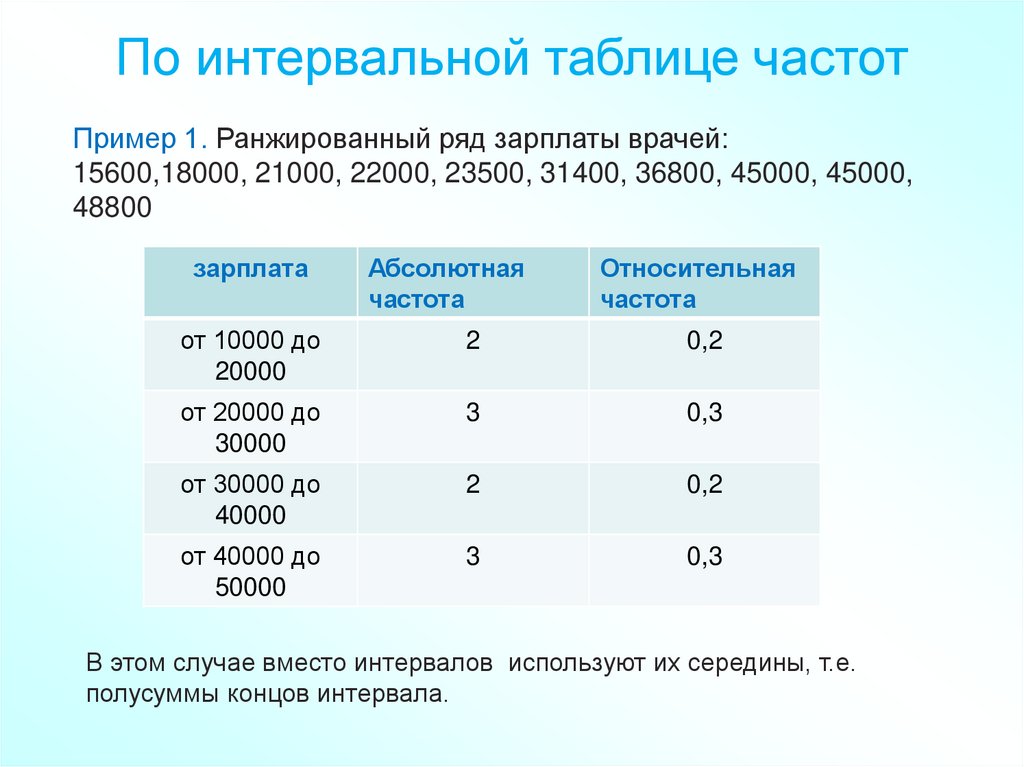
По интервальной таблице частот
Пример 1. Ранжированный ряд зарплаты врачей:
15600,18000, 21000, 22000, 23500, 31400, 36800, 45000, 45000,
48800
зарплата
Абсолютная
частота
Относительная
частота
от 10000 до
20000
2
0,2
от 20000 до
30000
3
0,3
от 30000 до
40000
2
0,2
от 40000 до
50000
3
0,3
В этом случае вместо интервалов используют их середины, т.е.
полусуммы концов интервала.

13.

По интервальной таблице частот
зарплата
Абсолютная
частота
Относительная
частота
от 10000 до
20000
2
0,2
от 20000 до
30000
3
0,3
от 30000 до
40000
2
0,2
от 40000 до
50000
3
0,3
С использованием абсолютных
частот:
С использованием относительных частот:

14.

Характеристики разброса
• Размах - это разность наибольшего и наименьшего
значений ряда данных.
• Дисперсия в статистике — это мера, которая
показывает разброс между результатами. Если все
они близки к среднему, дисперсия низкая. А если
результаты сильно различаются — высокая. Это один
из основных показателей в статистическом анализе.
Точка, вокруг которой считают разброс, — это обычно
среднее арифметическое из выборки,
математическое ожидание или какое-то целевое
значение.

15.

Характеристики разброса
• Дисперсией числового ряда называется среднее
квадратичное
отклонений от среднего арифметического:

16.

Характеристики разброса
Стандартным (или средним квадратичным)
отклонением числового ряда называется квадратный
корень из дисперсии