Похожие презентации:
Нахождение натуральной величины отрезка и плоской фигуры
1.
2. Способ прямоугольного треугольника
Применяется для определениянатуральной величины отрезка
прямой общего положения и углов
наклона к плоскостям проекций
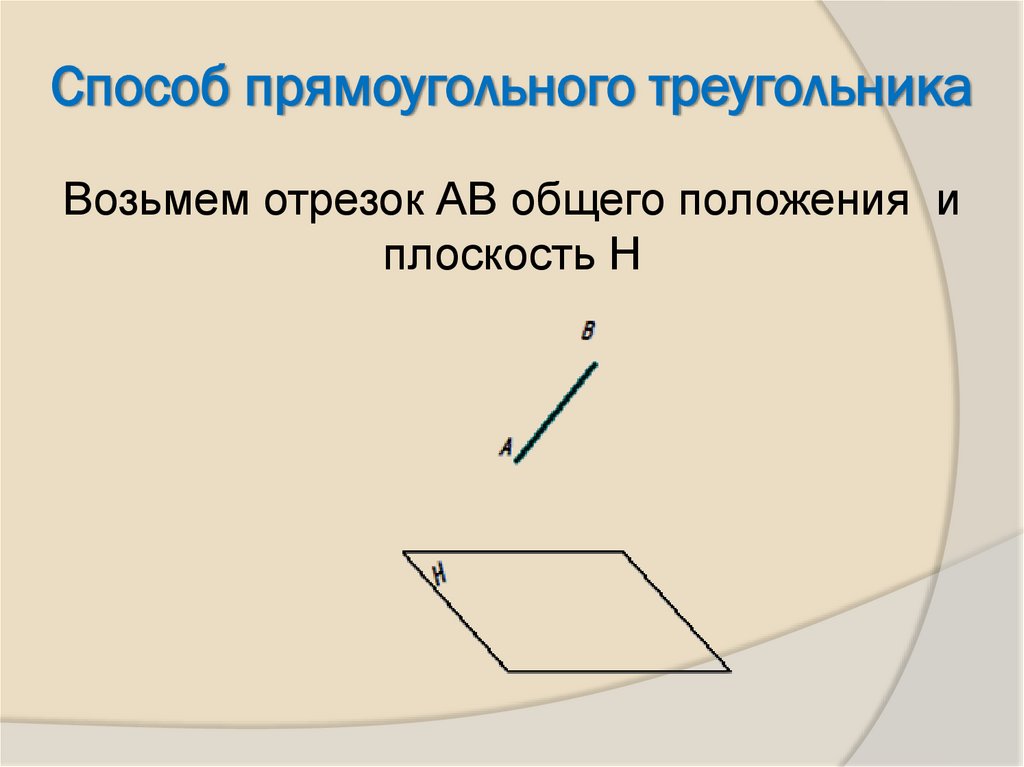
3. Способ прямоугольного треугольника
Возьмем отрезок АВ общего положения иплоскость Н
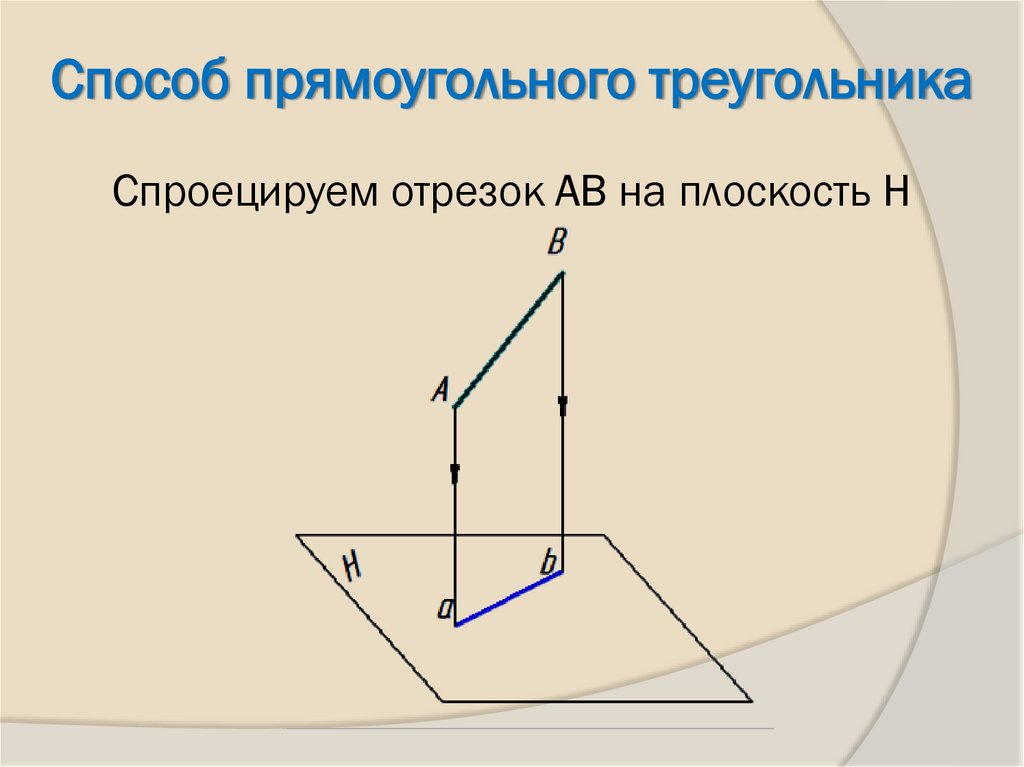
4. Спроецируем отрезок АВ на плоскость Н
Способ прямоугольного треугольникаСпроецируем отрезок АВ на плоскость Н
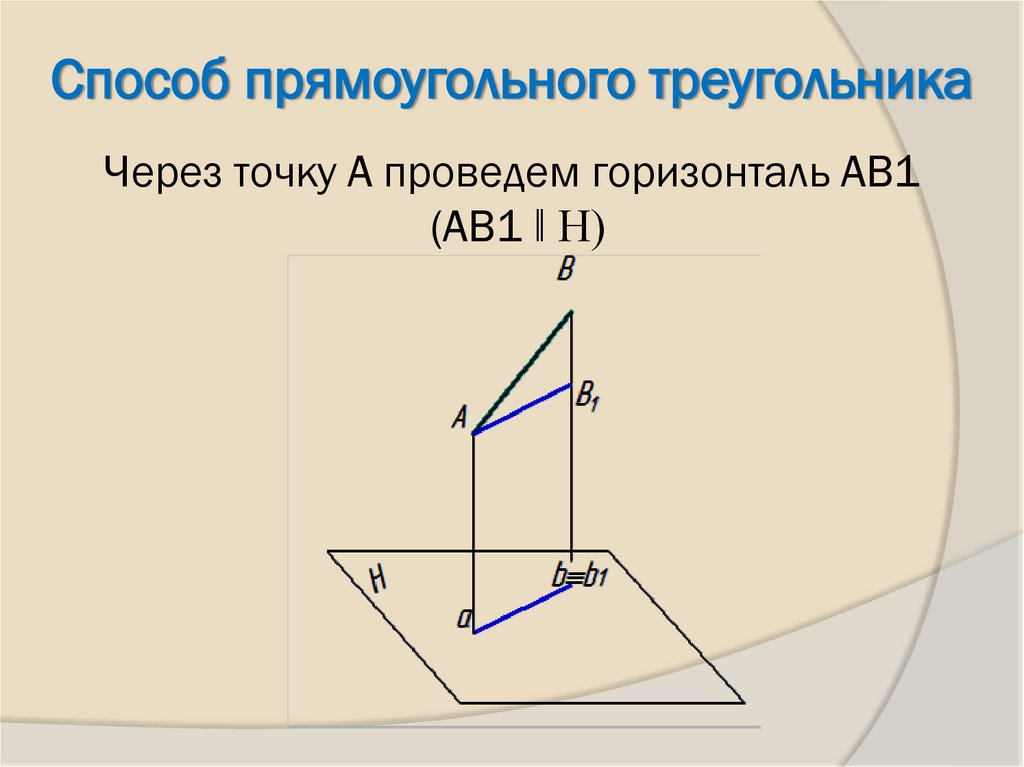
5. Через точку А проведем горизонталь АВ1 (АВ1 ǁ Н)
Способ прямоугольного треугольникаЧерез точку А проведем горизонталь АВ1
(АВ1 ǁ Н)
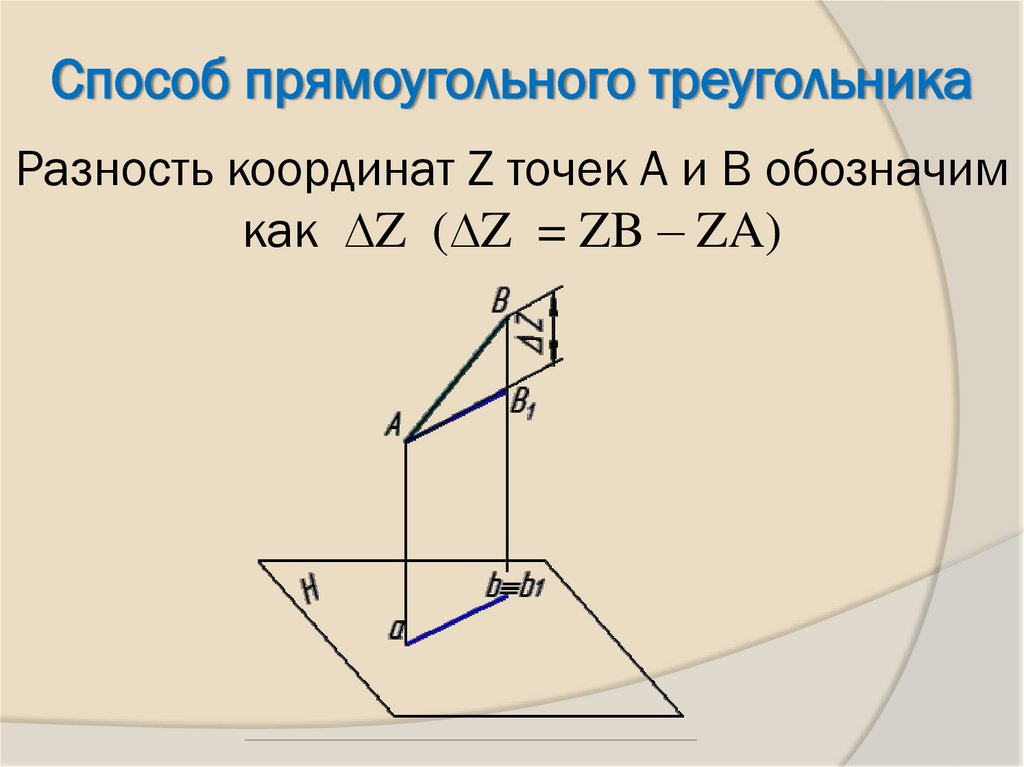
6. Разность координат Z точек А и В обозначим как ∆Z (∆Z = ZB – ZA)
Способ прямоугольного треугольникаРазность координат Z точек А и В обозначим
как ∆Z (∆Z = ZB – ZA)
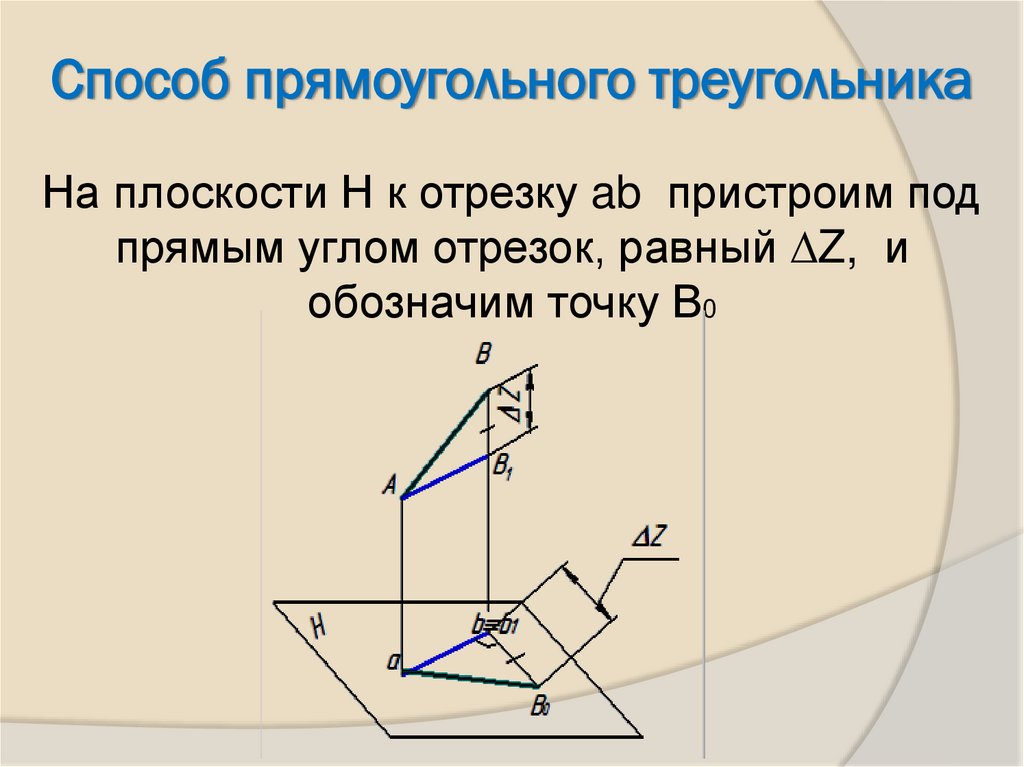
7. На плоскости Н к отрезку ab пристроим под прямым углом отрезок, равный ∆Z, и обозначим точку В0
Способ прямоугольного треугольникаНа плоскости Н к отрезку ab пристроим под
прямым углом отрезок, равный ∆Z, и
обозначим точку В0
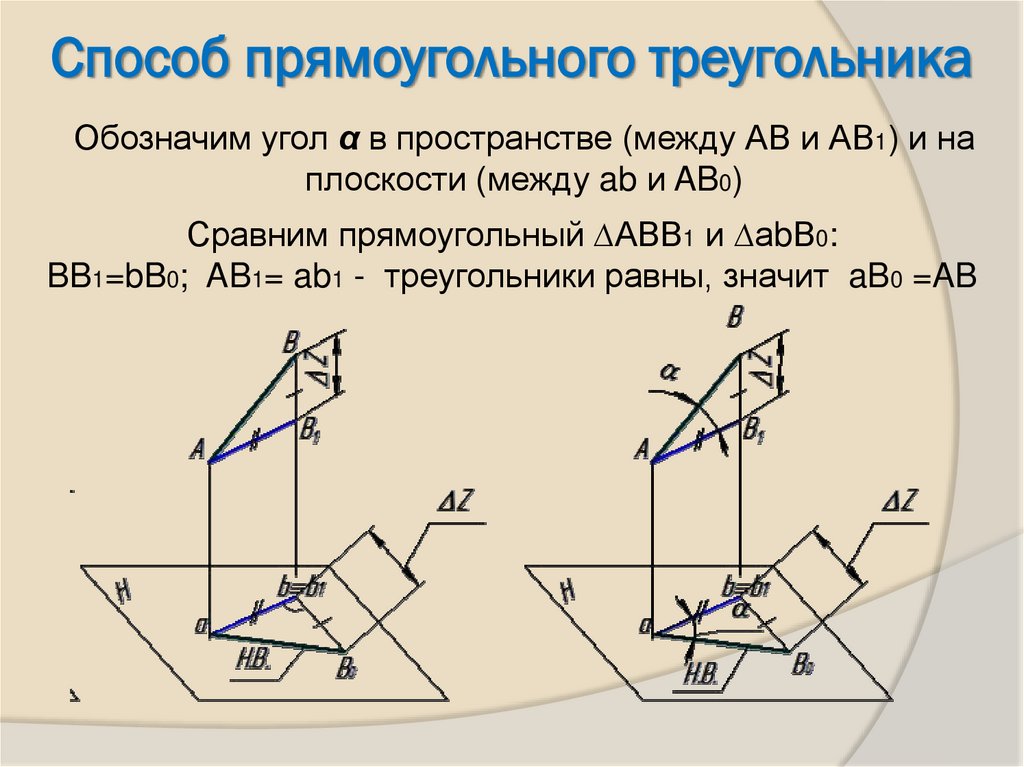
8. Обозначим угол α в пространстве (между АВ и АВ1) и на плоскости (между ab и AB0)
Способ прямоугольного треугольникаОбозначим угол α в пространстве (между АВ и АВ1) и на
плоскости (между ab и AB0)
Сравним прямоугольный ∆АВВ1 и ∆аbВ0:
BB1=bB0; AB1= ab1 - треугольники равны, значит aB0 =AB
9. Выводы:
Для определения натуральной величины отрезкапрямой общего положения и угла наклона его к
плоскости проекций необходимо построить
прямоугольный треугольник, у которого одним катетом
является проекция отрезка на эту плоскость, а другим
катетом –алгебраическая разность координат концов
отрезка от этой плоскости проекций.
Гипотенуза этого треугольника будет являться
натуральной величиной отрезка прямой
Угол между гипотенузой и проекцией отрезка будет
равен углу наклона прямой к плоскости проекций
10. Способ плоскопараллельного перемещения
Заданный геометрический объект совершаетплоскопараллельное движение, при котором
ВСЕ ЕГО ТОЧКИ движутся параллельно
некоторой плоскости до положения
параллельного или перпендикулярного
плоскости проекций
Линия по которой происходит перемещение всех
точек объекта находится В ПЛОСКОСТИ УРОВНЯ
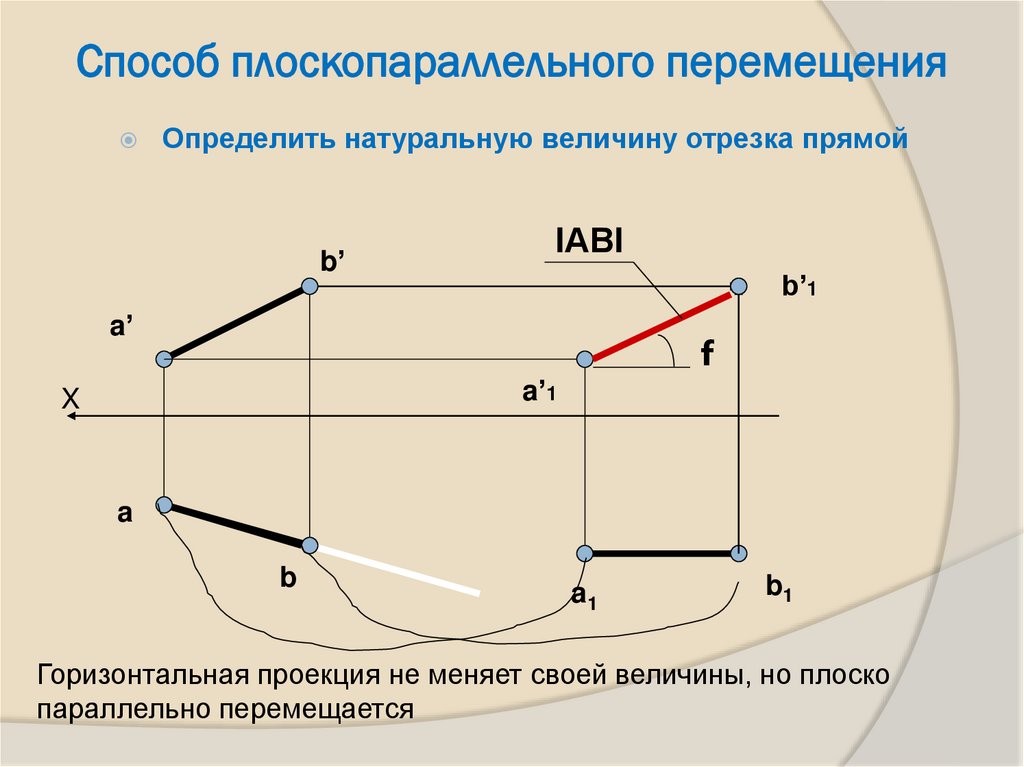
11. Способ плоскопараллельного перемещения
Определить натуральную величину отрезка прямойb’
IАВI
b’1
a’
f
a’1
X
a
b
a1
b1
Горизонтальная проекция не меняет своей величины, но плоско
параллельно перемещается
12.
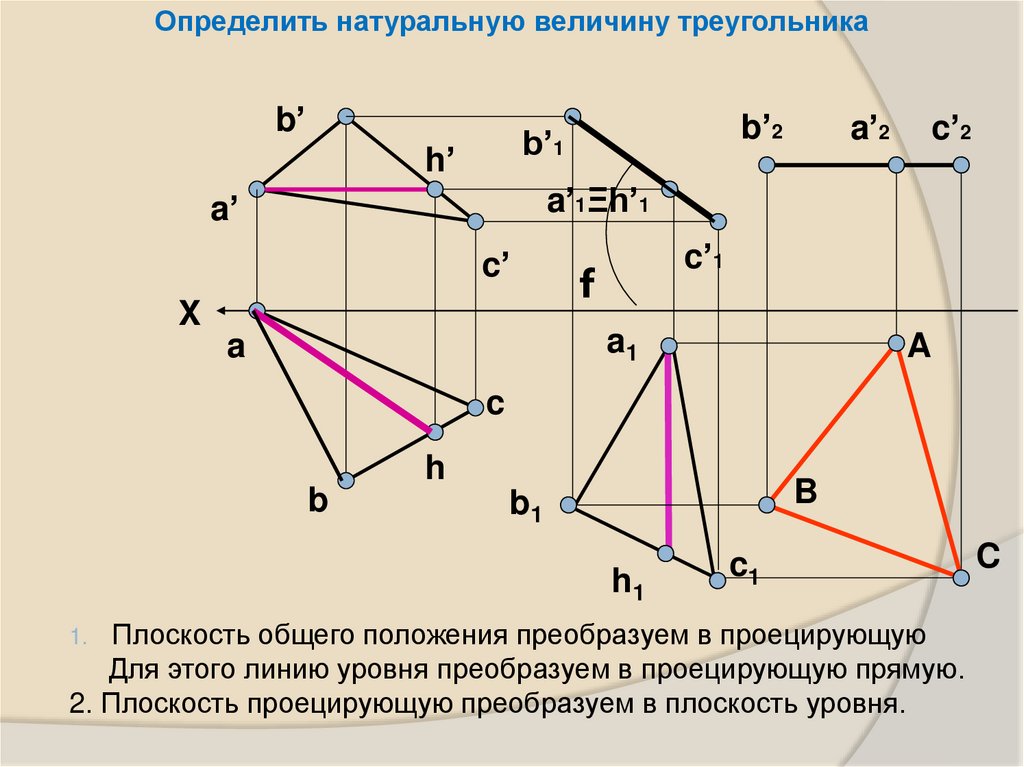
Определить натуральную величину треугольникаb’
b’2
b’1
h’
a’2
c’2
a’1Ξh’1
a’
c’
X
c’1
f
a1
a
A
c
h
b
B
b1
h1
c1
Плоскость общего положения преобразуем в проецирующую
Для этого линию уровня преобразуем в проецирующую прямую.
2. Плоскость проецирующую преобразуем в плоскость уровня.
1.
C
13.
Способ поворота вокруг проецирующей осиЗаданный геометрический объект вращается вокруг
оси до положения параллельного или
перпендикулярного какой-либо плоскости проекций.
Все точки объекта движутся по окружностям, которые
располагаются в плоскостях уровня,
перпендикулярных оси вращения.
14.
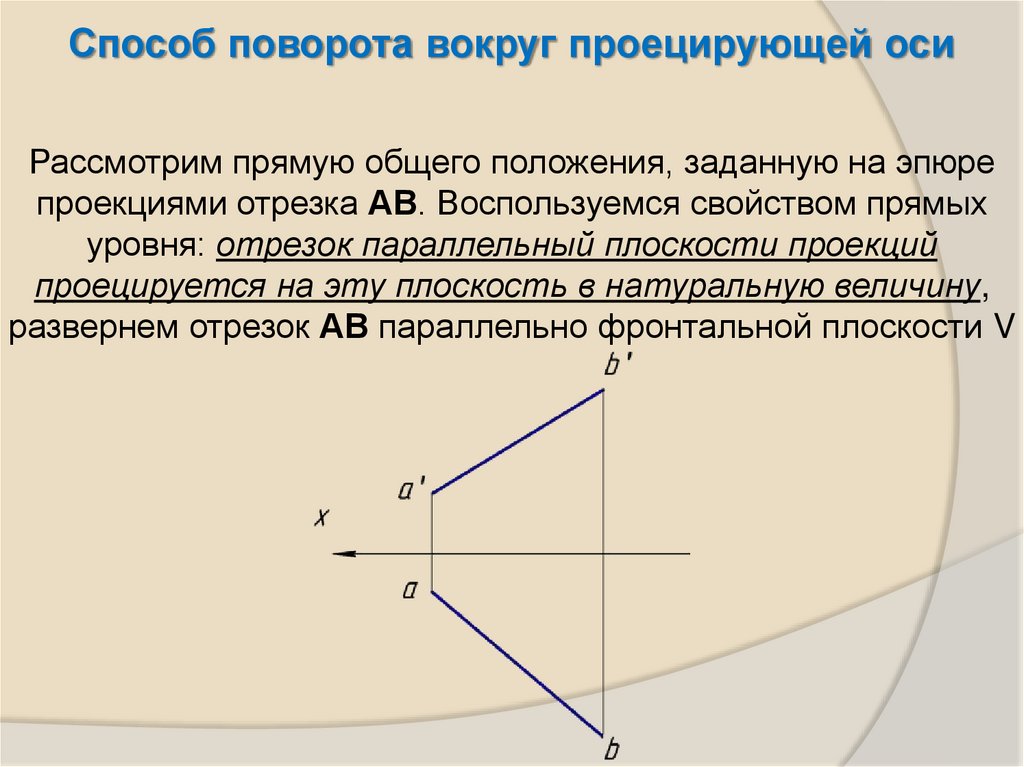
Способ поворота вокруг проецирующей осиРассмотрим прямую общего положения, заданную на эпюре
проекциями отрезка АВ. Воспользуемся свойством прямых
уровня: отрезок параллельный плоскости проекций
проецируется на эту плоскость в натуральную величину,
развернем отрезок АВ параллельно фронтальной плоскости V
15.
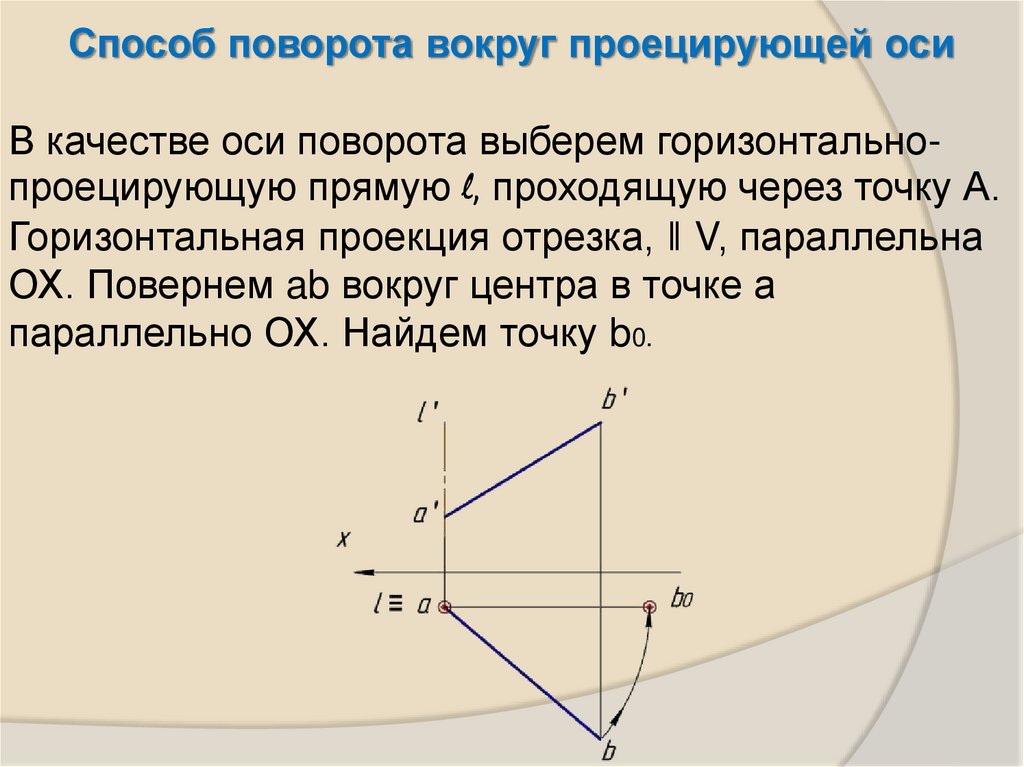
Способ поворота вокруг проецирующей осиВ качестве оси поворота выберем горизонтальнопроецирующую прямую l, проходящую через точку А.
Горизонтальная проекция отрезка, ‖ V, параллельна
ОХ. Повернем ab вокруг центра в точке а
параллельно ОХ. Найдем точку b0.
16.
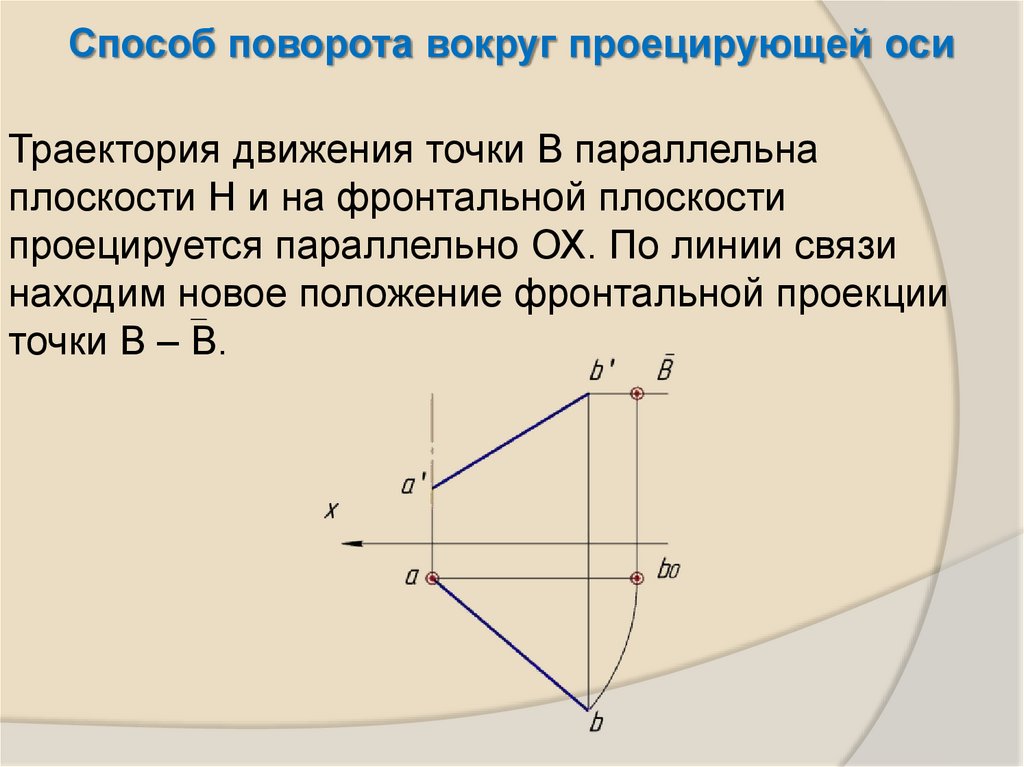
Способ поворота вокруг проецирующей осиТраектория движения точки В параллельна
плоскости Н и на фронтальной плоскости
проецируется параллельно ОХ. По линии связи
находим новое положение фронтальной проекции
точки В – В.
17.
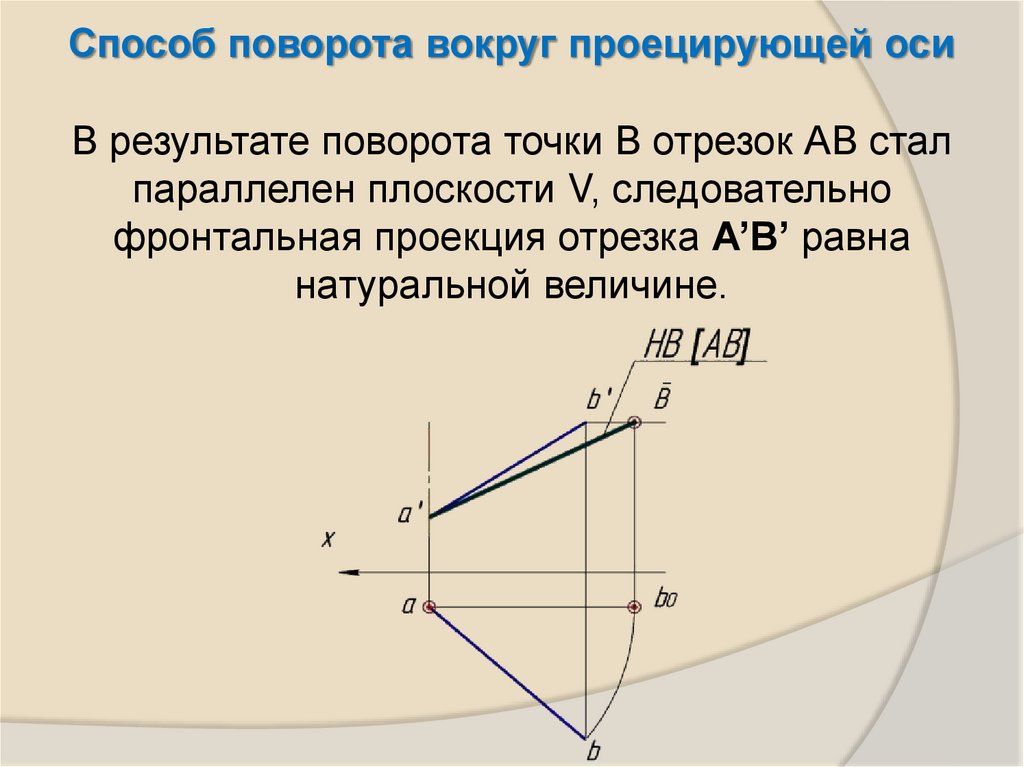
Способ поворота вокруг проецирующей осиВ результате поворота точки В отрезок АВ стал
параллелен плоскости V, следовательно
фронтальная проекция отрезка А’В’ равна
натуральной величине.
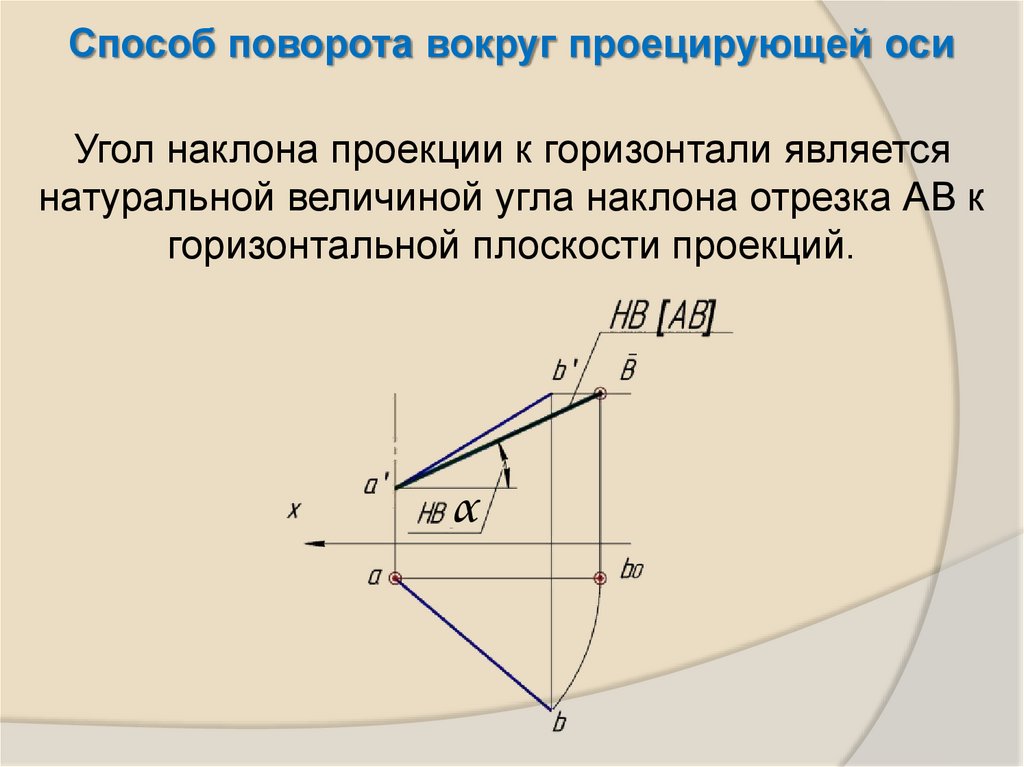
18.
Способ поворота вокруг проецирующей осиУгол наклона проекции к горизонтали является
натуральной величиной угла наклона отрезка АВ к
горизонтальной плоскости проекций.
α
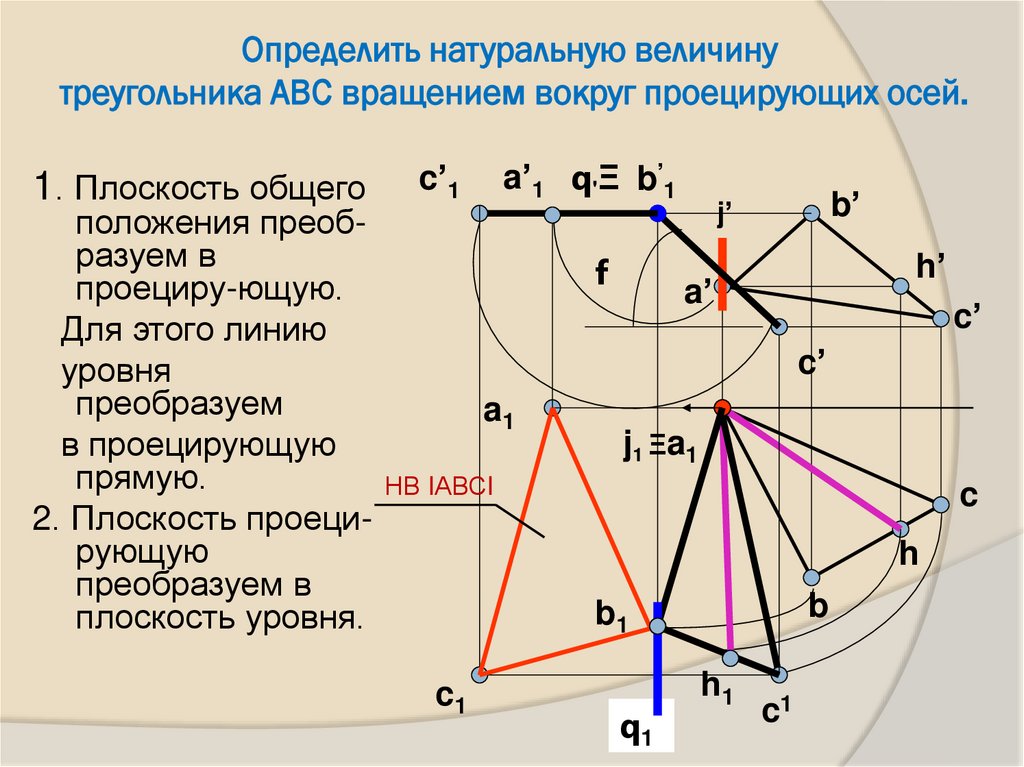
19. Определить натуральную величину треугольника АВС вращением вокруг проецирующих осей.
1. Плоскость общегоc’1
a’1 q'Ξ b’1
положения преобразуем в
проециру-ющую.
Для этого линию
уровня
преобразуем
a1
в проецирующую
прямую.
НВ IАВСI
2. Плоскость проецирующую
преобразуем в
плоскость уровня.
c1
f
b’
j’
h’
a’
c’
c’
j1 Ξa1
c
h
b
b1
q1
h1
c1
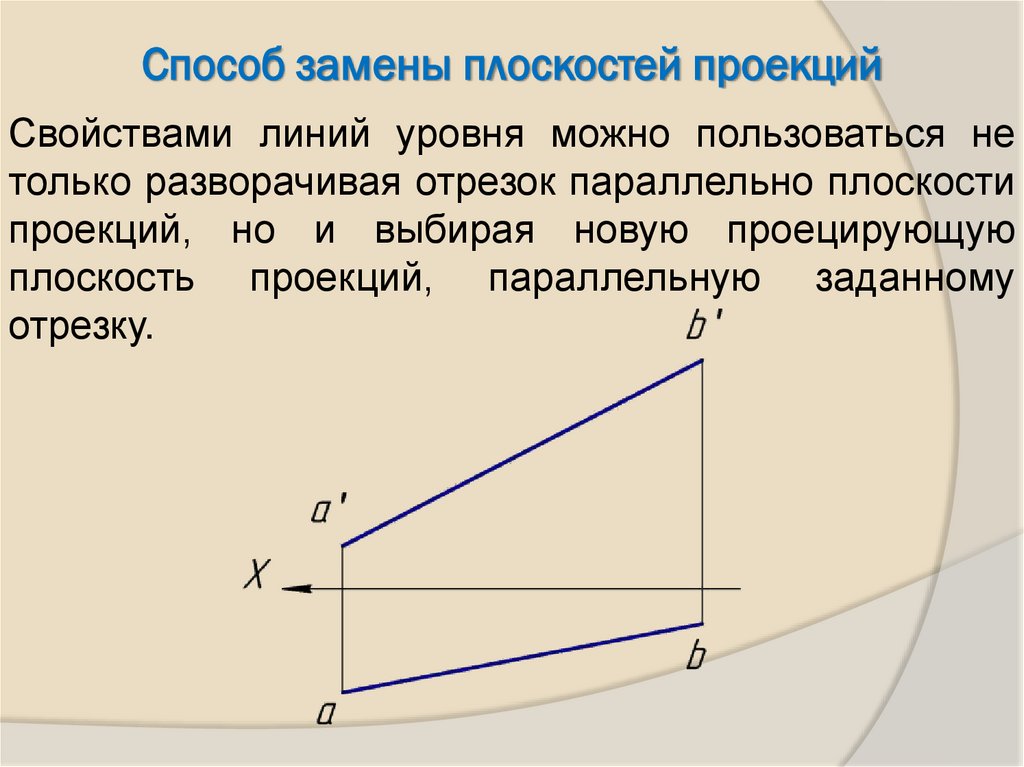
20.
Способ замены плоскостей проекцийСвойствами линий уровня можно пользоваться не
только разворачивая отрезок параллельно плоскости
проекций, но и выбирая новую проецирующую
плоскость проекций, параллельную заданному
отрезку.
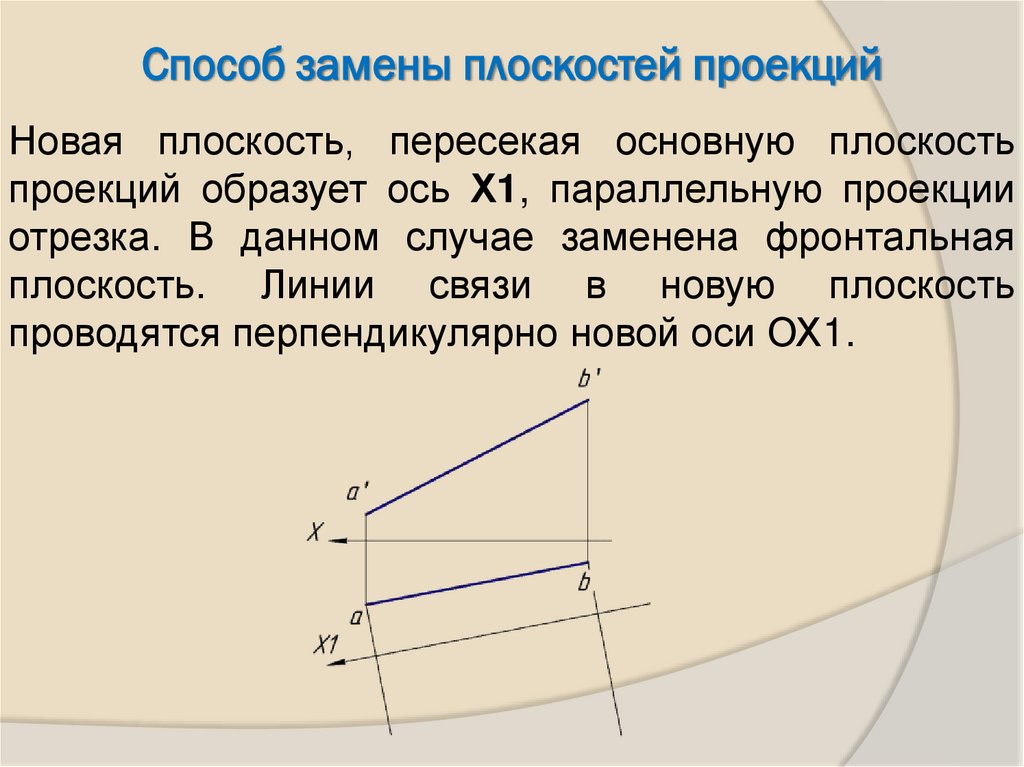
21.
Способ замены плоскостей проекцийНовая плоскость, пересекая основную плоскость
проекций образует ось Х1, параллельную проекции
отрезка. В данном случае заменена фронтальная
плоскость. Линии связи в новую плоскость
проводятся перпендикулярно новой оси ОХ1.
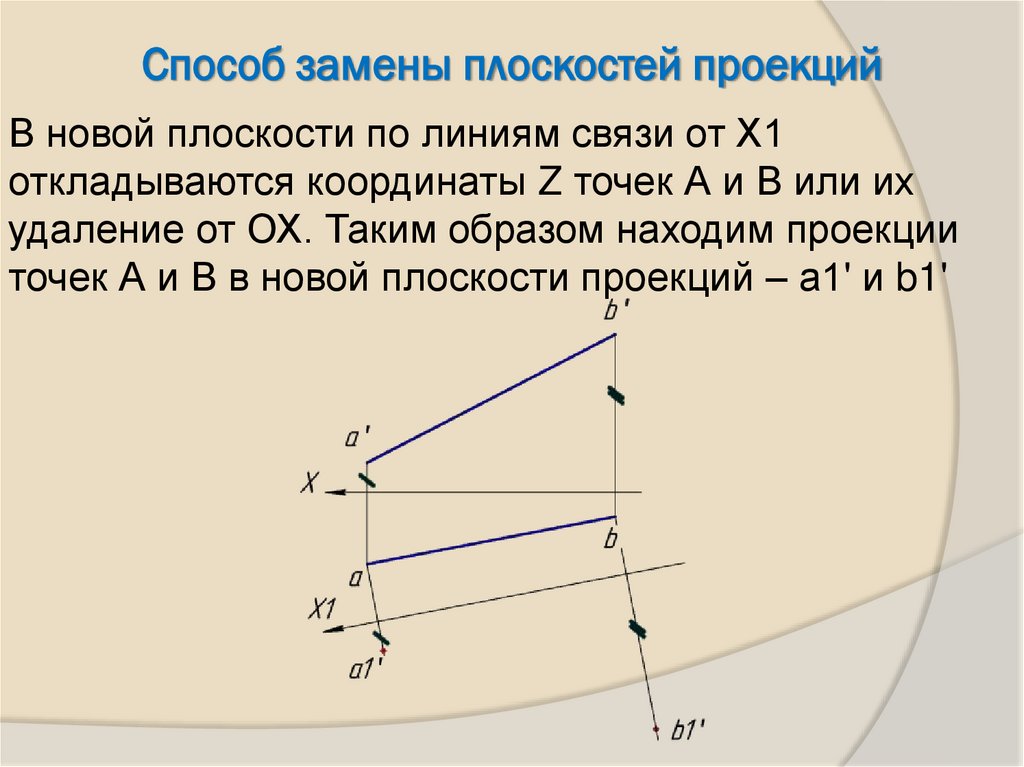
22.
Способ замены плоскостей проекцийВ новой плоскости по линиям связи от Х1
откладываются координаты Z точек А и В или их
удаление от ОХ. Таким образом находим проекции
точек А и В в новой плоскости проекций – а1' и b1'
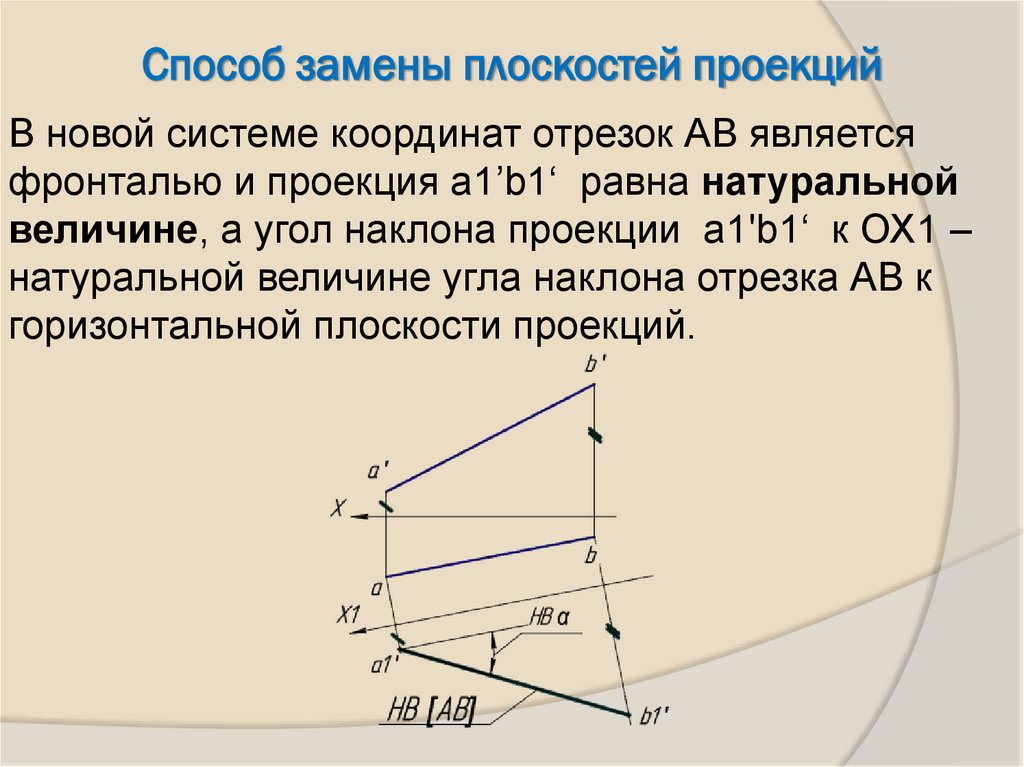
23.
Способ замены плоскостей проекцийВ новой системе координат отрезок АВ является
фронталью и проекция а1’b1‘ равна натуральной
величине, а угол наклона проекции а1'b1‘ к ОХ1 –
натуральной величине угла наклона отрезка АВ к
горизонтальной плоскости проекций.
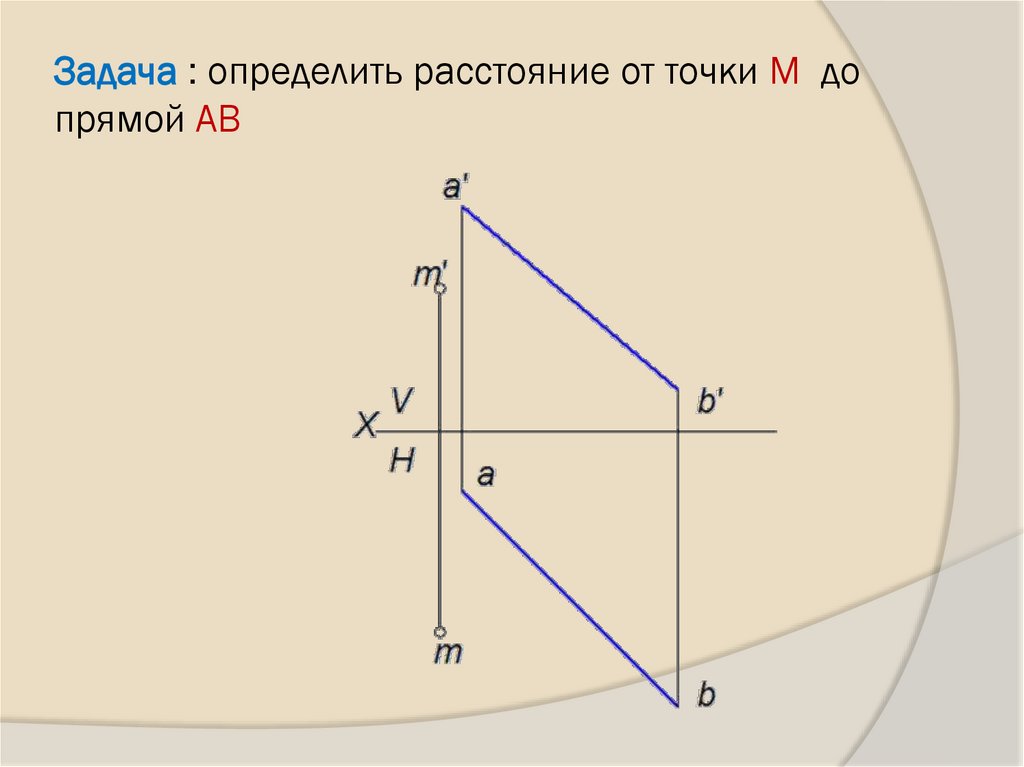
24. Задача : определить расстояние от точки М до прямой АВ
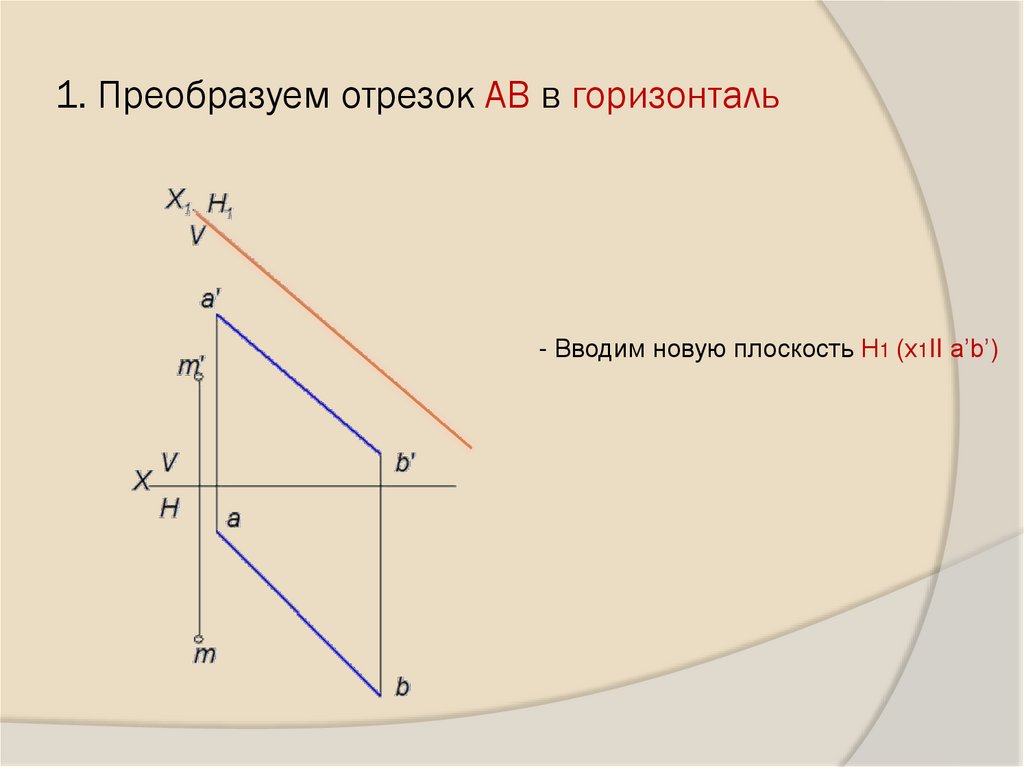
25. 1. Преобразуем отрезок АВ в горизонталь
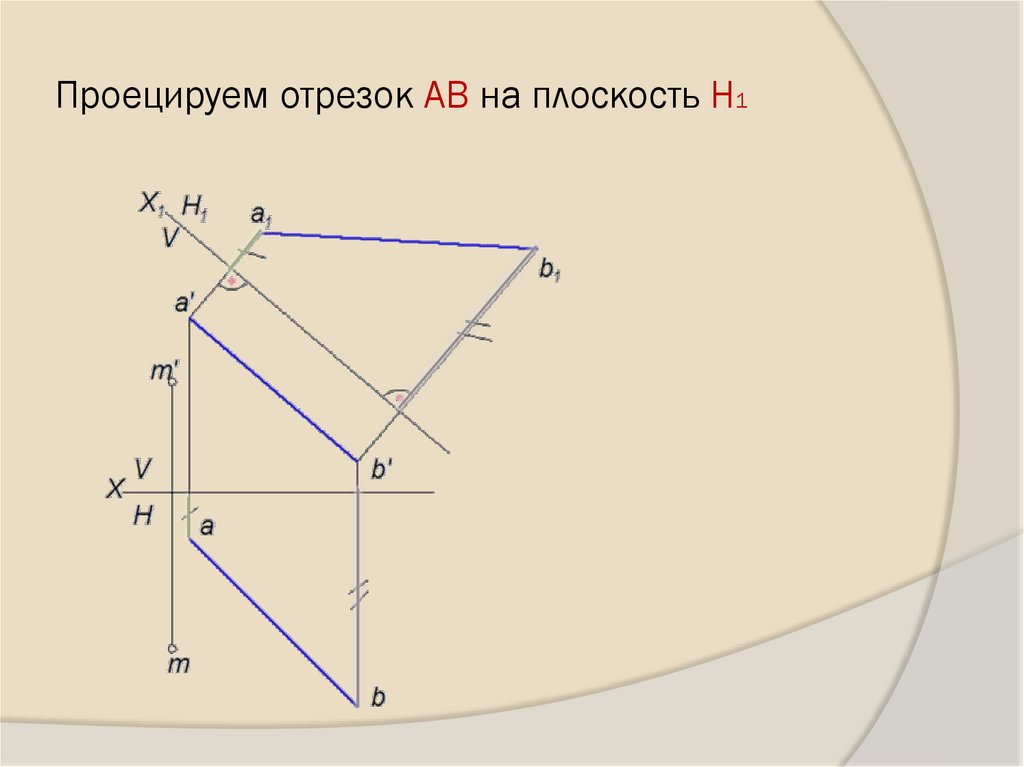
- Вводим новую плоскость Н1 (х1II a’b’)26. Проецируем отрезок АВ на плоскость Н1
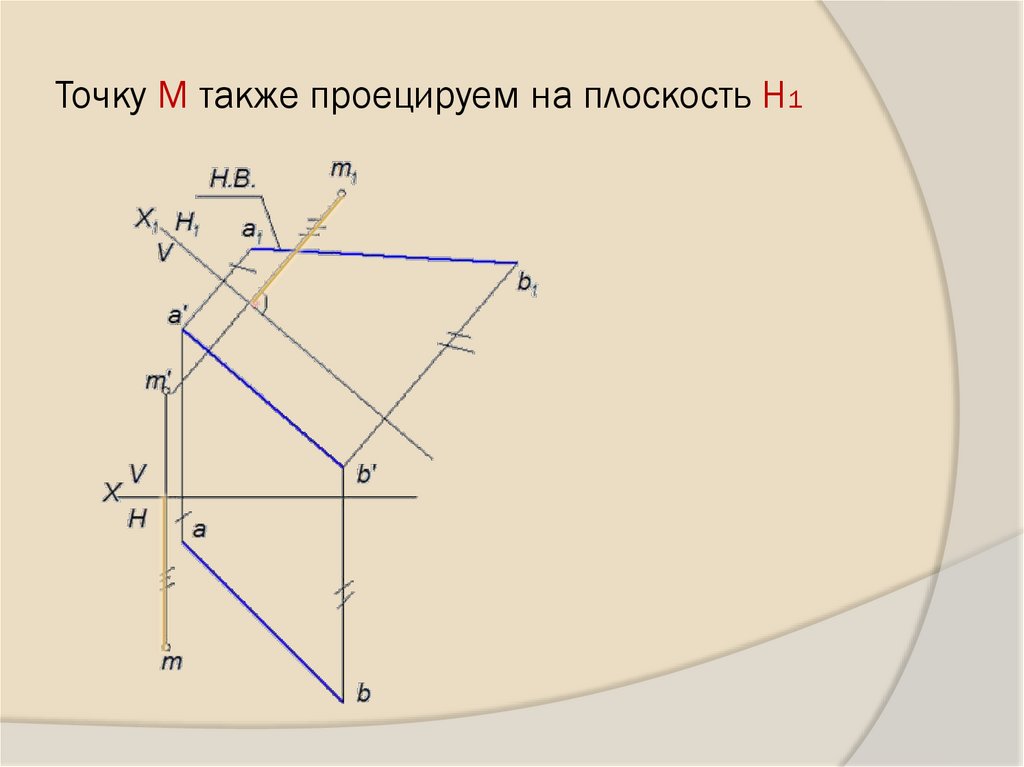
27. Точку М также проецируем на плоскость Н1
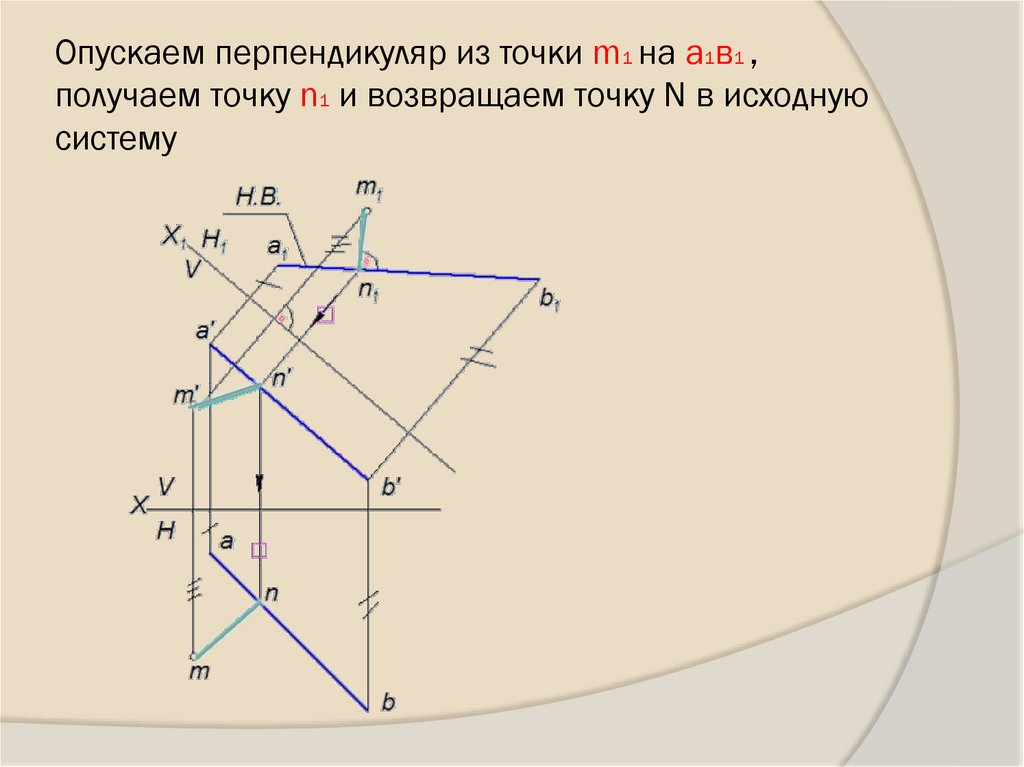
28. Опускаем перпендикуляр из точки m1 на а1в1 , получаем точку n1 и возвращаем точку N в исходную систему
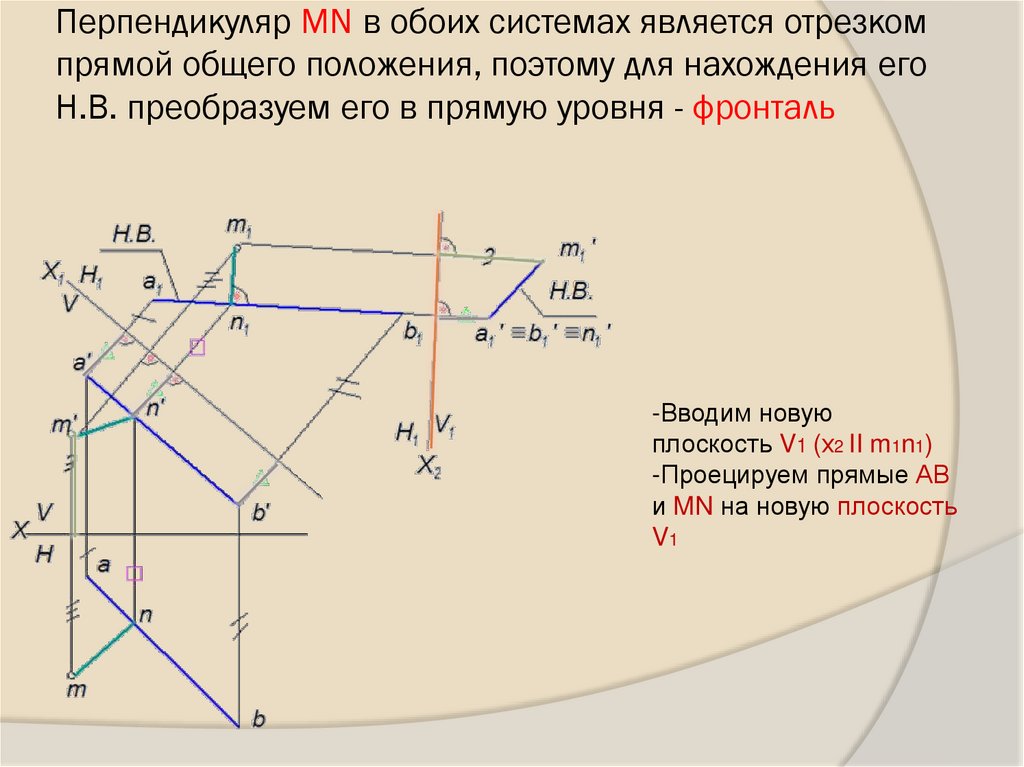
29. Перпендикуляр MN в обоих системах является отрезком прямой общего положения, поэтому для нахождения его Н.В. преобразуем его в
прямую уровня - фронталь-Вводим новую
плоскость V1 (х2 II m1n1)
-Проецируем прямые АВ
и MN на новую плоскость
V1
30.
СПАСИБО ЗАВНИМАНИЕ!





 Инженерная графика
Инженерная графика








