Проекции отрезков прямой

1. Проекции отрезков прямой

Лекция 2
Проекции
отрезка прямой
Прямые частного положения
Определение натуральной величины (НВ)
отрезка
Способ прямоугольного треугольника
Относительное положение прямых.
1

2. ПРЯМЫЕ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ

Прямая общего положения не имеет
проекций, параллельных или
перпендикулярных осям координат.
Прямые частного положения
параллельны или перпендикулярны
относительно какой-либо плоскости
проекций.
Параллельные прямые – линии уровня.
Такие прямые имеют проекции,
параллельные или перпендикулярные
осям координат.
2

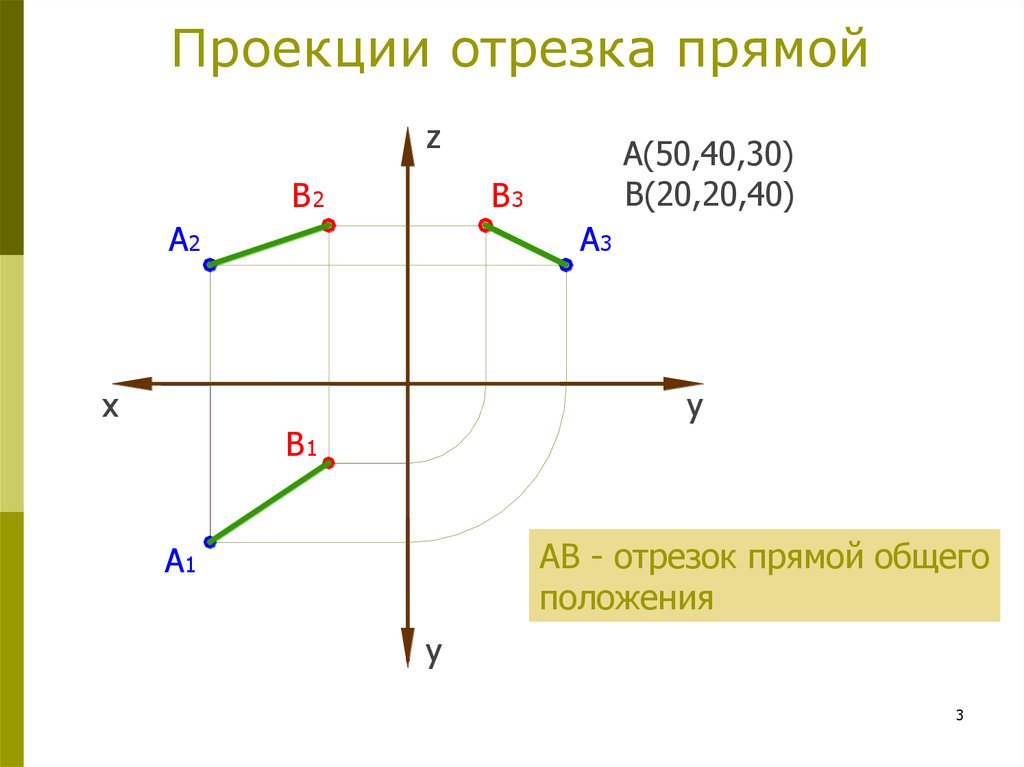
3. Проекции отрезка прямой

zz
B2
B3
A3
y = 40
y = 20
z = 30
z = 40
A2
xx
y
B1
A1
A(50,40,30)
B(20,20,40)
АВ - отрезок прямой общего
положения
x=
x=
2050
y
3

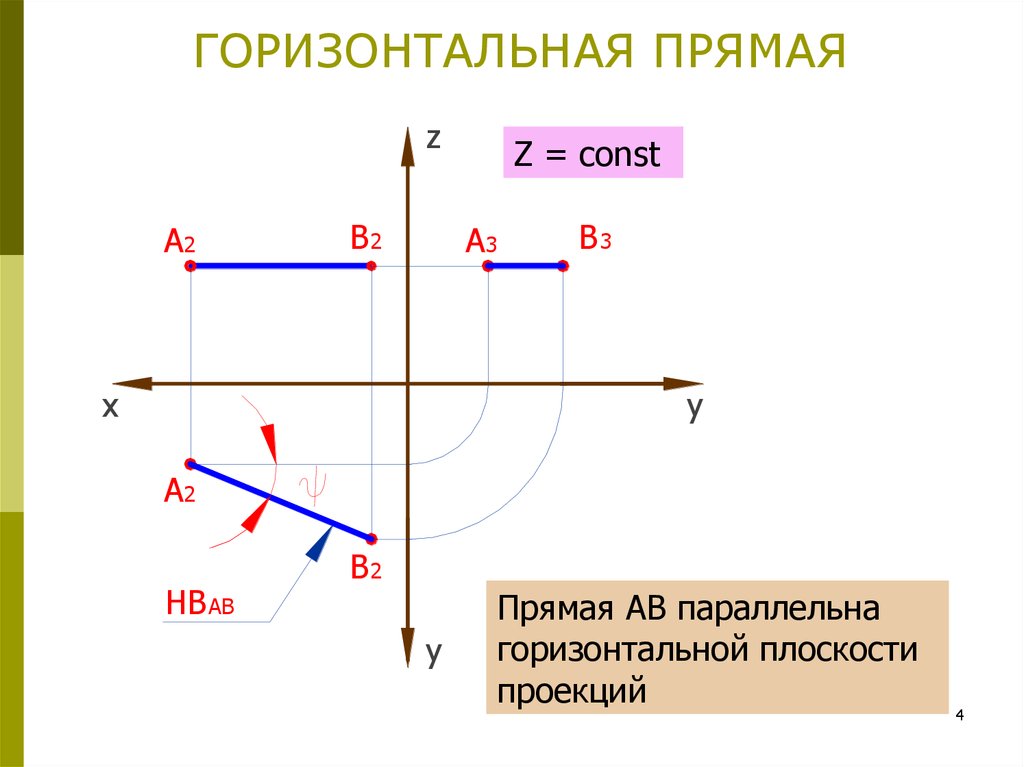
4. ГОРИЗОНТАЛЬНАЯ ПРЯМАЯ

z
A2
B2
Z = const
A3
x
B3
y
A2
HB AB
B2
y
Прямая АВ параллельна
горизонтальной плоскости
проекций
4

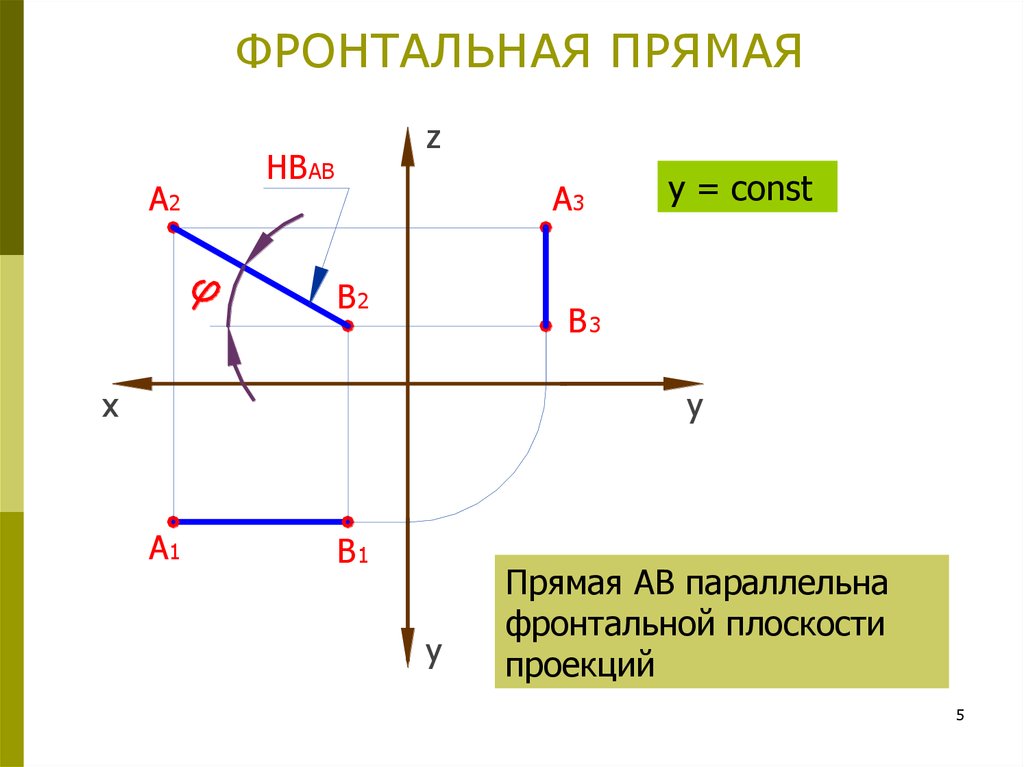
5. ФРОНТАЛЬНАЯ ПРЯМАЯ

A2
z
HB AB
A3
B2
y = const
B3
x
y
A1
B1
y
Прямая АВ параллельна
фронтальной плоскости
проекций
5

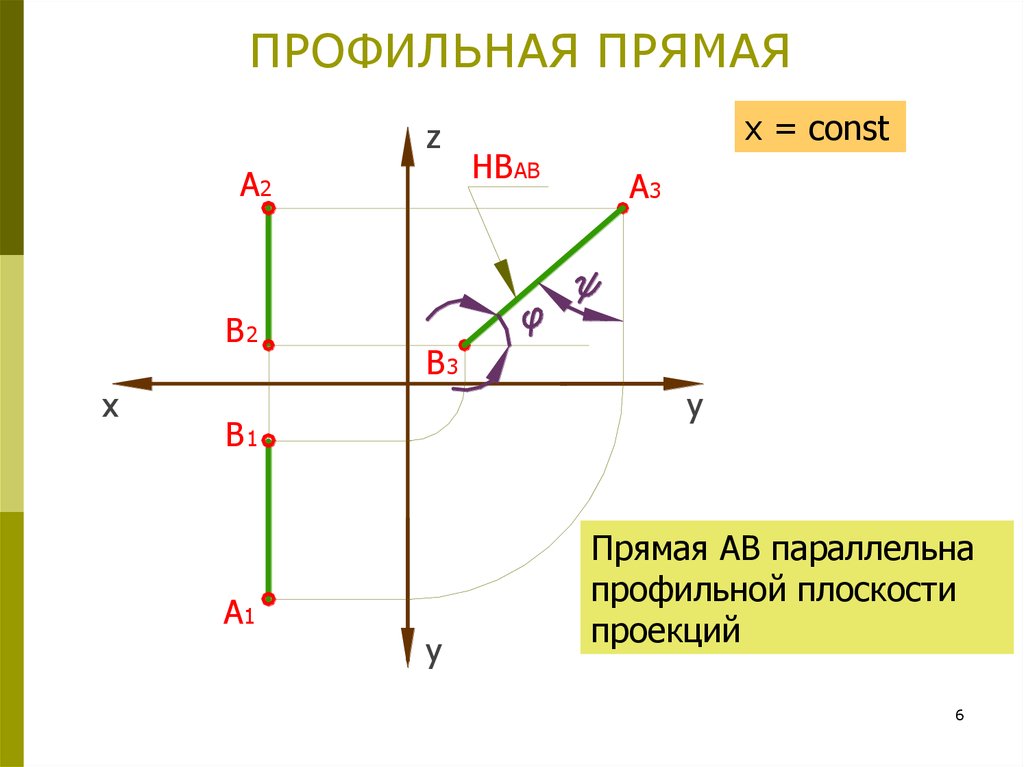
6. ПРОФИЛЬНАЯ ПРЯМАЯ

z
A2
B2
x
A3
B3
y
B1
A1
HB AB
x = const
y
Прямая АВ параллельна
профильной плоскости
проекций
6

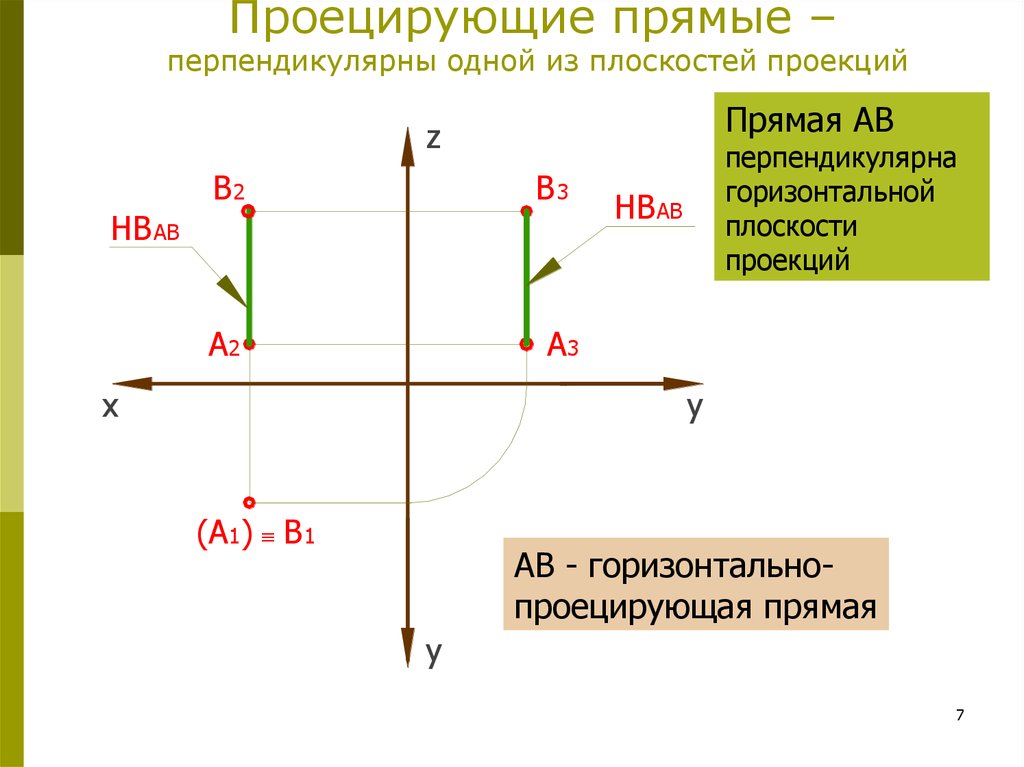
7. Проецирующие прямые – перпендикулярны одной из плоскостей проекций

Прямая АВ
z
B2
B3
HB AB
A2
перпендикулярна
горизонтальной
плоскости
проекций
HB AB
A3
x
y
A11 ) B 1B 1
(A
АВ - горизонтальнопроецирующая прямая
y
7

8.

z
HB AB
A3
A22 ) B 2B 2
(A
x
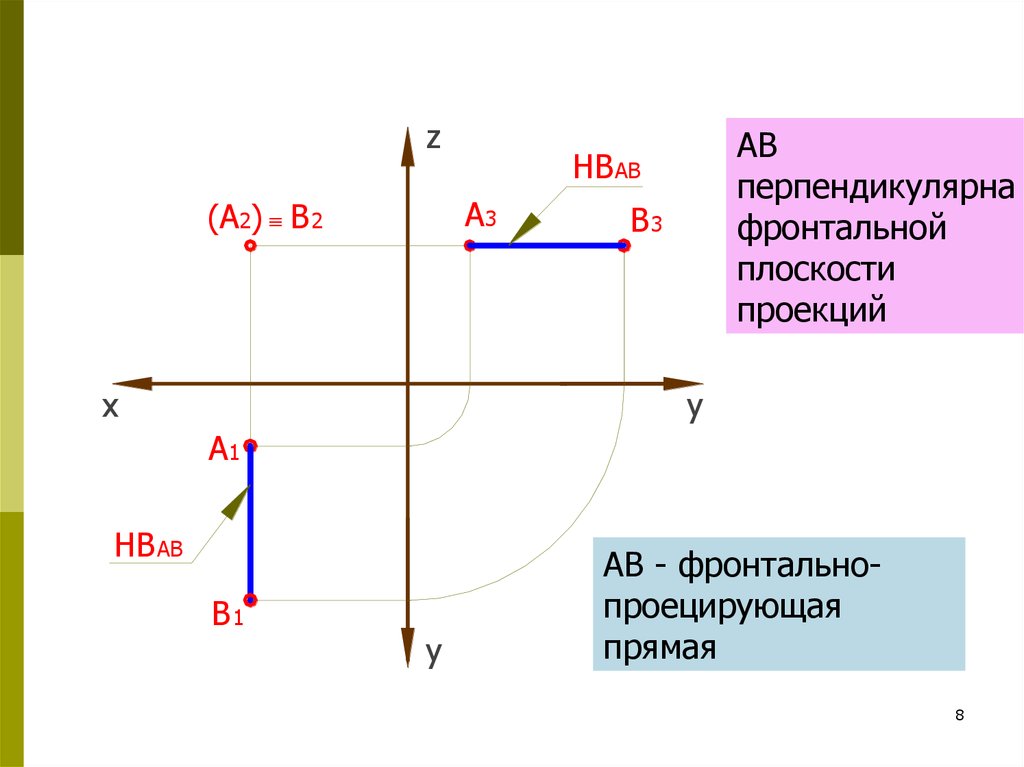
АВ
перпендикулярна
фронтальной
плоскости
проекций
B3
y
A1
HB AB
B1
y
АВ - фронтальнопроецирующая
прямая
8

9.

z
HB AB
A2
B2
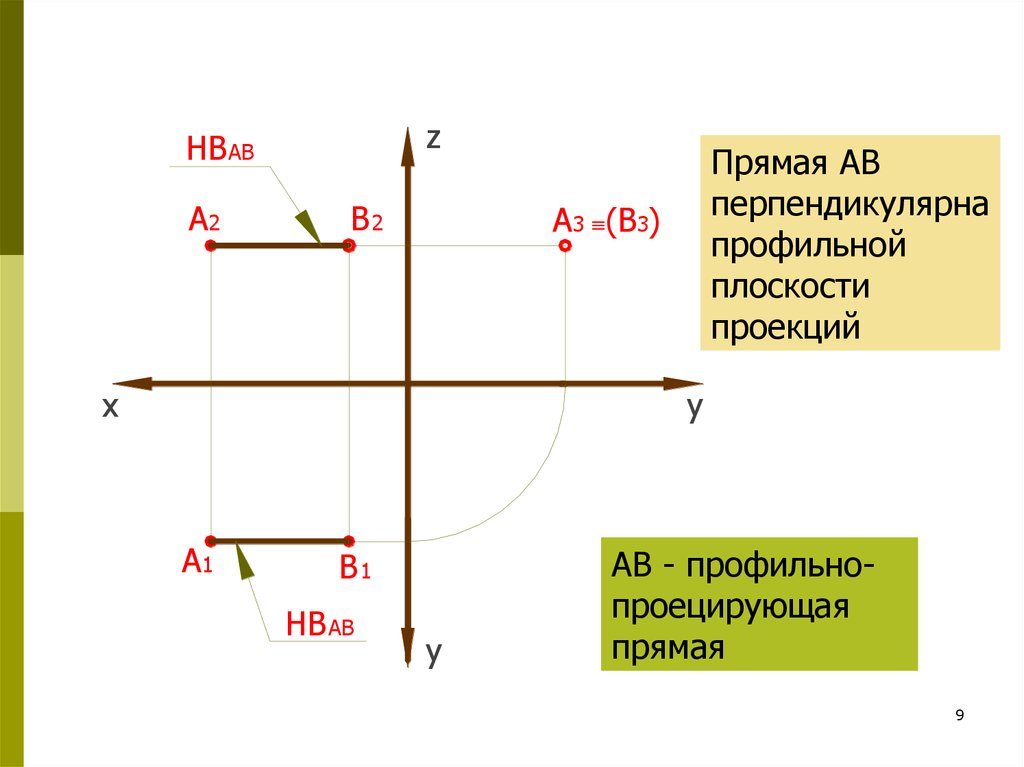
Прямая АВ
перпендикулярна
профильной
плоскости
проекций
B 33)
A3 (B
x
y
A1
B1
HB AB
y
АВ - профильнопроецирующая
прямая
9

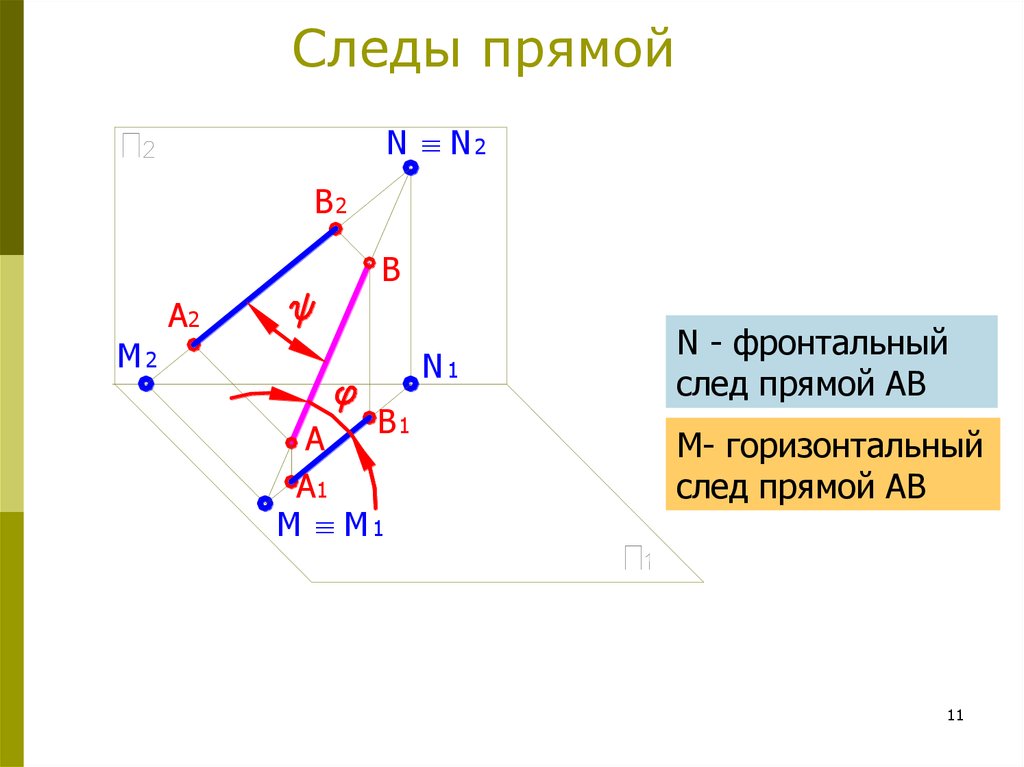
10. Следы прямой

Точки пересечения прямой линии с
плоскостями проекции называются следами
прямой.
Точка пересечения прямой с горизонтальной
плоскостью проекций называется
горизонтальным следом прямой.
Точка пересечения прямой с фронтальной
плоскостью проекций называется
фронтальным следом прямой.
10

11. Следы прямой

N N 2
B2
B
M 2
A2
N 12
B1
A
A1
M M 1
N - фронтальный
след прямой АВ
М- горизонтальный
след прямой АВ
11

12. Следы прямой

N2
B2
N - фронтальный
след прямой АВ
A2
x
M2
B1
A1
M1
N1
М - горизонтальный
след прямой АВ
12

13. Способы задания прямой

1. По координатам точек концов отрезка
прямой (проекциям отрезка прямой).
2. Параметрами отрезка прямой линии:
- натуральной величиной отрезка (НВ);
- углами наклона к плоскостям проекций - ( ₁)
и ( ₂);
- угол между линией отрезка и
горизонтальной плоскостью ( ₁);
- угол между линией отрезка и фронтальной
плоскостью ( ₂).
13

14. Способ прямоугольного треугольника

Натуральная величина отрезка прямой
общего положения равна гипотенузе
прямоугольного треугольника, одним
катетом которого является проекция
отрезка на любую плоскость проекций,
другим – разность расстояний концов
отрезка до той же плоскости проекций.
14

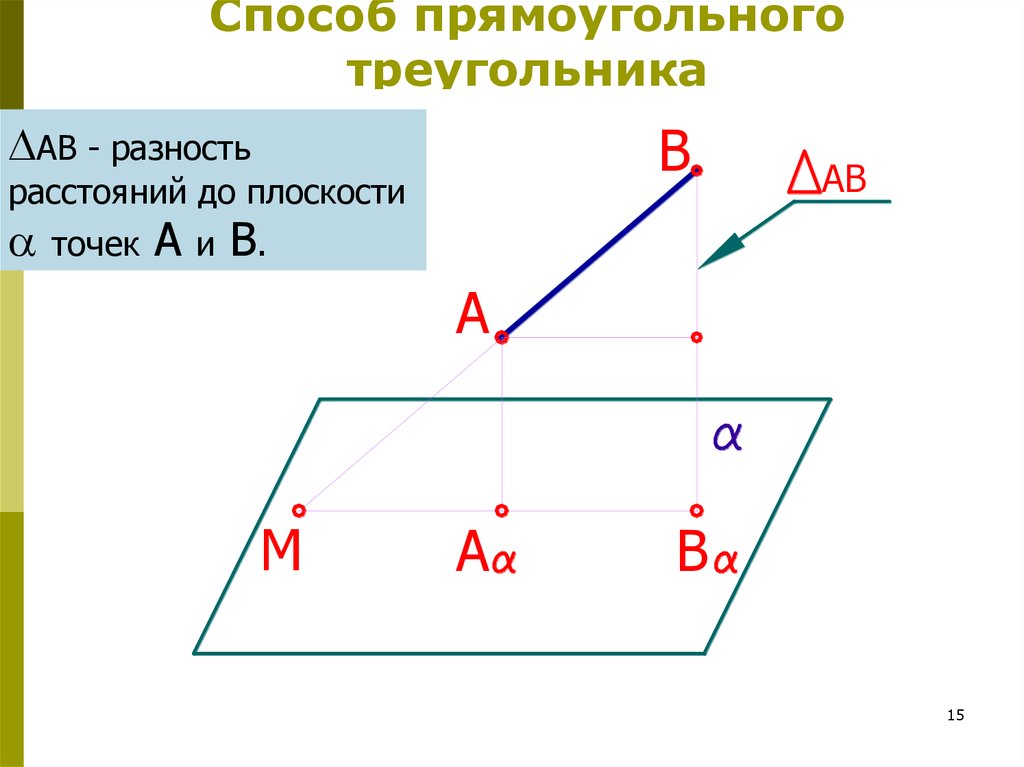
15. Способ прямоугольного треугольника

B
АВ - разность
расстояний до плоскости
точек
А
и
B
AB
В.
A
M
A
A
B
15

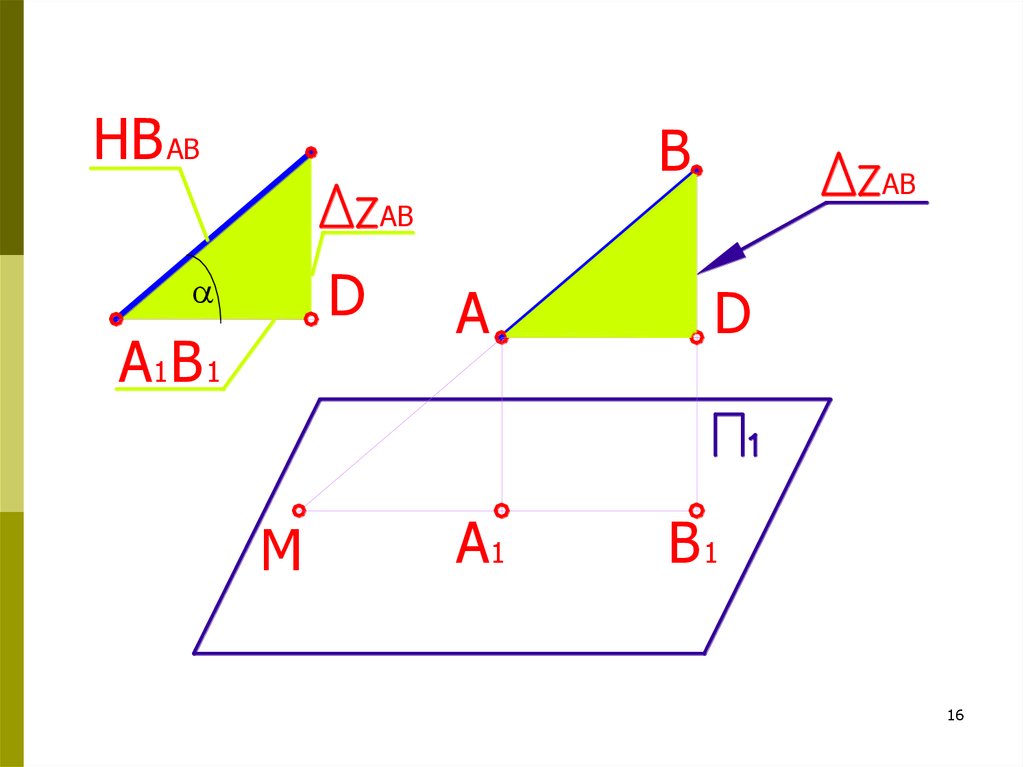
16.

HB AB
B
AB
AB
D
A1 B 1
M
A
A1
D
B1
16

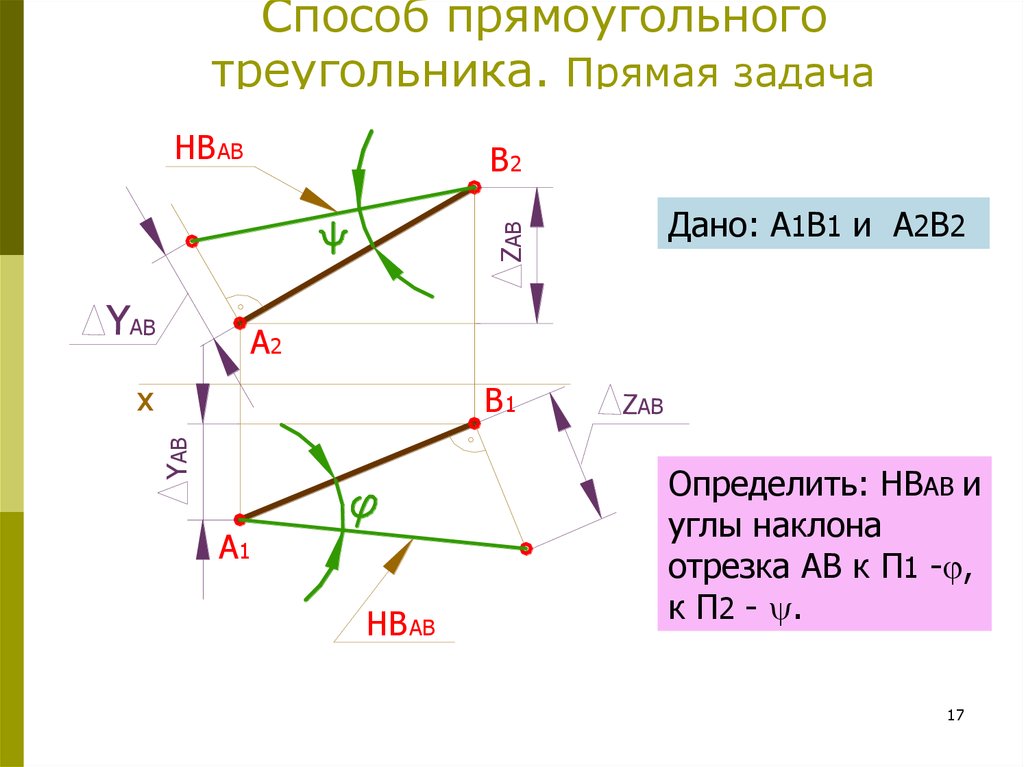
17. Способ прямоугольного треугольника. Прямая задача

HB AB
BB22
Z
ZAB
AB
Дано: А1В1 и А2В2
YYABAB A2 AA22
xx
Y
YAB
AB
BB11
A1
AA11
HB
HBAB
AB
ZZAB
AB
Определить: НВАВ и
углы наклона
отрезка АВ к П1 - ,
к П2 - .
17

18. Способ прямоугольного треугольника. Обратная задача

Дано: НВАВ,
1 1
R=
=30, =45 .
0
ZAB= 5
A1
B
AB
А(40,50,5)
1
A
A 2B 2
B
YAB
ZAB
ХА<ХВ, YA>YB,
B2
A2
x
ZA<ZB.
0
B1
YAB
Построить проекции
отрезка АВ.
A1
18

19. ВЫВОДЫ

По положению относительно плоскостей
проекций различают:
- прямые общего положения (непараллельные
и неперпендикулярные плоскостям
проекций),
- прямые частного положения: параллельные
или перпендикулярные плоскостям
проекций.
19

20. ВЫВОДЫ

Проекции прямых частного положения
дают ответы на вопросы позиционных и
метрических задач.
Способ прямоугольного треугольника
поясняет связи между натуральной
величиной отрезка, его проекциями и
углами наклона к плоскостям проекций.
20

21. Контрольные вопросы

1.
2.
Как по заданным проекциям
отрезка определить его
натуральную величину?
Как по заданным проекциям
отрезка определить углы наклона
его к плоскостям проекций?
21

22. Контрольные вопросы

3.
Какое положение прямой дает
проекцию отрезка этой прямой,
равную натуральной величине?
4.
Что такое «след прямой»?
Как его построить?
5.
22