Похожие презентации:
Энергетические характеристики молекул. Химическая связь
1.
Лекция 2.Энергетические характеристики
молекул. Химическая связь
2.
Молекула - динамическая система, состоящаяиз определенного числа ядер и электронов.
Важнейшей
характеристикой
молекулы
является химическая связь, ее длина и энергия.
Квантовомеханический подход к изучению
молекул тот же, что и к изучению атомов составляется и решается уравнение Шрёденгера
для систем из определенного числа ядер и
электронов.
3.
Точное решение уравнения Шрёдингера возможно толькодля атома водорода, поэтому для молекул используют
приближения, в частности принцип Борна-Оппенгеймера.
Сущность его в следующем, так как масса электронов в
тысячи раз меньше массы ядер, а скорость движения ядер очень
мала по сравнению со скоростью движения электронов, то
движение электронов в молекуле можно рассматривать, считая в
каждый данный момент ядра неподвижными.
Данному фиксированному положению ядер будет отвечать
определенное значение электронной энергии.
Если изменится положение ядер, то изменится поле, в
котором движутся электроны, изменится и энергия системы.
Таким образом, электронная энергия является функцией
межъядерного расстояния.
4.
Основные идеи метода молекулярных орбиталей(метод МО).
В основу метода МО положена модель
аналогичная методу самосогласованного поля,
используемому при описании атома:
5.
1. Молекула рассматривается как единое целое, а не каксовокупность сохраняющих некоторую индивидуальность
атомов. Каждый электрон принадлежит молекуле в целом и
движется в поле всех её ядер и электронов.
2. Состояние электрона описывается одноэлектронной
волновой функцией ψi, , характеризуемой определенным
набором квантовых чисел. Функция эта называется молекулярной
орбиталью (МО). В отличие от одноцентровой атомной орбитали
(АО),
молекулярная
орбиталь
в
общем
случае
многоцентровая. Квадрат волновой функции |ψi|2 определяет
плотность вероятности нахождения электрона в пространстве или
плотность электронного облака.
6.
3. Каждой МО соответствует определенная энергия Еi,приближенно характеризуемая потенциалом ионизации с
данной орбитали. Энергия электрона на МО складывается из его
кинетической энергии, потенциальной энергии притяжения ē ко
всем ядрам и отталкивания от других электронов.
4.Совокупность МО молекулы, занятых электронами,
называется её электронной конфигурацией.
Электронная конфигурация молекулы, так же как и для атома,
строится на основе двух фундаментальных положений принципа наименьшей энергии и принципа Паули.
Следовательно, для описания электронной конфигурации
основного состояния молекулы с 2n электронами требуется n
молекулярных орбиталей. Соблюдается также правило Гунда.
7.
5. Координатная волновая функция основного состояния молекулы внулевом приближении задается как произведение одноэлектронных
волновых функций занятых молекулярных орбиталей.
Ψмол = ψ1 ψ2 ψ3….. ψn
(I)
(метод Хартри-Фока)
Энергия системы при этом принимается равной сумме
орбитальных
энергий
занятых
МО
минус энергия их усредненного отталкивания:
Е=ѵΣEi – Eуср.отн. , (II)
где ѵ=1 или 2, в зависимости от заполнения орбиталей электронами.
Полная волновая функция с учетом спина должна строиться в
виде определителя, подобно функции Хартри-Фока с использованием
молекулярных спин-орбиталей.
Выражения (I) и (II) весьма
приближенные, они рассматривают движение электронов в молекуле как
взаимно независимое (точные результаты только для Н2+ и Н2).
8.
6. При переходе хотя бы одного электронамолекулы с занятой на более высокую свободную МО
молекула в целом переходит из основного состояния
(Ψмол) в возбужденное (Ψ*мол) . Волновая функция
возбужденного состояния в нулевом приближении
строится аналогично Ψмол = ψ1 ψ2 ψ3….. ψn (I) с
учетом занятой возбужденным электроном орбитали.
9.
Одним из способов приближенного описанияволновой функции электрона в молекуле является метод
выражения МО как линейной комбинации атомных
орбиталей (МО ЛКАО).
При построении МО по методу ЛКАО должны
соблюдаться условия, т. е.комбинируемые АО должны:
А) быть близкими по энергии;
Б) перекрываться достаточным образом;
В) обладать одинаковыми свойствами симметрии.
10.
Молекула Н2+ в методе МО ЛКАО.1. Расчет энергии и волновой функции по
вариационному методу:
11.
Рассмотрим приближенное решениеметодом МО ЛКАО уравнения
Шрёдингера для этой простейшей из
молекул, чтобы ознакомится с
характерными особенностями метода.
Для этого рассмотрим электрон в поле
двух протонов А и В, находящихся на
расстоянии RAB друг от друга.
12.
Построим МО в виде ЛКАО.Ψ = С1 ψ1 + С2 ψ2
(III) ,
где Ψ1 и Ψ2 – атомные орбитали атома водорода.
Они составляют базис молекулярной орбитали. Этот
базис – минимальный, меньшим числом АО при построении
данной МО обойтись нельзя. Ψ1 и Ψ2 выбираем как АО
основного состояния атома Н, т.е. 1S-АО.
13.
Нормированная волновая функция состояния 1Sзаписывается следующим образом:
Ψ1= (πа03)-1/2 e -r /a
Ψ2= (πа03)-1/2 e -r /a
a0 - радиус первой Боровской орбиты,
a0 = 0,529177*10-10 м,
rA1 и r B1 – расстояния электрона от ядер А и В.
A1
0
B1
0
14.
Решим задачу о коэффициентах волновойфункции (III) энергии системы Н2+ при помощи
вариационного метода.
Запишем уравнение Шрёдингера: Ĥψ=Еψ
15. (Ψ = С1 ψ1 + С2 ψ2 ) (III)
Данное уравнение домножим на ᴪ* и проинтегрируем:ᴪ*Ĥᴪ=Еᴪ*ᴪ →∫ᴪ* Ĥᴪdτ = Е∫ᴪ*ᴪdτ выведем отсюда Е:
Е=∫ᴪ* Ĥᴪdτ / ∫ᴪ*ᴪdτ
В выражение для энергии подставим пробную волновую функцию (III)
(Ψ = С1 ψ1 + С2 ψ2 ) (III)
16.
Выполнив соответствующие операции, получили:Е = С12 ∫ ψ1 Ĥ ψ1 dτ + С1С2 ∫ψ1 Ĥ ψ2 dτ + С2С1 ∫ ψ2 Ĥ ψ1 dτ + С22 ∫ ψ2 Ĥ ψ2 dτ
С12∫ ψ12dτ + С1С2∫ψ1ψ2 dτ + С2С1∫ψ2ψ1dτ + С22∫ψ22 dτ
(IV)
17.
Произведем упрощения записи, обозначивинтегралы символами:
∫ ψ1 Ĥ ψ1 dτ = Н11
∫ψ1 Ĥ ψ2 dτ = Н12
∫ ψ12 dτ = S11
∫ ψ2 Ĥ ψ2 dτ = Н22
∫ ψ2 Ĥ ψ1 dτ = Н21
∫ψ22 dτ = S22
∫ψ1 ψ2 dτ =S12
∫ψ2 ψ1 dτ = S21
18.
Из двух последних уравнений видно, что S12=S21 (A).Из свойств оператора Гамильтона следует также
Н12=Н21(В)
Учтём эти два равенства и подставим символы
интегралов в выражение (IV), получим:
19.
• Рассчитать энергию по (V) нельзя, т.к. не известныкоэффициенты С1 и С2. Для их нахождения
используем вариационный метод, согласно которому
лучшая функция Ψ типа (Ψ = С1 ψ1 + С2 ψ2 (III))
должна отвечать минимальной энергии, достигаемой
при определенных значениях С1 и С2.
• Условие минимума Е (V), как функции С1 и С2
известно: частные производные функции по каждому
из независимых переменных (С1 и С2) должны быть
равны нулю.
20.
Продифференцировав (V) по С1 при постоянном С2 и поС2 при постоянном С1 и проведя некоторые математические
преобразования, получим 2 уравнения:
С1 ( Н11 – Е S11) + C2( H12 – E S12)=0
С1 ( Н12 – Е S12) + C2( H22 – E S22)=0
(VI)
(VII)
Эти два уравнения представляют однородную систему
из двух линейных уравнений с двумя неизвестными С1 и С2.
Чтобы уравнения были совместны, определитель системы
должен быть равен нулю.
21.
Уравнения (VI) и (VII) называются вековымиуравнениями, а их определитель (VIII) – вековым
определителем. При учете равенств S12=S21 (А) и Н12=Н21 (В)
определитель (VIII) можно записать следующим образом :
Н11 – Е S 11
H12 – E S12
=0
Н21 – Е S 21
(VIII)
H22 – E S22
Цифры в индексах совпадают с номером строки (первая) и
номером столбца (вторая).
22.
Итак, при поисках двучленной МО по методу ЛКАОполучается определитель второго порядка, каждый элемент
которого записывается в форме (Нij – ESij), где i-номер
строки, j- номер столбца. Если функция является линейной
комбинацией n атомных орбиталей, то получают
определитель n-го порядка
Поэтому во многих случаях нет нужды проводить
дифференцированние выражения для Е, можно сразу
записать вековые уравнения или вековой определитель.
|Нij – Е Sij| =0
23.
Например, для иона Н3+, МО по методу ЛКАО имеет вид:ψ = С1 ψ1 + С2 ψ2 + С3ψ3, таким образом получаем вековой
определитель
Н11 – Е S 11
Н21 – Е S 21
Н31 – Е S 31
H12 – E S12
H22 – E S22
H32 – E S32
H13 – E S13
H23 – E S23 =0
H33 – E S33
(IX)
Определитель (VIII) для Н2+можно упростить:
Интегралы S11 = S22 = Sii =1 (из условия нормировки атомных волновых
функций ∫ ψi ψi dτ = Sii =1).
Единственный интеграл перекрывания S12 не нуждается в индексах,
обозначаем его через S (S12=S21=S).
24.
Интегралы Нii=Н11=Н22 (поскольку ψ1 и ψ2 – функции 1S дляодинаковых атомов водорода). Обозначим
их через α,
интеграл Н12 обозначим через β, определитель примет вид:
α–Е
β - ЕS
(IX)
β – ES α - E
Раскрыв этот определитель, получим уравнение второй
степени относительно Е:
(α – Е)2=(β– ЕS)2 или α – Е=±(β – ЕS)
Два корня квадратного уравнения обозначим через Еs и ЕА:
Es= (α+ β)/(1+S)
(X)
EA= (α- β)/(1-S)
(XI)
25.
Таким образом, мы пришли к выводу о существованиистрого определенных значений энергии для МО молекулы Н2+ –
собственных значений ψ функции уравнения Шрёдингера для
молекулы Н2+.
Определим коэффициенты волновой функции молекулы.
Из векового уравнения С1( Н11 – Е S11) + C2( H12 – E S12)=0 (VI)
выразим отношение С1/С2:
C1/C2 = (H12-ES12)/(ES11-H11)=(β–ES)/(E – α)
Подставим в это выражение вместо Е значение
Es= (α+ β)/(1+S), получим С1=С2=Сs (XII)
(S11=1)
26.
Аналогично из С1 ( Н12 – Е S12) + C2( H22 – E S22)=0 (VII)и EA= (α- β)/(1-S) (XI), получим
• С1/ С2= - 1
• С1 =-С2 = | CA |
• C1 = CA
C2 = - CA
(XIII)
27.
Подстановка полученных выражений для этихкоэффициентов (XII, XIII) в уравнении
Ψ = С1 ψ1 + С2 ψ2 (III) приводит к двум решениям
уравнения Шрёдингера для Н2+, к двум молекулярным
орбиталям:
Ψs= Сs (ψ1+ψ2)
ΨA= СA (ψ1-ψ2)
(XIV)
(XV)
28.
Для определения самих коэффициентов Сs и CA воспользуемсяусловием нормировки
∫(ψs)2 dτ=1, подставим сюда Ψs= Сs (ψ1+ψ2) (XIV), получим:
∫ Сs2(ψ1+ψ2)2 dτ = Сs2[∫ψ12 dτ +ꭍψ22 dτ +2ꭍψ1ψ2 dτ]=1
Первое и второе слагаемое в квадратных скобках равны единице,
т.к. ψ1 и ψ2 –нормированы. В третьем слагаемом стоит интеграл
перекрывания. Итак,
Сs 2[1+1+2S]=1
Сs=1/√2(1+S) (XVI)
Аналогично, находим из условия нормировки ψА коэффициент
СA=1/√2(1-S) (XVII)
Обычно пренебрегают интегралом S по сравнению с единицей
(хотя для Н2+ и Н2 этот интеграл не мал) в остальных случаях такое
допущение законно:
CA=CS=1/√2
29.
Отсюда из (XIV) и (XV) получаем двемолекулярные орбитали:
Ψs= 1/√2 (ψ1+ψ2) с энергией ЕS (XVIII)
ΨA= 1/√2 (ψ1-ψ2) с энергией ЕA
(XIX)
30.
Этот результат для молекулы с одинаковымиядрами может быть достигнут значительно проще, но на
примере Н2+ мы рассмотрели особенности
метода,
характерные для расчета более сложных систем.
Обе МО – приближенные решения уравнения
Шрёдингера, полученные вариационным методом. Из них
одна с более низкой энергией (ψS) отвечает основному,
вторая (ψА) – ближайшему высшему по энергии
состоянию.
31. ∫ѰsѰAdσ =∫1/√2 (Ѱ1+Ѱ2)•1/√2(Ѱ1-Ѱ2) dσ=1/√2[∫ Ѱ12dσ - ∫Ѱ22dσ ]=0
Эти орбитали ортогональны, то есть∫ѰsѰAdσ=0
Докажем это, подставим в это выражение выражения
XVIII и XIX, получим:
∫ѰsѰAdσ =∫1/√2 (Ѱ1+Ѱ2)•1/√2(Ѱ1-Ѱ2) dσ=1/√2[∫ Ѱ12dσ - ∫Ѱ22dσ ]=0
32.
Рассмотрим подробнее выражение для энергии (X) и (ХI).В них входят матричные элементы:
Н11=Н22=α Н12=Н21=β S12 =S21=S
Все эти элементы зависят от параметра RАВ –
межъядерного расстояния.
Н11=Н22=α называют кулоновским интегралом, потому что он
передает кулоновское взаимодействие частиц.
Он включает:
а) энергию электрона в атоме водорода в основном состоянии,
б) кулоновское отталкивание ядер и в) энергию кулоновского
взаимодействия второго протона с электронным облаком,
окружающим первый протон.
33.
• α = -1/2 + (1 + 1/R)•e-2R(ат.ед.)
• (1 ат. ед.= 4,35981•10-18Дж)
• На расстояниях порядка равновесного межъядерного
и выше этот интеграл отрицателен,
• а на больших, где отталкивание ядер мало, равен
энергии электрона на атомной орбитали (-1/2 ат.ед.),
а поэтому в нулевом приближении он принимается
равным энергии электрона в атоме.
• Только на очень малых по сравнению с rе
расстояниях он становится положительным и возрастает
неограниченно
34.
Н12=Н21=β называют обменным или резонансныминтегралом: β=[-1/2+1/R]S-(R+1)e-R (ат.ед)
Интеграл β описывает то добавочное понижение энергии,
которое возникает из-за возможности перехода электрона от ядра
А к ядру В, возможности движения в поле двух ядер, как бы
«обменивая» ядра при этом, обменивая ψ1 на ψ2. Этот интеграл
на бесконечности равен нулю, на всех других расстояниях,
кроме очень коротких - отрицателен. Только на очень коротких
расстояниях он становится положительным и возрастает
неограниченно при R→0. Его вклад и определяет энергию
химической связи: чем он больше по абсолютной величине, тем
прочнее связь. Не имеет аналога в классической физике.
35.
S12 =S21=S называют интеграл перекрывания.Этот интеграл служит мерой перекрывания
атомных орбиталей, образующих молекулярную орбиталь
S=(1/3R2+R+1)e-R
Интеграл перекрывания - величина безразмерная.
Он равен единице при RAB=0 и спадает до нуля при
возрастании межъядерного расстояния.
36.
На расстояниях между атомами, существующими вмолекулах, обменный интеграл тем больше по
абсолютной
величине,
чем
больше
интеграл
перекрывания. Поэтому принято считать, что чем больше
перекрываются атомные орбитали образующих МО, тем
прочнее связь.
Установив вид зависимости α, β и S от межъядерного
расстояния, можно найти взаимное расположение уровней
энергии Еs и ЕА. (Es= (α+ β)/(1+S) ; EA= (α- β)/(1-S) ).
Т.к. на всех расстояниях, кроме очень коротких, β<0, то
Еs <ЕА, т.е. Еs отвечает основному состоянию, а
ЕА – первому возбужденному состоянию молекулы водорода.
37.
Строгийфизический
смысл
имеет
только
энергия
Е
молекулы.
Составляющие же ее α и β имеют рассмотренный выше смысл только в рамках
приближения МО ЛКАО.
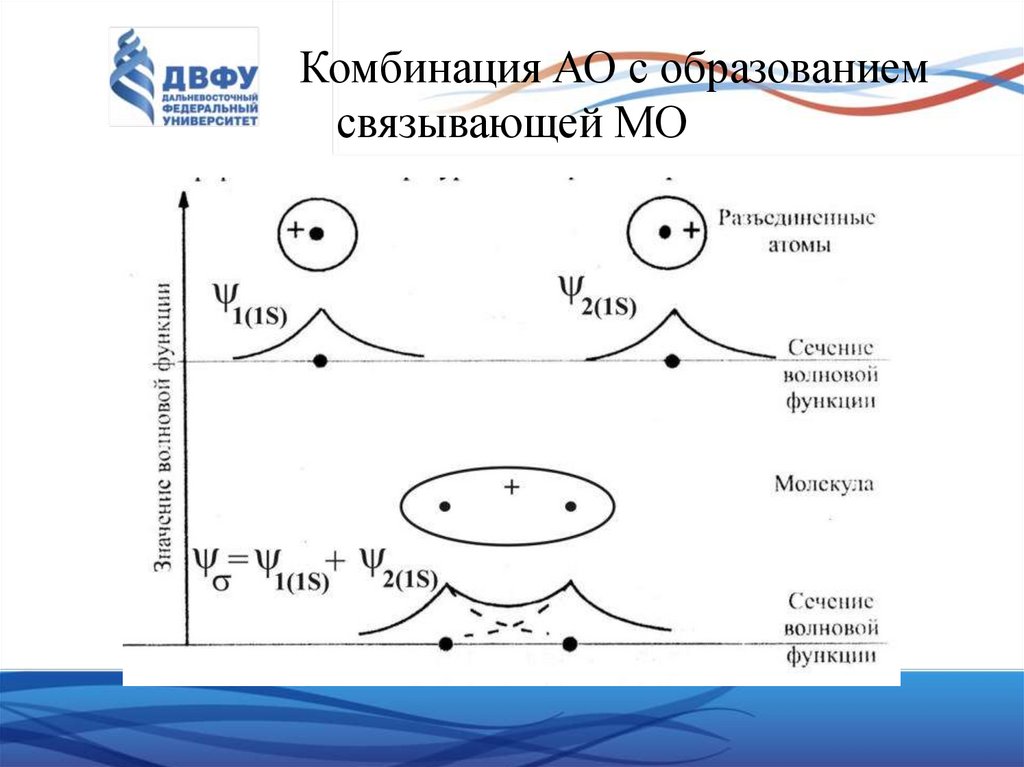
Функция ᴪS соответствует связывающей МО, а ᴪА – разрыхляющий.
Для ᴪS = 1/√2 (ᴪ1 + ᴪ2) волновые функции ᴪ1 и ᴪ2 имеют одинаковые знаки
и их поперечные сечения могут быть представлены графически следующим
образом:
38.
• Не трудно убедиться, что вероятность пребывания ē впространстве между ядрами большая и силы притяжения
преобладают над силами отталкивания, поэтому эта МО
называется связывающей.
• Квадрат |ᴪS|2, представленный графически, имеет вид:
39. Комбинация АО с образованием связывающей МО
40.
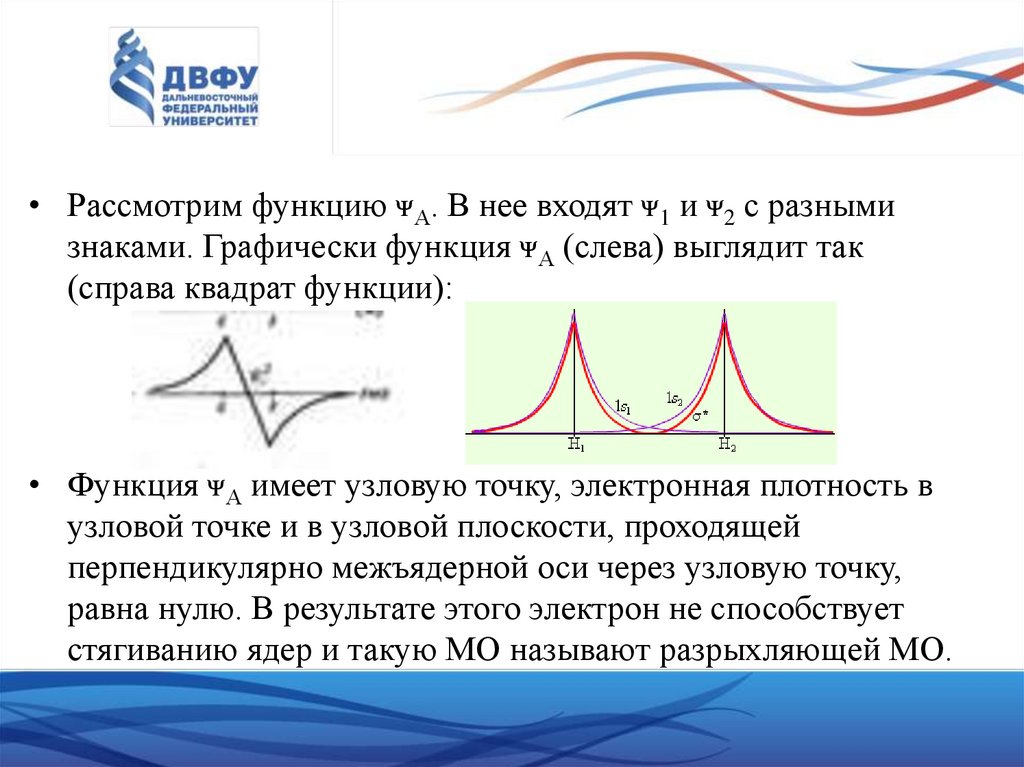
• Рассмотрим функцию ᴪА. В нее входят ᴪ1 и ᴪ2 с разнымизнаками. Графически функция ᴪА (слева) выглядит так
(справа квадрат функции):
• Функция ᴪА имеет узловую точку, электронная плотность в
узловой точке и в узловой плоскости, проходящей
перпендикулярно межъядерной оси через узловую точку,
равна нулю. В результате этого электрон не способствует
стягиванию ядер и такую МО называют разрыхляющей МО.






























![∫ѰsѰAdσ =∫1/√2 (Ѱ1+Ѱ2)•1/√2(Ѱ1-Ѱ2) dσ=1/√2[∫ Ѱ12dσ - ∫Ѱ22dσ ]=0 ∫ѰsѰAdσ =∫1/√2 (Ѱ1+Ѱ2)•1/√2(Ѱ1-Ѱ2) dσ=1/√2[∫ Ѱ12dσ - ∫Ѱ22dσ ]=0](https://cf5.ppt-online.org/files5/slide/f/FAVpTRnKcWlXOa9SNYer3LUgQvJIqtmi4M0uxj/slide-30.jpg)








 Химия
Химия








