5-6 Методы линейного программирования и симплекс-алгоритм (1)

1. ПЗ и ЛЗ 5-6: Методы линейного программирования и симплекс-алгоритм

ПЗ и ЛЗ 5-6: Методы линейного
программирования и симплексалгоритм

2. Цель лекции: Понять и применять метод линейного программирования. Изучить работу симплекс-алгоритма. Научиться использовать

Цель лекции:
Понять и применять метод
линейного программирования.
Изучить работу симплексалгоритма.
Научиться использовать данные
методы для решения
практических задач.

3. Метод линейного программирования

• Метод линейного программирования
• Линейное программирование — это метод принятия
решений с использованием линейных уравнений или
неравенств для эффективного распределения ресурсов.
• Области применения:
• Производство
• Логистика
• Финансы и инвестиции
• Цель:
Принятие оптимальных решений путем максимизации
или минимизации целевой функции.

4. Общий вид задачи ЛП

• 1. Целевая функция::
• Z = c1 * x1 + c2 * x2 + ... + cn * xn
• 2. Ограничения:
• a11 * x1 + a12 * x2 + ... + a1n * xn <= b1
• x1 >= 0, x2 >= 0, ... , xn >= 0

5. Симплекс алгоритм

• Симплекс-метод — это метод решения задач
линейного программирования.
• Этапы:
• Выбор начального решения
• Выполнение pivot-операции
• Улучшение значения целевой функции
• Повторение до окончания работы алгоритма
• Применение:
• Производственные планы
• Задачи транспортировки и логистики
• Распределение финансовых ресурсов

6. Пример: Производственный план

• Задача: Компания выпускает два продукта: A и B.
• Продукт A: требуется 3 часа работы и 2 единицы
материала, прибыль = 50 тг.
• Продукт B: требуется 4 часа работы и 3 единицы
материала, прибыль = 60 тг.
• Ресурсы компании:
• 120 часов работы
• 100 единиц материала
• Цель: Определить количество продуктов для
максимизации прибыли.

7. Математическая модель:

Целевая функция: Z = 50x1 + 60x2
• Ограничения:
• Труд: 3x1 + 4x2 ≤ 120
• Материал: 2x1 + 3x2 ≤ 100
• x1 ≥ 0, x2 ≥ 0
• Решение (симплекс-метод):
Оптимум: x1 = 20, x2 = 10
Прибыль: Z = 1600

8.

1-шаг: Приведение к стандартной форме
Чтобы решить задачу симплекс-методом, сначала приводим её к стандартной форме. В стандартной форме правые части ограничений должны быть неотрицательными, а сами ограничения — з
Введём переменные запаса s₁ и s₂ (s₁ ≥ 0, s₂ ≥ 0) и получим:
3x₁ + 4x₂ + s₁ = 120 (ограничение по труду)
2x₁ + 3x₂ + s₂ = 100 (ограничение по материалу)
Здесь s₁ и s₂ — переменные запаса.
2-шаг: Построение начальной симплекс-таблицы
Строим начальную симплекс-таблицу: строки соответствуют ограничениям, столбцы — переменным (x₁, x₂, s₁, s₂, RHS).
Базисными переменными на старте являются s₁ и s₂ (они равны правым частям).
В строке целевой функции Z коэффициенты записываются с отрицательными знаками, так как решается задача максимизации.
Базисные
переменные
(x_1)
(x_2)
(s_1)
(s_2)
(RHS)
(s_1)
3
4
1
0
120
(s_2)
2
3
0
1
100
Макс. пайда (Z)
-50
-60
0
0
0
Примечание:
Базисные переменные — s₁ и s₂, поскольку в начальном решении их значения больше нуля.
В строке Z (максимальная прибыль) коэффициенты целевой функции записываются со знаком «минус», так как решается задача максимизации.
Шаг 3. Выполнение pivot-операции
Выбор ведущего столбца. Берём самый отрицательный коэффициент в строке Z. Здесь это −60 (переменная x₂).
Проверка отношения (ratio test). Делим правую часть на положительные элементы в столбце x₂:
по 1-му ограничению: 120 / 4 = 30
по 2-му ограничению: 100 / 3 ≈ 33.33
Минимальное отношение — 30, значит ведущая строка — первая, x₂ входит в базис взамен s₁.
После pivot-операции пересчитываем строки и получаем новую таблицу. Процедуру повторяем до оптимальности.
4-шаг: Итоговое решение
По результатам симплекс-итераций получаем:
x₁ = 20 (количество продукта A)
x₂ = 10 (количество продукта B)
Прибыль:
Z = 50×20 + 60×10 = 1000 + 600 = 1600
Итог:
Продукт A: 20 ед.
Продукт B: 10 ед.
Максимальная прибыль: 1600 тг.

9. Симплекс-метод в Python

• from scipy.optimize import linprog
• c = [-50, -60] # коэффициенты (со знаком минус для
максимизации)
• A = [[3, 4], [2, 3]]
• b = [120, 100]
• res = linprog(c, A_ub=A, b_ub=b, bounds=(0, None),
method='simplex')
• print('Продукт A:', res.x[0])
• print('Продукт B:', res.x[1])
• print('Максимальная прибыль:', -res.fun)

10. Транспортная задача

Задача: Доставка товара со складов в магазины.
Склад 1: 150 ед.
Склад 2: 200 ед.
Магазин 1: 100 ед.
Магазин 2: 250 ед.
Затраты:
Склад 1 → Магазин 1: 5 тг
Склад 1 → Магазин 2: 6 тг
Склад 2 → Магазин 1: 4 тг
Склад 2 → Магазин 2: 3 тг
Цель: минимизировать затраты на транспортировку.

11. Транспортная задача

• Математическая модель:
Z = 5x1 + 6x2 + 4x3 + 3x4
• Ограничения:
• Склад 1: x1 + x2 = 150
• Склад 2: x3 + x4 = 200
• Магазин 1: x1 + x3 = 100
• Магазин 2: x2 + x4 = 250
• xi ≥ 0
• Решение (симплекс):
x1 = 100, x2 = 50, x3 = 0, x4 = 200
Минимальные затраты: Z = 1400

12.

Шаг 1. Математическая модель
Переменные:
x₁ — количество груза со Склада 1 в Магазин 1.
x₂ — количество груза со Склада 1 в Магазин 2.
x₃ — количество груза со Склада 2 в Магазин 1.
x₄ — количество груза со Склада 2 в Магазин 2.
Целевая функция (минимизация затрат):
Z = 5·x₁ + 6·x₂ + 4·x₃ + 3·x₄
Ограничения:
По отгрузке со Склада 1:
x₁ + x₂ = 150
По отгрузке со Склада 2:
x₃ + x₄ = 200
По спросу Магазина 1:
x₁ + x₃ = 100
По спросу Магазина 2:
x₂ + x₄ = 250
Неотрицательность:
x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0, x₄ ≥ 0.

13.

• Шаг 2. Подготовка к симплекс-методу
• Для применения симплекс-метода
необходимо преобразовать все ограничения в
равенства. Для этого вводятся
дополнительные переменные (переменные
запаса): s₁, s₂, s₃ и s₄.
• Ограничения в стандартной форме:
• Для Склада 1: x₁ + x₂ + s₁ = 150
• Для Склада 2: x₃ + x₄ + s₂ = 200
• Для Магазина 1: x₁ + x₃ + s₃ = 100
• Для Магазина 2: x₂ + x₄ + s₄ = 250
• Новая целевая функция:
Z = 5x₁ + 6x₂ + 4x₃ + 3x₄

14.

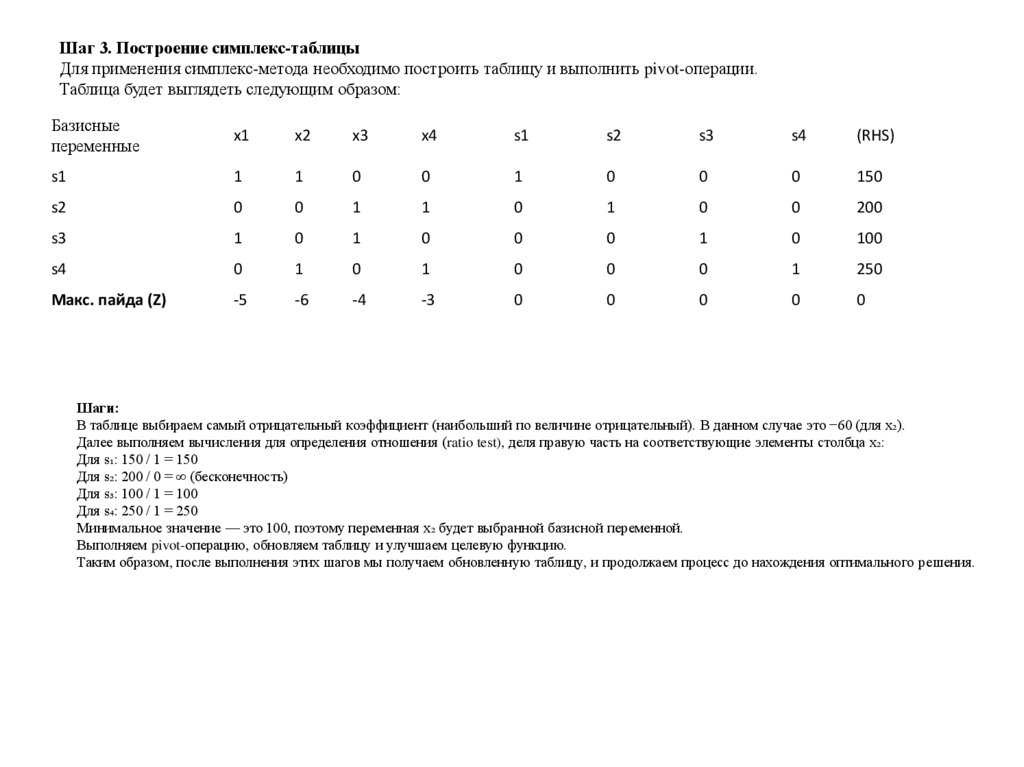
Шаг 3. Построение симплекс-таблицы
Для применения симплекс-метода необходимо построить таблицу и выполнить pivot-операции.
Таблица будет выглядеть следующим образом:
Базисные
переменные
x1
x2​
x3​
x4
s1
s2​
s3​
s4​
(RHS)
s1
1
1
0
0
1
0
0
0
150
s2
0
0
1
1
0
1
0
0
200
s3
1
0
1
0
0
0
1
0
100
s4
0
1
0
1
0
0
0
1
250
Макс. пайда (Z)
-5
-6
-4
-3
0
0
0
0
0
Шаги:
В таблице выбираем самый отрицательный коэффициент (наибольший по величине отрицательный). В данном случае это −60 (для x₂).
Далее выполняем вычисления для определения отношения (ratio test), деля правую часть на соответствующие элементы столбца x₂:
Для s₁: 150 / 1 = 150
Для s₂: 200 / 0 = ∞ (бесконечность)
Для s₃: 100 / 1 = 100
Для s₄: 250 / 1 = 250
Минимальное значение — это 100, поэтому переменная x₂ будет выбранной базисной переменной.
Выполняем pivot-операцию, обновляем таблицу и улучшаем целевую функцию.
Таким образом, после выполнения этих шагов мы получаем обновленную таблицу, и продолжаем процесс до нахождения оптимального решения.

15.

• Шаг 4. Новая таблица и результаты
• После выполнения симплекс-метода получаем следующие
результаты:
• x₁ = 100 (количество товара от Склада 1 в Магазин 1)
• x₂ = 50 (количество товара от Склада 1 в Магазин 2)
• x₃ = 0 (количество товара от Склада 2 в Магазин 1)
• x₄ = 200 (количество товара от Склада 2 в Магазин 2)
• Минимальные затраты:
Z = 5 × 100 + 6 × 50 + 4 × 0 + 3 × 200 = 500 + 300 + 600 = 1400
• Итог:
• От Склада 1 в Магазин 1 — 100 единиц товара.
• От Склада 1 в Магазин 2 — 50 единиц товара.
• От Склада 2 в Магазин 2 — 200 единиц товара.
• Минимальные затраты — 1400 тг.
• Это решение полностью удовлетворяет ресурсы складов и
спрос магазинов, минимизируя затраты на транспортировку.

16. Задания

Задача 1: Производственный план
Условие:
Компания выпускает два типа продукции: A и B.
Продукт A: требует 2 часа работы и 3 единицы материала, прибыль 60 тг.
Продукт B: требует 4 часа работы и 2 единицы материала, прибыль 80 тг.
Ресурсы компании:
120 часов работы.
100 единиц материала.
Цель: Определите, сколько единиц продукции нужно произвести, чтобы
максимизировать прибыль.
Математическая модель:
Целевая функция: Z = 60x₁ + 80x₂
Ограничения:
– 2x₁ + 4x₂ ≤ 120 (ограничение по времени работы)
– 3x₁ + 2x₂ ≤ 100 (ограничение по материалам)
– x₁, x₂ ≥ 0

17.

Задача 2: Транспортировка товара
Условие:
Компания должна транспортировать товар с двух складов на два магазина.
Склад 1: 150 единиц товара.
Склад 2: 200 единиц товара.
Магазин 1: требует 100 единиц товара.
Магазин 2: требует 250 единиц товара.
Затраты на транспортировку:
Склад 1 → Магазин 1: 4 тг.
Склад 1 → Магазин 2: 5 тг.
Склад 2 → Магазин 1: 6 тг.
Склад 2 → Магазин 2: 3 тг.
Цель: Минимизировать затраты на транспортировку.
Математическая модель:
Целевая функция: Z = 4x₁ + 5x₂ + 6x₃ + 3x₄
Ограничения:
–
–
–
–
–
x₁ + x₂ = 150 (ограничение по товару с Склад 1)
x₃ + x₄ = 200 (ограничение по товару с Склад 2)
x₁ + x₃ = 100 (ограничение по спросу Магазина 1)
x₂ + x₄ = 250 (ограничение по спросу Магазина 2)
x₁, x₂, x₃, x₄ ≥ 0

18.

• Задача 3: Распределение бюджета
• Условие:
Компания имеет бюджет 500 тыс. тг и хочет
инвестировать его в два проекта.
• Проект 1: инвестиции составляют 150 тыс. тг,
ожидаемая прибыль 300 тыс. тг.
• Проект 2: инвестиции составляют 200 тыс. тг,
ожидаемая прибыль 400 тыс. тг.
• Цель: Определить, сколько средств следует вложить в
каждый проект, чтобы максимизировать прибыль, не
превышая общий бюджет.
• Математическая модель:
• Целевая функция: Z = 300x₁ + 400x₂
• Ограничения:
– 150x₁ + 200x₂ ≤ 500 (ограничение по бюджету)
– x₁, x₂ ≥ 0

19.

• Задача 4: Планирование работы
• Условие:
Компания имеет два типа работы: установка оборудования и
обслуживание клиентов.
• Установка оборудования: требует 3 часа работы, прибыль 100
тг.
• Обслуживание клиентов: требует 2 часа работы, прибыль 80 тг.
• Ресурсы компании:
• 120 часов работы на проекте.
• Цель: Определить, сколько единиц работы каждого типа нужно
выполнить, чтобы максимизировать прибыль.
• Математическая модель:
• Целевая функция: Z = 100x₁ + 80x₂
• Ограничения:
– 3x₁ + 2x₂ ≤ 120 (ограничение по времени)
– x₁, x₂ ≥ 0

20.

Задача 5: Оптимизация транспортных затрат
Условие:
Компания должна организовать транспортировку товара между двумя
складами и двумя магазинами.
Склад 1: 100 единиц товара.
Склад 2: 150 единиц товара.
Магазин 1: требует 120 единиц товара.
Магазин 2: требует 130 единиц товара.
Затраты на транспортировку:
Склад 1 → Магазин 1: 6 тг.
Склад 1 → Магазин 2: 7 тг.
Склад 2 → Магазин 1: 8 тг.
Склад 2 → Магазин 2: 5 тг.
Цель: Минимизировать общие затраты на транспортировку.
Математическая модель:
Целевая функция: Z = 6x₁ + 7x₂ + 8x₃ + 5x₄
Ограничения:
–
–
–
–
–
x₁ + x₂ = 100 (ограничение по товару с Склад 1)
x₃ + x₄ = 150 (ограничение по товару с Склад 2)
x₁ + x₃ = 120 (ограничение по спросу Магазина 1)
x₂ + x₄ = 130 (ограничение по спросу Магазина 2)
x₁, x₂, x₃, x₄ ≥ 0