Похожие презентации:
سری 1[4351706]
1. دانشگاه آزاد اسلامی واحد شهرری دانشکده مهندسی برق
تهیه و تنظیم:علی جاللی فراهانی ،حامد حاجی علی اکبری ،امیرحسین احمدوند ،مجتبی کونانی ،حسن محمدی اقدم
دیماه 91
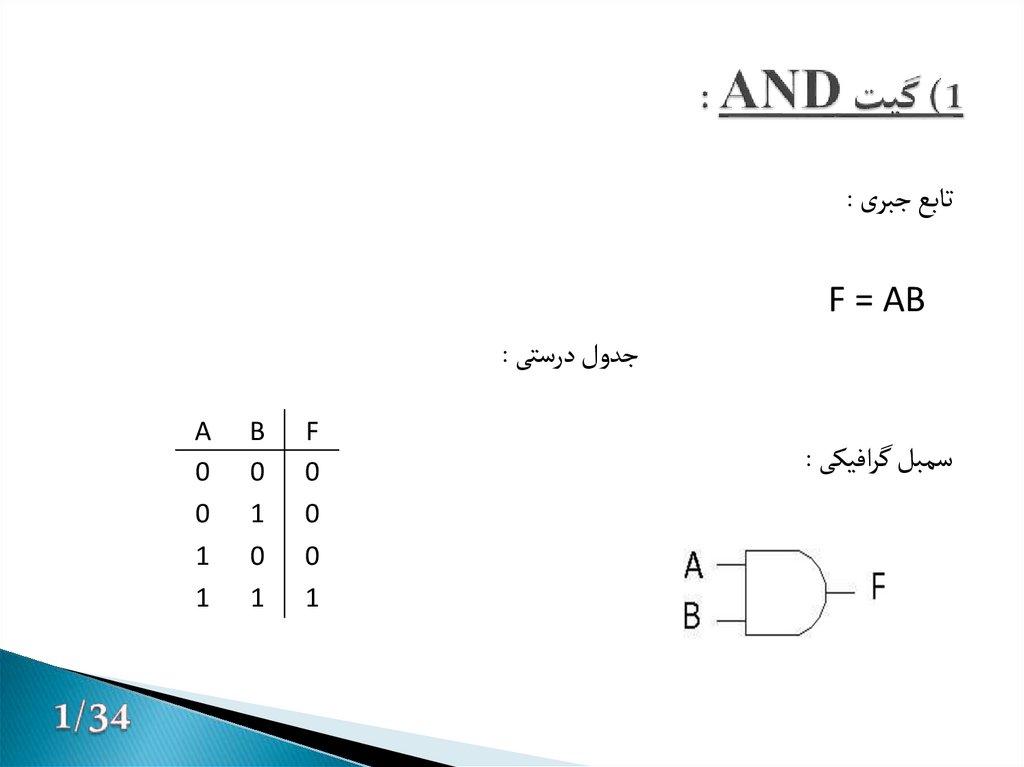
2. 1) گیت AND :
تابع جبری :F = AB
جدول درستی :
سمبل گرافیکی :
F
0
0
0
1
B
0
1
0
1
A
0
0
1
1
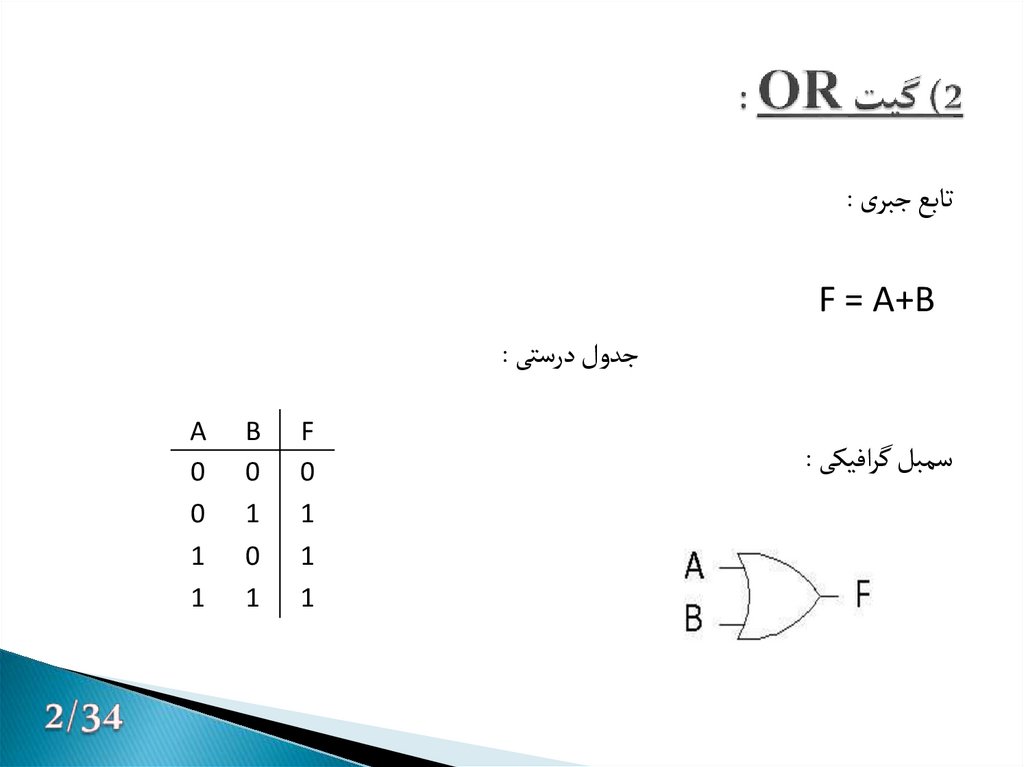
3. 2) گیت OR :
تابع جبری :F = A+B
جدول درستی :
سمبل گرافیکی :
F
0
1
1
1
B
0
1
0
1
A
0
0
1
1
4. 3) گیت NOT:
تابع جبری :´F = A
جدول درستی :
سمبل گرافیکی :
F
1
0
A
0
1
5. 4) گیت Buffer:
تابع جبری :F=A
جدول درستی :
سمبل گرافیکی :
F
0
1
A
0
1
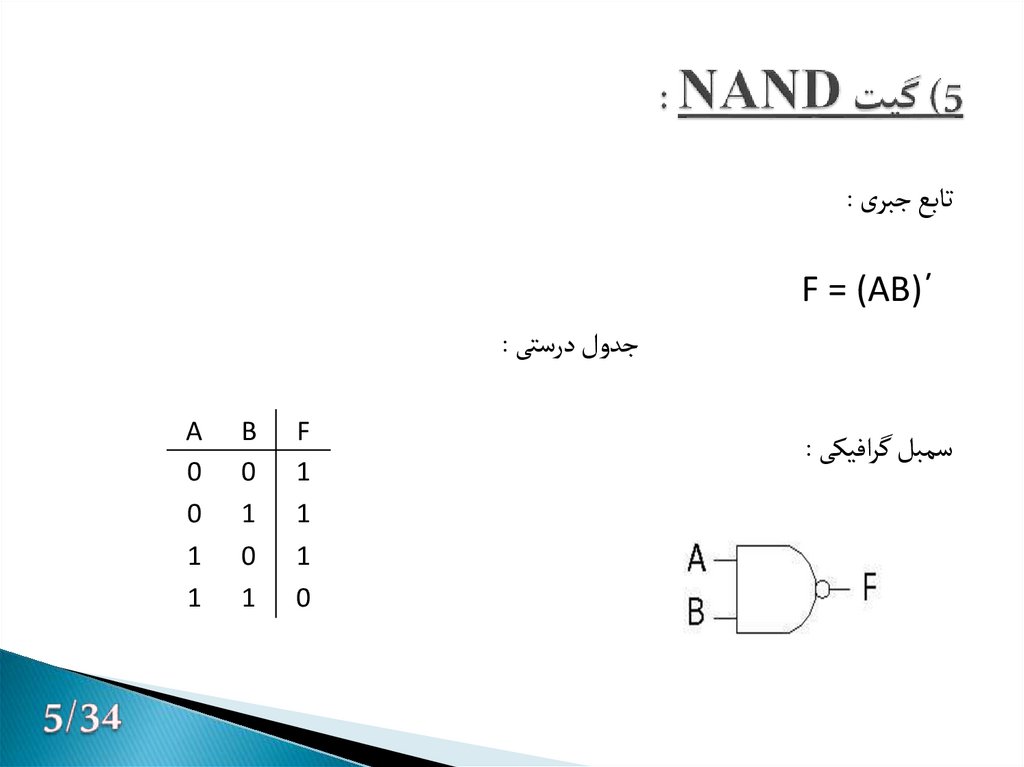
6. 5) گیت NAND :
تابع جبری :´)F = (AB
جدول درستی :
سمبل گرافیکی :
F
1
1
1
0
B
0
1
0
1
A
0
0
1
1
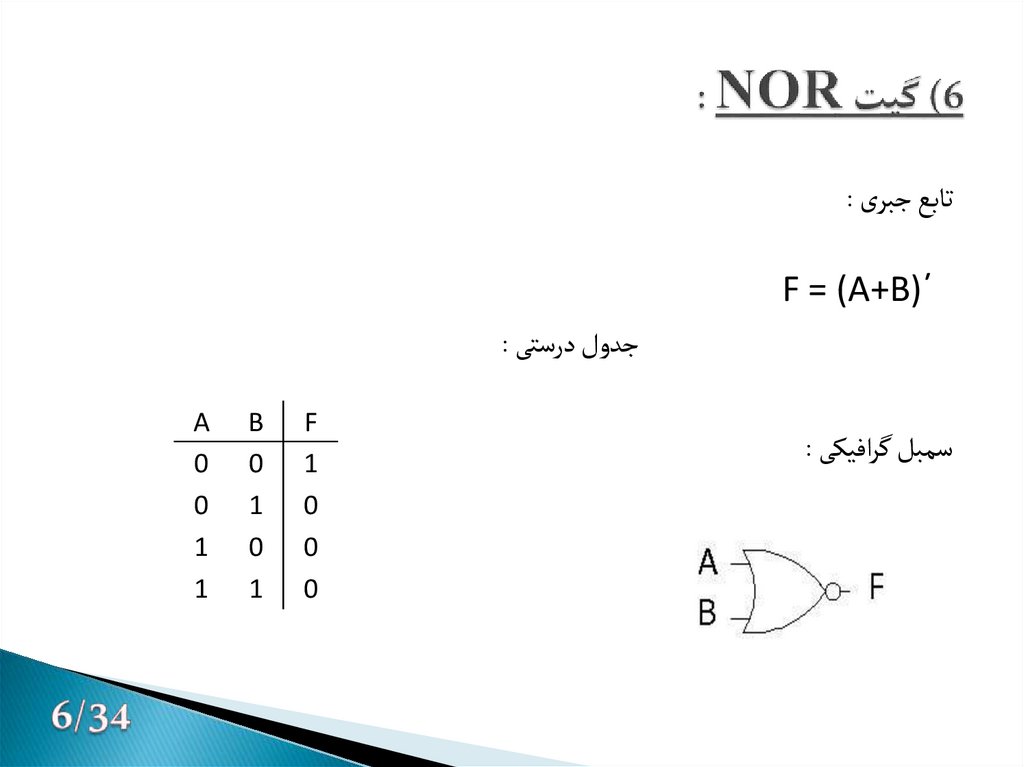
7. 6) گیت NOR :
تابع جبری :´)F = (A+B
جدول درستی :
سمبل گرافیکی :
F
1
0
0
0
B
0
1
0
1
A
0
0
1
1
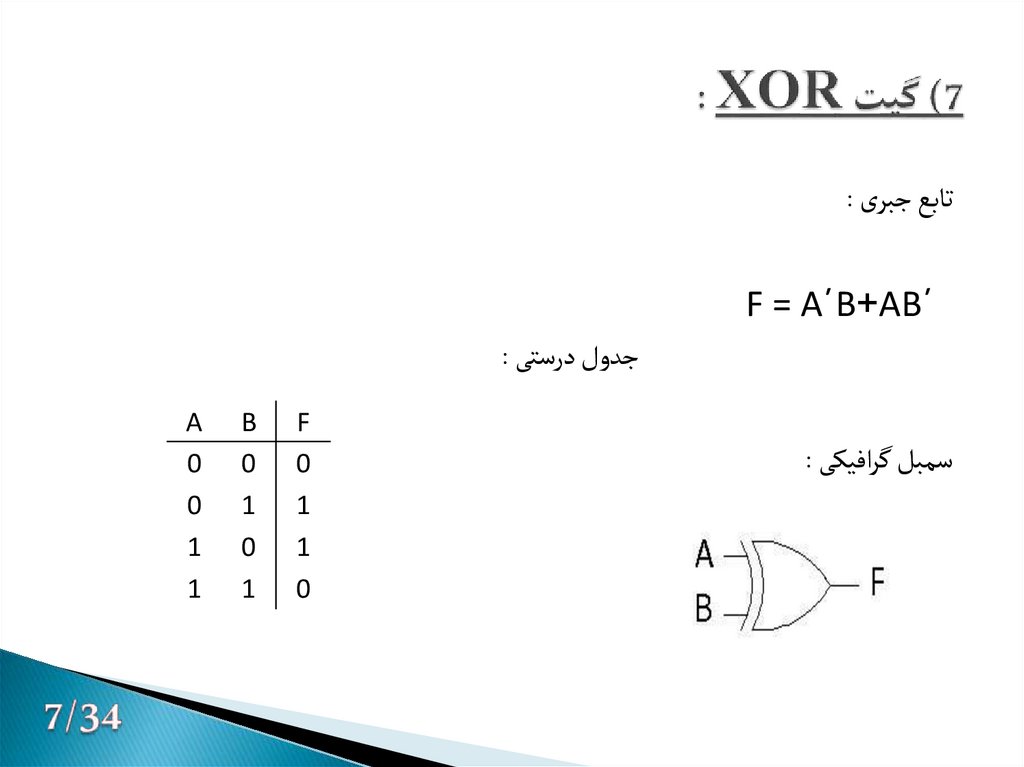
8. 7) گیت XOR :
تابع جبری :´F = A´B+AB
جدول درستی :
سمبل گرافیکی :
F
0
1
1
0
B
0
1
0
1
A
0
0
1
1
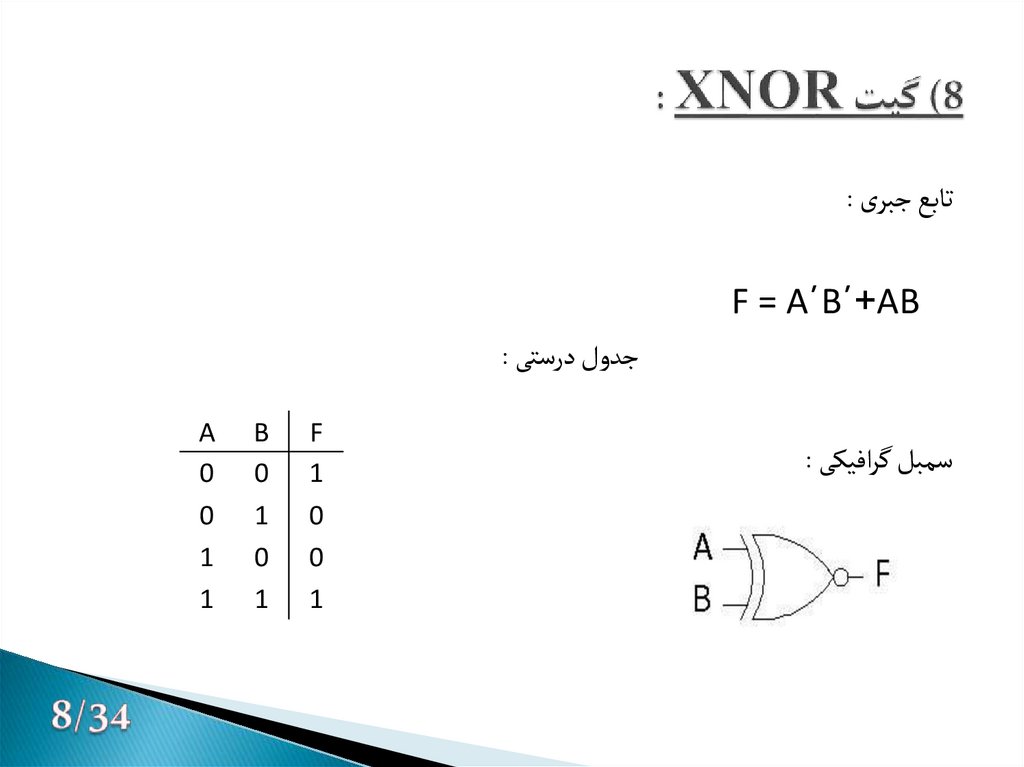
9. 8) گیت XNOR :
تابع جبری :F = A´B´+AB
جدول درستی :
سمبل گرافیکی :
F
1
0
0
1
B
0
1
0
1
A
0
0
1
1
10. انواع مدارهای منطقی:
)1مدار ترکیبی :حافظه ندارد. )2مدار ترتیبی :حافظه دارد.
مدار ترکیبی به مدارهای ی گ فته میشود که خروجی در هر لحظه به ورودی در همان لحظه وابسته است.اما در
مدارهای ترتیبی خروجی هر لحظه وابسته به لحظه قبل است.
: Half Adder
به مدار ترکیبی که جمع حسابی دو بیت را انجام دهد نیم جمع کننده گ فته میشود .برای ترسیم مدار داخلی نیم جمع
کننده جدول تغییرات ان را رسم کرده و سپس ارقام sو cمربوط به جمع دو بیت را محاسبه میکنیم
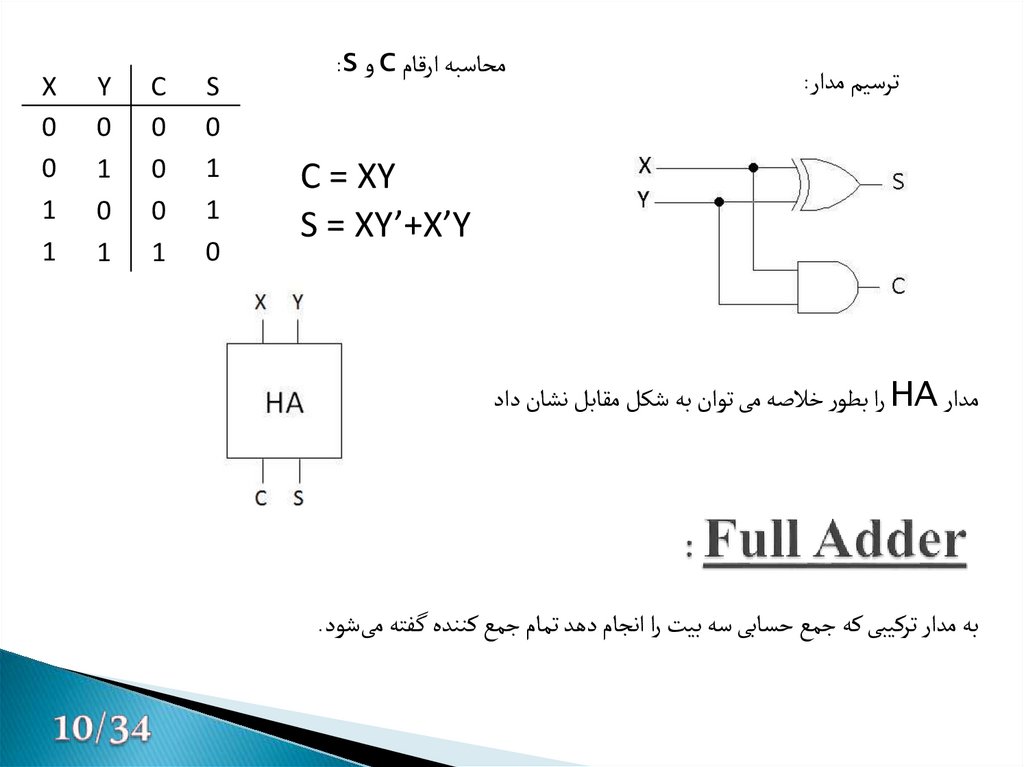
11. Full Adder :
ترسیم مدار:محاسبه ارقام cو :s
C = XY
S = XY’+X’Y
مدار HAرا بطور خالصه می توان به شکل مقابل نشان داد
به مدار ترکیبی که جمع حسابی سه بیت را انجام دهد تمام جمع کننده گ فته میشود.
S
0
1
1
0
C
0
0
0
1
Y
0
1
0
1
X
0
0
1
1
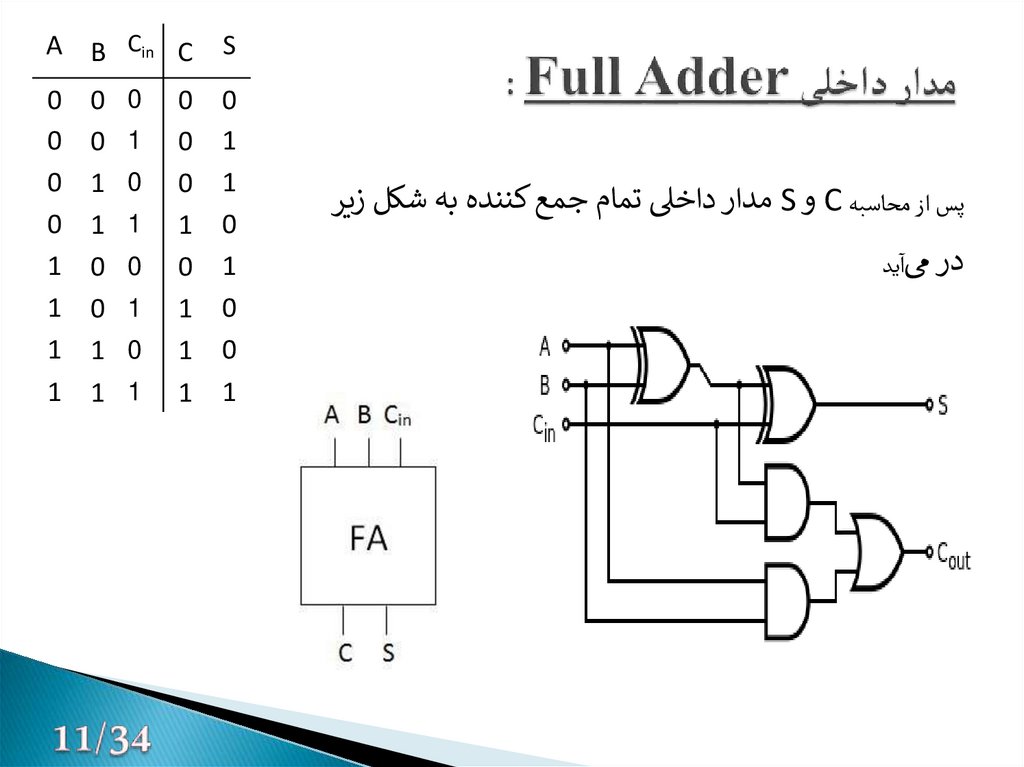
12. مدار داخلی Full Adder :
پس از محاسبه Cو Sمدار داخیل تمام جمع کننده به شکل زیردر یماید
S
A B Cin C
0
1
1
0
1
0
0
1
0
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
0
1
0
1
0
1
0
1
0
0
1
1
0
0
1
1
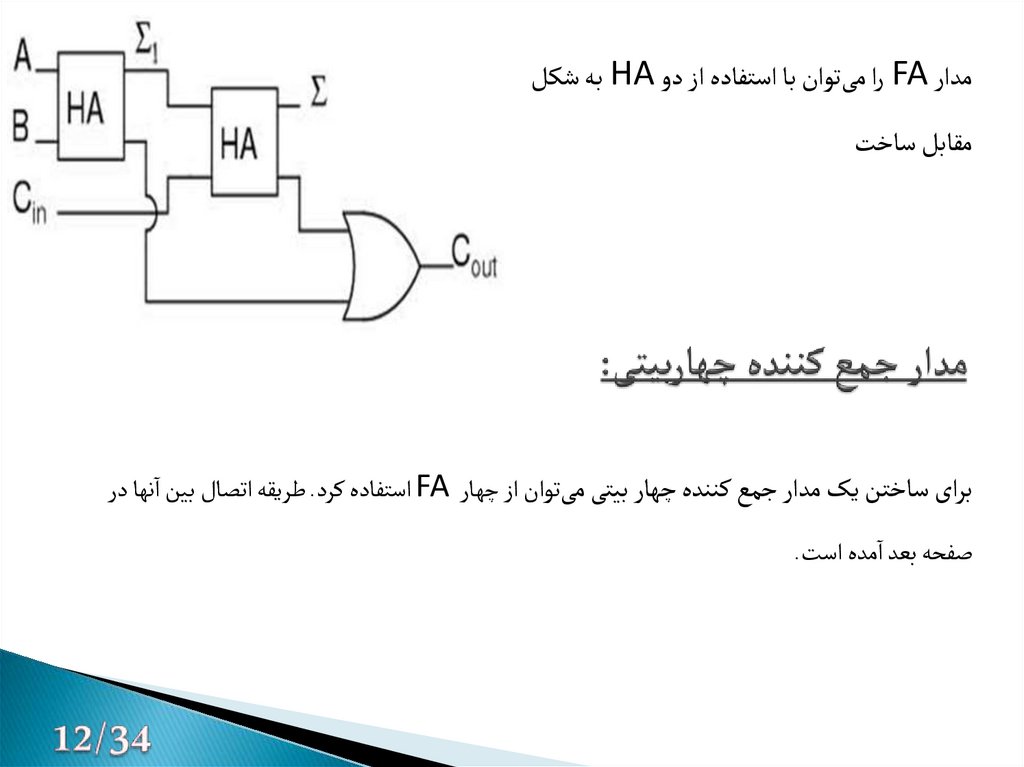
13. مدار جمع کننده چهاربیتی:
مدار FAرا میتوان با استفاده از دو HAبه شکلمقابل ساخت
برای ساختن یک مدار جمع کننده چهار بیتی میتوان از چهار FAاستفاده کرد .طریقه اتصال بین انها در
صفحه بعد امده است.
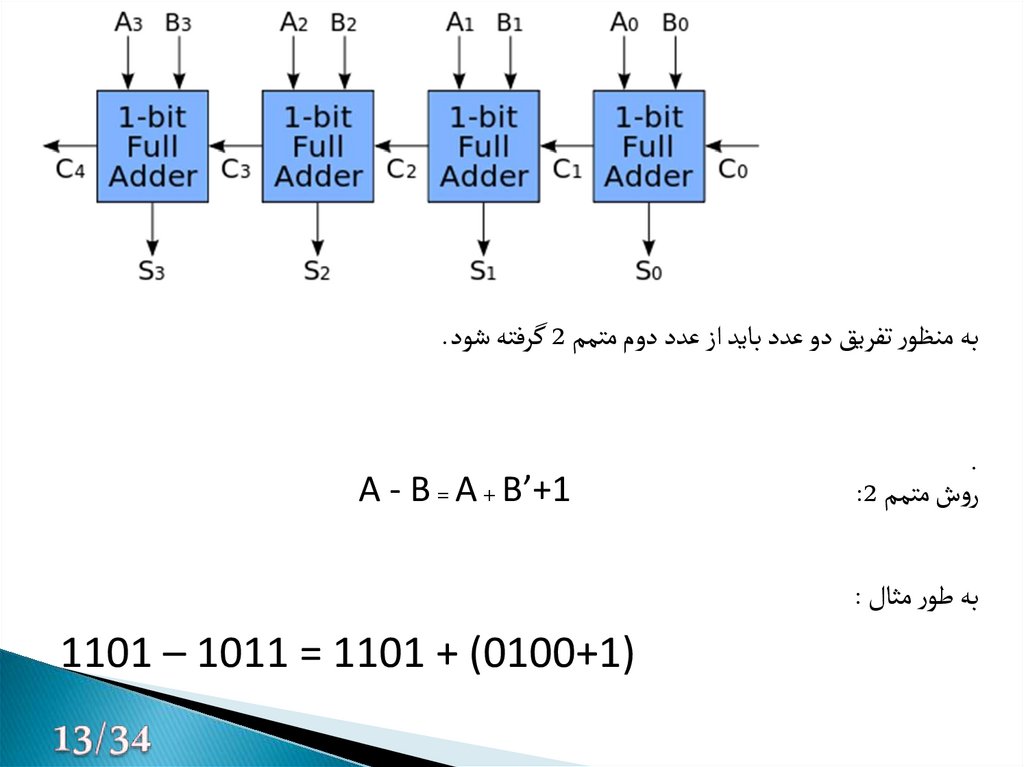
14.
به منظور تفریق دو عدد باید از عدد دوم متمم 2گرفته شود..
روش متمم :2
A - B = A + B’+1
به طور مثال :
)1101 – 1011 = 1101 + (0100+1
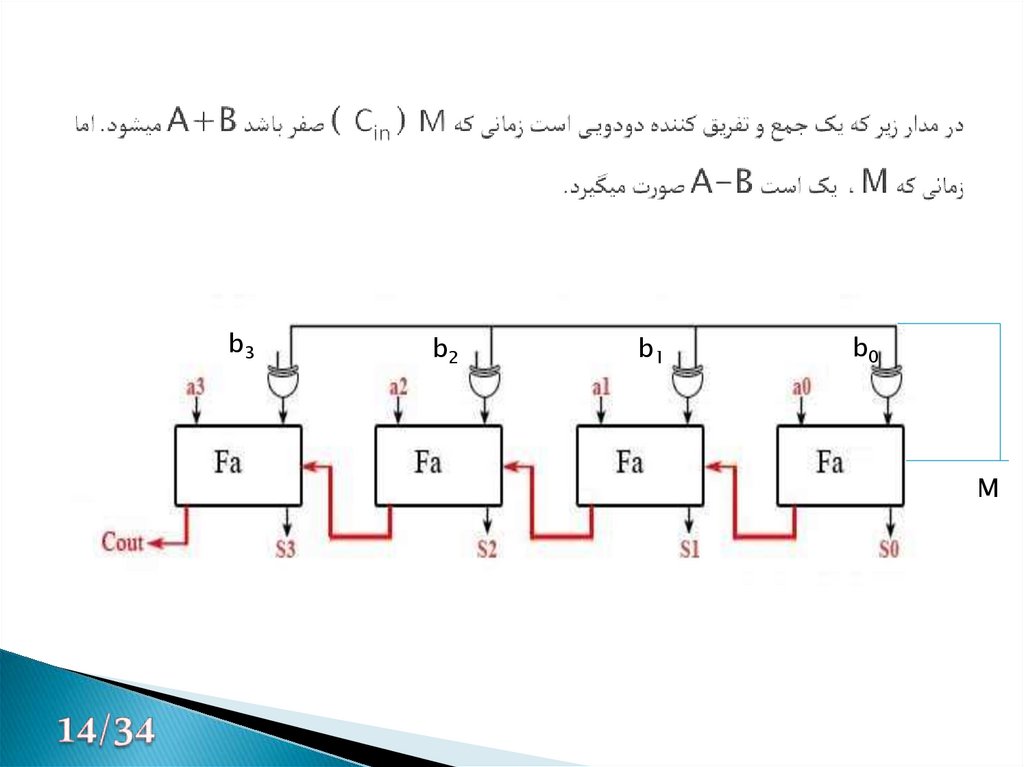
15. در مدار زیر که یک جمع و تفریق کننده دودویی است زمانی که ) M Cin ( صفر باشد A+B میشود. اما زمانی که M ، یک است A-B صورت میگیرد.
b3b2
b1
b0
M
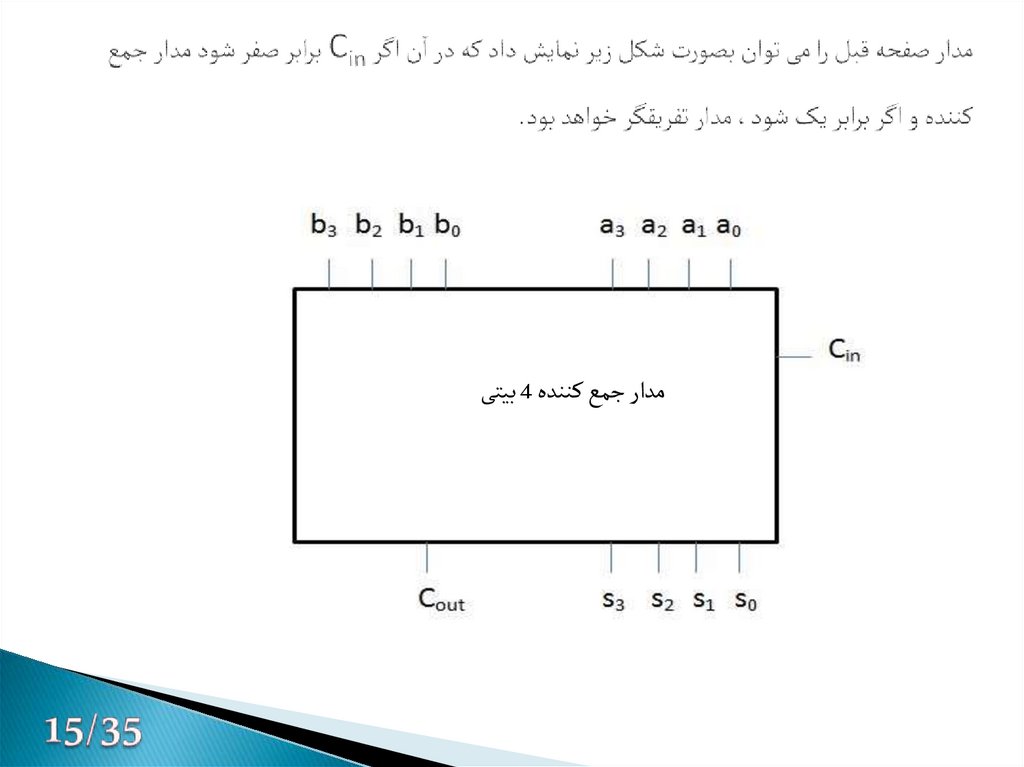
16. مدار صفحه قبل را می توان بصورت شکل زیر نمایش داد که در آن اگر Cin برابر صفر شود مدار جمع کننده و اگر برابر یک شود، مدار تفریقگر
مدار جمع کننده 4بیتی17. ساده سازی با جدول کارنو :
سریعترین و راحتترین راه برای ساده سازی توابع بولی دو ،سه و چهار متغیره استفاده از جدول کارنو است.بدین صورت که مقدار خروجی (که بصورت 0و 1است) در جدول قرار میگیرد .نقشه جدول کارنو برای توابع دو
،سه و چهار متغیره به همراه محل قرار گرفتن خروجیها به شکل زیر میباشد:
18.
* دو روش به منظور ساده سازی در جدول کارنو وجود دارد: -1استفاده از جمع حاصلضربها (مینترمها) :در این روش ان خانههای ی از جدول که با 1پر شده اند به
دستههای 4 ، 2 ، 1و بیشتر تقسیم میشوند (دستههای با ظرفیت باالتر در اولویت هستند) .سپس هر دسته به
صورت ضربی از متغیرهای ی که در ستونش قرار گرفته نوشته شده و در پایان عبارات مربوط به هر دسته با هم جمع
میشوند.
-2استفاده از ضرب حاصلجمعها (ماکسترمها) :این روش نیز همانند روش 1است ،با این تفاوت که دستهبندی
برای خانههای ی انجام میشود که با 0پر شدهاند .در پایان چون عبارات بدست امده متمم خروجی است ،یکبار ان
را Notکرده تا خروجی مورد نظر بصورت ضرب حاصلجمعها بدست اید.
19.
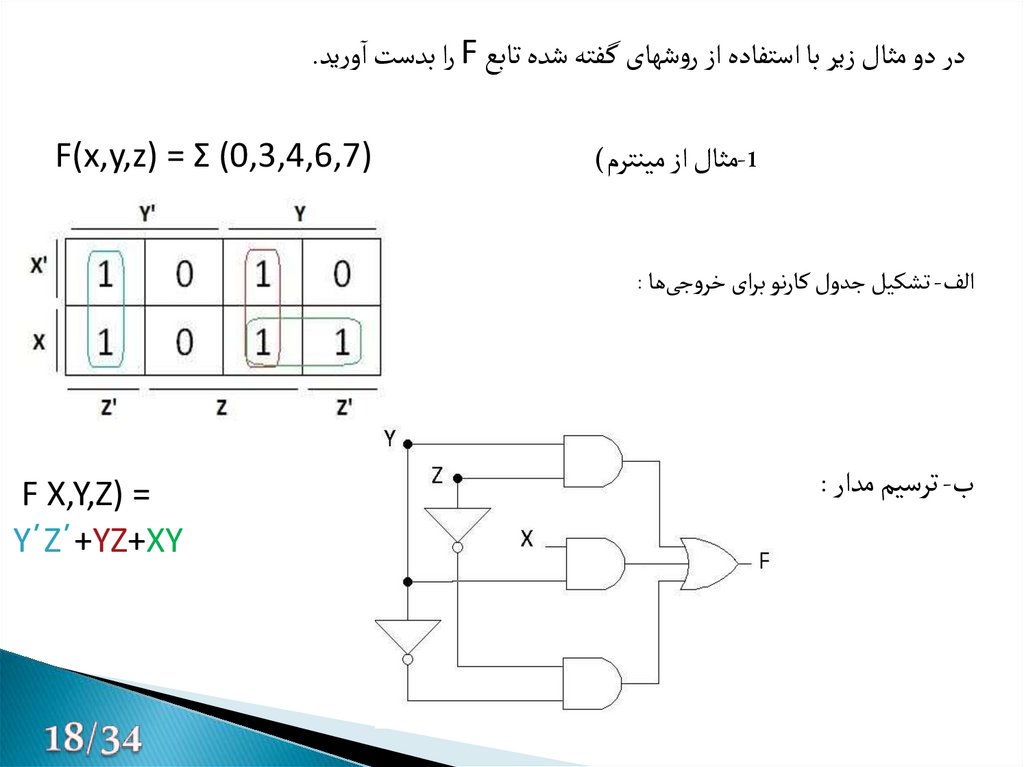
در دو مثال زیر با استفاده از روشهای گ فته شده تابع Fرا بدست اورید.-1مثال از مینترم)
)F(x,y,z) = Σ (0,3,4,6,7
الف -تشکیل جدول کارنو برای خروجیها :
ب -ترسیم مدار :
= )F X,Y,Z
Y´Z´+YZ+XY
20.
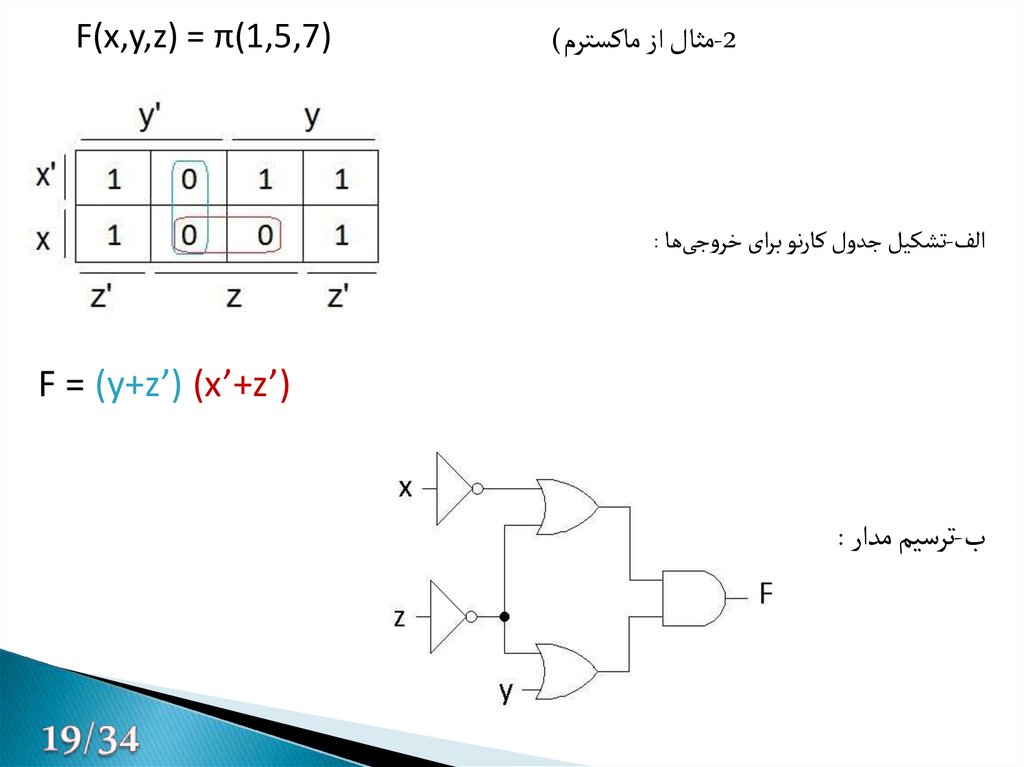
-2مثال از ماکسترم))F(x,y,z) = π(1,5,7
الف-تشکیل جدول کارنو برای خروجیها :
)’F = (y+z’) (x’+z
ب-ترسیم مدار :
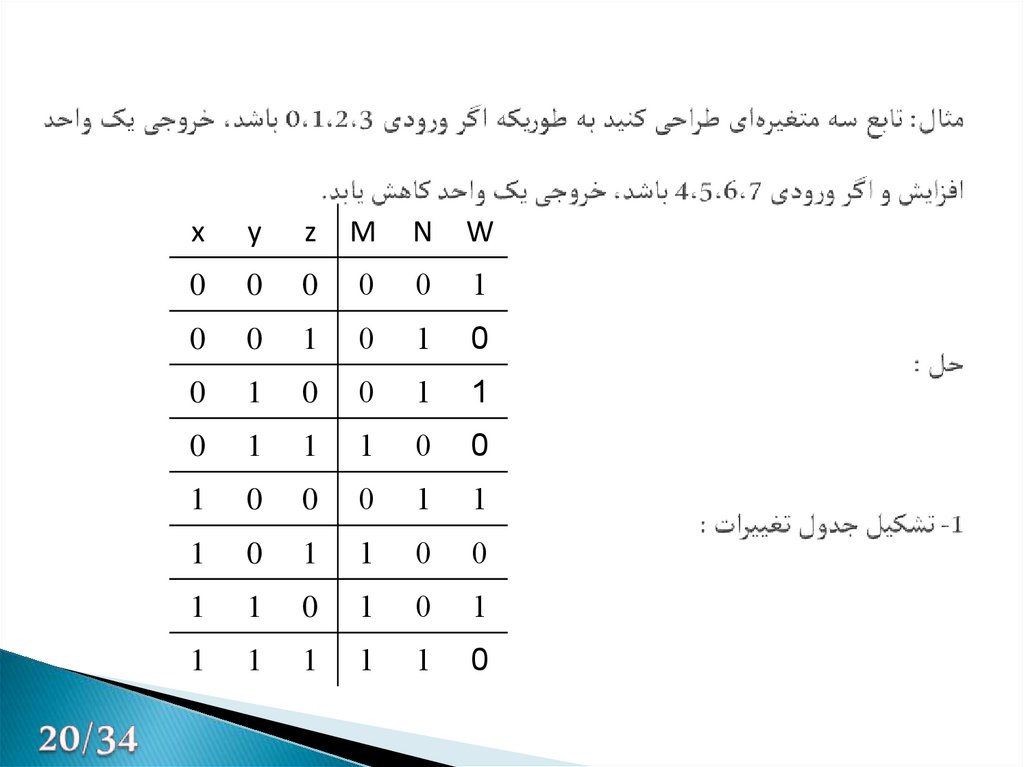
21. مثال: تابع سه متغیرهای طراحی کنید به طوریکه اگر ورودی 0،1،2،3 باشد، خروجی یک واحد افزایش و اگر ورودی 4،5،6،7 باشد، خروجی یک
xy
z
M
N
W
0
0
0
0
0
1
0
0
1
0
1
0
0
1
0
0
1
1
0
1
1
1
0
0
1
0
0
0
1
1
1
0
1
1
0
0
1
1
0
1
0
1
1
1
1
1
1
0
22.
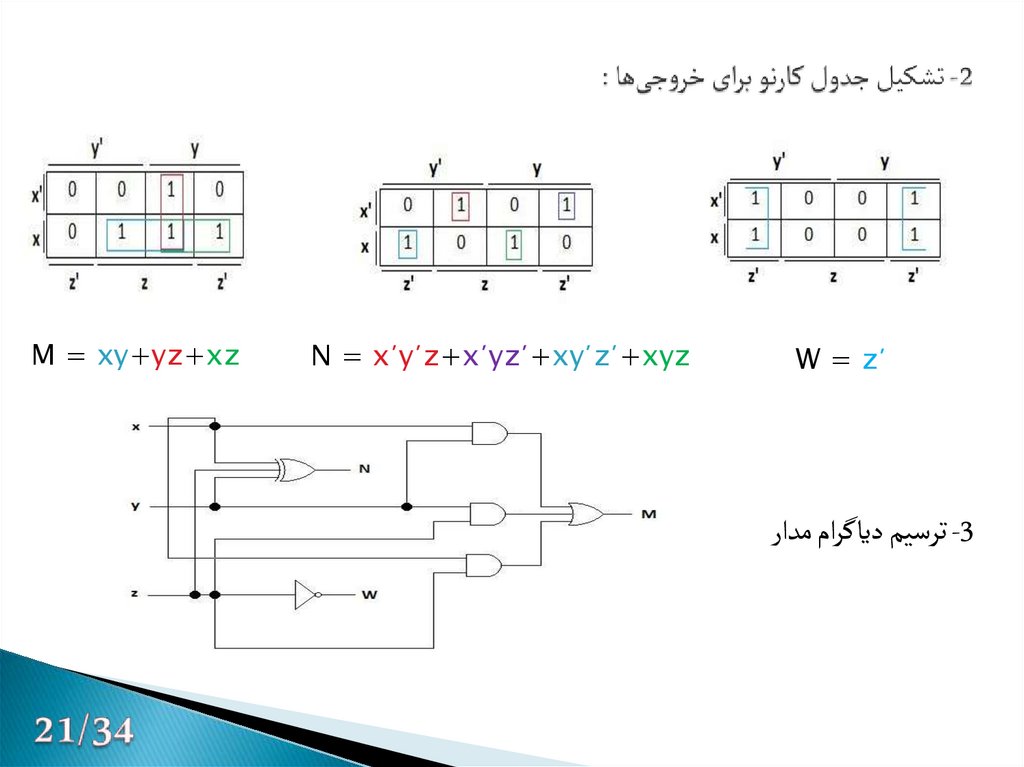
M = xy+yz+xzN = x´y´z+x´yz´+xy´z´+xyz
W = z´
ترسیم دیاگرام مدار-3
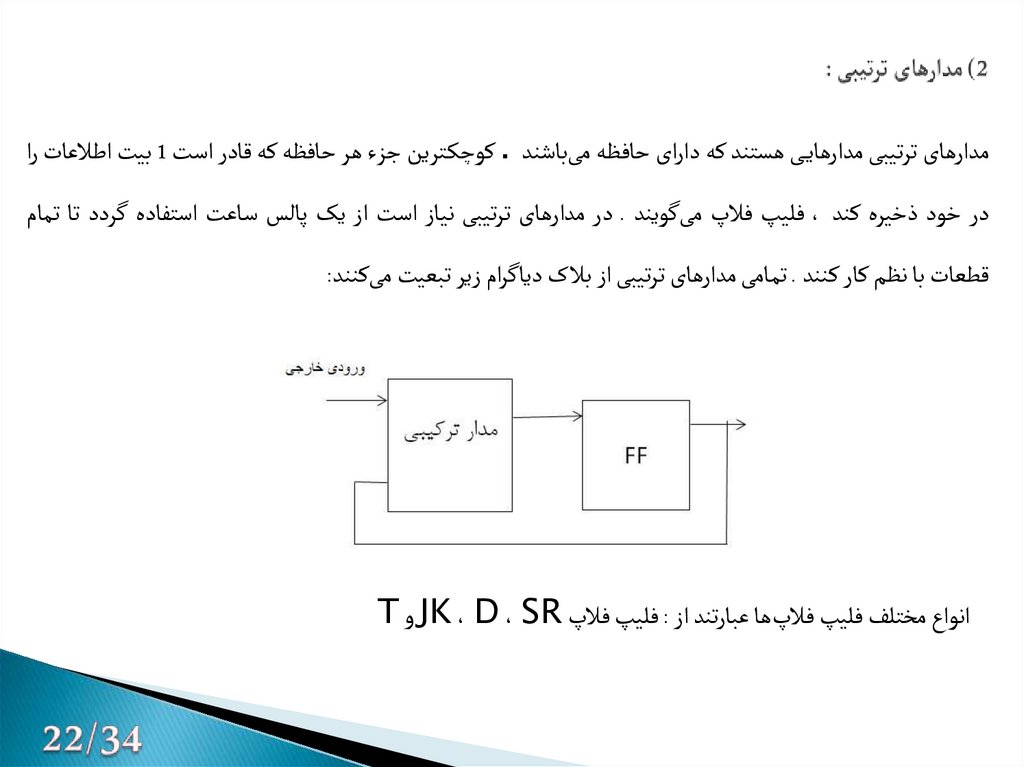
23. 2) مدارهای ترتیبی :
مدارهای ترتیبی مدارهای ی هستند که دارای حافظه میباشند .کوچک ترین جزء هر حافظه که قادر است 1بیت اطالعات رادر خود ذخیره کند ،فلیپ فالپ میگویند .در مدارهای ترتیبی نیاز است از یک پالس ساعت استفاده گردد تا تمام
قطعات با نظم کار کنند .تمامی مدارهای ترتیبی از بالک دیاگرام زیر تبعیت میکنند:
انواع مختلف فلیپ فالپها عبارتند از :فلیپ فالپ JK ، D ، SRو T
24.
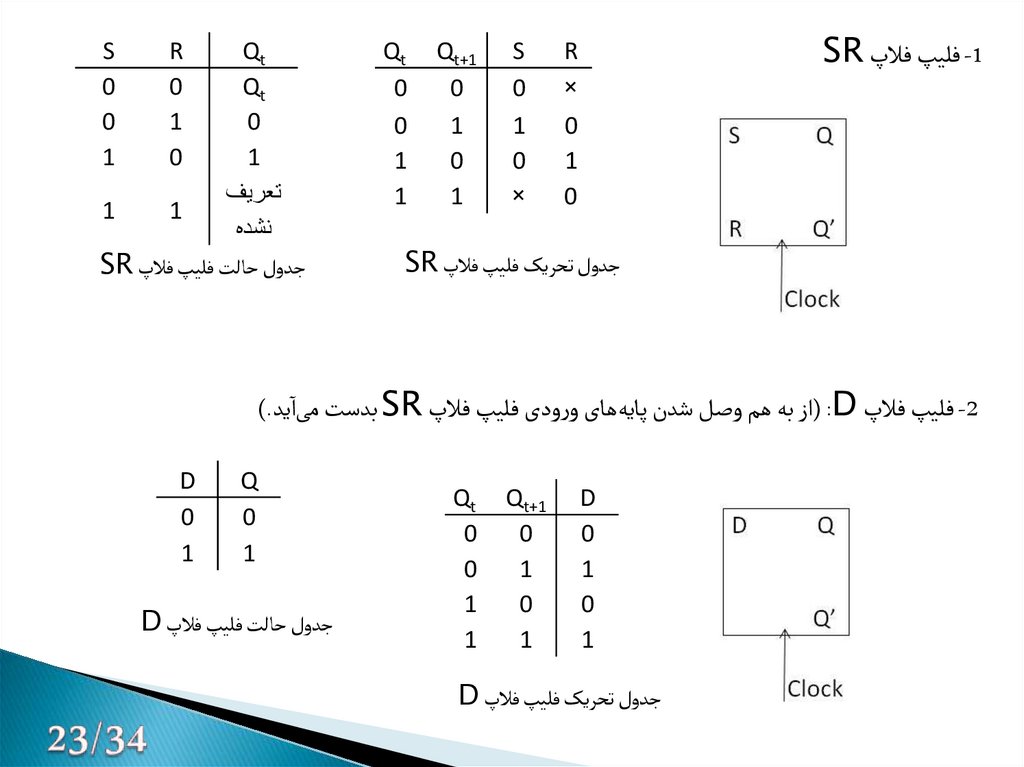
-1فلیپ فالپ SRR
×
0
1
0
S
0
1
0
×
Qt+1
0
1
0
1
Qt
0
0
1
1
جدول تحریک فلیپ فالپ SR
Qt
Qt
0
1
تعریف
نشده
R
0
1
0
S
0
0
1
1
1
جدول حالت فلیپ فالپ SR
-2فلیپ فالپ ( :Dاز به هم وصل شدن پایههای ورودی فلیپ فالپ SRبدست میاید).
D
0
1
0
1
Qt+1
0
1
0
1
Qt
0
0
1
1
جدول تحریک فلیپ فالپ D
Q
0
1
D
0
1
جدول حالت فلیپ فالپ D
25.
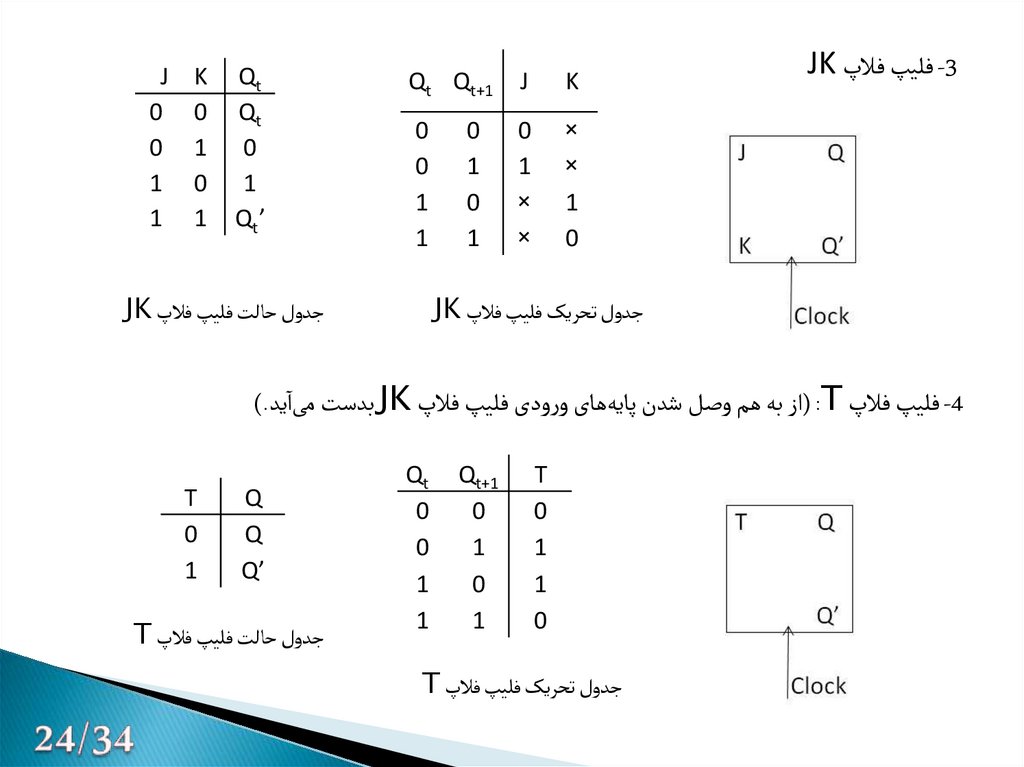
-3فلیپ فالپ JKK
J
Qt Qt+1
×
×
1
0
0
1
×
×
0
0
1
1
0
1
0
1
جدول تحریک فلیپ فالپ JK
Qt
Qt
0
1
’ Qt
J K
0 0
0 1
1 0
1 1
جدول حالت فلیپ فالپ JK
-4فلیپ فالپ ( :Tاز به هم وصل شدن پایههای ورودی فلیپ فالپ JKبدست میاید).
T
0
1
1
0
Qt+1
0
1
0
1
Qt
0
0
1
1
جدول تحریک فلیپ فالپ T
Q
Q
’Q
T
0
1
جدول حالت فلیپ فالپ T
26. * به طور کلی برای طراحی مدارهای ترتیبی باید مراحل زیر را طی نمود:
-1رسم دیاگرام حالت به صورت اشکال خط و دایره که هر حالت را با یک دایره و مسیر حرکت را از یک حالت به حالتدیگر نمایش میدهد.
-2رسم جدول تحریک .
-3رسم جداول کارنو و ساده سازی .
-4رسم مدار .
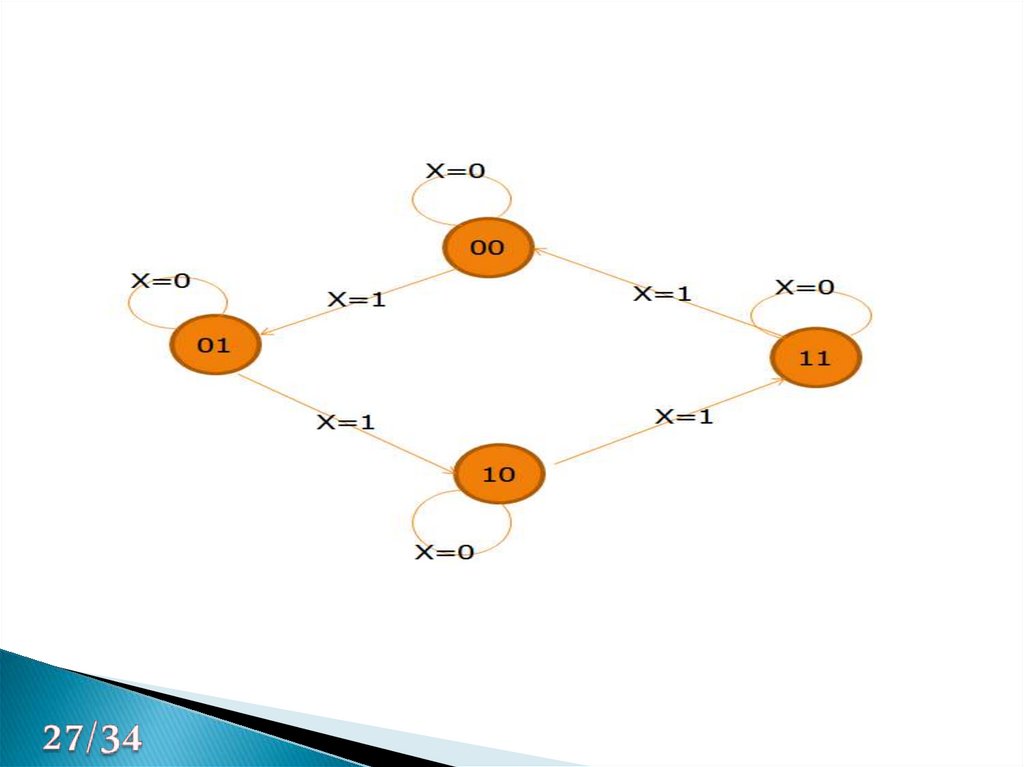
27.
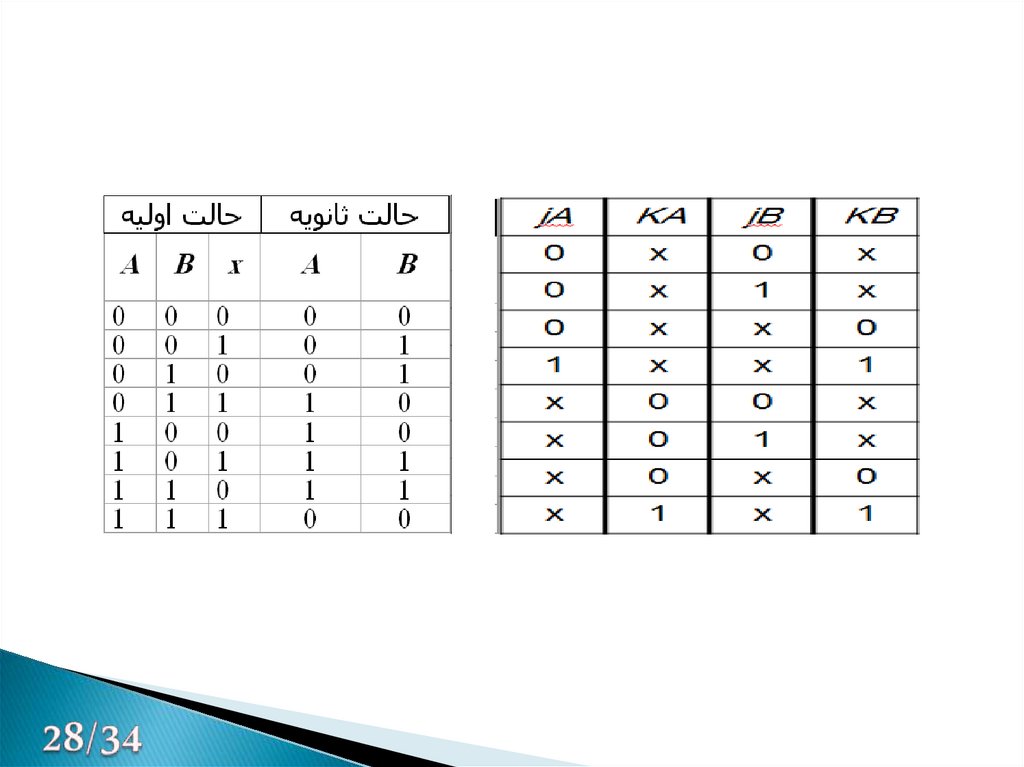
مداری طراحی نمایید که در صورتی که ورودی خارجی Xمساوی صفر است شمارشی صورتنگیرد و در زمانی که Xمساوی یک است رشته ی 00 11 10 01 00و تکرار ان را ادامه دهد.
28.
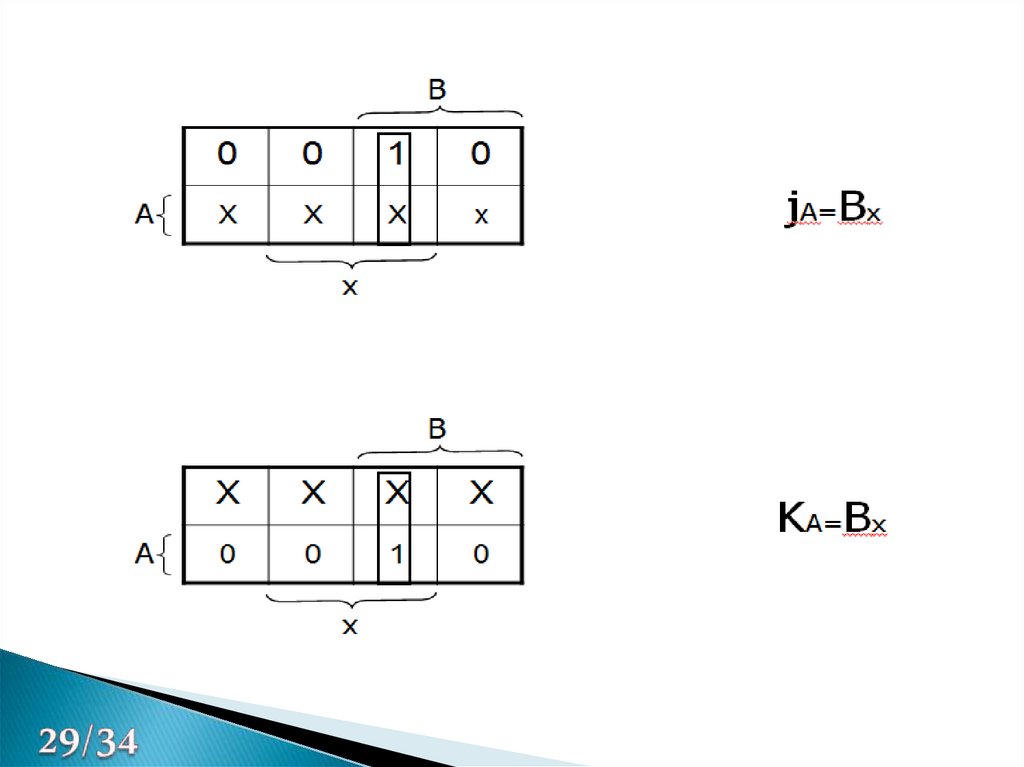
29.
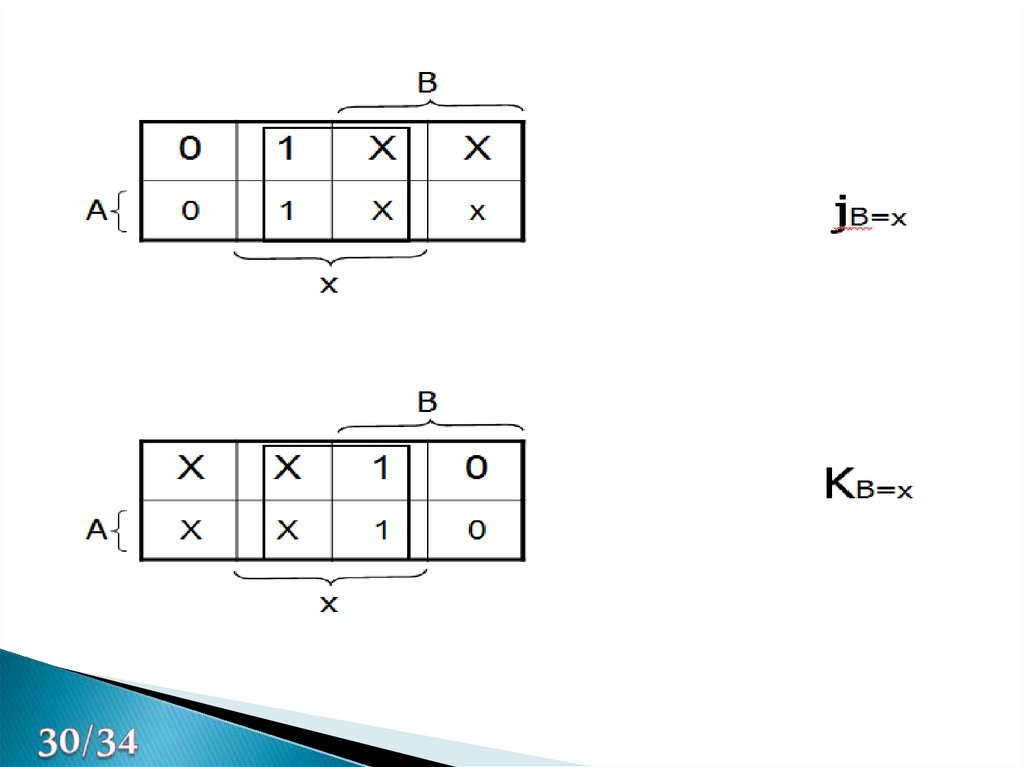
30.
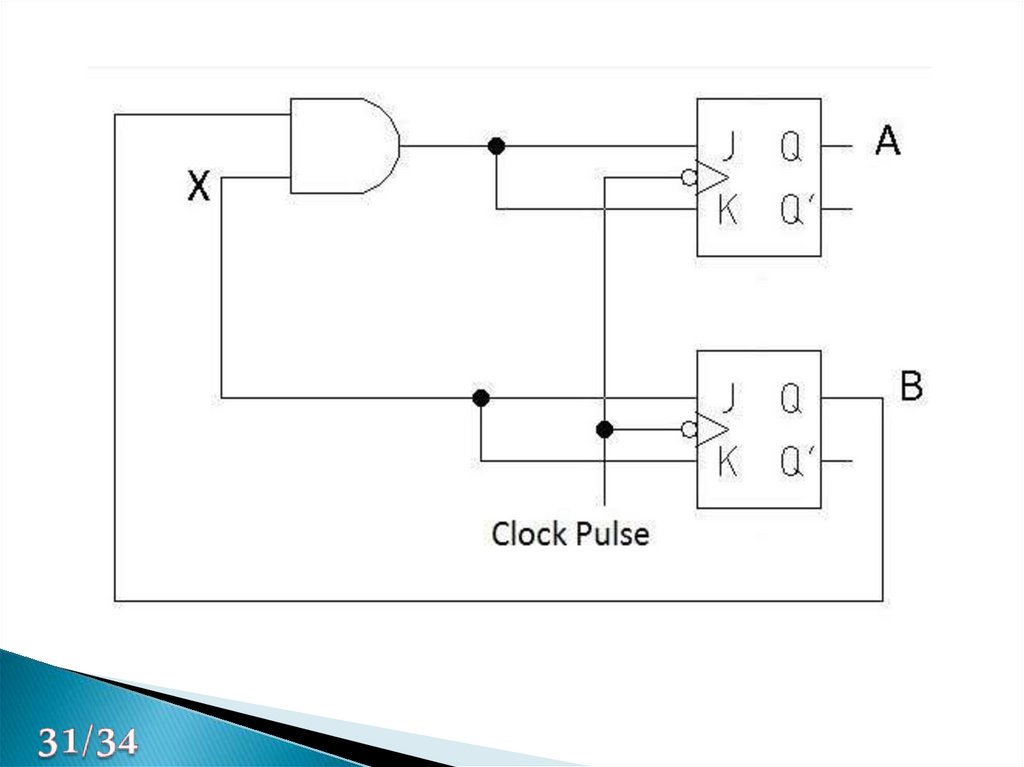
31.
32.
33.
تمرین :شمارنده 2بیتی طراحی کنید که دارای 2ورودی E , Xباشد زمانیکه Xیک است و Eصفر رشته 00 11 10 01 00و
تکراری از ان و زمانی که Xیک و Eیک می باشد رشته ی 11 00 01 10 11و تکرار ان و زمانی که Xصفر است در جای
خود باقی بماند .
34.
00000001
0010
0100
35.
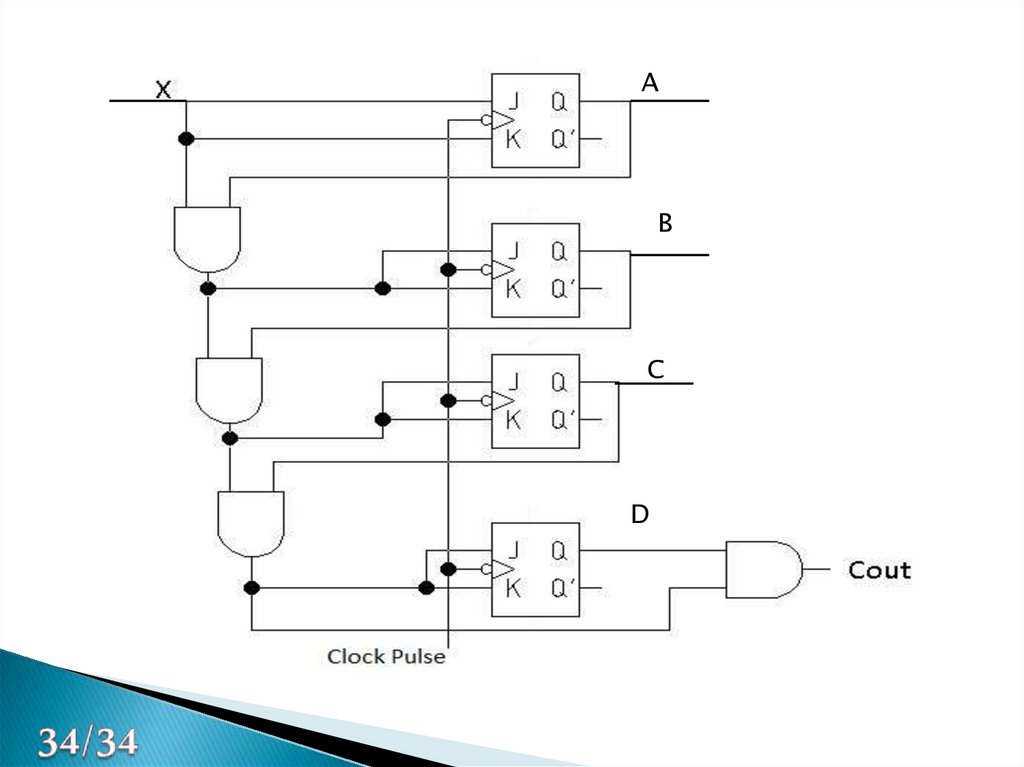
AB
C
D










 Математика
Математика








