Трапеция

1. Трапеция. Равнобокая и прямоугольная трапеции.

Подготовила:
учитель математики
МБОУ Г.ГОРЛОВКИ «ШКОЛА № 42
Рыбина М.В.

2. Определение

Четырёхугольник, две стороны которого параллельны, а две другие не
параллельны, называется трапецией. Параллельные стороны
называются основаниями трапеции, непараллельные стороны –
боковыми сторонами.
АВ CD, AB, CD- основания
AD, CB- боковые стороны

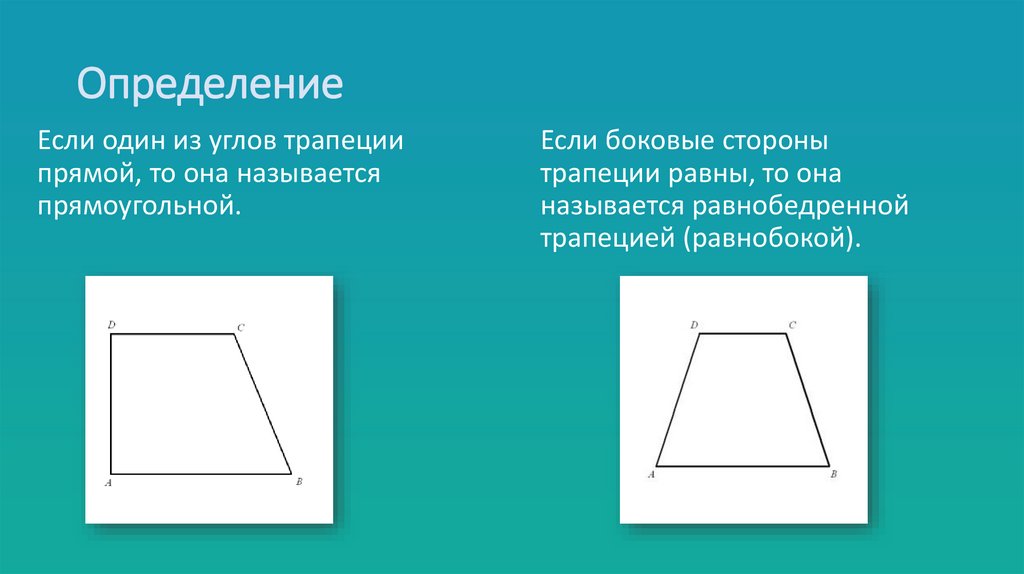
3. Определение

Если один из углов трапеции
прямой, то она называется
прямоугольной.
Если боковые стороны
трапеции равны, то она
называется равнобедренной
трапецией (равнобокой).

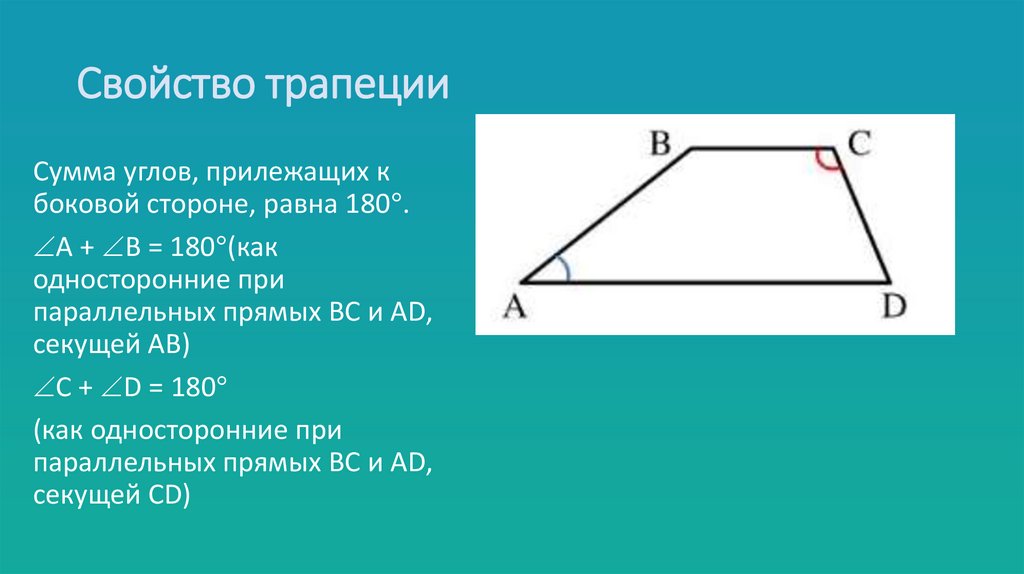
4. Свойство трапеции

Сумма углов, прилежащих к
боковой стороне, равна 180 .
А + В = 180 (как
односторонние при
параллельных прямых ВС и АD,
секущей АВ)
С + D = 180
(как односторонние при
параллельных прямых ВС и АD,
секущей CD)

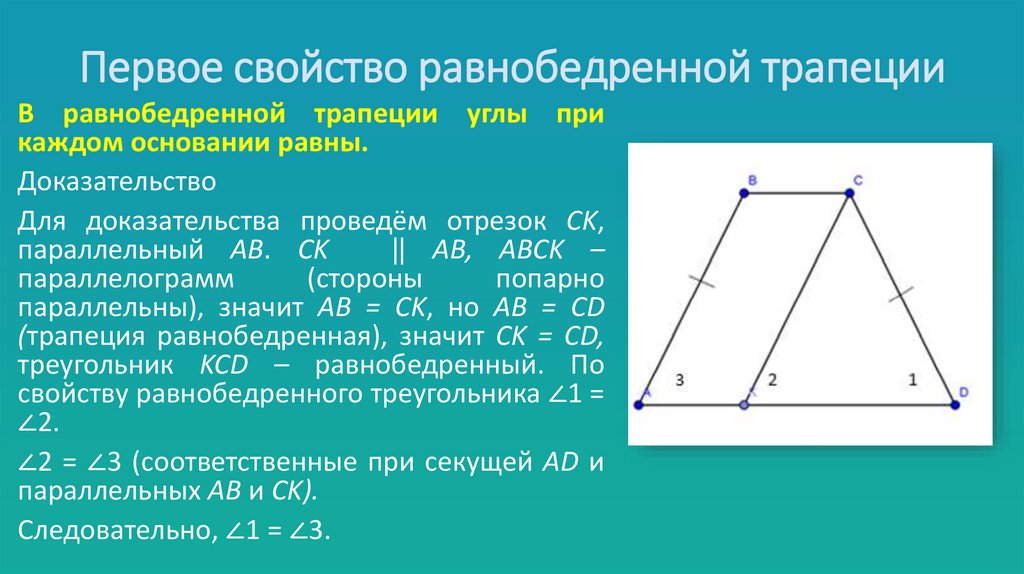
5. Первое свойство равнобедренной трапеции

В равнобедренной трапеции углы при
каждом основании равны.
Доказательство
Для доказательства проведём отрезок CK,
параллельный AB. CK
⃦ AB, ABCK –
параллелограмм
(стороны
попарно
параллельны), значит AB = CK, но AB = CD
(трапеция равнобедренная), значит CK = CD,
треугольник KCD – равнобедренный. По
свойству равнобедренного треугольника ∠1 =
∠2.
∠2 = ∠3 (соответственные при секущей AD и
параллельных AB и CK).
Следовательно, ∠1 = ∠3.

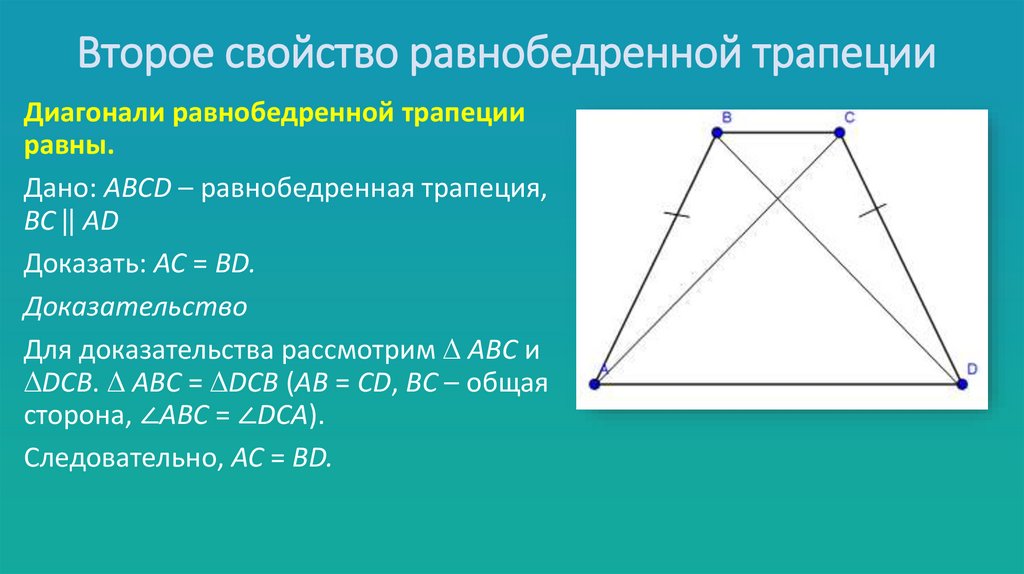
6. Второе свойство равнобедренной трапеции

Диагонали равнобедренной трапеции
равны.
Дано: ABCD – равнобедренная трапеция,
BC ⃦ AD
Доказать: AC = BD.
Доказательство
Для доказательства рассмотрим ABC и
DCB. ABC = DCB (AB = CD, BC – общая
сторона, ∠ABC = ∠DCA).
Следовательно, AC = BD.

7. Первый признак трапеции

Если углы при основании трапеции равны, то
трапеция является равнобедренной.
Дано: ABCD – трапеция, BC ⃦ AD
∠BAC = ∠CDA
Доказать: ABCD – равнобедренная трапеция
Доказательство:
Для доказательства проведем отрезок CK,
параллельный AB.
CK ⃦ AB, следовательно ABCK – параллелограмм,
тогда AB = CK, ∠A = ∠CKD.
Получится равнобедренный треугольник CKD (∠A
= ∠CKD и ∠A = ∠CDA), поэтому
CK = CD и AB = CK = CD. Следовательно, ABCD –
равнобедренная трапеция.

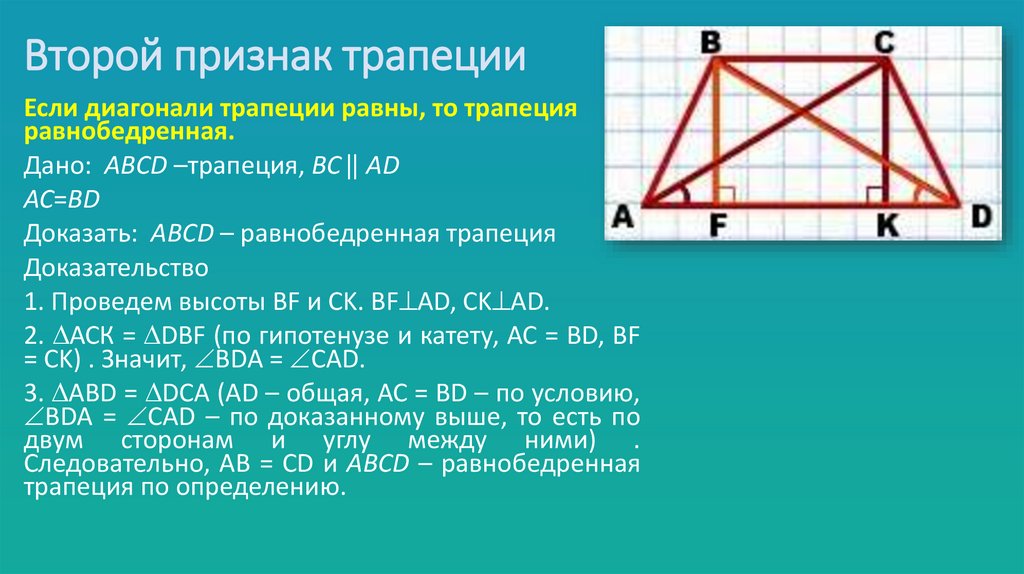
8. Второй признак трапеции

Если диагонали трапеции равны, то трапеция
равнобедренная.
Дано: ABCD –трапеция, BC ⃦ AD
AC=BD
Доказать: ABCD – равнобедренная трапеция
Доказательство
1. Проведем высоты BF и CK. BF AD, CK AD.
2. АСК = DBF (по гипотенузе и катету, АС = BD, BF
= CK) . Значит, BDA = CAD.
3. АBD = DCA (AD – общая, АС = BD – по условию,
BDA = CAD – по доказанному выше, то есть по
двум сторонам и углу между ними) .
Следовательно, AB = CD и ABCD – равнобедренная
трапеция по определению.

9. Проверь себя

10. Проверь себя

11. Проверь себя

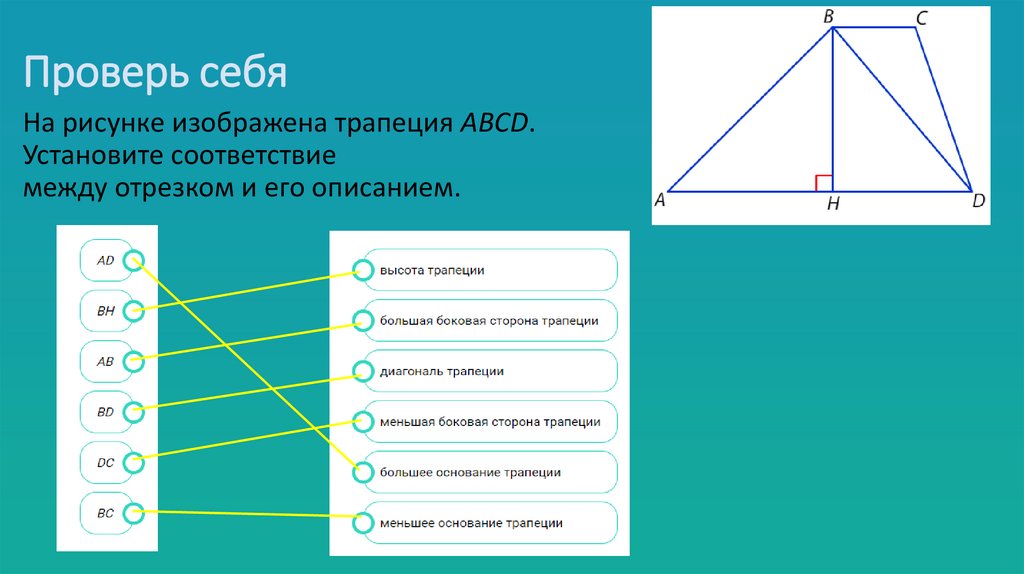
На рисунке изображена трапеция АВСD.
Установите соответствие
между отрезком и его описанием.

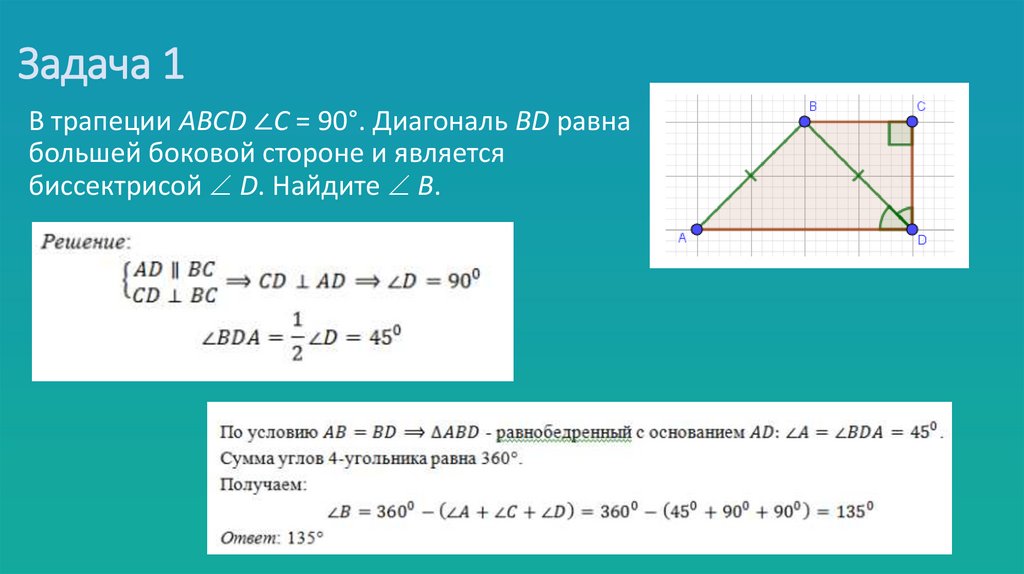
12. Задача 1

В трапеции АВСD ∠С = 90°. Диагональ BD равна
большей боковой стороне и является
биссектрисой D. Найдите B.

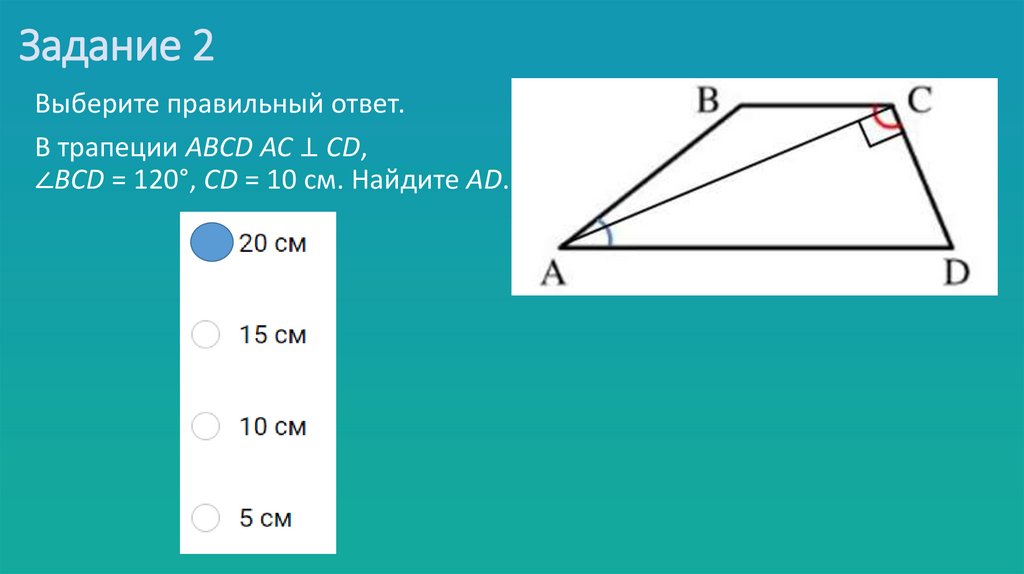
13. Задание 2

Выберите правильный ответ.
В трапеции АВСD AC ⊥ CD,
∠BCD = 120°, CD = 10 см. Найдите AD.

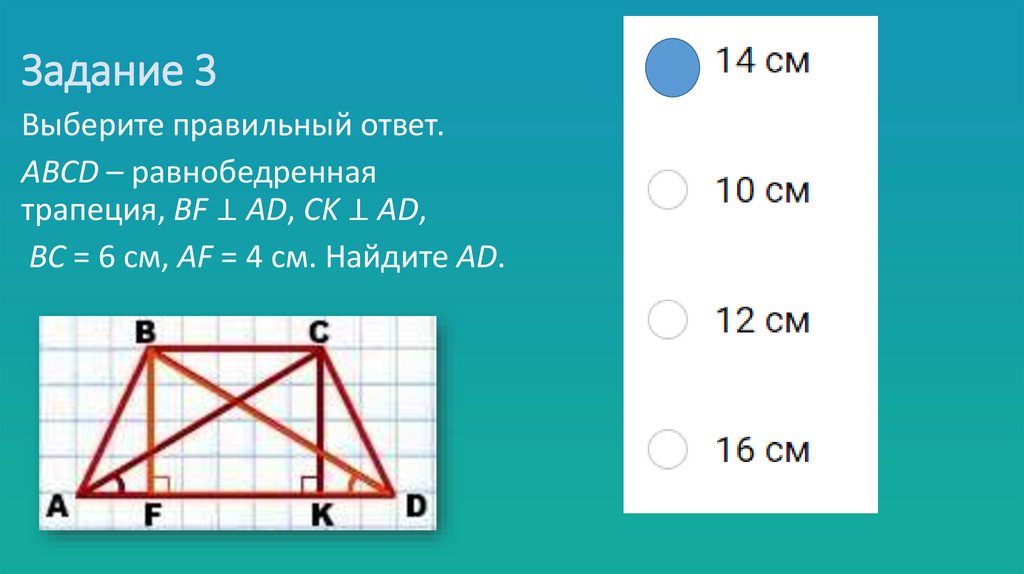
14. Задание 3

Выберите правильный ответ.
АВСD – равнобедренная
трапеция, ВF ⊥ AD, CK ⊥ AD,
ВС = 6 см, АF = 4 см. Найдите AD.

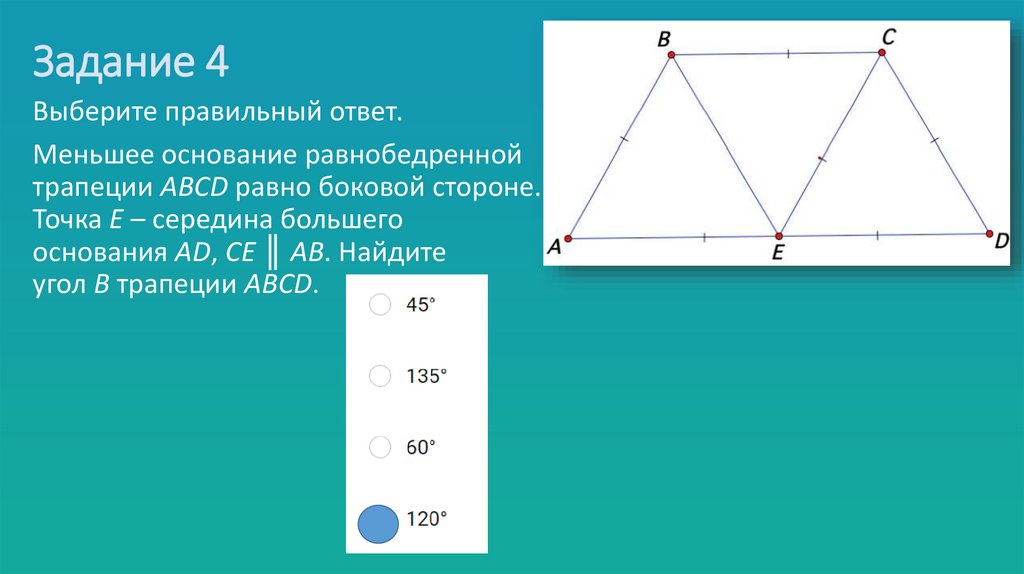
15. Задание 4

Выберите правильный ответ.
Меньшее основание равнобедренной
трапеции АВСD равно боковой стороне.
Точка E – середина большего
основания AD, CE ║ AB. Найдите
угол В трапеции АВСD.

16. Домашнее задание

Выучить правила § 2, п. 45
Выполнить в тетради № 387, 392 (а)

17. Использованные источники

• https://resh.edu.ru/subject/lesson/2009/conspect/

18. Скачано с www.znanio.ru