Похожие презентации:
Булевы функции
1.
БУЛЕВЫФУНКЦИИ
2. Введение
Постиндустриальное общество, в котором мы живем, постепеннопреобразуется в информационное. Напомню, что информационное
общество – это историческая фаза развития цивилизации, в которой
главными продуктами производства становятся информация и знания.
Огромное место в нашей жизни теперь занимает скорость получения
и обработки информации. Чрезвычайно важна ее актуальность. И на
фоне всего сказанного очень контрастирует тот факт, что решение
многих задач в обучении студенты вынуждены реализовывать «на
листочке». Хотя задачи являются алгоритмическими, легко
программируемыми, быстро решаемыми на современных ПК. На мой
взгляд обучаемый должен понять только принцип решения. Здесь
приводятся две программы, связанных с изучением булевых функций.
3. ДЖОРДЖ БУЛЬ (1815 – 1864)
Создателем алгебры логики является живший в ХIХ веке английский математикДжордж Буль, в честь которого эта алгебра названа булевой алгеброй
высказываний.
4.
Булевой алгебройАлгеброй Буля называется непустое множество A
с двумя бинарными операциями (конъюнкция, И),
(дизъюнкция, ИЛИ), унарной операцией (инверсия, НЕ) и двумя
выделенными элементами: 0 (или Ложь) и 1 (или Истина)
такими, что для всех a, b и c из множества A верны следующие
аксиомы:
ассоциативность
коммутативность
законы поглощения
дистрибутивность
дополнительность
5. Булевой функцией f(x1, x2, ... , xn) называется произвольная функция n переменных, аргументы которой x1, x2, ... , xn и сама
функция fпринимают значения 0 или 1
, т. е.
xi {0, 1}, i = 1, 2, ... , n; f (x1, x2, ... , xn)
{0, 1}.
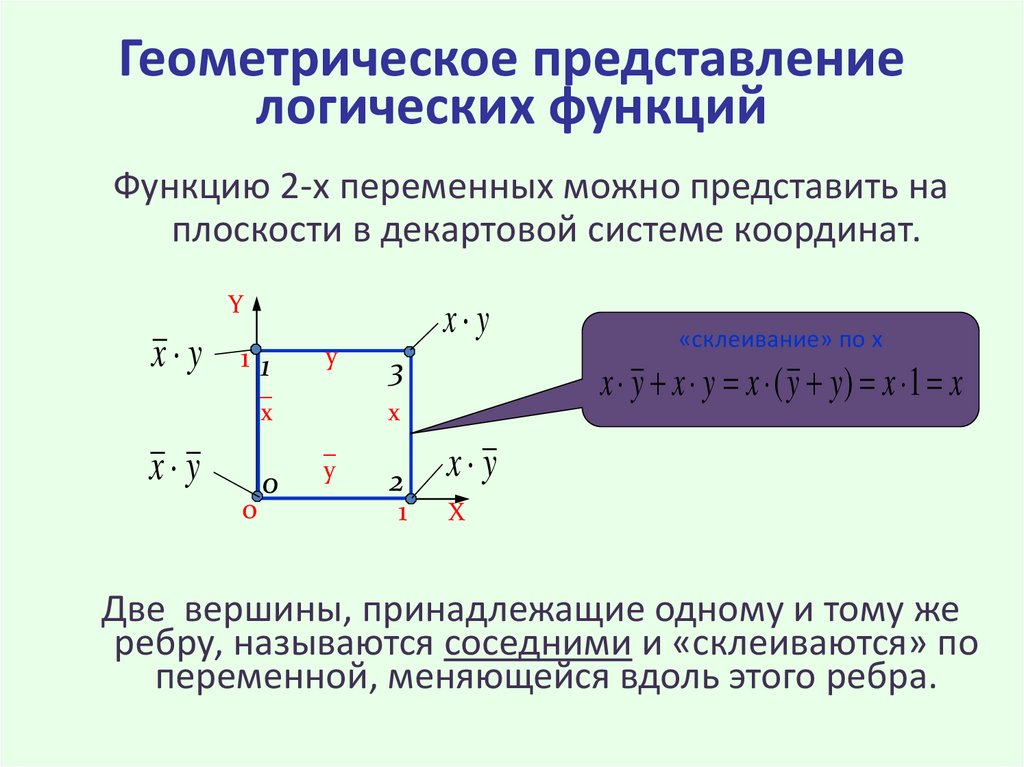
6. Геометрическое представление логических функций
Функцию 2-х переменных можно представить наплоскости в декартовой системе координат.
x y
Y
x y
11
y
x
x y
0
0
x y x y x ( y y) x 1 x
3
x
y
2
1
«склеивание» по х
x y
X
Две вершины, принадлежащие одному и тому же
ребру, называются соседними и «склеиваются» по
переменной, меняющейся вдоль этого ребра.
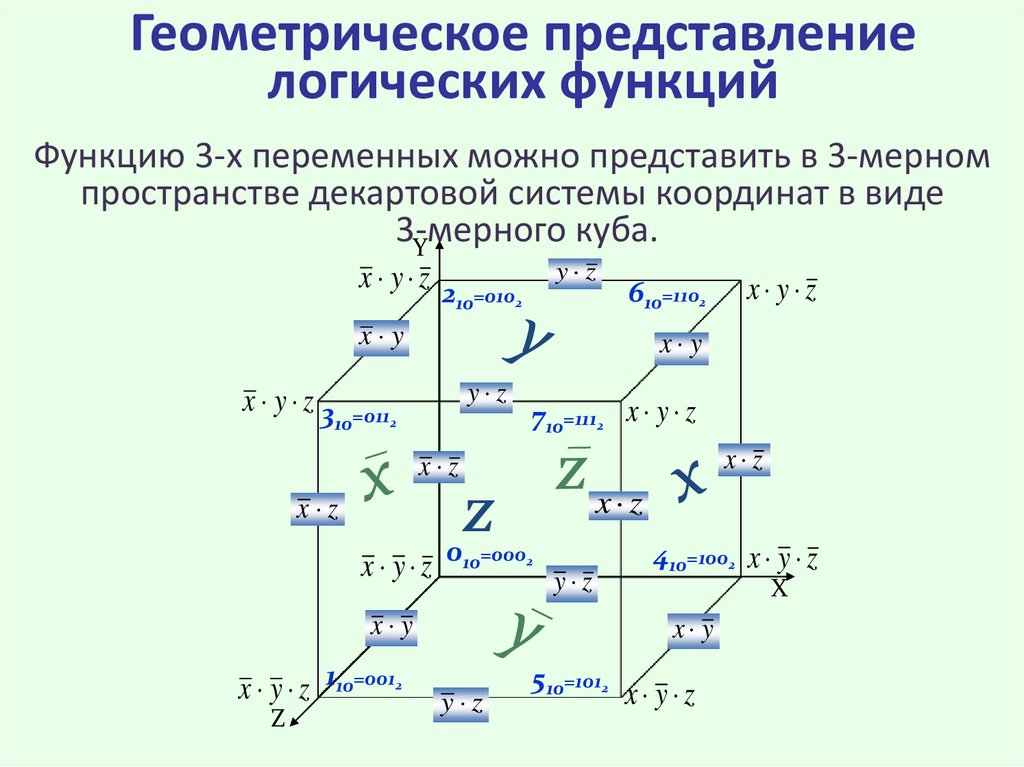
7. Геометрическое представление логических функций
Функцию 3-х переменных можно представить в 3-мерномпространстве декартовой системы координат в виде
3-мерного
куба.
Y
x y z 2 =010
2
10
y z
610=1102
x y
x y z 3
x y
y z
10=0112
710=1112 x y z
x z
x z
x z
x z
x y z 010=0002 y z
x y
x y z 110=0012
Z
x y z
410=1002 x y z
X
x y
y z
510=1012
x y z
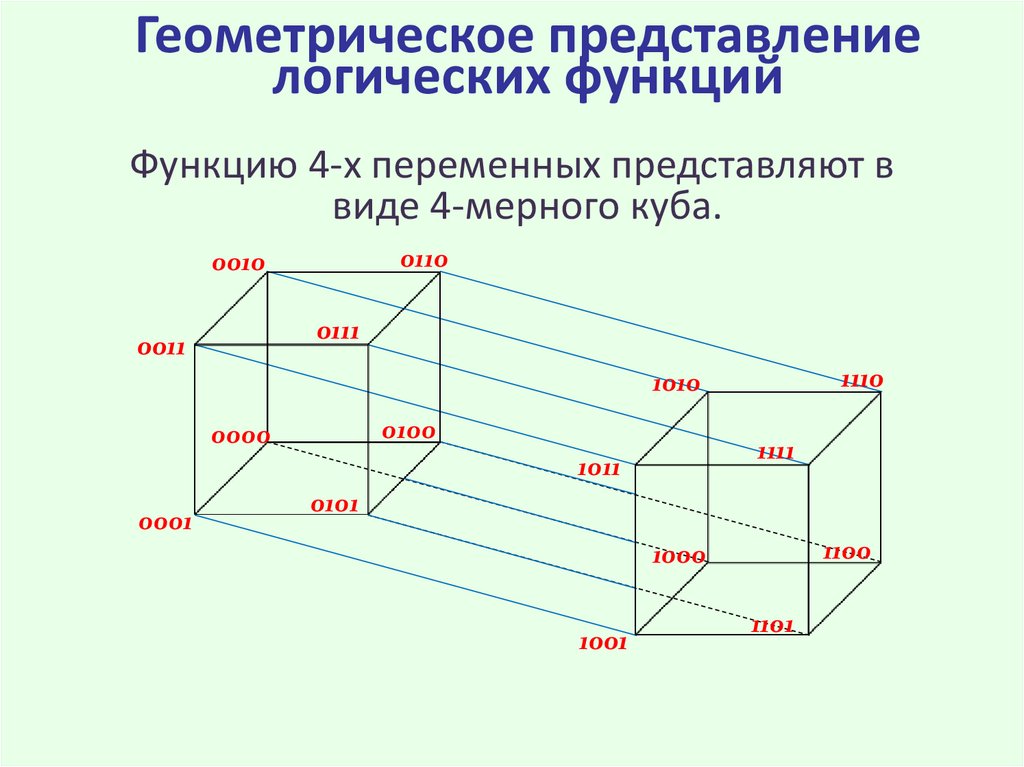
8. Геометрическое представление логических функций
Функцию 4-х переменных представляют ввиде 4-мерного куба.
0110
0010
0111
0011
1110
1010
0100
0000
1111
1011
0001
0101
1100
1000
1001
1101
9. Практически все булевы функции малых арностей (0, 1, 2 и 3) сложились исторически и имеют конкретные имена: Нульарные функции:
При n = 0 количество булевых функций сводится к двум 220 = 21 = 2,первая из них тождественно равна 0, а вторая 1. Их называют булевыми
константами — тождественный нуль и тождественная единица.
Унарные функции:
При n = 1 число булевых функций равно 221 = 22 = 4.
Бинарные функции:
При n = 2 число булевых функций равно 22² = 24 = 16.
Тернарные функции:
При n = 3 число булевых функций равно 22³ = 28 = 256.
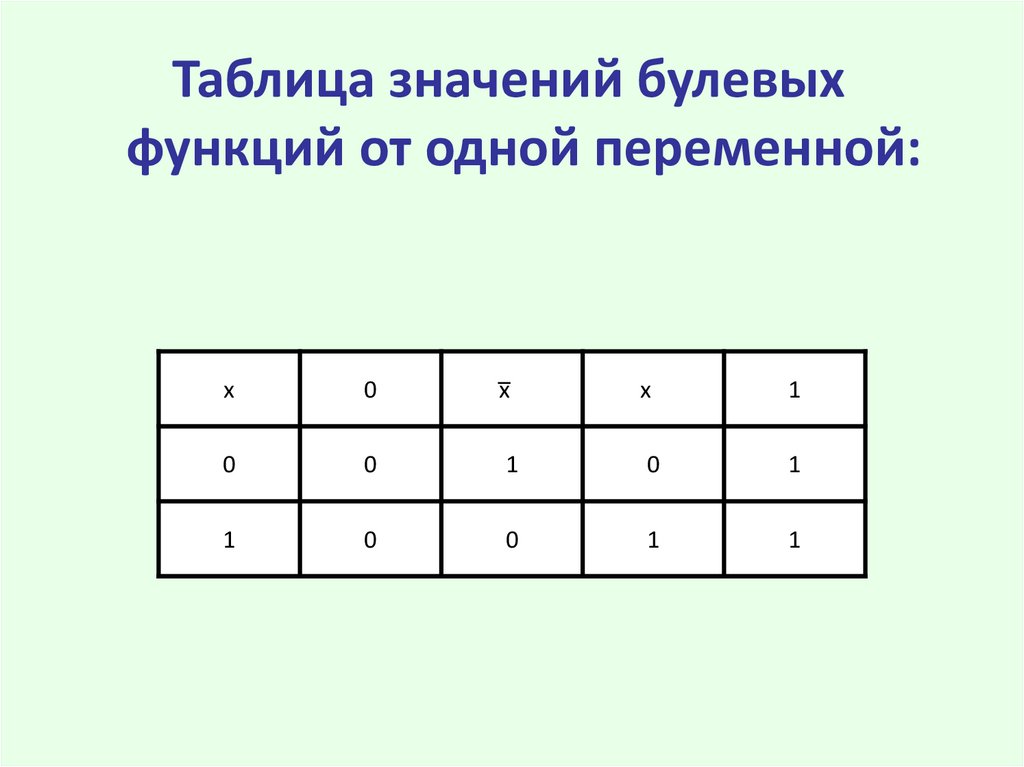
10.
Таблица значений булевыхфункций от одной переменной:
x
0
x̅
x
1
0
0
1
0
1
1
0
0
1
1
11. Названия булевых функций от одной переменной:
ОбозначениеНазвание
0
тождественный ноль, тождественная ложь, тождественное
"НЕТ" , константа
x̅
отрицание, логическое "НЕТ", "НЕ", "НИ"
x
тождественная функция, логическое "ДА",
1
тождественная единица, тождественная истина,
тождественное "ДА", константа
12. Легко, не правда ли? Даже человек, который первый раз видит материал, составит таблицу за минуту, как максимум. А если
переменных будет не 2, а 5, 10, 19?Или функция будет сложнее? Сколько времени
потребуется тогда? А если человек запутается,
сделает вычислительную ошибку (от которой на
100% застрахована ЭВМ)? Тогда вычисление
значения функции будет, как минимум, сильно
затруднено.
Здесь мы подошли к самому главному. Как
раз для тех случаев, где возможно исключить
рутинные расчеты, можно привести программу
на языке JavaScript, которая возьмет роль
счетовода на себя. И будет делать это в миллионы
раз быстрее (и точнее), чем человек.
13.
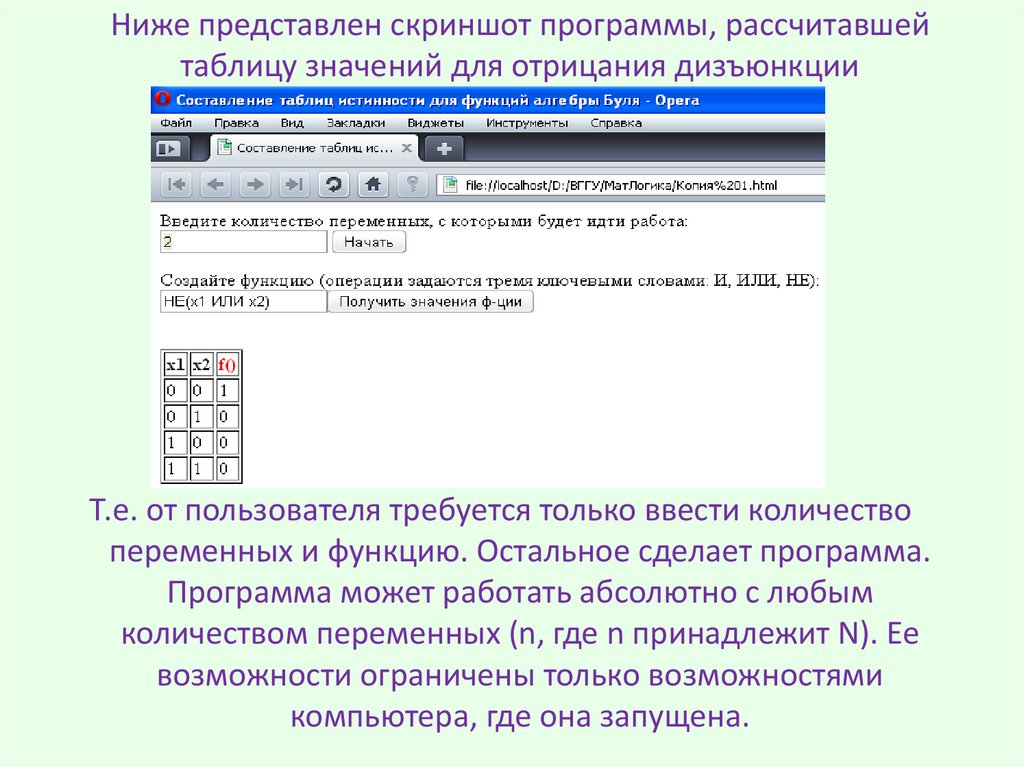
Ниже представлен скриншот программы, рассчитавшейтаблицу значений для отрицания дизъюнкции
Т.е. от пользователя требуется только ввести количество
переменных и функцию. Остальное сделает программа.
Программа может работать абсолютно с любым
количеством переменных (n, где n принадлежит N). Ее
возможности ограничены только возможностями
компьютера, где она запущена.
14.
Чуть выше мы рассмотрели само понятие булевой функции отn переменных. А сколько всего может быть функций nпеременных? Очевидно, что каждую функцию алгебры
логики можно задать с помощью таблицы истинности,
которая будет содержать 2n строк. Таким образом, функция
n переменных полностью определяется набором значений
из нулей и единиц длины 2n . Общее же число наборов,
состоящих из нулей и единиц, длины 2n равно 22n. Значит,
число различных функций алгебры логики n переменных
равно 22n.
Вторая программа как раз и составляет по известному
n всевозможные значения функций. Как вы понимаете, для
человека этот процесс будет очень трудоемок. Но было бы
неплохо иметь не только таблицу значений всевозможных
функций, но и их формулы. Тут мы плавно подходим к
такому понятию, как СДНФ.
Дизъюнктивной нормальной формой (ДНФ) формулы
А называется равносильная ей формула, представляющая
собой дизъюнкцию элементарных конъюнкций.
15.
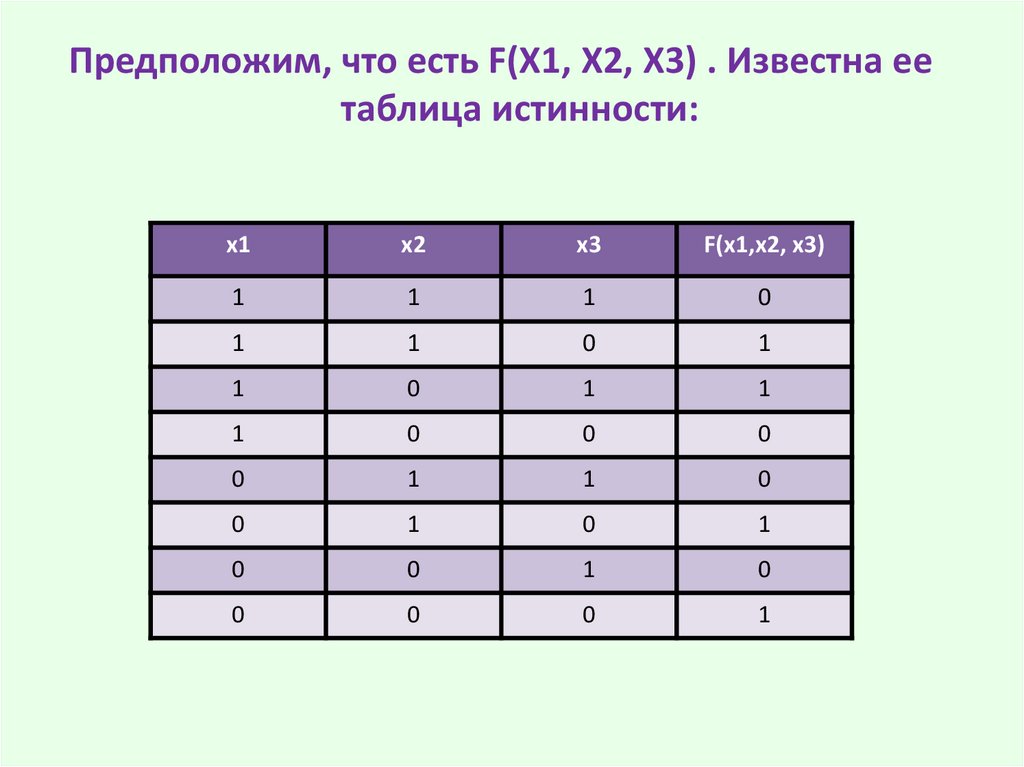
Предположим, что есть F(X1, X2, X3) . Известна еетаблица истинности:
x1
x2
x3
F(x1,x2, x3)
1
1
1
0
1
1
0
1
1
0
1
1
1
0
0
0
0
1
1
0
0
1
0
1
0
0
1
0
0
0
0
1
16.
Для наборов значений переменных (1,1,0), (1,0,1), (0,1,0), (0,0,0), накоторых функция принимает значение 1, запишем конъюнкции
Х1Х2¬Хз , Х1¬Х2Хз, ¬Х1Х2¬Хз, ¬Х1¬Х2¬Хз , а искомая формула,
свойствами совершенства, имеет вид: Х1Х2¬Хз V Х1¬Х2Хз V ¬Х1Х2¬Хз
V ¬Х1¬Х2¬Хз.
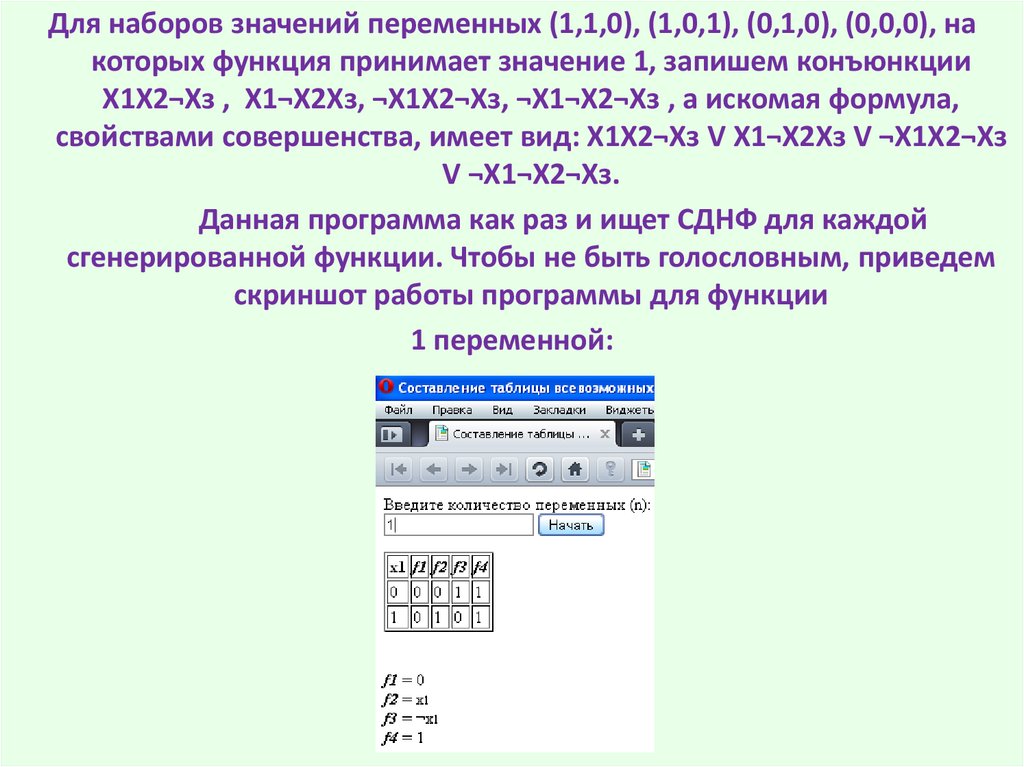
Данная программа как раз и ищет СДНФ для каждой
сгенерированной функции. Чтобы не быть голословным, приведем
скриншот работы программы для функции
1 переменной:









 Математика
Математика








