НГ лекции 1, 2 (3 ГР) (1)

1. Начертательная геометрия

ШИИ
Начертательная
геометрия
Лектор
Ширлина
Ирина Ивановна

2. Задания для выполнения контрольной работы для студентов групп ПГСб и АДб очно-заочной формы обучения

ШИИ
Задания для выполнения контрольной работы для студентов
групп ПГСб и АДб очно-заочной формы обучения
1. Задача № 2. Построение геометрического тела с вырезом.
Метод. указания к задаче 2 – стр.79. Варианты заданий – стр. 80-81. Пример
выполнения – рис. 1.118, стр. 82.
2. Задача № 3. Построение двух проекций конуса с вырезом. Развертку конуса не
выполнять.
Метод. указания к задаче 3 – стр. 83. Варианты заданий – стр. 84-85. Пример
выполнения – рас. 1.119, стр. 86.
3. Задача № 4. Построение линии пересечения двух гранных поверхностей.
Метод. указания к задаче 3 – стр.87. Варианты заданий – стр. 88-91. Пример
выполнения – рис. 1.120, 1.121 стр. 92
Форма контроля - ЗАЧЕТ

3.

ШИИ
1. Изучить методическое пособие по
начертательной геометрии, предложенное на
сайте.
2. Выполнить, необходимые контрольные задания
по варианту для получения допуска к экзамену.
3. Номер варианта:
№ зачетки (или студ. билета) минус 30.
Вычитать до тех пор, пока не останется число
от 1 до 30.
Например, номер зачетки 125:
125-30-30-30-30 = 5. Значит номер варианта 5.

4.

ШИИ
Начертательная геометрия – это раздел
геометрии, в котором изучаются методы
изображения пространственных фигур на
чертеже и способы решения различных
геометрических задач.
Основоположником начертательной
геометрии считается Госпар Монж
(1746-1818).
Его работа «Начертательная
геометрия» была напечатана в 1795г.

5.

ШИИ
Основные обозначения
1, 2, 3 – плоскости проекций (горизонтальная, фронтальная,
профильная;
А, В, С – точки в пространстве (объекты проецирования);
А1 , А2 , А3 – проекции точки А на плоскости проекций 1, 2, 3;
a, b, c – линии в пространстве (прямые и кривые);
α, β, γ – плоскости (поверхности) в пространстве.
Символы отношений
= – совпадение (a=b);
// – параллельность (a // b);
– перпендикулярность (a b);
∩ – пересечение (a ∩ b= К);
– скрещивание (a
b);
– объединение (Сф Сф);
h ( ) – принадлежность (А b);
– касание (α
Сф);

6.

ШИИ
Основной метод
начертательной геометрии
для получения изображений
- метод проекций
Проекция - это изображение
Проецирование – это процесс
Существует 2 метода проецирования:
- центральное и параллельное

7.

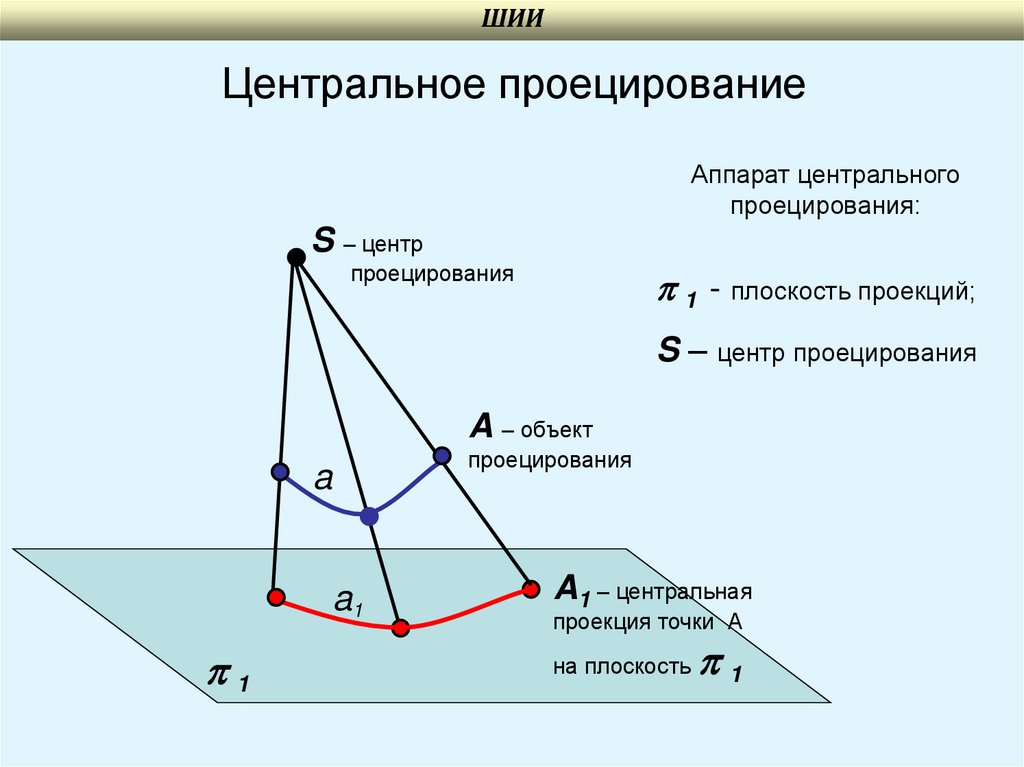
ШИИ
Центральное проецирование
Аппарат центрального
проецирования:
S – центр
проецирования
1 - плоскость проекций;
S – центр проецирования
A – объект
проецирования
a
a1
1
A1 – центральная
проекция точки А
на плоскость
1

8.

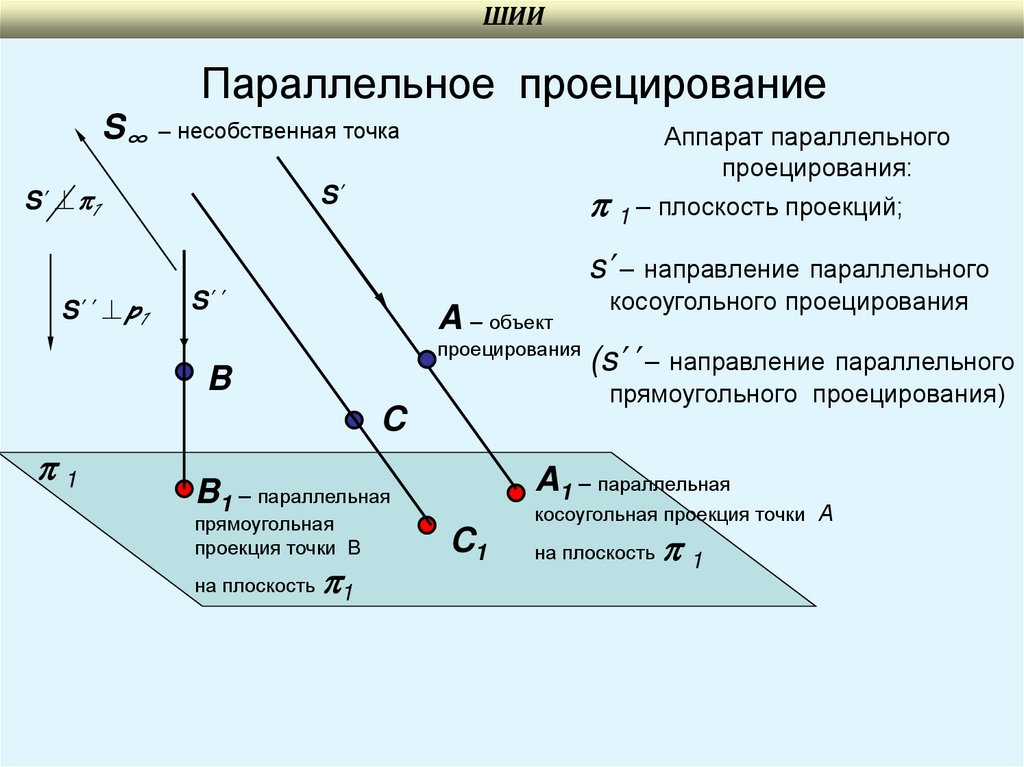
ШИИ
Параллельное проецирование
S∞ – несобственная точка
Аппарат параллельного
проецирования:
1 – плоскость проекций;
S’
S’⊥ 1
s’– направление параллельного
S’’⊥p1
S’’
A – объект
проецирования
B
A1 – параллельная
B1 – параллельная
прямоугольная
проекция точки B
на плоскость
1
(s’’– направление параллельного
прямоугольного проецирования)
C
1
косоугольного проецирования
косоугольная проекция точки А
C1
на плоскость
1

9.

ШИИ
Ортогональное
проецирование точки.
Проекционная модель
Г. Монжа.

10.

ШИИ
Проекционный чертеж должен
отвечать требованиям
обратимости, то есть возможности
реконструировать предмет по
чертежу в пространстве с
точностью его позиционных и
метрических свойств.

11.

ШИИ
Модель Г. Монжа:
2 ортогональные (т.е. взаимно перпендикулярные)
плоскости и система координат.
Метод Монжа заключатся в прямоугольном
проецировании предметов на две взаимно
перпендикулярные плоскости, называемые
плоскостями проекций.
1 - горизонтальная плоскость проекций;
2 - фронтальная плоскость проекций.

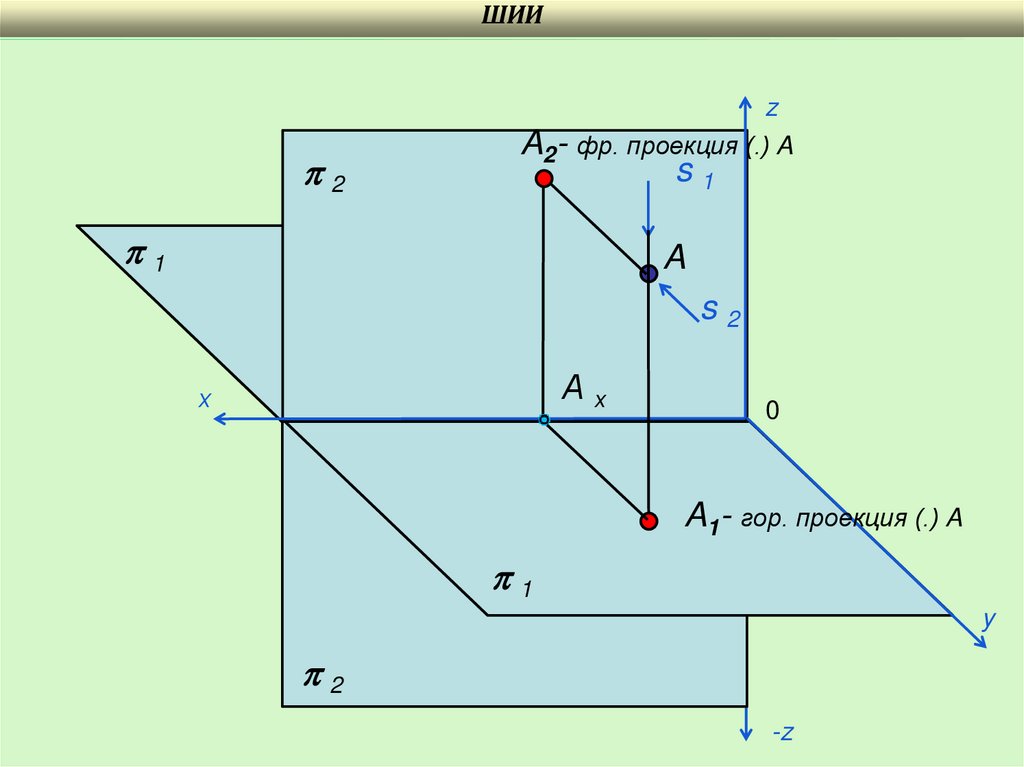
12.

ШИИ
2
z
A2- фр. проекция (.) A
s1
1
A
s2
Ах
х
0
A1- гор. проекция (.) A
1
y
2
-z

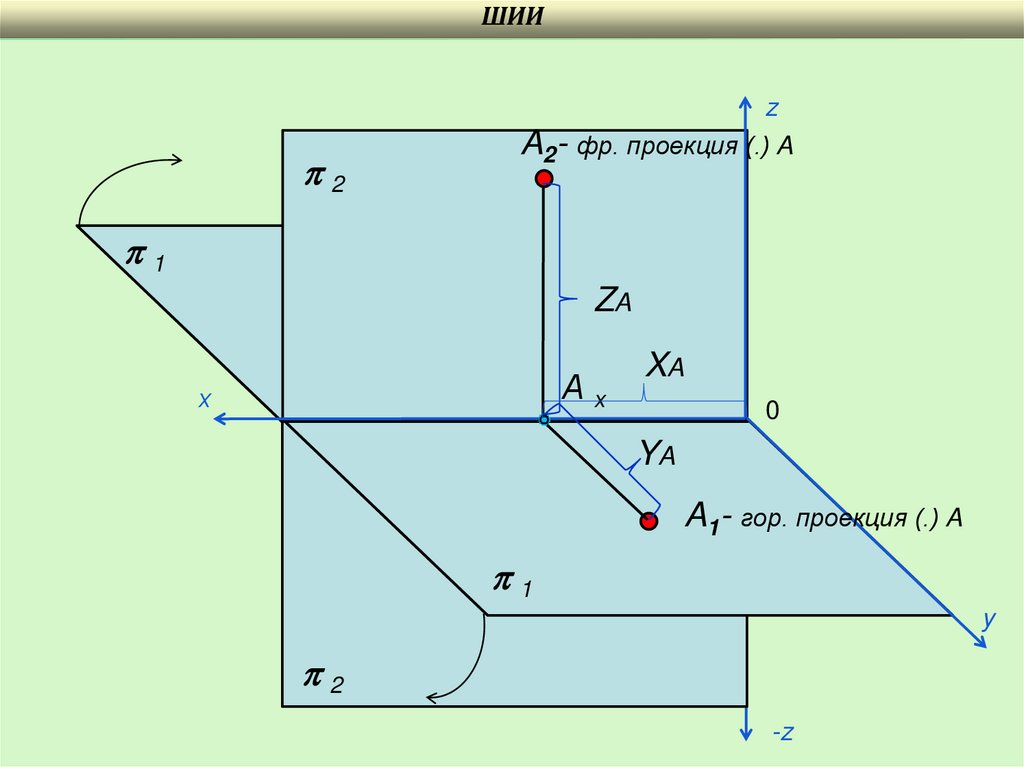
13.

ШИИ
2
z
A2- фр. проекция (.) A
1
ZA
Ах
х
XA
0
YA
A1- гор. проекция (.) A
1
y
2
-z

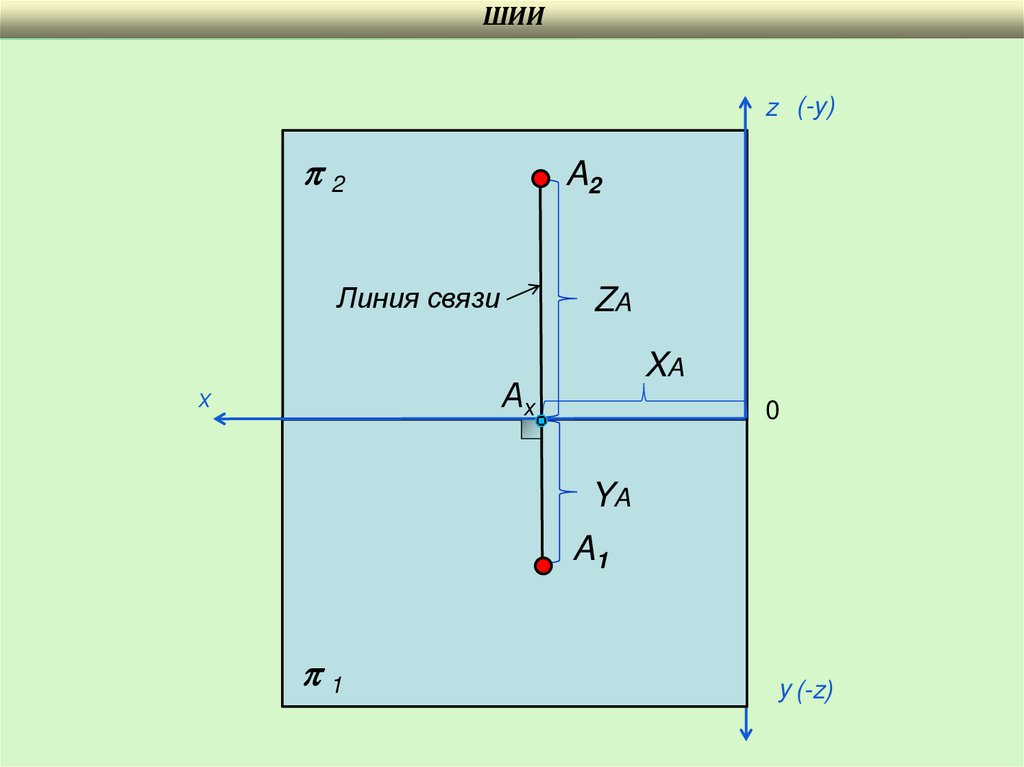
14.

ШИИ
z (-y)
2
A2
Линия связи
ZA
XA
Ах
х
0
YA
A1
1
y (-z)

15.

ШИИ
Проецирование точки на
три плоскости проекций.

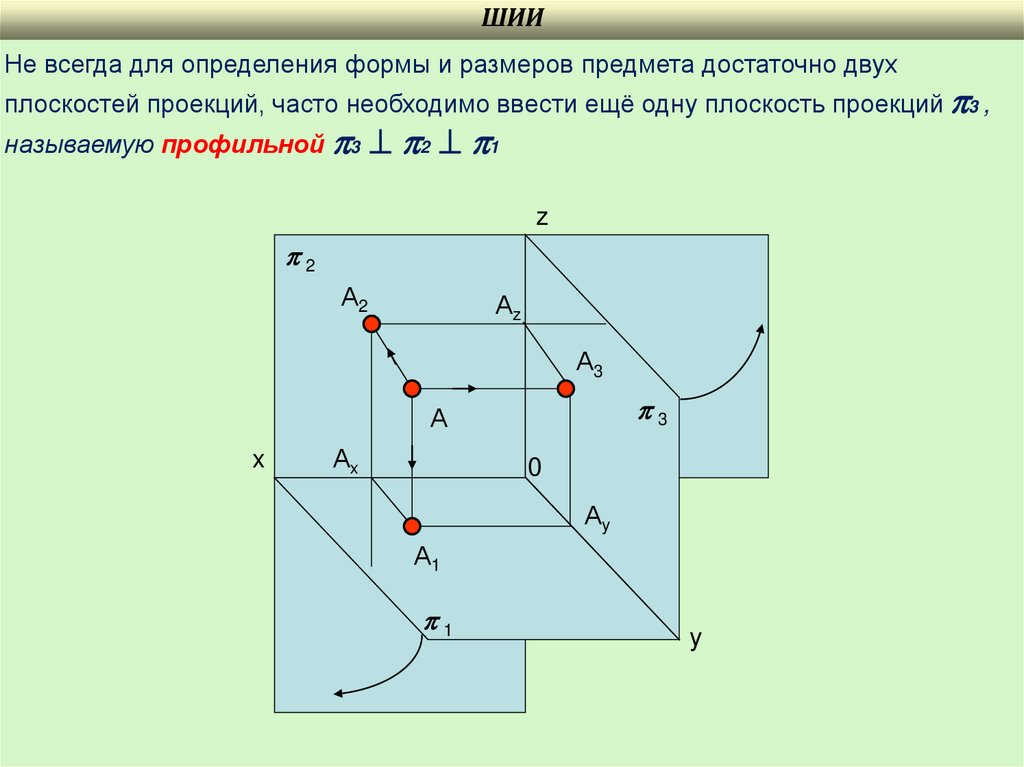
16.

ШИИ
Не всегда для определения формы и размеров предмета достаточно двух
плоскостей проекций, часто необходимо ввести ещё одну плоскость проекций 3 ,
называемую профильной 3 2 1
z
2
А2
Аz
А3
3
А
x
Ах
0
Аy
А1
1
y

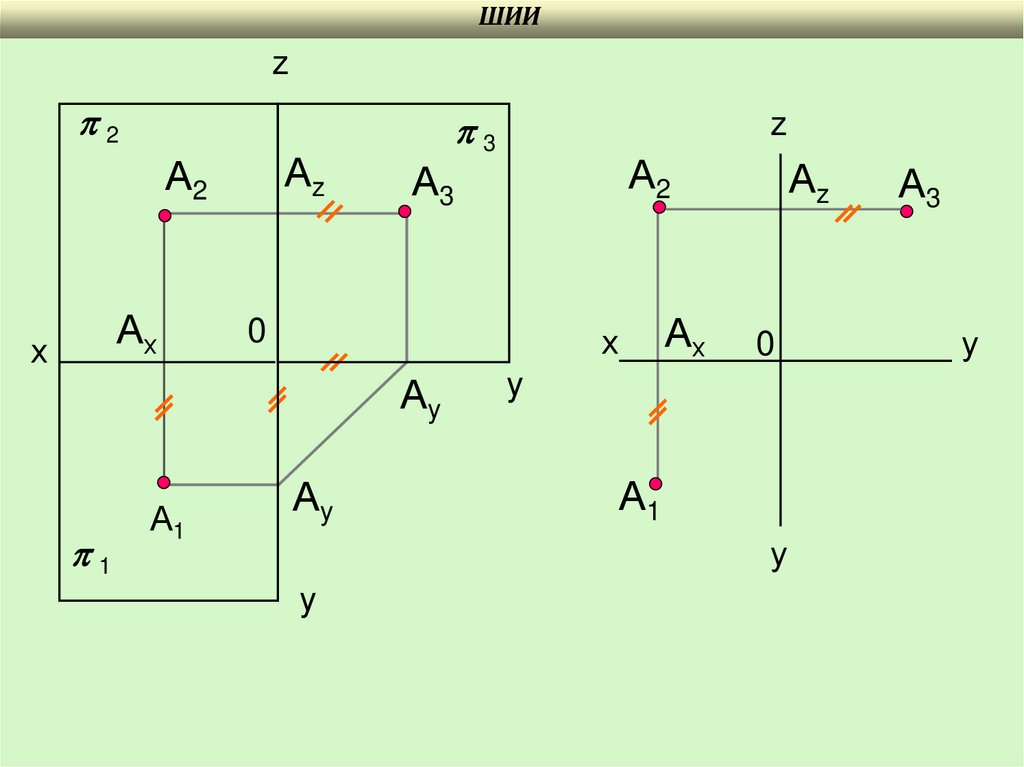
17.

ШИИ
z
2
Аz
А2
Ах
х
3
1
А2
А3
0
Ах
х
Аy
А1
z
Аy
Аz
0
y
А1
у
y
А3
у

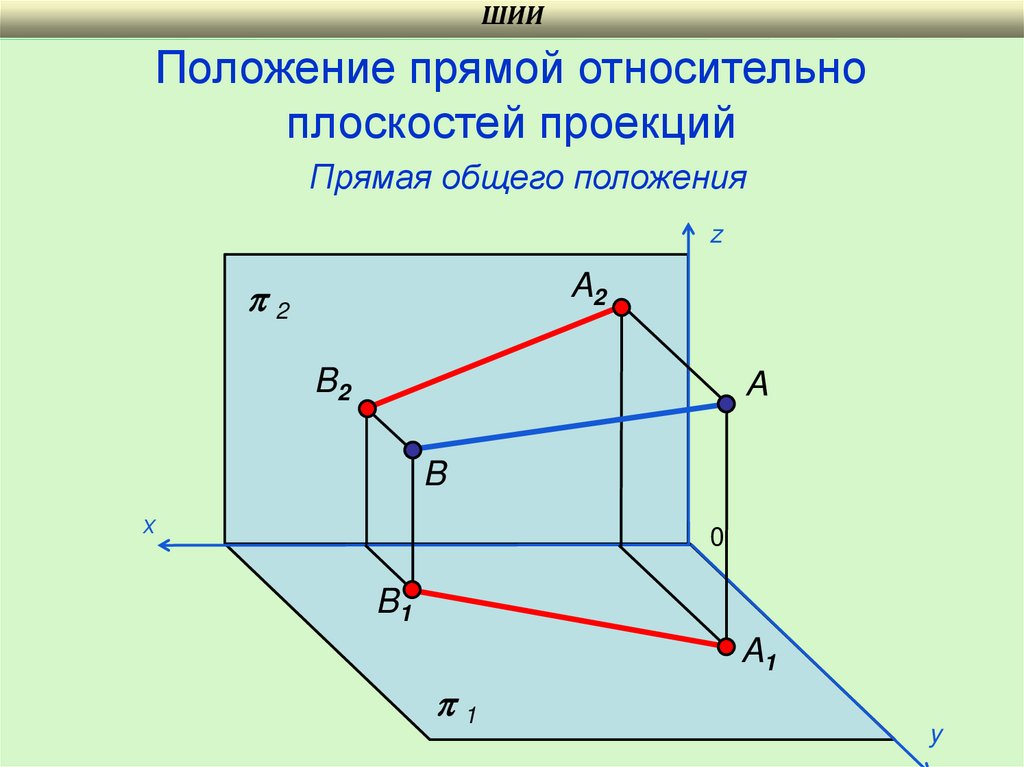
18.

ШИИ
Положение прямой относительно
плоскостей проекций
Прямая общего положения
z
A2
2
B2
A
B
х
0
B1
A1
1
y

19.

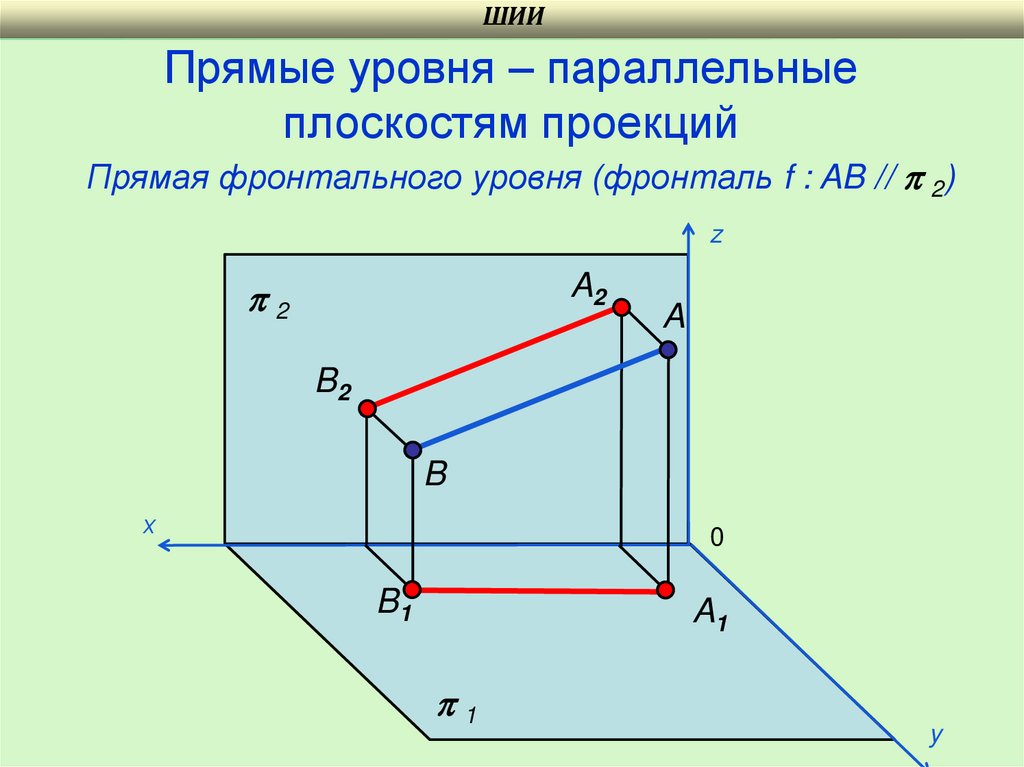
ШИИ
Прямые уровня – параллельные
плоскостям проекций
Прямая фронтального уровня (фронталь f : AB // 2)
z
A2
2
A
B2
B
х
0
B1
A1
1
y

20.

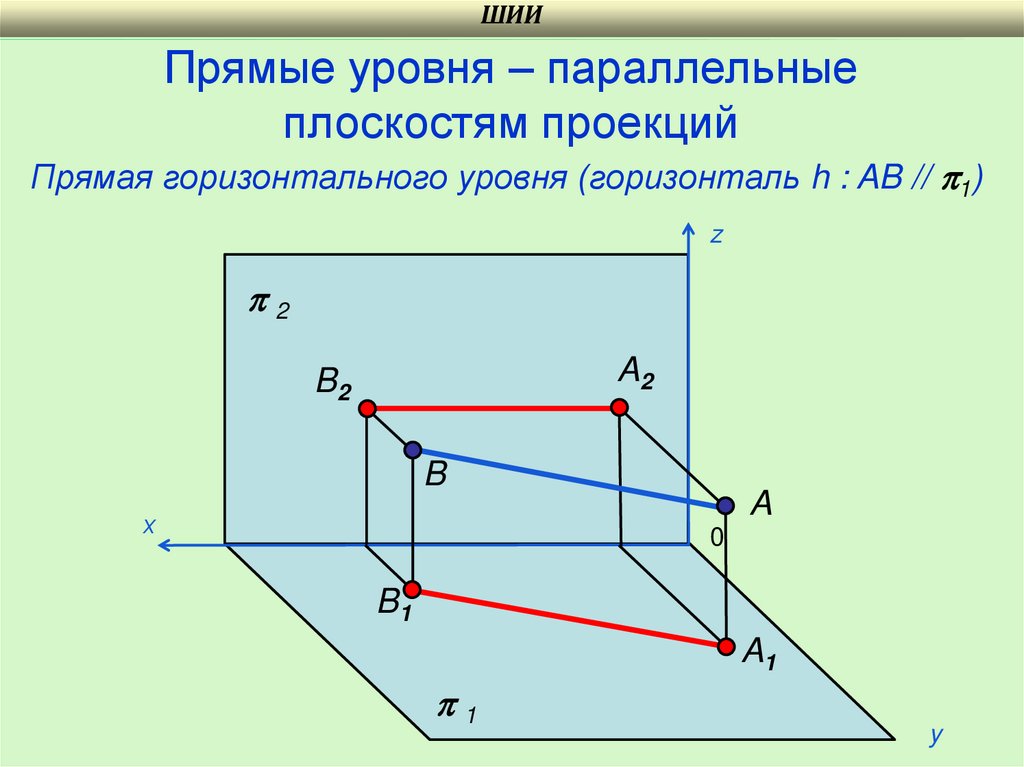
ШИИ
Прямые уровня – параллельные
плоскостям проекций
Прямая горизонтального уровня (горизонталь h : AB // 1)
z
2
A2
B2
B
х
A
0
B1
A1
1
y

21.

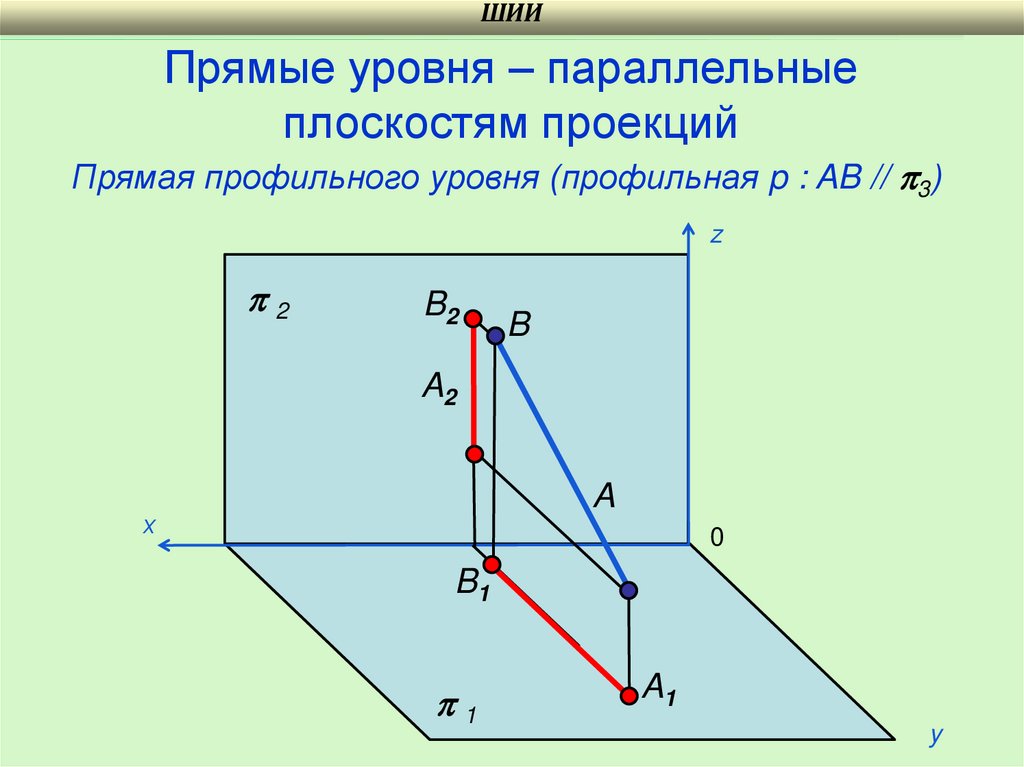
ШИИ
Прямые уровня – параллельные
плоскостям проекций
Прямая профильного уровня (профильная p : AB // 3)
z
2
B2
B
A2
A
х
0
B1
1
A1
y

22.

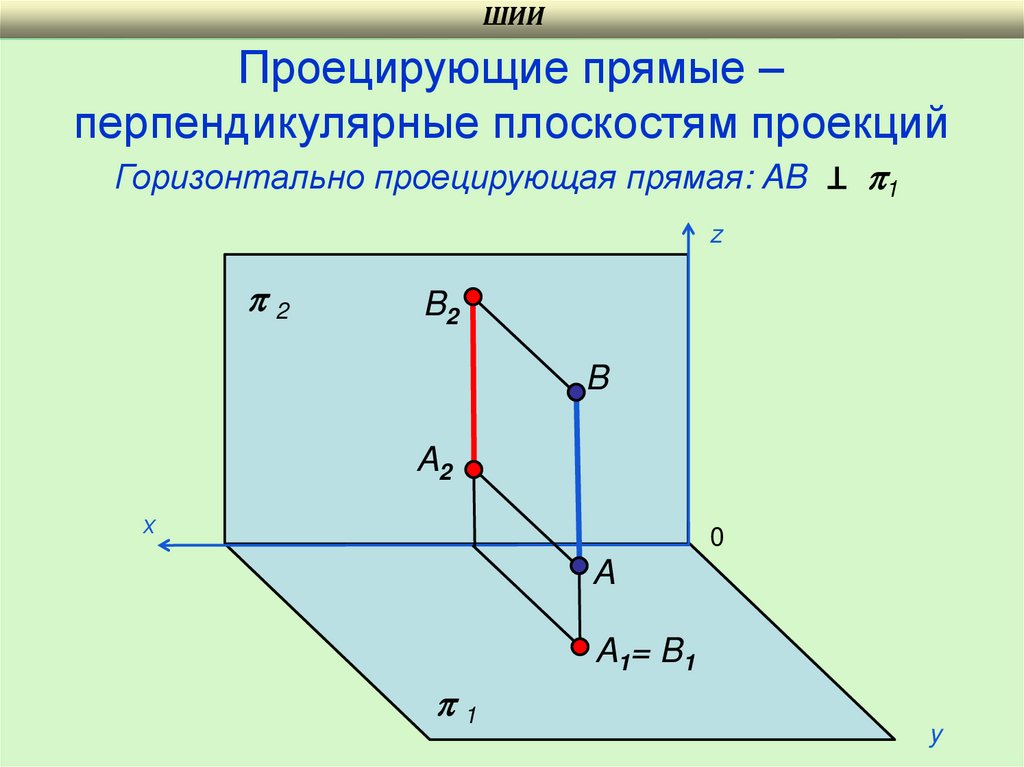
ШИИ
Проецирующие прямые –
перпендикулярные плоскостям проекций
Горизонтально проецирующая прямая: AB ⊥ 1
z
2
B2
B
A2
х
0
A
A1= B1
1
y

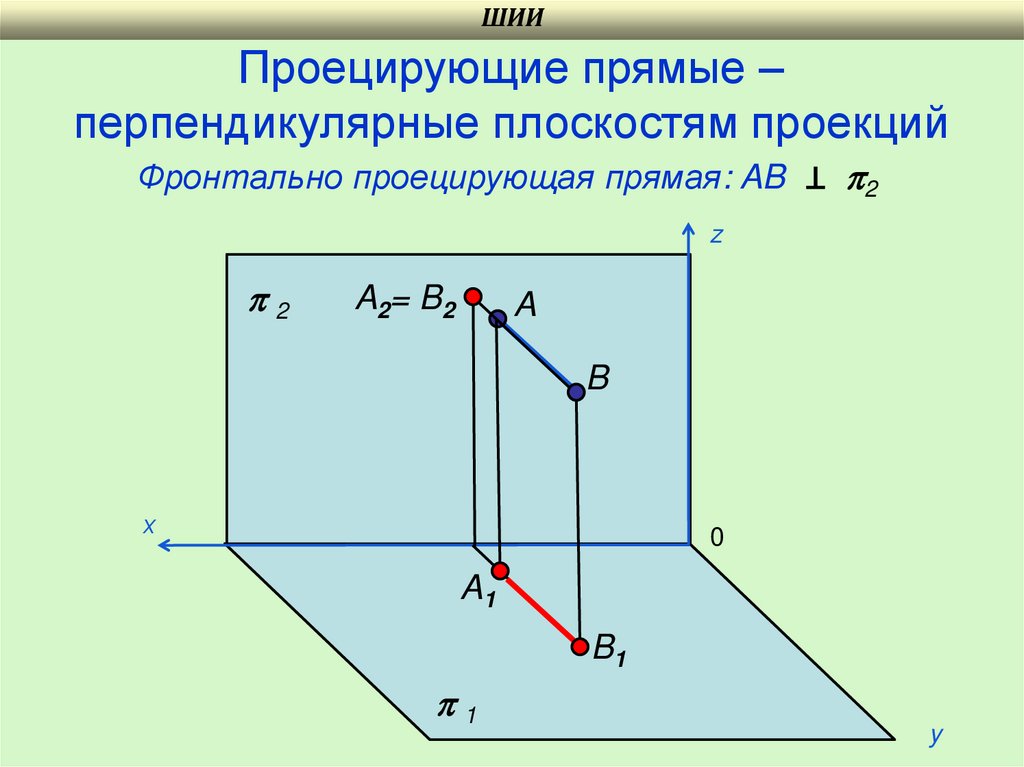
23.

ШИИ
Проецирующие прямые –
перпендикулярные плоскостям проекций
Фронтально проецирующая прямая: AB ⊥ 2
z
2
A2= B2
A
B
х
0
A1
B1
1
y

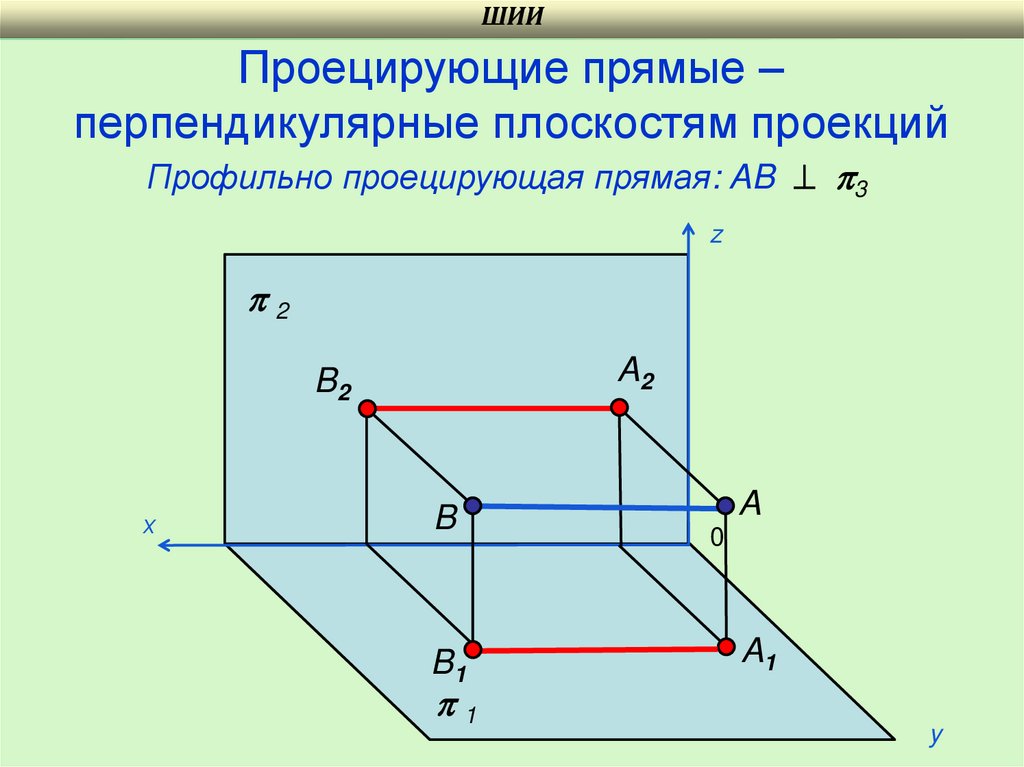
24.

ШИИ
Проецирующие прямые –
перпендикулярные плоскостям проекций
Профильно проецирующая прямая: AB 3
z
2
A2
B2
х
B
B1
1
A
0
A1
y

25. Взаимное расположение прямых

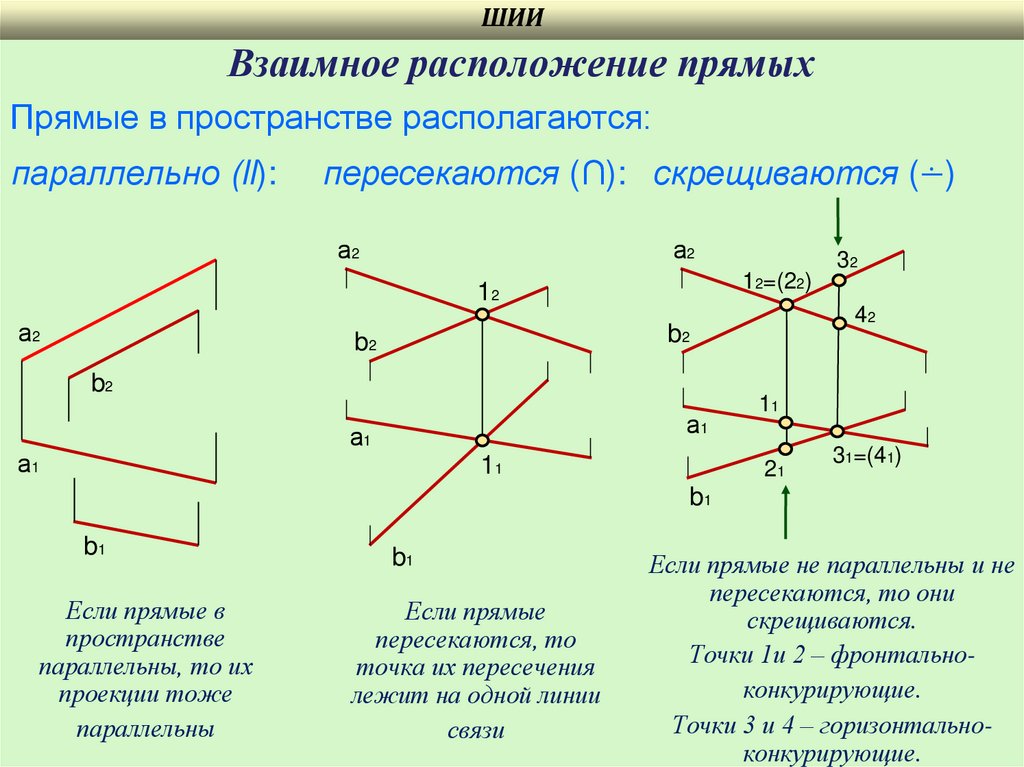
ШИИ
Взаимное расположение прямых
Прямые в пространстве располагаются:
параллельно (ll):
пересекаются (∩): скрещиваются (∸)
а2
а2
12
а2
42
b2
b2
b2
а1
а1
а1
32
12=(22)
11
11
21
31=(41)
b1
b1
Если прямые в
пространстве
параллельны, то их
проекции тоже
параллельны
b1
Если прямые
пересекаются, то
точка их пересечения
лежит на одной линии
связи
Если прямые не параллельны и не
пересекаются, то они
скрещиваются.
Точки 1и 2 – фронтальноконкурирующие.
Точки 3 и 4 – горизонтальноконкурирующие.

26.

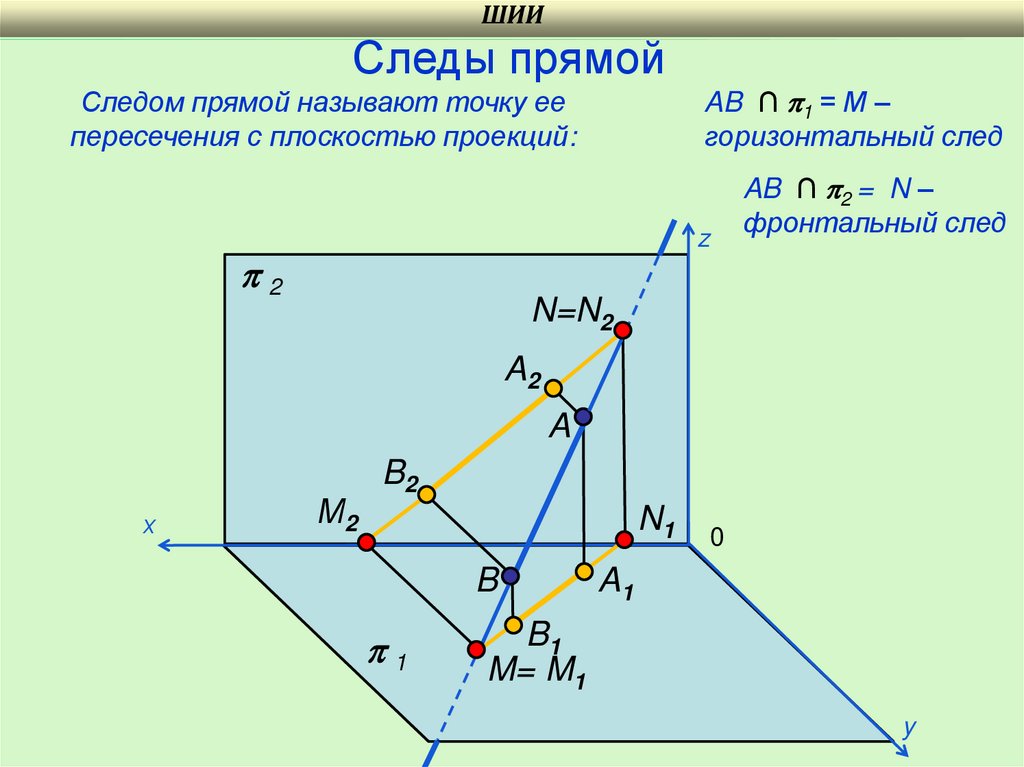
ШИИ
Следы прямой
Следом прямой называют точку ее
пересечения с плоскостью проекций:
AB ∩ 1 = М –
горизонтальный след
z
2
AB ∩ 2 = N –
фронтальный след
N=N2
A2
A
х
М2
B2
N1
B
1
0
A1
B1
M= M1
y

27.

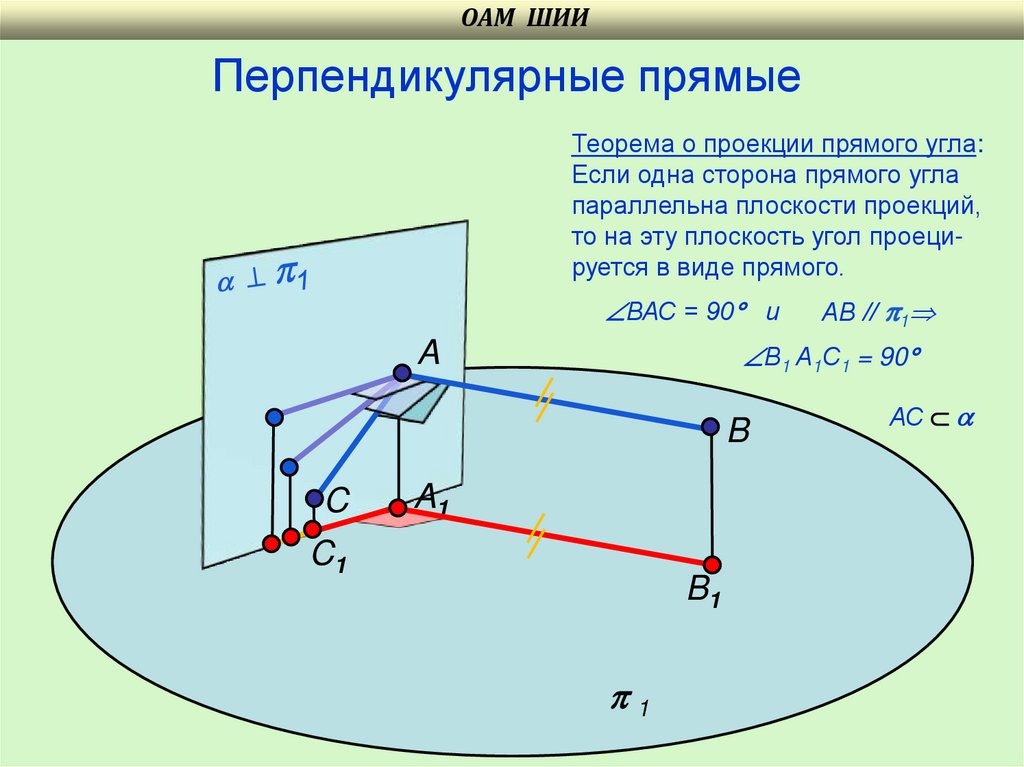
ОАМ ШИИ
Перпендикулярные прямые
Теорема о проекции прямого угла:
Если одна сторона прямого угла
параллельна плоскости проекций,
то на эту плоскость угол проецируется в виде прямого.
ВАС = 90 и
В1 А1С1 = 90
A
B
C
АВ // 1
A1
C1
B1
1
АС

28.

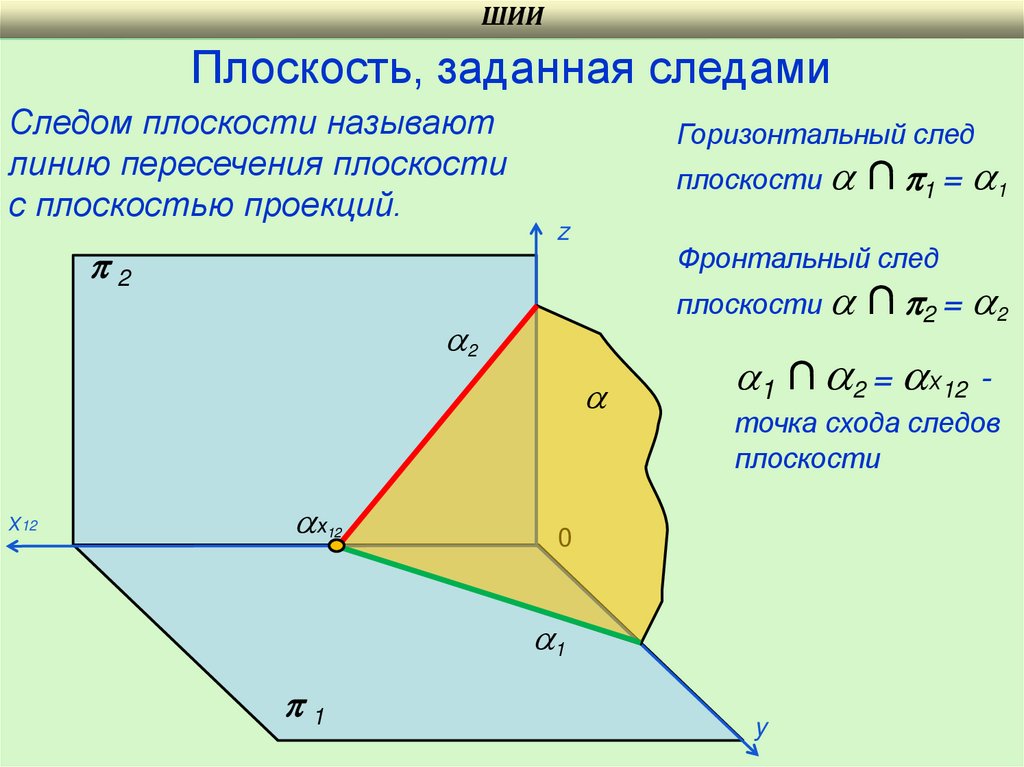
ШИИ
Плоскость, заданная следами
Следом плоскости называют
линию пересечения плоскости
с плоскостью проекций.
2
Горизонтальный след
плоскости ∩ 1 = 1
z
Фронтальный след
плоскости ∩ 2 = 2
2
х12
х
12
1 ∩ 2 = х12 точка схода следов
плоскости
0
1
1
y

29.

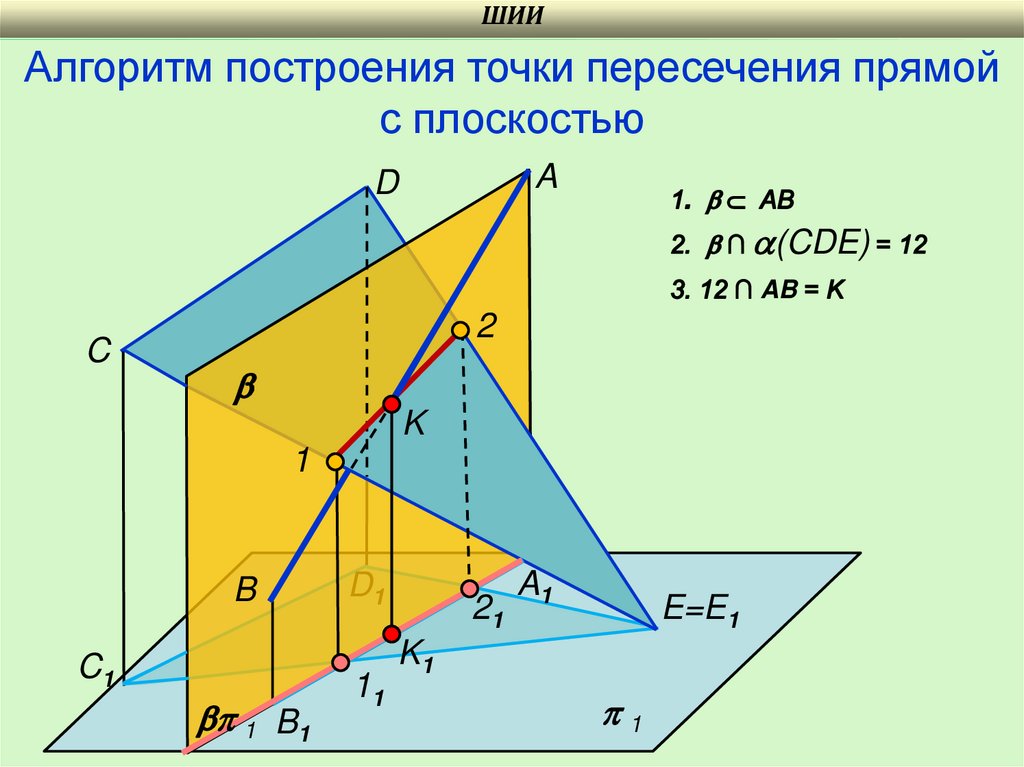
ШИИ
Алгоритм построения точки пересечения прямой
с плоскостью
A
D
(CDE)
AB
2
C
K
1
B
C1
1 B1
D1
11
21
A1
E=E1
K1
1

30.

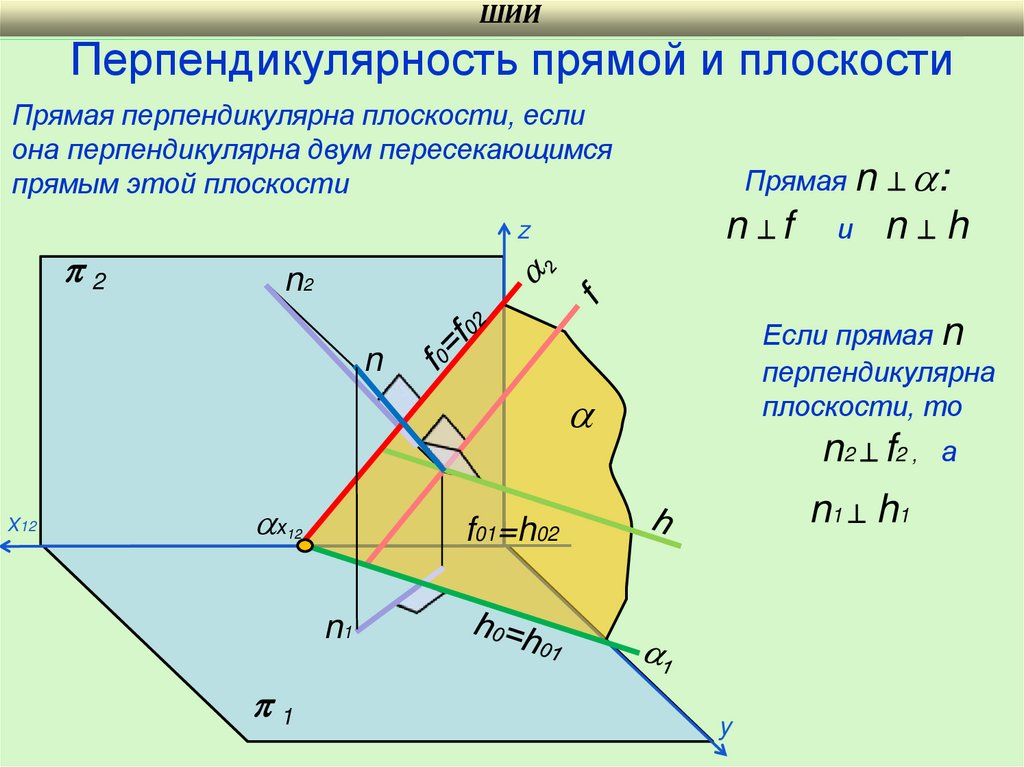
ШИИ
Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если
она перпендикулярна двум пересекающимся
прямым этой плоскости
n f
z
2
Прямая n :
n h
n2
Если прямая n
перпендикулярна
плоскости, то
n
х12
и
х
n 2 f2 , а
n 1 h1
f01=h02
12
n1
1
y

31.

Лекция 1
OAM
ШИИ
Проецирование точки на
три плоскости проекций.
(Способ замены плоскостей
проекций.)
с.19

32.

Лекция 1
с.20
OAM
ШИИ
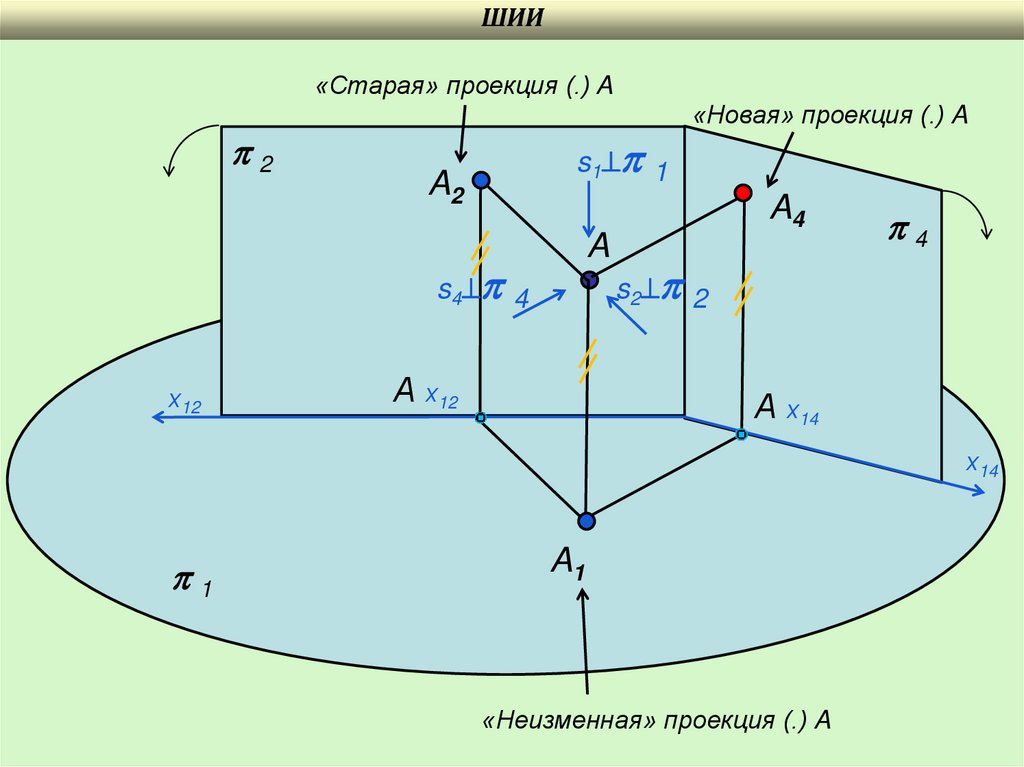
«Старая» проекция (.) A
2
«Новая» проекция (.) A
s 1 1
A2
A4
A
s 4 4
х12
А х12
4
s 2 2
А х14
х14
1
A1
«Неизменная» проекция (.) A

33.

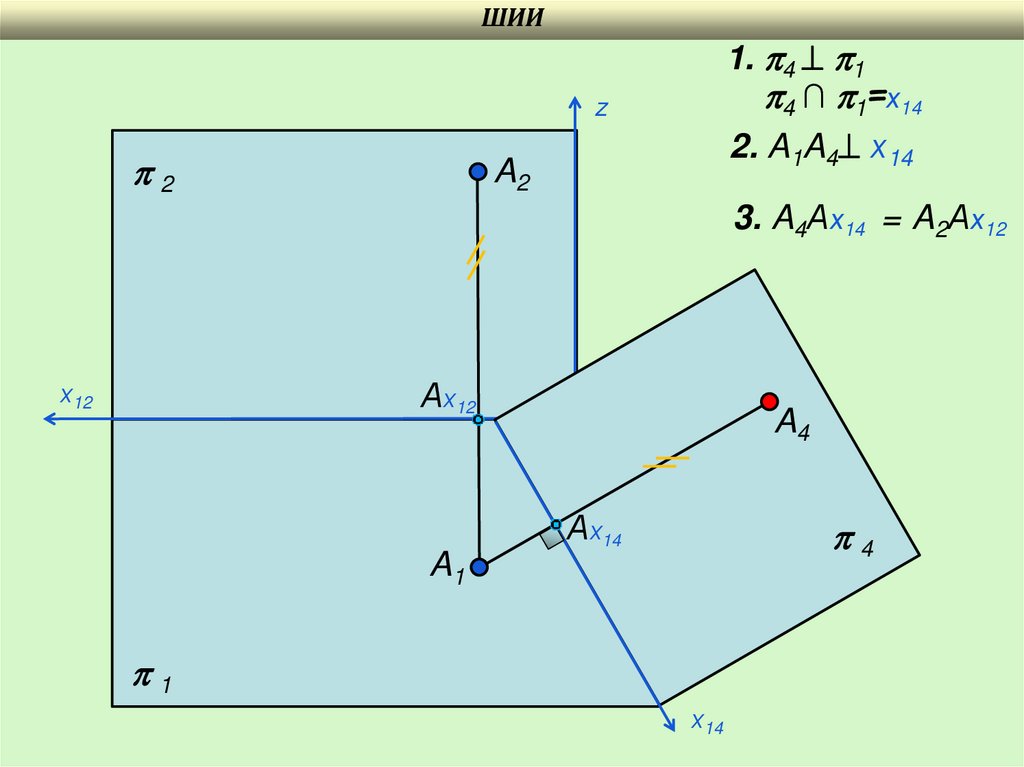
ШИИ
1. 4 1
4 ∩ 1=х14
2. A1A4 х14
z
2
A2
3. A4Ах14 = A2Ах12
Ах12
х12
A4
Ах14
4
A1
1
х14

34. Пример. Определить длину отрезка АВ и угол наклона его к плоскости П1.

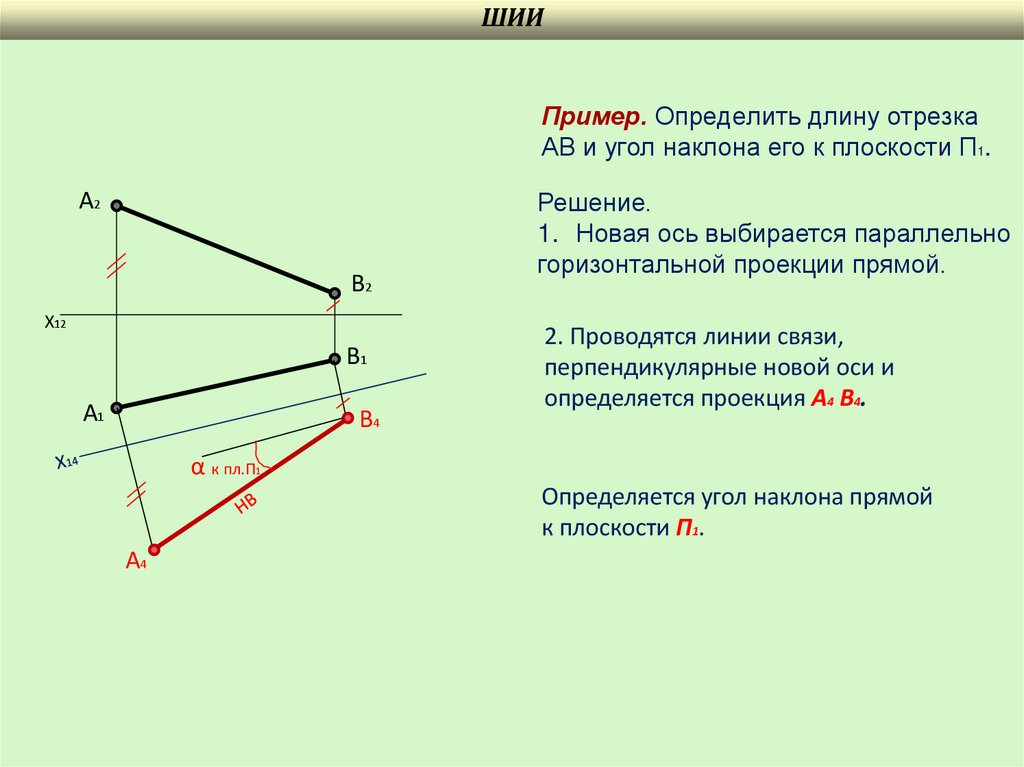
ШИИ
Пример. Определить длину отрезка
АВ и угол наклона его к плоскости П1.
А2
В2
Х12
В1
А1
В4
Решение.
1. Новая ось выбирается параллельно
горизонтальной проекции прямой.
2. Проводятся линии связи,
перпендикулярные новой оси и
определяется проекция А4 В4.
α к пл.П1
Определяется угол наклона прямой
к плоскости П1.
А4

35.

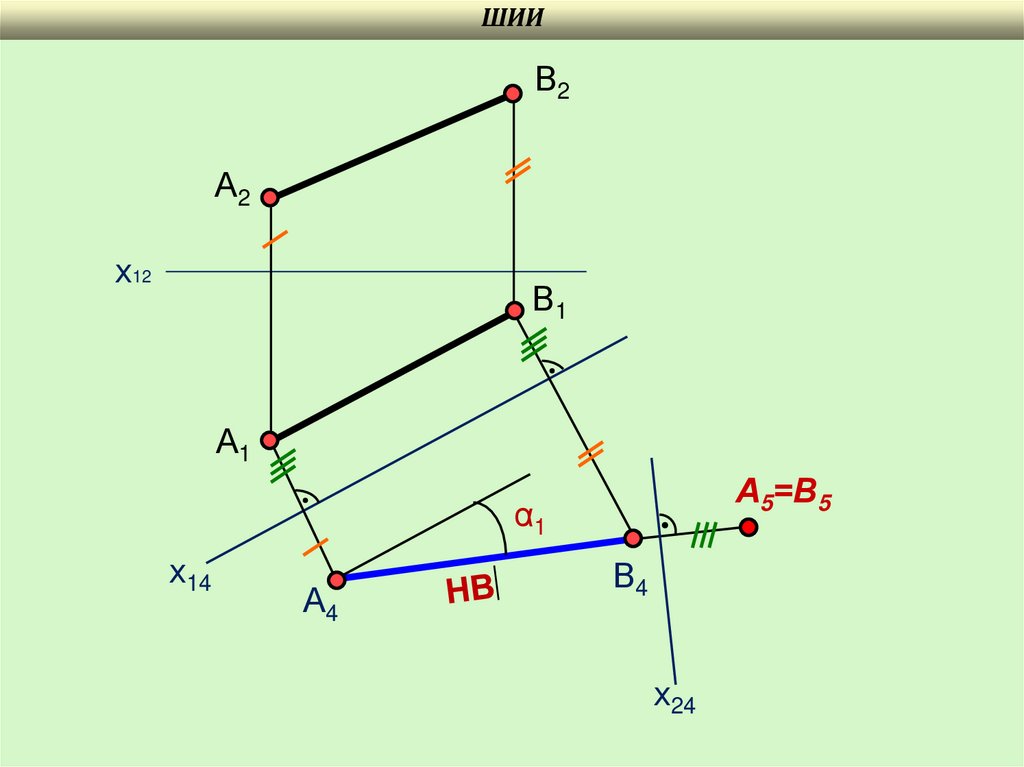
Замена двух и более плоскостей проекций
При второй и последующих заменах плоскостей проекций поступают так же,
как и при первой замене, принимая результат предыдущей замены за
исходную систему.
Пример: Преобразовать прямую АВ в точку и определить угол наклона ее к
горизонтальной плоскости проекций.
1. Новая ось выбирается параллельно горизонтальной проекции прямой.
2. Проводятся линии связи, перпендикулярные новой оси и определяется
проекция А4 В4.
3. Определяется угол наклона прямой к плоскости П1 (угол между натуральной
величиной и осью Х14).
4. Новая ось Х45 выбирается перпендикулярно А4 В4.
5. Проводятся линии связи перпендикулярно Х45 и определяется проекция А5 В5.

36.

ШИИ
В2
А2
х12
В1
А1
А5=В5
α1
х14
А4
В4
х24

37.

ШИИ
Вращение вокруг проецирующих прямых
При вращении элементов чертежа вокруг проецирующих прямых одна проекция
элементов не изменяется по величине и форме.
Поэтому одной проекции сразу можно придать положение, удобное для решения
задачи, считая, что вращение произошло.
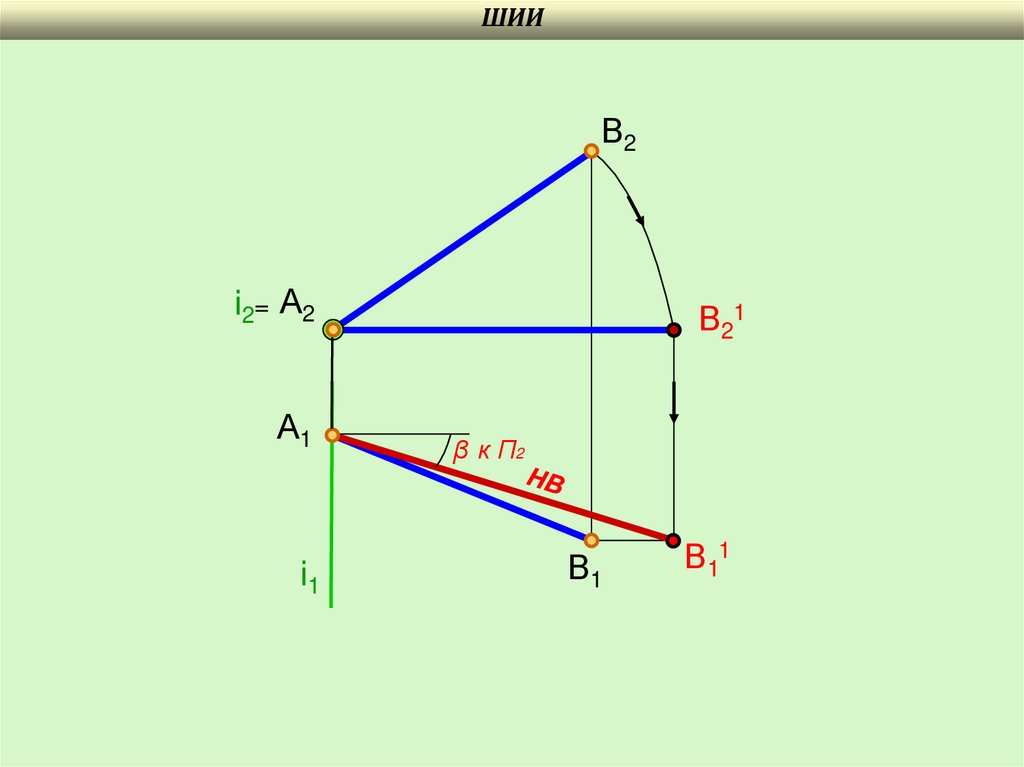
Пример. Определить натуральную величину отрезка прямой АВ
i – ось вращения
i П2
А2В2 – радиус вращения точки В2
Прямую АВ вращают до положения горизонтали
А1В11 - НВ прямой АВ

38.

ШИИ
В2
i2= А2
А1
i1
В21
β к П2
В1
В11

39.

ШИИ
Способ плоскопараллельного перемещения
Плоское движение геометрической фигуры, при котором
все ее точки движутся параллельно некоторой плоскости.
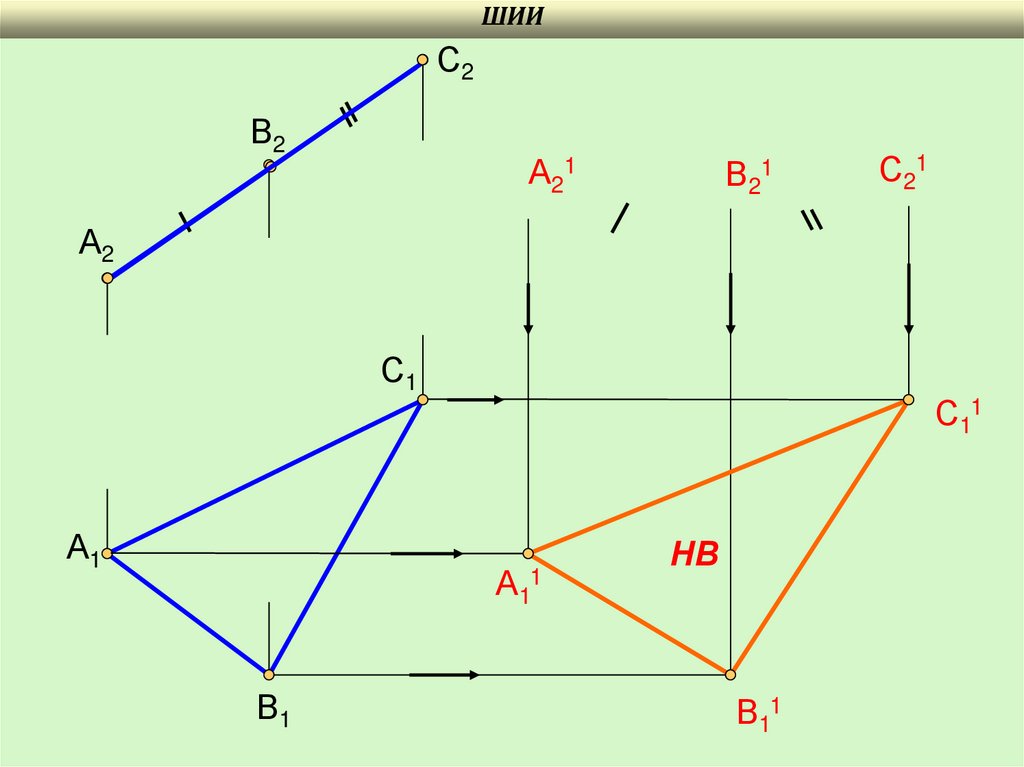
Пример. Определить натуральную величину плоскости треугольника АВС.

40.

ШИИ
С2
В2
А21
В21
С21
А2
С1
А1
С11
А11
В1
НВ
В11

41. ПОВЕРХНОСТИ

ШИИ
ПОВЕРХНОСТИ
Поверхностью называют общую часть двух смежных областей
пространства.
Поверхностью называют совокупность всех
последовательных положений перемещающейся линии. Эту
линию называют образующей, а линия, по которой
перемещается образующая, называется направляющей.
Главу 5 «Кривые линии и поверхности» изучить
самостоятельно.

42.

Лекция 1
с.6
OAM
ШИИ
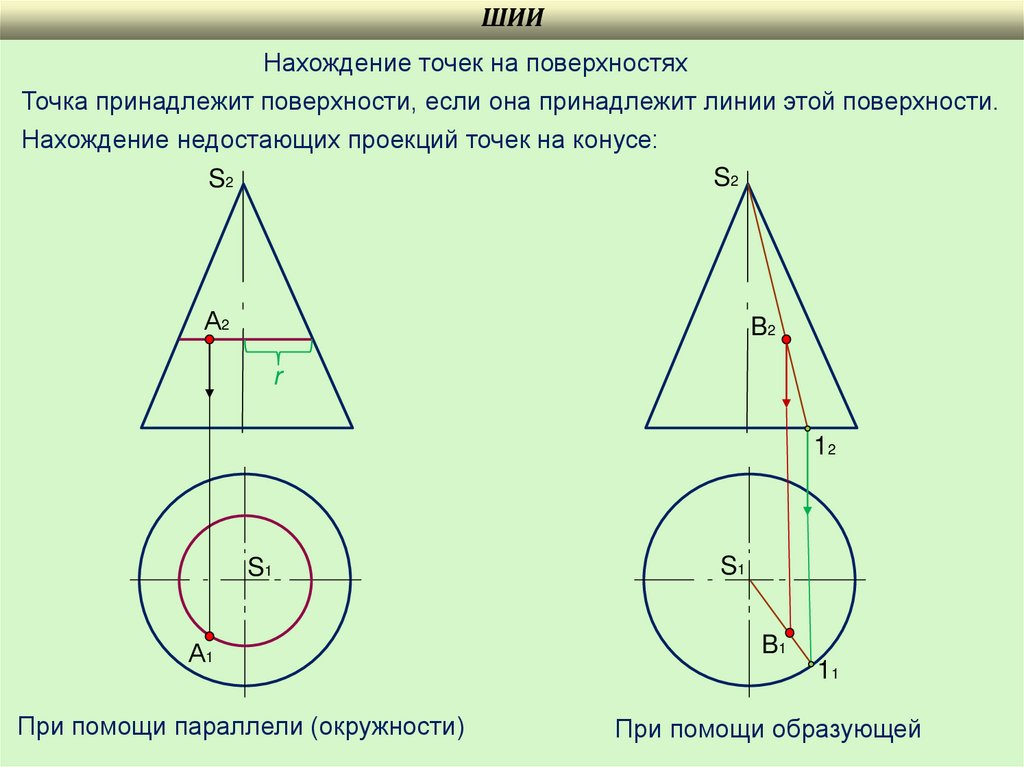
Нахождение точек на поверхностях
Точка принадлежит поверхности, если она принадлежит линии этой поверхности.
Нахождение недостающих проекций точек на конусе:
S2
S2
А2
B2
r
12
S1
А1
При помощи параллели (окружности)
S1
B1
11
При помощи образующей

43.

Лекция 1
OAM
ШИИ
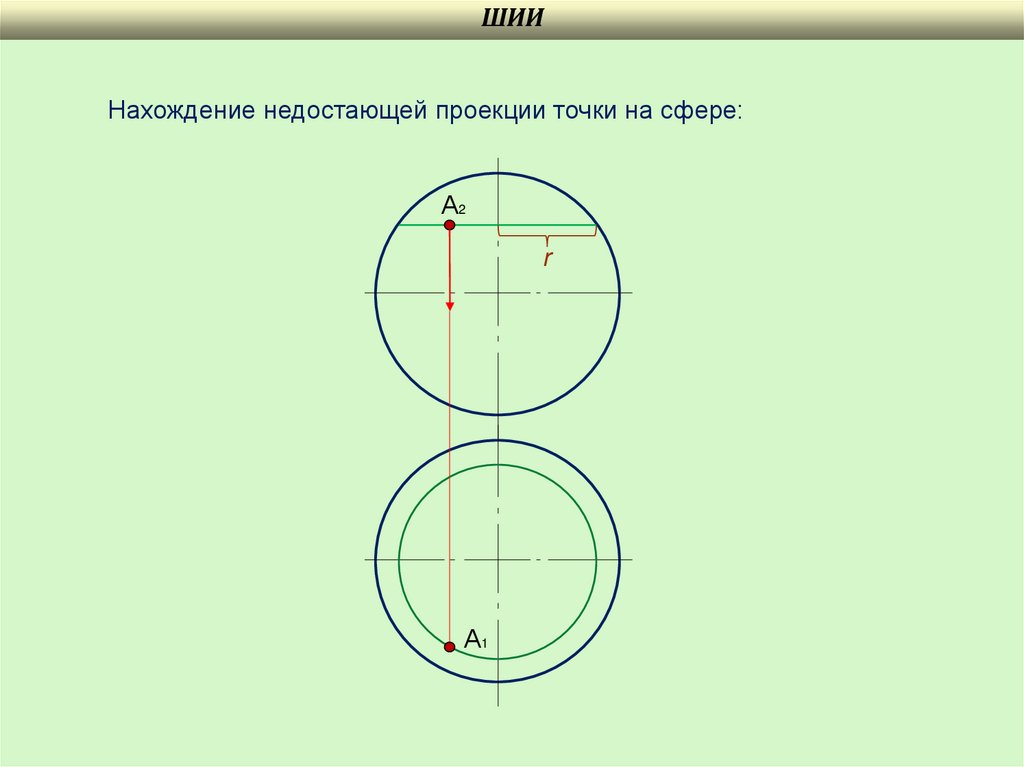
Нахождение недостающей проекции точки на сфере:
А2
r
А1
с.6