Постоянный ток. Магнитное поле

1. Курс общей физики

КУРС
ОБЩЕЙ
ФИЗИКИ
ЛЕКЦИЯ 10
ПОСТОЯННЫЙ ТОК. МАГНИТНОЕ ПОЛЕ

2. Постоянный электрический ток

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Электрический ток – это упорядоченное движение носителей
заряда. Различают следующие разновидности электрического тока:
1. ток проводимости;
2. ток поляризации;
3. ток в вакууме;
4. конвекционный ток.
Постоянный электрический ток – это упорядоченное движение
носителей заряда, скорость направленного движения которых неизменна.
Условились, что направление тока совпадает с направлением
упорядоченного движения положительных зарядов, образующих данный
ток. Количественно электрический ток характеризуют с помощью силы тока.
Сила тока – это скалярная величина, равная заряду dq, переносимому
носителями через некоторую поверхность за единицу времени dt
dq
I=
dt

3. Постоянный электрический ток

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
В случае постоянного тока, сила тока определяется как
I=
q
t
Единицей силы тока в СИ является А – ампер. Из определения силы тока
следует, что 1 А = 1 Кл/ 1 с.
Т.к. в общем случае электрический ток может быть неравномерно
распределен по поверхности, через которую он течет, то для описания
такого распределения необходима соответствующая физическая величина.
Такой
величиной
является
плотность
тока
.
Плотность тока – это векторная физическая величина, численно равная
отношению тока dI через расположенную перпендикулярно направлению
тока площадку dS┴ к величине этой площадки
dI
j=
dS

4. Постоянный электрический ток

ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Направление плотности тока такое же, как и направление скорости
упорядоченного движения положительных носителей заряда данного тока.
Плотность тока можно определить и несколько иначе. Пусть в единице
объема однородного изотропного проводника имеется n+ носителей
положительного заряда и n- носителей отрицательного заряда. Величина
зарядов носителей e+ и e -, а их скорость направленного движения u + и u соответственно. Тогда через единичную площадку проводника за единицу
времени пройдут n+u + + n - u - носителей заряда, которые перенесут заряд
равный e+ n+u + + e - n - u -. Данная величина численно равна плотности тока, т.е.
j =e n u +e n u
+
+
Поток плотности тока через данную поверхность равна силе тока через данную
поверхность. Этот факт отражает взаимосвязь данных физических величин
I jdS
s

5. Электродвижущая сила источника тока. Напряжение

ЭЛЕКТРОДВИЖУЩАЯ СИЛА
ИСТОЧНИКА ТОКА. НАПРЯЖЕНИЕ
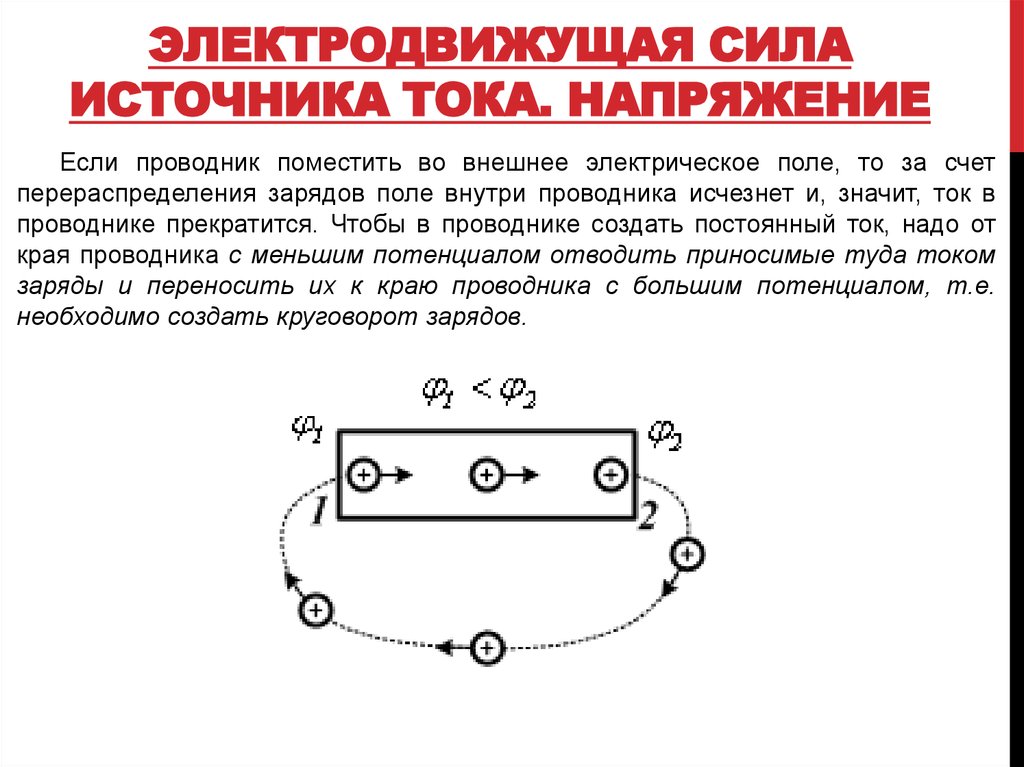
Если проводник поместить во внешнее электрическое поле, то за счет
перераспределения зарядов поле внутри проводника исчезнет и, значит, ток в
проводнике прекратится. Чтобы в проводнике создать постоянный ток, надо от
края проводника с меньшим потенциалом отводить приносимые туда током
заряды и переносить их к краю проводника с большим потенциалом, т.е.
необходимо создать круговорот зарядов.

6. Электродвижущая сила источника тока. Напряжение

ЭЛЕКТРОДВИЖУЩАЯ СИЛА
ИСТОЧНИКА ТОКА. НАПРЯЖЕНИЕ
Данный «круговорот» возможен лишь за счет работы сторонних сил, т.е. сил
неэлектростатической природы. Такие силы обусловлены, например,
протеканием химических процессов в гальванических элементах.
Электродвижущей силой (ЭДС) называется величина, численно равная
работе сторонних сил, по перемещению единичного положительного заряда в
электрической цепи или на ее участке
Añò î ð
q
ЭДС в замкнутой цепи запишется как
Eñò î ð dl
Отсюда, ЭДС равна циркуляции вектора напряженности сторонних сил по
замкнутой электрической цепи.

7. Электродвижущая сила источника тока. Напряжение

ЭЛЕКТРОДВИЖУЩАЯ СИЛА
ИСТОЧНИКА ТОКА. НАПРЯЖЕНИЕ
В электрической цепи на носители заряда кроме сторонних сил действуют
силы электростатического поля. Поэтому, результирующая сила, действующая
в каждой точке цепи на заряд равна
F=q Å+Eñò î ð
Данная сила совершает работу над зарядом q на участке цепи, что
выражается как
2
2
1
1
À12 = Fdl q E+Eñò î ð dl q( 1 2 ) q 12
Напряжение U (падение напряжения) на участке электрической цепи 1-2 – это
величина, численно равная работе, совершаемой электрическими и сторонними
силами над единичным положительным зарядом на данном участке
U 12 =
A12
= ( 1 2 )
q

8. Закон Ома

ЗАКОН ОМА
В 1826 г. немецкий физик Ом Г. экспериментально открыл одноименный
закон:
сила тока, текущего по однородному металлическому проводнику,
пропорциональна падению напряжения на проводнике
1
I = U
R
где R – электрическое сопротивление проводника постоянному току (еще
называют
активное
или
омическое
сопротивление).
Электрическое сопротивление – это физическая величина, характеризующая
противодействие проводника электрическому току.
Единицей измерения
электрического сопротивления в системе СИ является Ом. В случае
однородного проводника постоянного сечения электрическое сопротивление
равно
l
R
S

9. Закон Ома

ЗАКОН ОМА
где – удельное сопротивление, измеряемое в Ом∙м; ℓ – длина проводника; S –
площадь поперечного сечения проводника. Удельное сопротивление
определяется свойствами материала и условиями, в которых он находится;
численно равно электрическому сопротивлению проводника при ℓ=1 м и S=1
м2. Для большинства металлов зависимость удельного сопротивления от
температуры дается выражением
0 1 t o
где 0 – удельное сопротивление проводника при 0 ºС; – температурный
коэффициент сопротивления; tº - температура проводника по шкале Цельсия.
При переходе к шкале Кельвина получим
0 T

10. Закон Ома

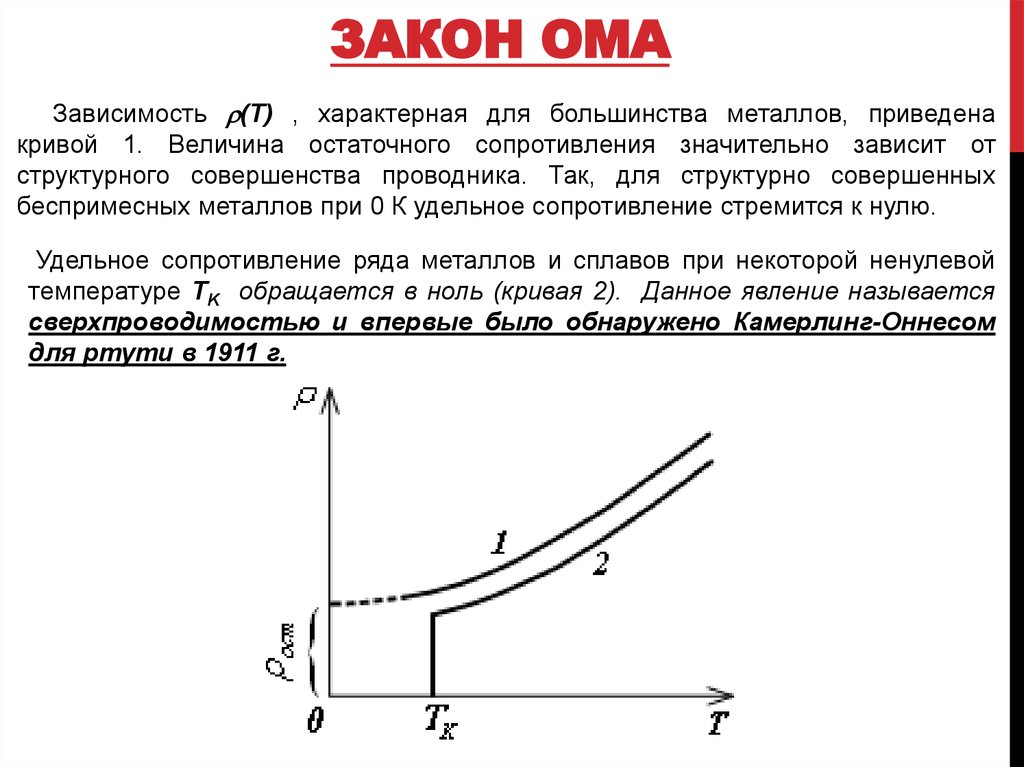
ЗАКОН ОМА
Зависимость (T) , характерная для большинства металлов, приведена
кривой 1. Величина остаточного сопротивления значительно зависит от
структурного совершенства проводника. Так, для структурно совершенных
беспримесных металлов при 0 К удельное сопротивление стремится к нулю.
Удельное сопротивление ряда металлов и сплавов при некоторой ненулевой
температуре TK обращается в ноль (кривая 2). Данное явление называется
сверхпроводимостью и впервые было обнаружено Камерлинг-Оннесом
для ртути в 1911 г.

11. Закон Ома

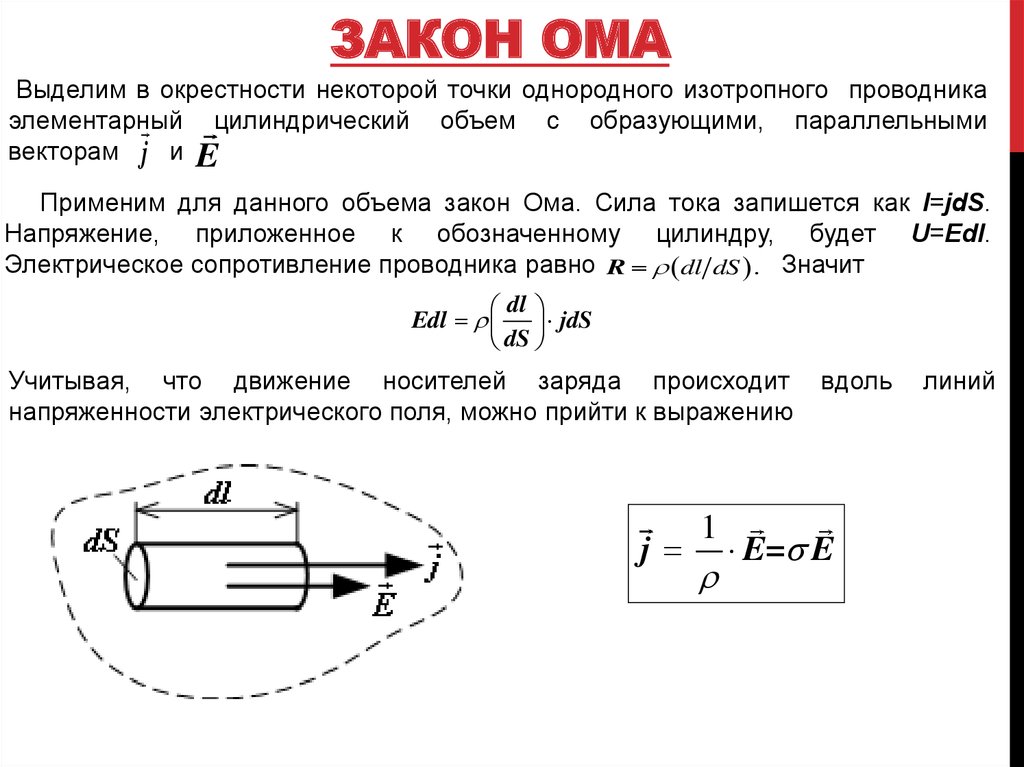
ЗАКОН ОМА
Выделим в окрестности некоторой точки однородного изотропного проводника
элементарный цилиндрический объем с образующими, параллельными
векторам j и E
Применим для данного объема закон Ома. Сила тока запишется как I=jdS.
Напряжение, приложенное к обозначенному цилиндру, будет U=Edl.
Электрическое сопротивление проводника равно R dl dS . Значит
dl
Edl jdS
dS
Учитывая, что движение носителей заряда происходит
напряженности электрического поля, можно прийти к выражению
j
1
вдоль
E= E
линий

12. Закон Ома

ЗАКОН ОМА
Рассмотрим
неоднородный
участок
электрической цепи, т.е. такой участок, на
котором действуют сторонние силы.
Запишем для данного участка закон
Ома в дифференциальной форме
j E+EÑÒÎ Ð
Как поле электростатическое, так и поле сторонних сил выполняет работу над
носителями заряда на участке электрической цепи 12, что записывается в виде
2
A12
Edl ,
1
2
A12 ÑÒÎ Ð
E
ÑÒÎ Ð
1
dl .

13. Закон Ома

ЗАКОН ОМА
Преобразуем записанный выше закон Ома следующим образом:
j dl E+EÑÒÎ Ð dl ,
где dl – элементарное перемещение носителя заряда на участке электрической
цепи 12.
Проинтегрировав данное выражение для участка 12 а также, учитывая, что A12
= j1 – j2 и A12 СТОР = 12, получим
l
jl12 1 2 12 I 12 1 2 12 IR12 1 2 12 .
S
Последнее выражение и есть закон Ома для неоднородного участка цепи.
Данную формулу часто представляю в виде
I
1 2 12
R12

14. Закон Ома

ЗАКОН ОМА
В случае, если цепь замкнутая, т.е. j1 = j2, на основании закона Ома для
неоднородного участка электрической цепи, можно получить закон Ома
для замкнутой цепи:
I
R
где
– ЭДС, действующая в замкнутой цепи; R – омическое
электросопротивление цепи.

15. Закон Джоуля – Ленца

ЗАКОН ДЖОУЛЯ – ЛЕНЦА
Как известно, проводник нагревается при протекании по нему электрического
тока. В 1831-1842 гг. Джоуль Дж. и независимо от него Ленц Э.Х.
экспериментально установили, что при этом количество выделяющейся теплоты
определяется как
Q I 2 Rt
где I – сила тока в проводнике; R – электросопротивление проводника; t –
время протекания тока.
Проводник нагревается за счет работы сил электрического поля над носителями
заряда. Данная работа также равна A I 2 Rt Заметим, что используя закон
Ома для однородного участка цепи и понятие силы тока приведенным
выражениям можно придать вид
2
U
Q A I 2 Rt IU t
t qU .
R

16. Закон Джоуля – Ленца

ЗАКОН ДЖОУЛЯ – ЛЕНЦА
Выделим в проводнике элементарный цилиндрический объем dV с площадью
поперечного сечения dS и длиной dl. В данном объеме за время dt выделится
количество теплоты
dl
2
dQ I 2 Rd t j dS d t j 2 dl dS d t j 2 dV d t.
dS
Разделив выражение на dV dt получим удельную мощность тока –
количество теплоты, выделяющейся за единицу времени в единице
объема проводника
j E
2
2
Это закон Джоуля – Ленца в дифференциальной форме.

17. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

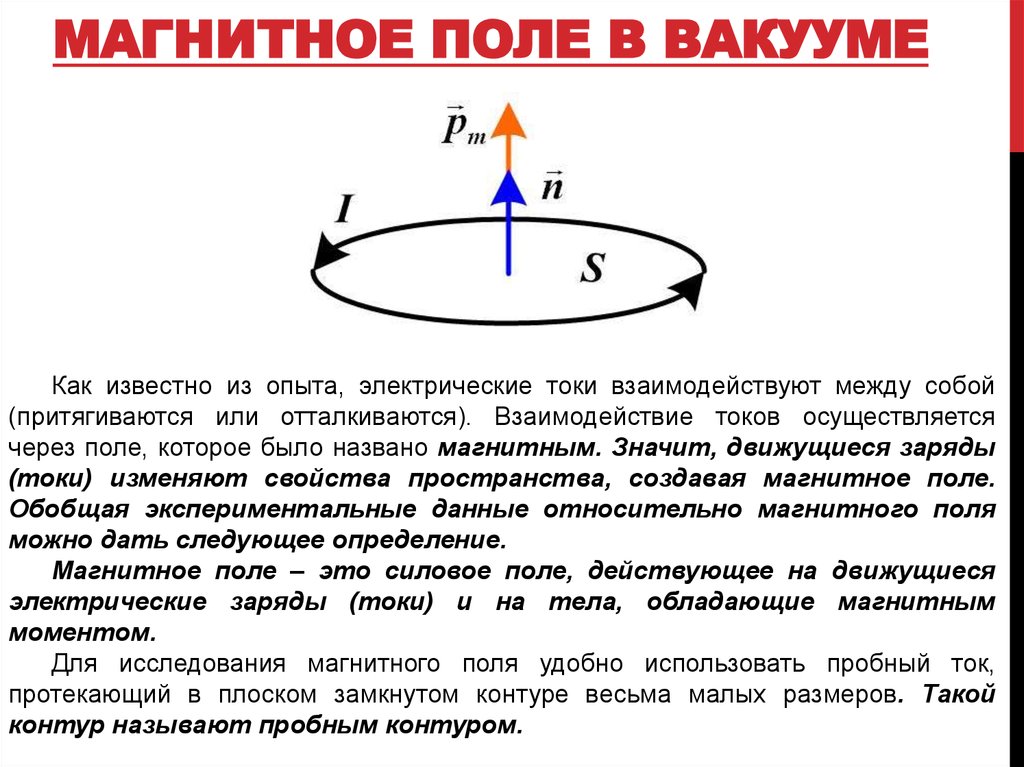
Как известно из опыта, электрические токи взаимодействуют между собой
(притягиваются или отталкиваются). Взаимодействие токов осуществляется
через поле, которое было названо магнитным. Значит, движущиеся заряды
(токи) изменяют свойства пространства, создавая магнитное поле.
Обобщая экспериментальные данные относительно магнитного поля
можно дать следующее определение.
Магнитное поле – это силовое поле, действующее на движущиеся
электрические заряды (токи) и на тела, обладающие магнитным
моментом.
Для исследования магнитного поля удобно использовать пробный ток,
протекающий в плоском замкнутом контуре весьма малых размеров. Такой
контур называют пробным контуром.

18. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

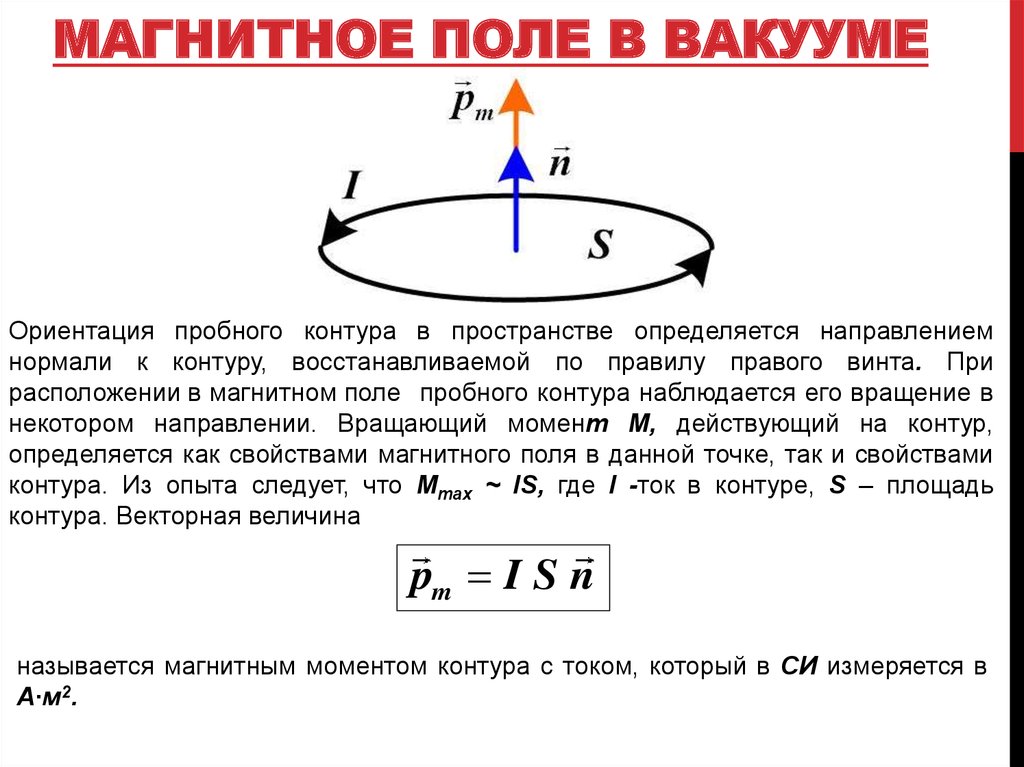
Ориентация пробного контура в пространстве определяется направлением
нормали к контуру, восстанавливаемой по правилу правого винта. При
расположении в магнитном поле пробного контура наблюдается его вращение в
некотором направлении. Вращающий момент М, действующий на контур,
определяется как свойствами магнитного поля в данной точке, так и свойствами
контура. Из опыта следует, что Мmax ~ IS, где I -ток в контуре, S – площадь
контура. Векторная величина
pm I S n
называется магнитным моментом контура с током, который в СИ измеряется в
А∙м2.

19. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

Наблюдая в данной точке магнитного поля пробные контуры с
различными рm, можно сделать вывод, что на контуры действуют разные по
величине Мmax. В то же время отношение Мmax / рm будет для всех контуров
одинаково. Данное отношение можно использовать как силовую характеристику
магнитного поля. Данная характеристика называется магнитной индукцией.
Магнитная индукция – вектор B, направление которого определяется
равновесным направлением нормали к пробному контуру, а модуль B Mmax pm
Поле вектора B можно представить с помощью силовых линий.
Магнитная индукция в СИ измеряется в теслах. 1 Тесла равен магнитной
индукции однородного поля, в котором на плоский контур с током с магнитным
моментом 1 А∙м2, действует максимальный вращающий момент, равный 1 Н м.

20. Закон Био - Савара - Лапласа

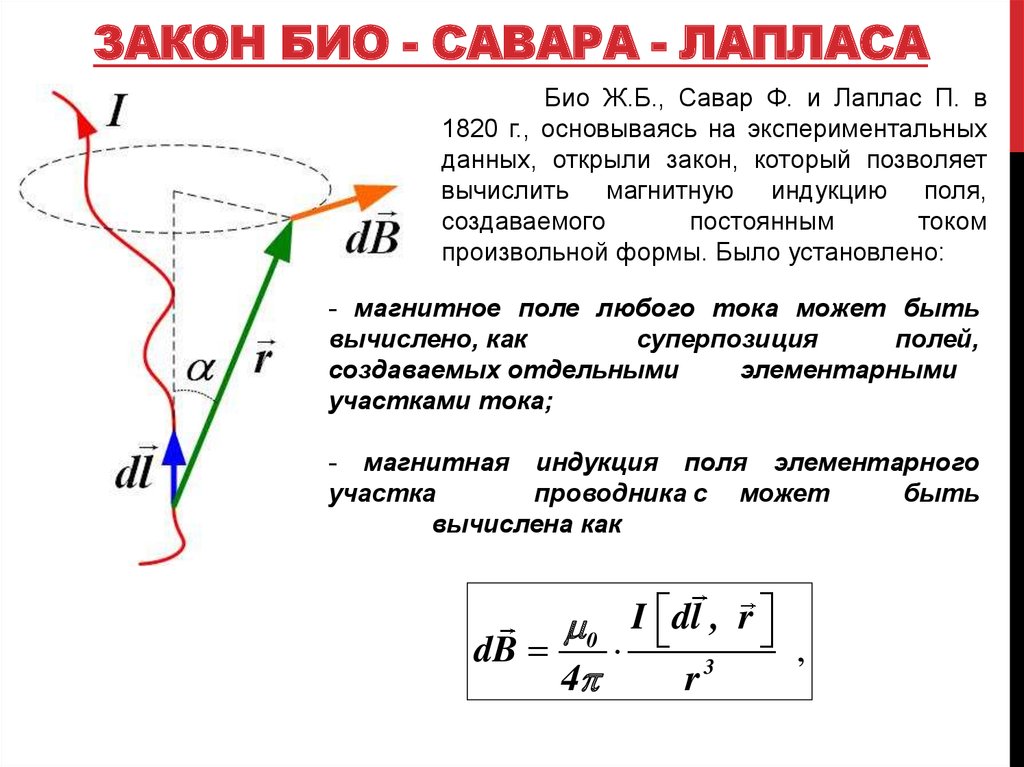
ЗАКОН БИО - САВАРА - ЛАПЛАСА
Био Ж.Б., Савар Ф. и Лаплас П. в
1820 г., основываясь на экспериментальных
данных, открыли закон, который позволяет
вычислить магнитную индукцию поля,
создаваемого
постоянным
током
произвольной формы. Было установлено:
- магнитное поле любого тока может быть
вычислено, как
суперпозиция
полей,
создаваемых отдельными
элементарными
участками тока;
- магнитная индукция поля элементарного
участка
проводника с может
быть
вычислена как
0 I dl , r
dB
,
3
4
r

21. Закон Био - Савара - Лапласа

ЗАКОН БИО - САВАРА - ЛАПЛАСА
0
=
I
–
где
4 ∙ 10-7 Гн/м – магнитная
постоянная;
сила
тока
в
проводнике;
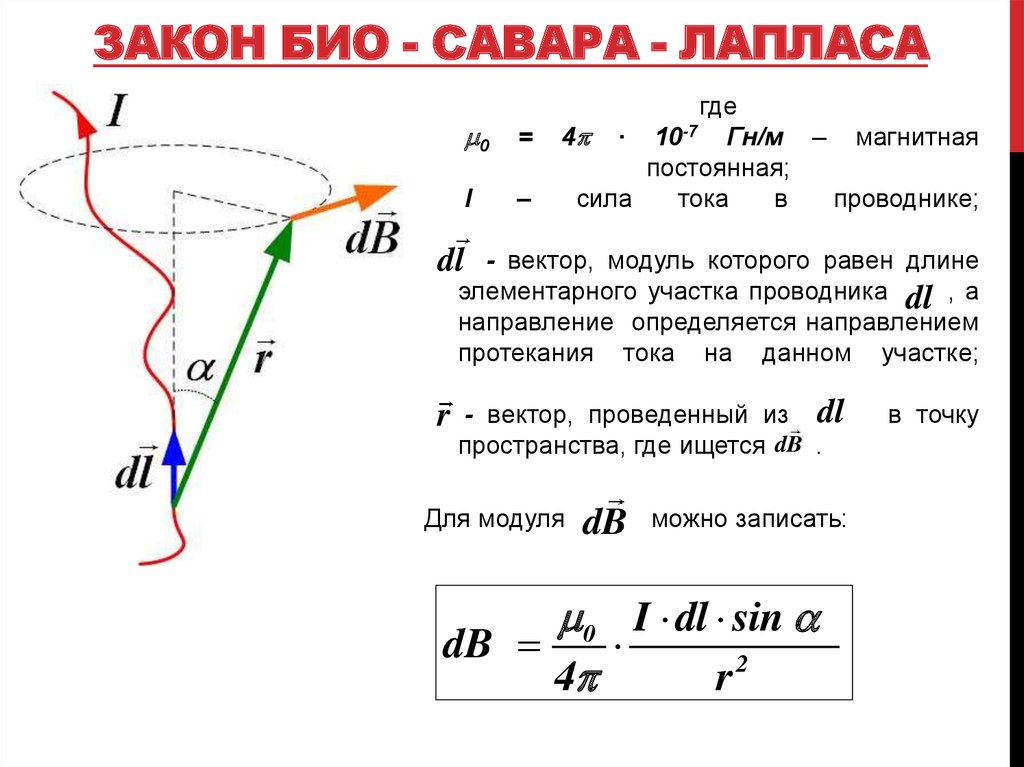
- вектор, модуль которого равен длине
элементарного участка проводника dl , а
направление определяется направлением
протекания тока на данном участке;
dl
r
- вектор, проведенный из dl
пространства, где ищется dB .
Для модуля
dB
можно записать:
0 I dl sin
dB
2
4
r
в точку

22. Закон Био - Савара - Лапласа

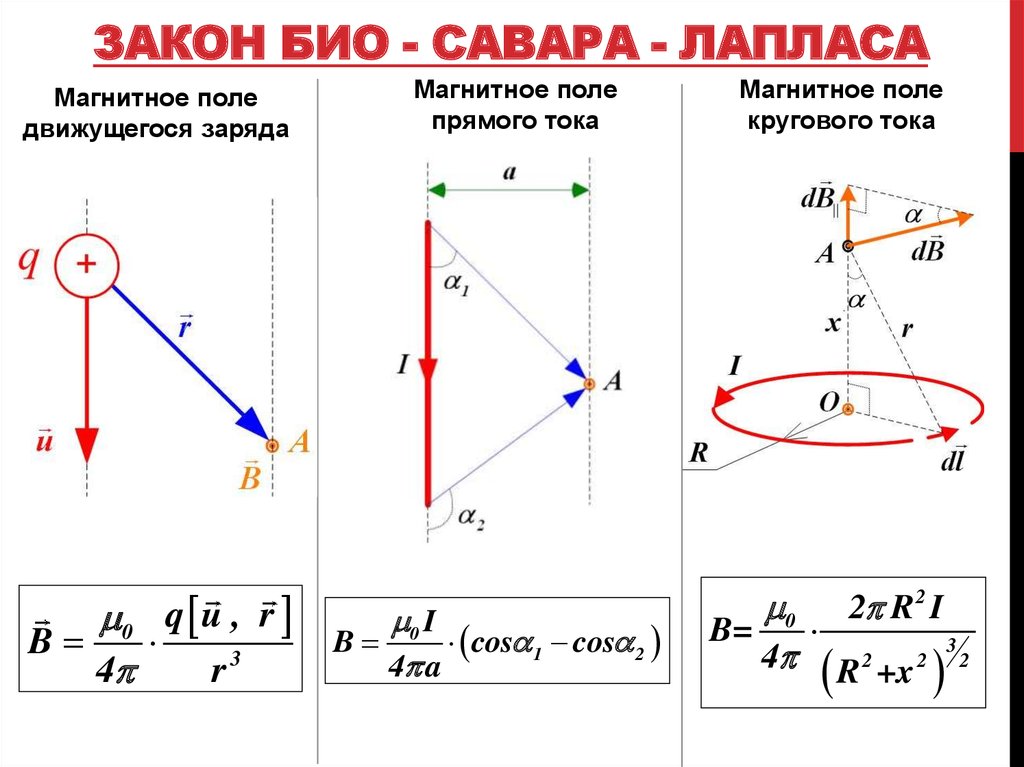
ЗАКОН БИО - САВАРА - ЛАПЛАСА
Магнитное поле
движущегося заряда
0 q u , r
B
4
r3
Магнитное поле
прямого тока
0 I
B
cos 1 cos 2
4 a
Магнитное поле
кругового тока
0 2 R 2 I
B=
4 R 2 +x 2 3 2

23. Закон АМПЕРА

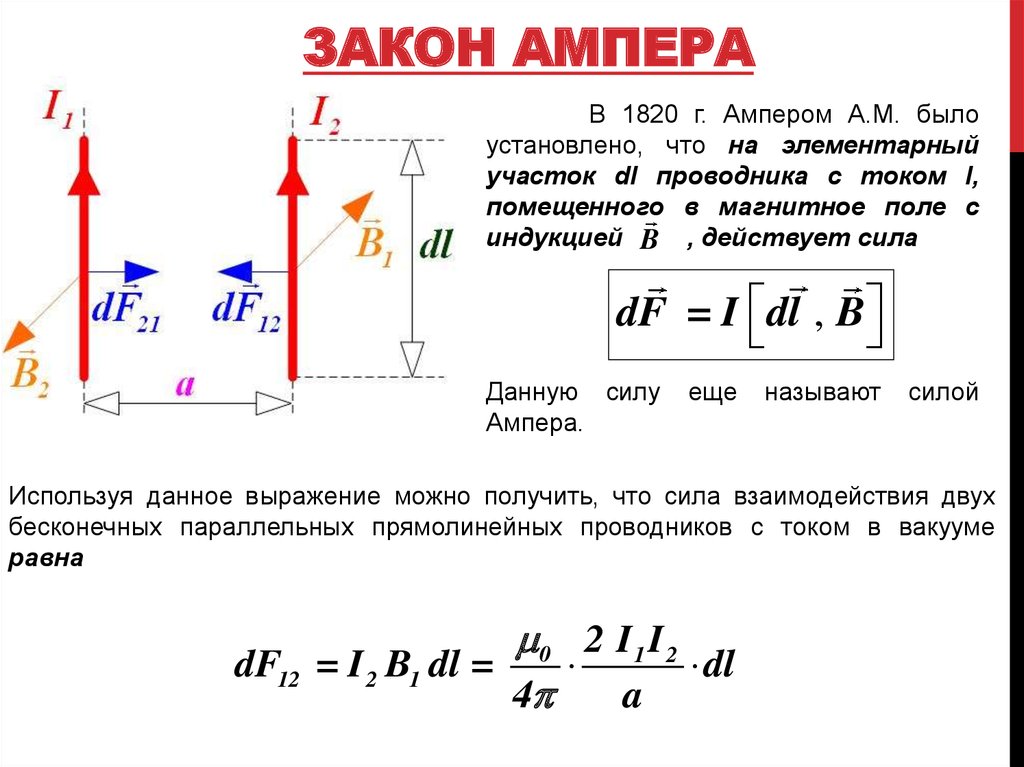
ЗАКОН АМПЕРА
В 1820 г. Ампером А.М. было
установлено, что на элементарный
участок dl проводника с током I,
помещенного в магнитное поле с
индукцией B , действует сила
dF = I dl , B
Данную силу
Ампера.
еще
называют
силой
Используя данное выражение можно получить, что сила взаимодействия двух
бесконечных параллельных прямолинейных проводников с током в вакууме
равна
0 2 I 1 I 2
dF12 = I 2 B1 dl =
dl
4
a

24. Закон АМПЕРА

ЗАКОН АМПЕРА
Это сила, действующая со стороны
проводника с током I1 на проводник с
током I2. Величина силы dF21 такая же.
Т.о. сила приходящаяся на единицу
длины проводника равна
dF 0 2 I 1 I 2
=
dl
4
a
Исходя из последнего соотношения устанавливается единица силы тока в
СИ.
Ампер – это такая сила постоянного тока, который проходя по двум
параллельным прямолинейным проводникам бесконечной длины и ничтожно
малого сечения, расположенным на расстоянии 1 м друг от друга в вакууме,
вызывал бы между данными проводниками силу взаимодействия 2∙10-7 Н.

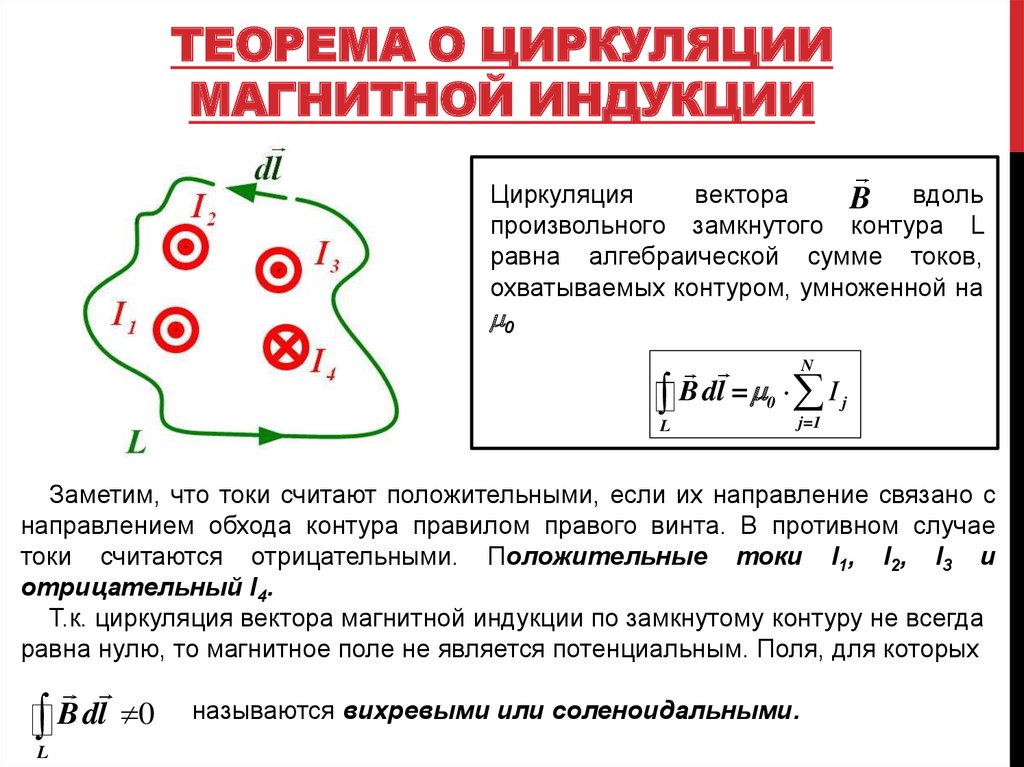
25. ТЕОРЕМА О ЦИРКУЛЯЦИИ МАГНИТНОЙ ИНДУКЦИИ

Циркуляция
вектора
B вдоль
произвольного замкнутого контура L
равна алгебраической сумме токов,
охватываемых контуром, умноженной на
0
N
B dl = I
0
L
j
j=1
Заметим, что токи считают положительными, если их направление связано с
направлением обхода контура правилом правого винта. В противном случае
токи считаются отрицательными. Положительные токи I1, I2, I3 и
отрицательный I4.
Т.к. циркуляция вектора магнитной индукции по замкнутому контуру не всегда
равна нулю, то магнитное поле не является потенциальным. Поля, для которых
B dl 0
L
называются вихревыми или соленоидальными.