https___school.mos.ru_ej_attachments_files_217_319_781_original_%D0%9F%D0%B0%D1%80%D0%B0%D0%BB%D0%BB%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%8C%20%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D0%B9%20%D0%B8%20%D0%BF%D0%BB%D0

1.

2.

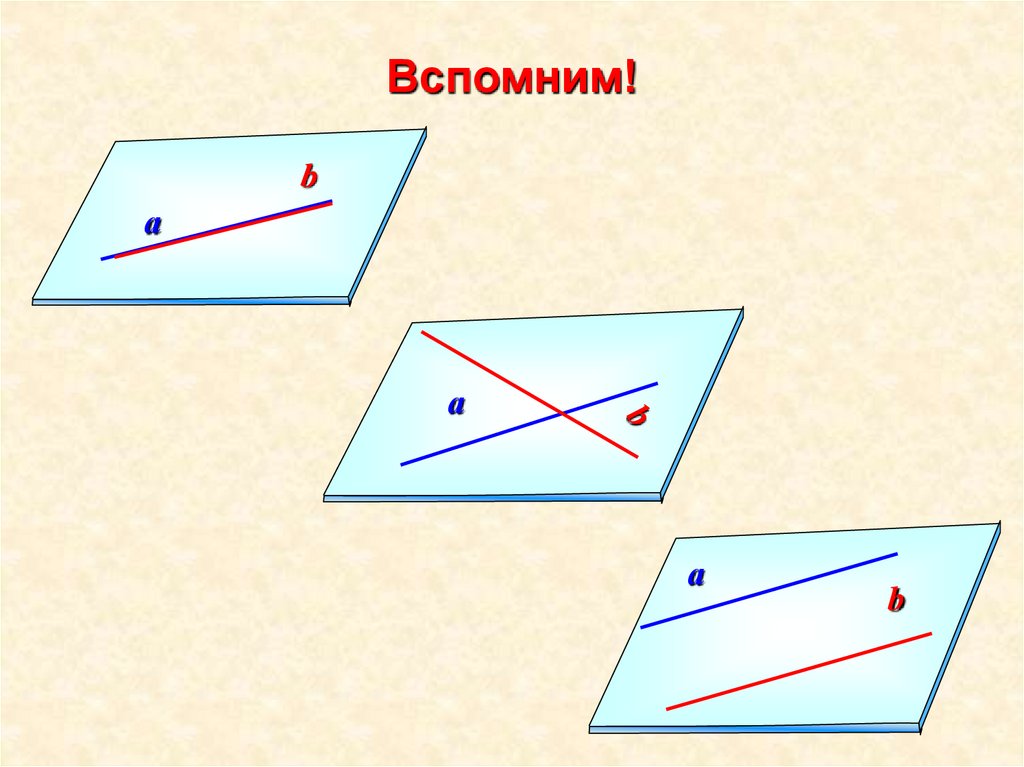
Вспомним!
а
а
а
b

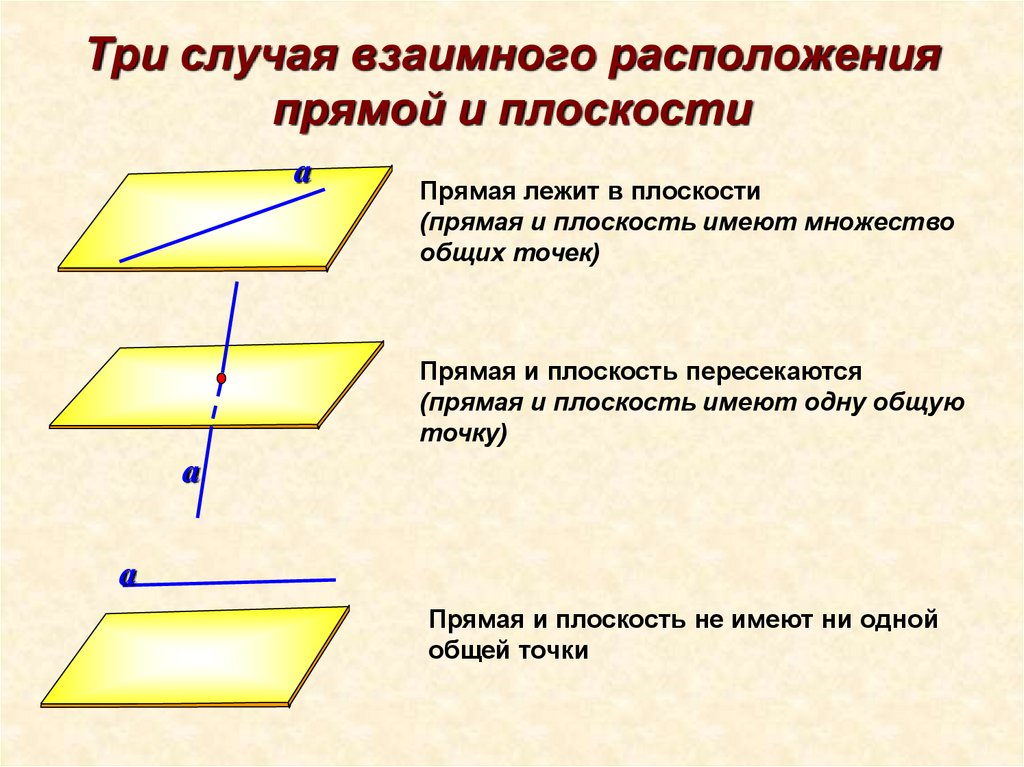
3. Три случая взаимного расположения прямой и плоскости

a
Прямая лежит в плоскости
(прямая и плоскость имеют множество
общих точек)
Прямая и плоскость пересекаются
(прямая и плоскость имеют одну общую
точку)
a
a
Прямая и плоскость не имеют ни одной
общей точки

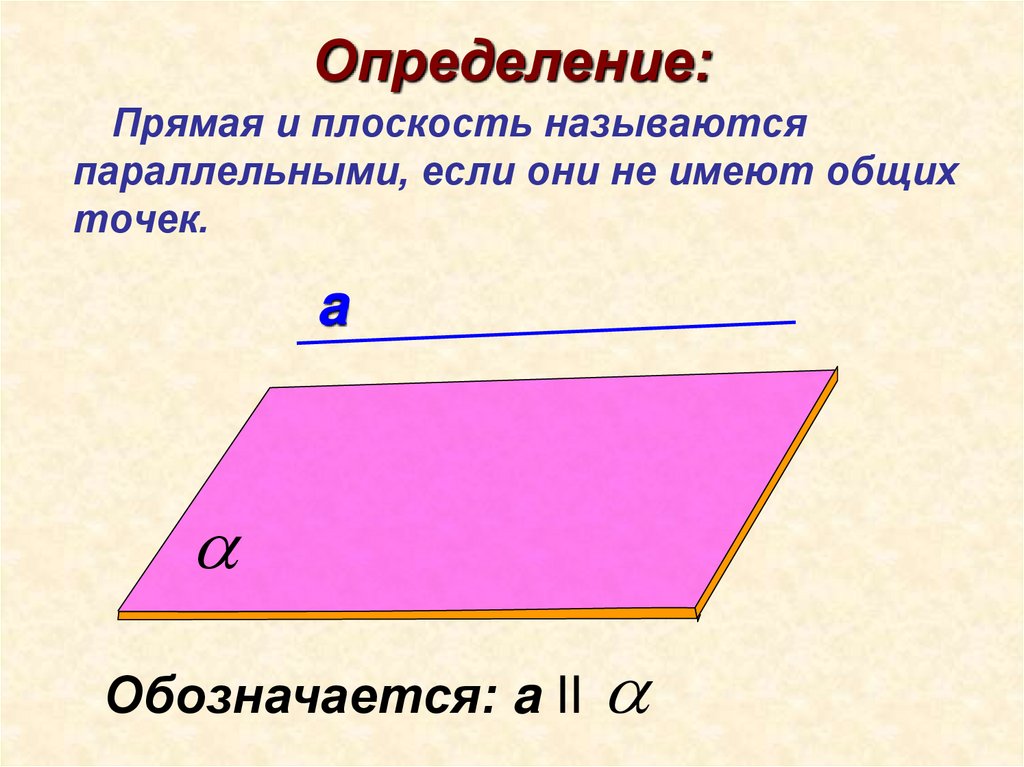
4. Определение:

Прямая и плоскость называются
параллельными, если они не имеют общих
точек.
a
Обозначается: a II

5.

6.

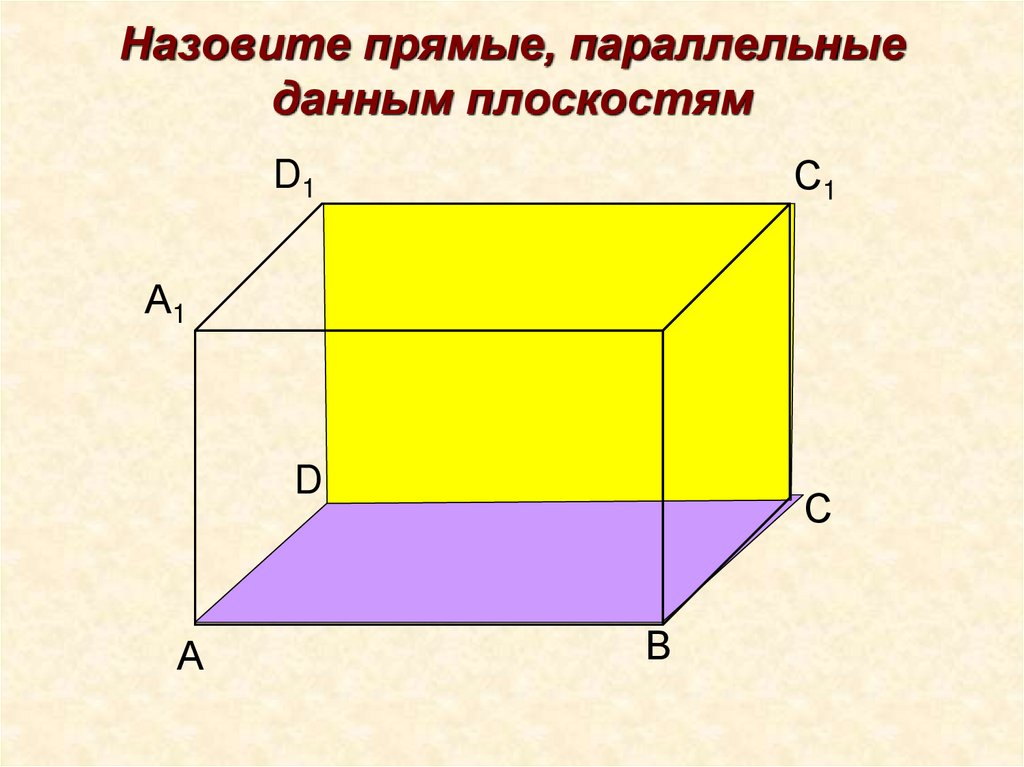
а

7. Назовите прямые, параллельные данным плоскостям

С1
D1
А1
D
А
С
В

8.

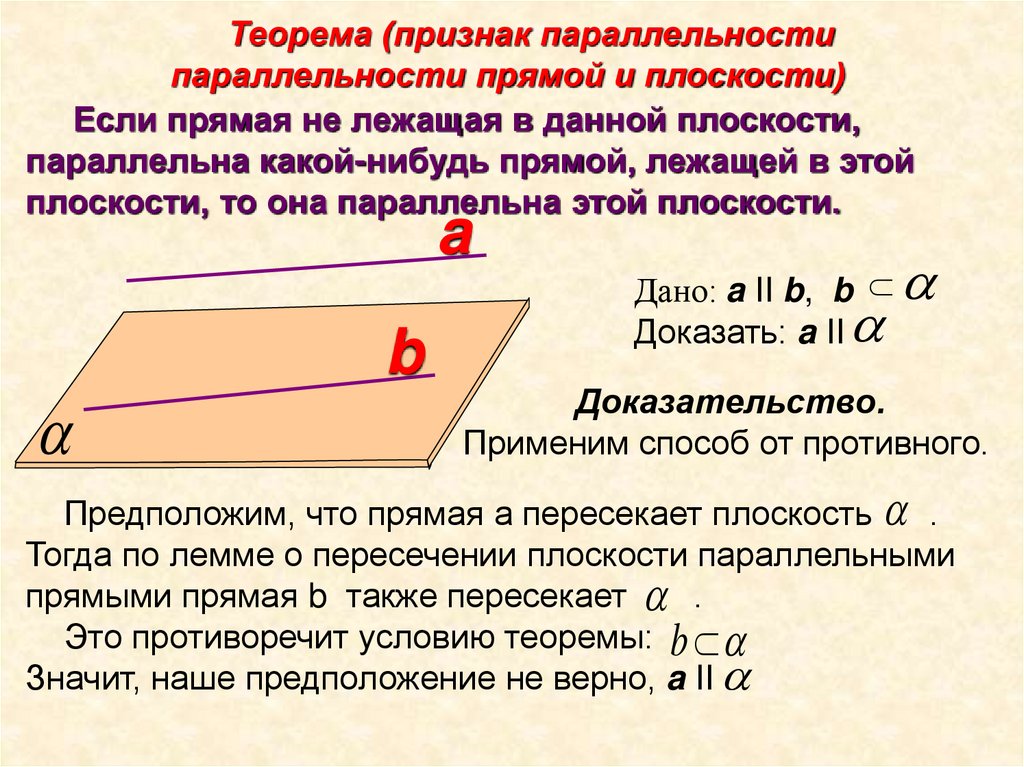
Теорема (признак параллельности
параллельности прямой и плоскости)
Если прямая не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой
плоскости, то она параллельна этой плоскости.
a
b
Дано: a II b, b
Доказать: a II
Доказательство.
Применим способ от противного.
Предположим, что прямая а пересекает плоскость .
Тогда по лемме о пересечении плоскости параллельными
прямыми прямая b также пересекает .
Это противоречит условию теоремы: b
Значит, наше предположение не верно, a II

9.

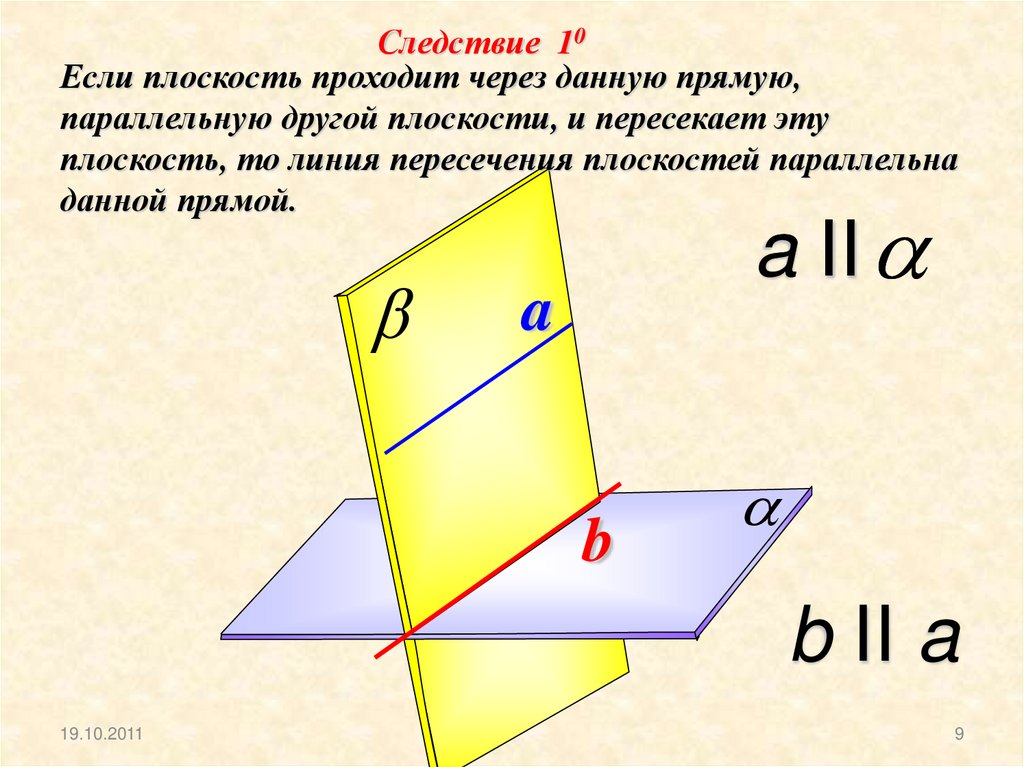
Следствие 10
Если плоскость проходит через данную прямую,
параллельную другой плоскости, и пересекает эту
плоскость, то линия пересечения плоскостей параллельна
данной прямой.
a II
a
b
b II a
19.10.2011
9

10.

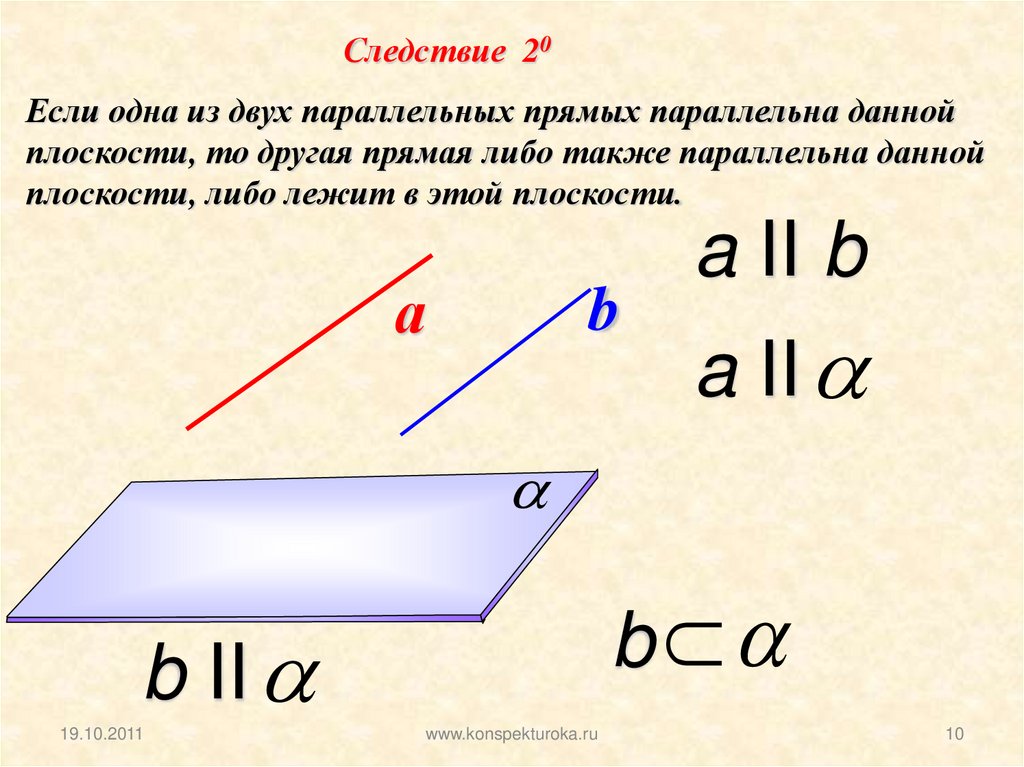
Следствие 20
Если одна из двух параллельных прямых параллельна данной
плоскости, то другая прямая либо также параллельна данной
плоскости, либо лежит в этой плоскости.
а
b
a II b
a II
b
b II
19.10.2011
www.konspekturoka.ru
10

11.

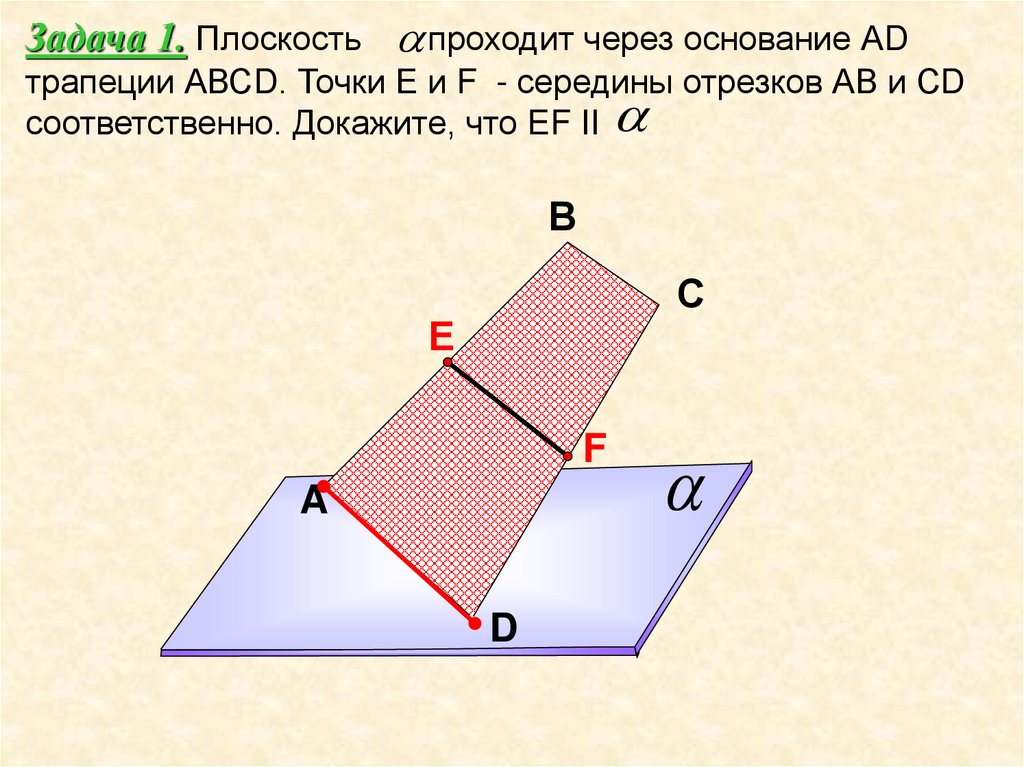
Задача 1. Плоскость проходит через основание АD
трапеции АВСD. Точки Е и F - середины отрезков АВ и СD
соответственно. Докажите, что EF II
В
С
Е
F
A
D

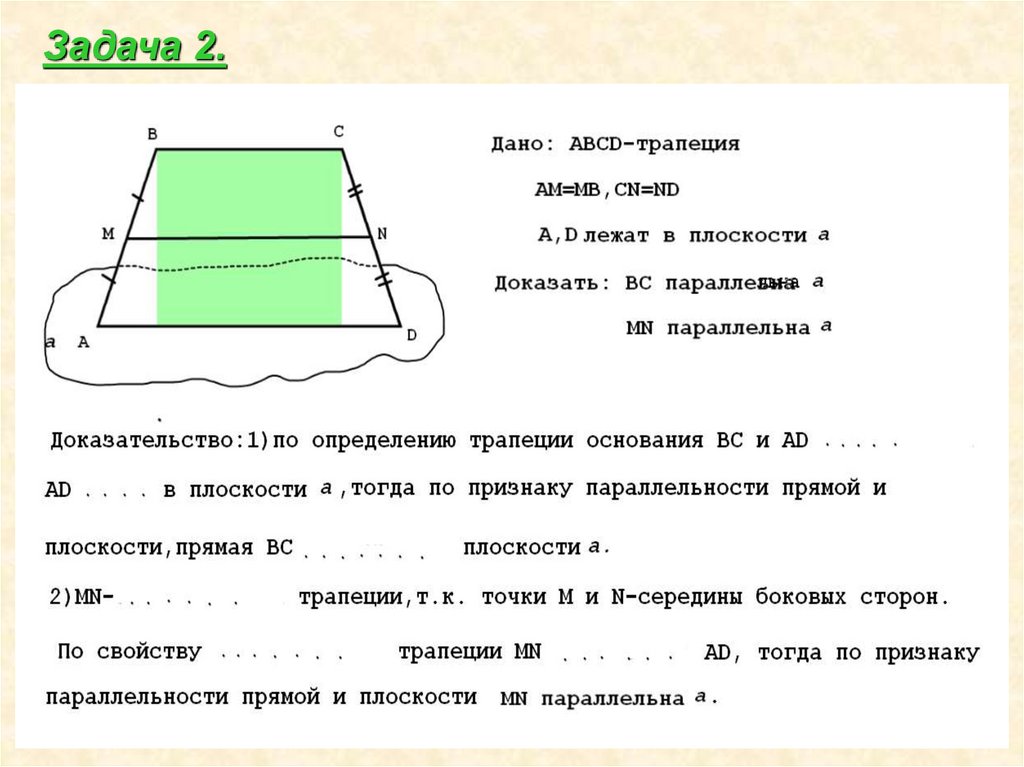
12.

Задача 2.

13. Подведение итогов занятия.

Назовите три случая взаимного расположения
прямой и плоскости.
Какие прямая и плоскость называются
параллельными?
Назовите признак параллельности прямой и
плоскости.
Домашнее задание!
Изучить §1, пункт 6, решить задачу № 20.