9e2e21d39b614c798866bb2561ec566e

1. Функция, способы задания функции. Взаимно обратные функции. График функции. Область определения и множество значений функции.

Нули функции.
Промежутки знакопостоянства

2. Исторические сведения

Немецкий философ Вильгельм Лейбниц
(1646-1716) использовал этот термин для
обозначения весьма разнообразных понятий
в алгебре, геометрии, механике.
Леонард Эйлер (1707-1783) швейцарский, немецкий и
российский математик, трактовал математическую
функцию в максимальной общности: «Когда некоторые
количества зависят от других таким образом, что при
изменении последних и сами они подвергаются изменению,
то первые называются функциями…»
Серьезный вклад принадлежит
российскому математику Николаю
Ивановичу Лобачевскому (1792-1856)
и немецкому математику Иоганну
Дирихле (1805-1859)

3. Исторические сведения

Джузеппе Пиано (1858-1932) итальянский
математик; «Отображение f: X
Y
множество Х в множество Y
Исаак Ньютон (1642-1727) английский
физик и математик опубликовал правила
исследования функций с помощью
производной
Исторически первыми
были использованы
таблично заданные
тригонометрические
функциив астрономии
древнегреческим ученым
Клавдием Птолимеем (ок.
87-165) и индийским
астрономом и математиком
Ариабхатой (476-ок. 550)

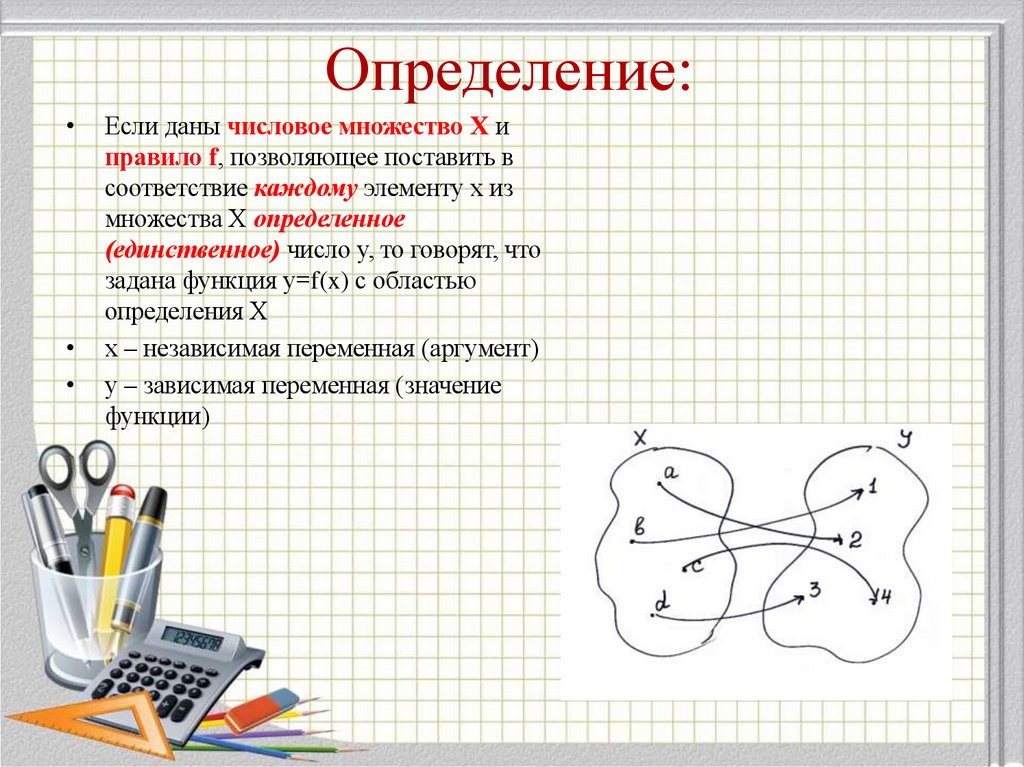
4. Определение:

Если даны числовое множество Х и
правило f, позволяющее поставить в
соответствие каждому элементу х из
множества Х определенное
(единственное) число у, то говорят, что
задана функция у=f(x) с областью
определения Х
х – независимая переменная (аргумент)
у – зависимая переменная (значение
функции)

5.

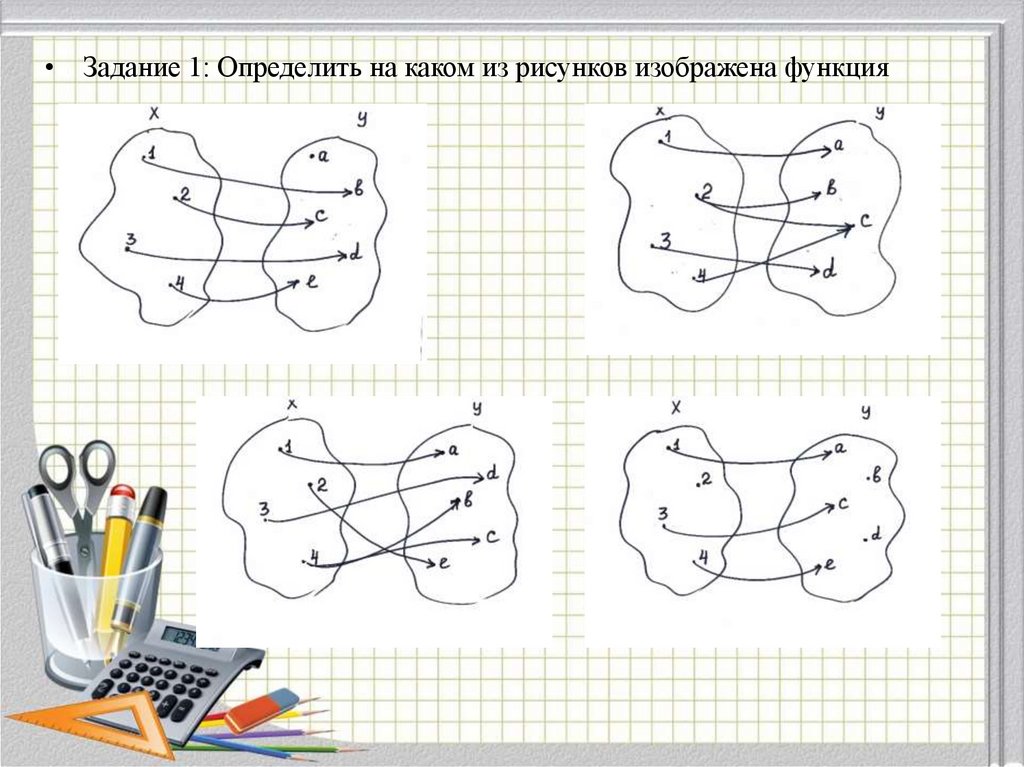
• Задание 1: Определить на каком из рисунков изображена функция

6.

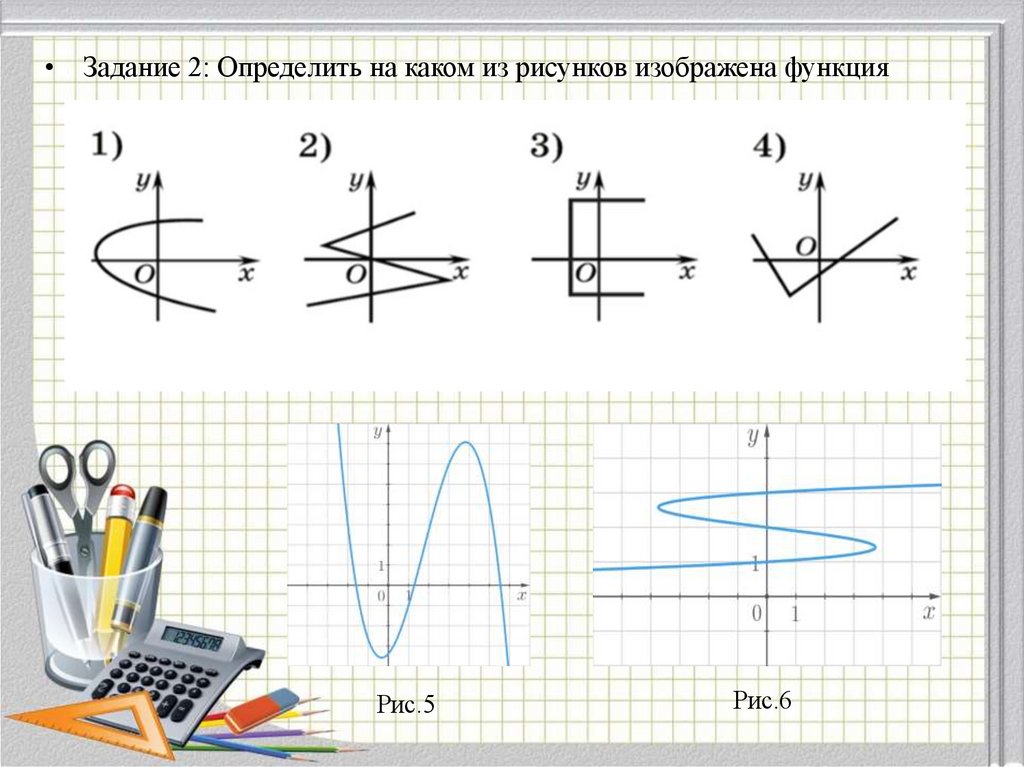
• Задание 2: Определить на каком из рисунков изображена функция
Рис.5
Рис.6

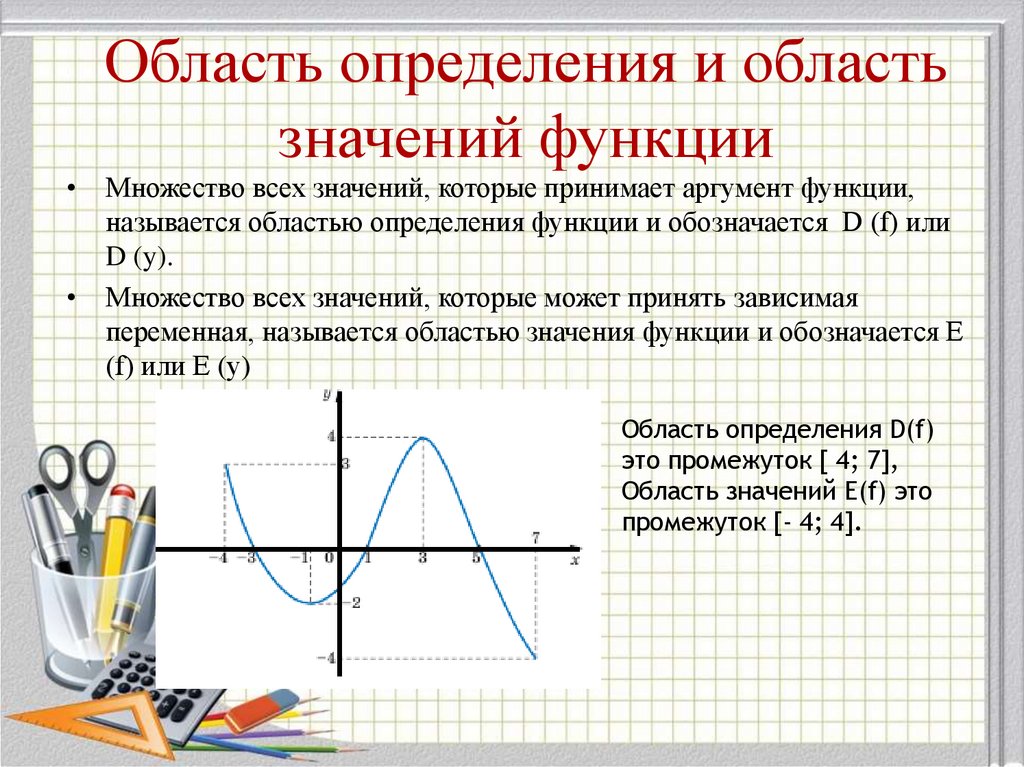
7. Область определения и область значений функции

• Множество всех значений, которые принимает аргумент функции,
называется областью определения функции и обозначается D (f) или
D (y).
• Множество всех значений, которые может принять зависимая
переменная, называется областью значения функции и обозначается E
(f) или E (y)
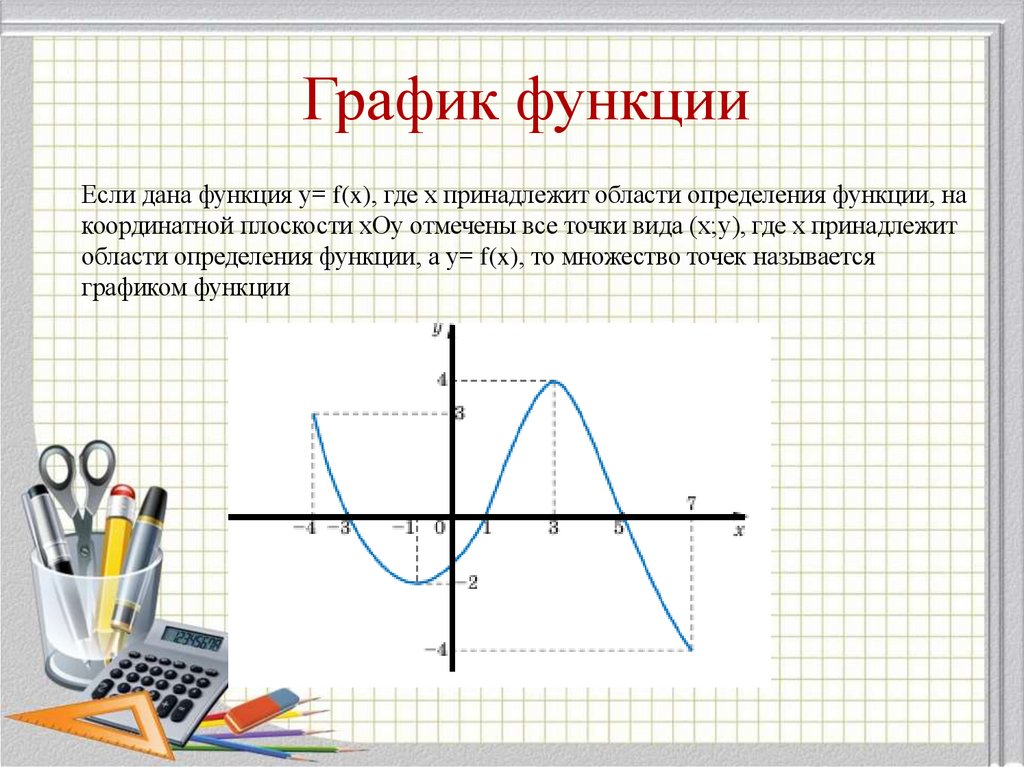
Область определения D(f)
это промежуток [ 4; 7],
Область значений E(f) это
промежуток [- 4; 4].

8.

• Задание 3: Найди область определения функции
Ответ:

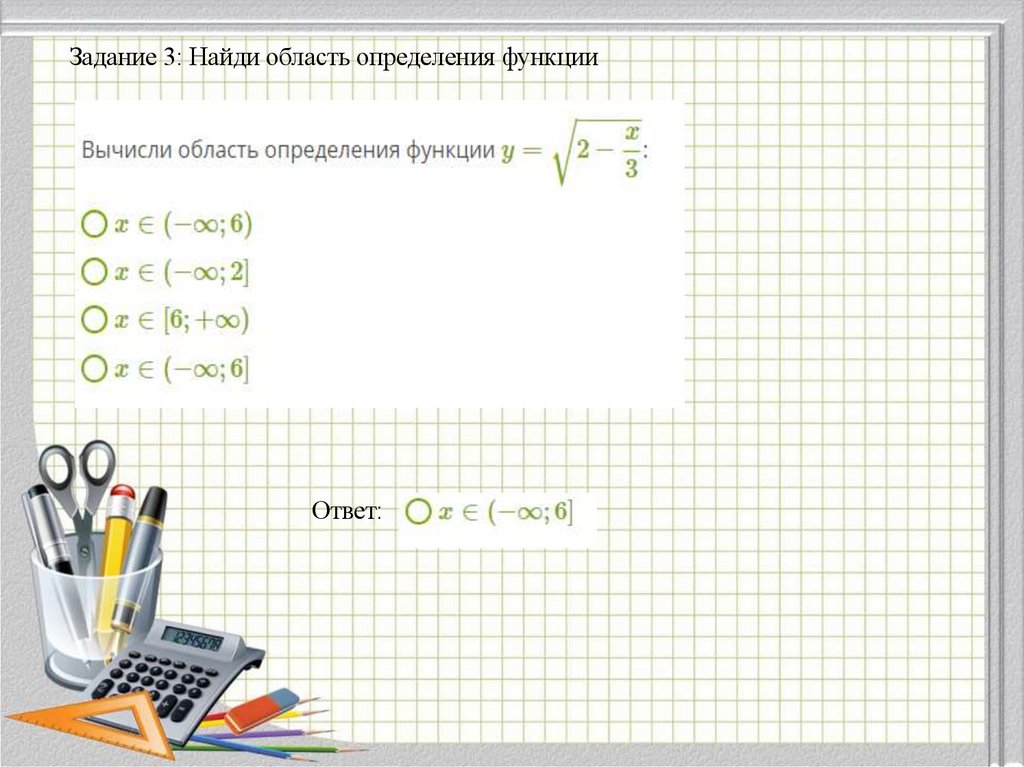
9.

Задание 3: Найди область определения функции
Ответ:

10. Способы задания функции

1.
2.
Описательный. Этот способ состоит в том, что функциональная зависимость
выражается словами.
Графический. Множество всех точек плоскости, координаты которых
удовлетворяют данному уравнению
3.
Аналитический. Закон, устанавливающий связь между аргументом и
функцией, задается посредством формул.
4.
Табличный. Заключается в задании таблицы отдельных значений аргумента и
соответствующих им значений функции
х 1
4
9
16
у 1
2
3
4
у=2х+3

11. Взаимно обратные функции

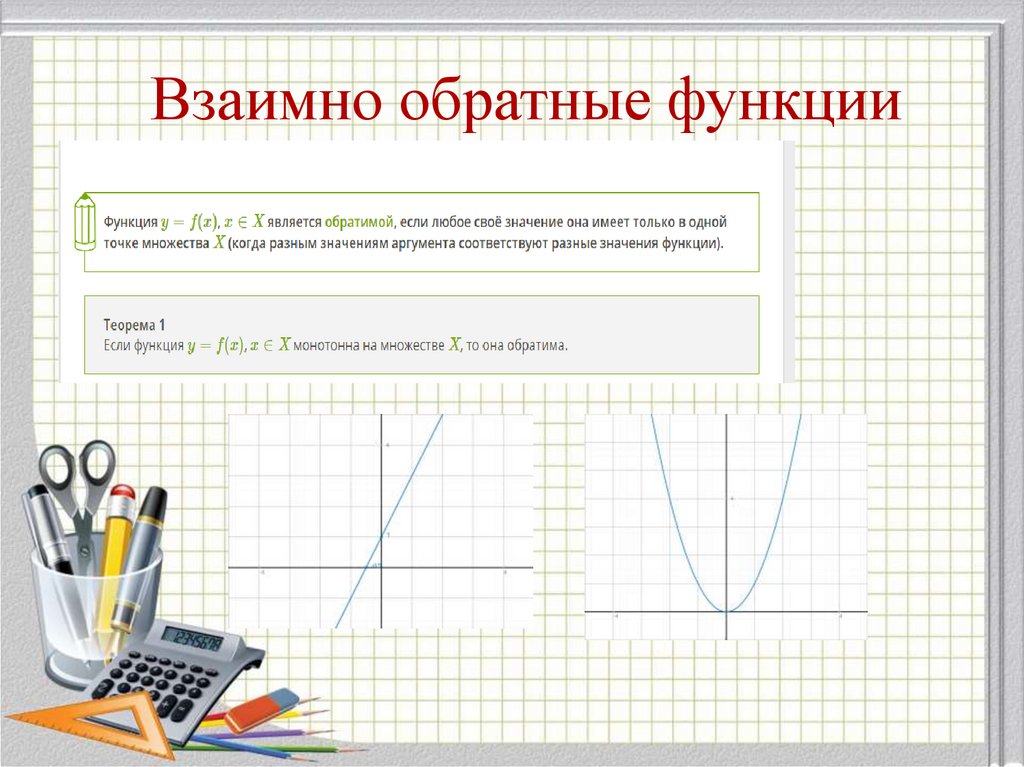
12. Взаимно обратные функции

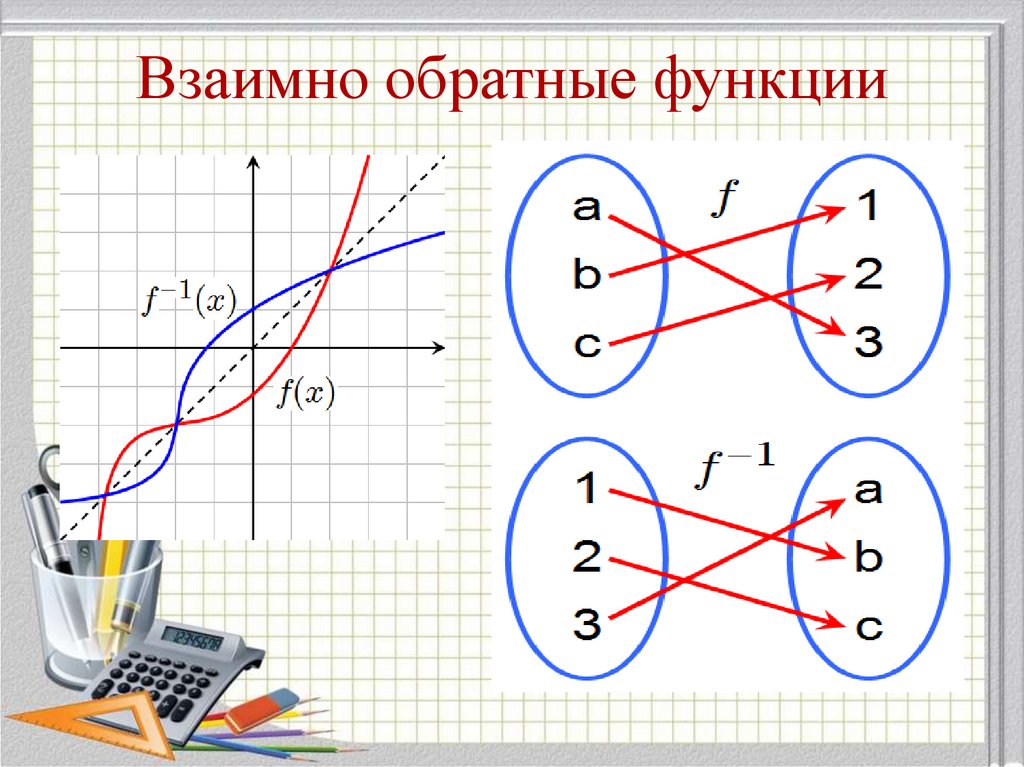
13. Взаимно обратные функции

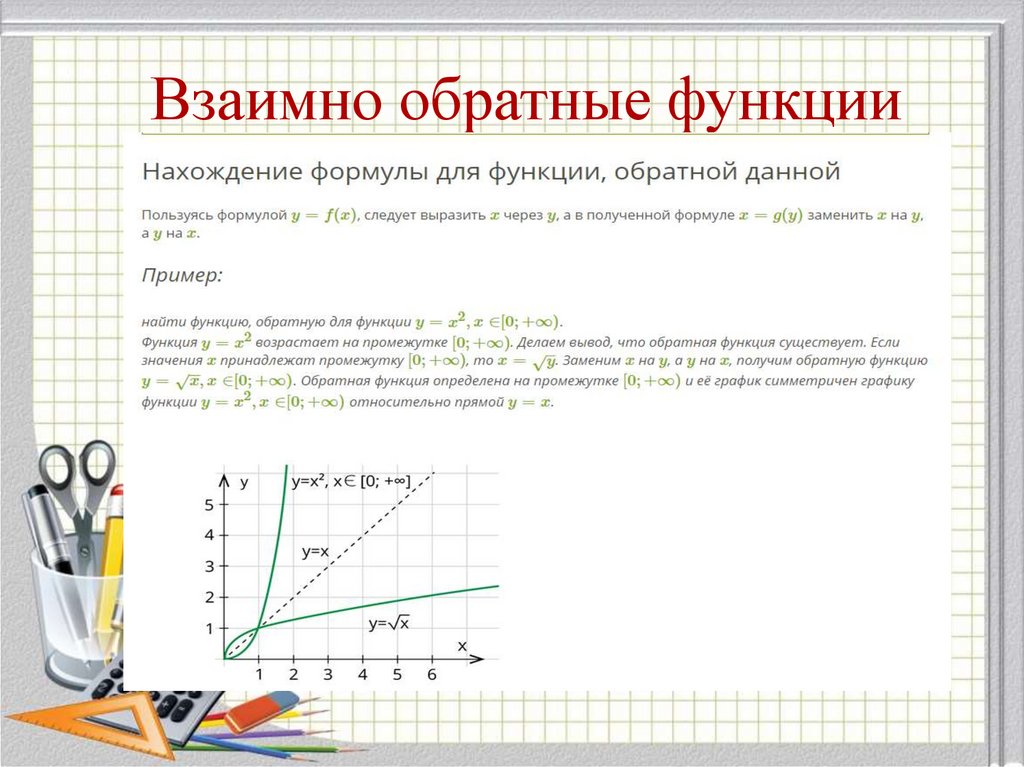
14. Взаимно обратные функции

15.

Задание 1
Задание 3
Задание 2
Задание 4

16. График функции

Если дана функция у= f(x), где х принадлежит области определения функции, на
координатной плоскости хОу отмечены все точки вида (х;у), где х принадлежит
области определения функции, а у= f(x), то множество точек называется
графиком функции

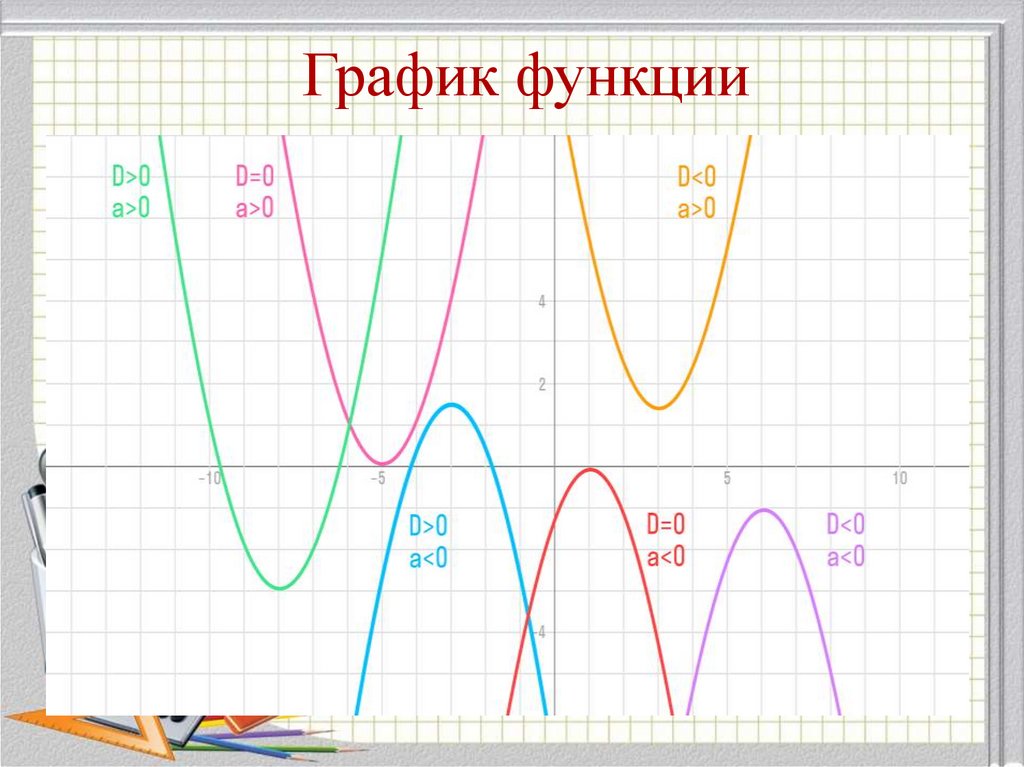
17. График функции

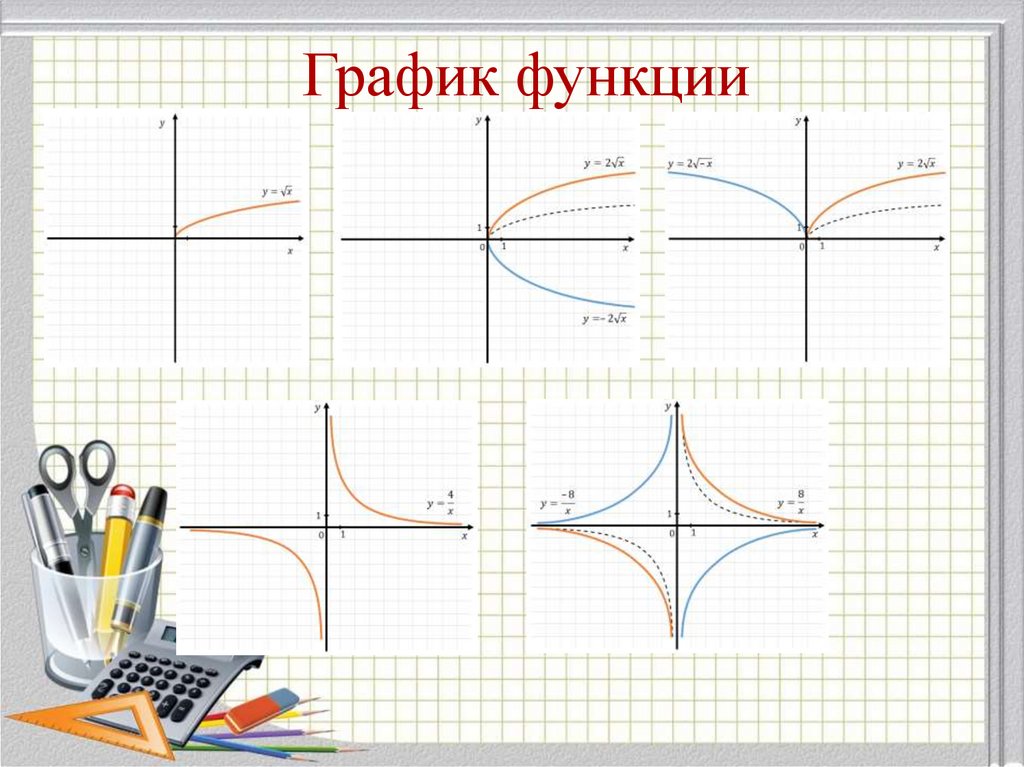
18. График функции

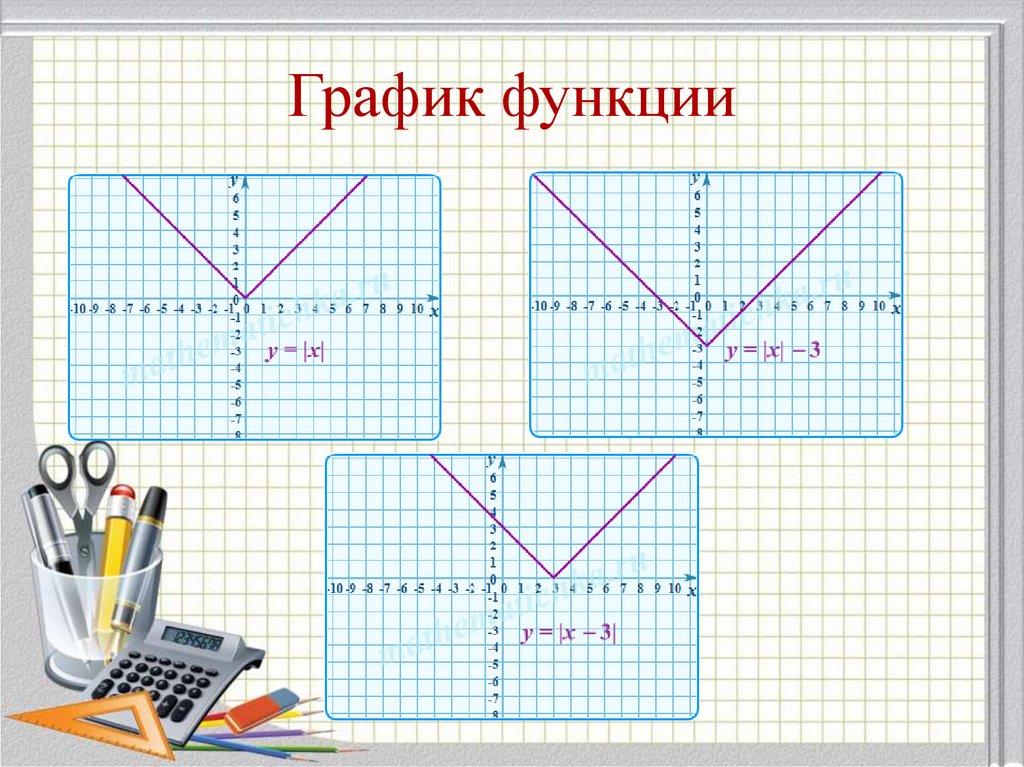
19. График функции

20. График функции

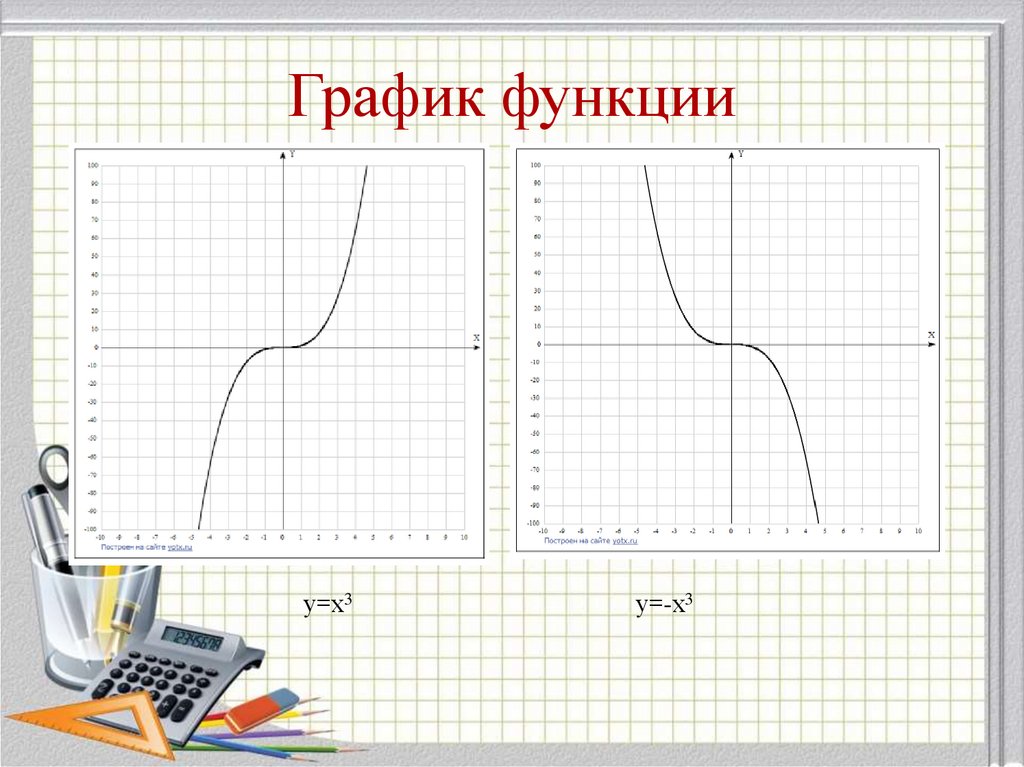
21. График функции

у=х3
у=-х3

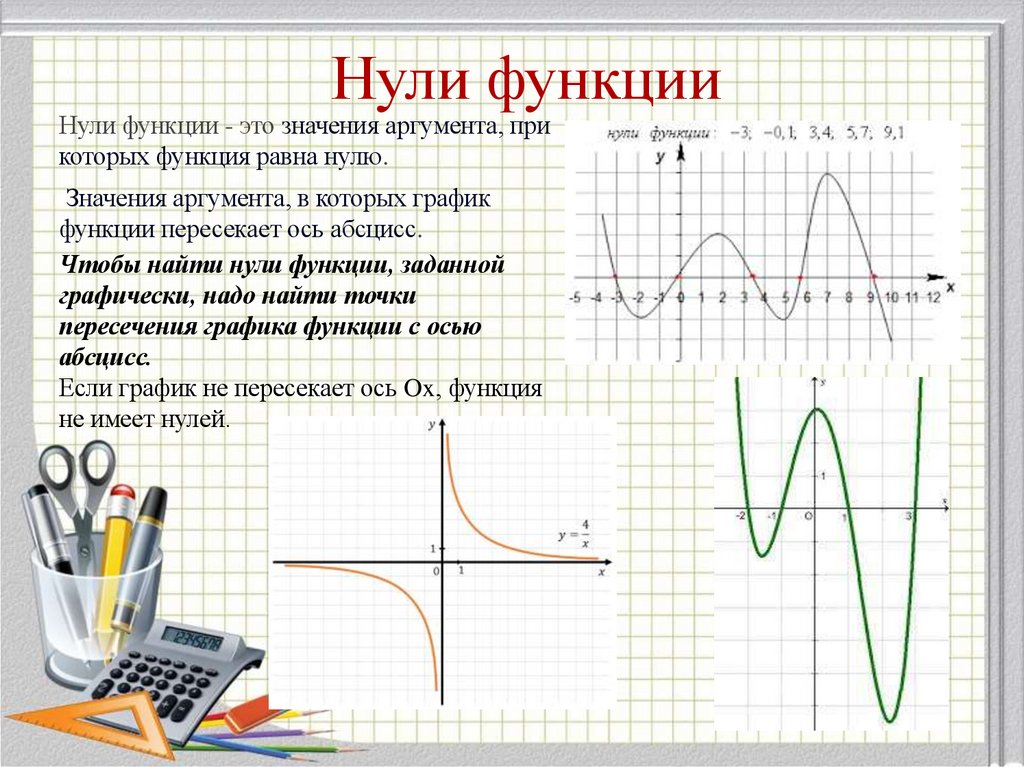
22. Нули функции

Нули функции - это значения аргумента, при
которых функция равна нулю.
Значения аргумента, в которых график
функции пересекает ось абсцисс.
Чтобы найти нули функции, заданной
графически, надо найти точки
пересечения графика функции с осью
абсцисс.
Если график не пересекает ось Ox, функция
не имеет нулей.

23. Нули функции

Чтобы найти нули функции, заданной
формулой y = f (x), надо решить
уравнение f (x) = 0.
Если уравнение не имеет корней, нулей
у функции нет.
2) Найти нули квадратичной
функции f(x)=x²-7x+12.
Решение:
Для нахождения нулей функции
решим квадратное уравнение
x²-7x+12=0.
Его корни x1=3 и x2=4 являются
нулями данной функции.
Ответ: x=3; x=4.
1) Найти нули линейной
функции y=3x+15.
Решение:
Чтобы найти нули функции,
решим уравнение 3x+15=0.
3x=-15; x= -5.
Таким образом, нуль
функции y=3x+15 — x= -5.
Ответ:x= -5.
Найти нули функции

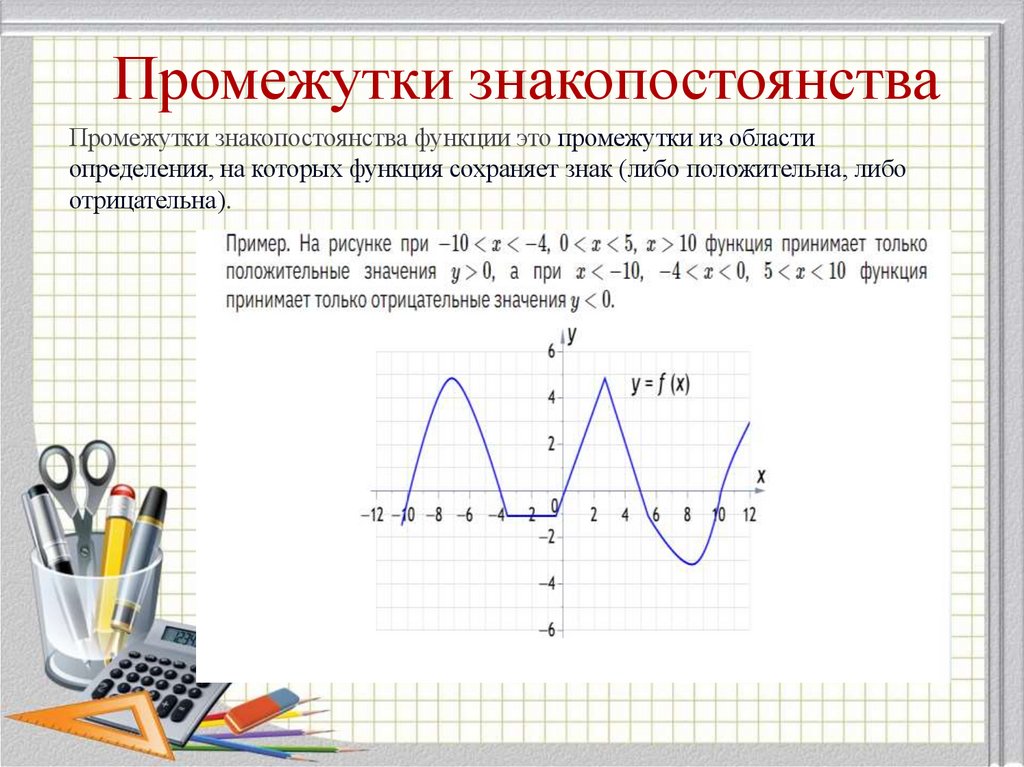
24. Промежутки знакопостоянства

Промежутки знакопостоянства функции это промежутки из области
определения, на которых функция сохраняет знак (либо положительна, либо
отрицательна).

25. Промежутки знакопостоянства

Алгоритм метода интервалов
1. Найти область определения функции
2. Найти нули функции
3. Сделать схематический чертеж (на оси х
откладываем точки разрыва и нули функции)
4. Определяем знак функции на интервалах,
входящих в область определения
Найти промежутки знакопостоянства

26. Интернет-ресурсы

1.
https://www.yaklass.ru/p/algebra/10-klass/chto-my-znaem-o-chislovykhfunktciiakh-9133/obratimaia-i-obratnaia-funktcii-9159
2. https://foxford.ru/wiki/matematika/grafikfunktsii?srsltid=AfmBOopWeVaO8fftz708MGk4ixVm7FNhvxS4AtfL6Stzy
9M9ZlJg1A8G
3. https://nado5.ru/e-book/funkciya-oblast-opredeleniya-i-oblast-znacheniifunkcii
4. https://www.algebraclass.ru/nuli-funkcii/
5. https://oblakoz.ru/conspect/508707/nuli-i-promezhutki-znakopostoyanstvafunkciy
6. http://mathprofi.ru/nuli_funkcii_intervaly_znakopostoyanstva_metod_interv
alov.html
7. https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%
82%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA
%D1%86%D0%B8%D1%8F
8. https://skysmart.ru/articles/mathematic/grafik
9. https://maximumtest.ru/uchebnik/8-klass/matematika/funktsiya
10. http://pedsovet.su/