Похожие презентации:
матлогика_презентации_ОКОНЧАТЕЛЬНЫЕ (1)
1. История математической логики
Логика(др.-греч. λογοζ (логос) —
«искусство рассуждения») —
наука, изучающая законы и
формы мышления.
Содержание
2. История математической логики
Как самостоятельная наука логикаоформилась в трудах греческого
философа Аристотеля (384-322 г.г до н.э.).
Он систематизировал известные до него
сведения, и эта система стала
впоследствии называться формальной
или Аристотелевой логикой.
Содержание
3. История математической логики
Впервые в истории идеи о построениилогики на математической основе были
высказаны немецким математиком Г.
Лейбницем (1646-1716) в конце XVII века. Он
считал, что основные понятия логики
должны быть обозначены символами,
которые соединяются по особым правилам.
Это позволит всякое рассуждение
заменить вычислением.
Содержание
4. История математической логики
Реализация идеи Лейбница принадлежитанглийскому учёному Д. Булю. Он создал алгебру, в
которой буквами обозначены высказывания.
Введение символических обозначений в логику
имело для этой науки такое же решающее
значение, как и введение буквенных обозначений
для математики. Именно благодаря введению
символов в логику была получена основа для
создания новой науки – МАТЕМАТИЧЕСКОЙ
ЛОГИКИ
Содержание
5. Высказывания
Высказыванием называется повествовательноепредложение, которое может быть либо истинным,
либо ложным.
И (1) - истина, Л (0) - ложь
Примеры:
1) ”Волга впадает в Каспийское море” - истинное
высказывание.
2) 2 2=5 - ложное высказывание.
3) Х+3=7 - не является высказыванием, т.к.
истинность этого равенства зависит от значения Х.
Содержание
6.
Высказываниеобозначается
большими
латинскими буквами А, В, …
Подобно тому, как из заданных чисел можно
получить другие числа с помощью операций
сложения, вычитания, умножения и деления, так из
заданных высказываний получаются новые с
помощью операций, имеющих специальные
названия: конъюнкция, дизъюнкция, импликация,
эквивалентность и отрицание. Эти операции
означают соединение отдельных предложений
связками «и», «или», «если…,то…», «тогда и
только тогда, когда…» и присоединение к
высказыванию частицы «не».
Содержание
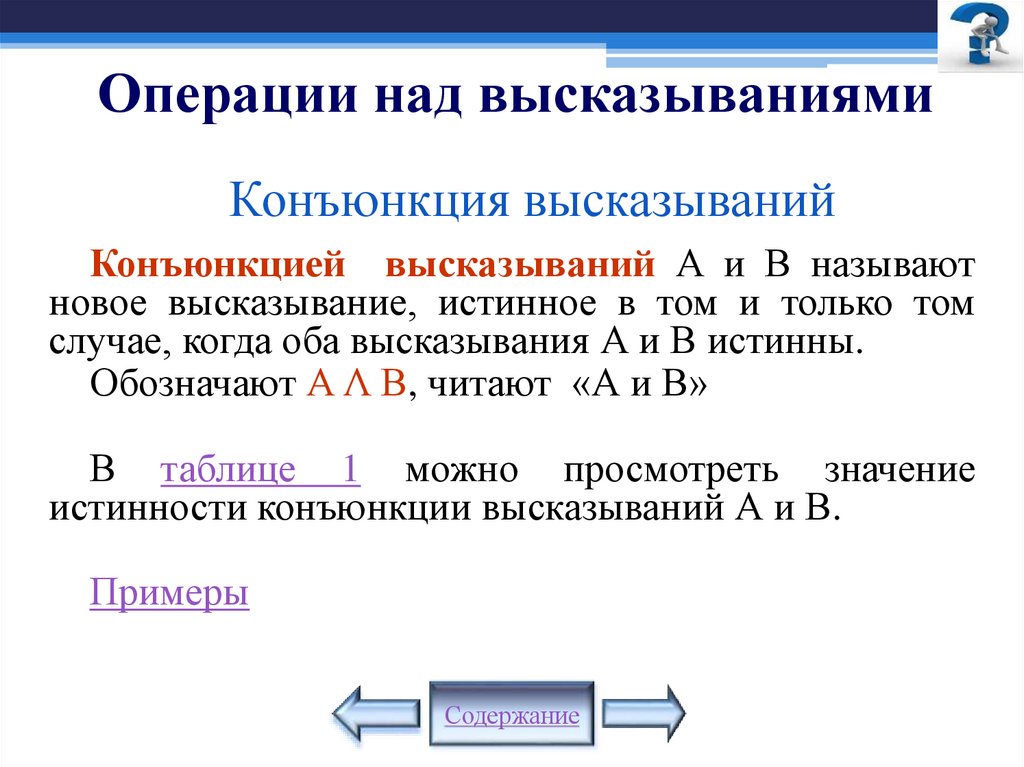
7. Операции над высказываниями
Конъюнкция высказыванийКонъюнкцией высказываний А и В называют
новое высказывание, истинное в том и только том
случае, когда оба высказывания А и В истинны.
Обозначают А Λ В, читают «А и В»
В таблице 1 можно просмотреть значение
истинности конъюнкции высказываний А и В.
Примеры
Содержание
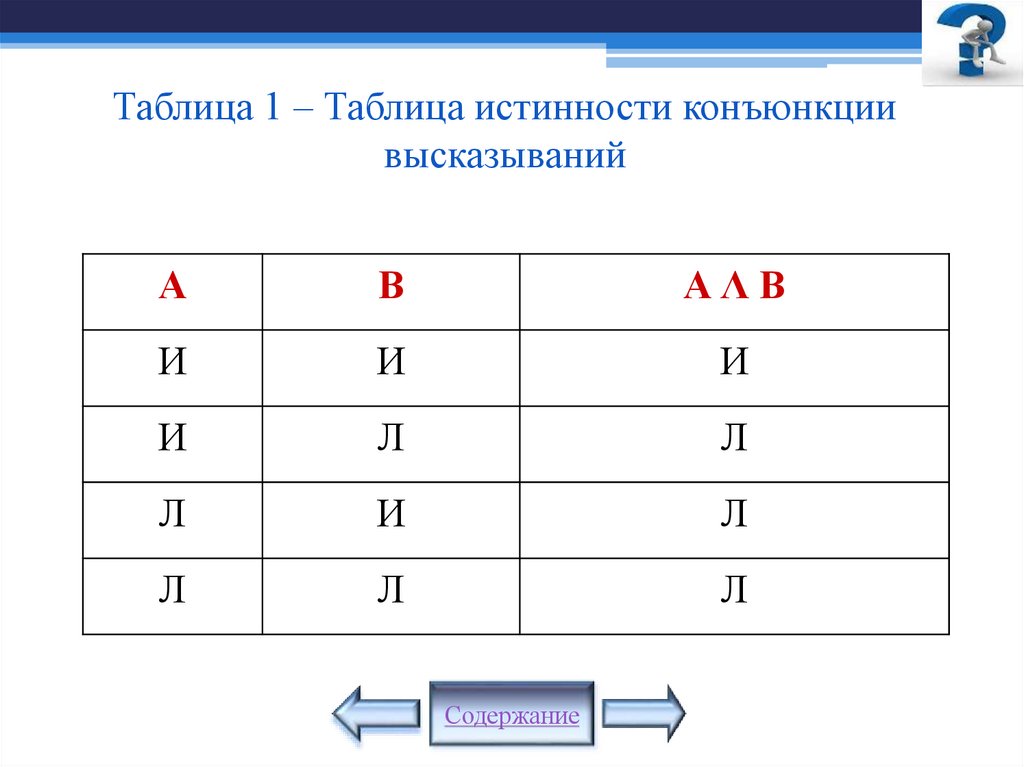
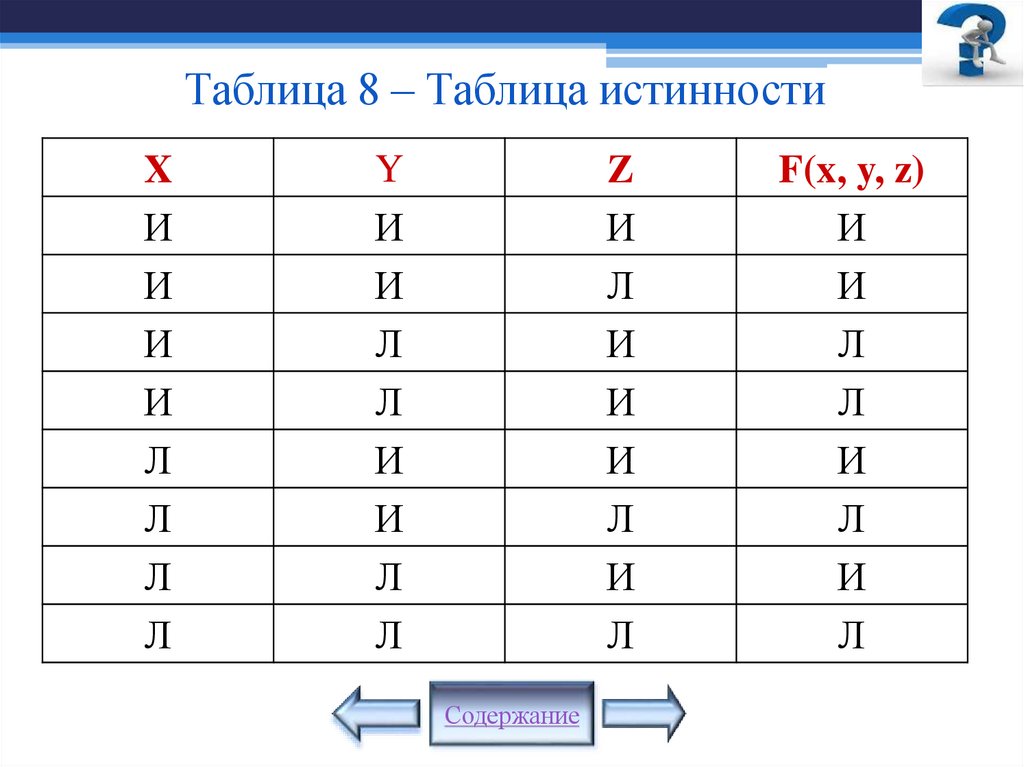
8.
Таблица 1 – Таблица истинности конъюнкциивысказываний
А
В
АΛВ
И
И
И
И
Л
Л
Л
И
Л
Л
Л
Л
Содержание
9. Примеры: 1. Даны высказывания: А: «Число 2- четное» – и В: «Число 2-простое» – и Тогда АΛВ: «Число 2-четное и простое» – и 2.
Даны высказывания:А: « 3<12» – и
В: «12<10» – л
Тогда АΛВ: «3<12<10» – л
Содержание
10. Дизъюнкция высказывания
Дизъюнкцией высказываний называется такоеновое высказывание, которое ложно лишь в одном
случае, когда оба высказывания ложны.
Обозначают АV В, читают «А или В»
В таблице 2 можно просмотреть значение
истинности дизъюнкции высказываний А и В.
Примеры
Содержание
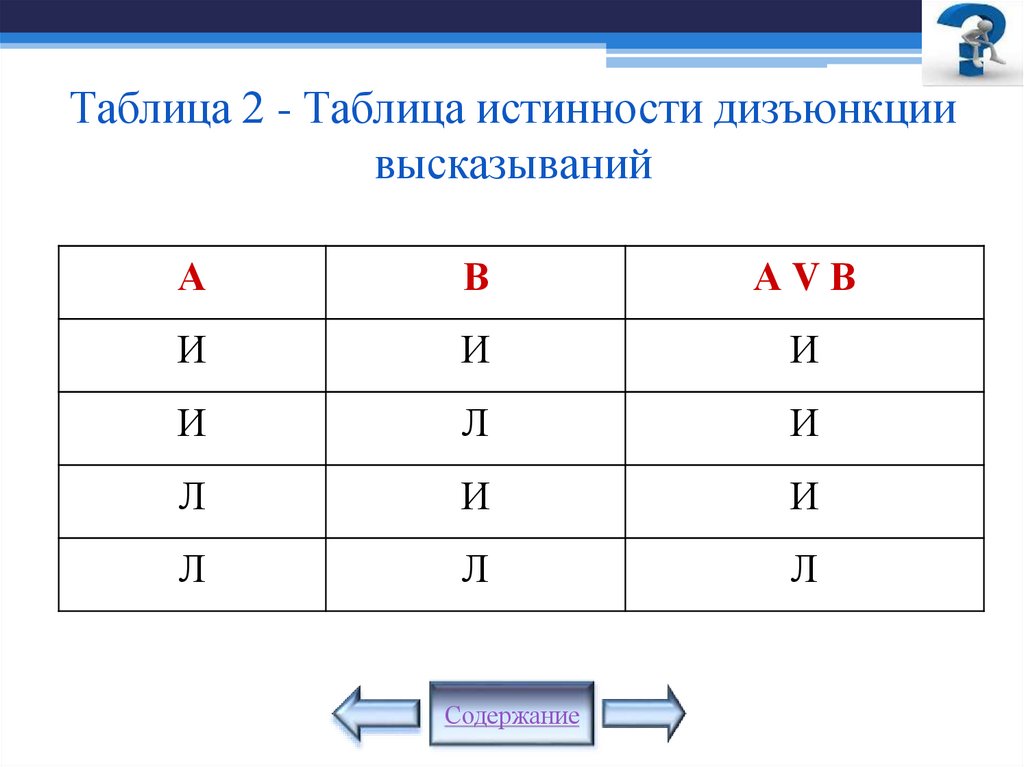
11. Таблица 2 - Таблица истинности дизъюнкции высказываний
АВ
АVВ
И
И
И
И
Л
И
Л
И
И
Л
Л
Л
Содержание
12. Примеры: 1. Даны высказывания: А: «22 двузначное число» – и В: «22 нечетное число» – л Тогда АВ: «22 двузначное или нечетное
Примеры:1. Даны высказывания:
А: «22 двузначное число» – и
В: «22 нечетное число» – л
Тогда А В: «22 двузначное или нечетное
число» и
2. Дано А В: «3≤3» - и
Тогда А: «3<3» л, В: «3=3» – и
Вывод: «Дизъюнкция нескольких высказываний
истина, если истинно хотя бы одно из этих
высказываний»
Содержание
13. Импликация высказываний
Импликацией высказываний А и В называютвысказывание ложное лишь в одном случае, когда
А - истинно, а В - ложно.
Обозначают А В, читают
«если А, то В»
В таблице 3 можно просмотреть значение
истинности импликации высказываний А и В.
Примеры
Содержание
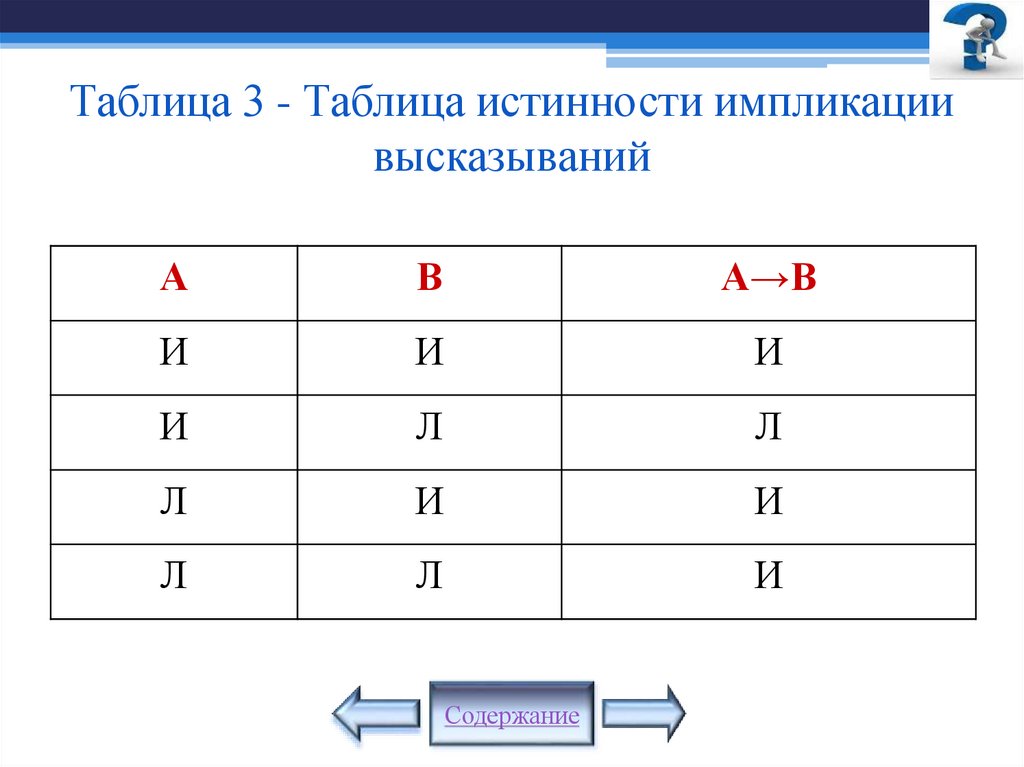
14. Таблица 3 - Таблица истинности импликации высказываний
АВ
А→В
И
И
И
И
Л
Л
Л
И
И
Л
Л
И
Содержание
15. Пример: Даны высказывания: А: «Последняя цифра числа 15 равна 5»и В: «Число 15 делится на 5»и Тогда А→В: «Если последняя
Пример:Даны высказывания:
А: «Последняя цифра числа 15 равна 5» и
В: «Число 15 делится на 5» и
Тогда А→В: «Если последняя цифра числа
15 равна 5, то число 15 делится
на 5» и
Содержание
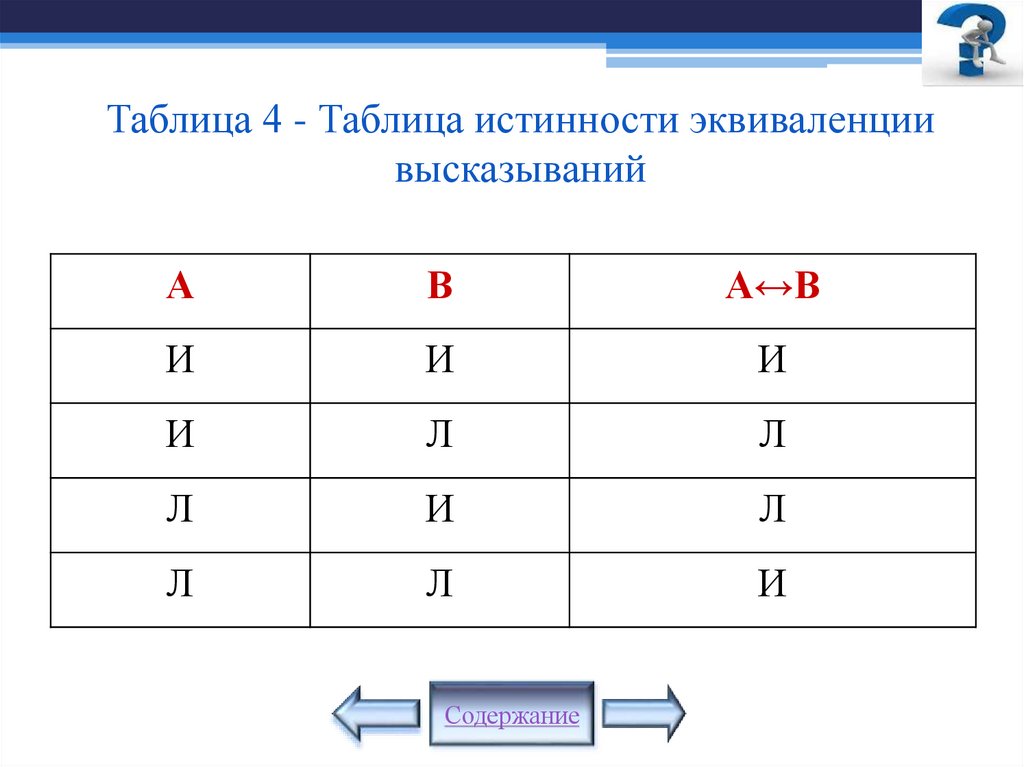
16. Эквиваленция высказываний
Эквиваленцией высказыванийА и В
называют высказывание, которое истинно, если оба
высказывания А и В истинны или оба высказывания
ложны.
Обозначают А↔В, читают
тогда, когда В»
«А тогда и только
В таблице 4 можно просмотреть значение
истинности эквиваленции высказываний А и В.
Содержание
17. Таблица 4 - Таблица истинности эквиваленции высказываний
АВ
А↔В
И
И
И
И
Л
Л
Л
И
Л
Л
Л
И
Содержание
18. Отрицание высказываний
Отрицанием высказывания А называют новоевысказывание, истинное в том и только том случае,
когда высказывание А ложно.
Обозначают А, читают «не А»
В таблице 5 можно просмотреть значение
истинности отрицания высказывания А.
Примеры
Содержание
19. Таблица 5 - Таблица истинности отрицания высказывания
АА
И
Л
Л
И
Содержание
20. Примеры: 1) Дано высказывание А: «Петя не умеет говорить по-английски». Тогда отрицание высказывания А будет высказывание: А :
«Петя умеет говорить по-английски».2) Дано высказывание А: «5>10»
Тогда А: «5≤10»
Содержание
21. Выражение, составленное из высказываний с помощью операций отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции
Выражение,помощью
составленное
операций
из
высказываний
отрицания,
с
конъюнкции,
дизъюнкции, импликации, эквиваленции называется
логической формулой.
Содержание
22. Формулы алгебры высказываний
ПустьХ, Y, Z – элементарные высказывания
(высказывания, которые могут принимать значения
истина или ложь).
Формулой алгебры высказываний называется:
1) A, B, C – элементарные высказывания;
2) Если А, В – формулы алгебры высказываний, то
формулами будут: АVB, A ΛB, A→B, A↔B;
3) Ни что иное не есть формула.
Содержание
23. Примеры:
1) (А Λ В) V B → C – формулаалгебры высказываний;
2) (А + В) : B → C – не является
формулой алгебры высказываний;
Содержание
24. Приоритет выполнения операций в формулах алгебры высказываний
43 2
5
1
А ν (В С) ∧ А → (В ν С)
1
1. Действия в скобках
2. Отрицание
3. Конъюнкция
4. Дизъюнкция
5. Импликация, эквиваленция
Содержание
25. Формула называется тождественно истинной, если она принимает значение истина при любом наборе значений переменных высказываний.
Формула называется тождественно ложной, еслиона принимает значение ложь, при любом наборе
значений
переменных
высказываний.
Формула называется выполнимой, если существует
хотя бы один набор значений переменных
высказываний, на которых формула принимает
значение
истинно.
Содержание
26. Замечание: Любое тождественно истинное высказывание является выполнимым, обратное неверно. Вывод: Для множества формул в логике
высказываний существуют два алгоритма, спомощью которых можно установить является ли
формула тождественно истинной, тождественно
ложной
или
только
выполнимой:
- с помощью построения таблиц истинности;
- с помощью равносильных преобразований.
Содержание
27. Законы логики. Равносильные преобразования
Формулы А и В называют равносильными, еслиони принимают одинаковые значения на одних и тех
же наборах значений переменных высказываний
(Равносильные
формулы
имеют
одинаковые
таблицы истинности).
Обозначают А ≡ В
Наиболее часто используемые равносильные
формулы получили название законов логики
высказываний.
Содержание
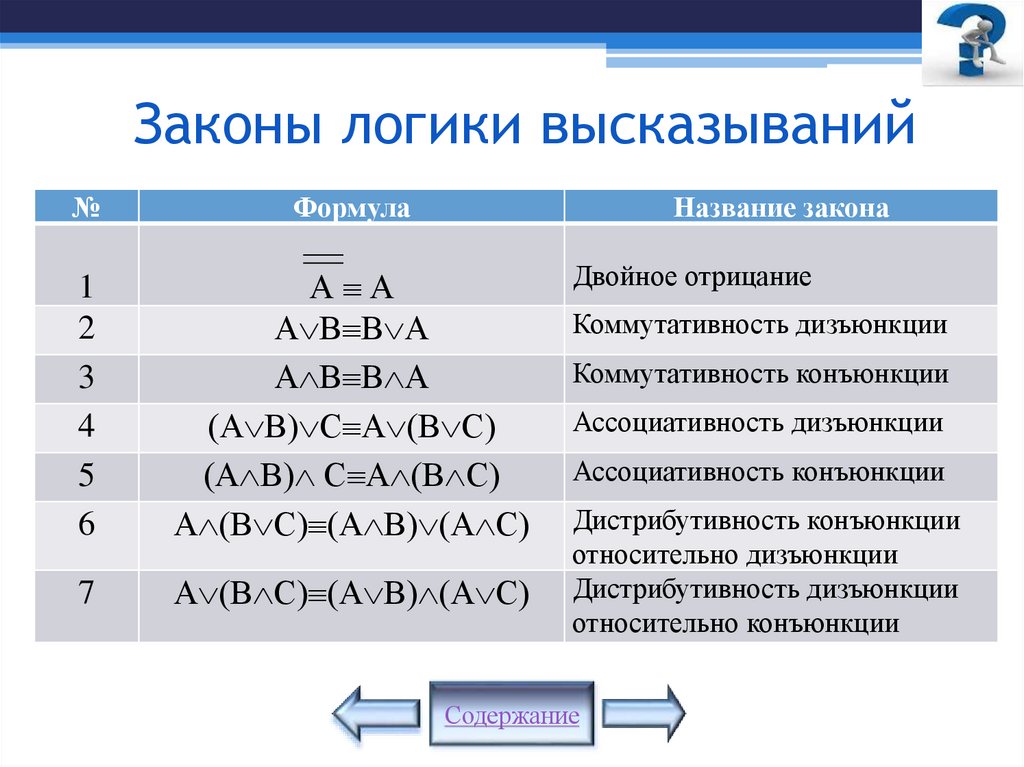
28. Законы логики высказываний
№Формула
Название закона
1
2
3
4
5
6
А А
А В В А
А В В А
(А В) С А (В С)
(А В) С А (В С)
А (В С) (А В) (А С)
7
А (В С) (А В) (А С)
Двойное отрицание
Коммутативность дизъюнкции
Коммутативность конъюнкции
Ассоциативность дизъюнкции
Ассоциативность конъюнкции
Дистрибутивность конъюнкции
относительно дизъюнкции
Дистрибутивность дизъюнкции
относительно конъюнкции
Содержание
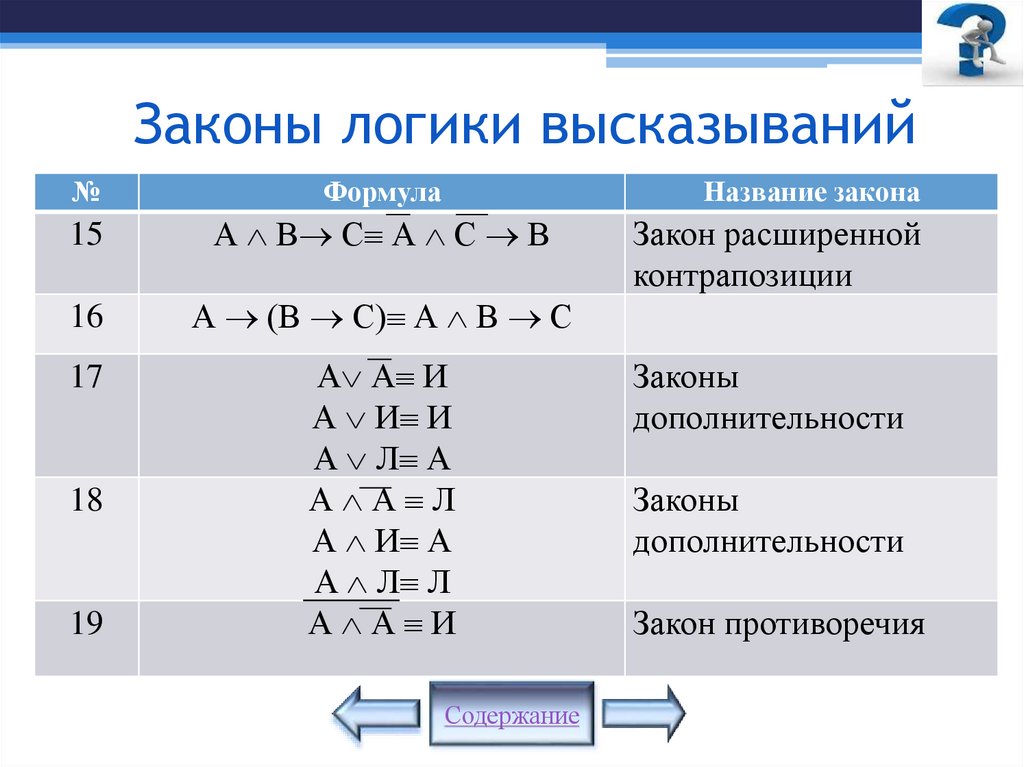
29. Законы логики высказываний
№Формула
8
9
А В А В
А В А В
10
А В А В


































































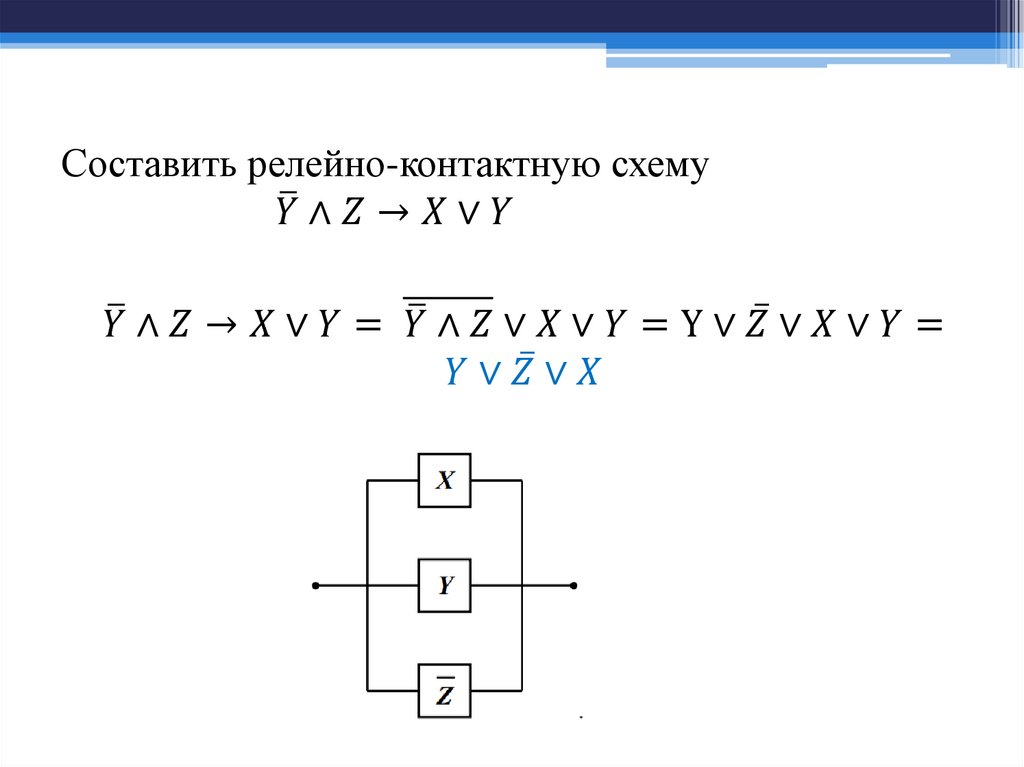
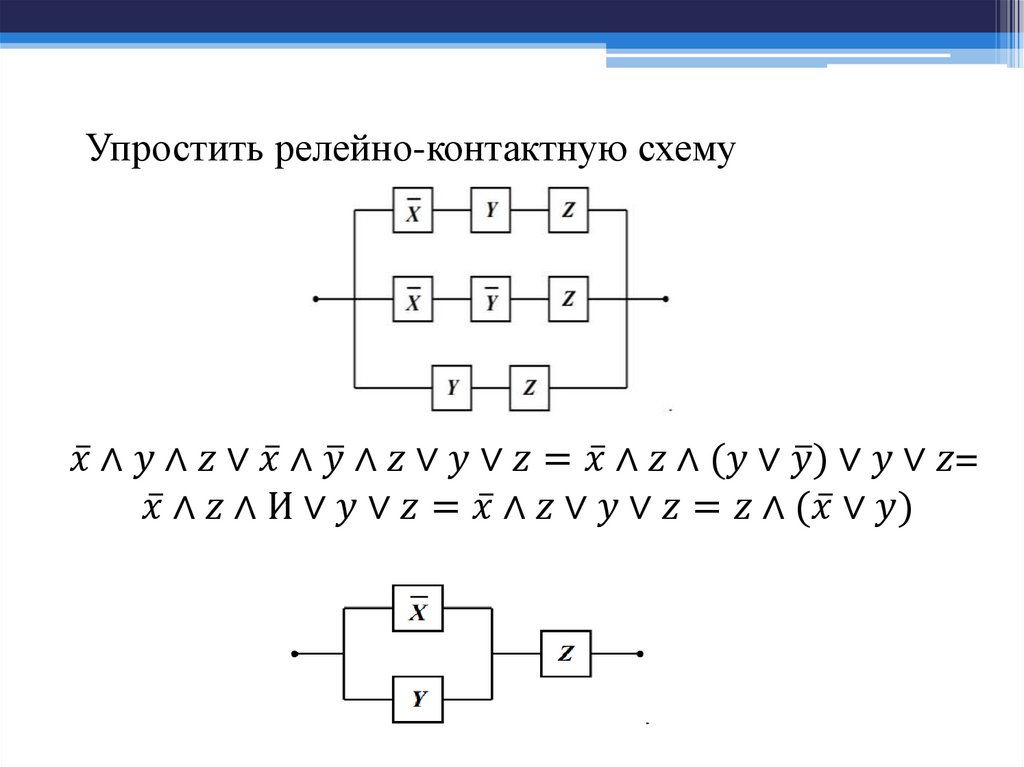

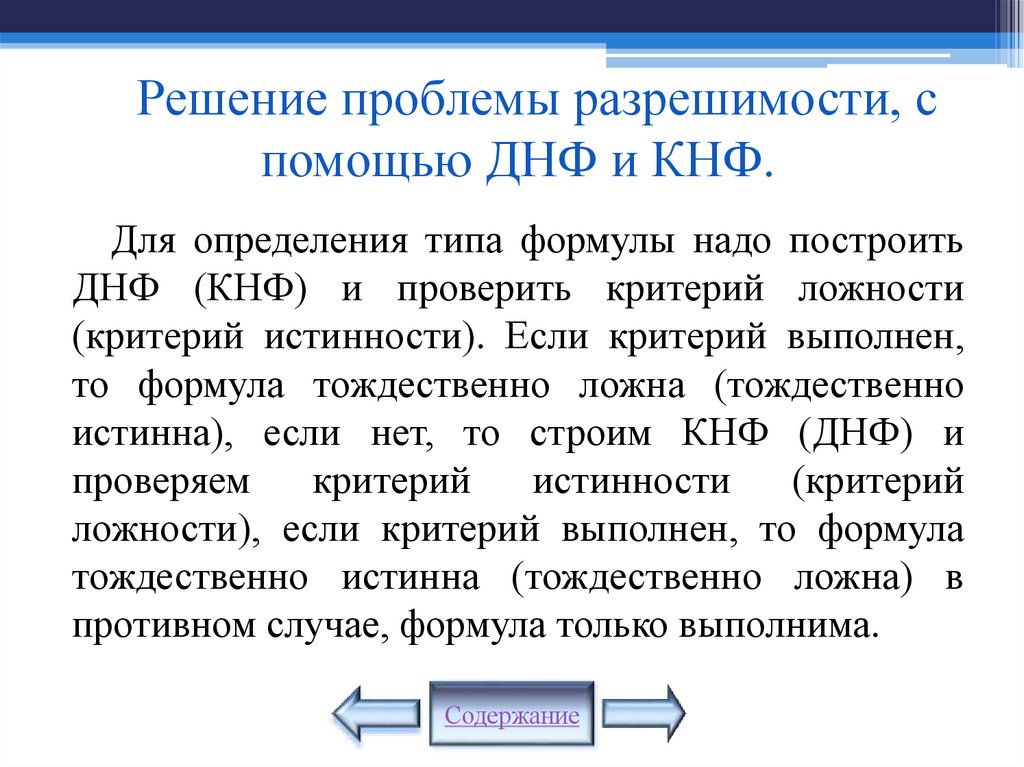


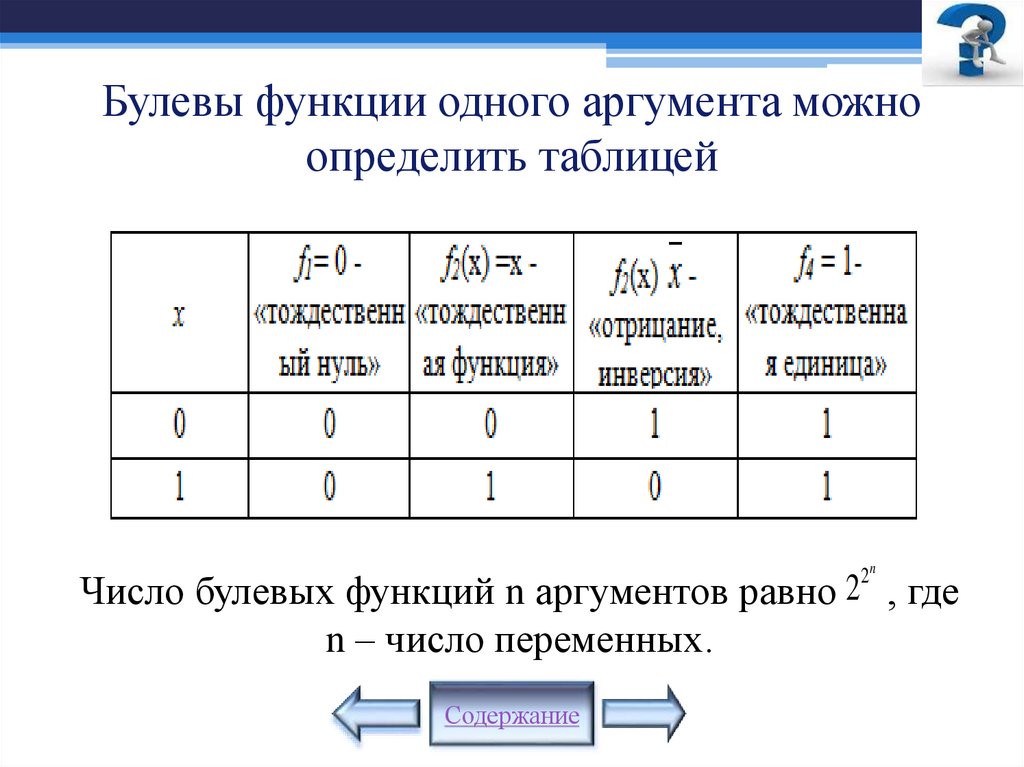
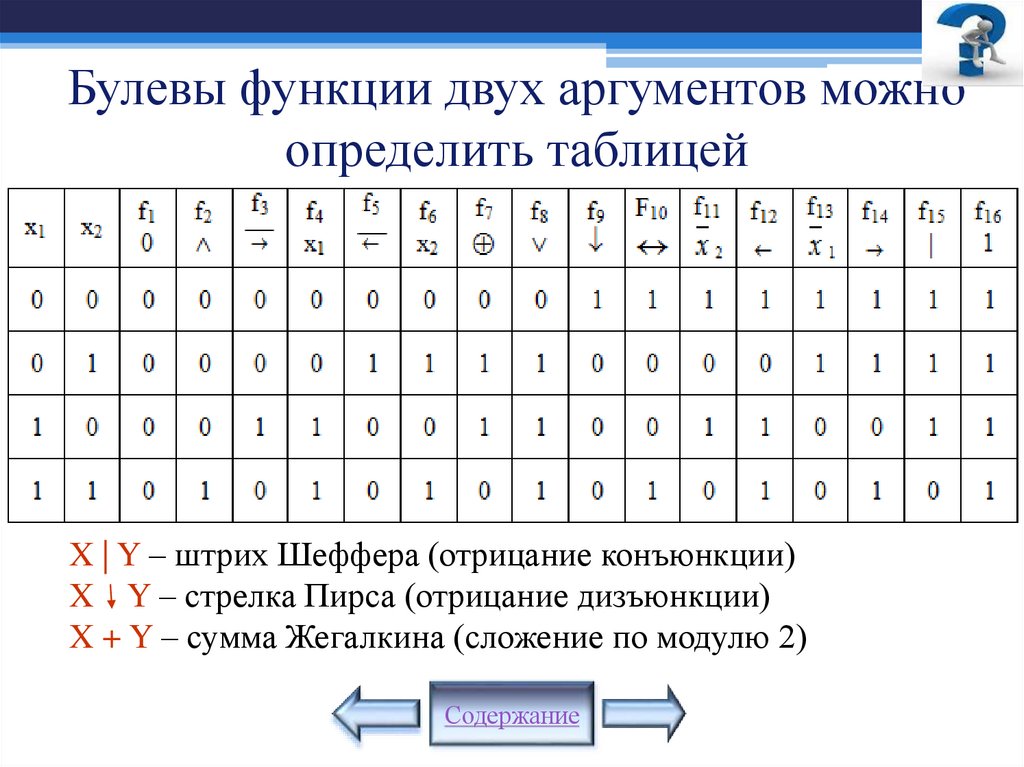












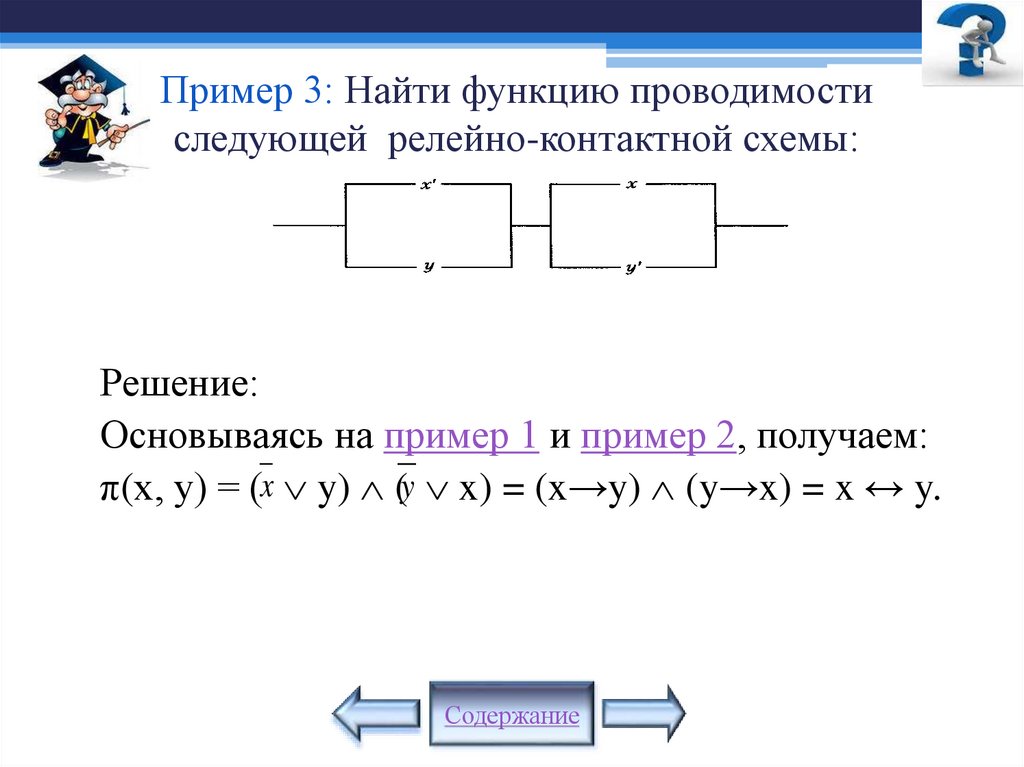
 Математика
Математика








