механика теория

1. Механика

- Это раздел физики, наука, изучающая
движение материальных тел и
взаимодействие между ними; при этом
движением в механике называют
изменение во времени взаимного
положения тел или их частей в
пространстве.

2.

Механика
•Кинематика
•Динамика
•Статика
•Законы сохранения

3.

Кинематика
•Основные понятия
•Действия с векторами
•Прямолинейное движение
•Криволинейное движение

4.

Действия с векторами
•Сложение векторов
•Вычитание векторов
•Умножение вектора на скаляр
•Проекции векторов

5.

Прямолинейное движение
•Равномерное
•Равноускоренное
•Средняя скорость

6.

Криволинейное движение
•Тело, брошенное вертикально
•Тело, брошенное горизонтально
•Тело, брошенное под углом к горизонту
•Движение тела по окружности

7.

Динамика
• Явление инерции
• Законы Ньютона
1 Закон
2 Закон
3 Закон
• Закон всемирного тяготения
• Сила тяжести
• Вес тела
• Космические скорости
• Сила упругости
• Сила трения

8.

Законы сохранения
•Импульс
•Закон сохранения импульса
•Работа
•Мощность
•Энергия
Кинетическая
Потенциальная
•Закон сохранения энергии

9.

Статика
•1 условие равновесия
•2 условие равновесия

10.

Кинематика
Механическое движение – это изменение положения
тела относительно других тел с течением времени.
Основная задача механики – определить положение тела в
любой момент времени.
Система отсчета состоит из:
•Тела отсчета
•Системы координат
•Прибора для измерения времени

11.

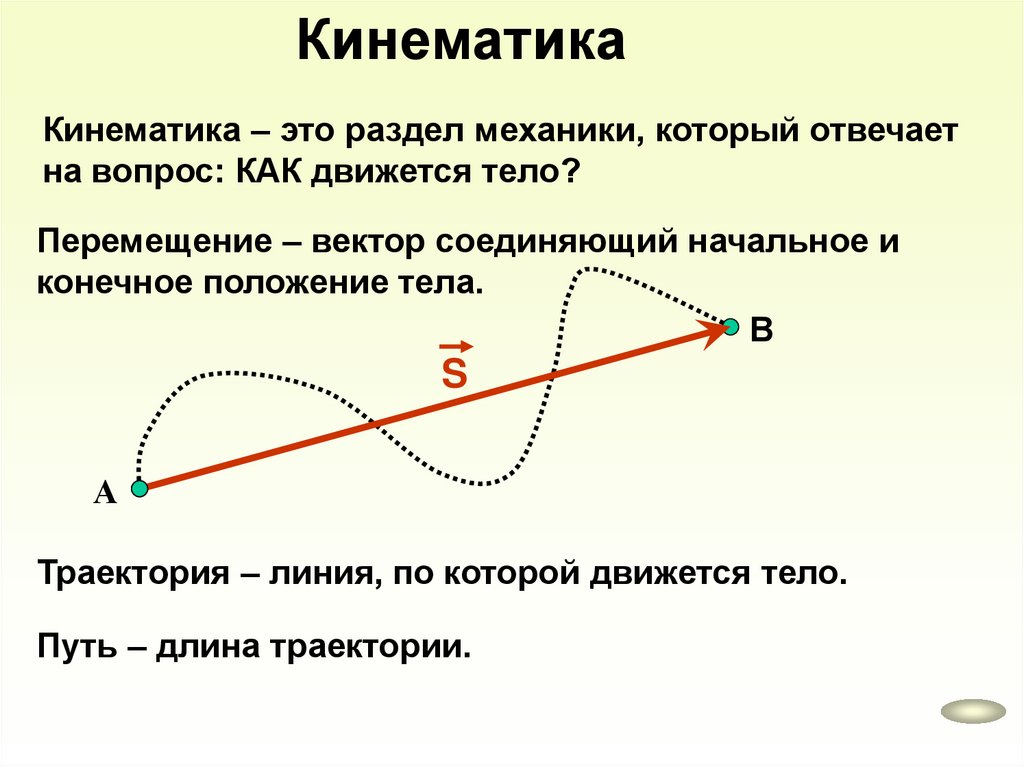
Кинематика
Кинематика – это раздел механики, который отвечает
на вопрос: КАК движется тело?
Перемещение – вектор соединяющий начальное и
конечное положение тела.
В
S
А
Траектория – линия, по которой движется тело.
Путь – длина траектории.

12.

Кинематика

13.

Кинематика
Материальная точка – тело, размерами которого
можно пренебречь.
Материальной точкой тело можно считать если:
•Его размеры малы по сравнению с пройденным
расстоянием
•Движение тела поступательно
Поступательное движение – это движение тела, при
котором траектории всех его точек одинаковы.

14.

Кинематика
Поступательное движение – это движение тела, при
котором траектории всех его точек одинаковы.

15.

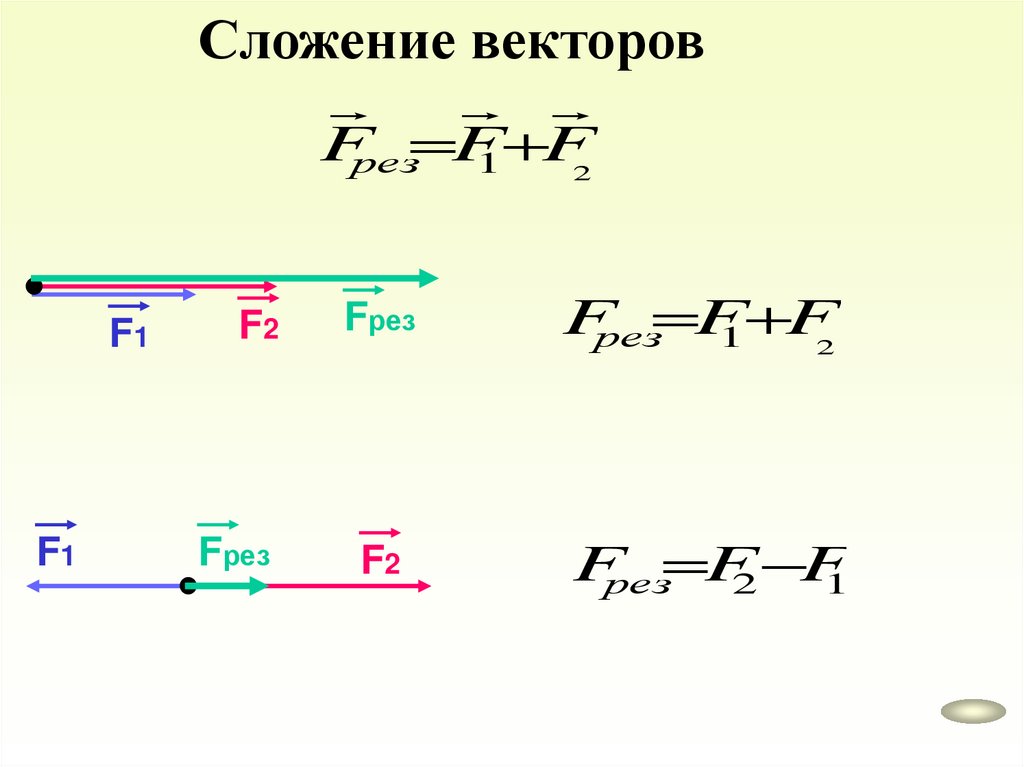
Сложение векторов
Fрез F
1 F
2
F1
F1
F2
Fрез
Fрез F
1 F
2
Fрез
F2
Fрез F2 F
1

16.

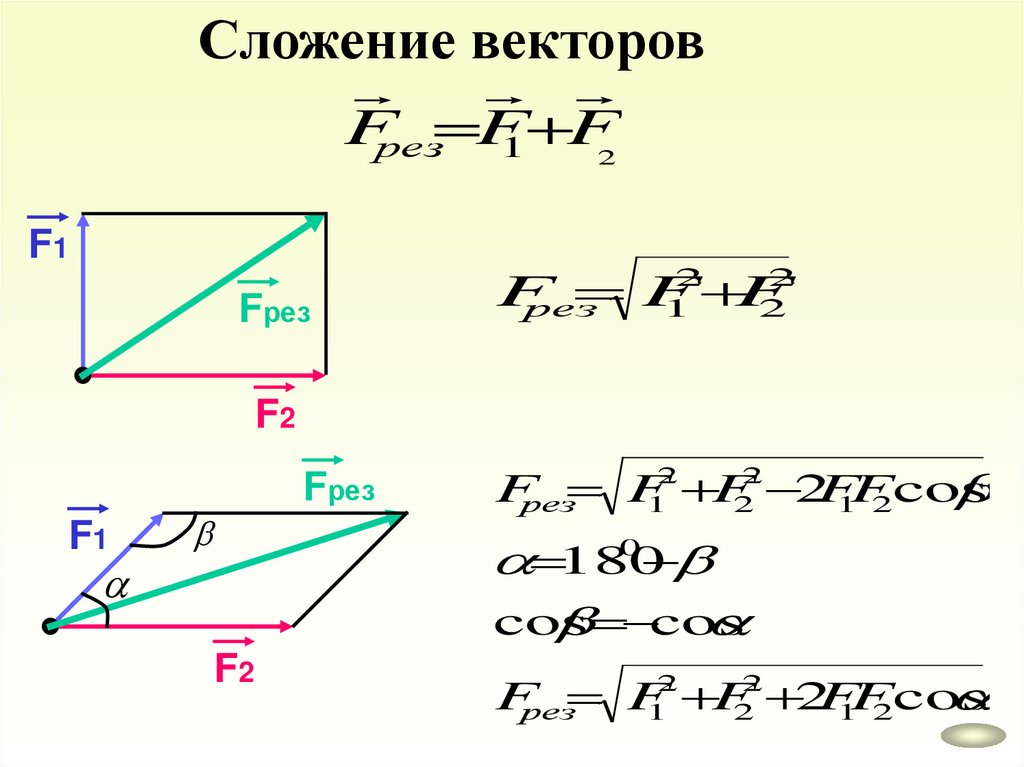
Сложение векторов
Fрез F
1 F
2
F1
Fрез
2
2
F
F
F
рез
1
2
F2
F1
Fрез
Fрез F F 2F
1F
2cos
2
1
2
2
0
180
cos
cos
F2
2
2
Fрез F
F
F
1
2 2
1F
2cos

17.

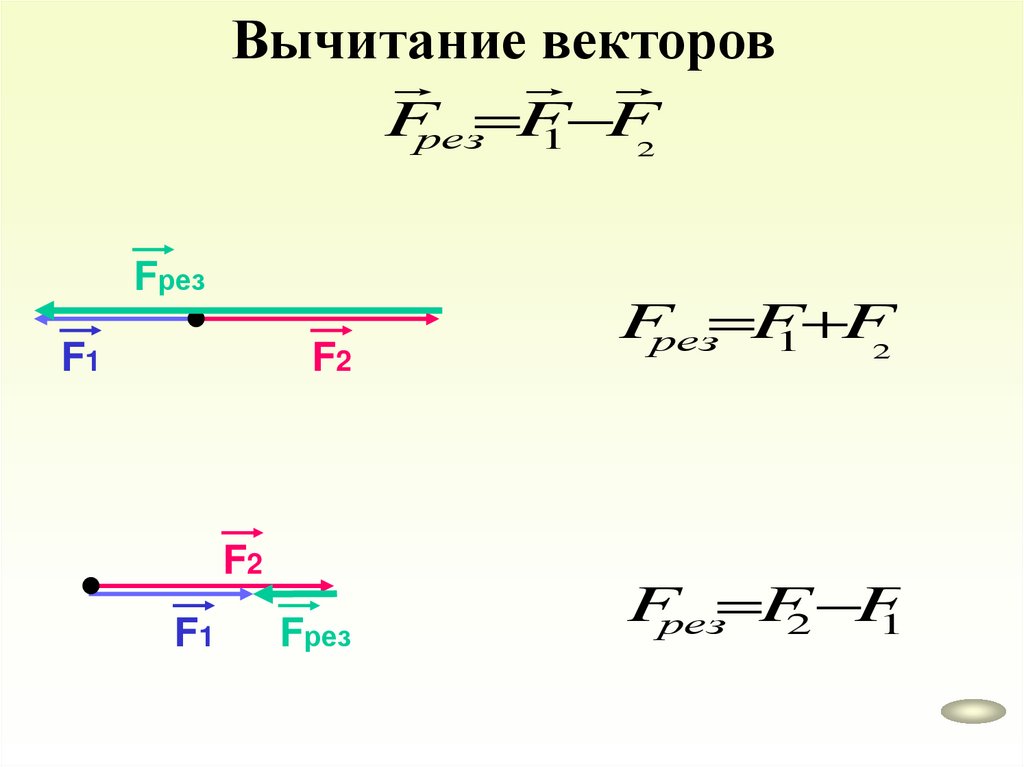
Вычитание векторов
Fрез F
1 F
2
Fрез
F1
F2
Fрез F
1 F
2
Fрез
Fрез F2 F
1
F2
F1

18.

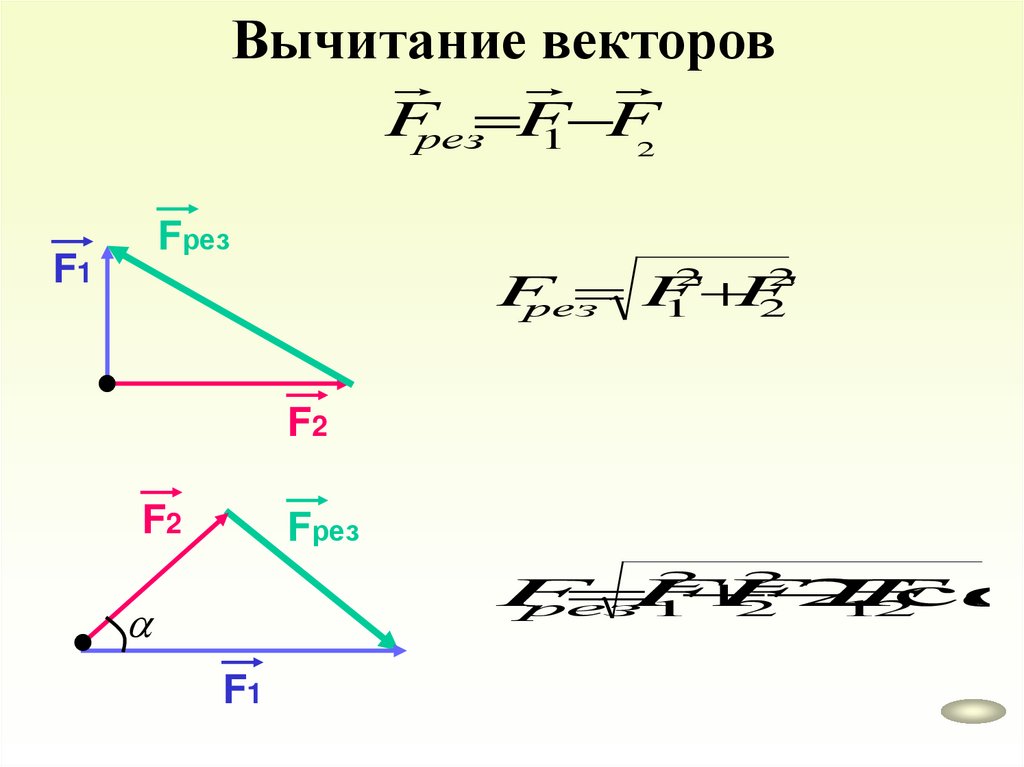
Вычитание векторов
Fрез F
1 F
2
Fрез
F1
2
2
F
F
F
рез
1
2
F2
F2
Fрез
2
2
F
F
F
2
F
F
co
рез 1
2
1
2
F1

19.

Умножение вектора на скаляр
F1 F0 a
F0
a 0
F2
F1
F1 F0 a
F0
F2 F0 b
b 0
F2 F0 b

20.

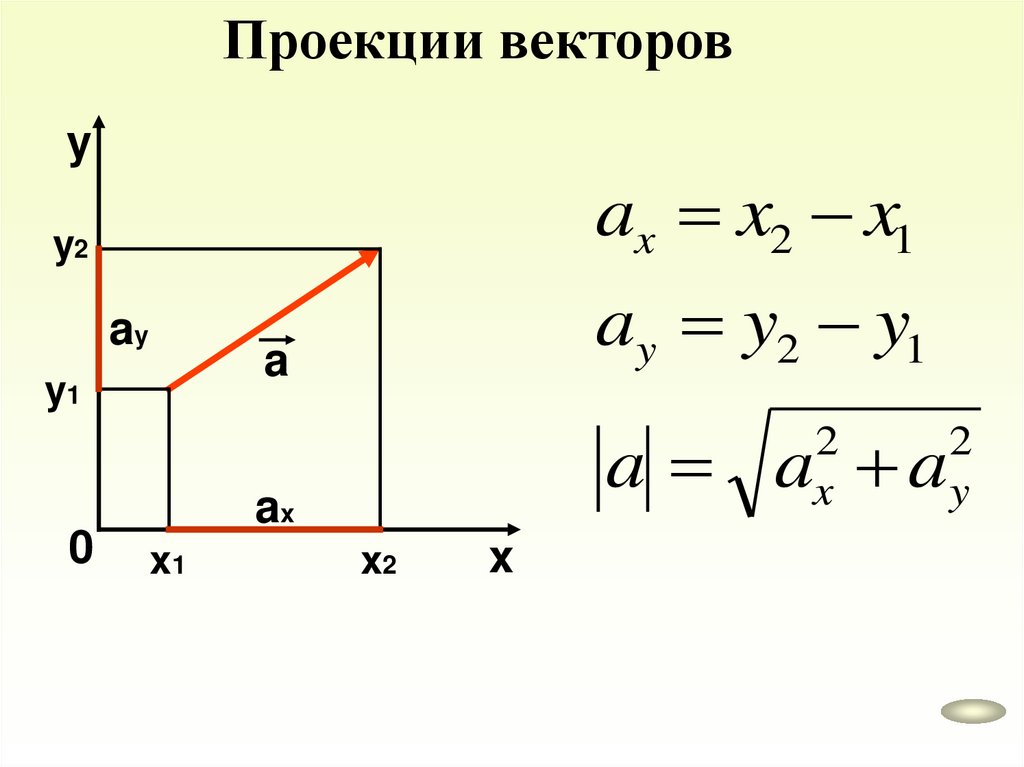
Проекции векторов
y
ax x2 x1
y2
ay
a
y1
0
ay y2 y1
a a a
2
x
ax
x1
x2
x
2
y

21.

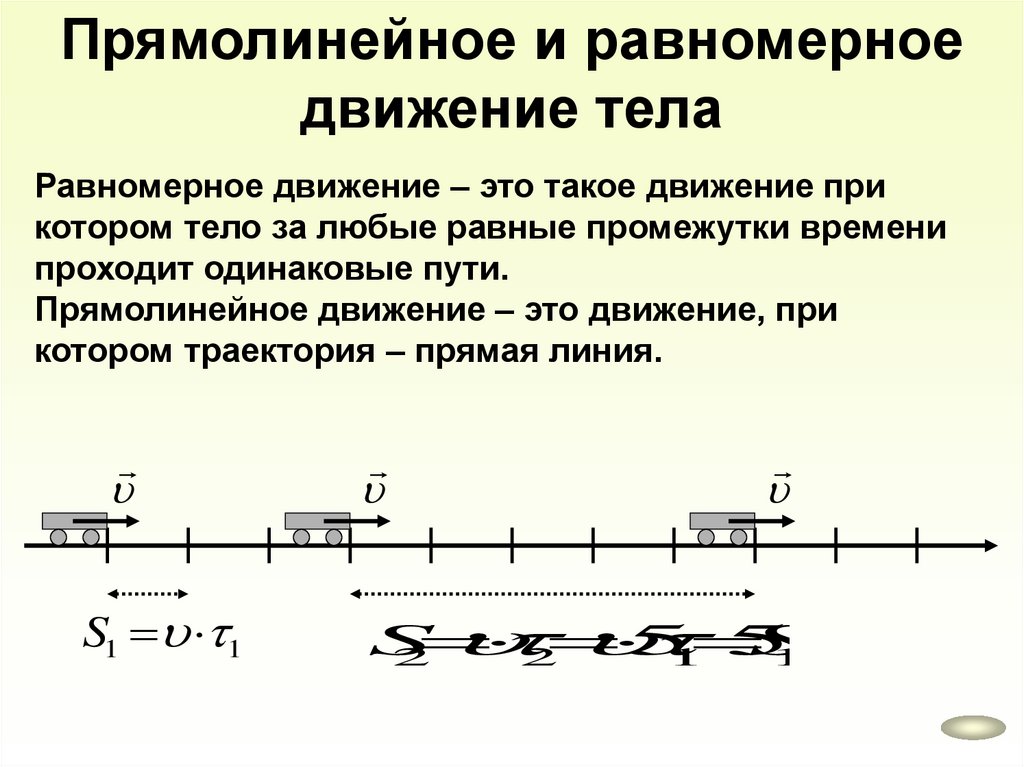
Прямолинейное и равномерное
движение тела
Равномерное движение – это такое движение при
котором тело за любые равные промежутки времени
проходит одинаковые пути.
Прямолинейное движение – это движение, при
котором траектория – прямая линия.
S1 1
S
5
5
S
2
2
1
1

22.

Прямолинейное и равномерное
движение тела
S
t
Sx
x
t
S
х
0
x0
x x0 S x
Sx
x
x
S x xt
x x0 xt

23.

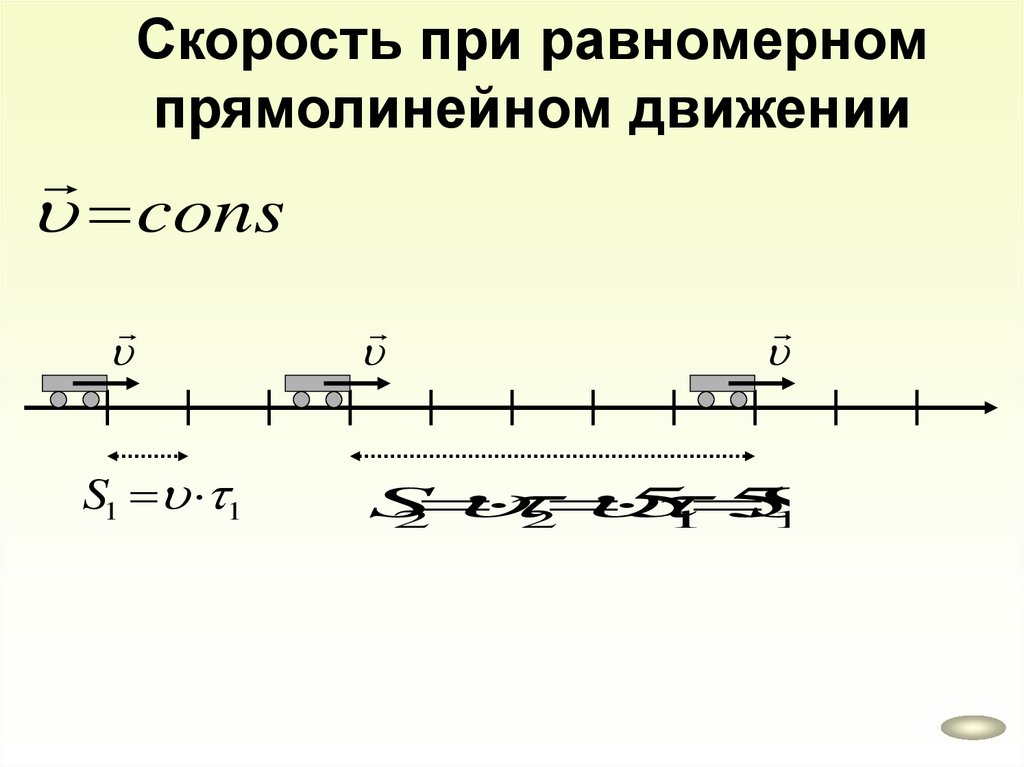
Скорость при равномерном
прямолинейном движении
const
S1 1
S
5
5
S
2
2
1
1

24.

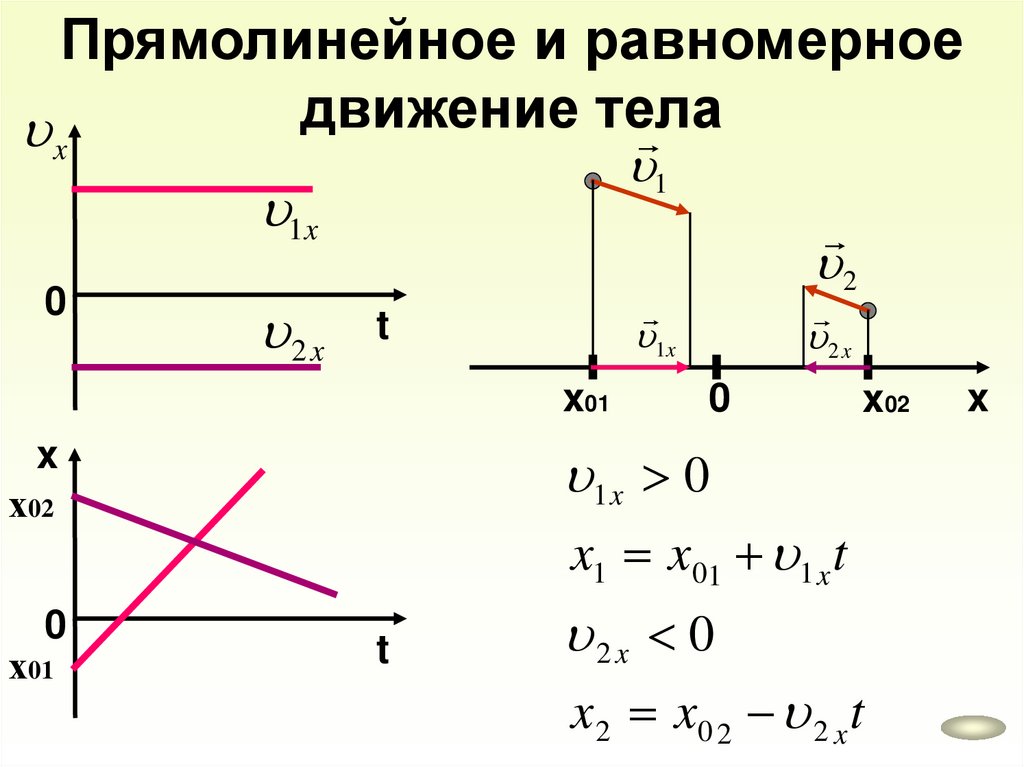
Прямолинейное и равномерное
движение тела
1
x
1x
0
2 x
1x
2 x
0
x02
1 x 0
x
х02
х01
t
x01
0
2
x1 x01 1 x t
t
2x 0
x 2 x0 2 2 x t
x

25.

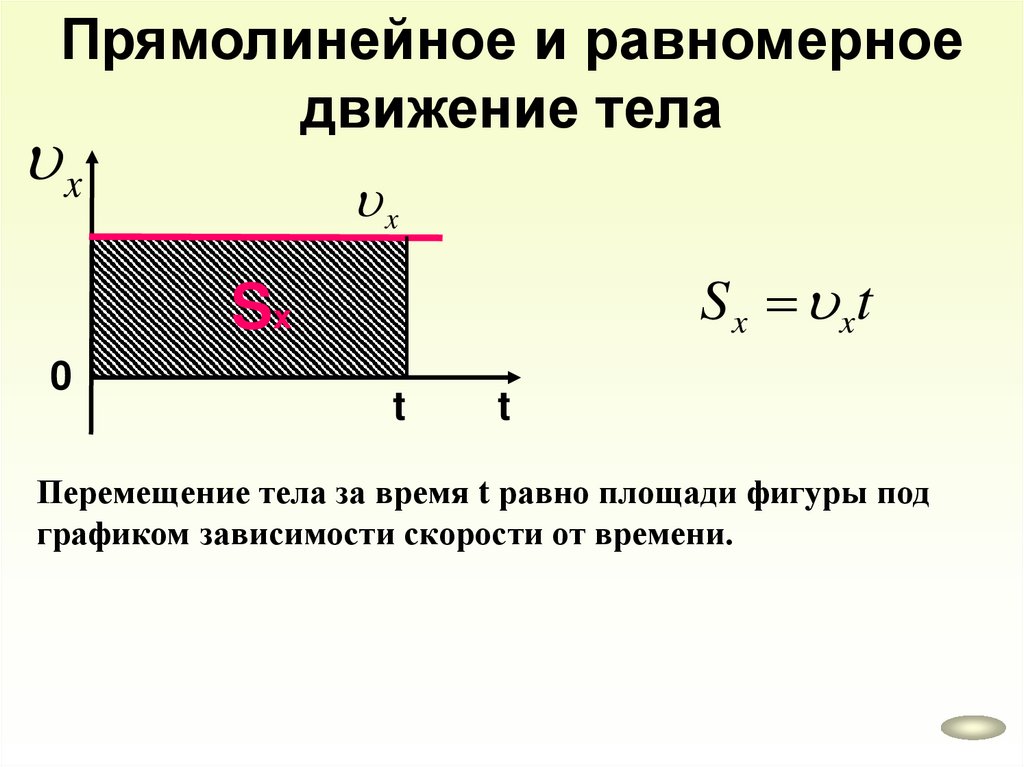
Прямолинейное и равномерное
движение тела
x
x
S x xt
Sх
0
t
t
Перемещение тела за время t равно площади фигуры под
графиком зависимости скорости от времени.

26.

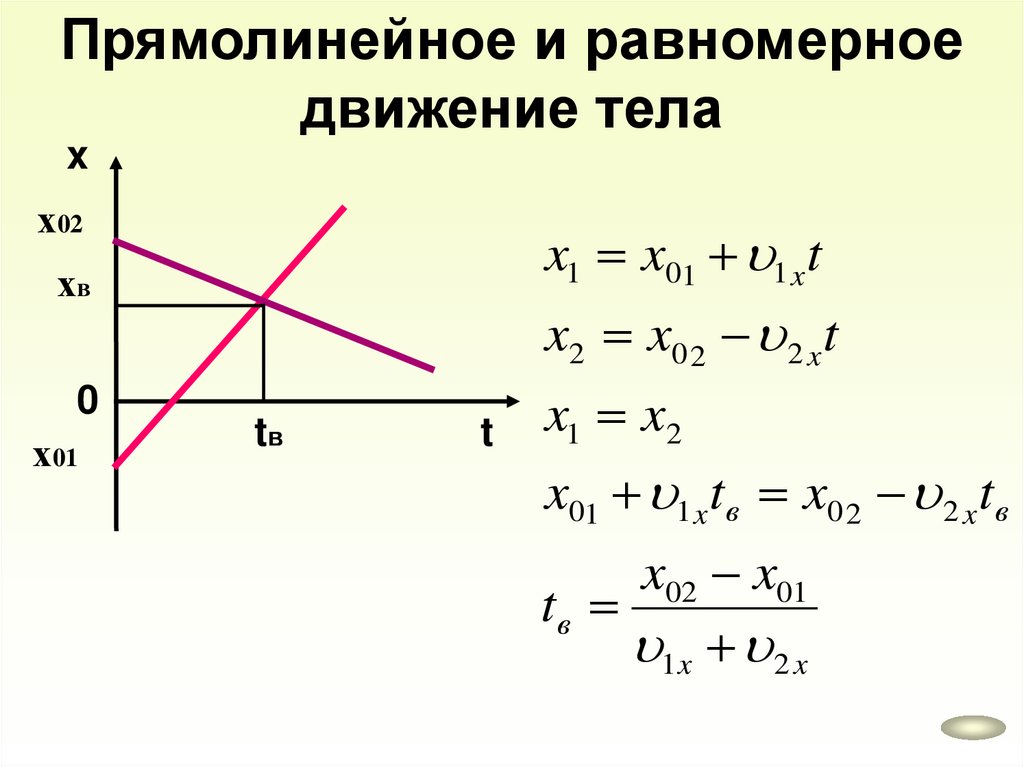
Прямолинейное и равномерное
движение тела
x
х02
x1 x01 1 x t
хв
0
х01
x2 x0 2 2 x t
tв
t
x1 x2
x01 1 x tв x0 2 2 x tв
x02 x01
tв
1x 2 x

27.

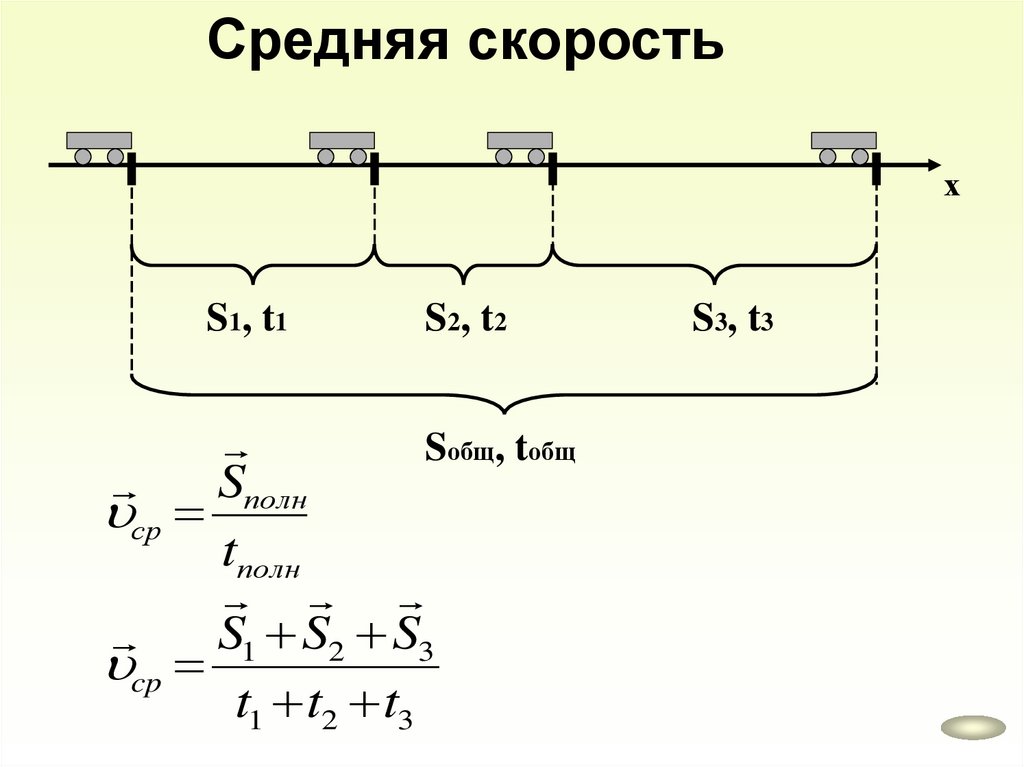
Средняя скорость
х
S1, t1
S2, t2
Sобщ, tобщ
Sполн
ср
tполн
S1 S2 S3
cp
t1 t2 t3
S3, t3

28.

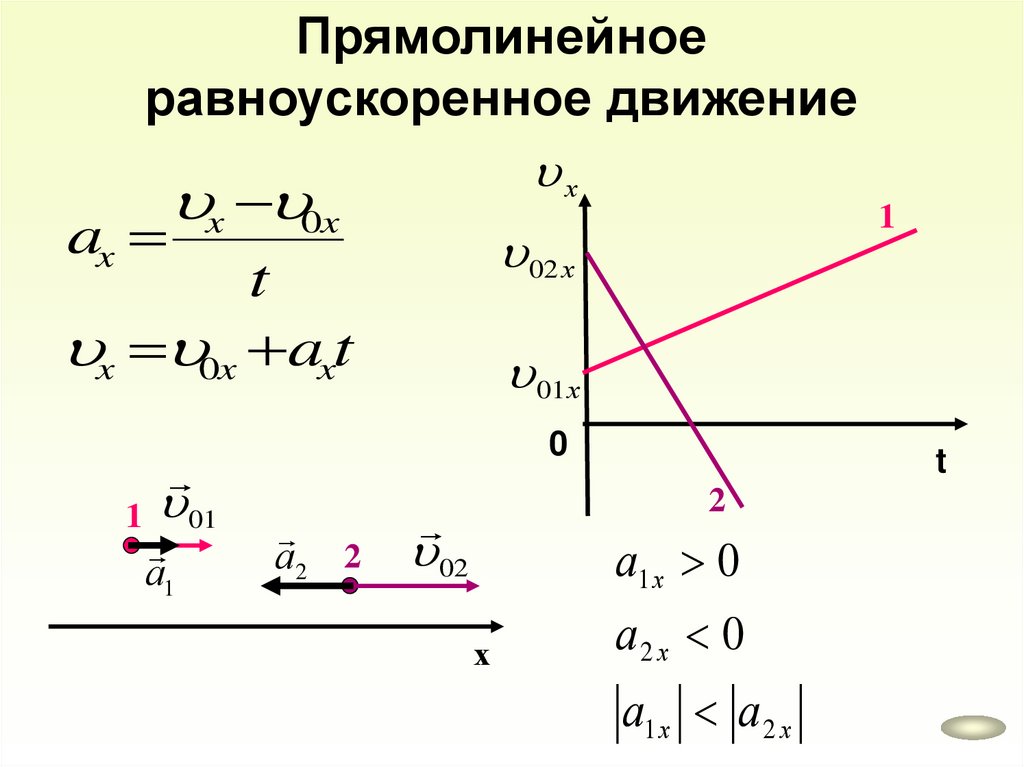
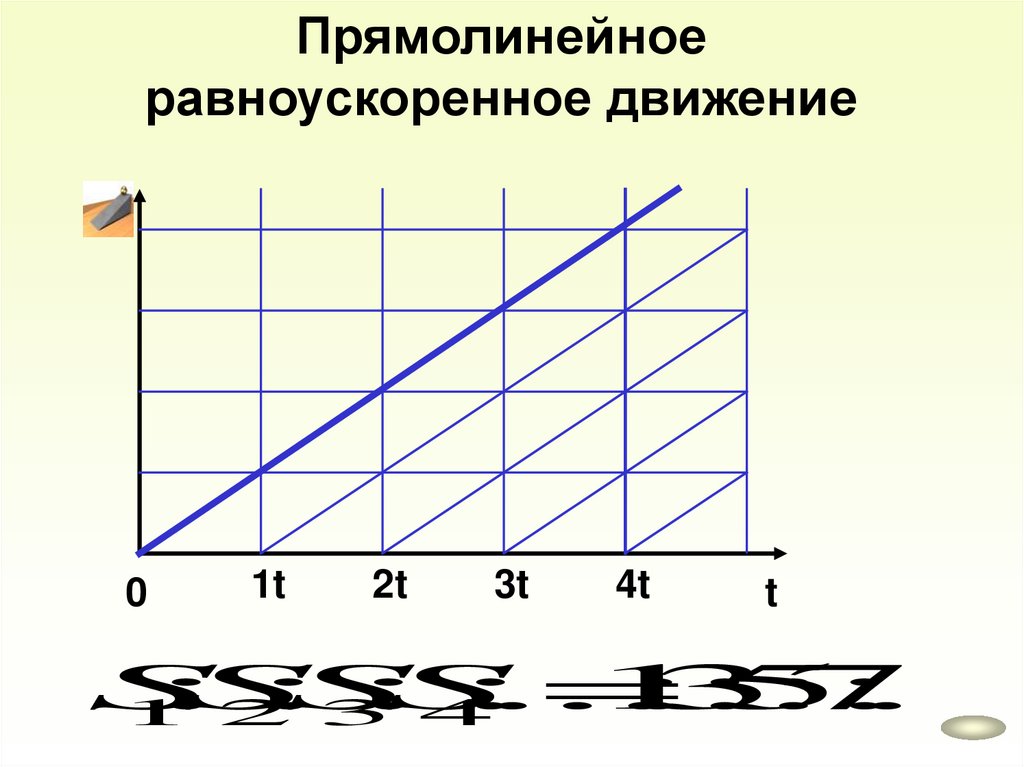
Прямолинейное
равноускоренное движение
Равноускоренное движение – это движение при
котором скорость тела за равные промежутки времени
меняется одинаково.
0
a
t
a
t
0 at
Ускорение – величина, равная
отношению изменения скорости к
промежутку времени, за которое
это изменение произошло.
м
м
с
а 2
с с

29.

Прямолинейное
равноускоренное движение
ax
х
x 0x
02 х
t
x 0x axt
01х
0
1 01
а1
1
а2 2
t
2
02
а1 х 0
х
а2 х 0
а1 х а 2 х

30.

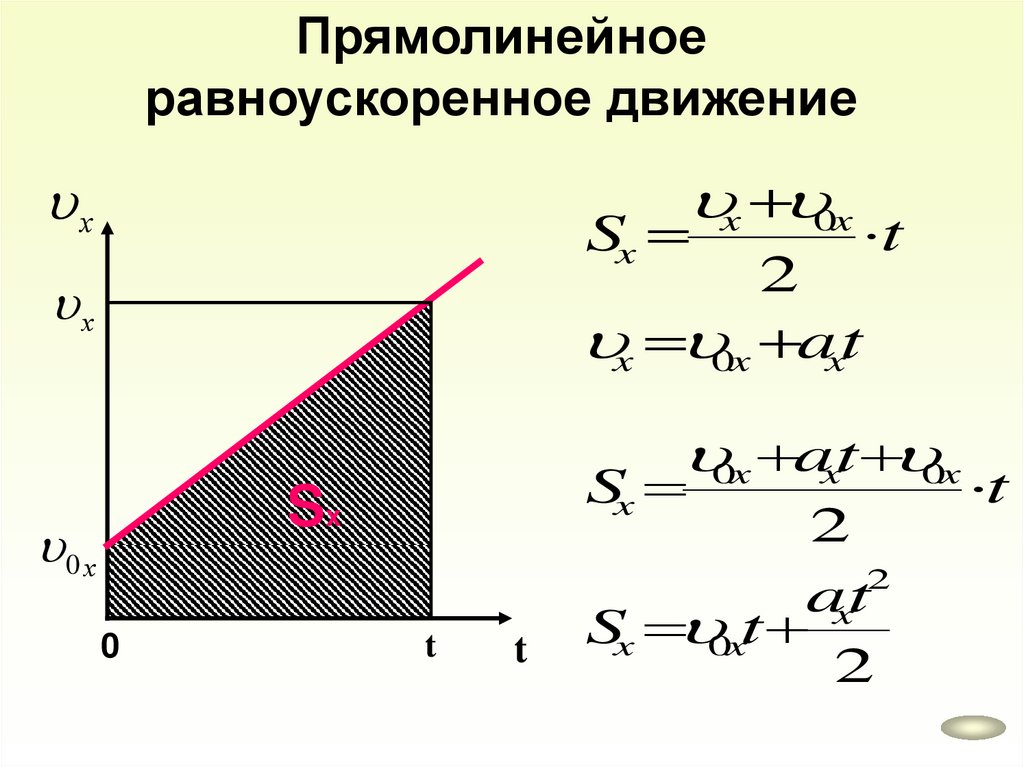
Прямолинейное
равноускоренное движение
x 0x
х
Sx
t
2
x 0x axt
х
0x axt 0x
Sx
Sx
0 х
0
t
t
2
2
axt
Sx 0xt
2
t

31.

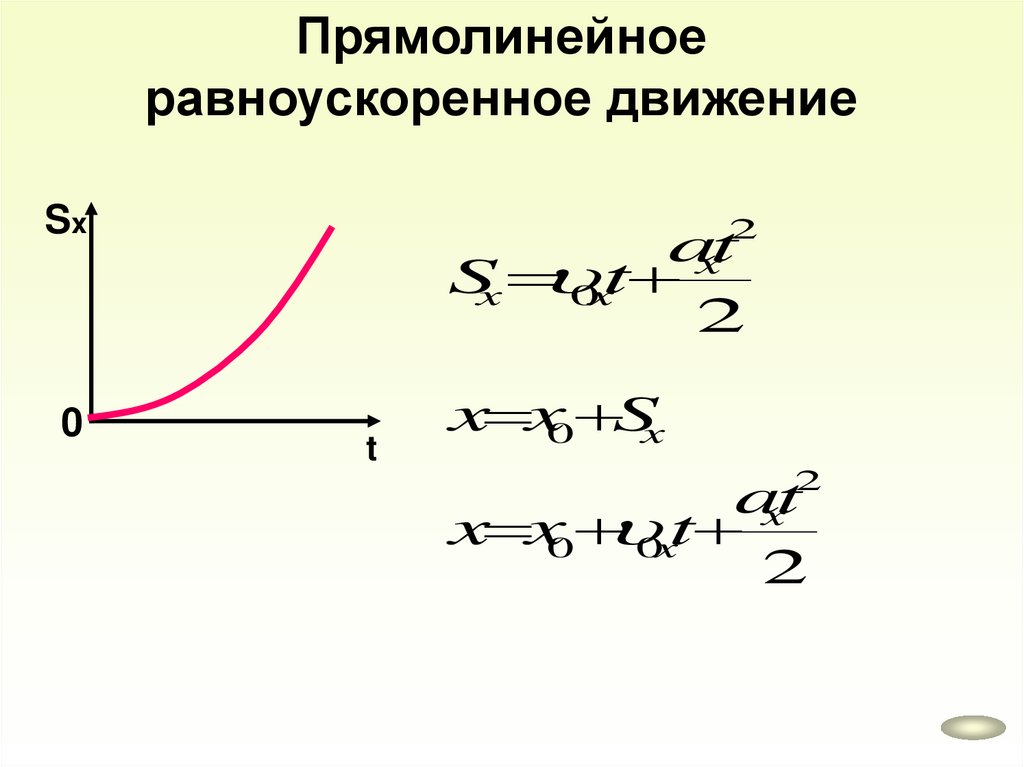
Прямолинейное
равноускоренное движение
Sx
0
2
axt
Sx
0xt
2
t
x x0 Sx
2
axt
x x0 0xt
2

32.

Прямолинейное
равноускоренное движение
2
axt
Sx
0xt
2
x 0x
ax
t
x2 02x
Sx
2a
x 0x
Sx
2
t

33.

Прямолинейное
равноускоренное движение
0
1t
2t
3t
4t
t
S
:
S
:
S
:
S
:
...
1
:
3
:
5
:
7
:
...
1
2
3
4

34.

35.

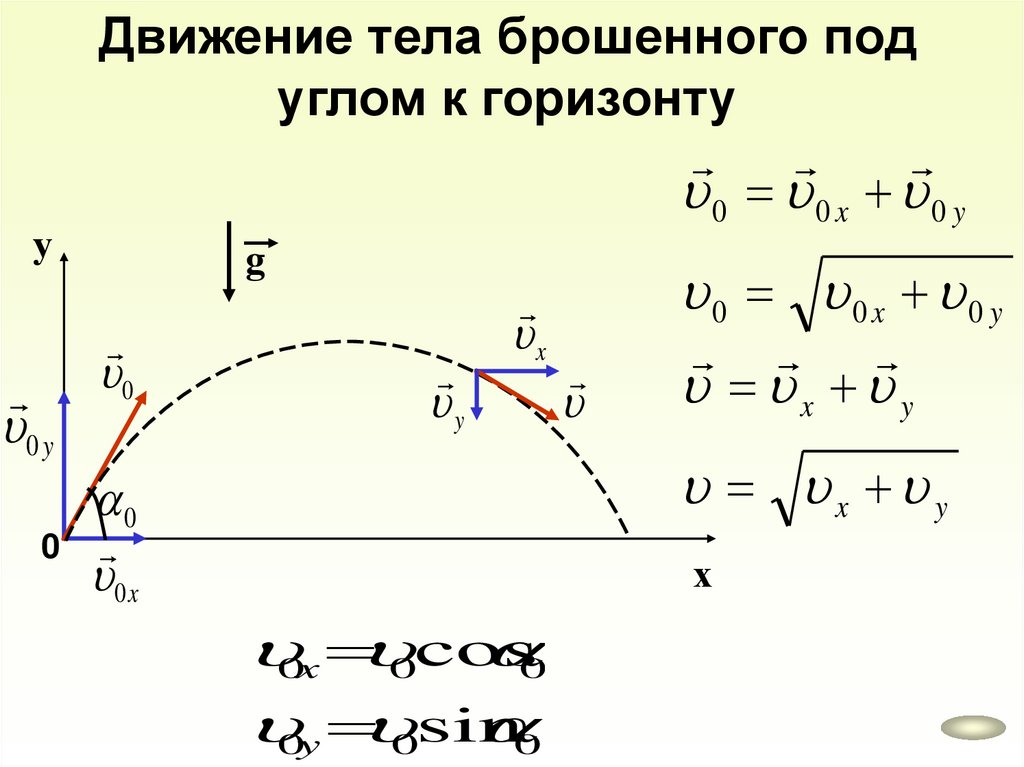
Движение тела брошенного под
углом к горизонту

36.

у
Движение тела брошенного под
углом к горизонту
g
0 y
0
0
y
x
0
0 x
х
x x0 xt
2
gt
y y0 0yt
2
x 0x const
y 0y gt

37.

Движение тела брошенного под
углом к горизонту
0 0x 0 y
у
0 y
g
0
0
0
0 x
y
x
0 0x 0 y
x y
x y
х
0x 0cos
0
0y 0sin
0

38.

Движение тела брошенного под
углом к горизонту
у
0 y
g
0
0
0
0 x
х
tm
0 0y g
2
2 0 y
tm
g
2 0 sin 0
tm
g

39.

Движение тела брошенного под
углом к горизонту
у
g
0 y
0
0
0
0x
xmax х
xmax 0xtm
2 0 sin 0
xmax 0 cos
0
g
02 sin 2 0
xmax
g

40.

у
0 y
Движение тела брошенного под
углом к горизонту
g
0
0
0
0x
ymax
х
0y
tm
g
g
g
tm
2
0y
ymax 0y 0y
2
2
g
2
2
0y2
ymax
2g
2
02sin
0
ymax
2g
2

41.

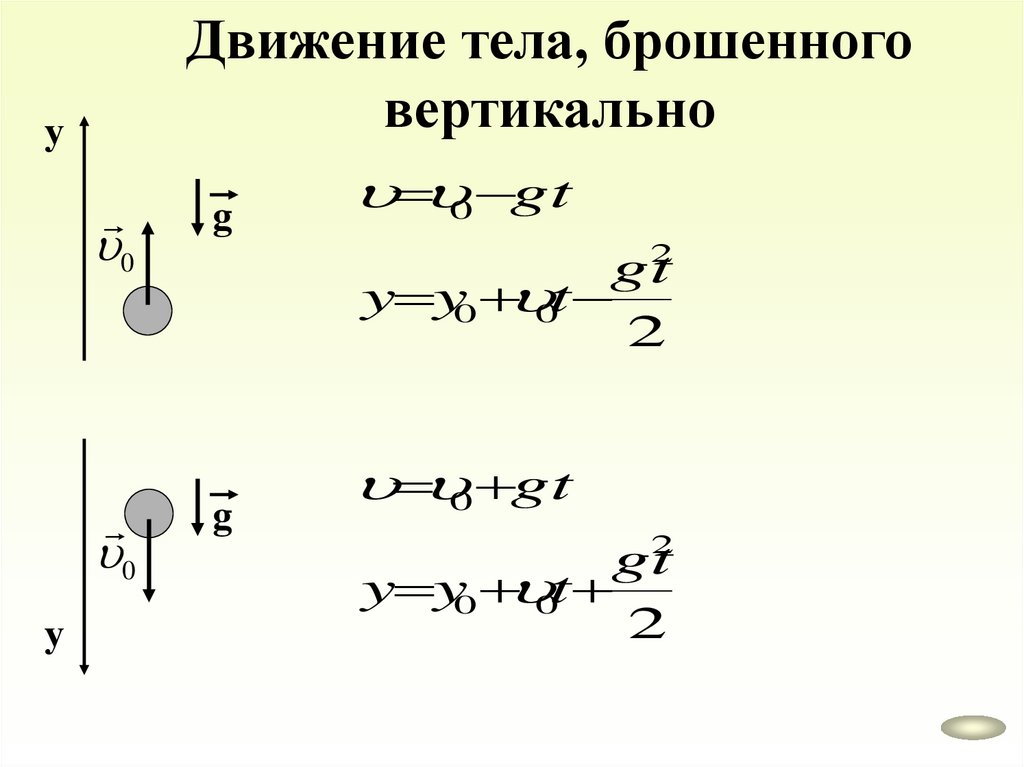
Движение тела, брошенного
вертикально
у
0
0
у
g
0 gt
gt2
y y0 0t
2
g
0 gt
gt2
y y0 0t
2

42.

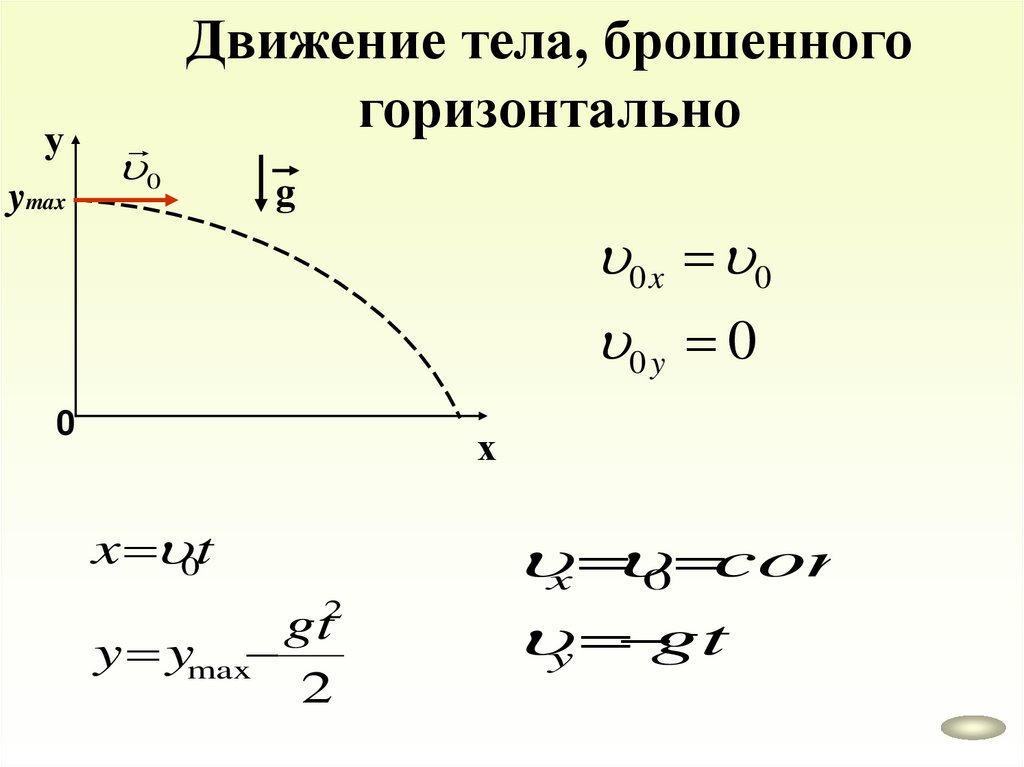
у
ymax
Движение тела, брошенного
горизонтально
0
g
0 x 0
0 y 0
0
х
x 0t
2
gt
y ymax
2
x 0 const
y gt

43.

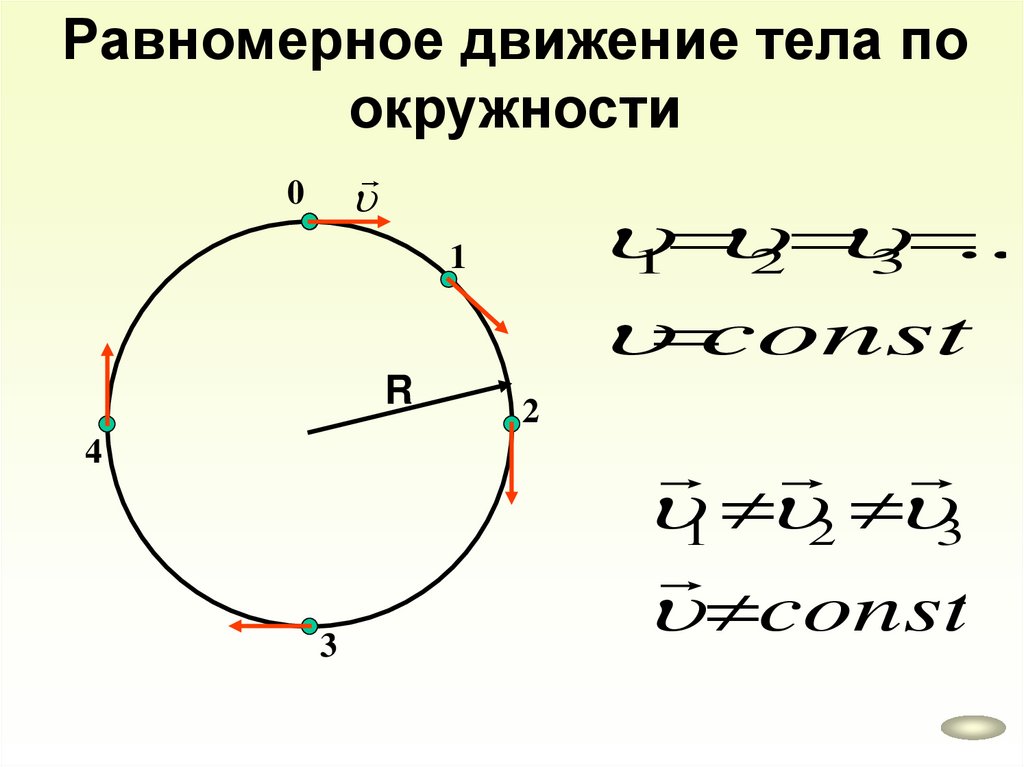
Равномерное движение тела по
окружности
0
2 3 ...
1
const
1
R
2
4
3
1 2 3
const

44.

Равномерное движение тела по
окружности
0 0
aц
R
1
1
0
a
t
t
a const
R
2
aц
R

45.

Динамика
Динамика – раздел механики, который отвечает на вопрос:
ПОЧЕМУ движется тело?
Причина изменения скорости тела – воздействие на него
других тел.
Если на тело не действуют другие тела, то оно либо
покоится, либо движется прямолинейно и равномерно.

46.

Законы Ньютона
1 закон Ньютона:
Существуют такие системы отсчета, относительно которых
тело движется прямолинейно и равномерно или покоится
при отсутствии внешних воздействий. Такие с.о. называются
инерциальными (ИСО).
Инерция – явление при котором скорость тела
остается неизменной при отсутствии на него внешних
воздействий.

47.

Законы Ньютона
Инертность – свойство тела сохранять свою скорость
при отсутствии внешних воздействий.
Мера инертности – масса тела. (Чем больше масса
тела, тем труднее изменить его скорость).
m кг
Сила – количественная мера взаимодействия тел.
F Н
F1
Равнодействующая – векторная
сумма всех сил, действующих на
тело.
Fрез
F2

48.

Законы Ньютона
2 закон Ньютона:
Ускорение тела прямо пропорционально силе,
действующей на тело и обратно пропорционально
массе этого тела.
a
F ma
м
Н кг 2
с
Fрез
m

49.

Законы Ньютона
3 закон Ньютона:
Силы, с которыми тела действуют друг на друга,
равны по модулю и противоположны по направлению.
F1 F 2
m 1a1 m 2 a 2
m 1a1 m 2 a 2
m1 a2
m 2 a1

50.

Законы Ньютона
N
Земля
P
Fпр
FУ
Fпр
F
Луна
Силы, возникающие при взаимодействии тел не могут
скомпенсировать друг друга, так как действуют на
разные тела.

51.

Закон всемирного
тяготения
Исаак Ньютон
Все тела во Вселенной притягиваются друг к другу с
силами прямо пропорциональными произведению их
масс и обратно пропорциональными квадрату
расстояния между их центрами.
F1
F2
r
m
1m
2
F G 2
r

52.

Закон всемирного
тяготения
F r
G
m1m2
2
Гравитационная постоянная – величина.
Численно равная силе взаимодействия
двух тел массами по 1 кг , находящихся
на расстоянии 1 м друг от друга.
2
H
м
11
G
6
,672
10 2
кг
1798 г. Генри Кавендиш

53.

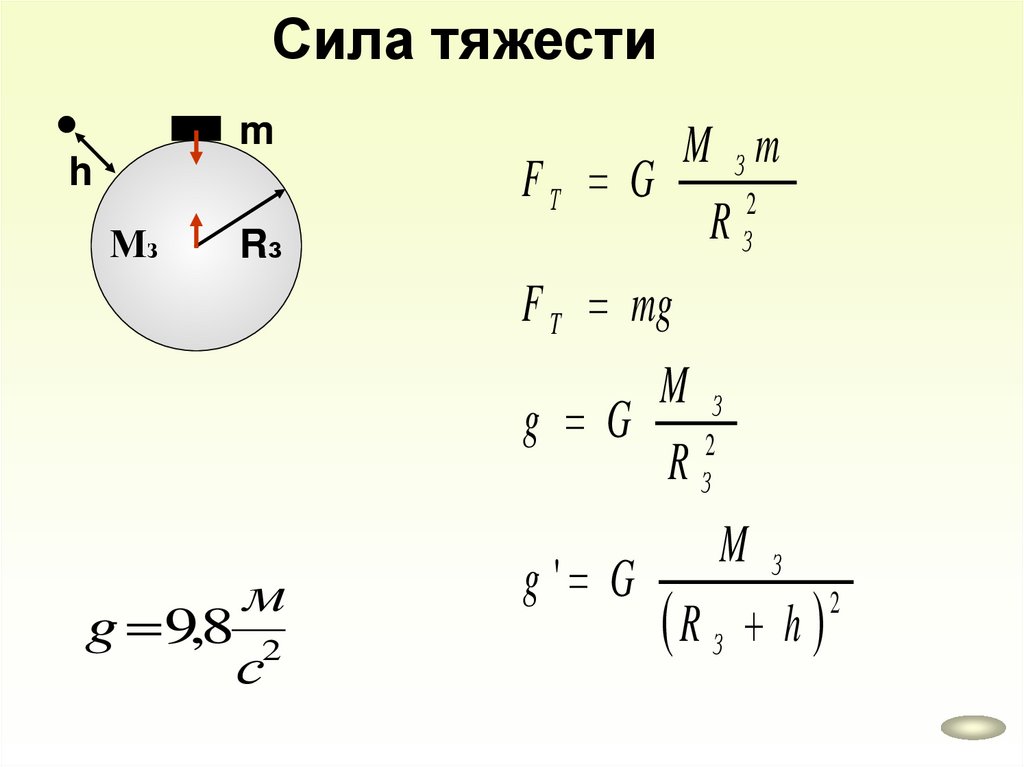
Сила тяжести
m
h
Мз
Rз
M Зm
FТ G
2
RЗ
F T mg
M З
g G 2
RЗ
м
g 9,8 2
с
M З
g ' G
2
R З h

54.

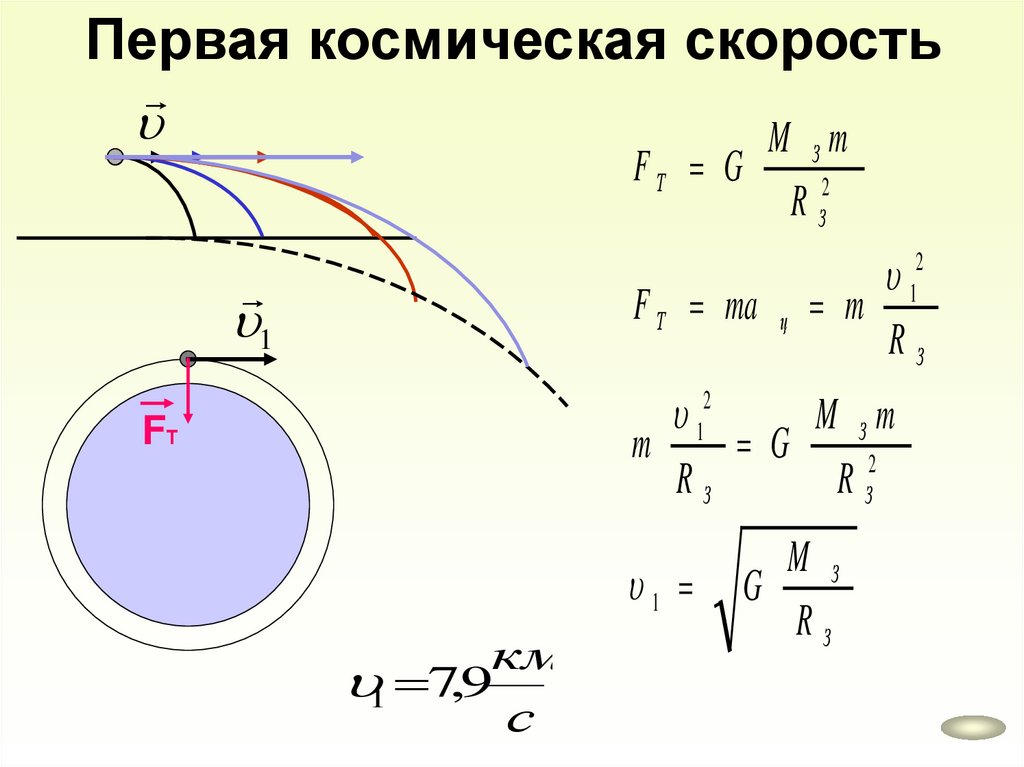
Первая космическая скорость
M Зm
FТ G
2
RЗ
F Т ma ц m
RЗ
2
1
1
M Зm
m
G
RЗ
R З2
2
1
FТ
1
км
1 7,9
с
M З
G
RЗ

55.

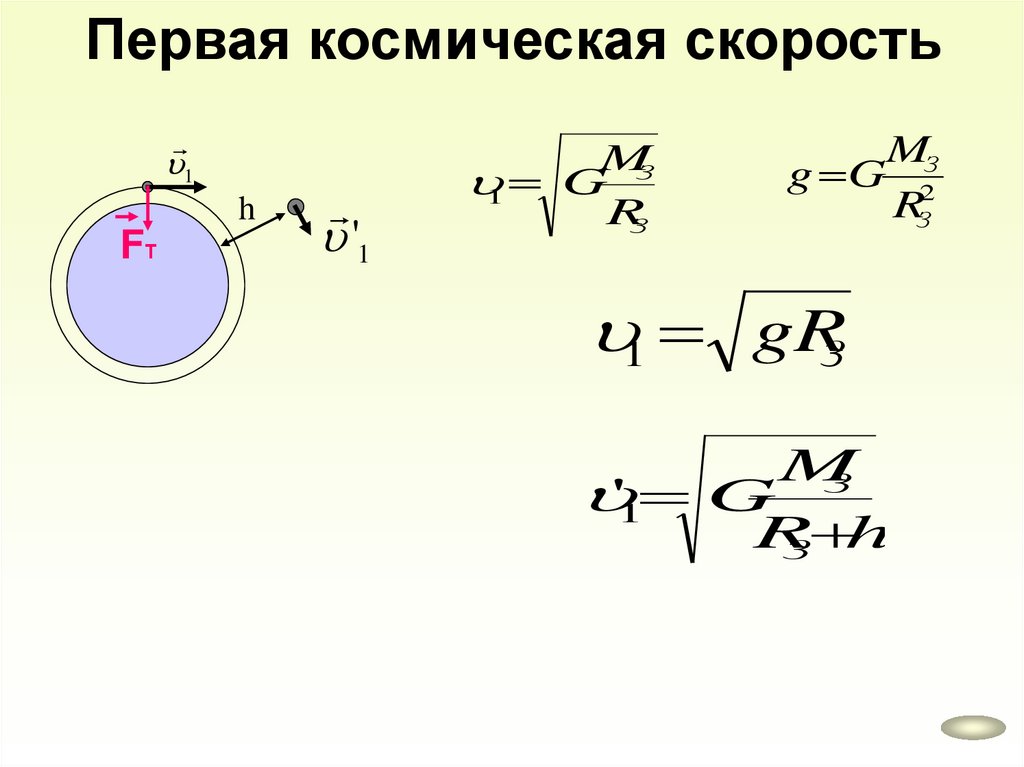
Первая космическая скорость
1
h
FТ
'1
MЗ
1 G
RЗ
MЗ
g G 2
RЗ
1 gRЗ
M
'1 G З
R
h
З

56.

Космические скорости
км
1 7,9
с
1 2
M
2 2G З
R
З
км
2 11
,2
с
км
3 16
,7
с

57.

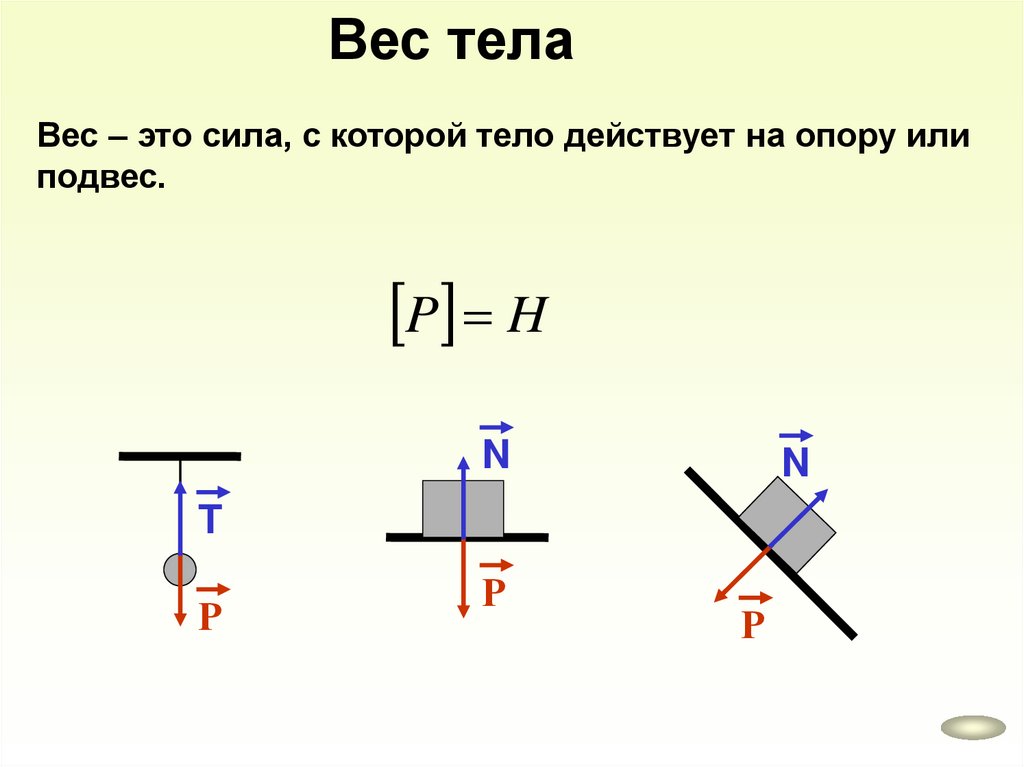
Вес тела
Вес – это сила, с которой тело действует на опору или
подвес.
P H
N
N
T
Р
Р
Р

58.

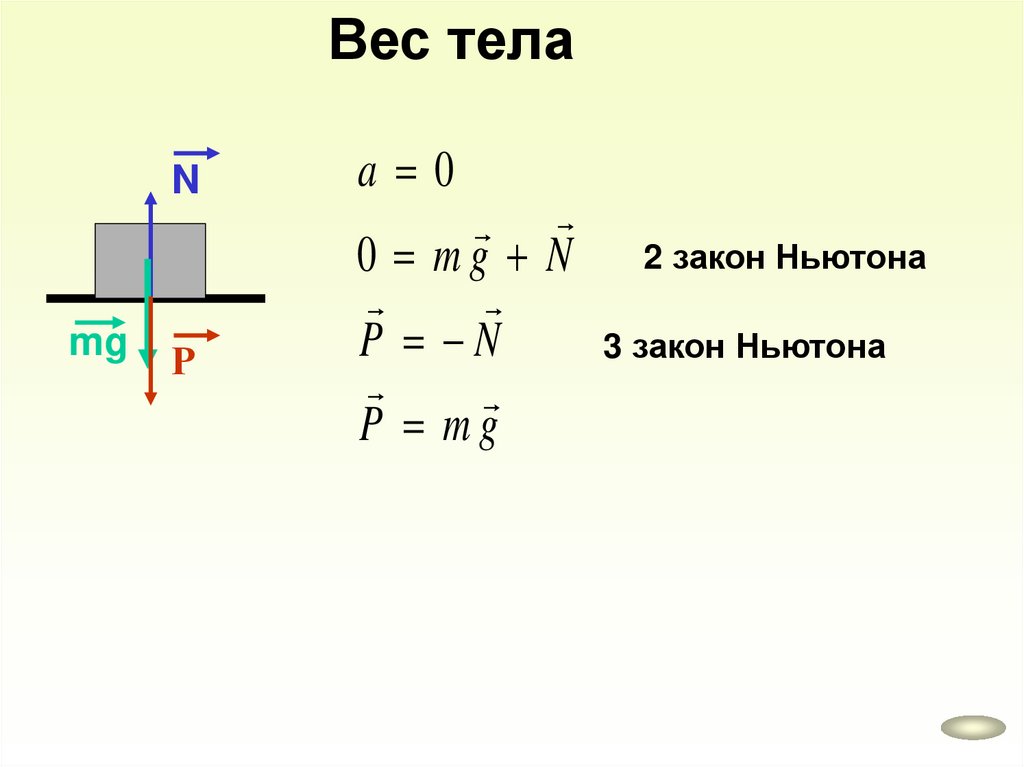
Вес тела
N
mg
Р
a 0
0 m g N 2 закон Ньютона
P N
3 закон Ньютона
P mg

59.

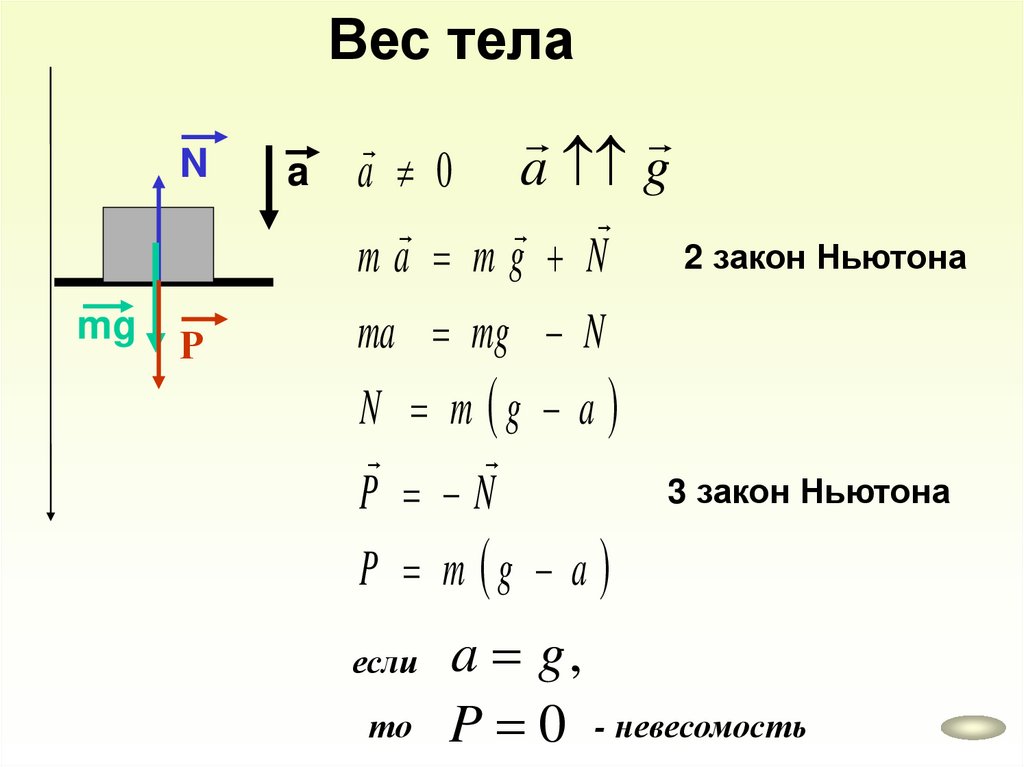
Вес тела
N
mg
Р
a
a 0 a g
2 закон Ньютона
ma mg N
ma mg N
N m g a
3 закон Ньютона
P N
P m g a
a g,
то P 0 - невесомость
если

60.

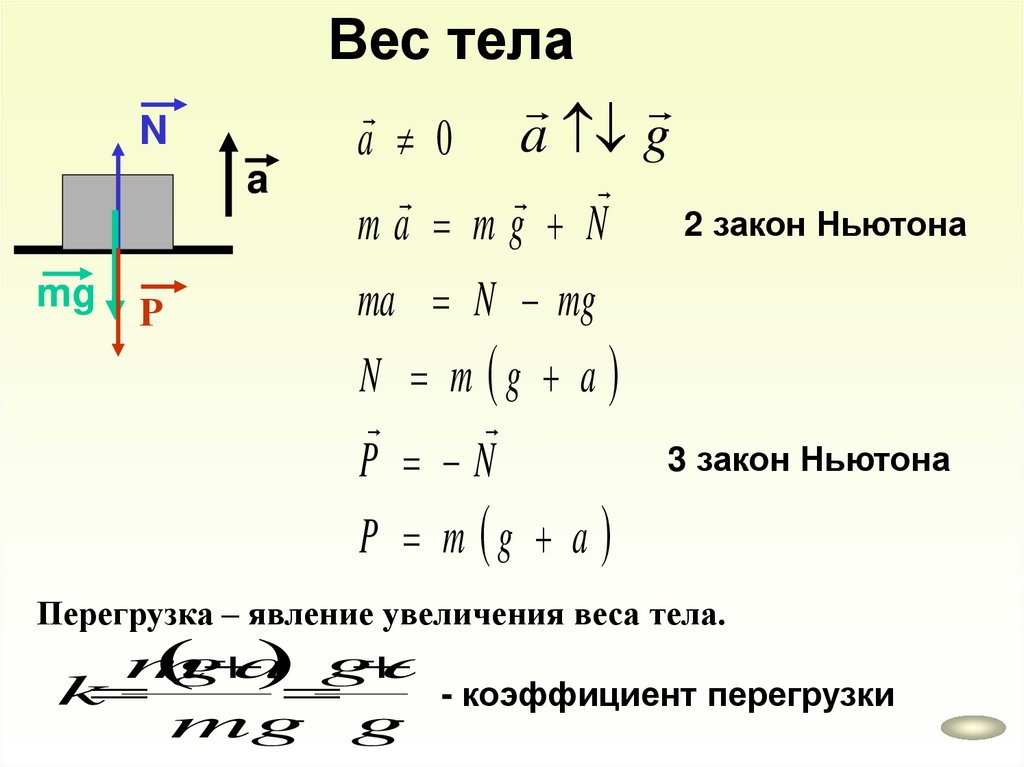
N
a
mg
Р
Вес тела
a 0 a g
ma mg N
ma N mg
N m g a
P N
P m g a
2 закон Ньютона
3 закон Ньютона
Перегрузка – явление увеличения веса тела.
m
g
a
g
a
k
- коэффициент перегрузки
mg g

61.

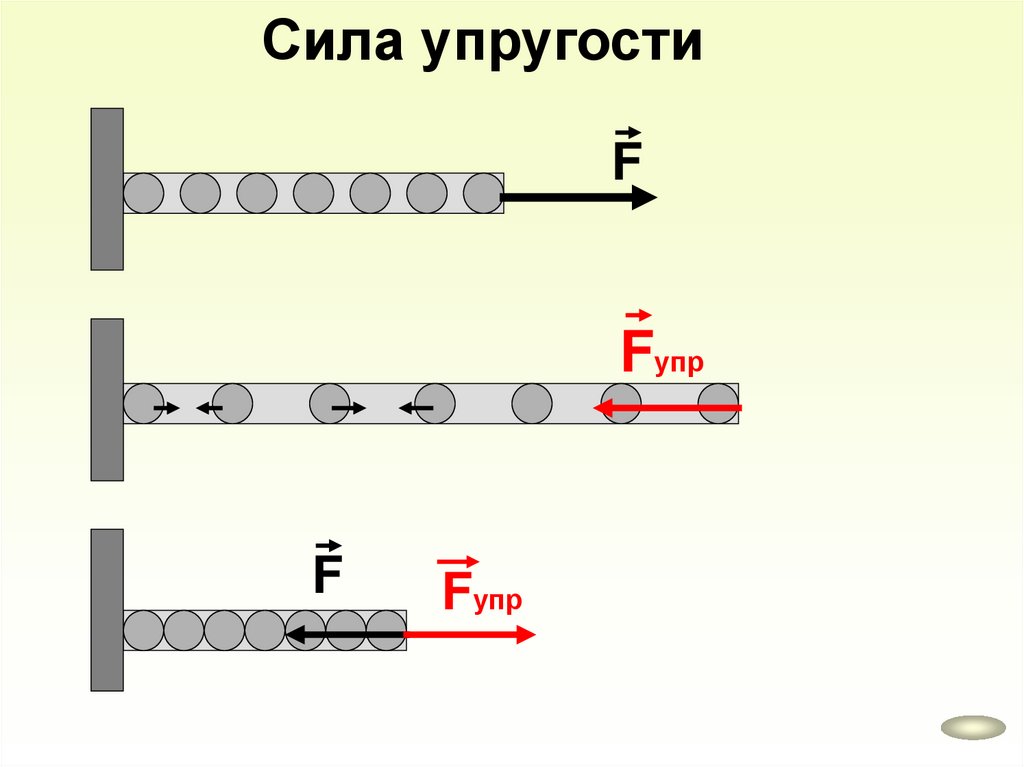
Сила упругости
F
Fупр
F
Fупр

62.

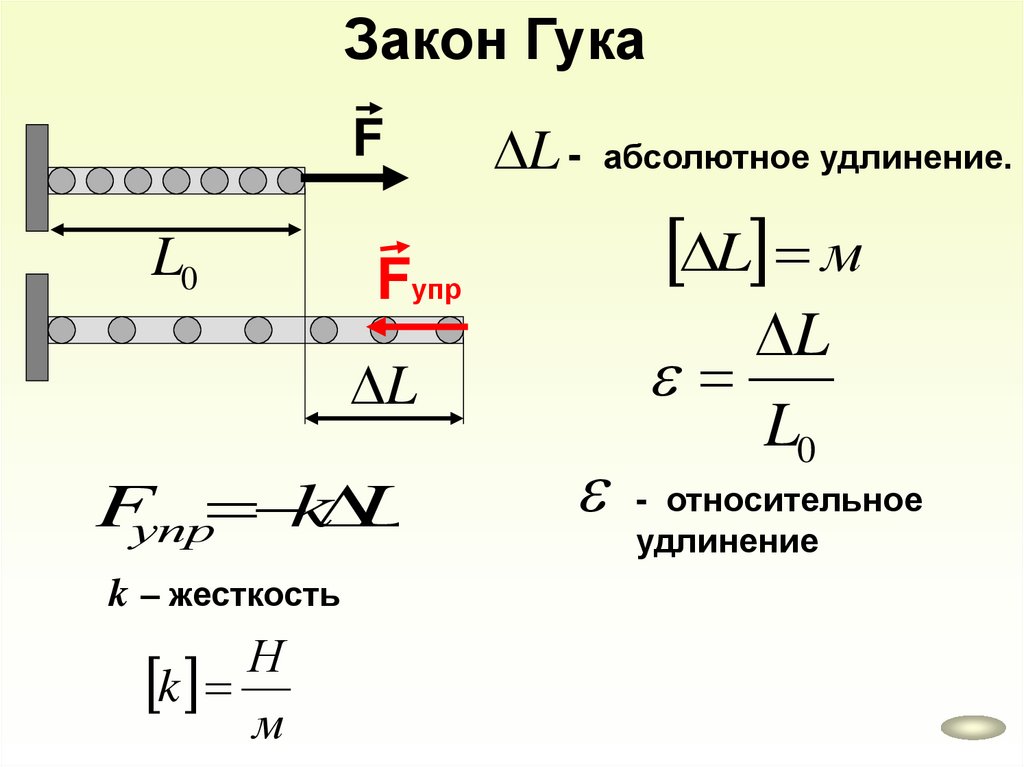
Закон Гука
F
L0
Fупр
L
Fупр k L
k – жесткость
Н
k
м
L - абсолютное удлинение.
L м
L
L0
- относительное
удлинение

63.

Закон Гука
F
- механическое напряжение
S
Н
2 Па
м
пч - предел прочности – максимальное механическое
напряжение, которое выдерживает данное
вещество
Е
1660 г.
Е – модуль Юнга
Е Па

64.

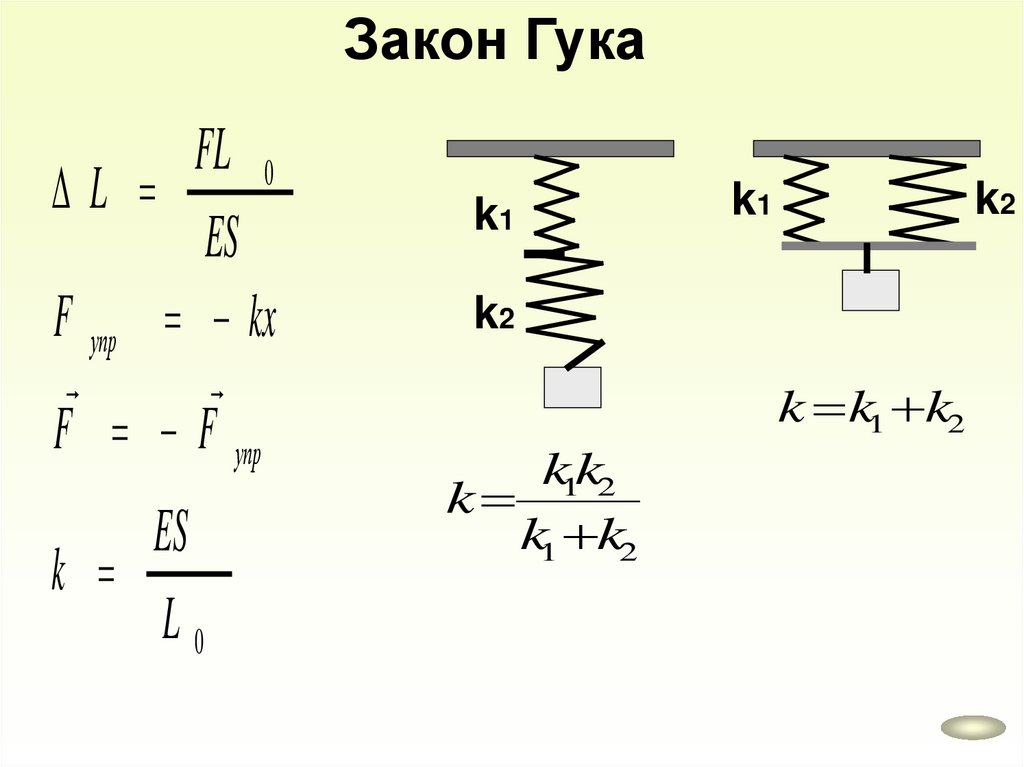
Закон Гука
FL 0
L
ES
F упр kx
F F упр
ES
k
L0
k1
k2
k1
k2
k k1 k2
k1k2
k
k1 k2

65.

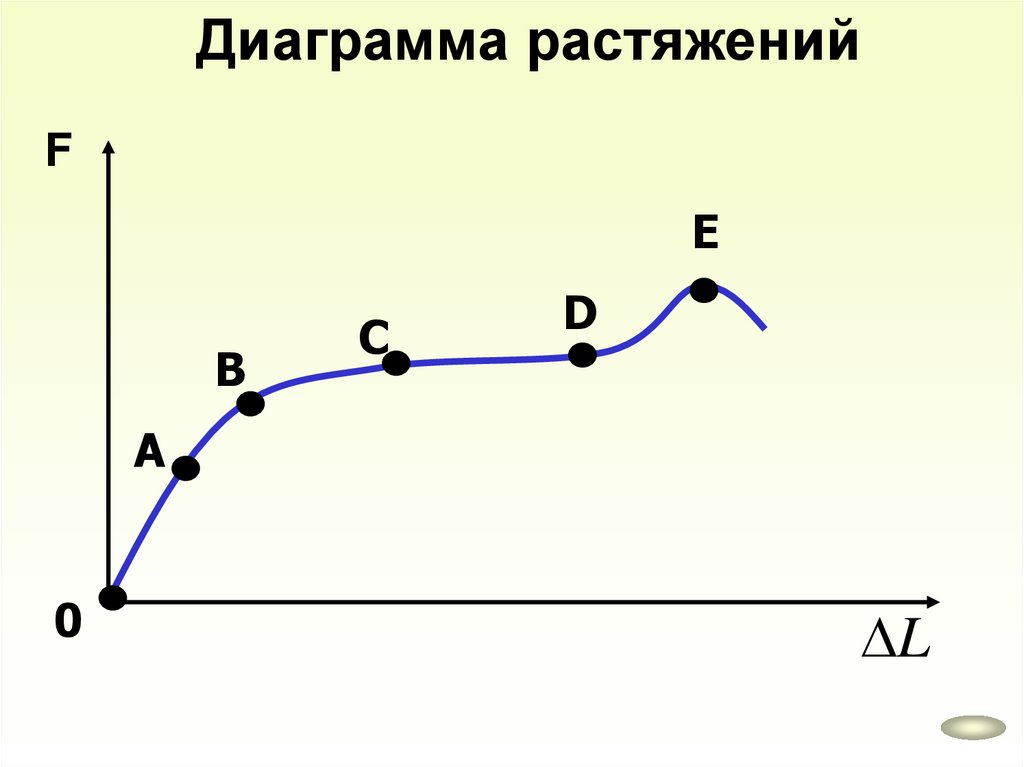
Диаграмма растяжений
F
Е
В
С
D
А
0
L

66.

Сила трения
N
Fтяги
Fтр
mg
Cилу трения, действующую между двумя телами,
неподвижными относительно друг друга называют
силой трения покоя.
Наибольшее значение силы трения, при котором
скольжение еще не наступает, называется
максимальной силой трения покоя.
Fтр.max N
Сила трения не зависит от площади соприкосновения
тел.

67.

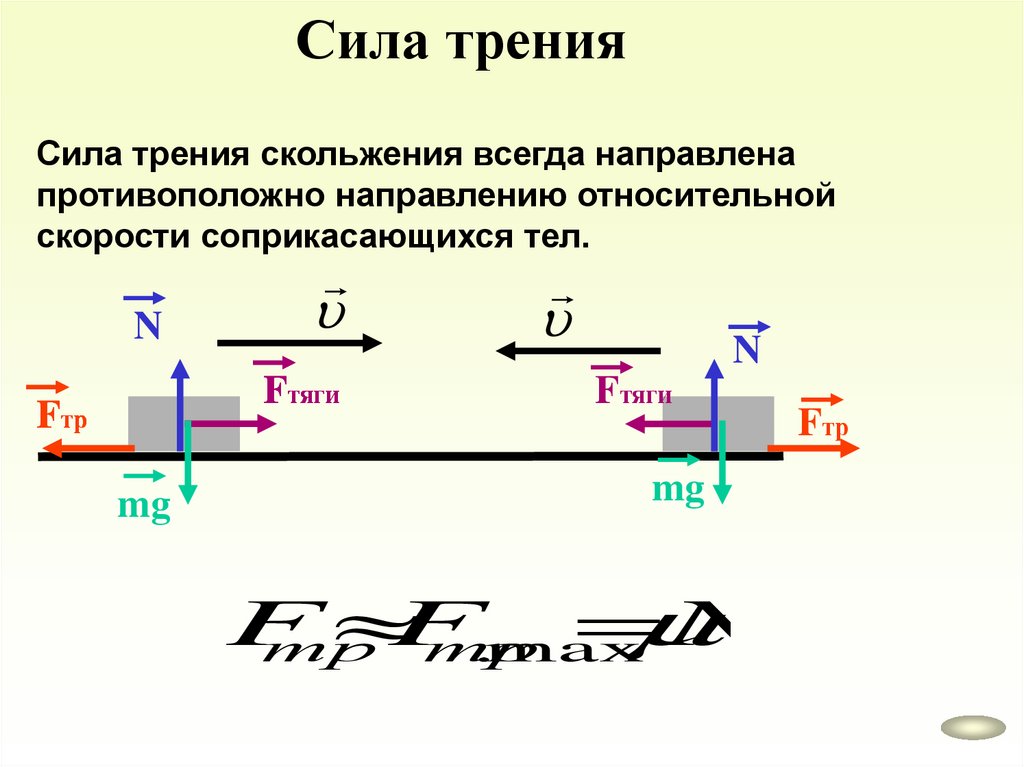
Сила трения
Сила трения скольжения всегда направлена
противоположно направлению относительной
скорости соприкасающихся тел.
N
Fтяги
Fтр
mg
N
Fтяги
mg
F
F
N
тр
тр
.max
Fтр

68.

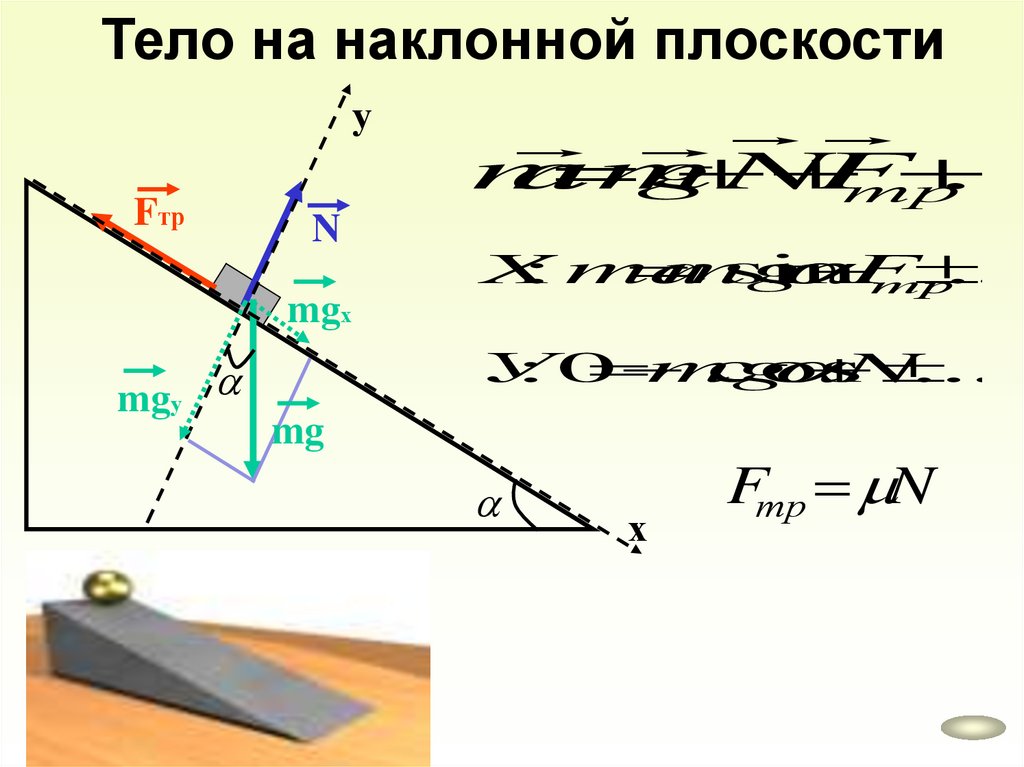
Тело на наклонной плоскости
у
m
a
m
g
N
F
...
тр
Fтр
N
mgх
mgу
X
: ma
mg
sin
F
...
тр
У
:0
mg
cos
N
...
mg
х
Fтр N

69.

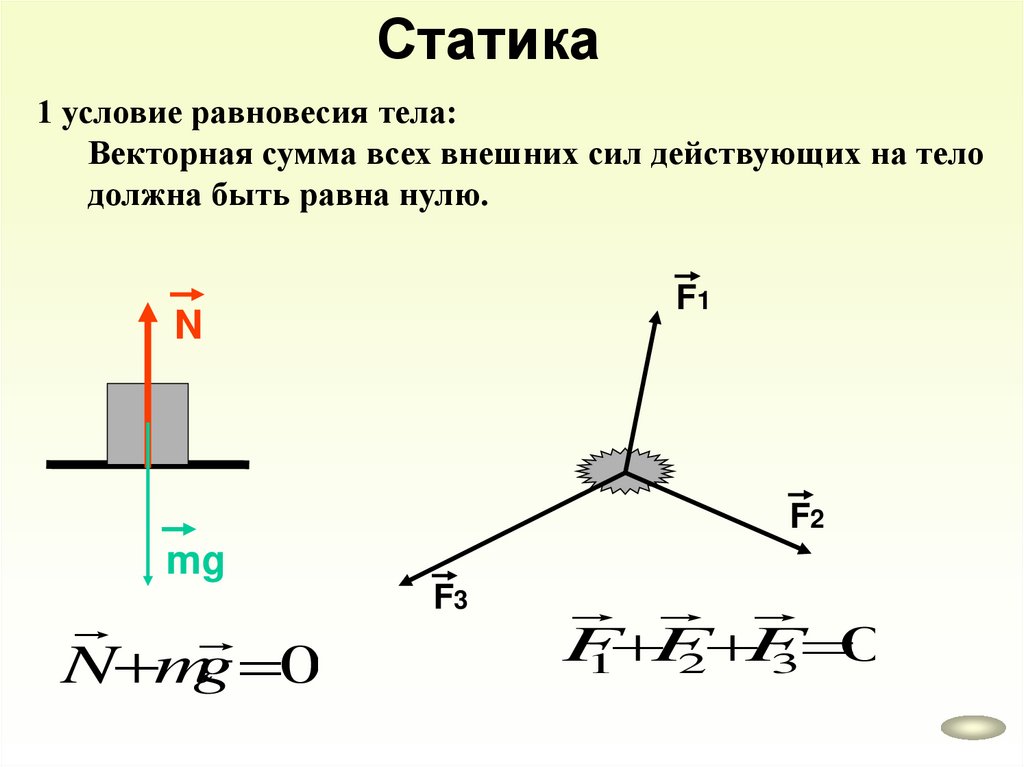
Статика
1 условие равновесия тела:
Векторная сумма всех внешних сил действующих на тело
должна быть равна нулю.
F1
N
F2
mg
N mg 0
F3
F
F
F
0
1
2
3

70.

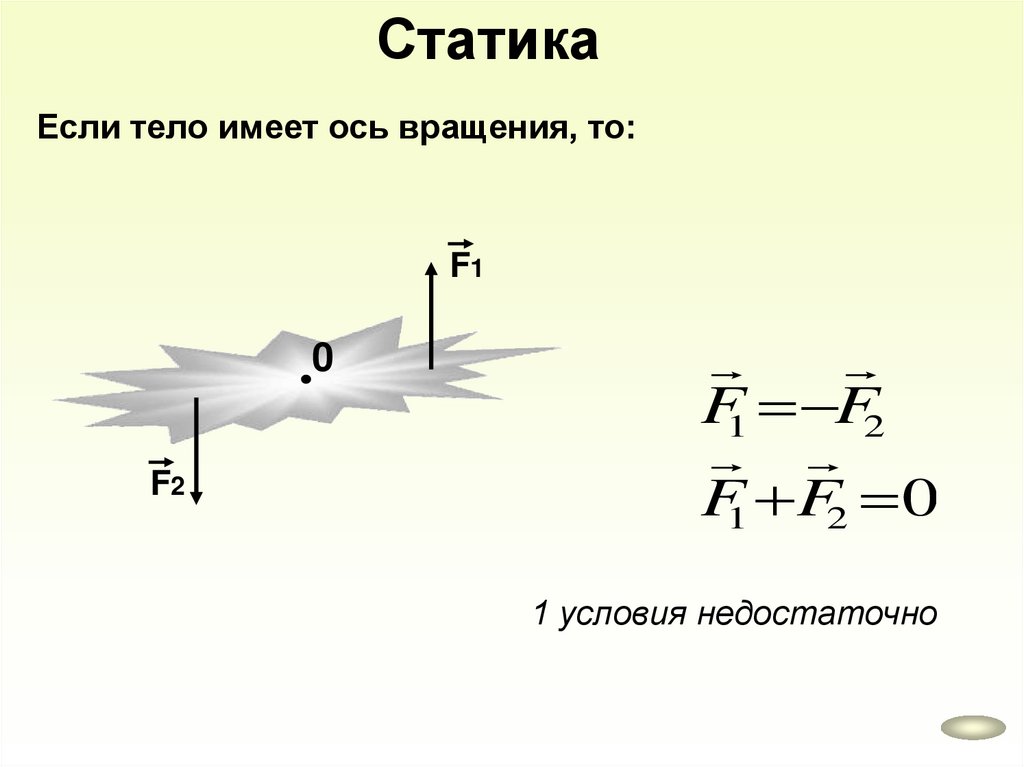
Статика
Если тело имеет ось вращения, то:
F1
0
F2
F1 F2
F1 F2 0
1 условия недостаточно

71.

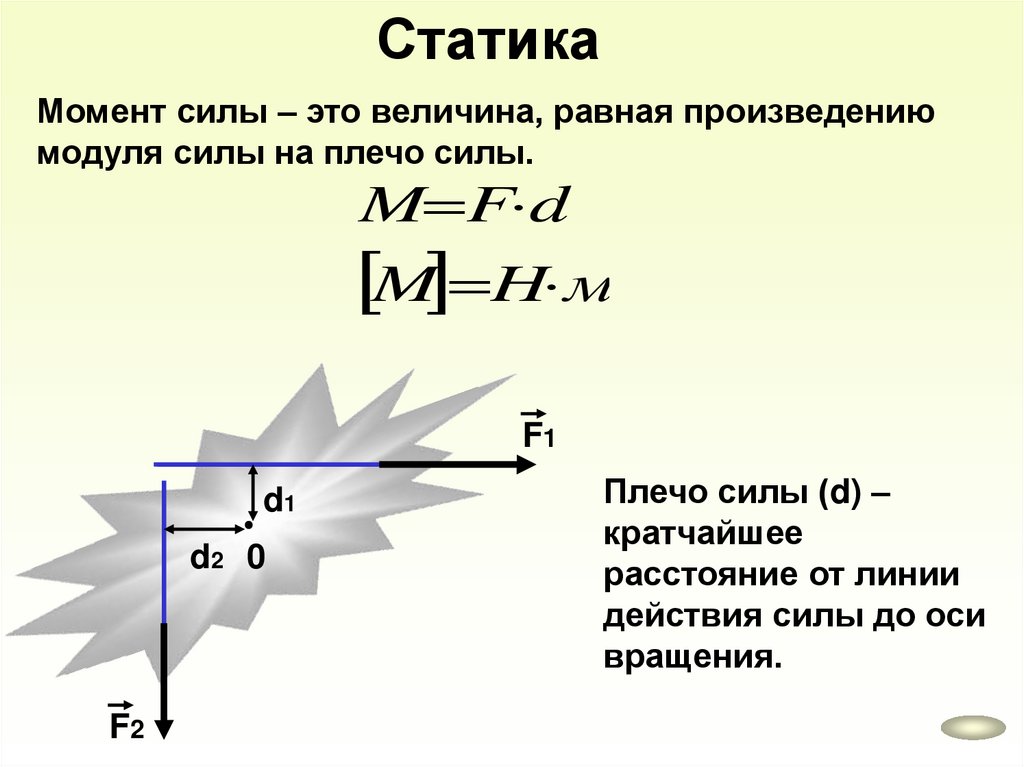
Статика
Момент силы – это величина, равная произведению
модуля силы на плечо силы.
M F d
M H м
F1
d1
d2 0
F2
Плечо силы (d) –
кратчайшее
расстояние от линии
действия силы до оси
вращения.

72.

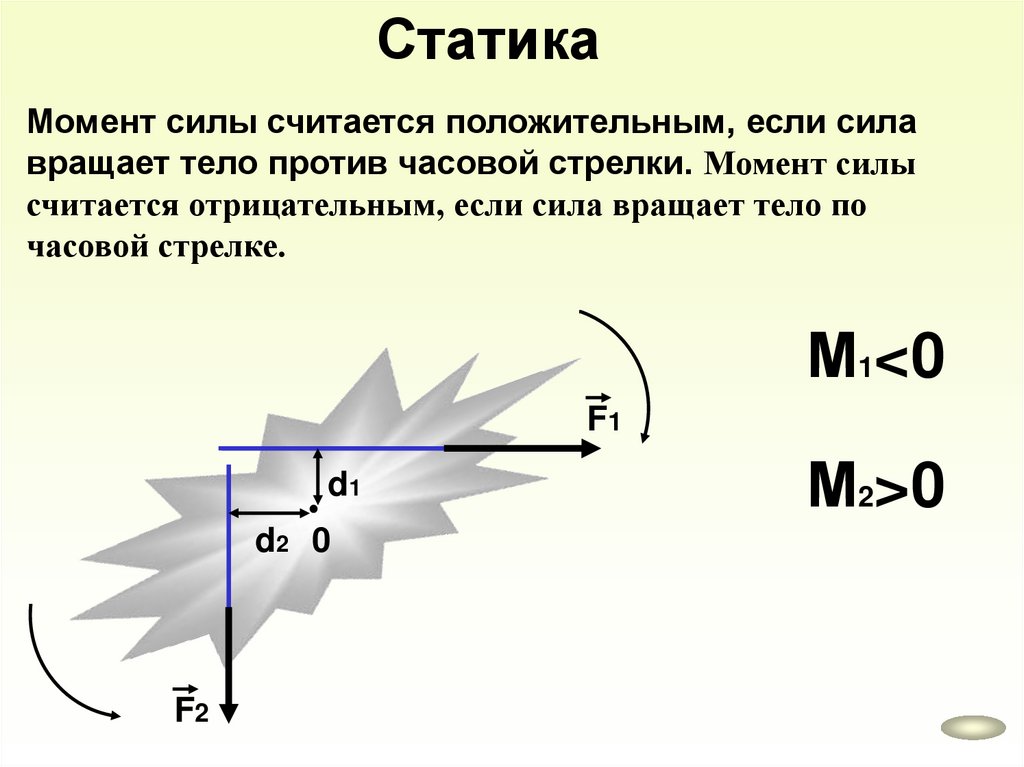
Статика
Момент силы считается положительным, если сила
вращает тело против часовой стрелки. Момент силы
считается отрицательным, если сила вращает тело по
часовой стрелке.
М1<0
F1
d1
d2 0
F2
М2>0

73.

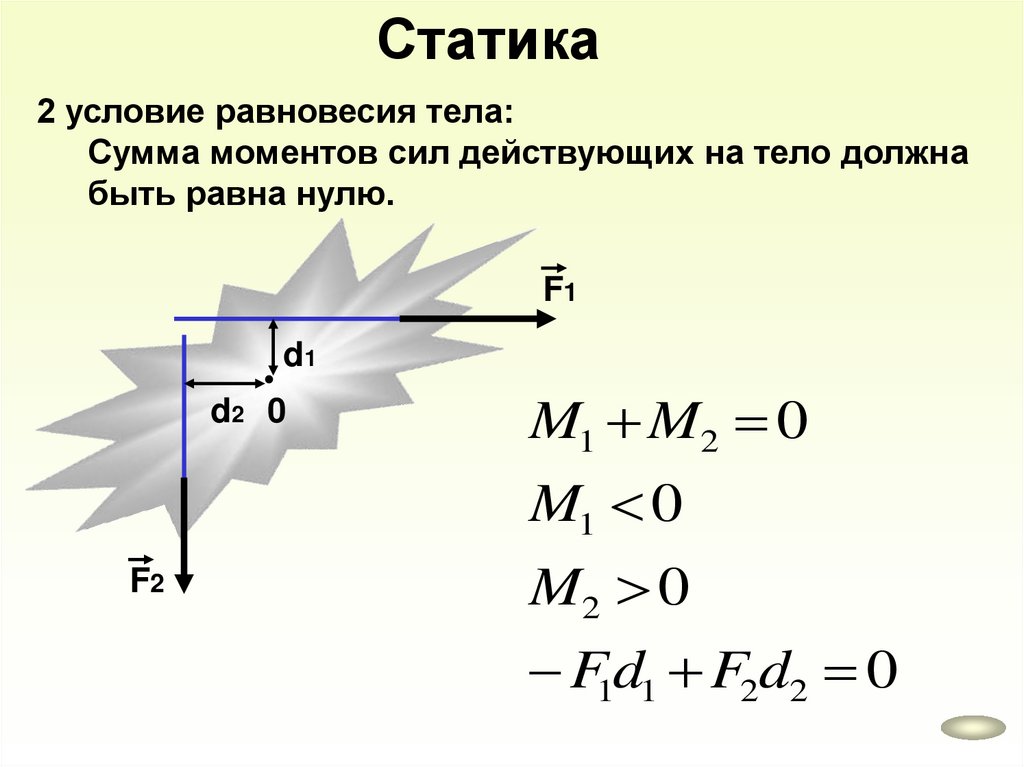
Статика
2 условие равновесия тела:
Сумма моментов сил действующих на тело должна
быть равна нулю.
F1
d1
d2 0
M1 M2 0
M1 0
F2
M2 0
F1d1 F2d2 0

74.

Импульс
F
a
m
0
a
t
Ft m m o
Ft - импульс силы
P m - импульс тела
Ft P P0
Ft P
Ft Н с
кг м
P
с
кг
м кг
м
Н
с
2 с
с
с

75.

Закон сохранения импульса
F
t m
m
o
F
F
1
2
m
1 m
01 m
2 m
02
1
1
2
2
m
01 m
02 m
1 m
2
1
2
1
2
P
P
P
P
01
02
1
2

76.

Закон сохранения импульса
m
m
m
m
1
01
2
02
1
1
2
2
P
P
P
P
01
02
1
2
упругий удар

77.

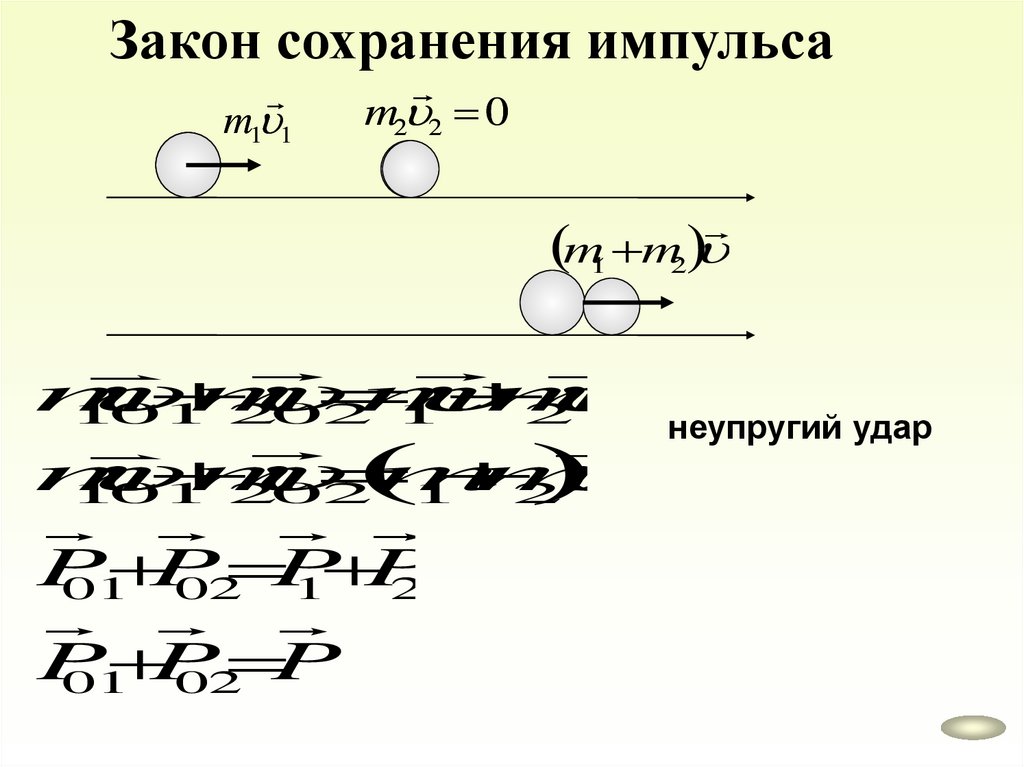
Закон сохранения импульса
m1 1
m2 2 0
m1 m2
m
m
m
m
неупругий удар
1
01
2
02
1
2
m
m
m
m
1
01
2
02
1
2
P
P
P
P
01
02
1
2
P
P
P
01
02

78.

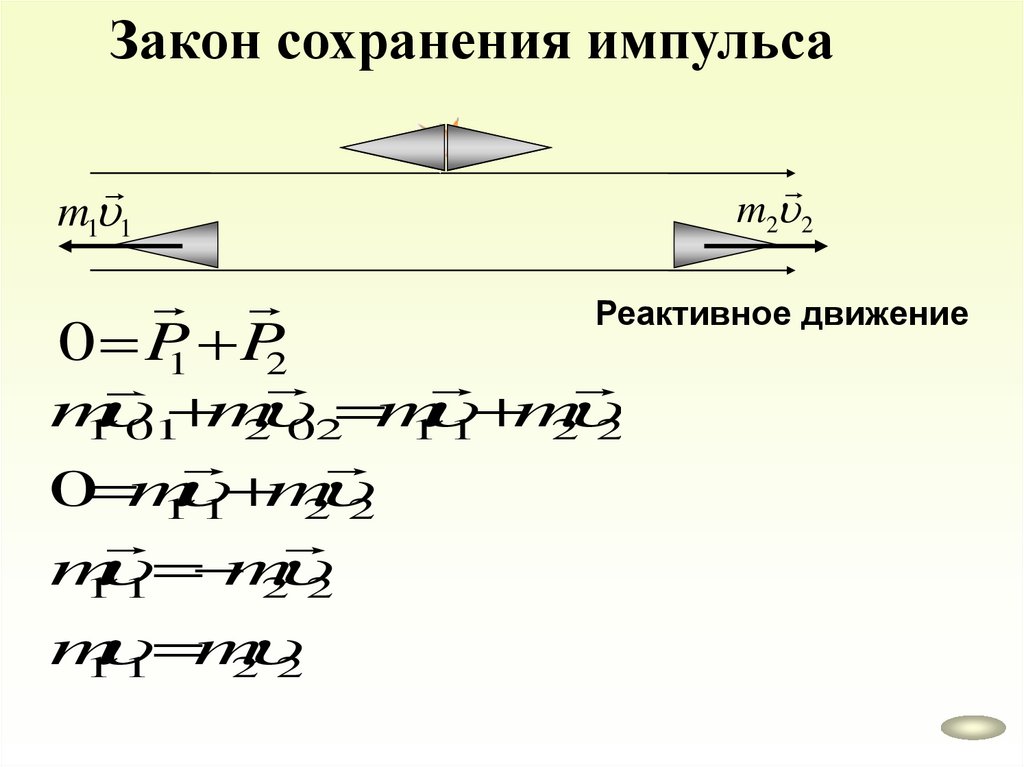
Закон сохранения импульса
m1 1
0 P1 P2
m2 2
Реактивное движение
m
01 m
02 m
1 m
2
1
2
1
2
0 m
1 m
2
1
2
m
1 m
2
1
2
m
1 m
2
1
2

79.

Закон сохранения импульса
m
m
m
n
n
n
ц
m m m m gh
2
n
ц
2
n
ц

80.

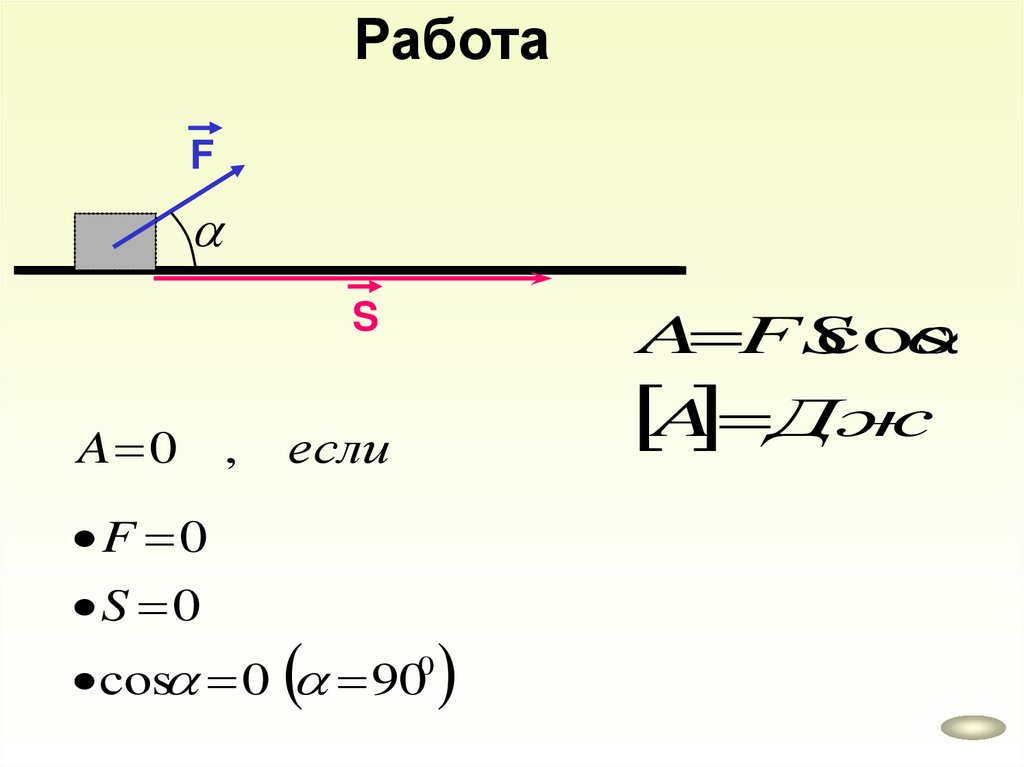
Работа
F
A FS
cos
A Дж
S
A 0
F 0
S 0
,
если
cos 0 900

81.

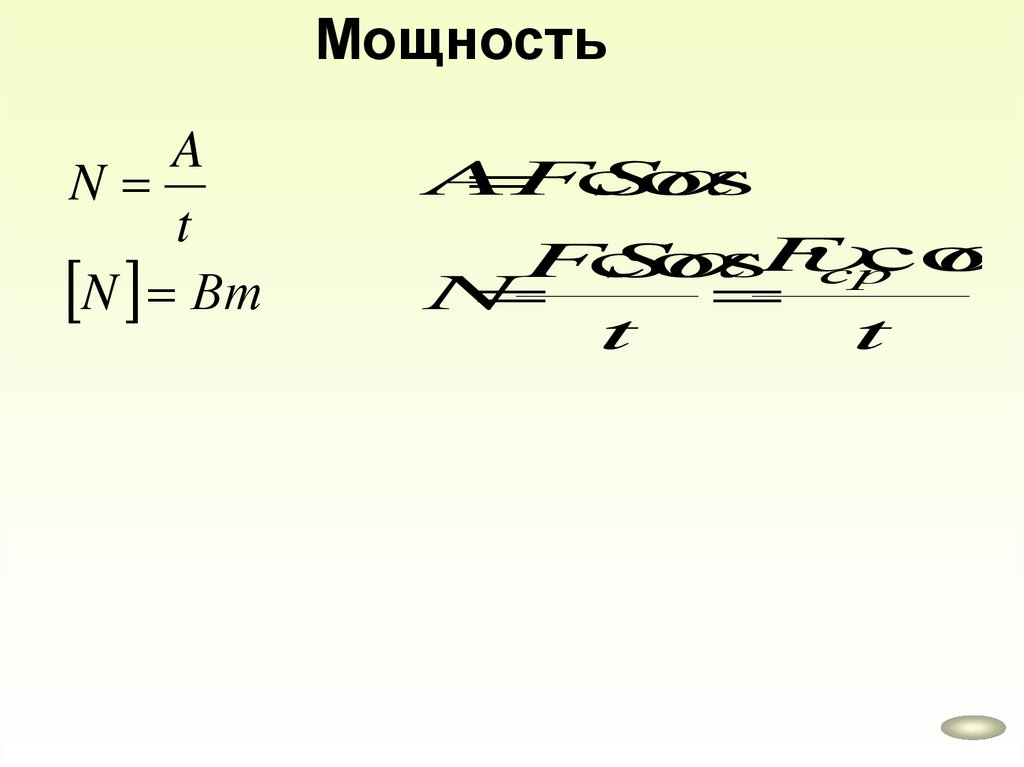
Мощность
A
N
t
N Вт
A
FS
cos
F
cos
FS
cos
ср
N
t
t

82.

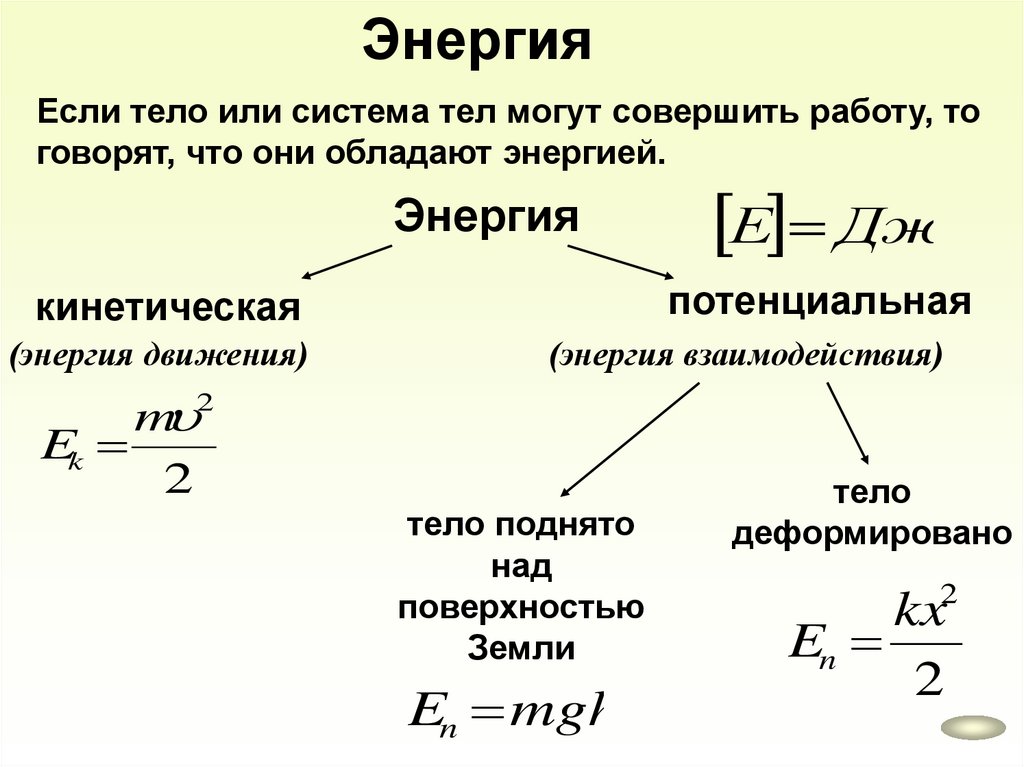
Энергия
Если тело или система тел могут совершить работу, то
говорят, что они обладают энергией.
Энергия
потенциальная
кинетическая
(энергия движения)
Е Дж
(энергия взаимодействия)
m 2
Ek
2
тело поднято
над
поверхностью
Земли
En mgh
тело
деформировано
2
kx
En
2

83.

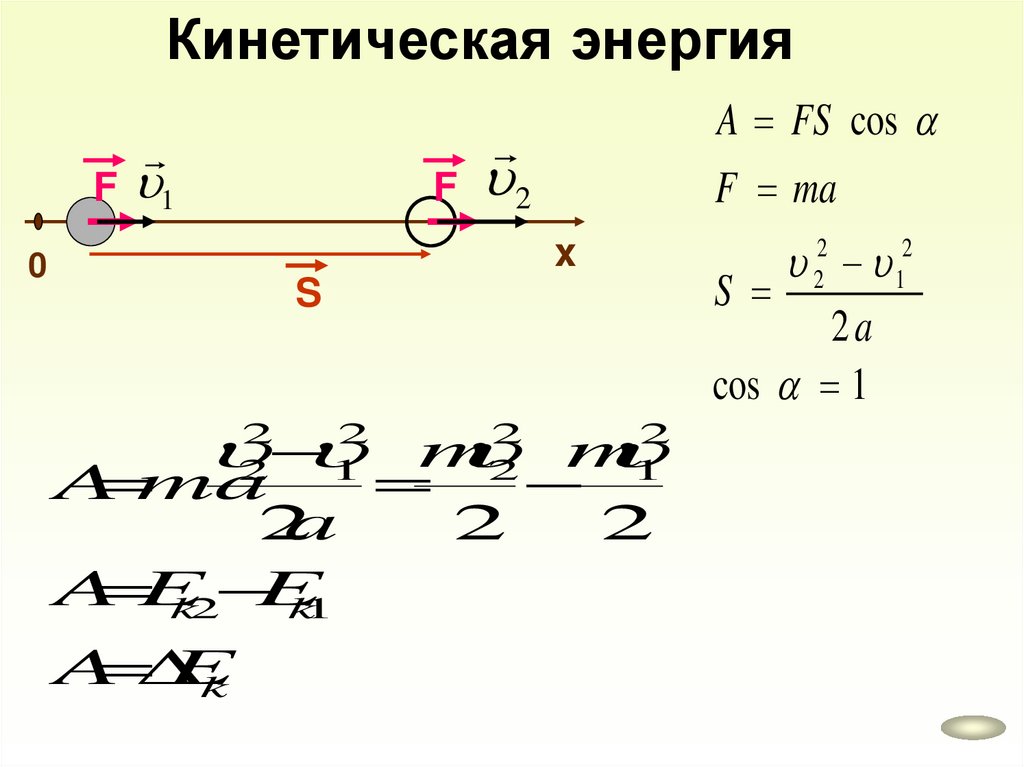
Кинетическая энергия
A FS cos
F ma
F 2
F 1
x
0
S
m
m
2
2
2
1
2
2
2
1
A ma
2
a
2
2
A E
E
k2
k1
A
E
k
22 12
S
2a
cos 1

84.

Потенциальная энергия
mg
h h1
h2
A FScos
F mg
S h h1 h2
cos 1
A mg h1 h2 mgh1 mgh2
A En1 En2 En2 En1
A En

85.

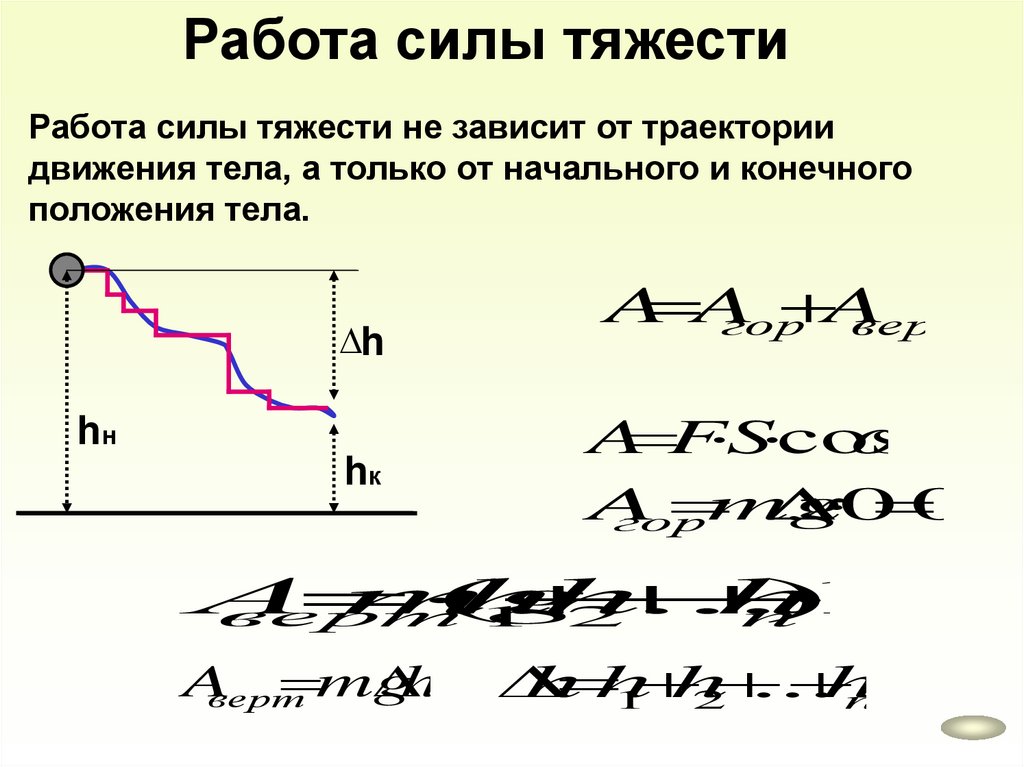
Работа силы тяжести
Работа силы тяжести не зависит от траектории
движения тела, а только от начального и конечного
положения тела.
h
hн
hк
A A
A
гор
верт
A F S cos
A
mg
х 0
0
гор
А
mg
(
h
h
...
h
)
1
верт
1
2
n
A
mg
h
верт
h
h
h
...
h
1
2
n

86.

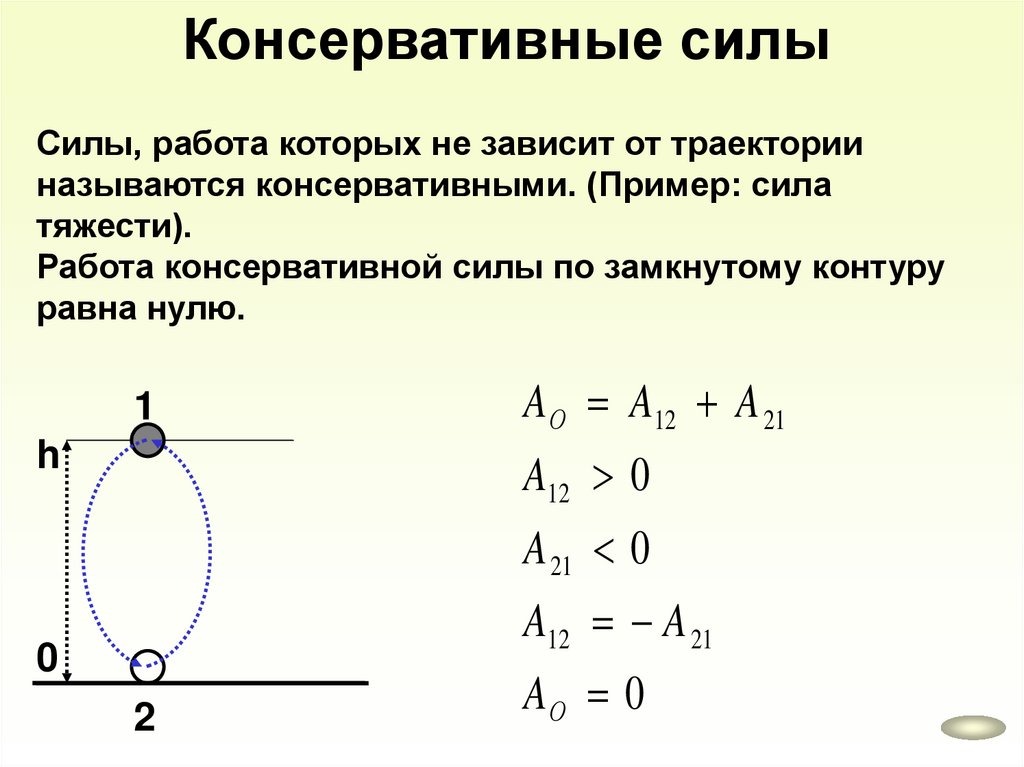
Консервативные силы
Силы, работа которых не зависит от траектории
называются консервативными. (Пример: сила
тяжести).
Работа консервативной силы по замкнутому контуру
равна нулю.
1
h
A О A12 A 21
A12 0
A 21 0
A12 A 21
0
2
AО 0

87.

Потенциальная энергия
FУ1
FУ2
Х2
Х
Х1
A FScos
F kx
S x x1 x2
cos 1
0
F1 F2 k x1 x2
Fср
2
2
k x1 x2
x1 x2
A
2
2
2
2
2
k x1 x2 kx1 kx2
A
2
2
2
A En1 En 2 En 2 En1
A En

88.

Закон сохранения энергии
A Ek
A En
Ek En
Ek 2 Ek1 ( En 2 En1 )
Ek1 En1 Ek 2 En 2
E Е
до
после
- закон сохранения энергии
для замкнутой системы, в
которой действуют только
консервативные силы.

89.

Закон сохранения энергии
Если присутствуют неконсервативные силы
(например силы трения), то закон сохранения энергии
имеет вид:
E
E
E
E
А
k
1
n
1
k
2
n
2
тр
E
Е
А
до
после
тр