Лекция 2 ОИКС

1.

Лекции № 3, 4
Населенность энергетических уровней
Объекты, состоящие из большого числа элементарных квантовых
систем, рассматриваются с точки зрения их распределения по
стационарным состояниям внутри макроскопического ансамбля.
Распределение Больцмана
Если рассмотреть макроскопический ансамбль слабовзаимодействующих,
одинаковых, но различимых квантовых систем, что его можно характеризовать
числами квантовых систем N m , находящихся в стационарном состоянии с
энергией Wm .
По статистике Больцмана распределение по энергиям внутри невырожденного
ансамбля квантовых систем, находящихся в термодинамическом равновесии
друг с другом и окружающей средой при температуре T
W Wm
N m N n exp n
, Wm Wn
kT
N m – распределение населенностей квантовых систем по энергетическим
уровням внутри ансамбля;

2.

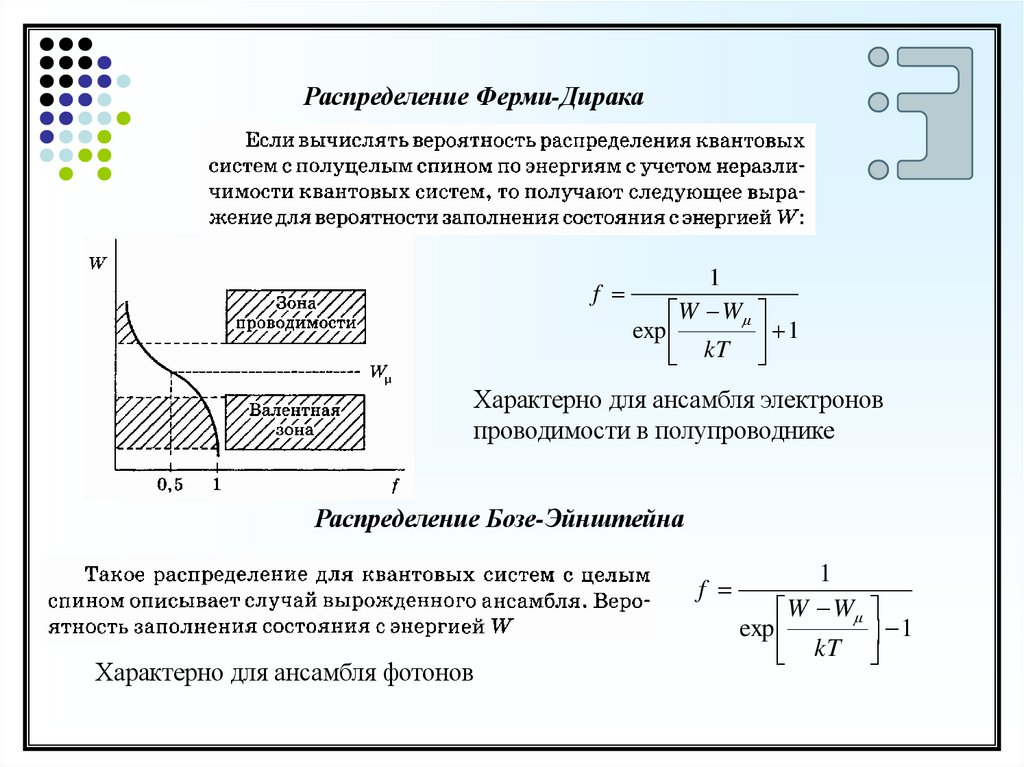
Распределение Ферми-Дирака
f
1
W W
exp
1
kT
Характерно для ансамбля электронов
проводимости в полупроводнике
Распределение Бозе-Эйнштейна
f
Характерно для ансамбля фотонов
1
W W
exp
1
kT

3.

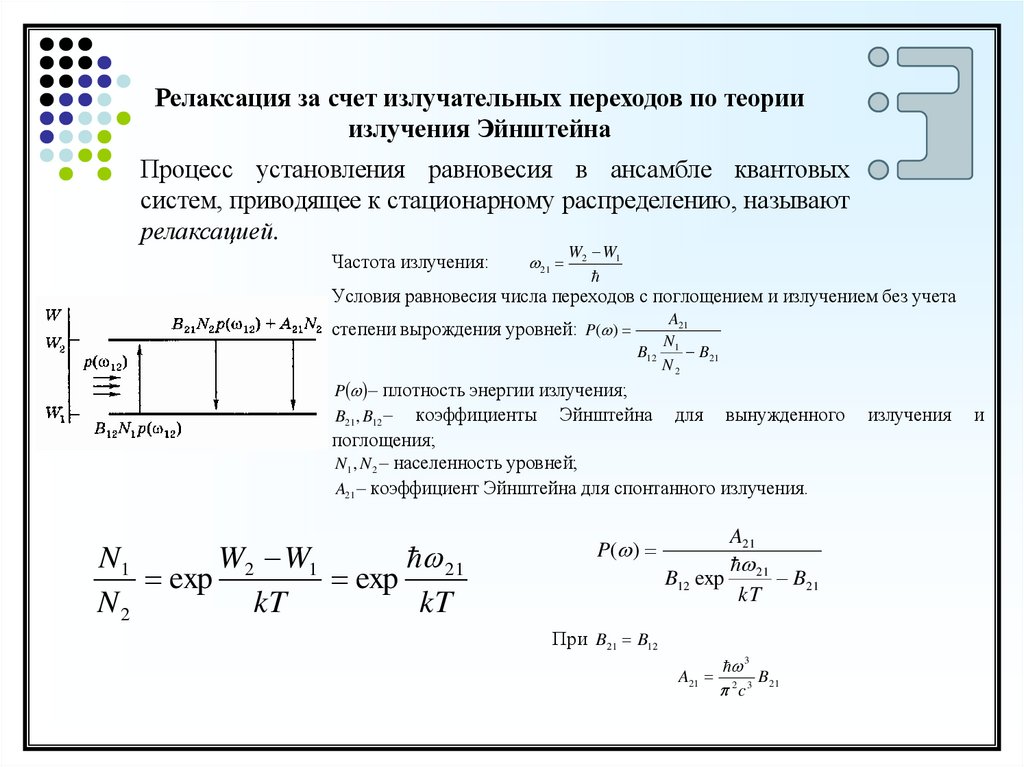
Релаксация за счет излучательных переходов по теории
излучения Эйнштейна
Процесс установления равновесия в ансамбле квантовых
систем, приводящее к стационарному распределению, называют
релаксацией.
Частота излучения:
21
W2 W1
Условия равновесия числа переходов с поглощением и излучением без учета
степени вырождения уровней: P( )
A21
N1
B12
B21
N2
P – плотность энергии излучения;
B21 , B12 – коэффициенты Эйнштейна
для
вынужденного
поглощения;
N1 , N 2 – населенность уровней;
A21 – коэффициент Эйнштейна для спонтанного излучения.
N1
W2 W1
21
exp
exp
N2
kT
kT
P( )
A21
21
B12 exp
B21
kT
При B21 B12
A21
3
B21
2c3
излучения
и

4.

Инверсия населенностей уровней
В условиях термодинамического равновесия число атомов на низшем уровне
превышает число атомов, находящихся в возбужденном состоянии, то есть
N1 N 2 . Однако для того чтобы число индуцированных полем переходов с
излучением превышало число переходов с поглощением P BN 2 P BN 1
необходимо: N 2 N1 (инверсная населенность уровней).
С учетом степени вырождения:
N2
g2y
g1 y
N1 .
Схемы создания инверсии населенностей
dN m
Wнак bmn N n N m a nm N n a mn N m
dt
n

5.

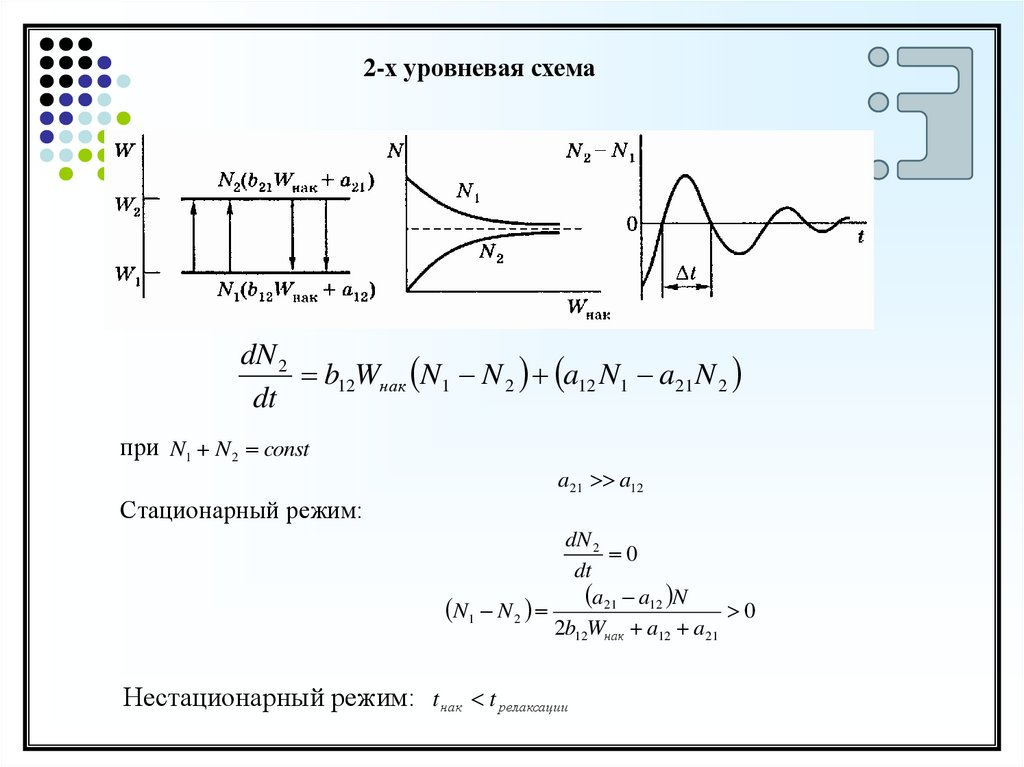
2-х уровневая схема
dN 2
b12Wнак N1 N 2 a12 N1 a21 N 2
dt
при N1 N 2 const
a21 a12
Стационарный режим:
dN 2
0
dt
N1 N 2 a21 a12 N 0
2b12Wнак a12 a21
Нестационарный режим: t нак t рел аксации

6.

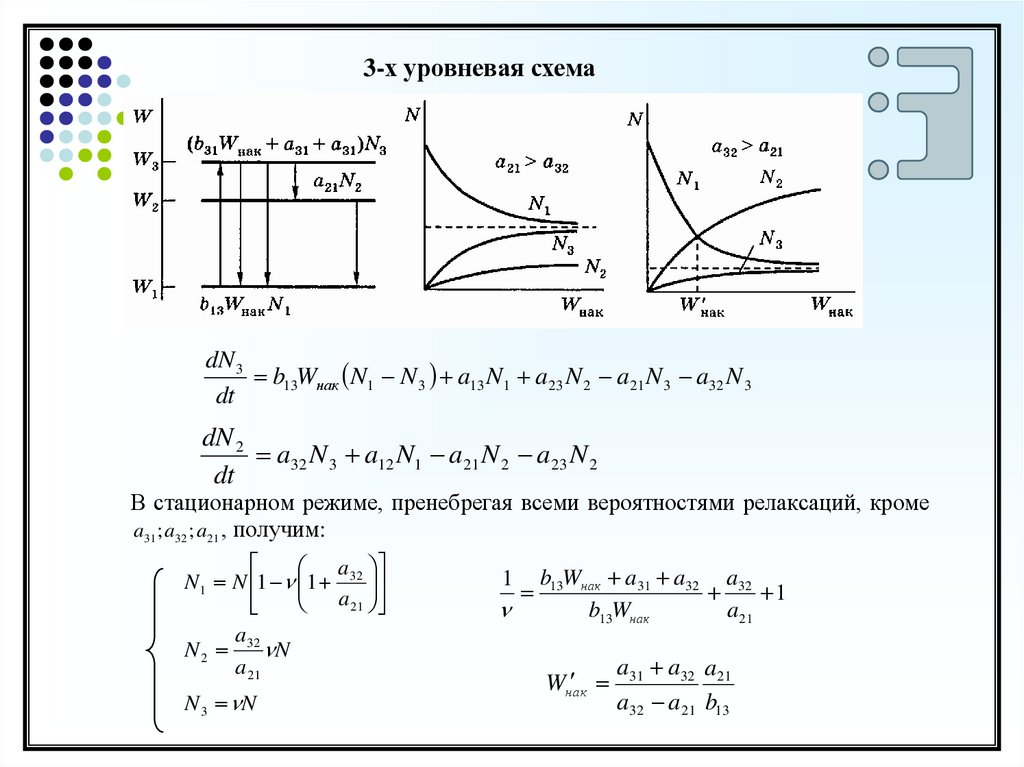
3-х уровневая схема
dN 3
b13Wнак N1 N 3 a13 N1 a23 N 2 a21 N 3 a32 N 3
dt
dN 2
a32 N 3 a12 N1 a21 N 2 a23 N 2
dt
В стационарном режиме, пренебрегая всеми вероятностями релаксаций, кроме
a31 ; a32 ; a21 , получим:
a
N 1 N 1 1 32
a 21
a
N 2 32 N
a21
N 3 N
1
b13Wнак a31 a32 a32
1
b13Wнак
a21
Wнак
a31 a32 a21
a32 a 21 b13

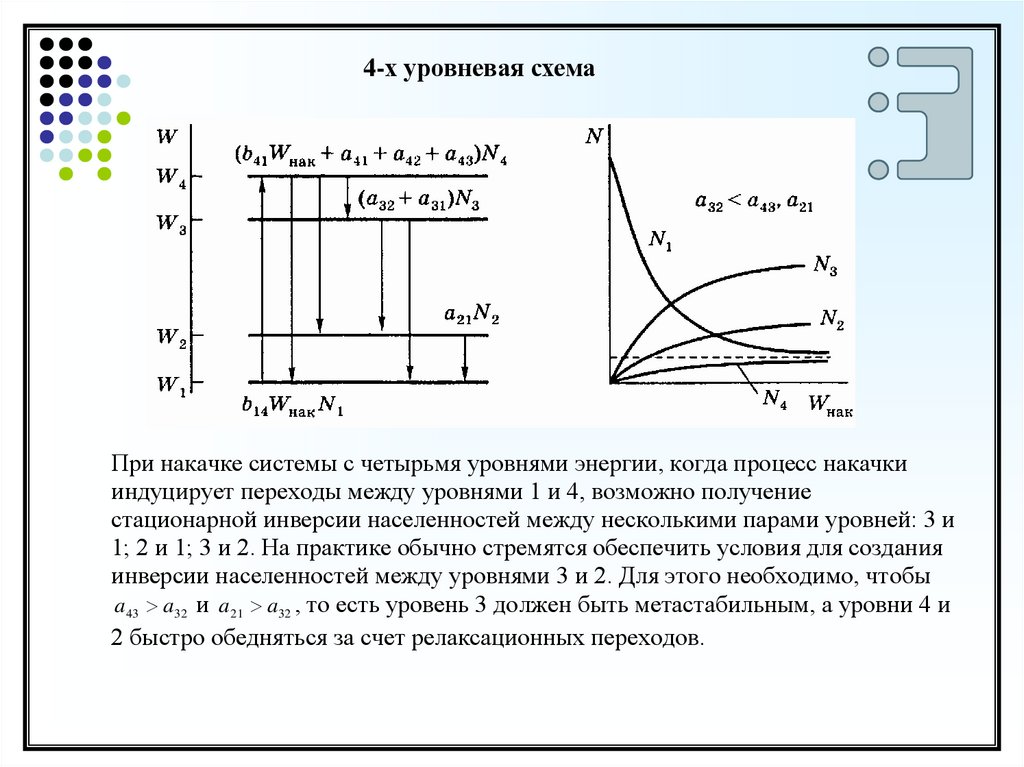
7.

4-х уровневая схема
При накачке системы с четырьмя уровнями энергии, когда процесс накачки
индуцирует переходы между уровнями 1 и 4, возможно получение
стационарной инверсии населенностей между несколькими парами уровней: 3 и
1; 2 и 1; 3 и 2. На практике обычно стремятся обеспечить условия для создания
инверсии населенностей между уровнями 3 и 2. Для этого необходимо, чтобы
a 43 a32 и a 21 a32 , то есть уровень 3 должен быть метастабильным, а уровни 4 и
2 быстро обедняться за счет релаксационных переходов.

8.

Многоуровневые схемы