Матанализ_Лекция-7-_1_-_1_

1. Математический анализ

ЛЕКЦИЯ № 7
Непрерывные функции.

2.

§ 1. Непрерывные функции
Пусть в Rn в некоторой окрестности т. M 0 определена функция
y f (M ) .
Определение 10. Функция f M называется непрерывной в т. M 0 , если
а) f M определена в т. M 0 ,
б) существует предел lim f M ,
в) lim f M f M 0 .
M 0
M M 0
Если нарушено хотя бы из условий а), б), в), то M 0 называют точкой
разрыва функции y f M . Из в) следует, что под знаком непрерывной
функции можно переходить к пределу, т.е. lim f ( x) f lim x .
x x0
x x0
Рассмотрим свойства непрерывных функций для функция одной
переменной y f (x).
Определение 11. Если f x непрерывна в т. a , то f a 0 f a 0 f a .

3.

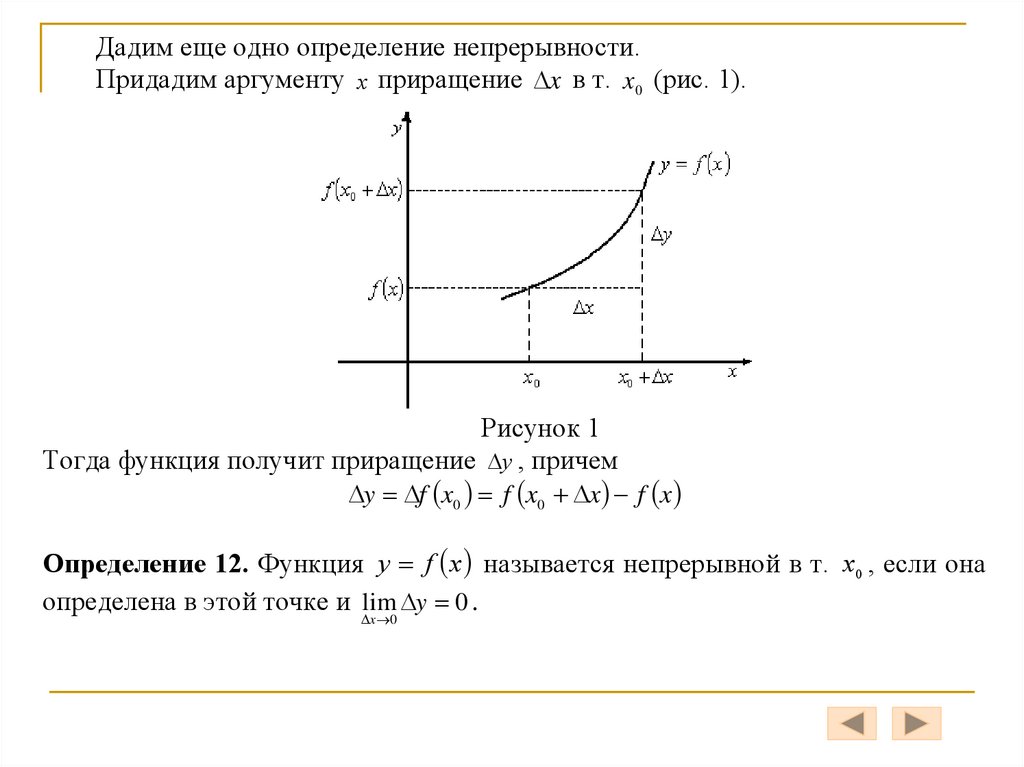
Дадим еще одно определение непрерывности.
Придадим аргументу x приращение x в т. x 0 (рис. 1).
Рисунок 1
Тогда функция получит приращение y , причем
y f x0 f x0 x f x
Определение 12. Функция y f x называется непрерывной в т. x 0 , если она
y 0 .
определена в этой точке и lim
x 0

4.

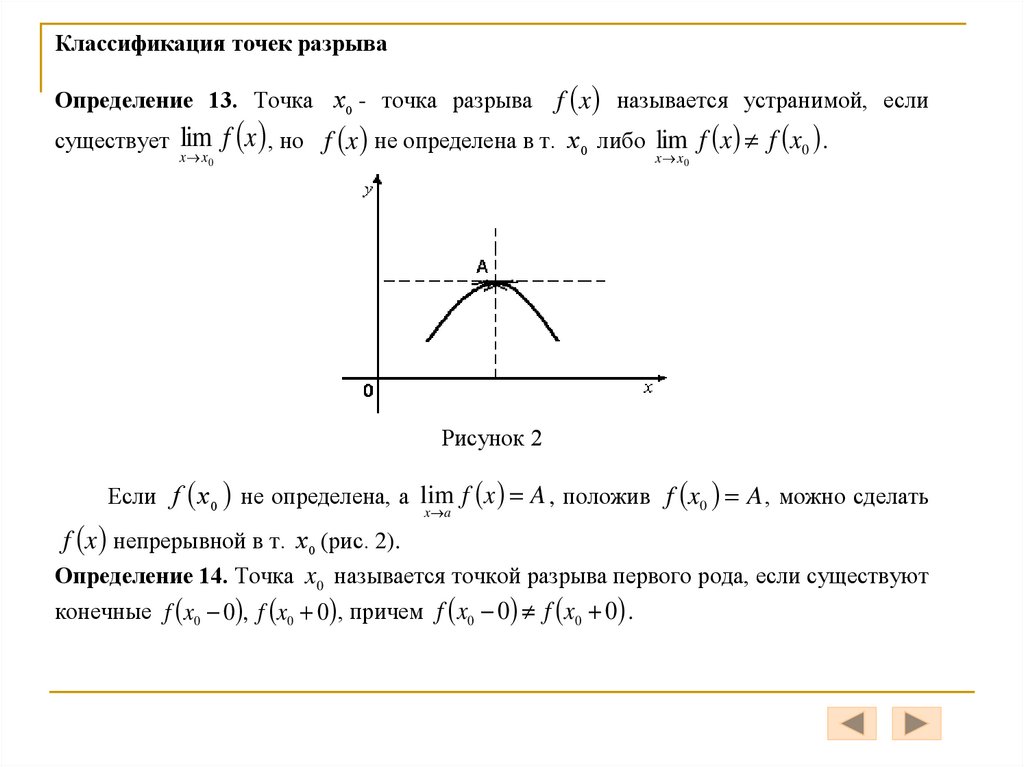
Классификация точек разрыва
f x называется устранимой, если
существует lim f x , но f x не определена в т. x 0 либо lim f x f x0 .
Определение 13. Точка x 0 - точка разрыва
x x0
x x0
Рисунок 2
Если f x 0 не определена, а lim f x A , положив f x0 A , можно сделать
x a
f x непрерывной в т. x 0 (рис. 2).
Определение 14. Точка x0 называется точкой разрыва первого рода, если существуют
конечные f x0 0 , f x0 0 , причем f x0 0 f x0 0 .

5.

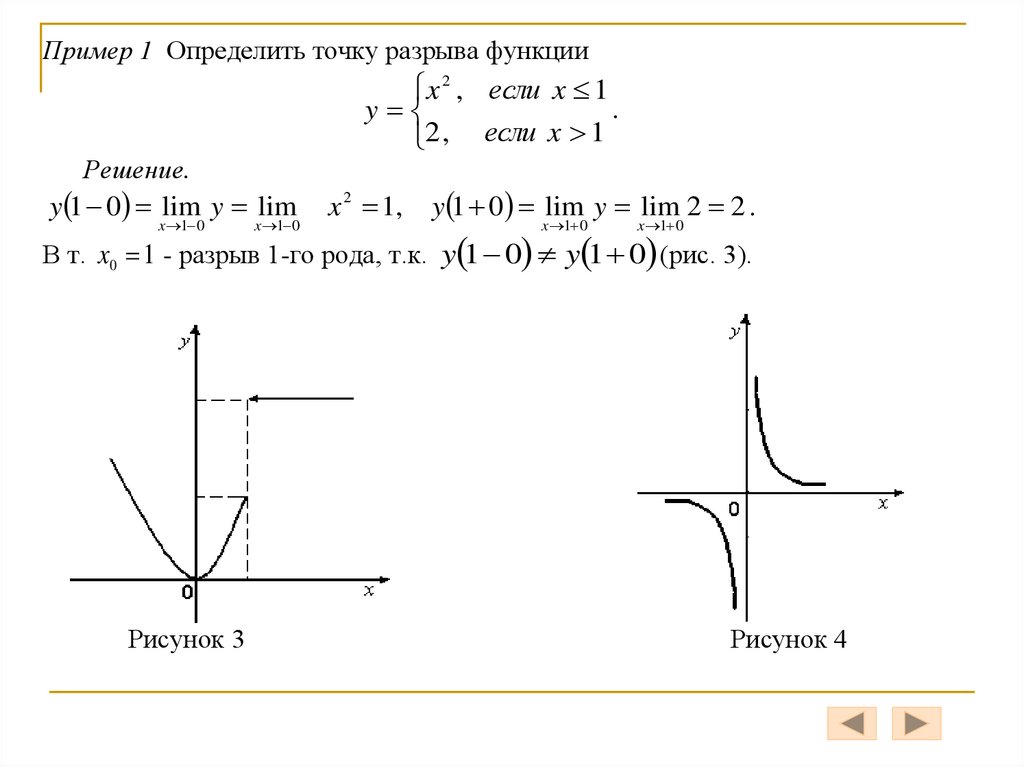
Пример 1 Определить точку разрыва функции
x 2 , если x 1
.
y
2 , если x 1
Решение.
y 1 0 lim y lim
x 1 0
x 1 0
x 2 1,
y 1 0 lim y lim 2 2 .
x 1 0
x 1 0
В т. x0 1 - разрыв 1-го рода, т.к. y 1 0 y 1 0 (рис. 3).
Рисунок 3
Рисунок 4

6.

Определение 15. Если у функции не существует правого или левого
предела, или же эти пределы бесконечны, то говорят, что она имеет
разрыв второго рода в этой точке.
1
Пример 2. y , x0 0 (рис. 4).
x
Решение.
lim y , lim y . Следовательно, т.0 – точка разрыва 2-ого
x 0
x 0
рода.