НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ (заочники лекция 1)

1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Пьянкова Жанна Анатольевна
канд. пед. наук, доцент кафедры
«Проектирование и эксплуатация автомобилей»
(ПиЭА)
Ауд. Б1-72

2. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ -

наука о способах изображения
пространственных форм на
плоскости или другой
поверхности и методах
решения геометрических задач
по этим изображениям
2

3. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

3

4.

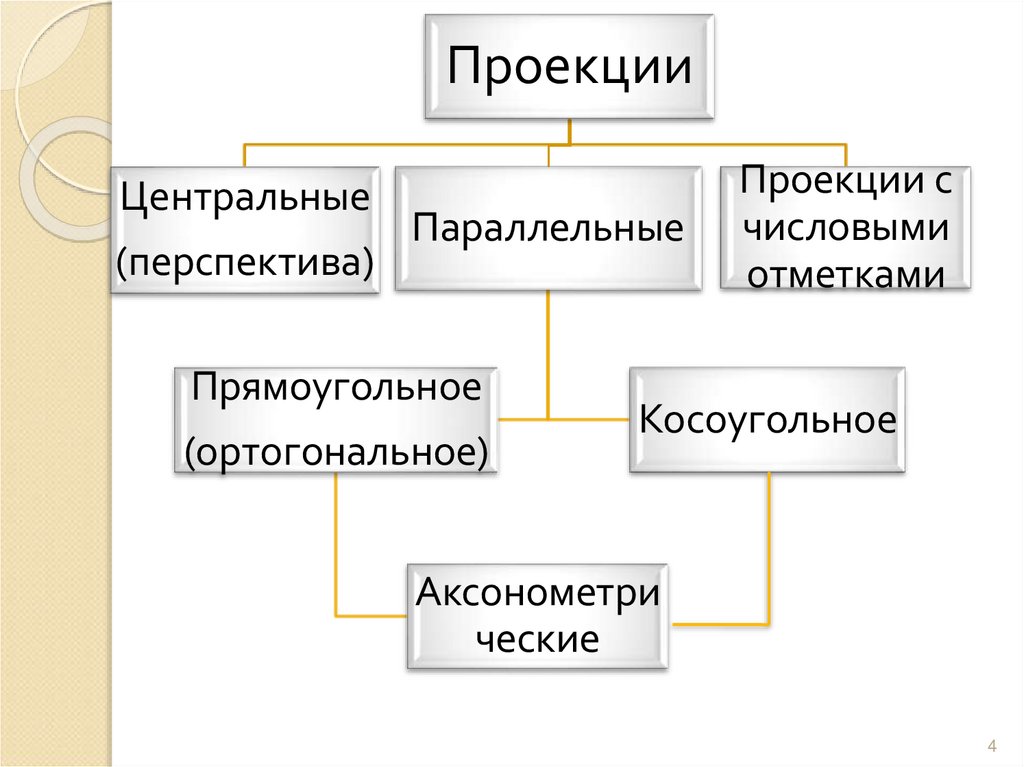
Проекции
Центральные
(перспектива)
Параллельные
Прямоугольное
(ортогональное)
Проекции с
числовыми
отметками
Косоугольное
Аксонометри
ческие
4

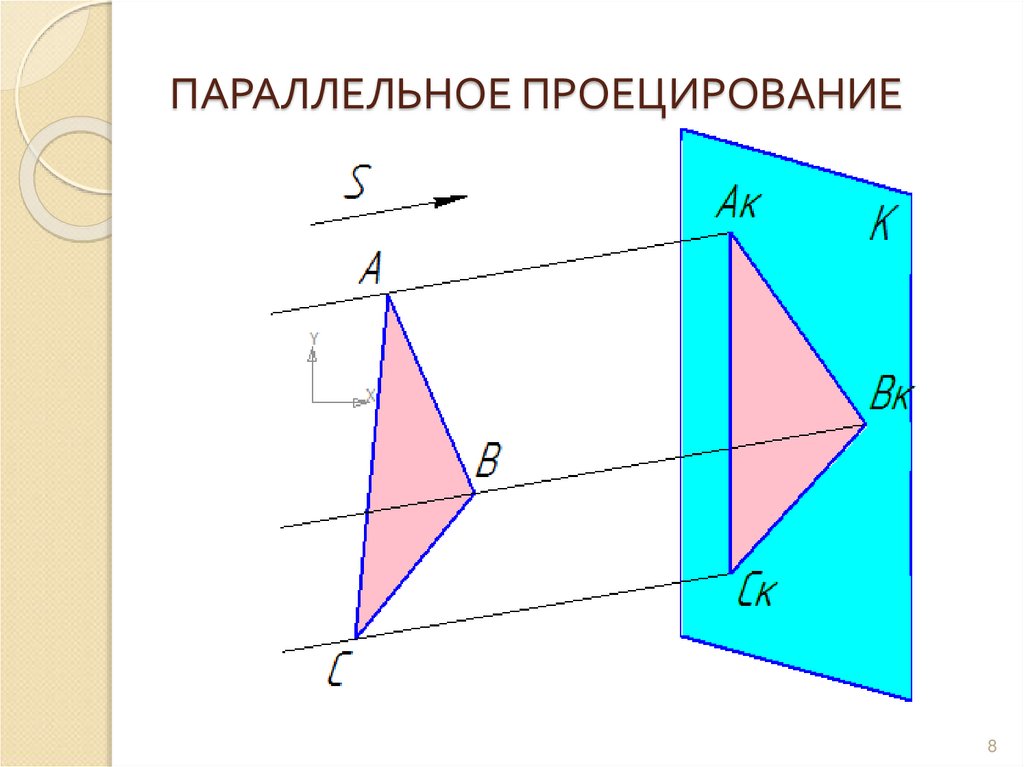
5. ПАРАЛЛЕЛЬНЫЕ ПРОЕКЦИИ:

Прямоугольные – если
проецирующие лучи направлены к
плоскости проекций под прямым
углом
Косоугольные - если
проецирующие лучи направлены к
плоскости проекций под углом, не
равным прямому
5

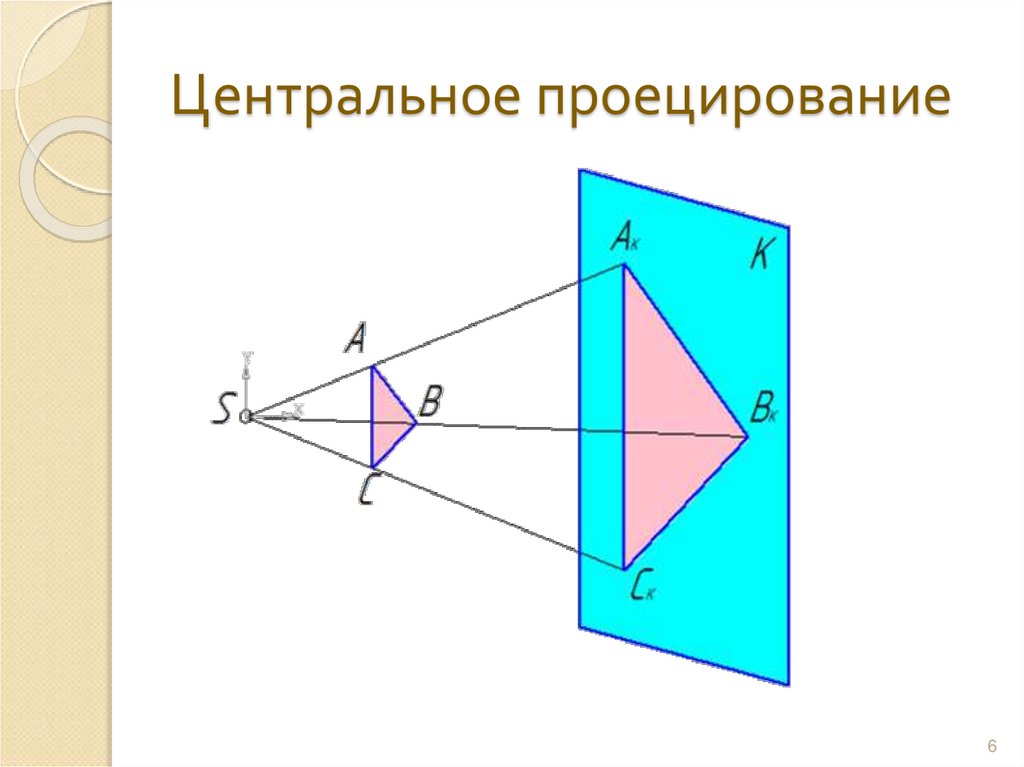
6. Центральное проецирование

6

7. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

S – центр проецирования
К – проецирующая плоскость
АВС – треугольник в пространстве
АкВкСк – центральная проекция
треугольника АВС на плоскость К
SАк, SBк, SCк – проецирующие
лучи
7

8. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

8

9. Метод Монжа -

метод параллельного
прямоугольного
проецирования на две
взаимно перпендикулярные
плоскости
9

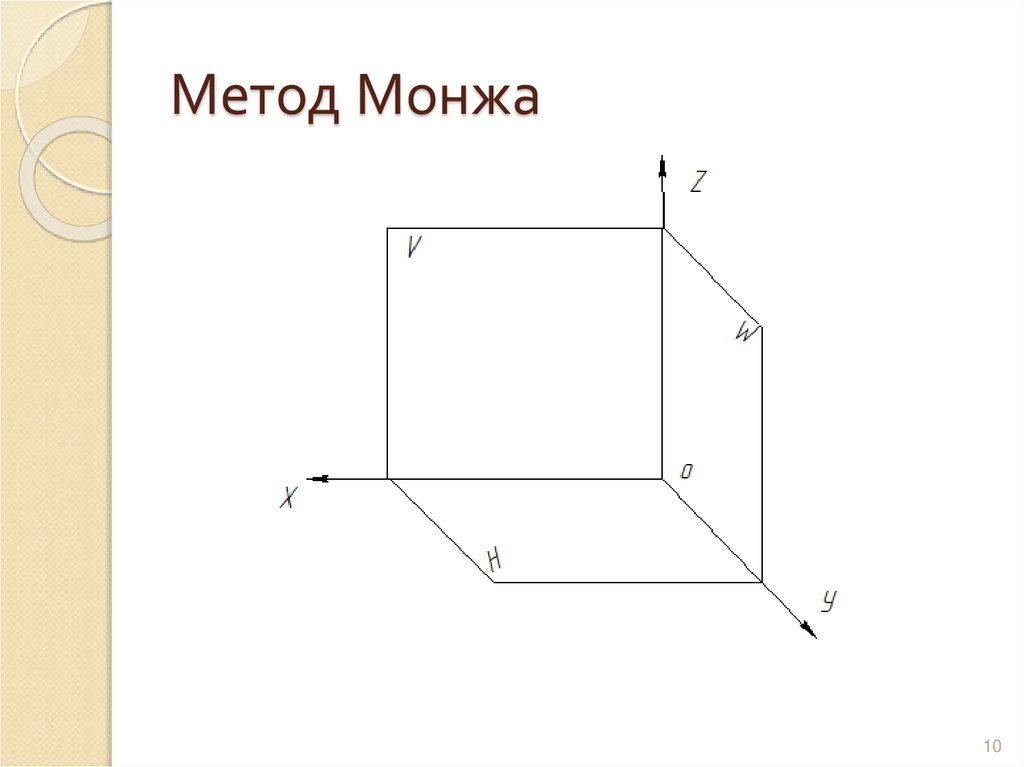
10. Метод Монжа

10

11. Обозначения и понятия

V – фронтальная плоскость проекций
H – горизонтальная плоскость
проекций
W – профильная плоскость проекций
0 – начало координат
0Х – ось абсцисс
0Y – ось ординат
0Z – ось аппликат
11

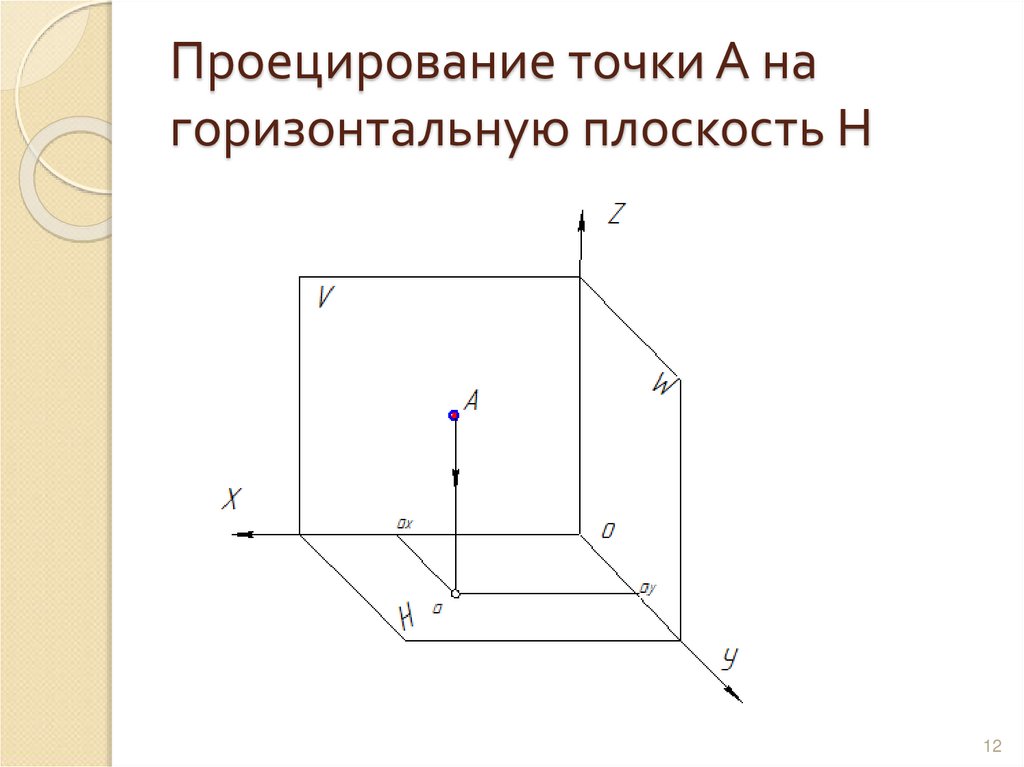
12. Проецирование точки А на горизонтальную плоскость Н

12

13. Обозначения и понятия

А – точка в пространстве
а – горизонтальная проекция точки А
ах – абсцисса (координата Х) точки А
ау – ордината (координата Y) точки А
Аа – линия проекционной связи
(проекция проецирующего луча)
13

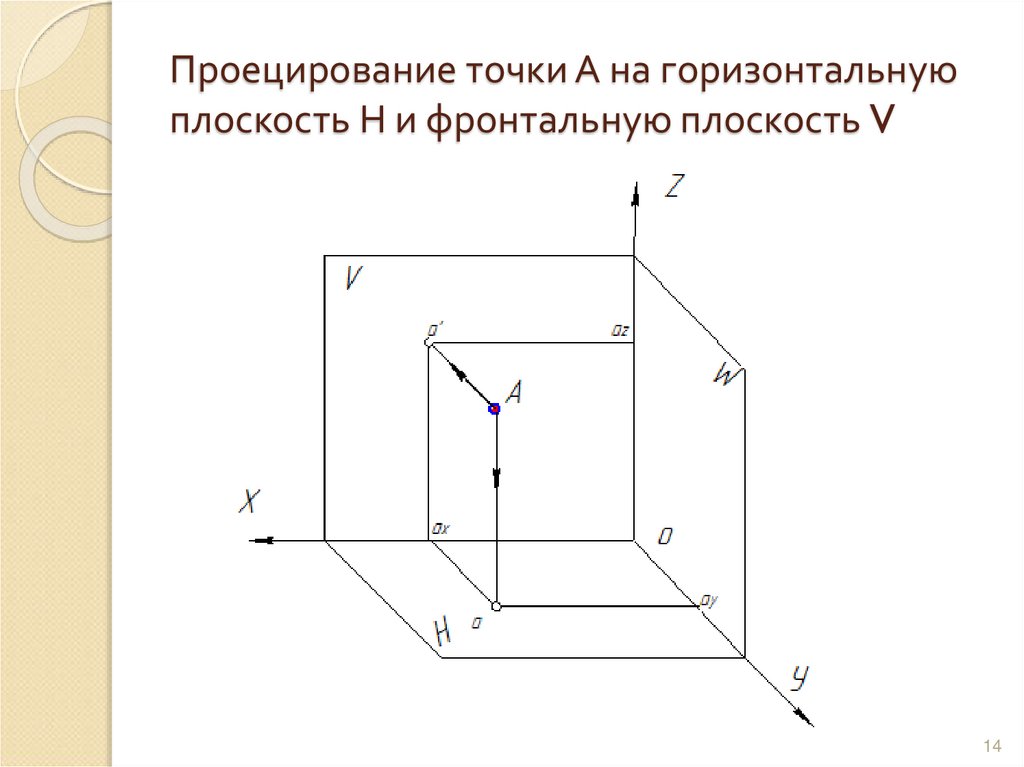
14. Проецирование точки А на горизонтальную плоскость Н и фронтальную плоскость V

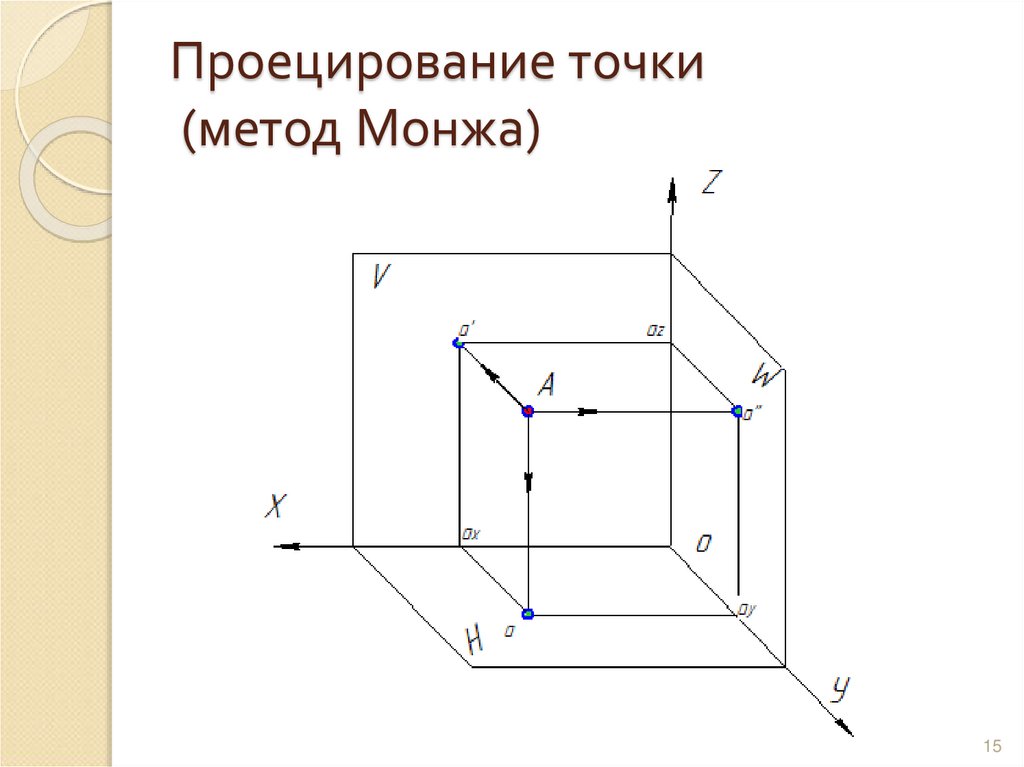
14

15. Проецирование точки (метод Монжа)

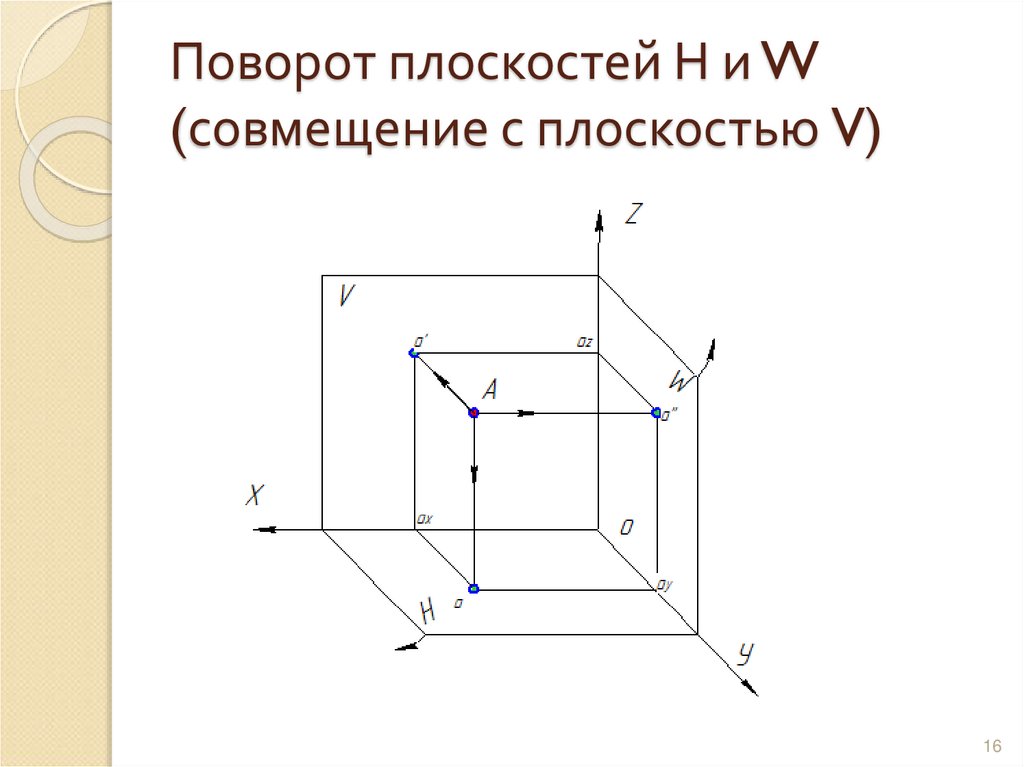
15

16. Поворот плоскостей Н и W (совмещение с плоскостью V)

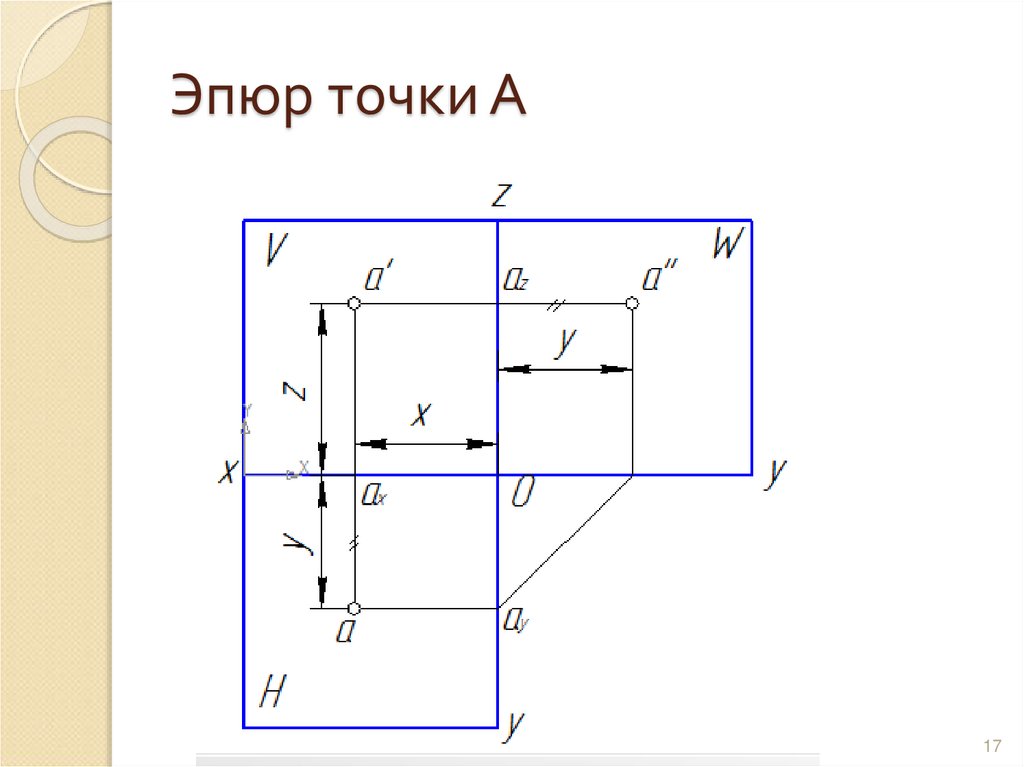
16

17. Эпюр точки А

17

18. Вывод:

По одной центральной или
параллельной проекции фигуры
нельзя определить ее положение в
пространстве, т.к. все точки,
лежащие на проецирующем луче,
проецируются в одну и ту же точку
18

19. ЭПЮР –

это плоский чертеж,
построенный методом
прямоугольного параллельного
проецирования на совмещенных
плоскостях проекций
19

20. Ортогональные проекции -

это прямоугольные
проекции на взаимно
перпендикулярных
плоскостях проекций
20

21. СВОЙСТВА ОРТОГОНАЛЬНЫХ ПРОЕЦИЙ ТОЧКИ:

Две разноименные проекции
точки расположены на одной
линии связи
По двум проекциям точки всегда
можно построить недостающую
третью проекцию
По двум проекциям точки всегда
можно определить положение
самой точки в пространстве
21

22. АЛГОРИТМ ПОСТРОЕНИЯ ТОЧКИ

1.
2.
3.
Отложить координату х А (х, у, z)
Через ах провести линию х. Линия
связи – это прямая,
перпендикулярная координатным
осям и несущая проекции точки
Отложить y, получаем
горизонтальную проекцию точки а
(у => а - горизонтальная)
22

23.

4.
5.
6.
На линии связи отложить z
(z => а’ - фронтальная)
Через а’ провести линию связи
на профильную плоскость
Отложить координату у
(у => а’’ - профильная)
(задача 1)
23

24. ПРЯМАЯ

Положение прямой относительно
плоскостей проекций:
1. Параллельно – прямые уровня
(горизонталь, фронталь, профильная
прямая)
2.
Перпендикулярно – проецирующие
прямые (задача 4)
3.
Под углом, отличным от прямого –
прямые общего положения
24

25. Способы задания прямой на эпюре

1.
Координатами 2 точек,
принадлежащих этой прямой
2.
Координатами 1 точки,
принадлежащей прямой и углом
наклона этой прямой к плоскости
проекций
25

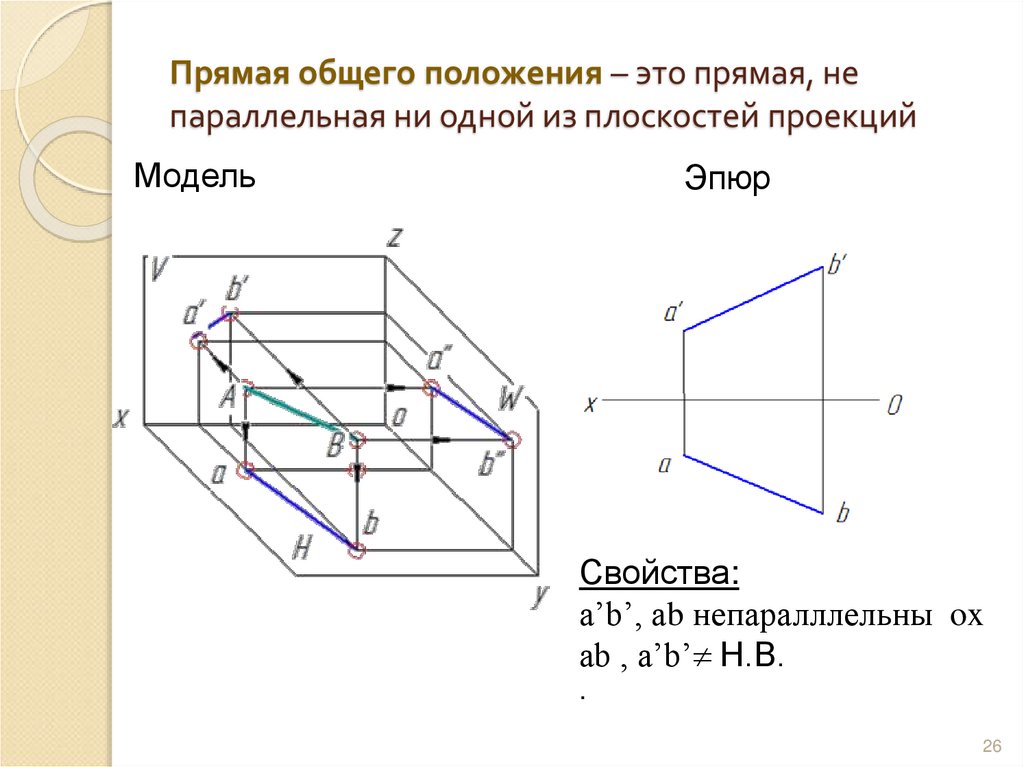
26. Прямая общего положения – это прямая, не параллельная ни одной из плоскостей проекций

Модель
Эпюр
Свойства:
a’b’, аb непаралллельны ox
ab , a’b’ Н.В.
.
26

27. Линии уровня -

Линии уровня прямые, параллельные плоскостям
проекций:
горизонталь (задача 6)
фронталь (задача 5)
профильная прямая
27

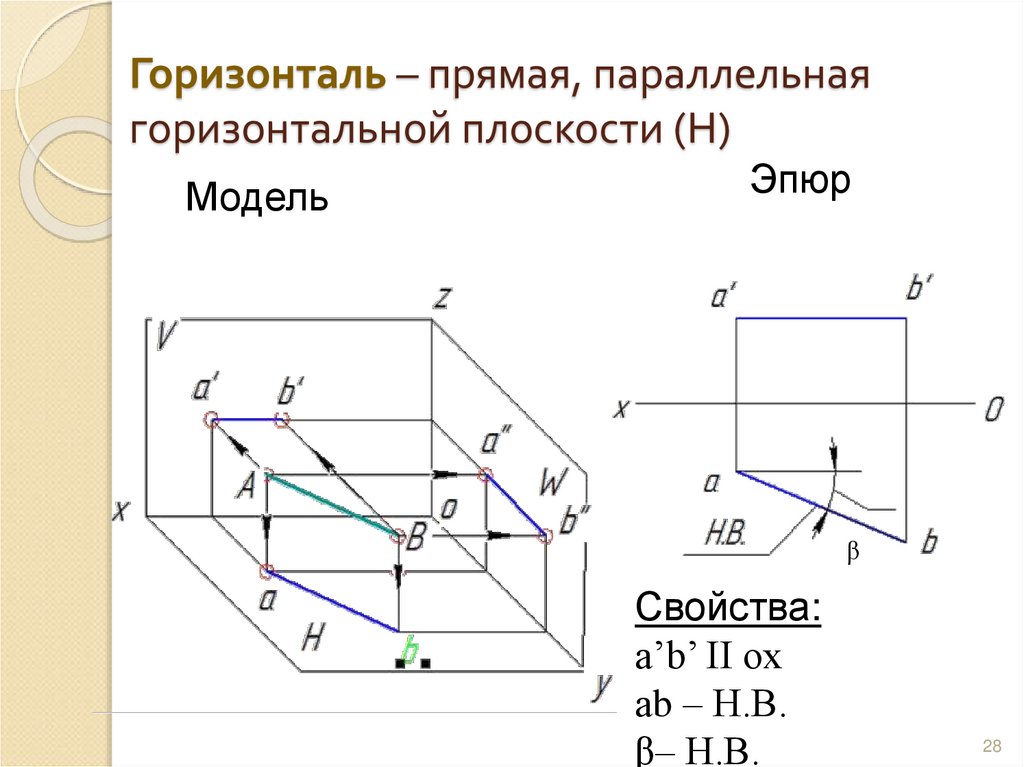
28. Горизонталь – прямая, параллельная горизонтальной плоскости (Н)

Модель
Эпюр
β
Свойства:
a’b’ II ox
аb – Н.В.
β– Н.В.
28

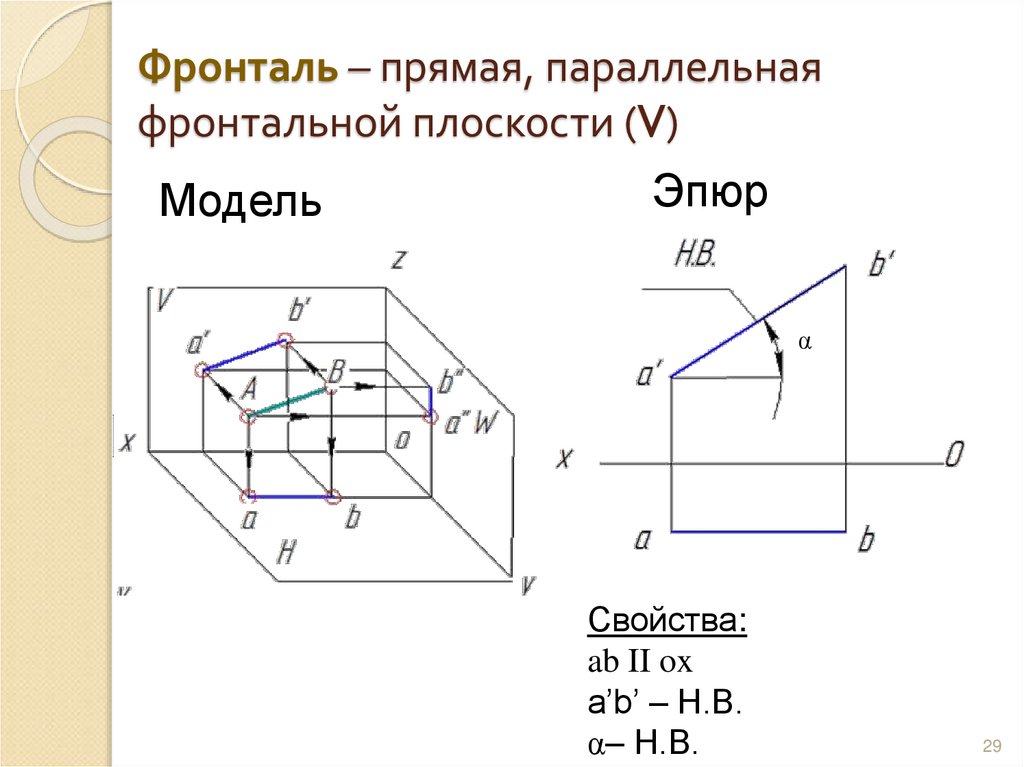
29. Фронталь – прямая, параллельная фронтальной плоскости (V)

Модель
Эпюр
α
Свойства:
ab II ox
a’b’ – Н.В.
α– Н.В.
29

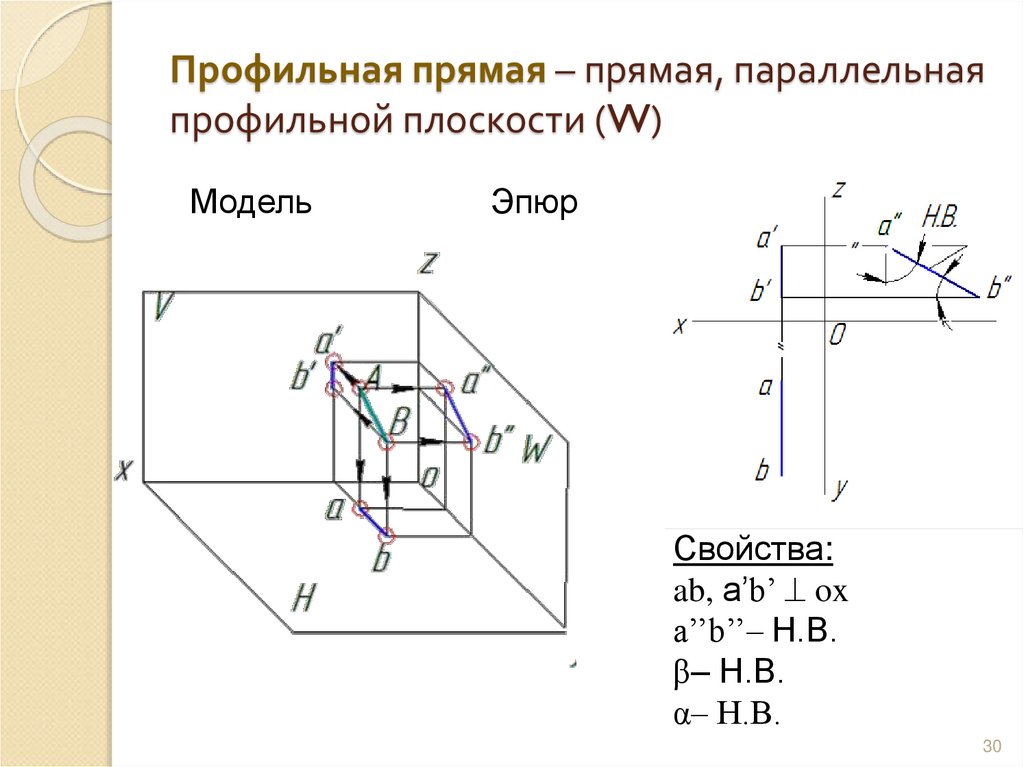
30. Профильная прямая – прямая, параллельная профильной плоскости (W)

Модель
Эпюр
Свойства:
ab, а’b’ ox
a’’b’’– Н.В.
β– Н.В.
α– Н.В.
30

31. Проецирующие прямые -

Проецирующие прямые Прямые, перпендикулярные к
плоскостям проекций:
горизонтально-проецирующая
фронтально-проецирующая
профильно-проецирующая
31

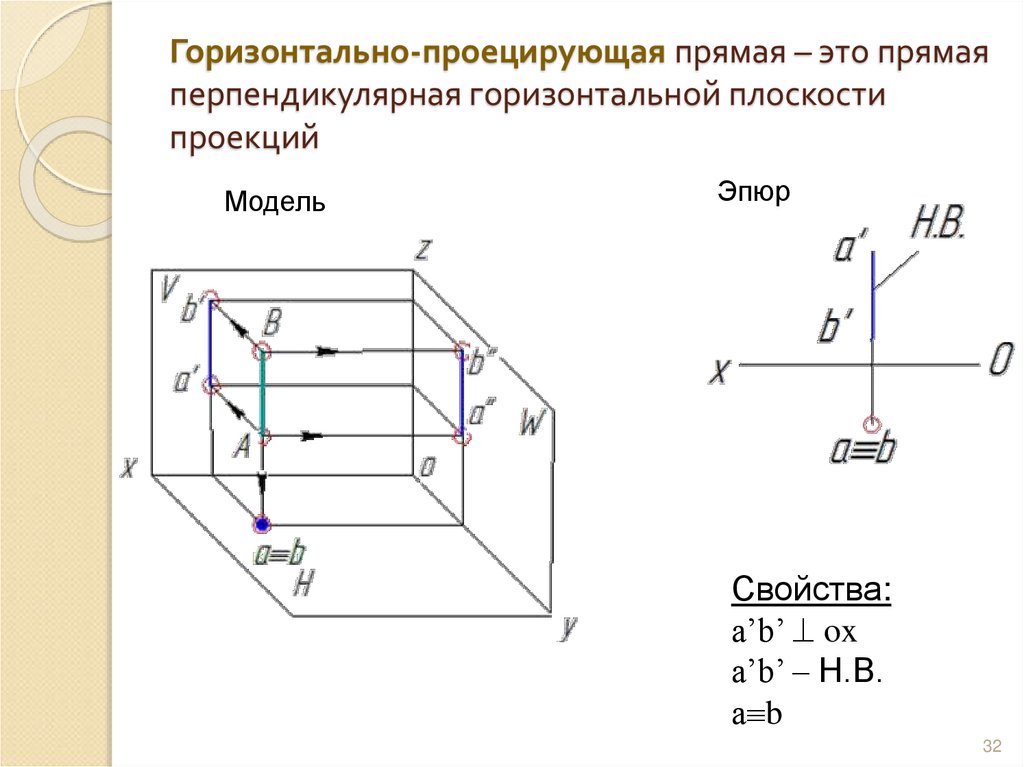
32. Горизонтально-проецирующая прямая – это прямая перпендикулярная горизонтальной плоскости проекций

Модель
Эпюр
Свойства:
a’b’ ox
a’b’ – Н.В.
а b
32

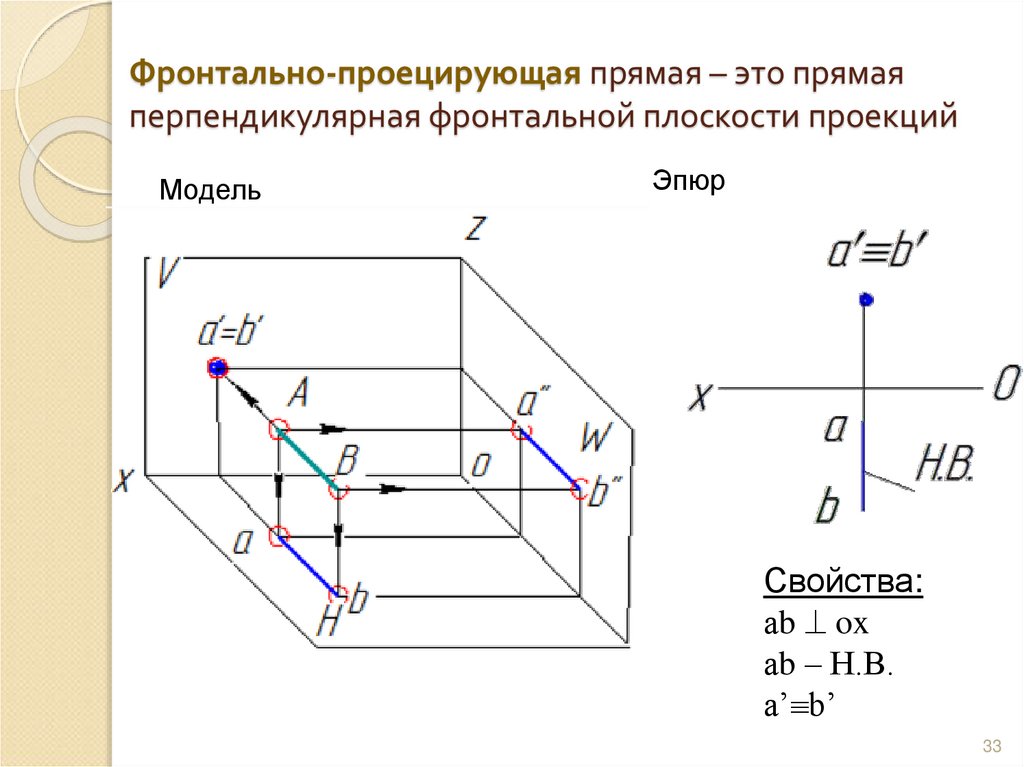
33. Фронтально-проецирующая прямая – это прямая перпендикулярная фронтальной плоскости проекций

Модель
Эпюр
Свойства:
аb ox
аb – Н.В.
a’ b’
33

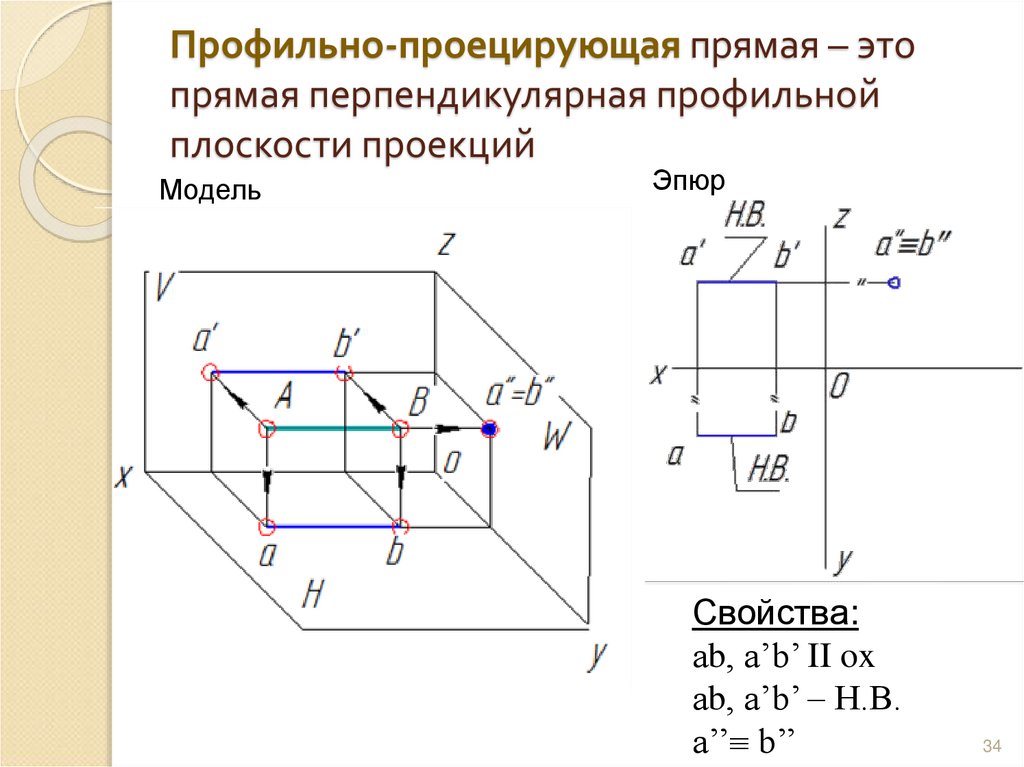
34. Профильно-проецирующая прямая – это прямая перпендикулярная профильной плоскости проекций

Модель
Эпюр
Свойства:
аb, а’b’ II ox
аb, а’b’ – Н.В.
a’’ b’’
34

35. Принадлежность точки к прямой линии

Если точка принадлежит прямой, то ее
проекции расположены на одноименных
проекциях этой прямой
(задача 7)
35

36. Взаимное положение двух прямых

По отношению друг к другу прямые в
пространстве могут быть расположены:
1.
паралллельно
2.
перпендикулярно
3.
скрещиваться
36

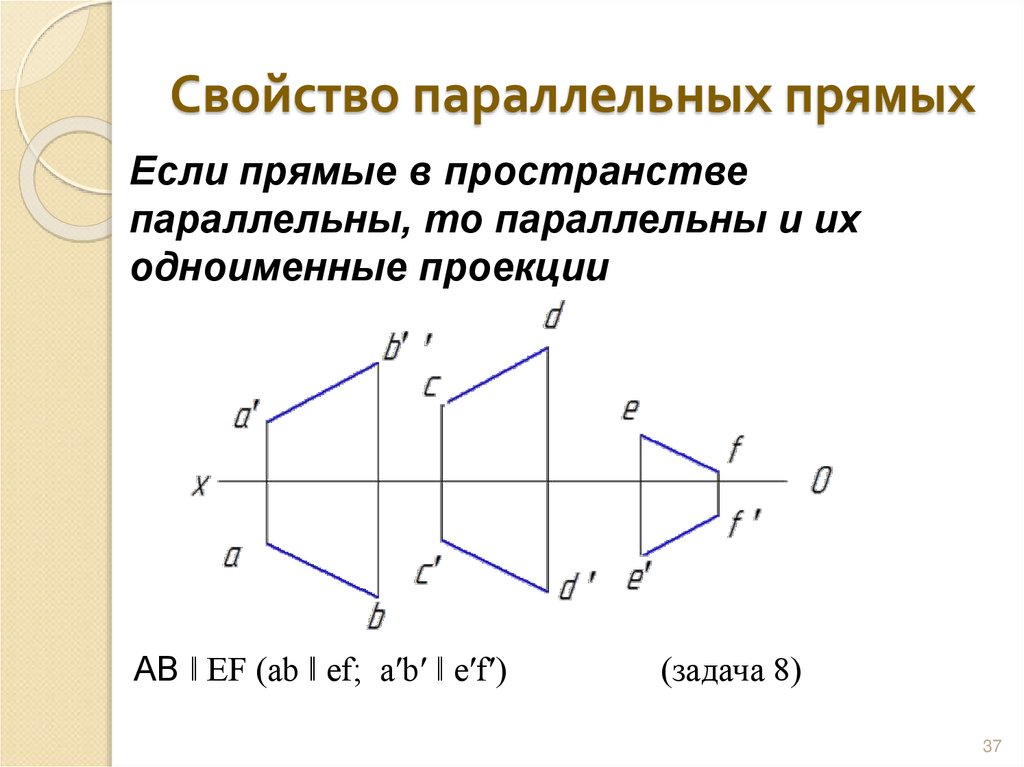
37. Свойство параллельных прямых

Если прямые в пространстве
параллельны, то параллельны и их
одноименные проекции
АВ ǁ EF (ab ǁ ef; aʹbʹ ǁ eʹfʹ)
(задача 8)
37

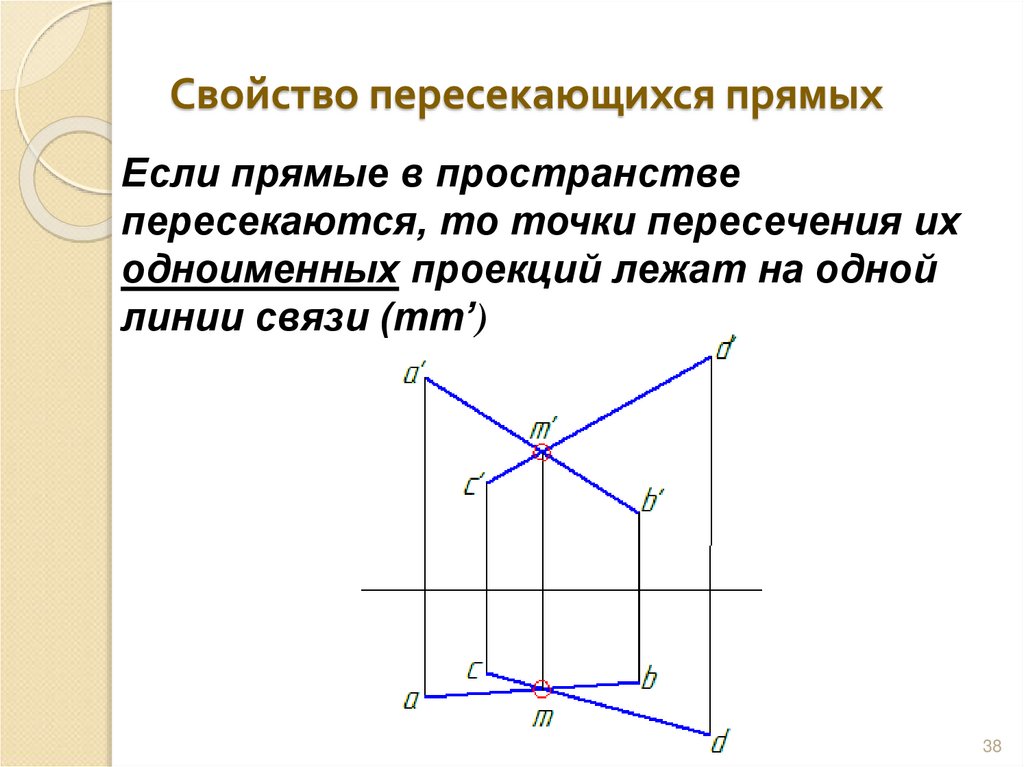
38. Свойство пересекающихся прямых

Если прямые в пространстве
пересекаются, то точки пересечения их
одноименных проекций лежат на одной
линии связи (mm’)
38

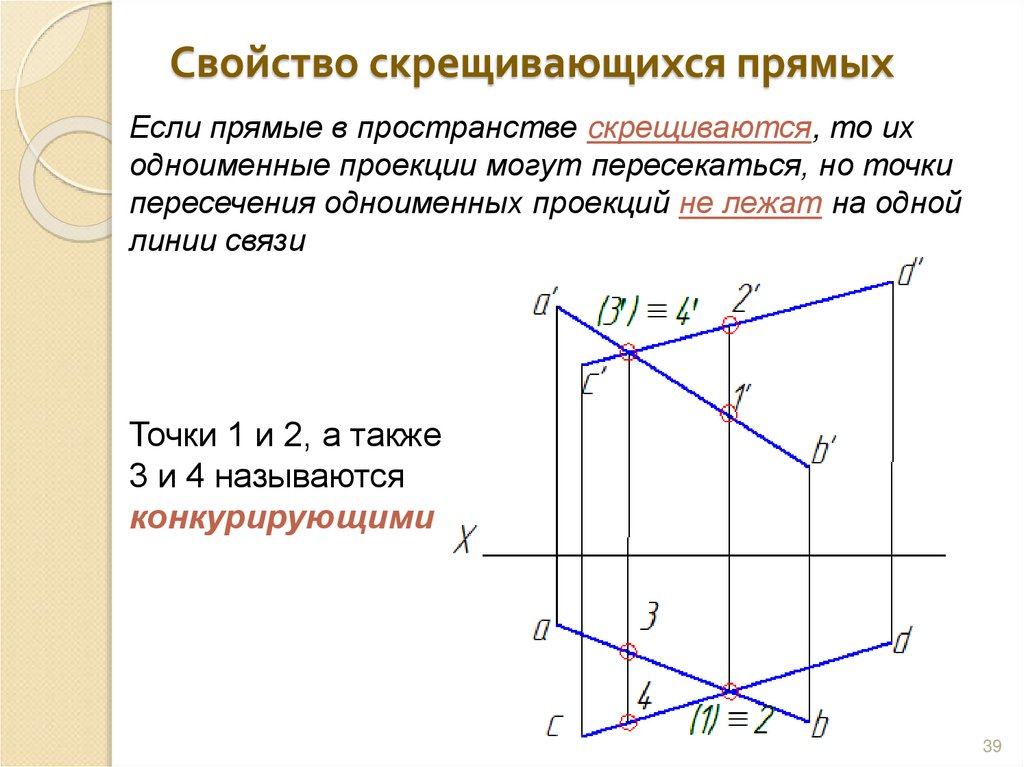
39. Свойство скрещивающихся прямых

Если прямые в пространстве cкрещиваются, то их
одноименные проекции могут пересекаться, но точки
пересечения одноименных проекций не лежат на одной
линии связи
Точки 1 и 2, а также
3 и 4 называются
конкурирующими
39

40. Конкурирующие точки

это точки, проекции которых на какую-
либо плоскость проекций совпадают
из двух конкурирующих точек
видимой будет та точка, проекция
которой расположена дальше от оси
40

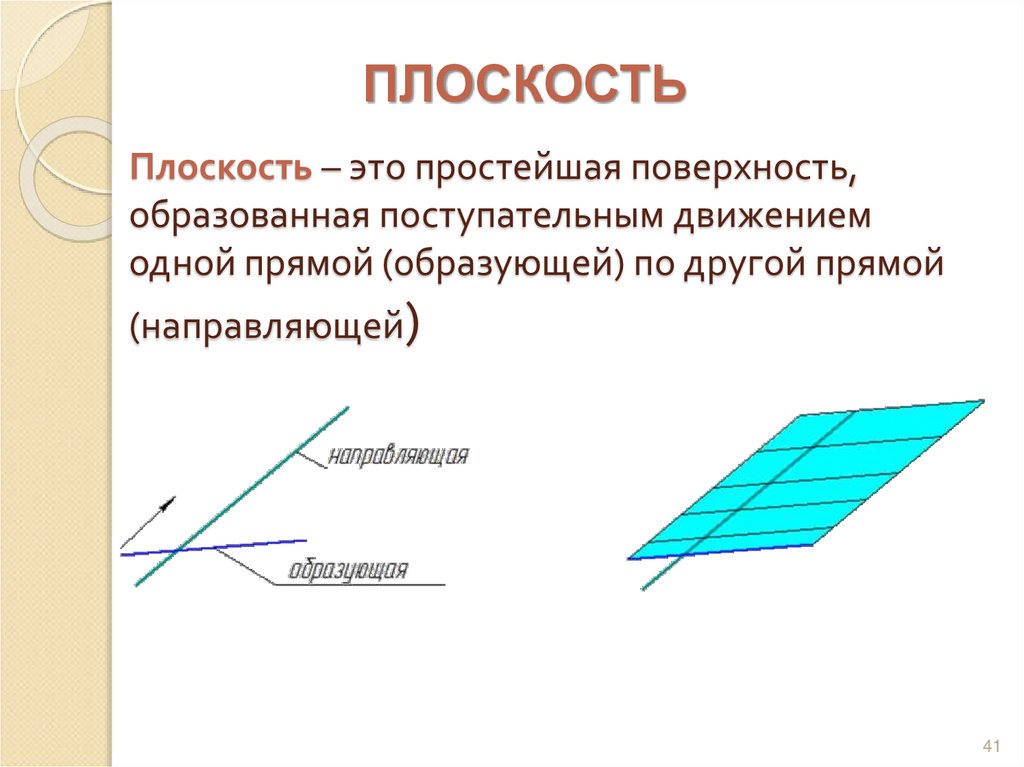
41. Плоскость – это простейшая поверхность, образованная поступательным движением одной прямой (образующей) по другой прямой

ПЛОСКОСТЬ
Плоскость – это простейшая поверхность,
образованная поступательным движением
одной прямой (образующей) по другой прямой
(направляющей)
41

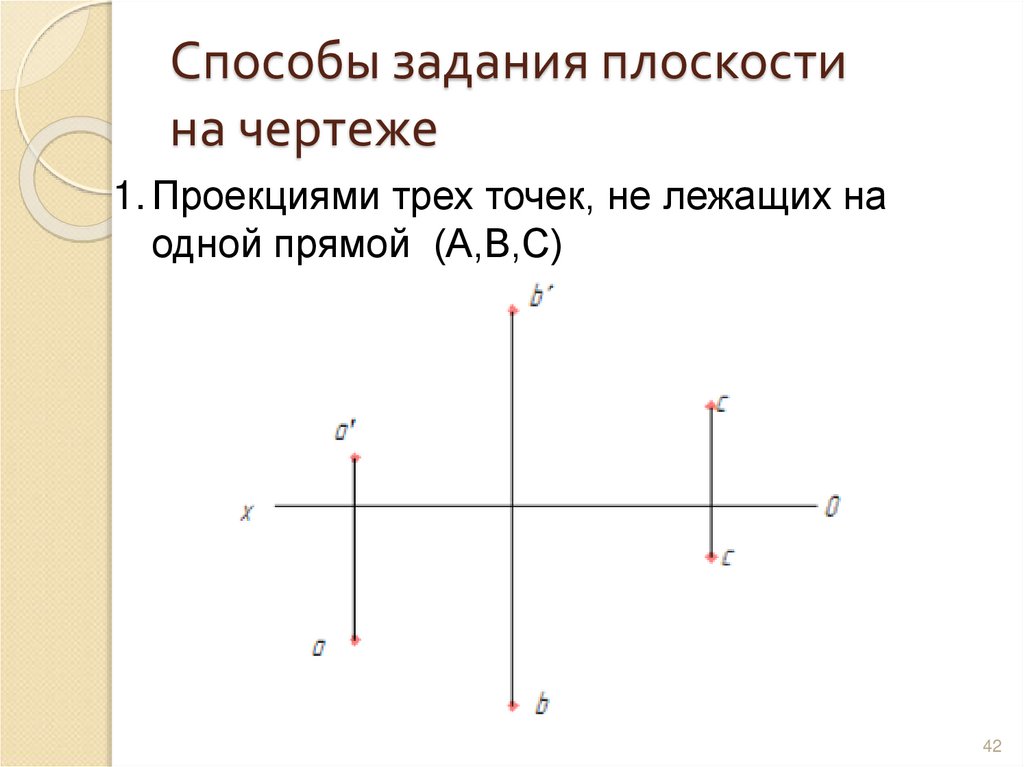
42. Способы задания плоскости на чертеже

1. Проекциями трех точек, не лежащих на
одной прямой (А,В,С)
42

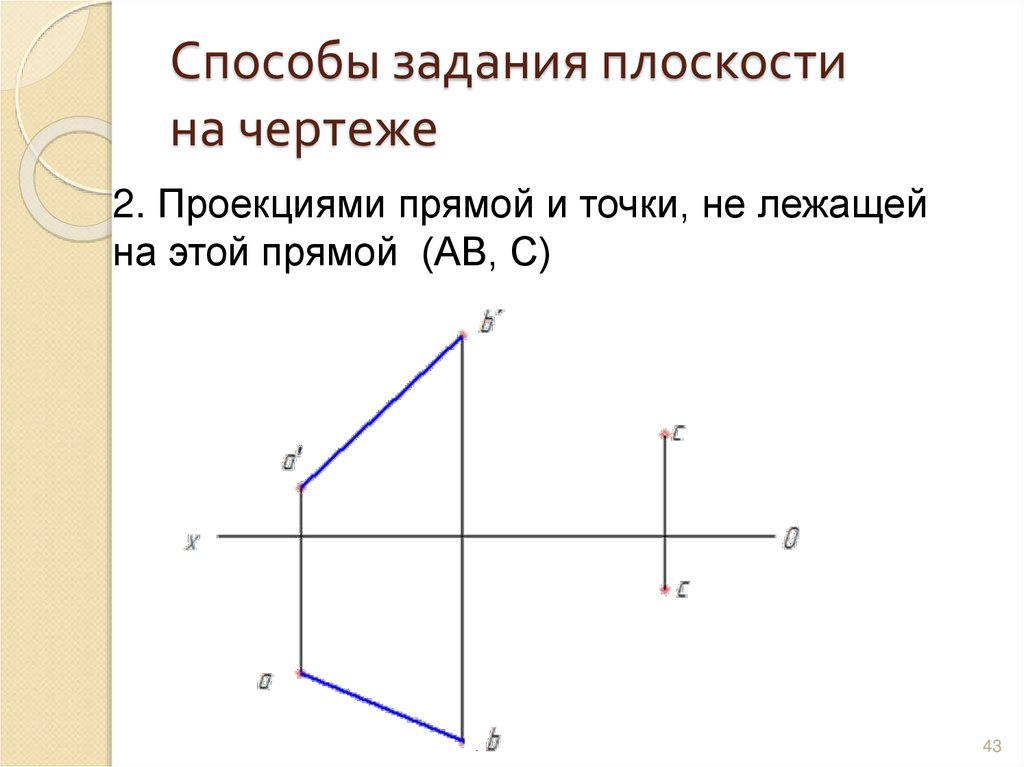
43. Способы задания плоскости на чертеже

2. Проекциями прямой и точки, не лежащей
на этой прямой (АВ, С)
43

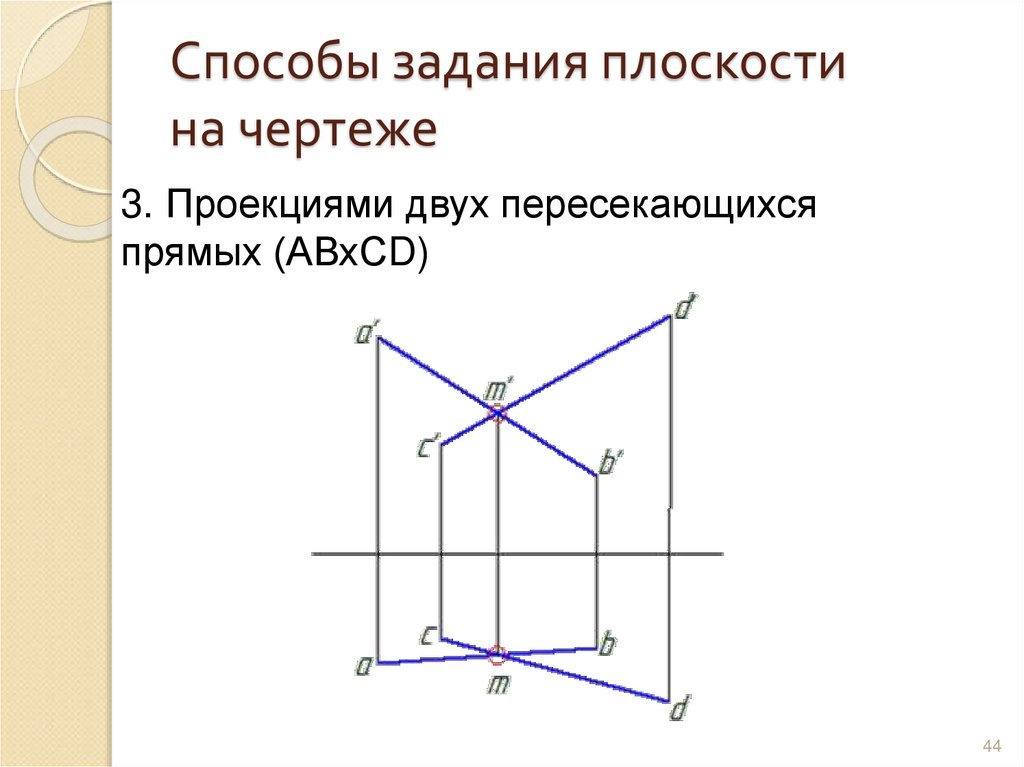
44. Способы задания плоскости на чертеже

3. Проекциями двух пересекающихся
прямых (АВхСD)
44

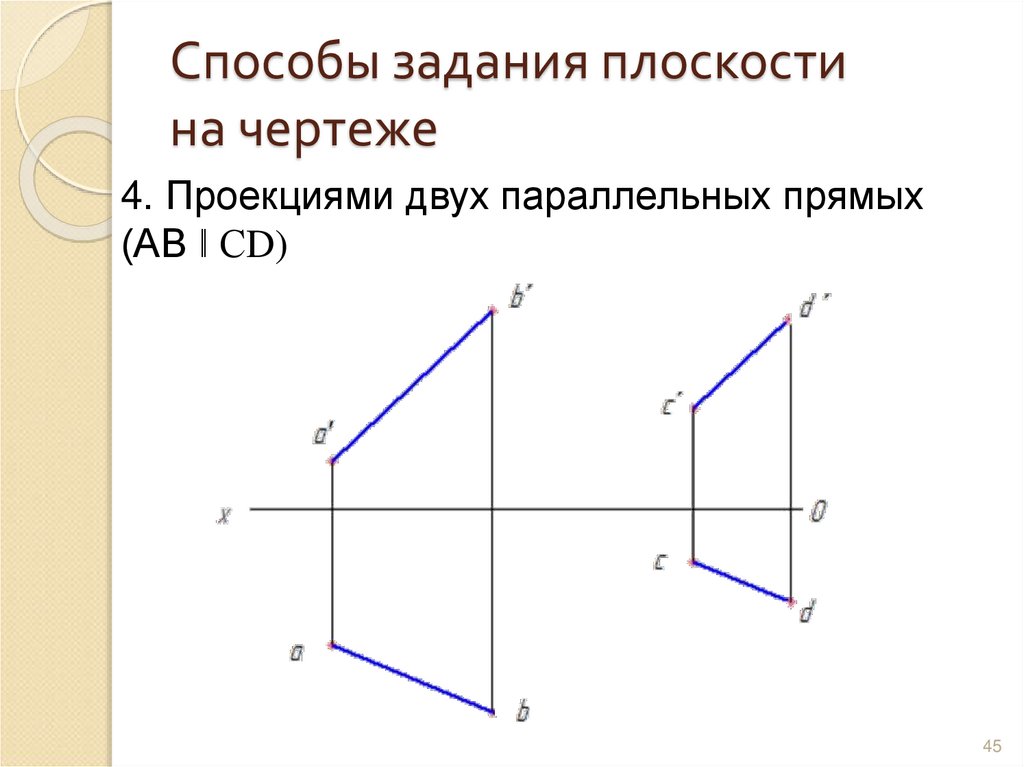
45. Способы задания плоскости на чертеже

4. Проекциями двух параллельных прямых
(АВ ǁ СD)
45

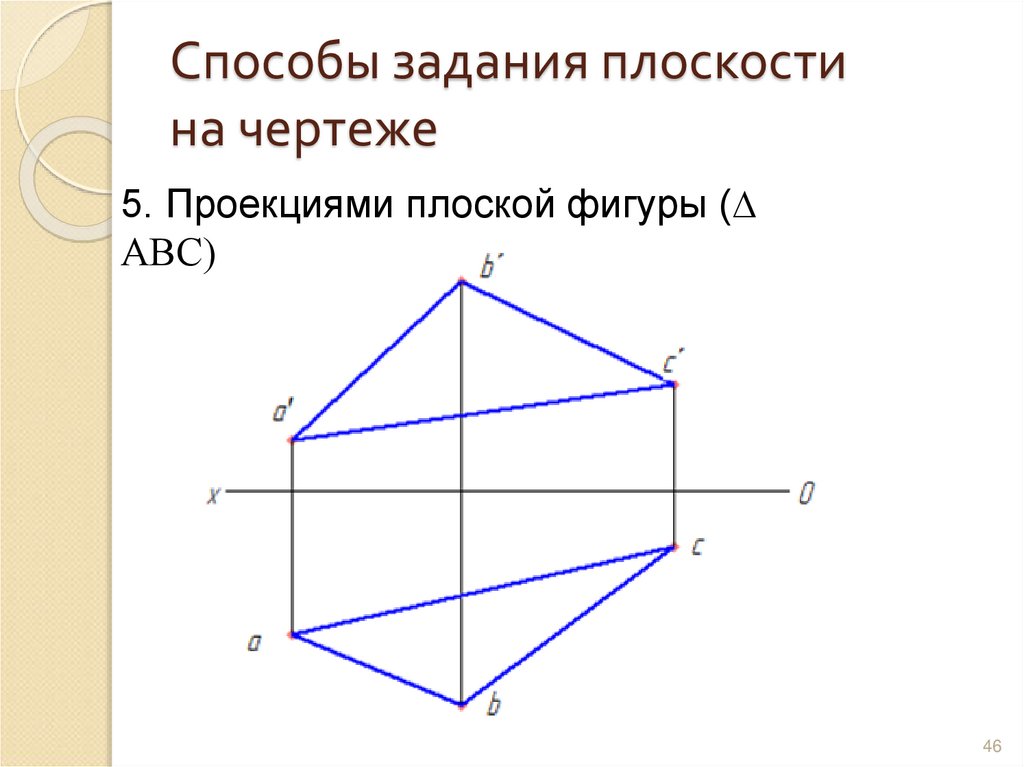
46. Способы задания плоскости на чертеже

5. Проекциями плоской фигуры (∆
АВС)
46

47. Способы задания плоскости на чертеже

6. Следами плоскости
47

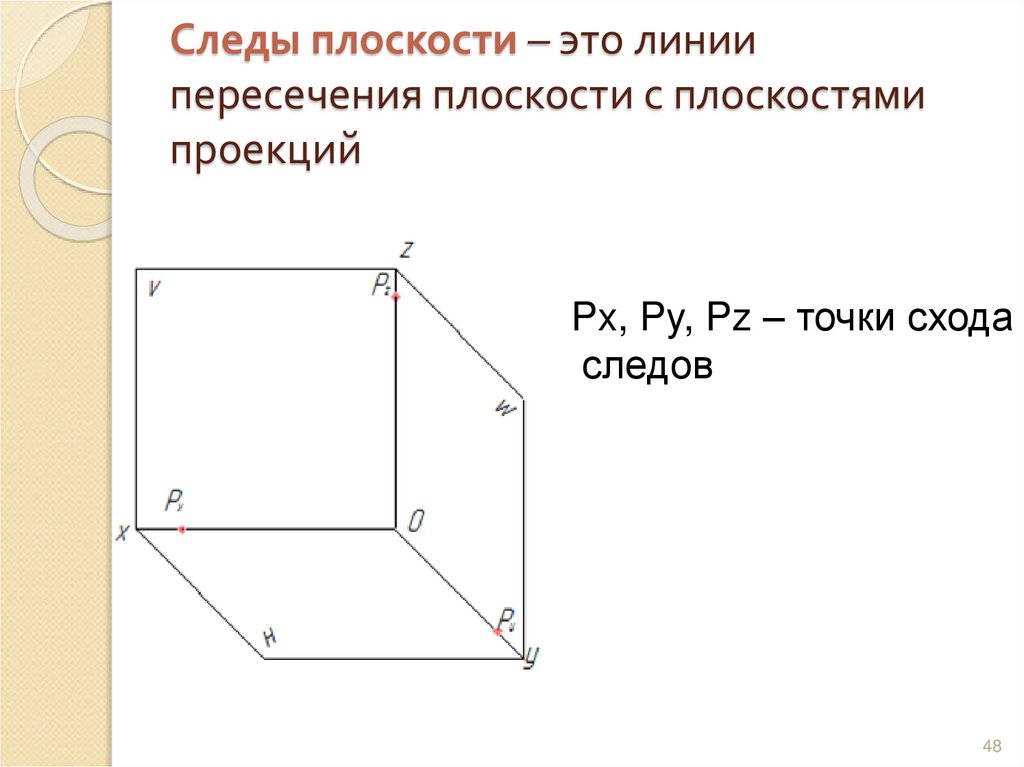
48. Следы плоскости – это линии пересечения плоскости с плоскостями проекций

Px, Py, Pz – точки схода
следов
48

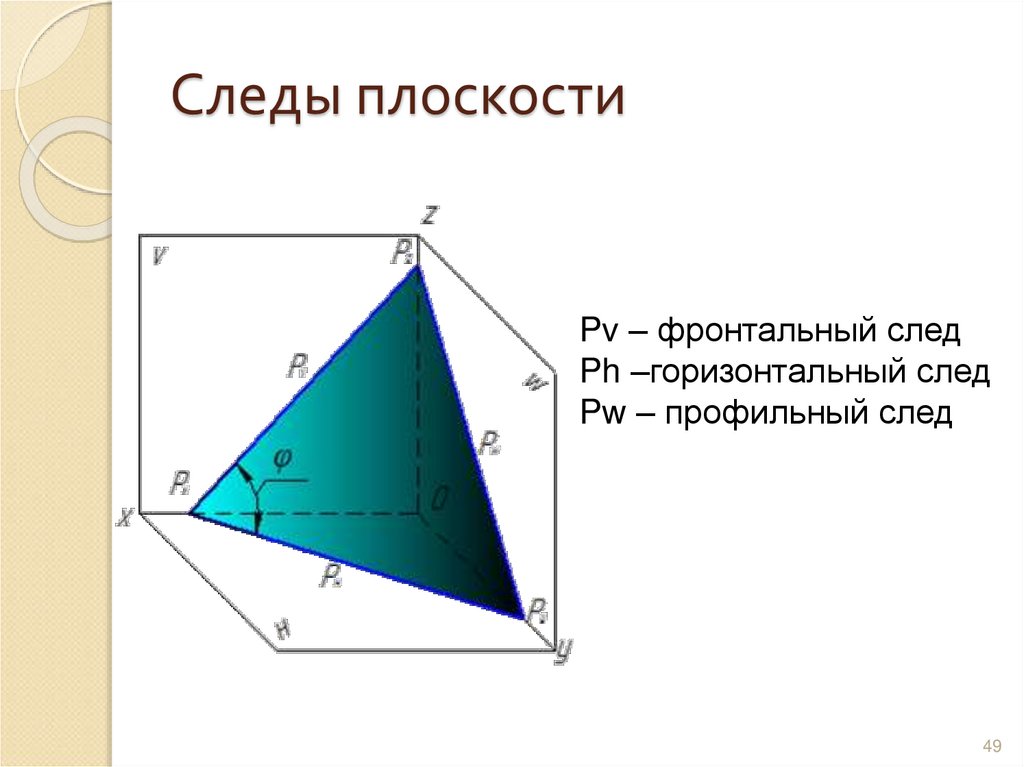
49. Следы плоскости

Pv – фронтальный след
Ph –горизонтальный след
Pw – профильный след
49

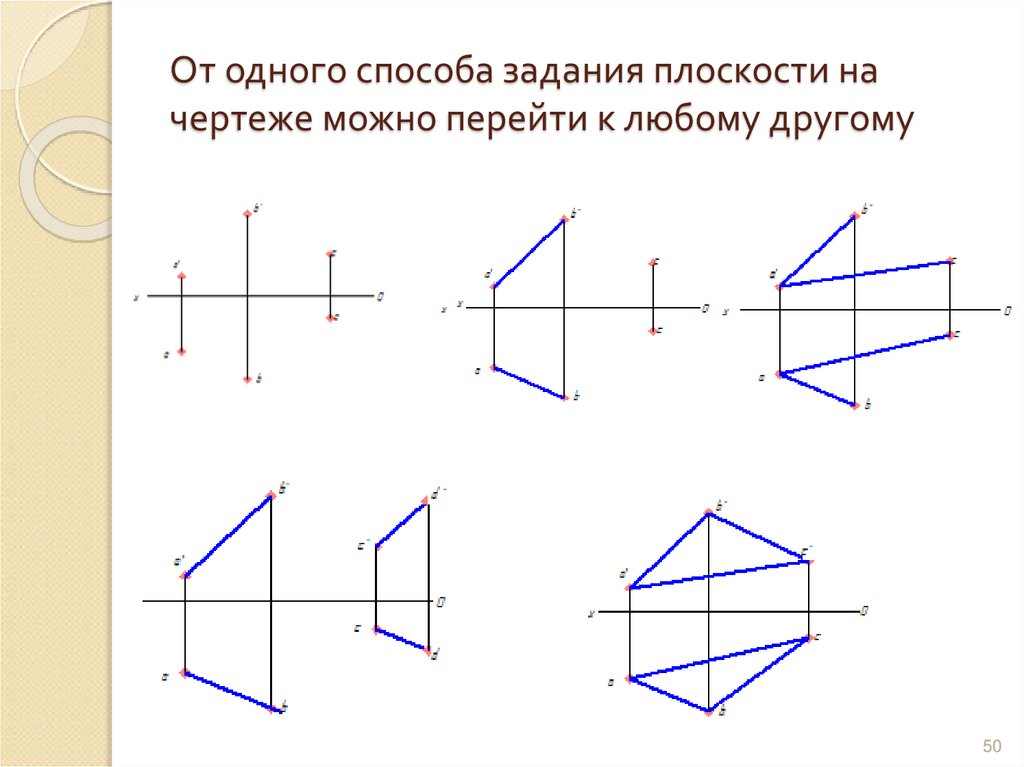
50. От одного способа задания плоскости на чертеже можно перейти к любому другому

50

51. Положение плоскости относительно плоскостей проекций:

Параллельно – плоскости уровня;
Перпендикулярно – проецирующие
плоскости
Под любым углом, отличным от
прямого – плоскости общего
положения
51

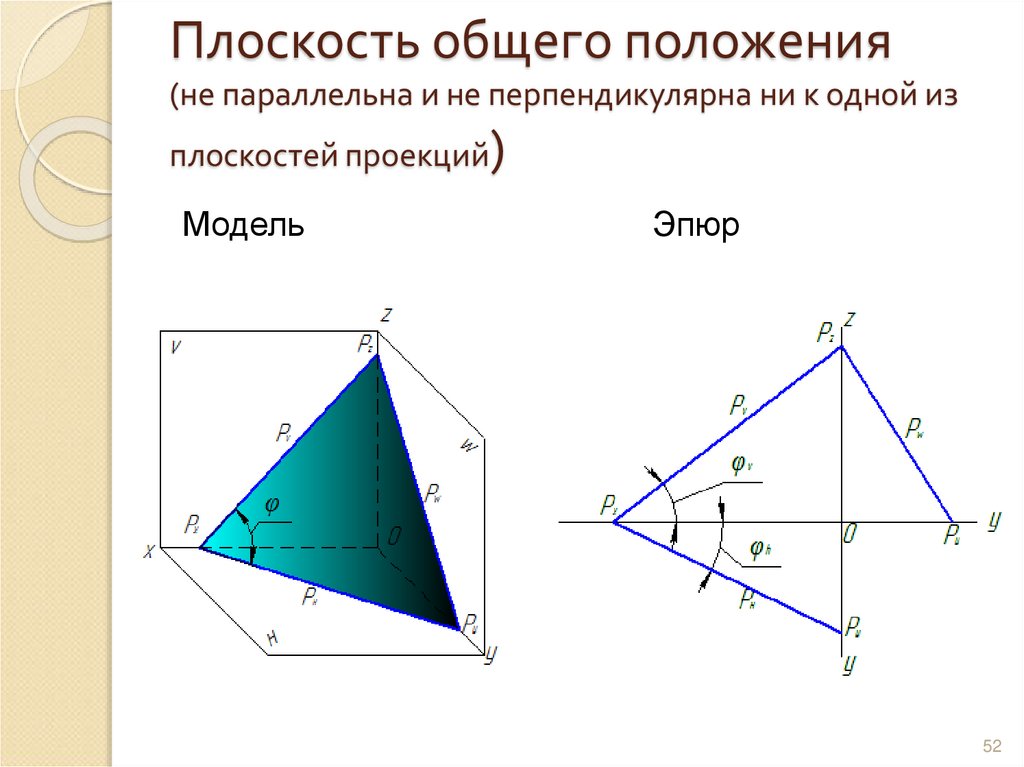
52. Плоскость общего положения (не параллельна и не перпендикулярна ни к одной из плоскостей проекций)

Плоскость общего положения
(не параллельна и не перпендикулярна ни к одной из
)
плоскостей проекций
Модель
Эпюр
52

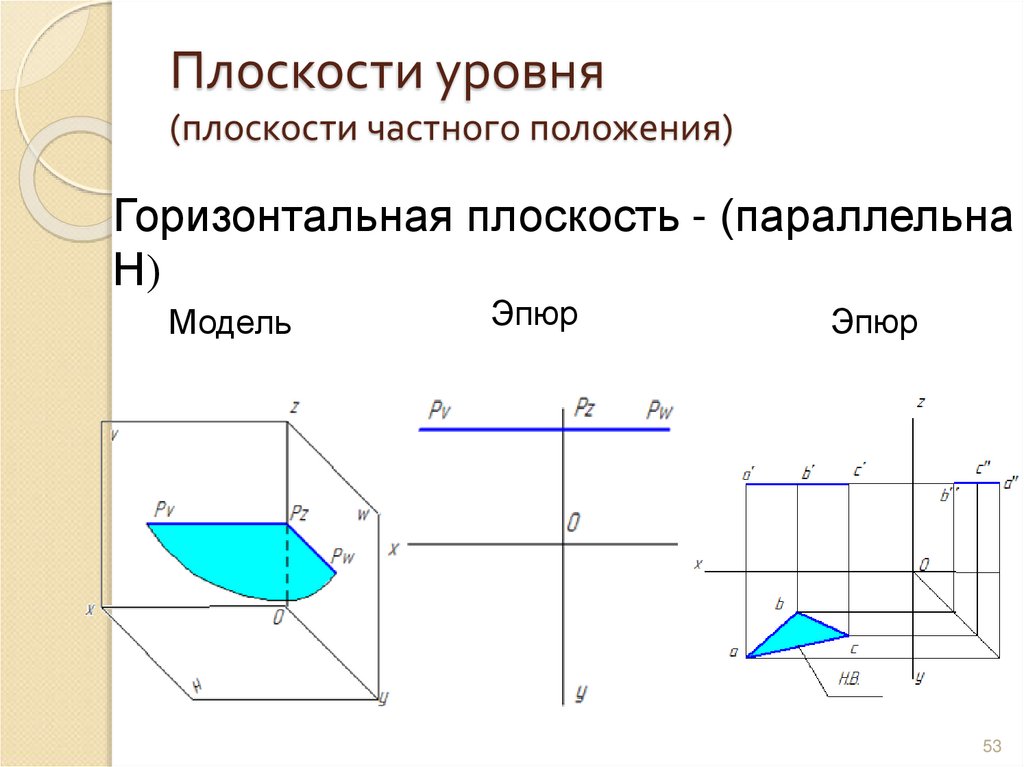
53. Плоскости уровня (плоскости частного положения)

Горизонтальная плоскость - (параллельна
Н)
Модель
Эпюр
Эпюр
53

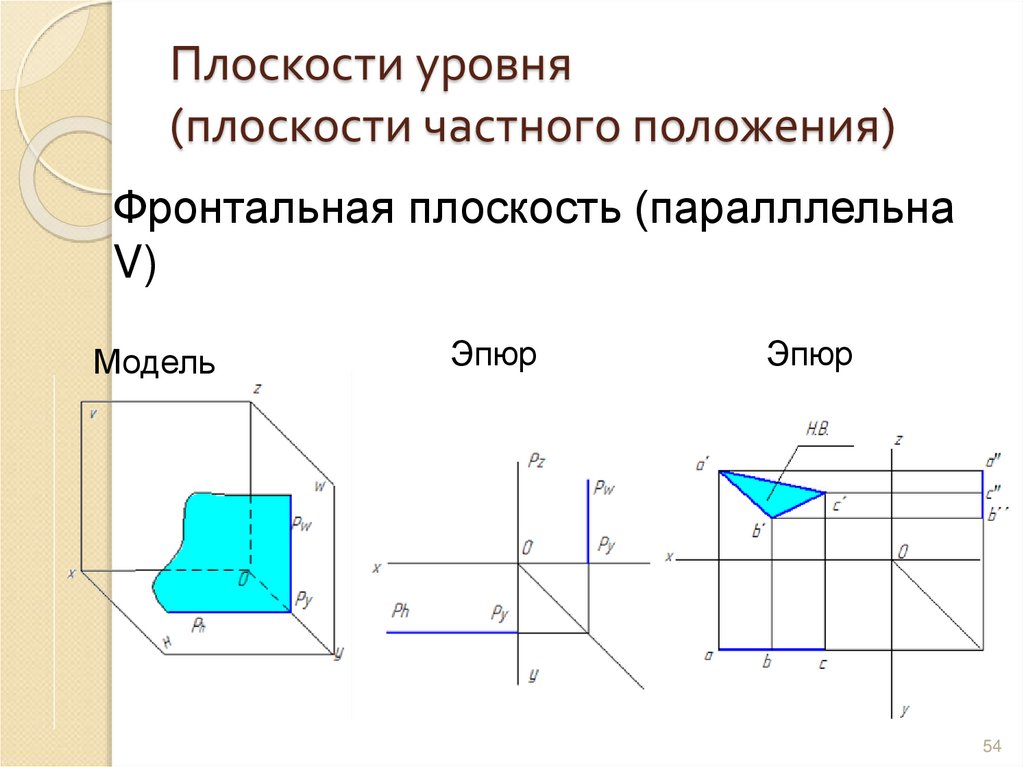
54. Плоскости уровня (плоскости частного положения)

Фронтальная плоскость (паралллельна
V)
Модель
Эпюр
Эпюр
54

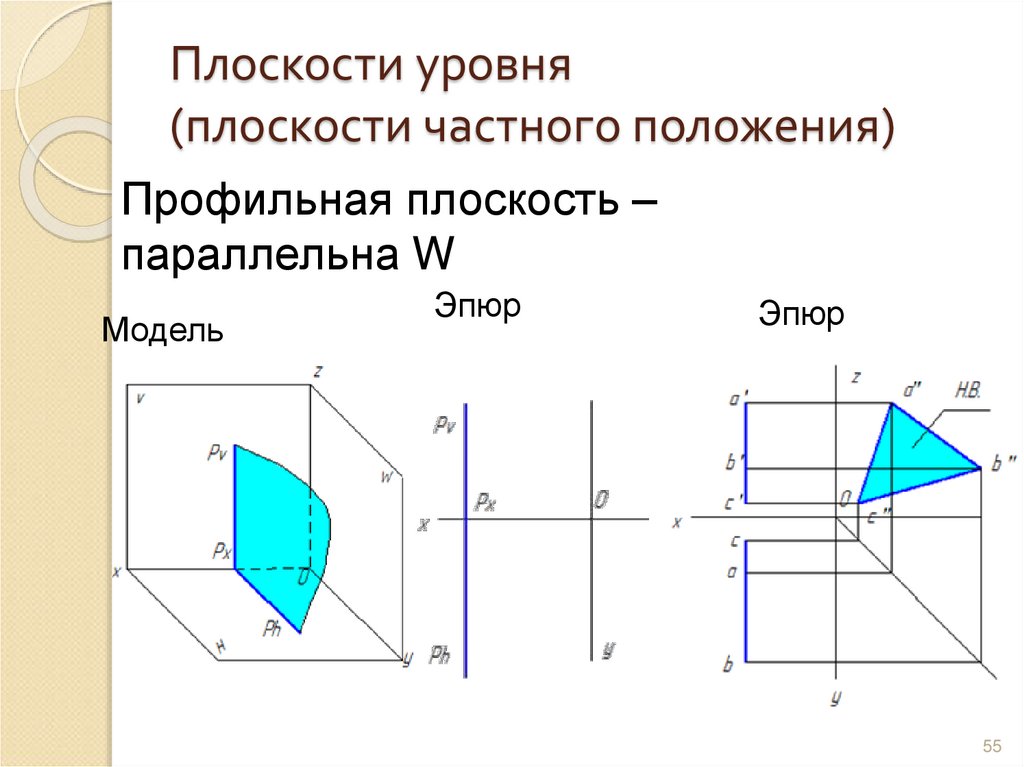
55. Плоскости уровня (плоскости частного положения)

Профильная плоскость –
параллельна W
Модель
Эпюр
Эпюр
55

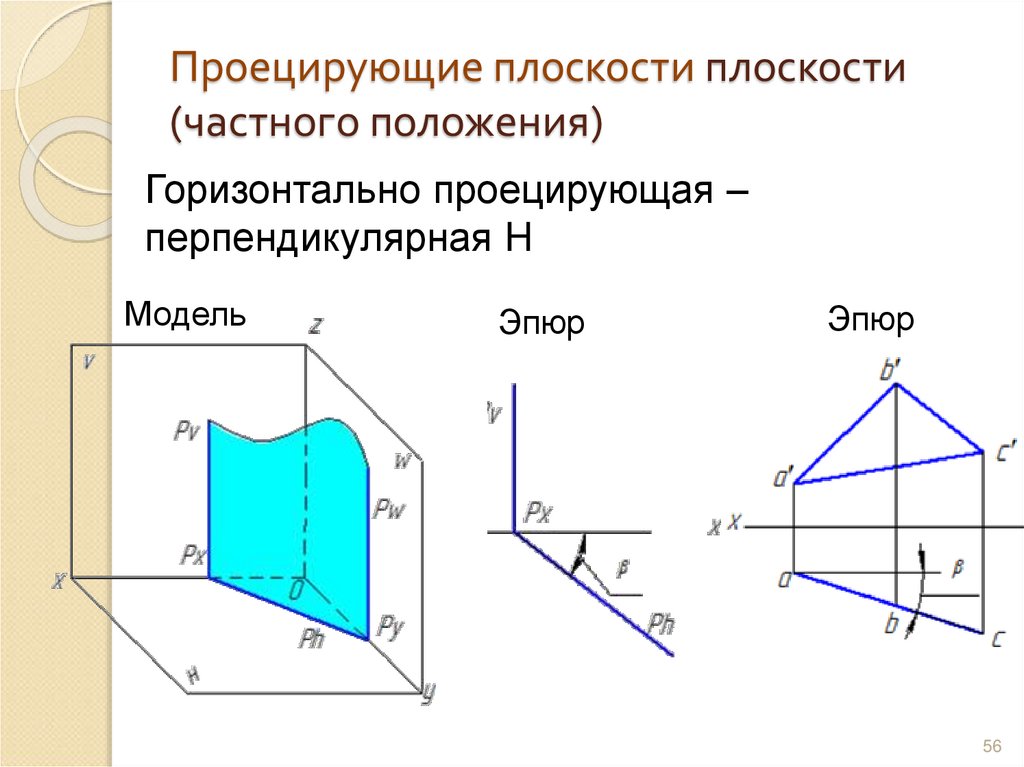
56. Проецирующие плоскости плоскости (частного положения)

Горизонтально проецирующая –
перпендикулярная H
Модель
Эпюр
Эпюр
56

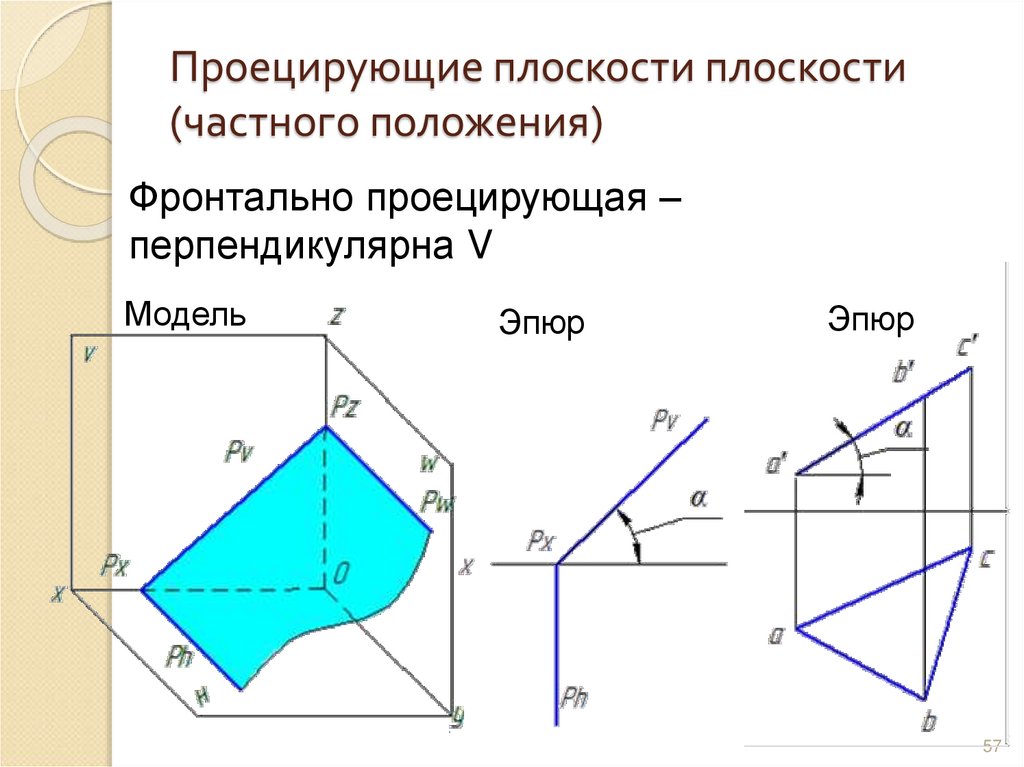
57. Проецирующие плоскости плоскости (частного положения)

Фронтально проецирующая –
перпендикулярна V
Модель
Эпюр
Эпюр
57

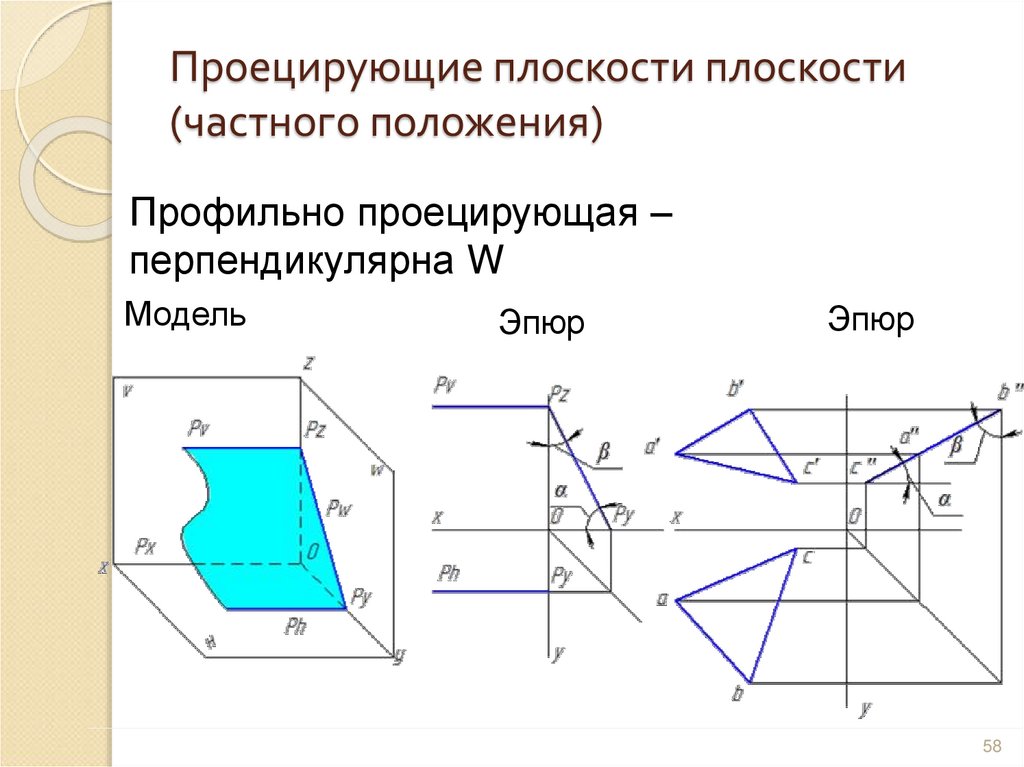
58. Проецирующие плоскости плоскости (частного положения)

Профильно проецирующая –
перпендикулярна W
Модель
Эпюр
Эпюр
58

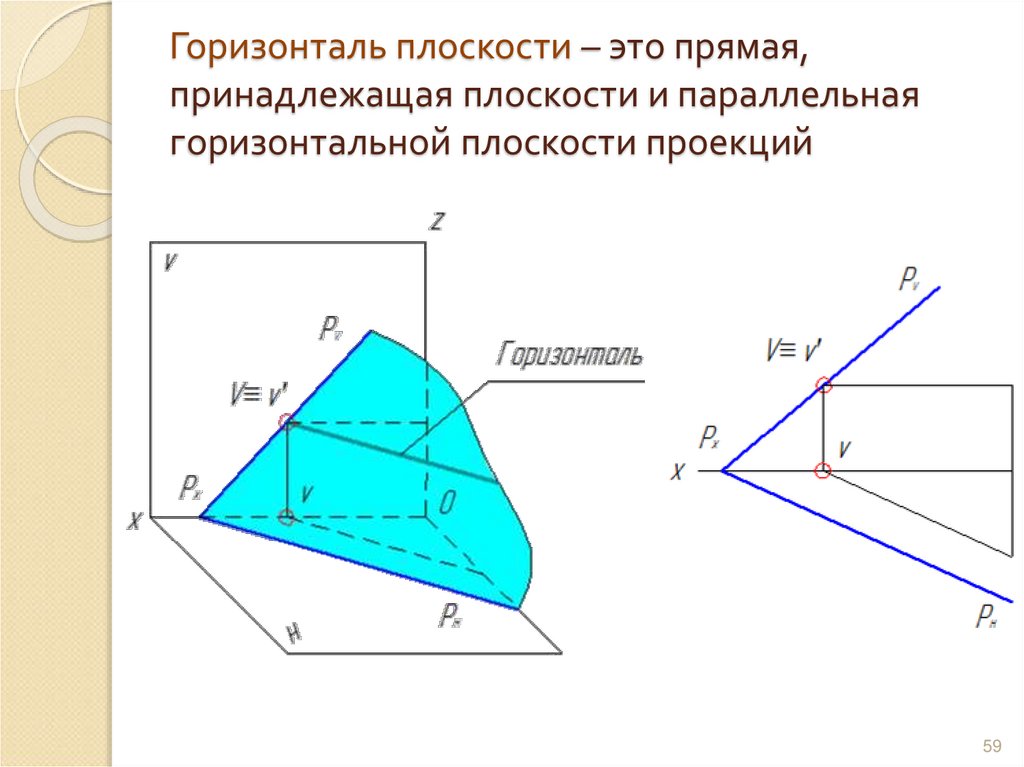
59. Горизонталь плоскости – это прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций

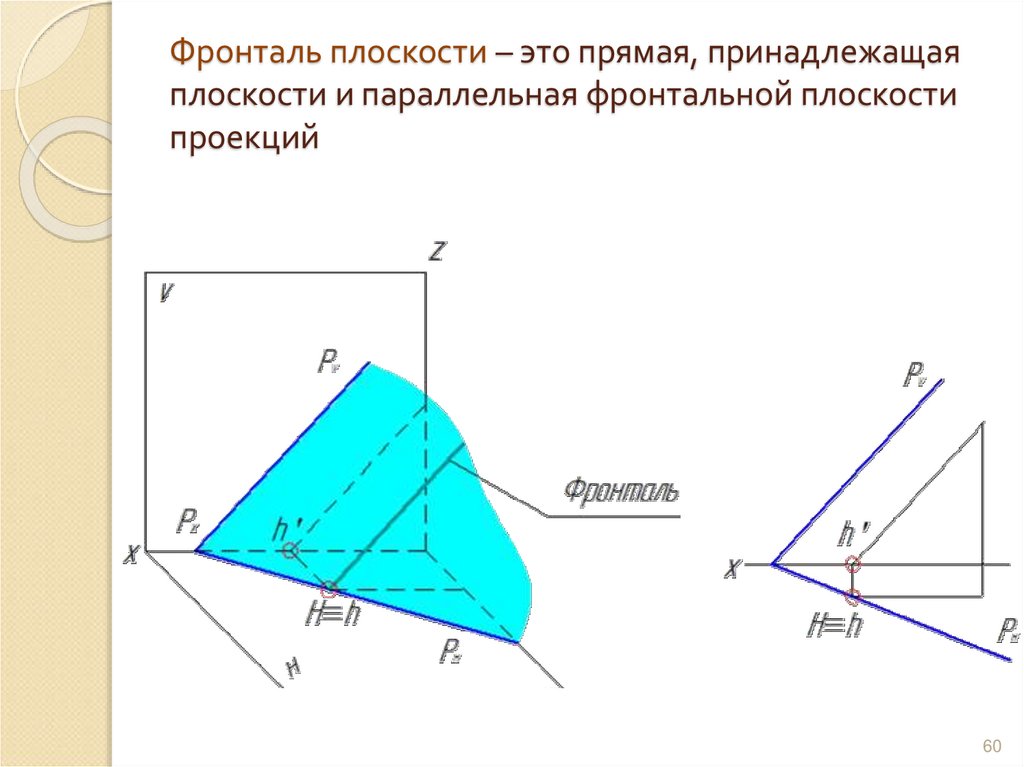
59

60. Фронталь плоскости – это прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций

60

61. Взаимное положение прямой и плоскости

Прямая принадлежит плоскости
Прямая параллельна плоскости
Прямая пересекает плоскость
Прямая перпендикулярна плоскости
61

62. Прямая и точка в плоскости

Прямая принадлежит плоскости, если
она имеет с этой плоскостью две
общие точки
Чтобы построить точку в плоскости,
необходимо построить прямую,
принадлежащую этой плоскости и на
ней найти точку
62

63. Прямая параллельна плоскости,

если она параллельна хотя бы одной
прямой, лежащей в этой плоскости
63

64. Пересечение прямой с плоскостью

Аксиома:
Если прямая не принадлежит плоскости
и не параллельна ей, то она эту
плоскость пересекает
64

65. Пересечение прямой с плоскостью общего положения (задачи 23-25)

65

66. ЗАМЕНА ПЛОСКОСТЕЙ

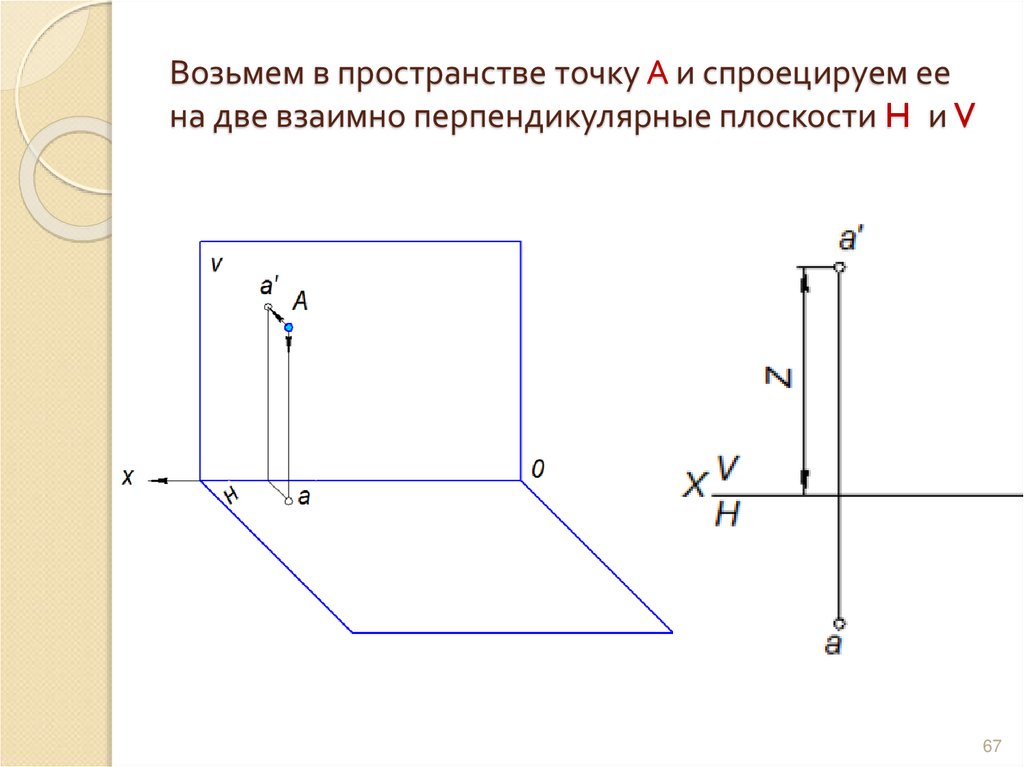
66

67. Возьмем в пространстве точку А и спроецируем ее на две взаимно перпендикулярные плоскости H и V

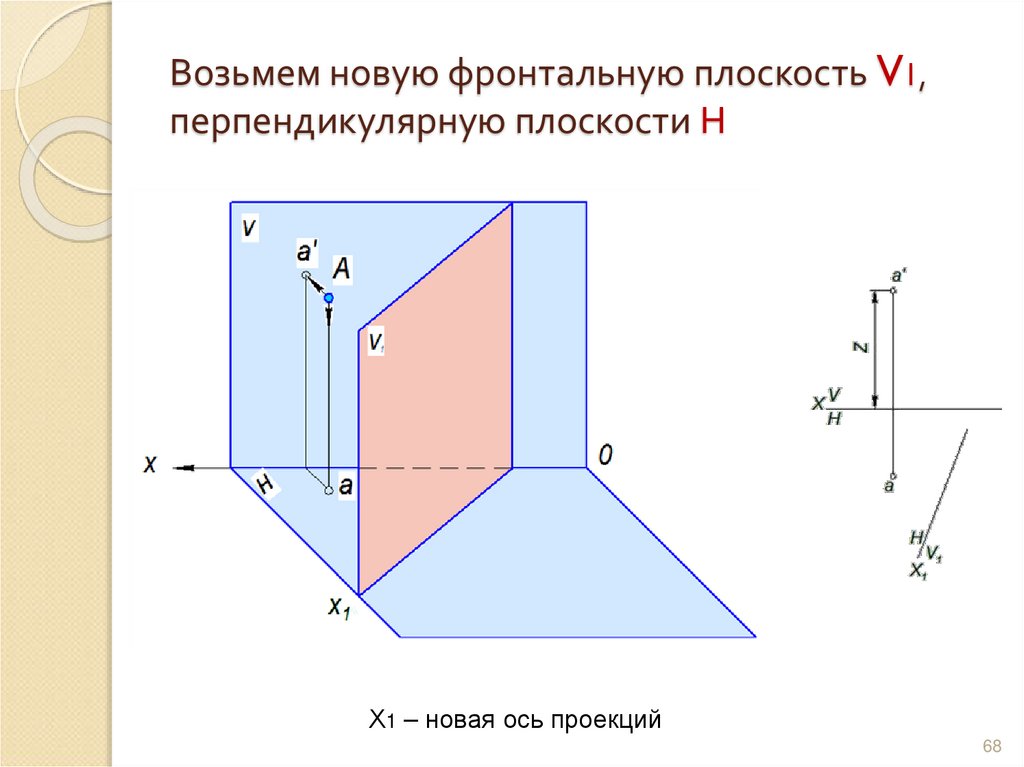
67

68. Возьмем новую фронтальную плоскость V1, перпендикулярную плоскости Н

Х1 – новая ось проекций
68

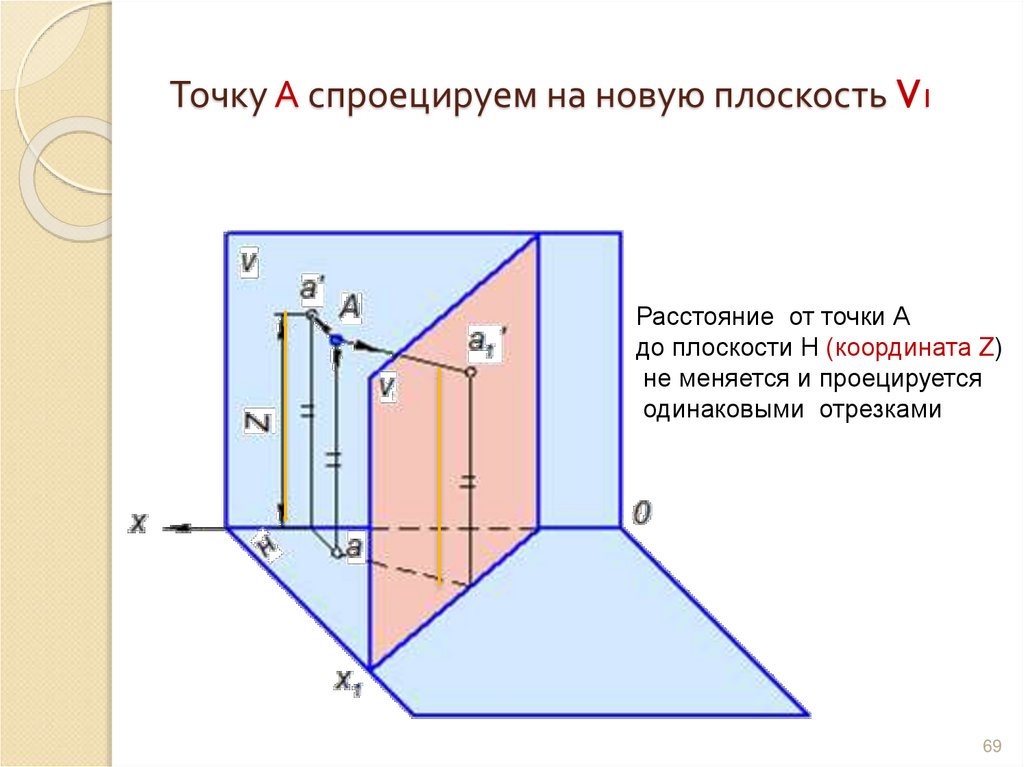
69. Точку А спроецируем на новую плоскость V1

Расстояние от точки А
до плоскости Н (координата Z)
не меняется и проецируется
одинаковыми отрезками
69

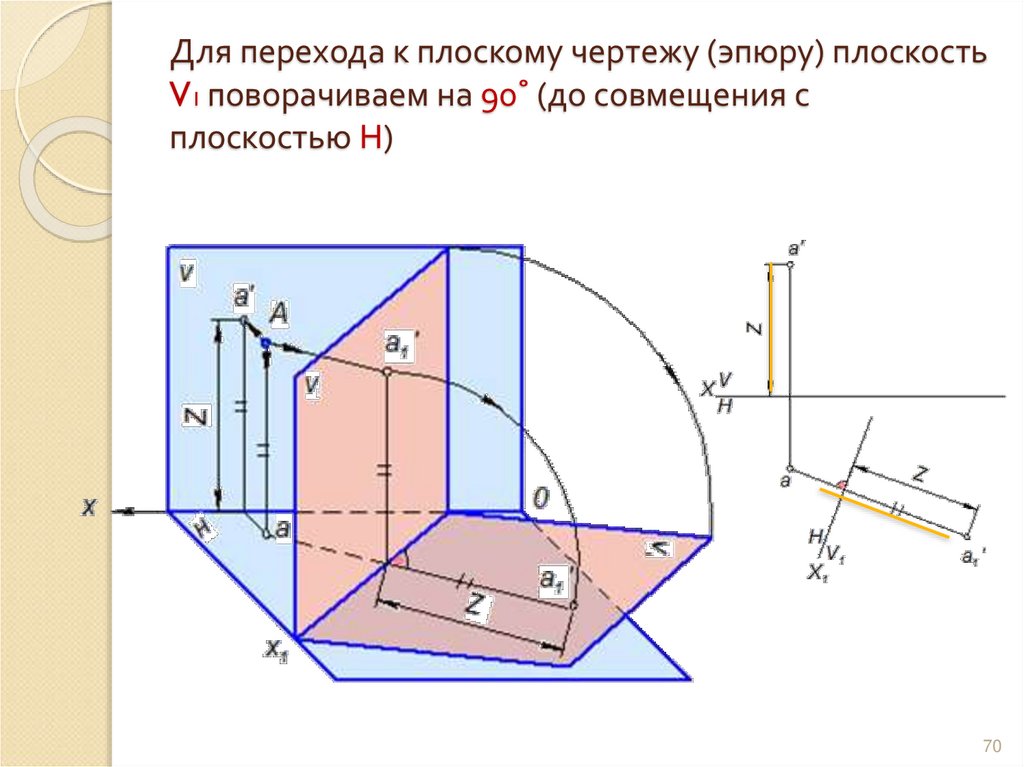
70. Для перехода к плоскому чертежу (эпюру) плоскость V1 поворачиваем на 90˚ (до совмещения с плоскостью Н)

70

71.

При замене плоскости проекций V на новую
плоскость V1 положение новой прямоугольной
проекции точки определяется ее аппликатой
(координатой Z)
71

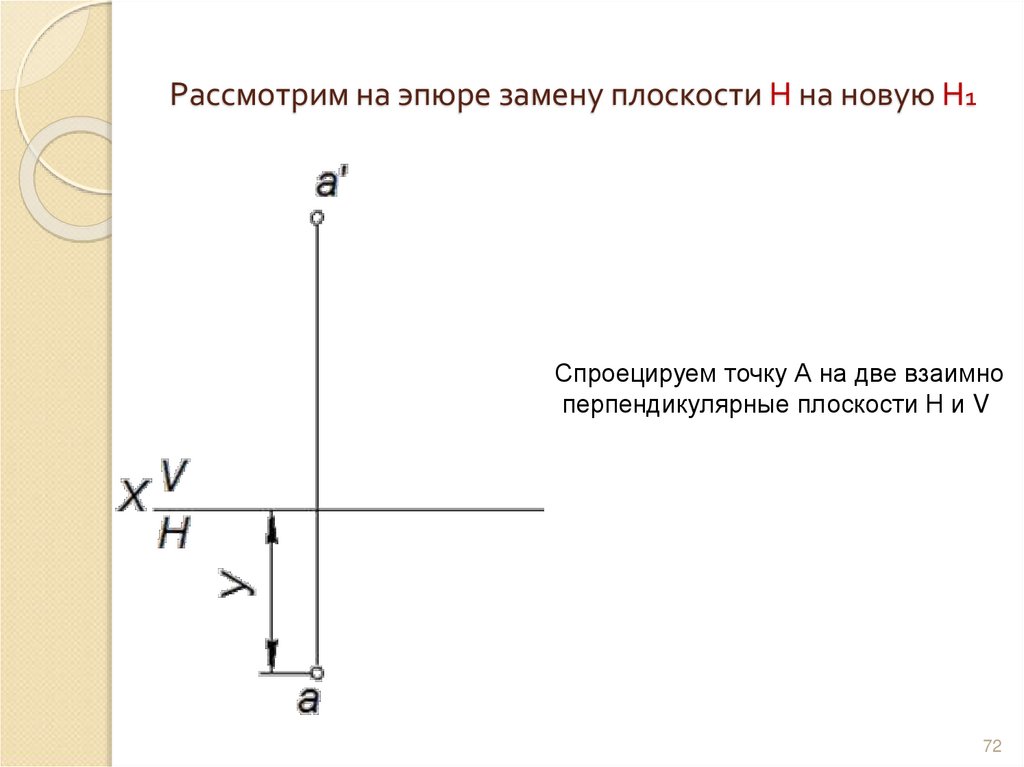
72. Рассмотрим на эпюре замену плоскости Н на новую Н1

Спроецируем точку А на две взаимно
перпендикулярные плоскости Н и V
72

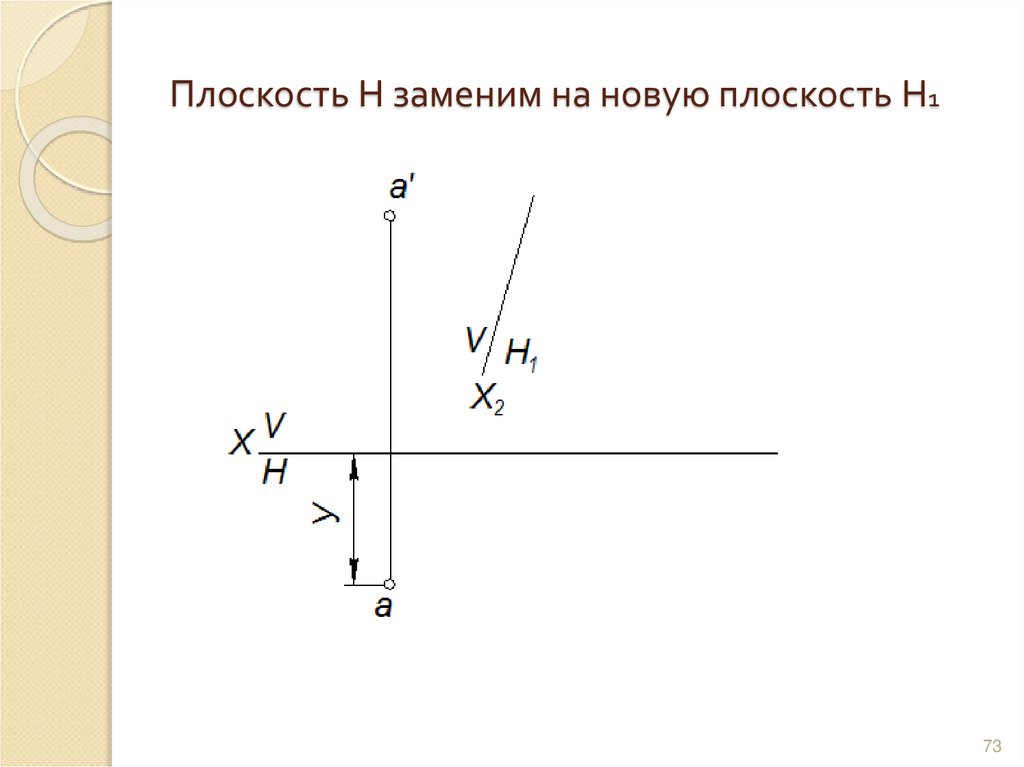
73. Плоскость Н заменим на новую плоскость Н1

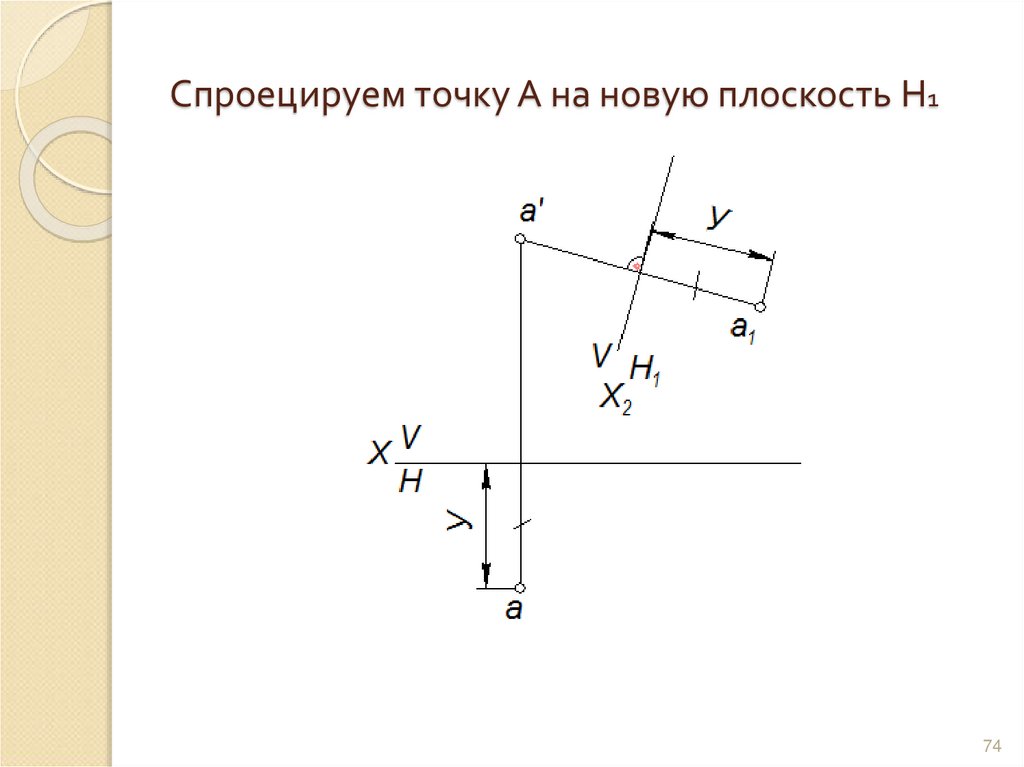
73

74. Спроецируем точку А на новую плоскость Н1

74

75. Вывод

При замене плоскости проекций H на новую
плоскость H1 положение новой
прямоугольной проекции точки определяется
ее ординатой (координатой Y)
75

76. Способ вращения

Вращение вокруг проецирующей
прямой
Плоско-параллельное перемещение
Вращение вокруг линий уровня
Совмещение (вращение вокруг следа
плоскости
76

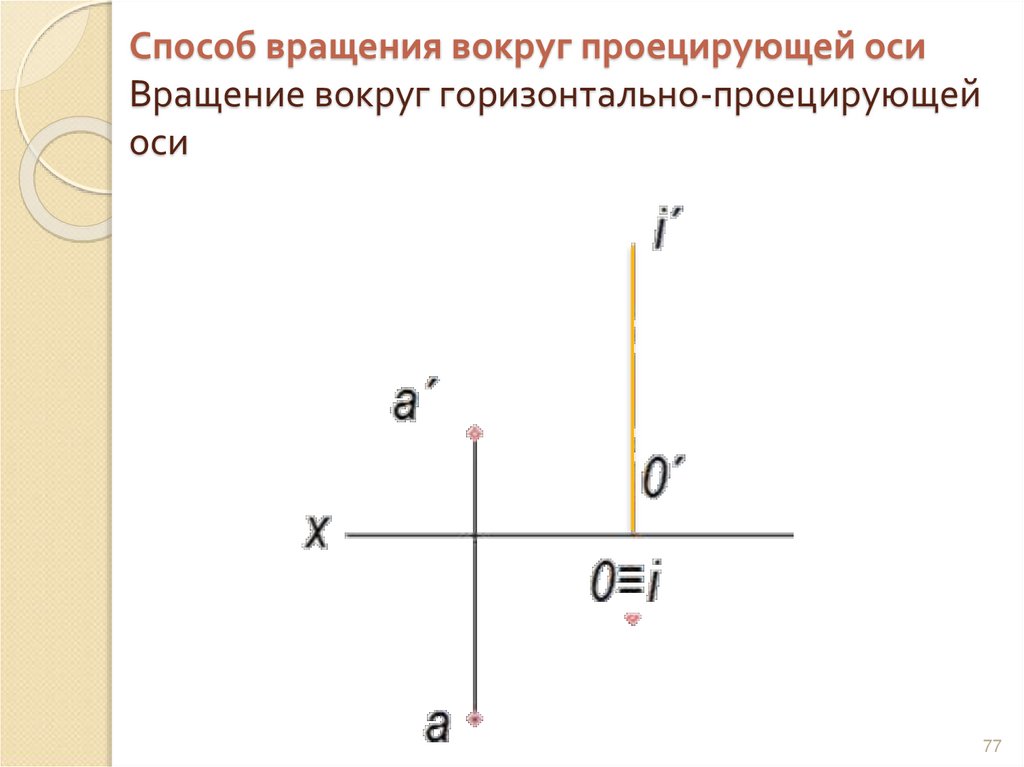
77. Способ вращения вокруг проецирующей оси Вращение вокруг горизонтально-проецирующей оси

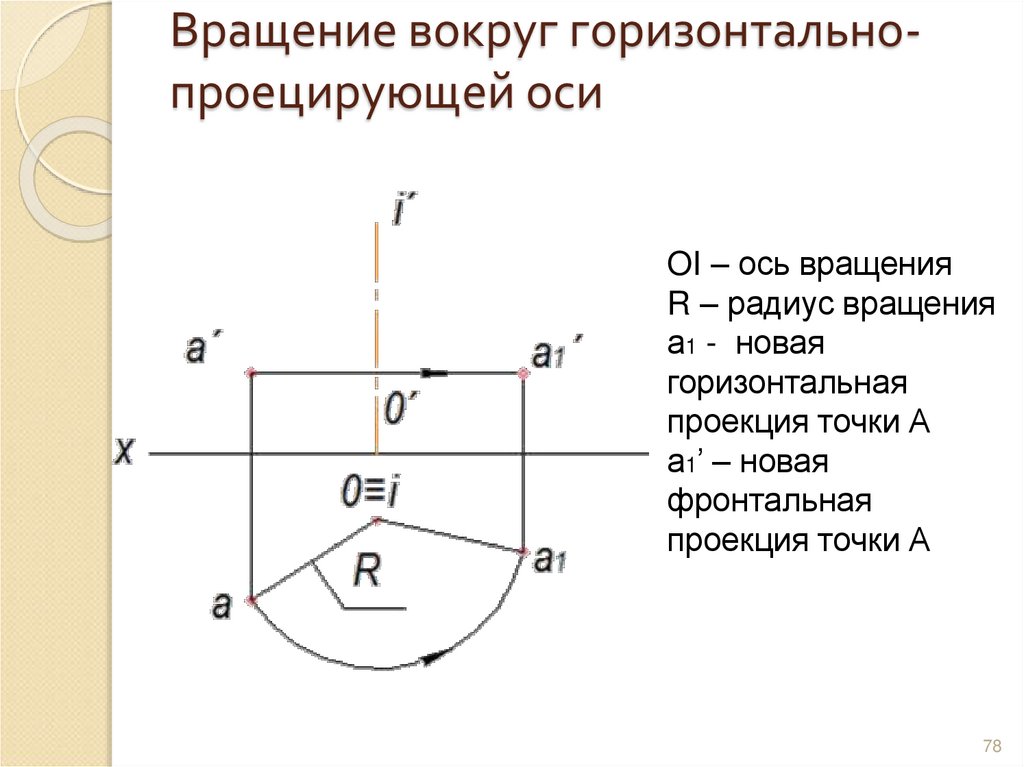
77

78. Вращение вокруг горизонтально- проецирующей оси

Вращение вокруг горизонтальнопроецирующей оси
OI – ось вращения
R – радиус вращения
а1 - новая
горизонтальная
проекция точки А
а1’ – новая
фронтальная
проекция точки А
78

79. Выводы:

Вращая в пространстве точку А в положение
А1 вокруг горизонтально –проецирующей оси OI,
точка А описывает дугу окружности радиусом АО с
центром O на оси вращения.
Эта дуга на плоскость Н проецируется в
натуральную величину, а на плоскость V – отрезком
прямой , параллельным оси Х.
Горизонтальная проекция точки перемещается по
окружности, а фронтальная – по прямой,
параллельной оси Х.
79

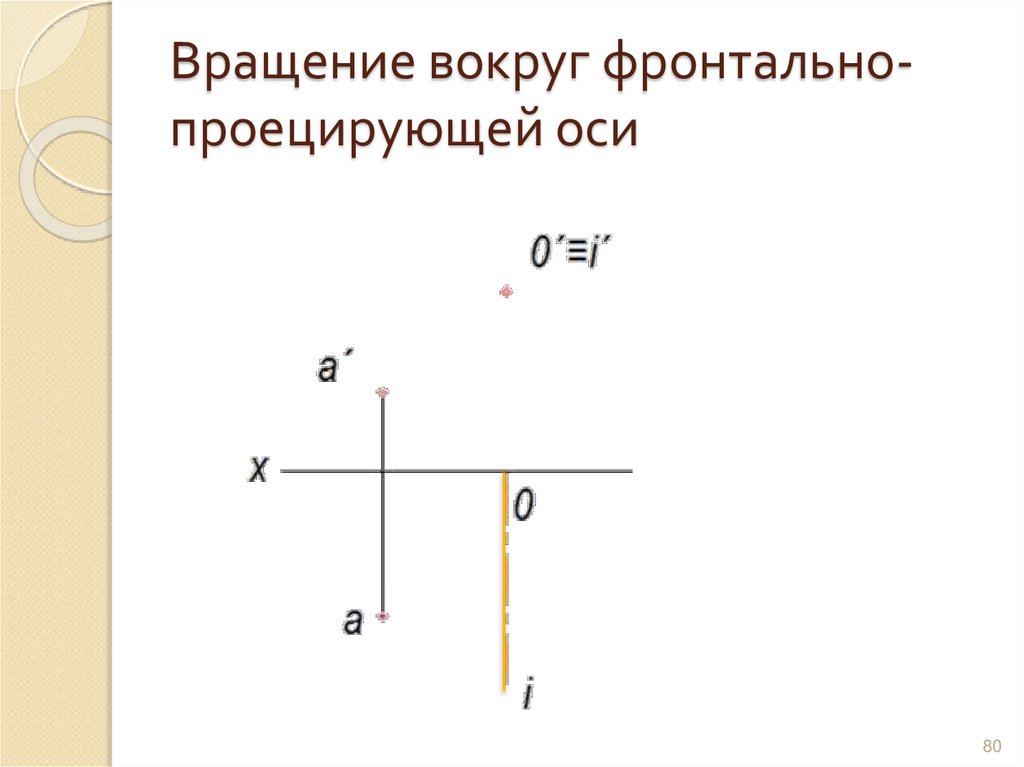
80. Вращение вокруг фронтально- проецирующей оси

Вращение вокруг фронтальнопроецирующей оси
80

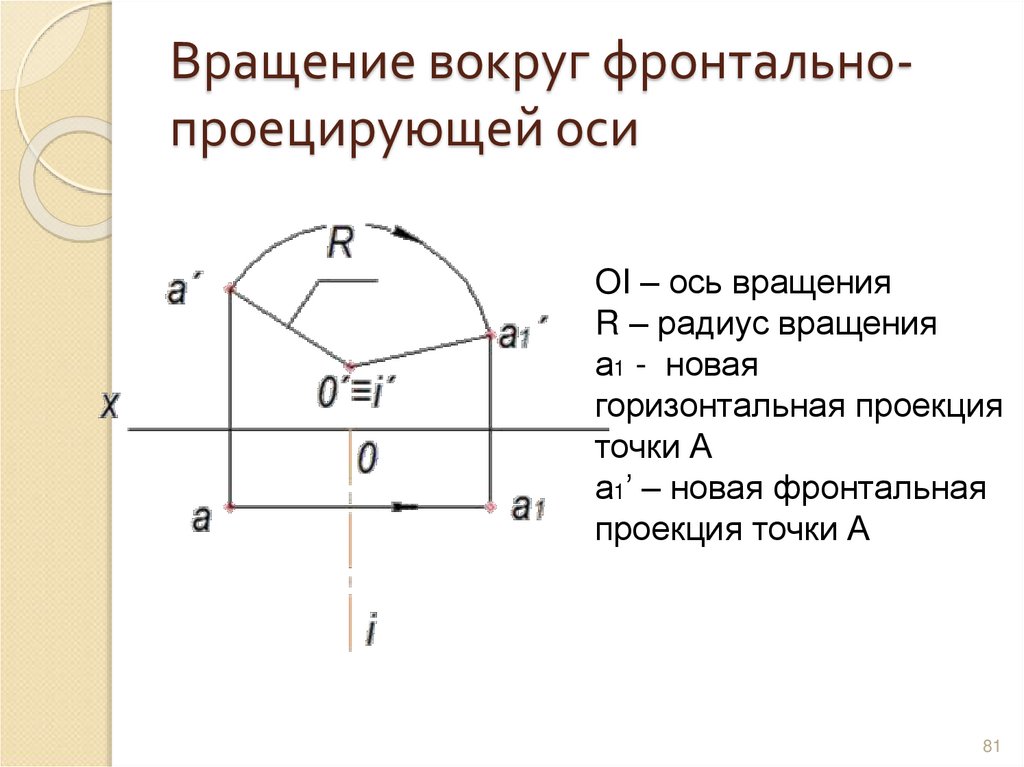
81. Вращение вокруг фронтально- проецирующей оси

Вращение вокруг фронтальнопроецирующей оси
OI – ось вращения
R – радиус вращения
а1 - новая
горизонтальная проекция
точки А
а1’ – новая фронтальная
проекция точки А
81

82. Выводы:

Вращая в пространстве точку А в
положение А1 вокруг фронтально –
проецирующей оси OI, точка А описывает
дугу окружности радиусом АО с центром
O на оси вращения.
Эта дуга на плоскость V проецируется в
натуральную величину, а на плоскость H
– отрезком прямой , параллельным оси Х.
Фронтальная проекция точки
перемещается по окружности, а
горизонтальная – по прямой,
параллельной оси Х.
82

83. Сечения геометрических тел плоскостью. Определение Н.В. сечений

Сечение – плоская фигура, полученная в
пересечении поверхности тела
плоскостью
83

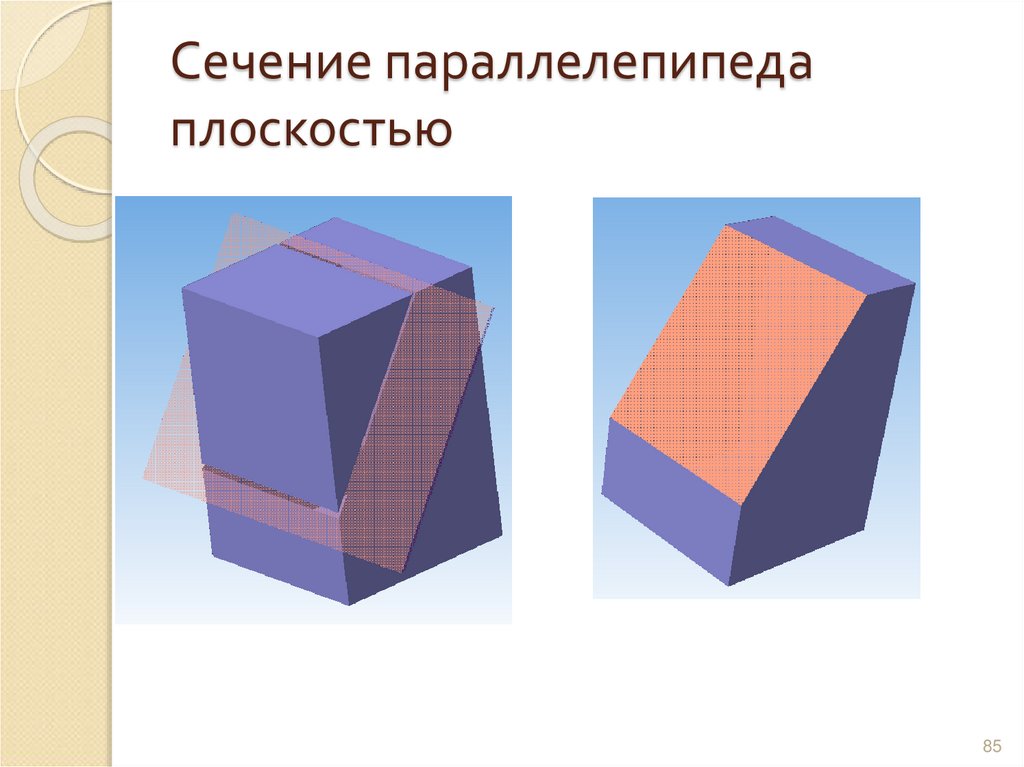
84. Характерные сечения тел плоскостью

В сечении многогранника плоскостью многоугольник
84

85. Сечение параллелепипеда плоскостью

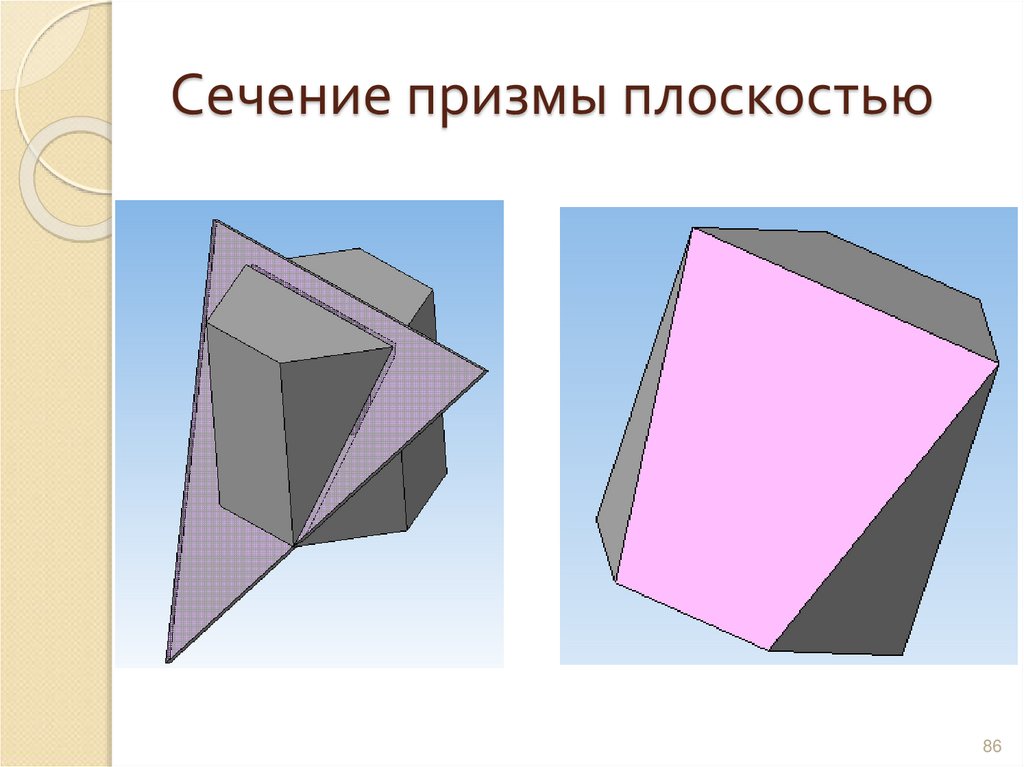
85

86. Сечение призмы плоскостью

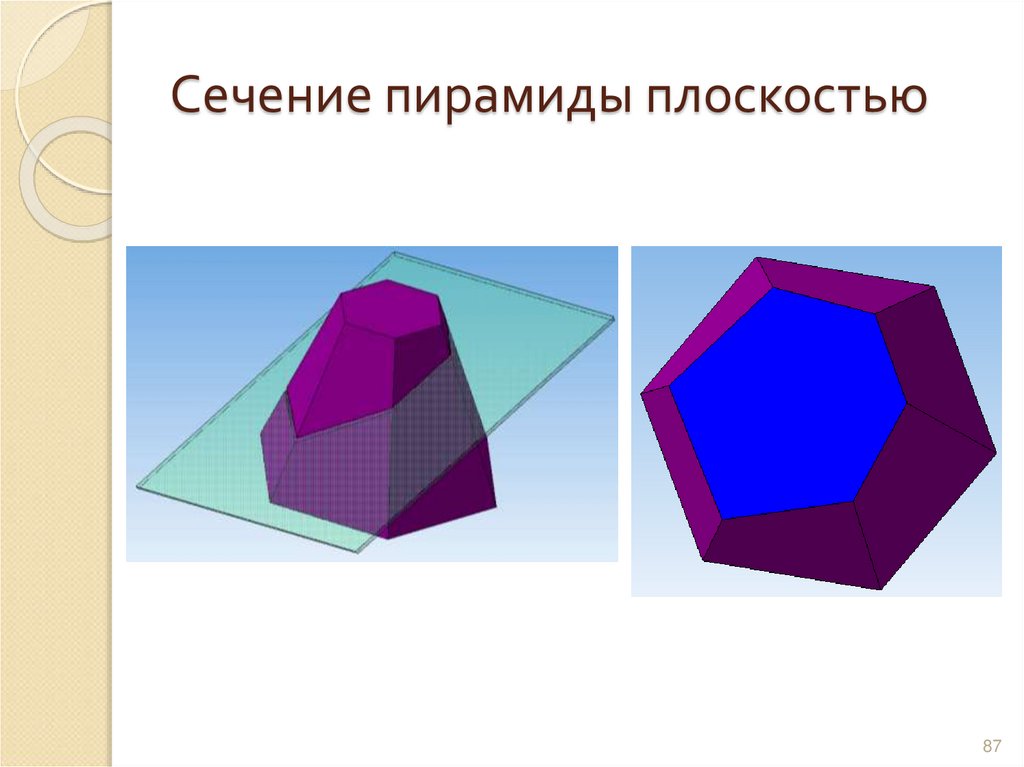
86

87. Сечение пирамиды плоскостью

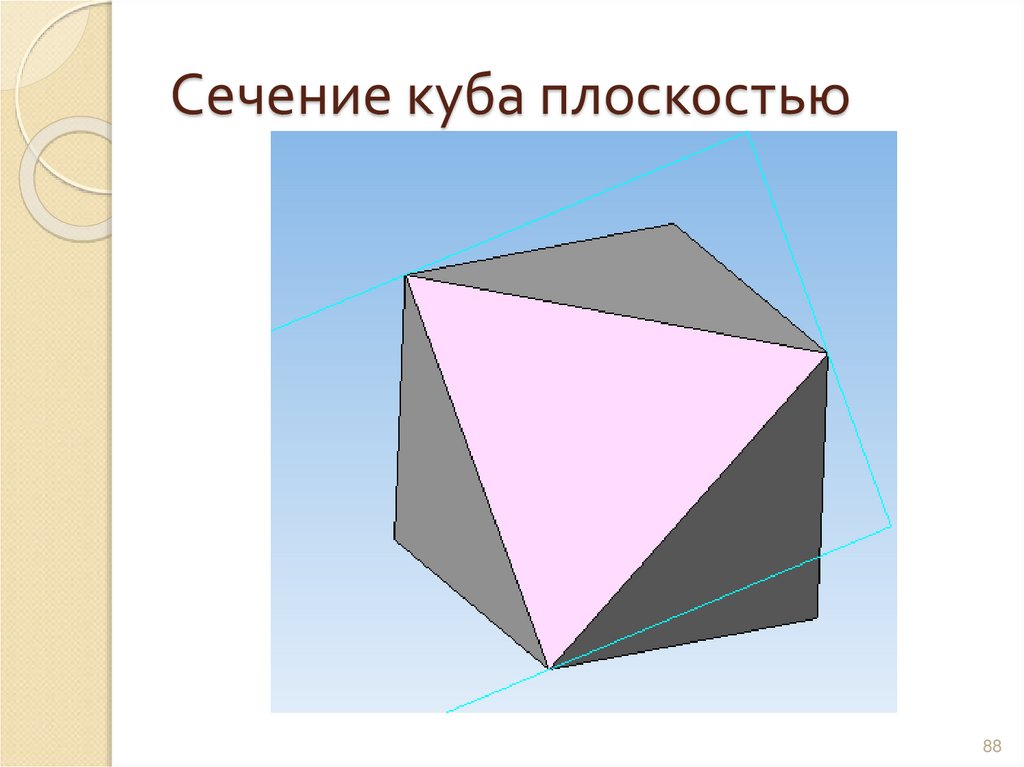
87

88. Сечение куба плоскостью

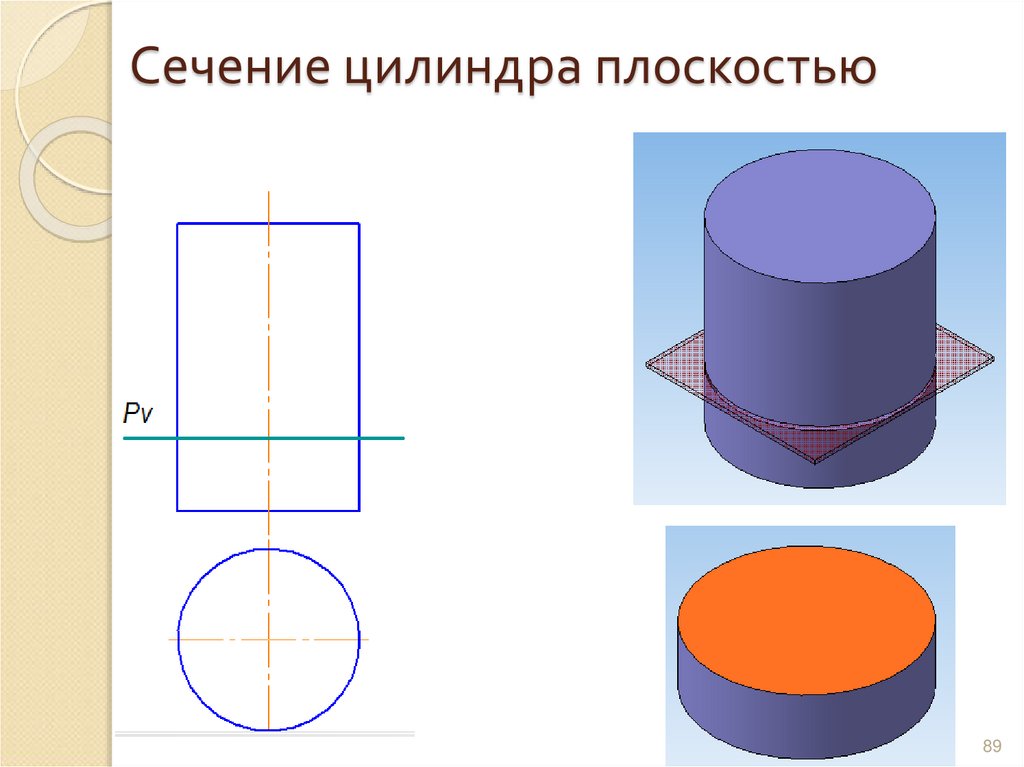
88

89. Сечение цилиндра плоскостью

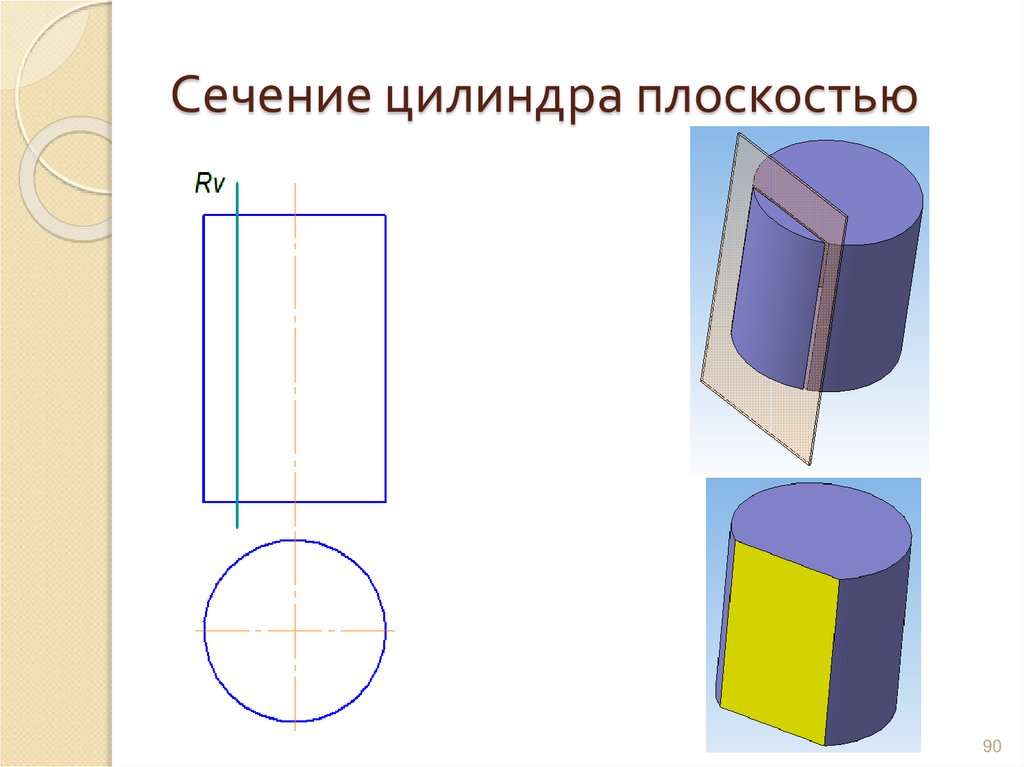
89

90. Сечение цилиндра плоскостью

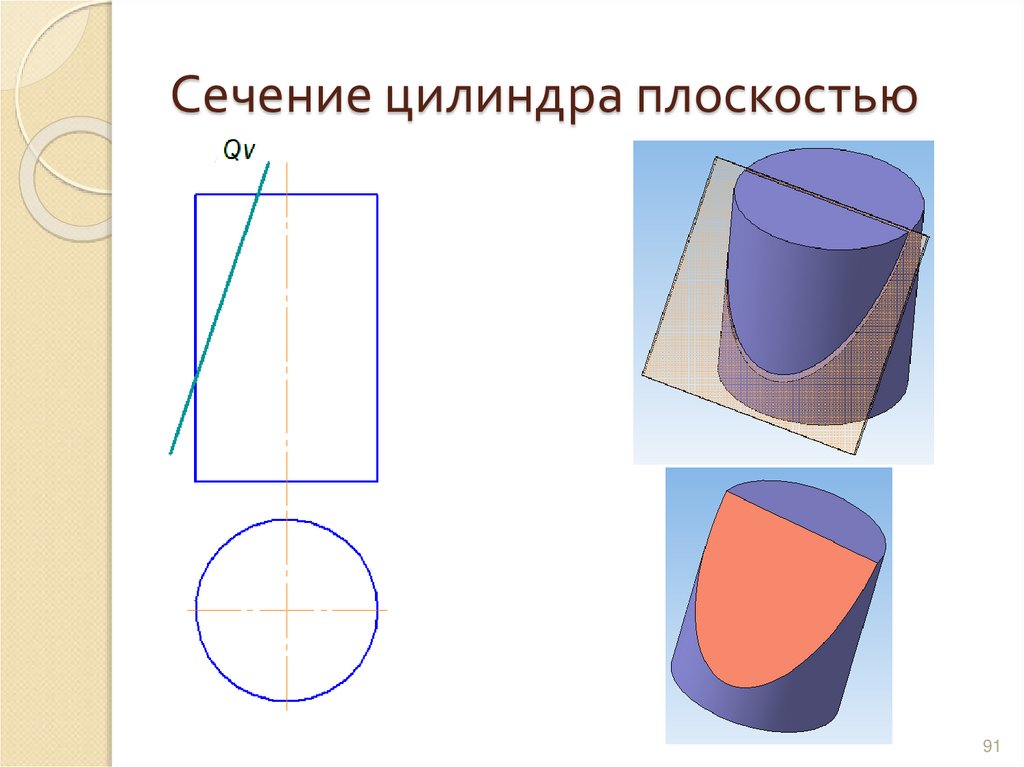
90

91. Сечение цилиндра плоскостью

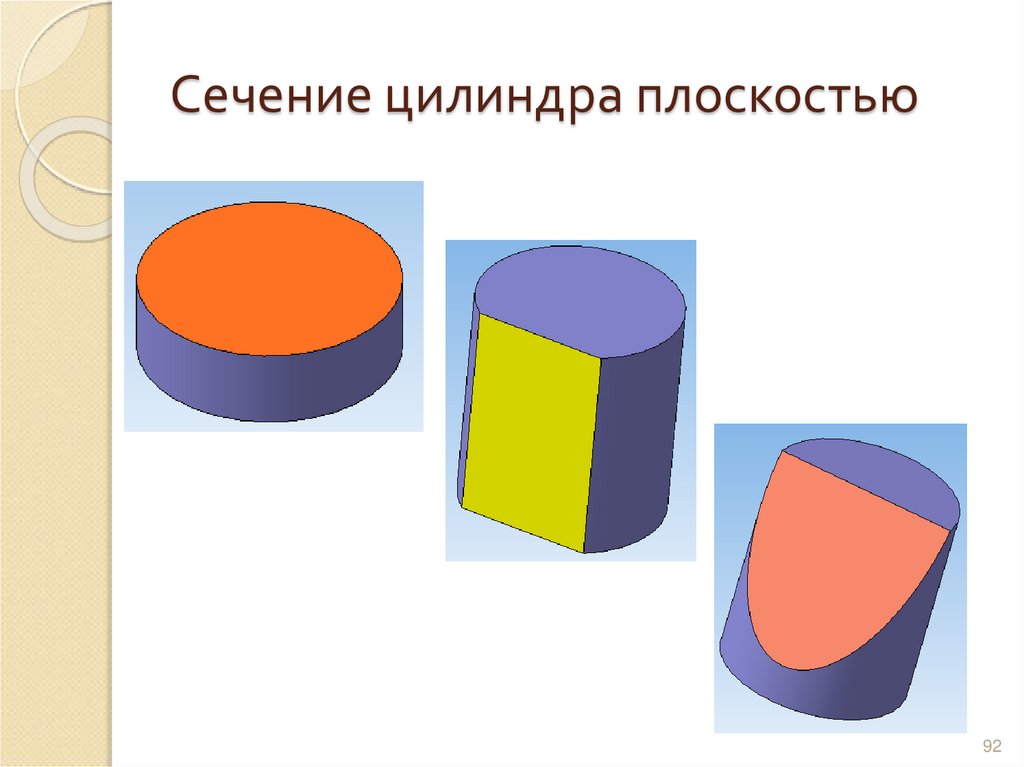
91

92. Сечение цилиндра плоскостью

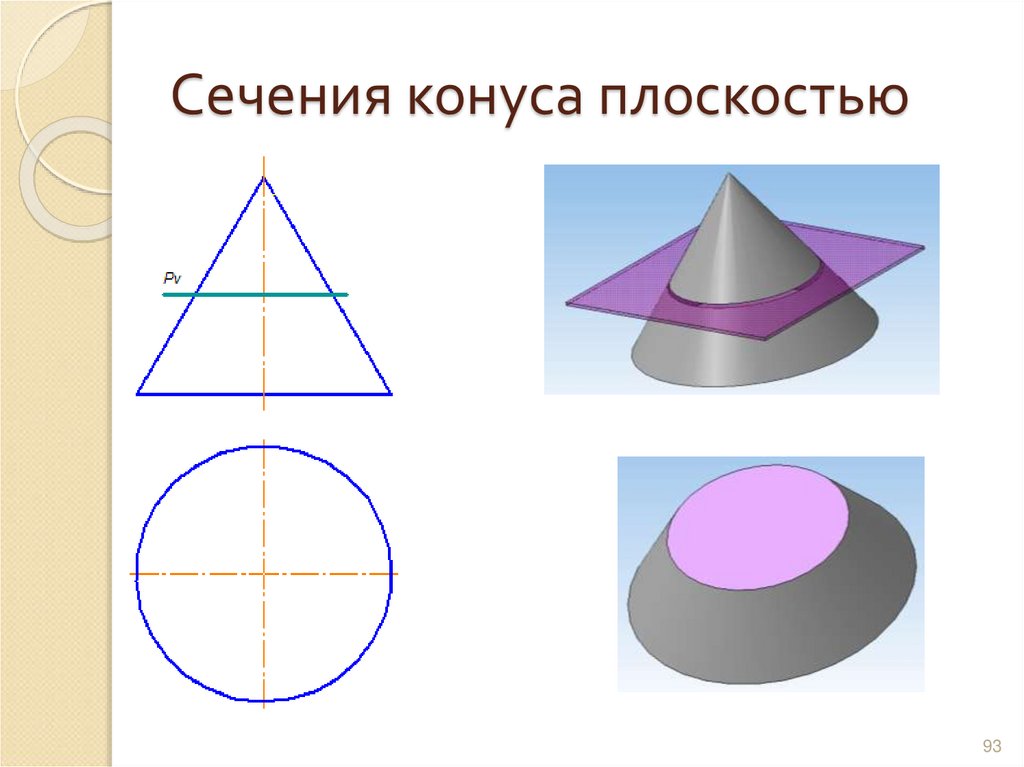
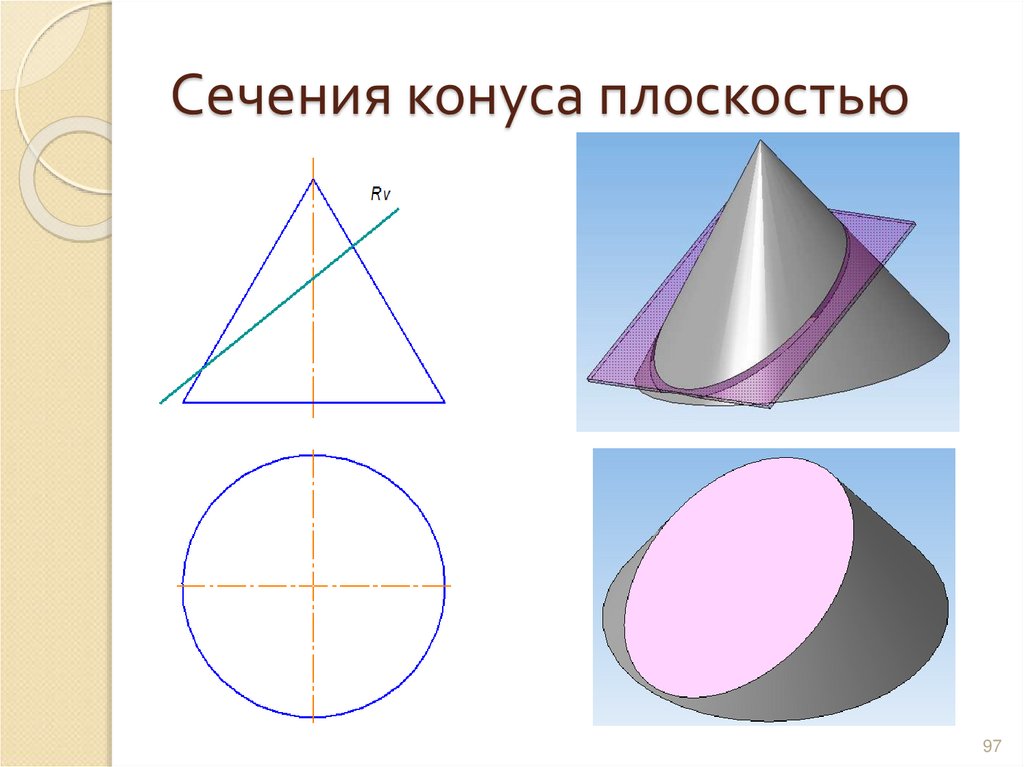
92

93. Сечения конуса плоскостью

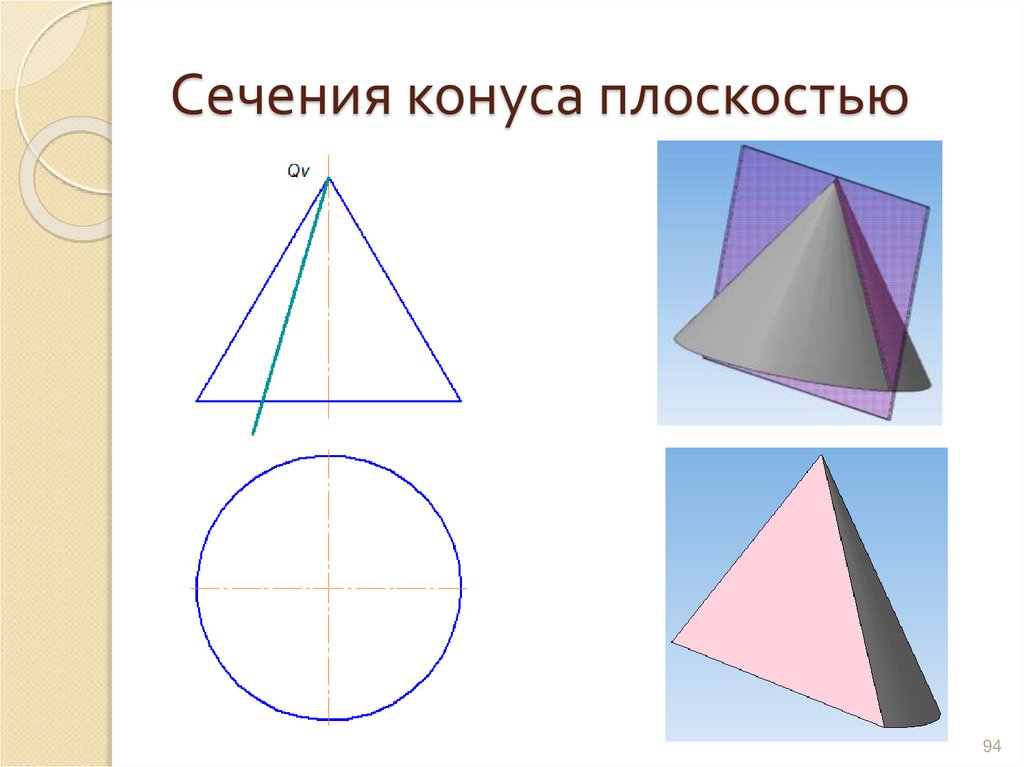
93

94. Сечения конуса плоскостью

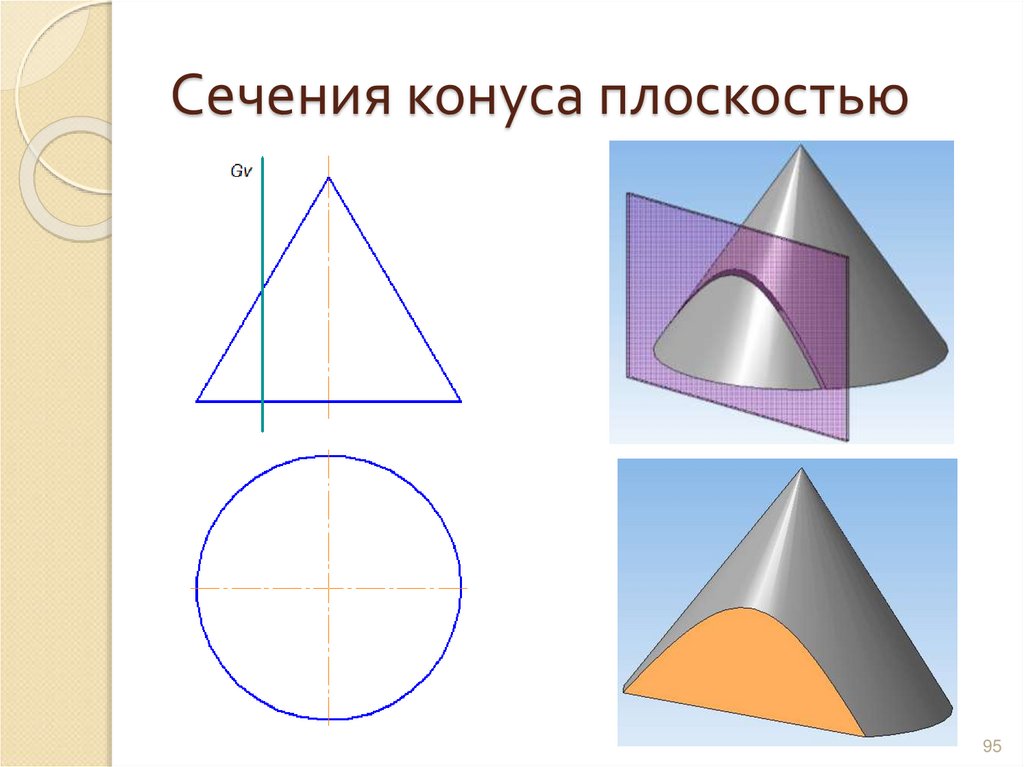
94

95. Сечения конуса плоскостью

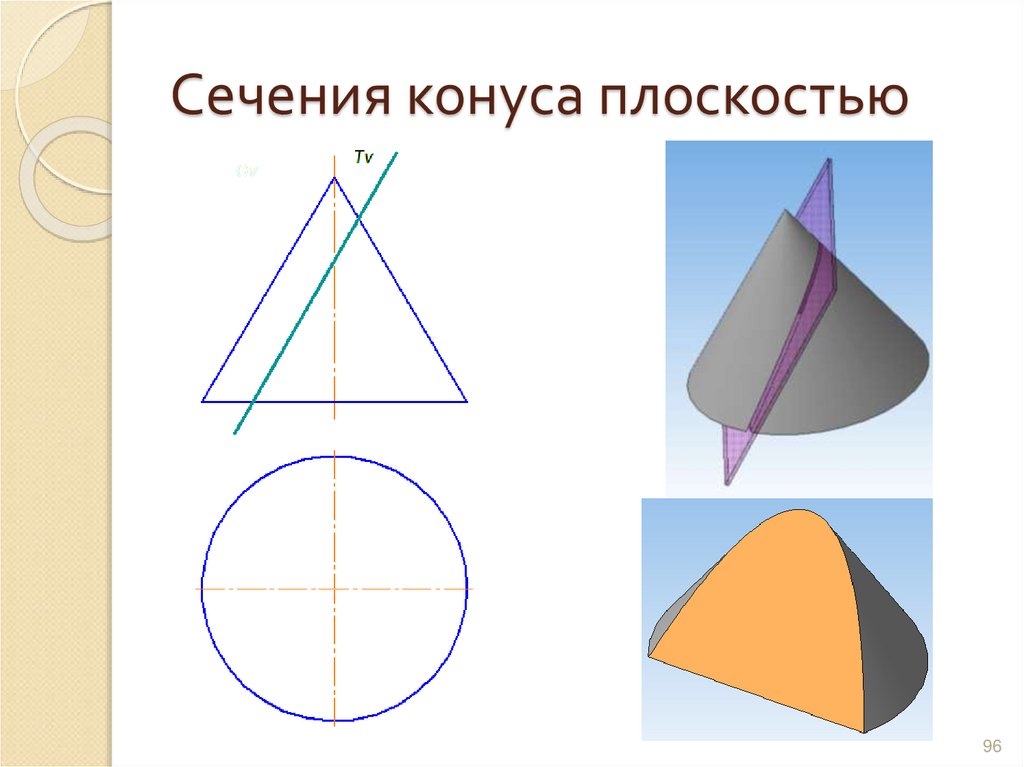
95

96. Сечения конуса плоскостью

96

97. Сечения конуса плоскостью

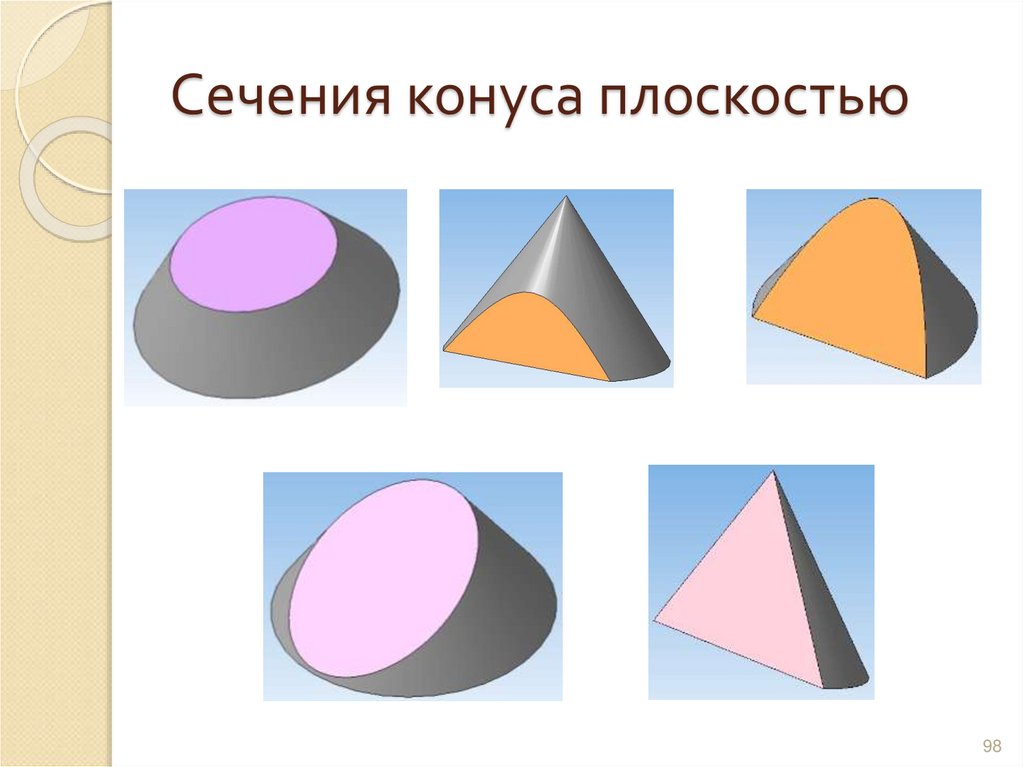
97

98. Сечения конуса плоскостью

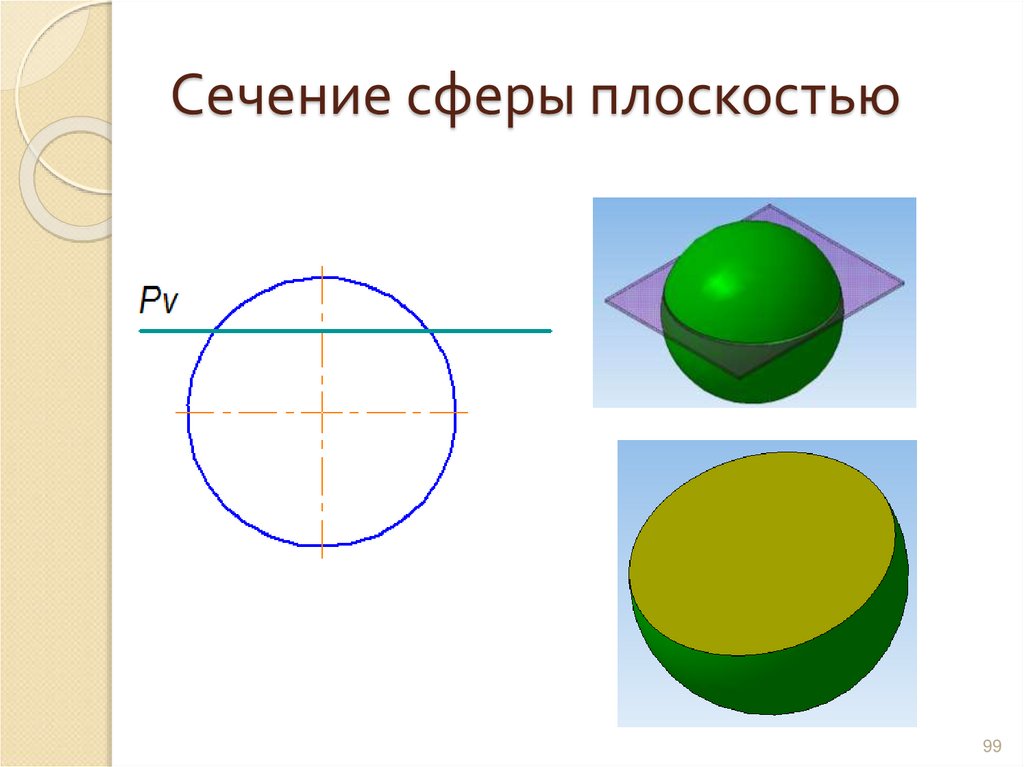
98

99. Сечение сферы плоскостью

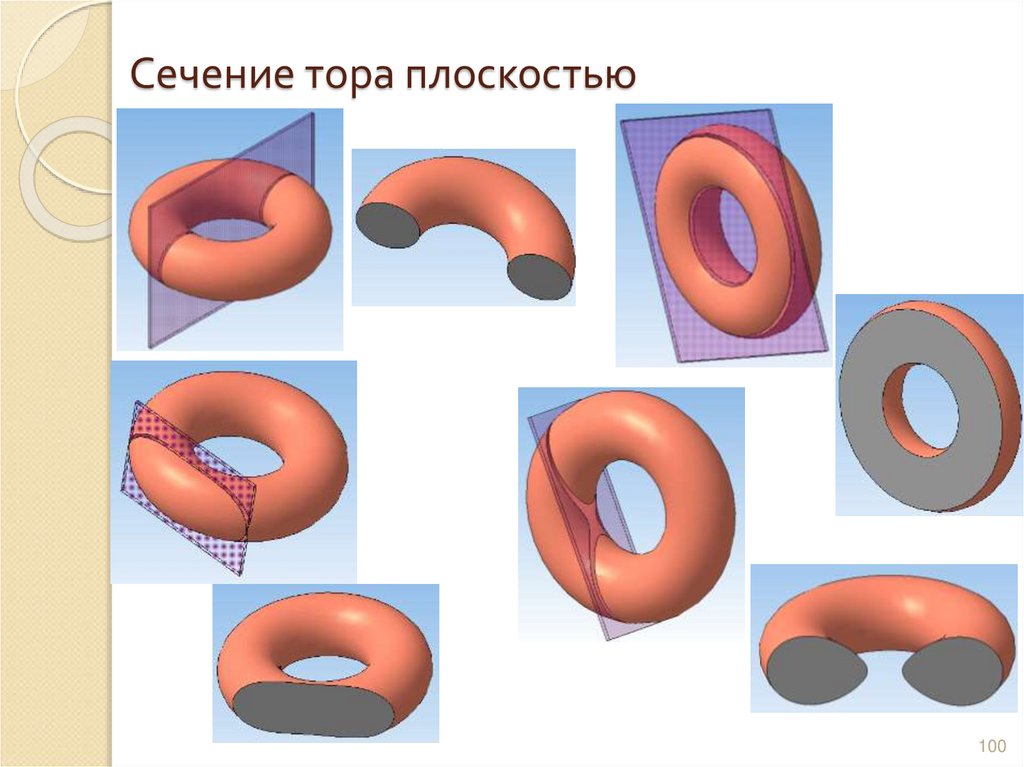
99

100. Сечение тора плоскостью

100

101. Алгоритм построения линии пересечения тела плоскостью

1. Определить форму линии пересечения в
пространстве;
2. Построить характерные точки искомой линии (точки
пересечения с плоскостью ребер многогранника,
контурных образующих кривых поверхностей, точки
изменения видимости, верхние, нижние и др.);
3. Построить промежуточные точки (для уточнения
линии пересечения);
4. Соединить полученные точки прямыми или кривыми
линиями в зависимости от их формы;
5. Определить видимость линии пересечения и
геометрического тела
101

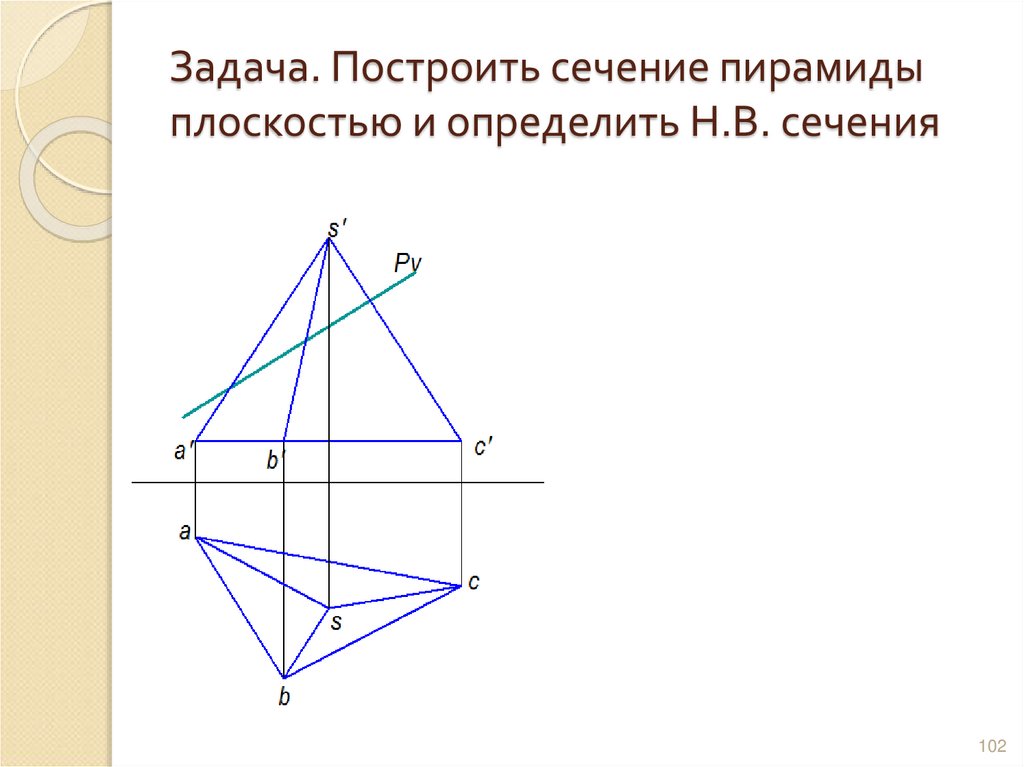
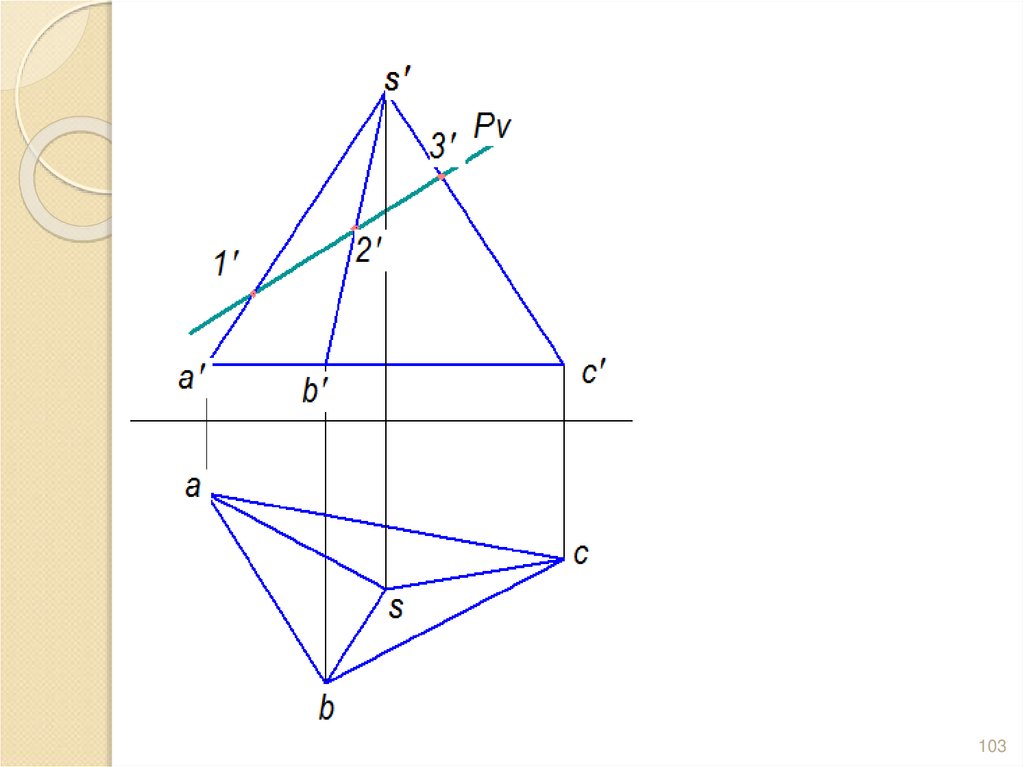
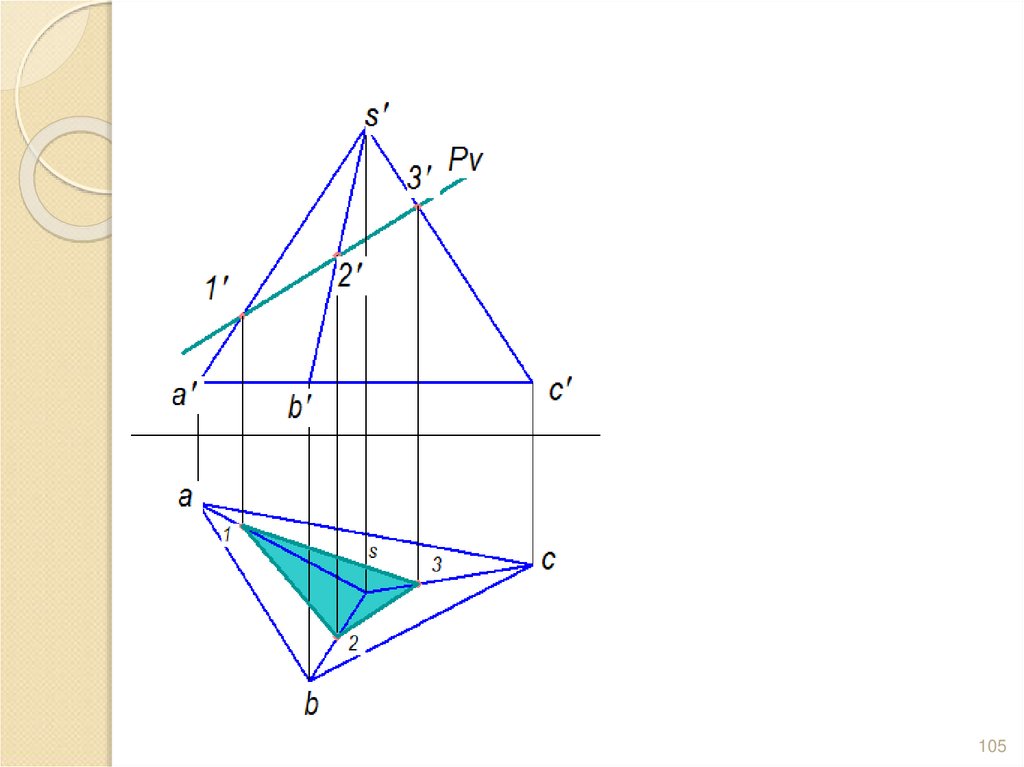
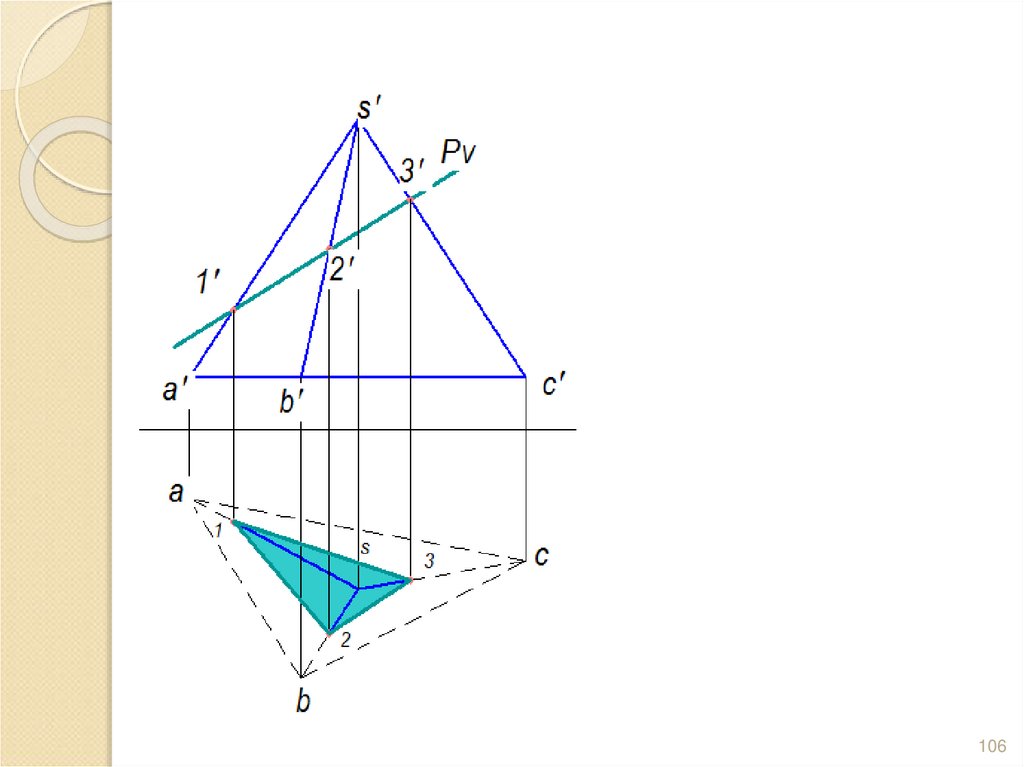
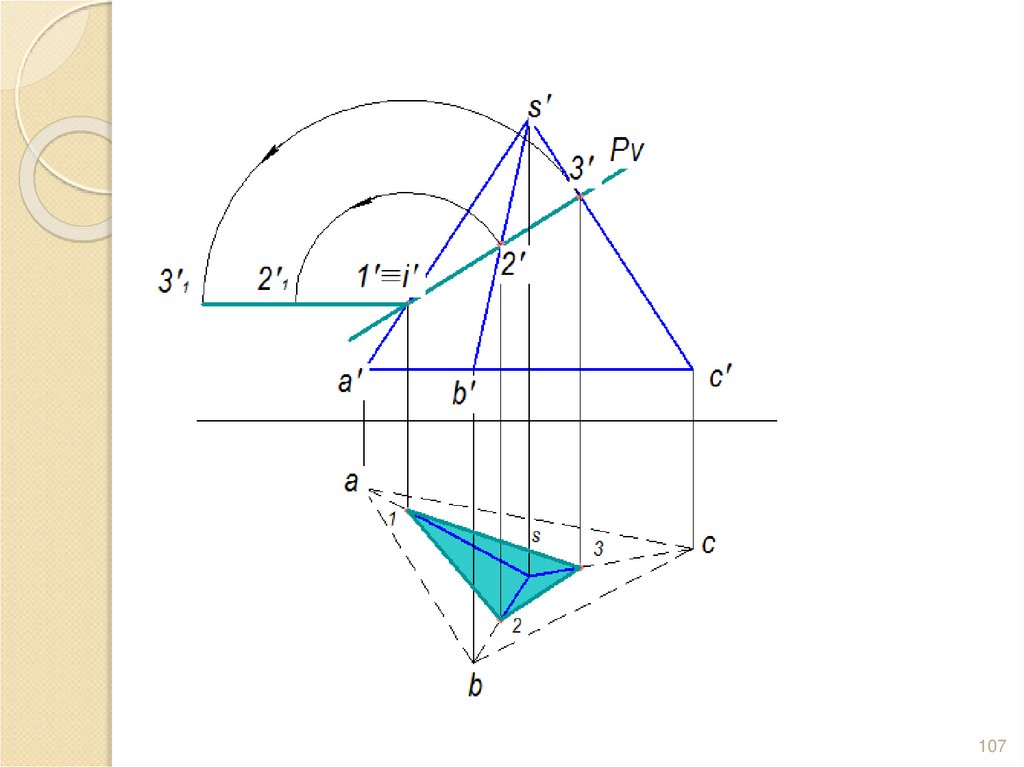
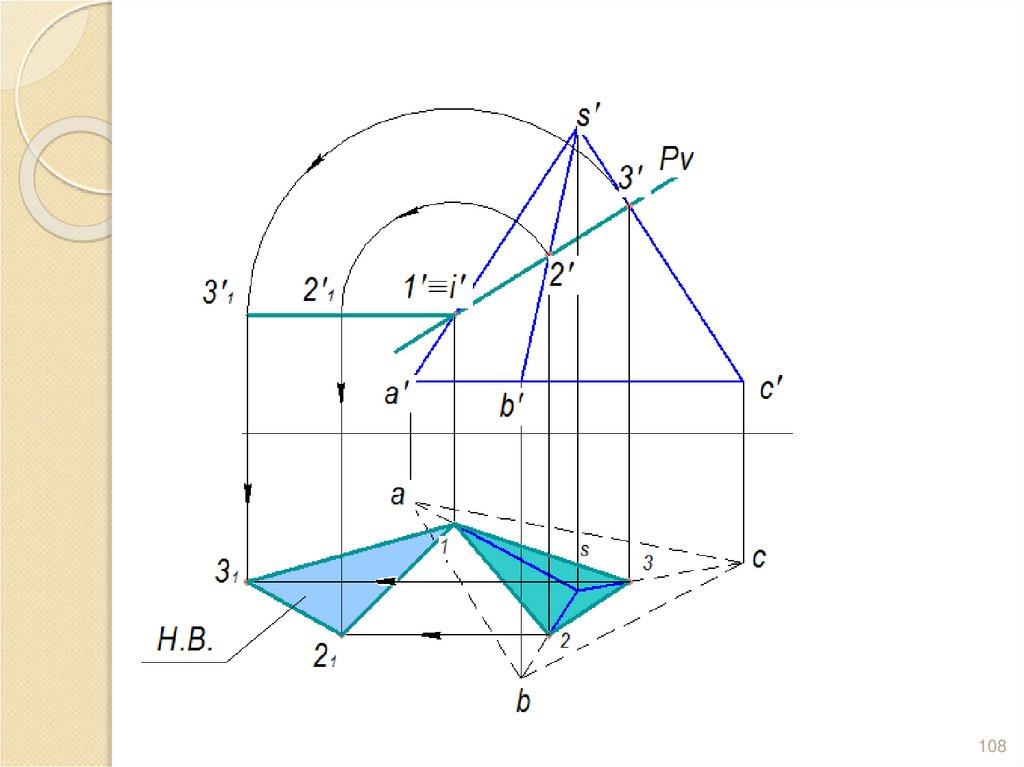
102. Задача. Построить сечение пирамиды плоскостью и определить Н.В. сечения

102

103.

103

104.

104

105.

105

106.

106

107.

107

108.

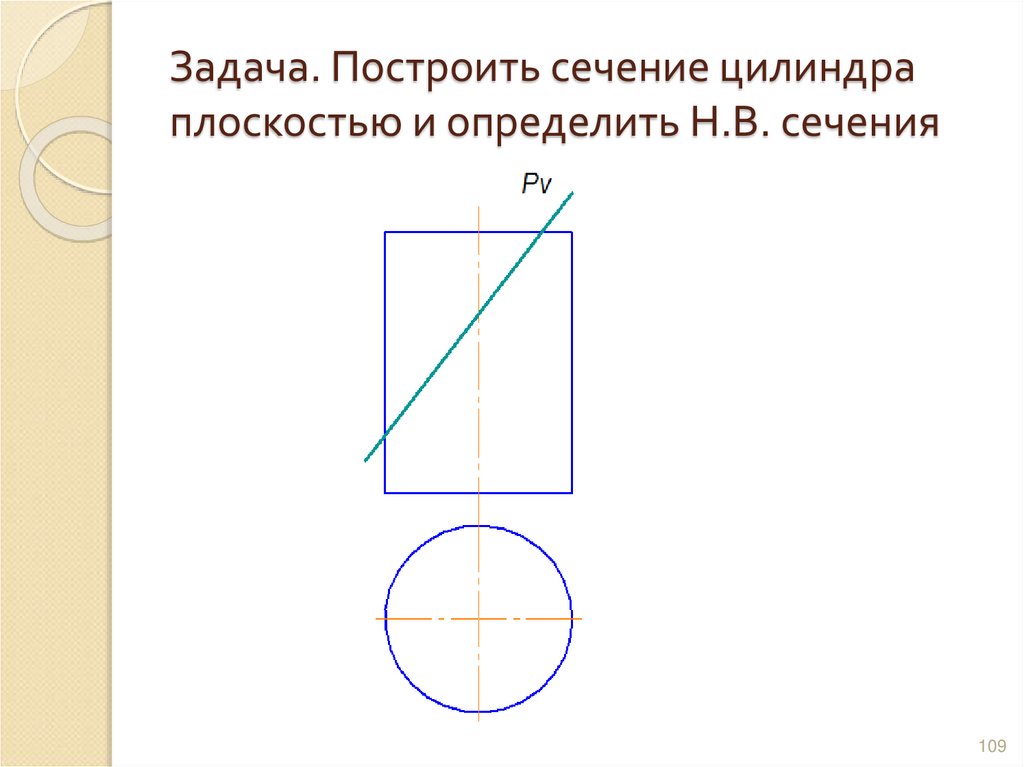
108

109. Задача. Построить сечение цилиндра плоскостью и определить Н.В. сечения

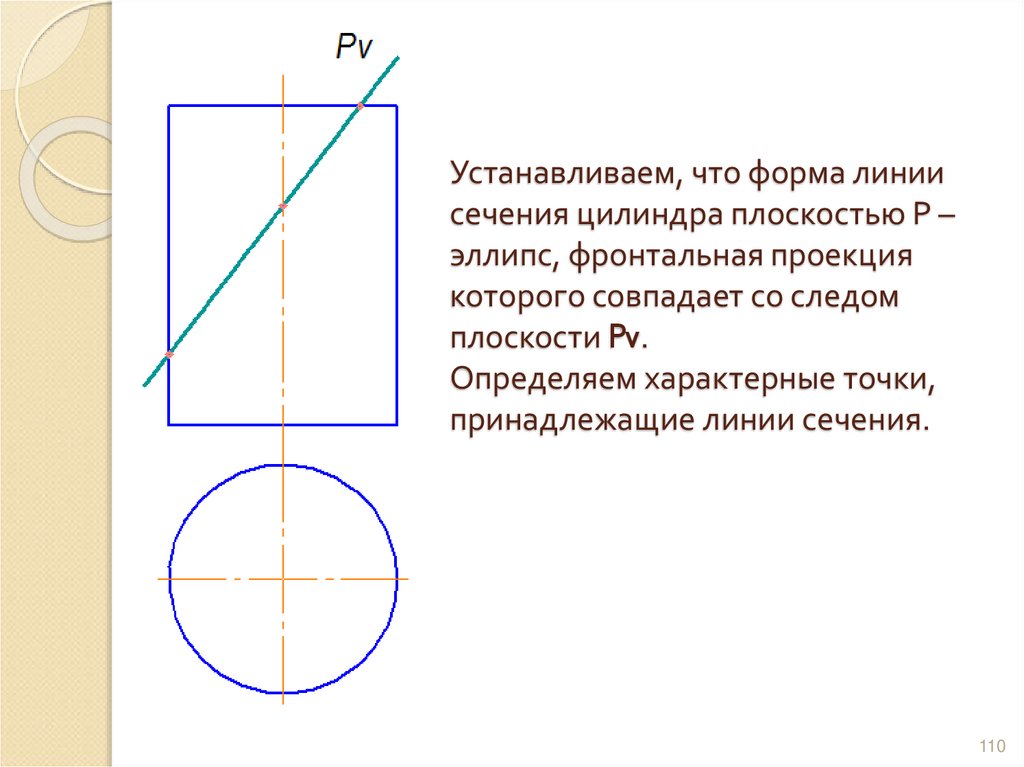
109

110. Устанавливаем, что форма линии сечения цилиндра плоскостью Р – эллипс, фронтальная проекция которого совпадает со следом

плоскости Pv.
Определяем характерные точки,
принадлежащие линии сечения.
110

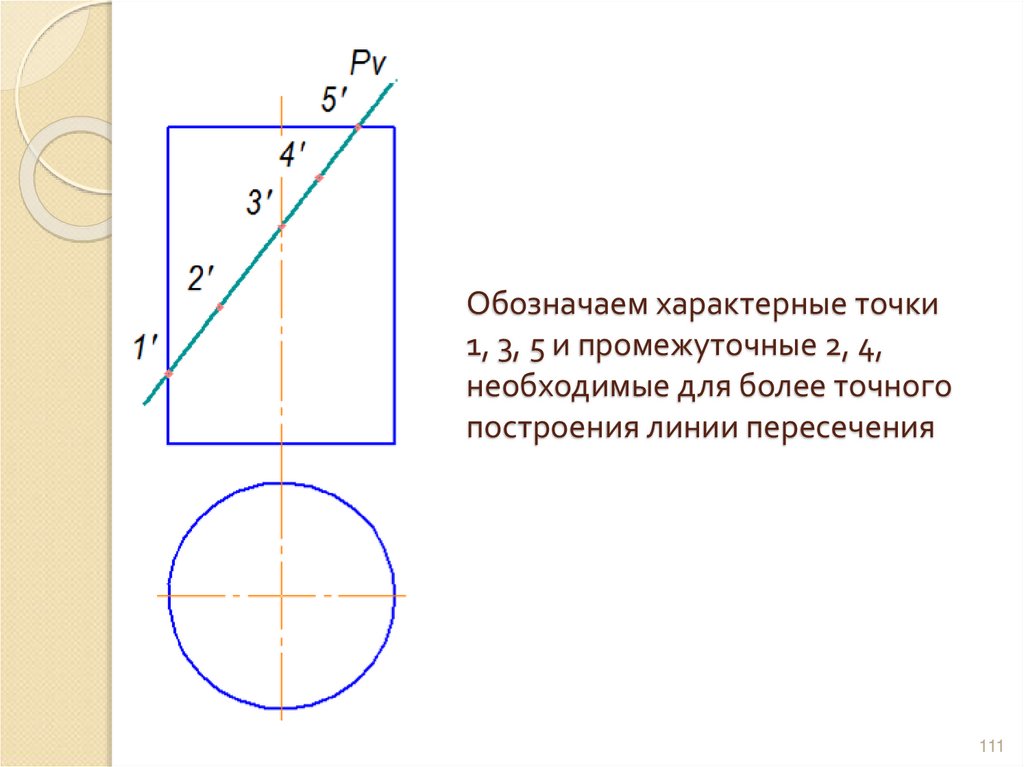
111. Обозначаем характерные точки 1, 3, 5 и промежуточные 2, 4, необходимые для более точного построения линии пересечения

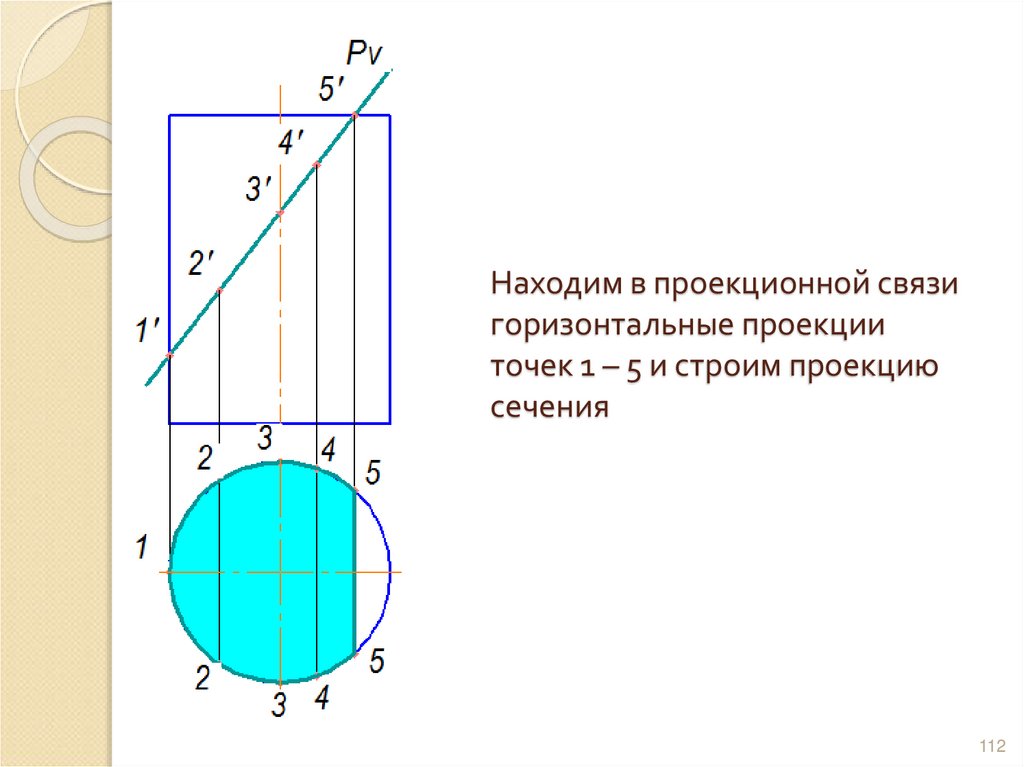
111

112. Находим в проекционной связи горизонтальные проекции точек 1 – 5 и строим проекцию сечения

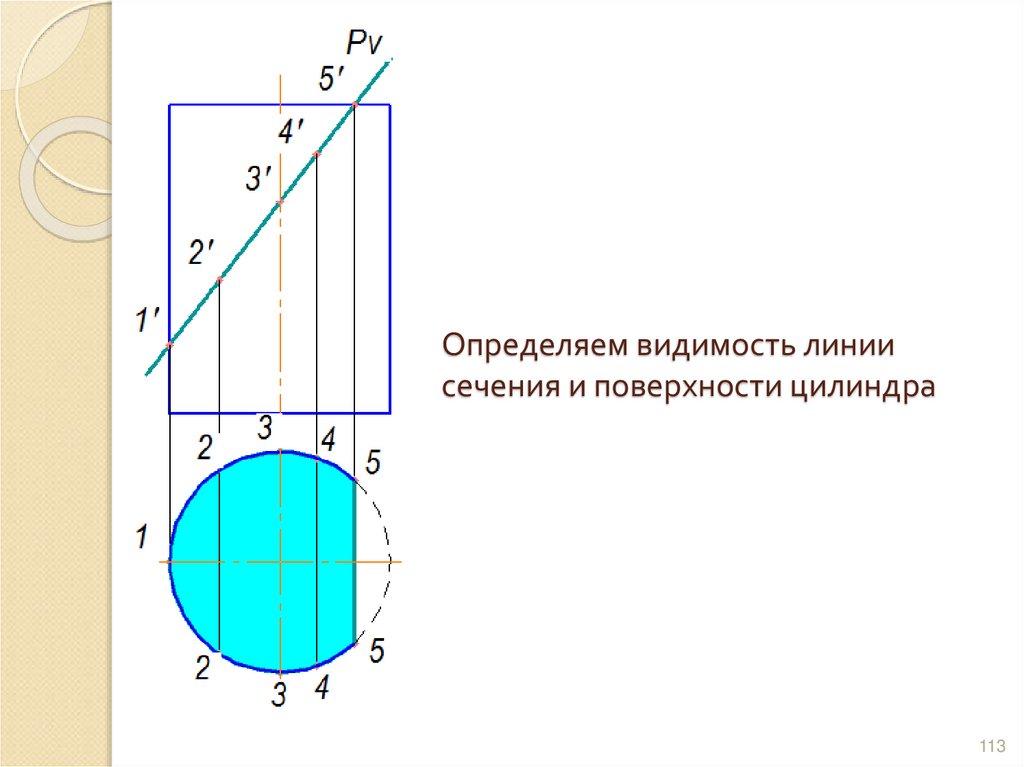
112

113. Определяем видимость линии сечения и поверхности цилиндра

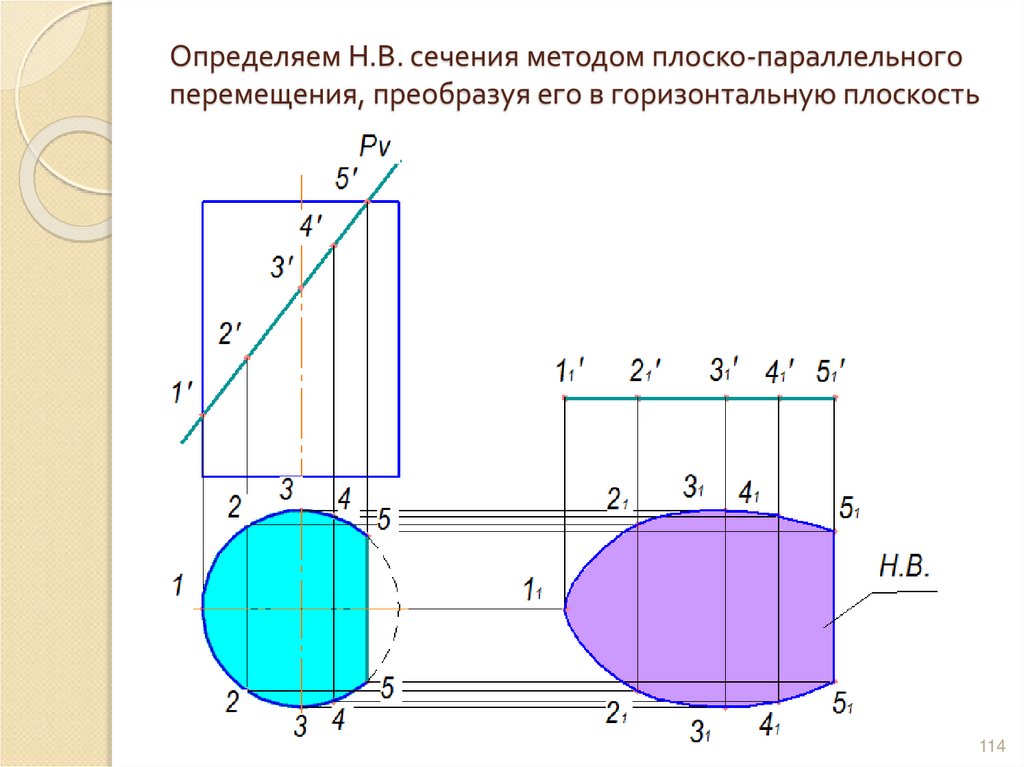
113

114. Определяем Н.В. сечения методом плоско-параллельного перемещения, преобразуя его в горизонтальную плоскость уровня

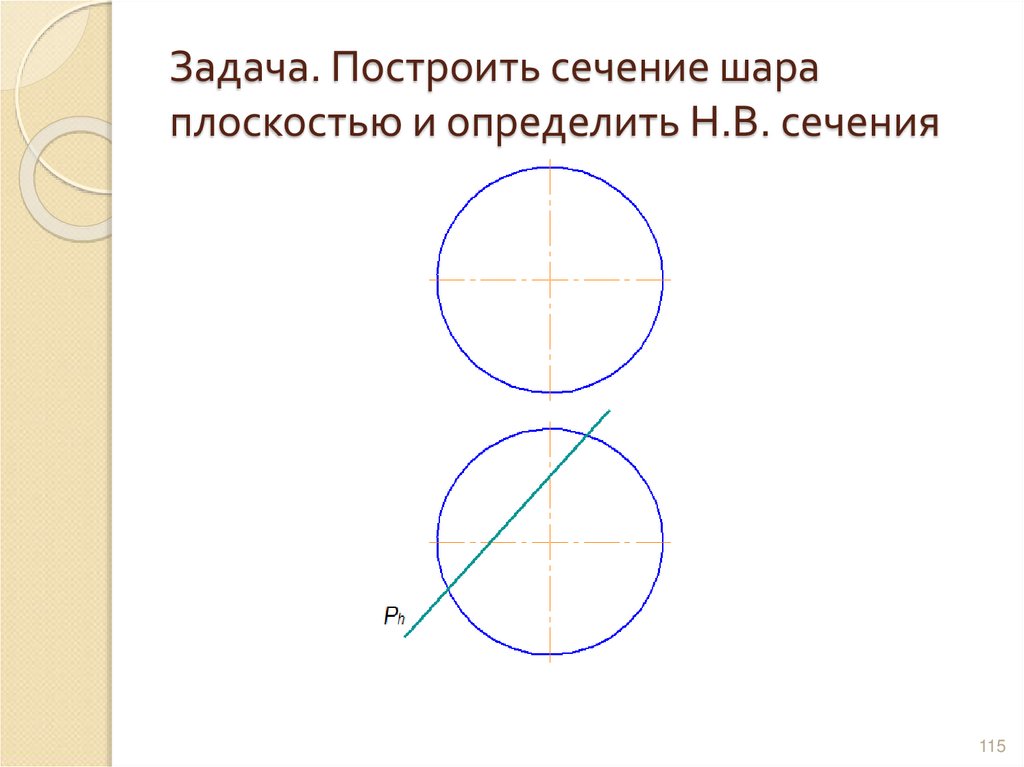
114

115. Задача. Построить сечение шара плоскостью и определить Н.В. сечения

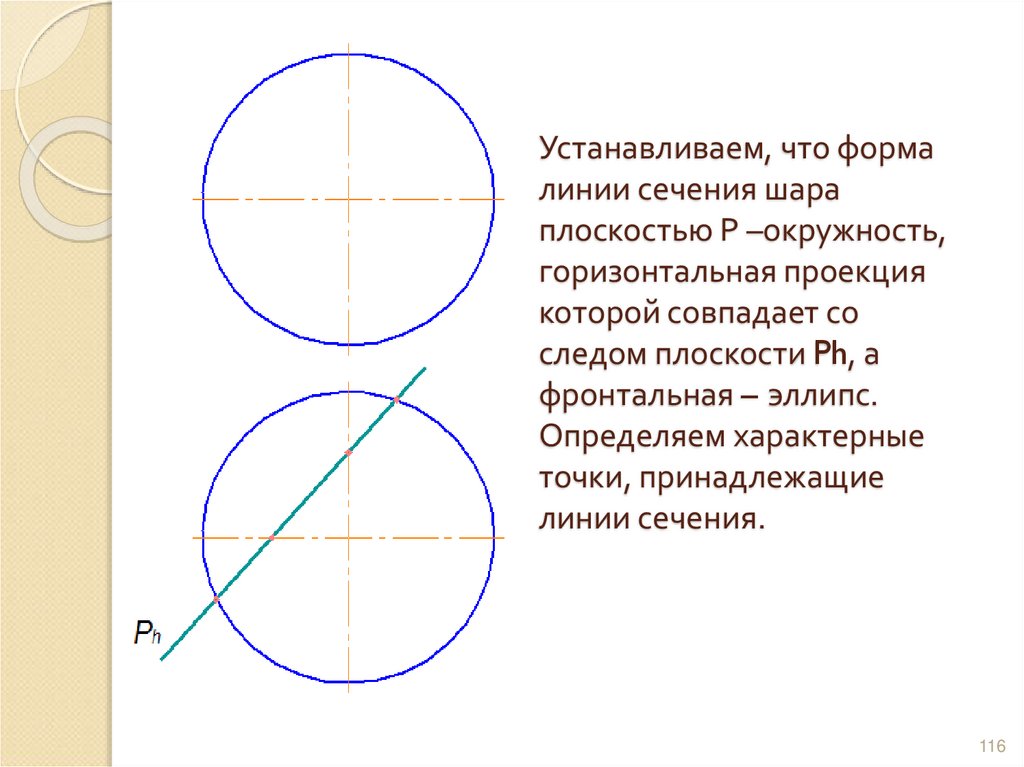
115

116. Устанавливаем, что форма линии сечения шара плоскостью Р –окружность, горизонтальная проекция которой совпадает со следом

плоскости Ph, а
фронтальная – эллипс.
Определяем характерные
точки, принадлежащие
линии сечения.
116

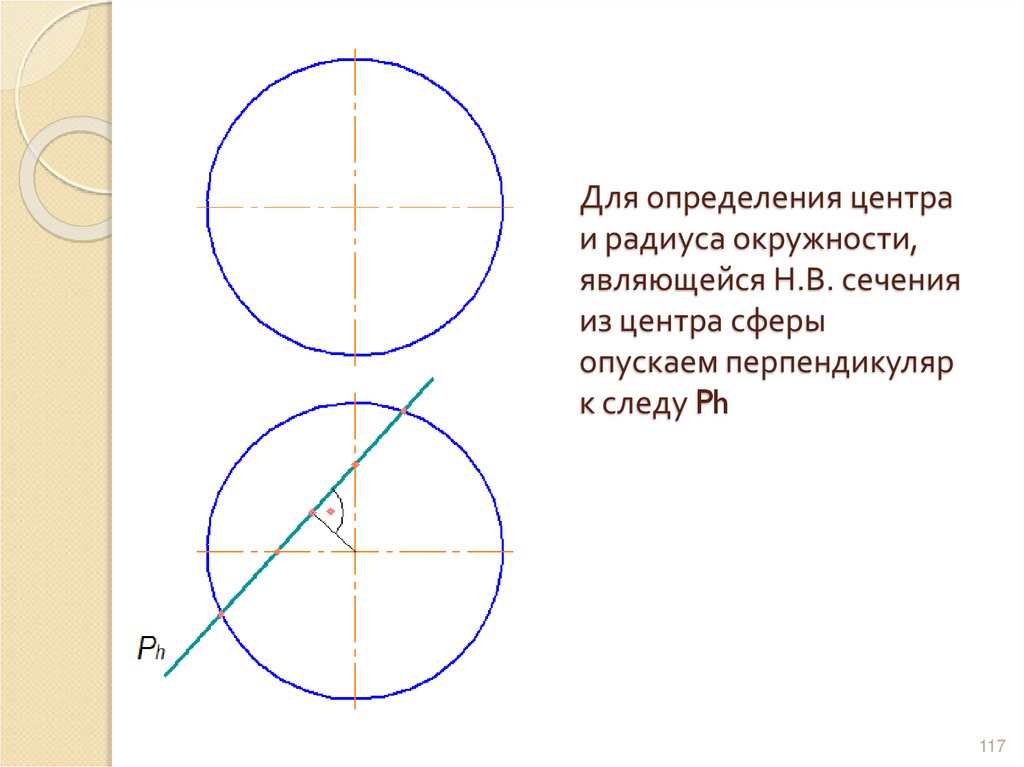
117. Для определения центра и радиуса окружности, являющейся Н.В. сечения из центра сферы опускаем перпендикуляр к следу Ph

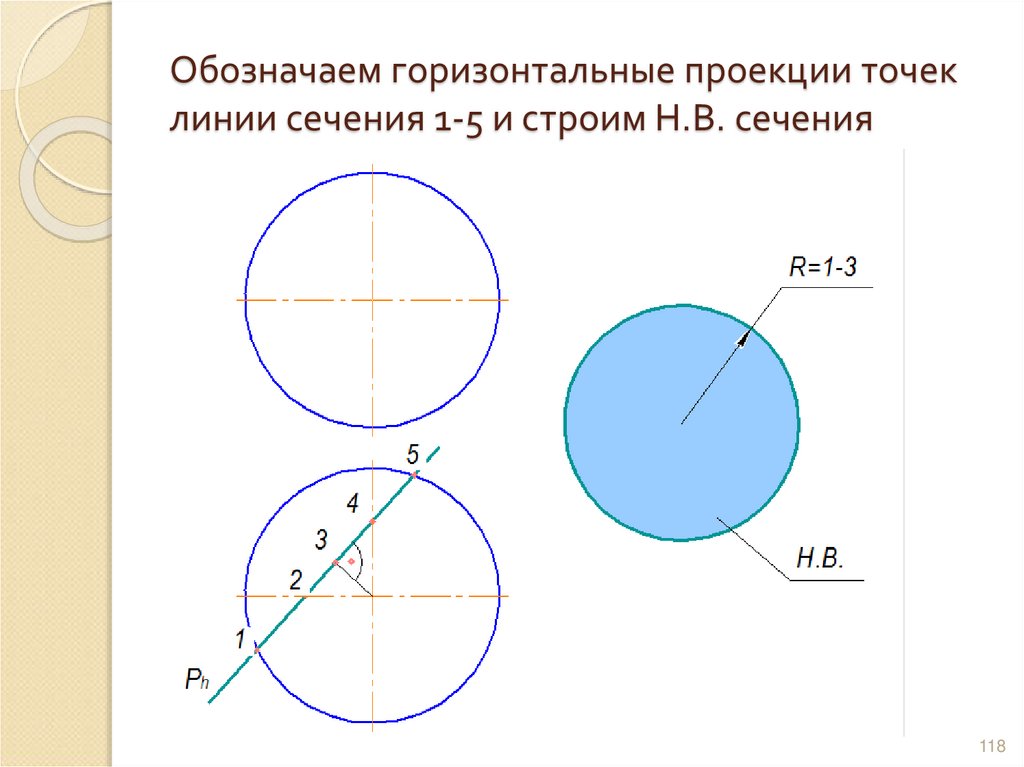
117

118. Обозначаем горизонтальные проекции точек линии сечения 1-5 и строим Н.В. сечения

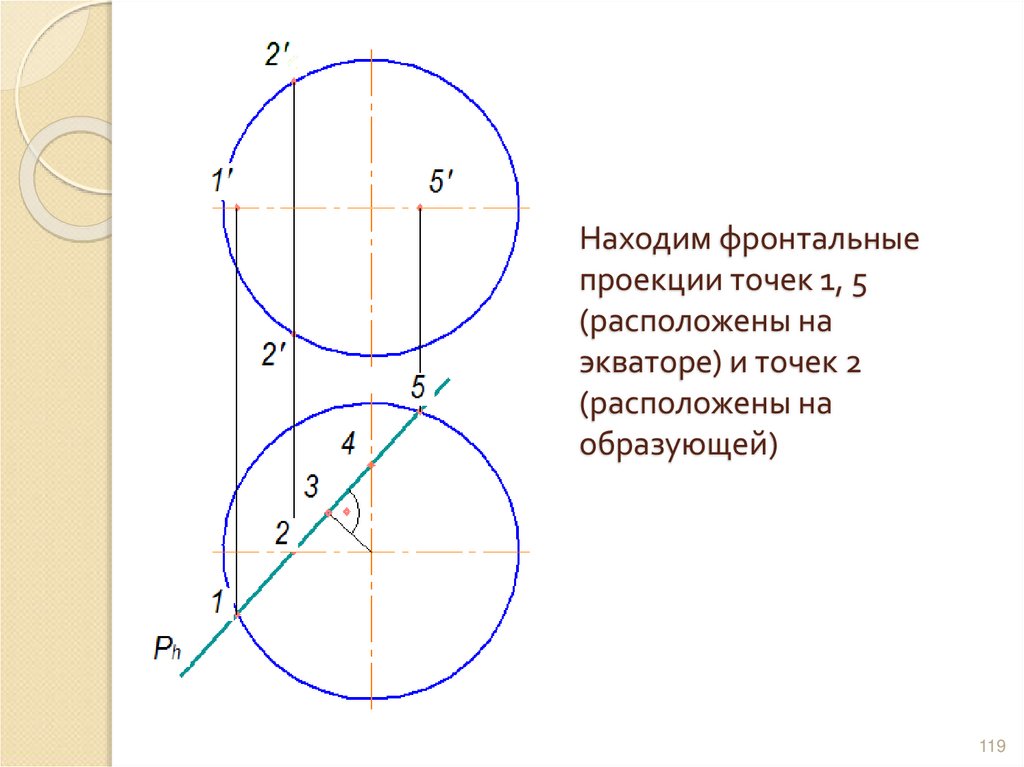
118

119. Находим фронтальные проекции точек 1, 5 (расположены на экваторе) и точек 2 (расположены на образующей)

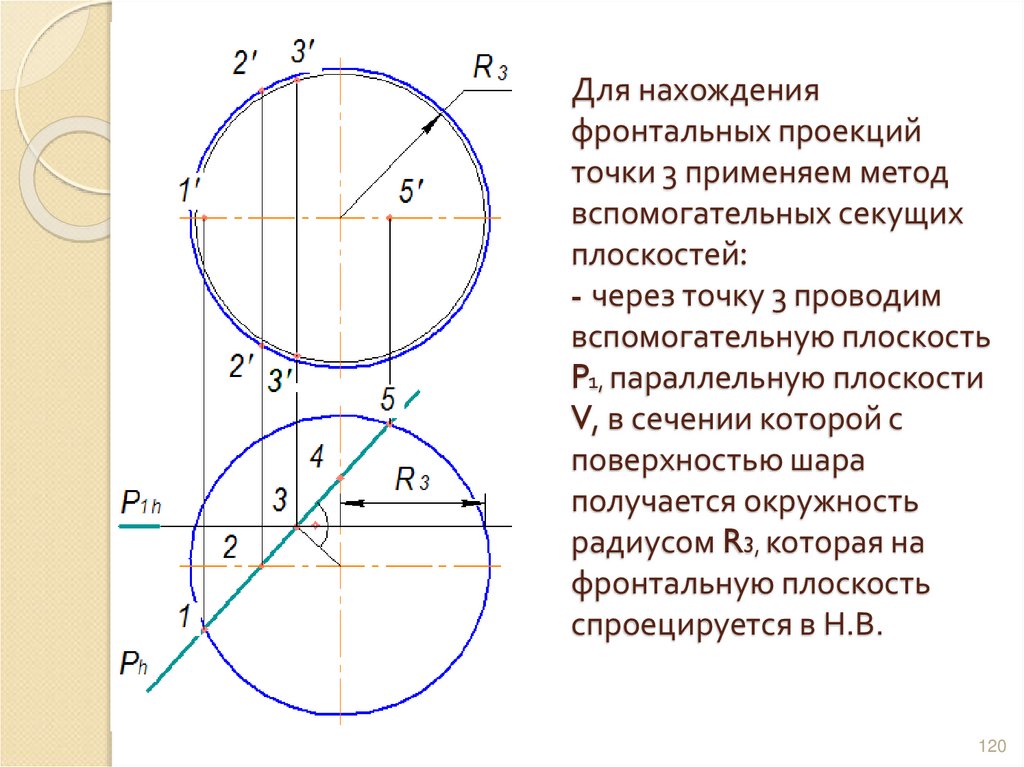
119

120. Для нахождения фронтальных проекций точки 3 применяем метод вспомогательных секущих плоскостей: - через точку 3 проводим

вспомогательную плоскость
P1, параллельную плоскости
V, в сечении которой с
поверхностью шара
получается окружность
радиусом R3, которая на
фронтальную плоскость
спроецируется в Н.В.
120

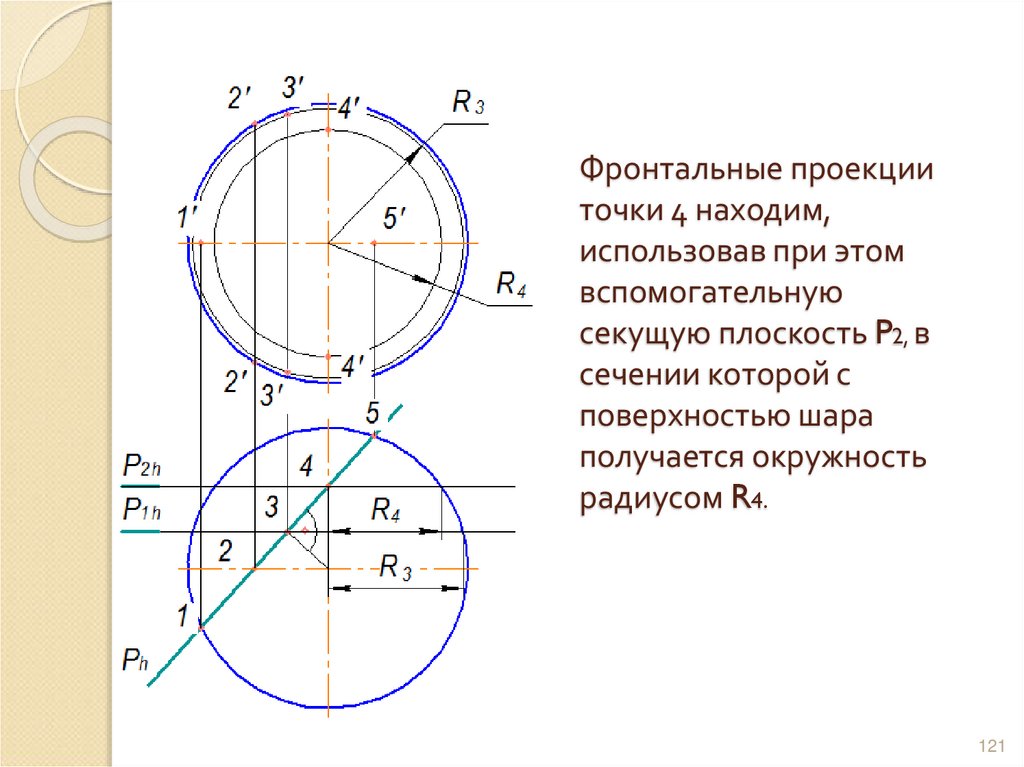
121. Фронтальные проекции точки 4 находим, использовав при этом вспомогательную секущую плоскость P2, в сечении которой с

поверхностью шара
получается окружность
радиусом R4.
121

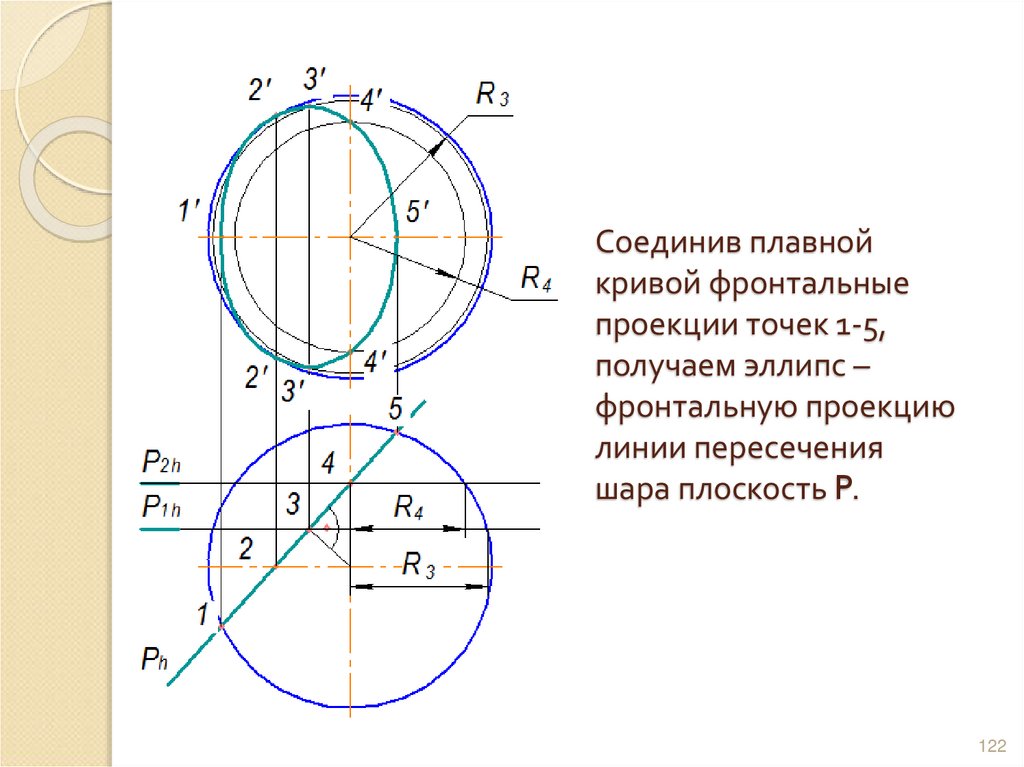
122. Соединив плавной кривой фронтальные проекции точек 1-5, получаем эллипс – фронтальную проекцию линии пересечения шара плоскость

P.
122

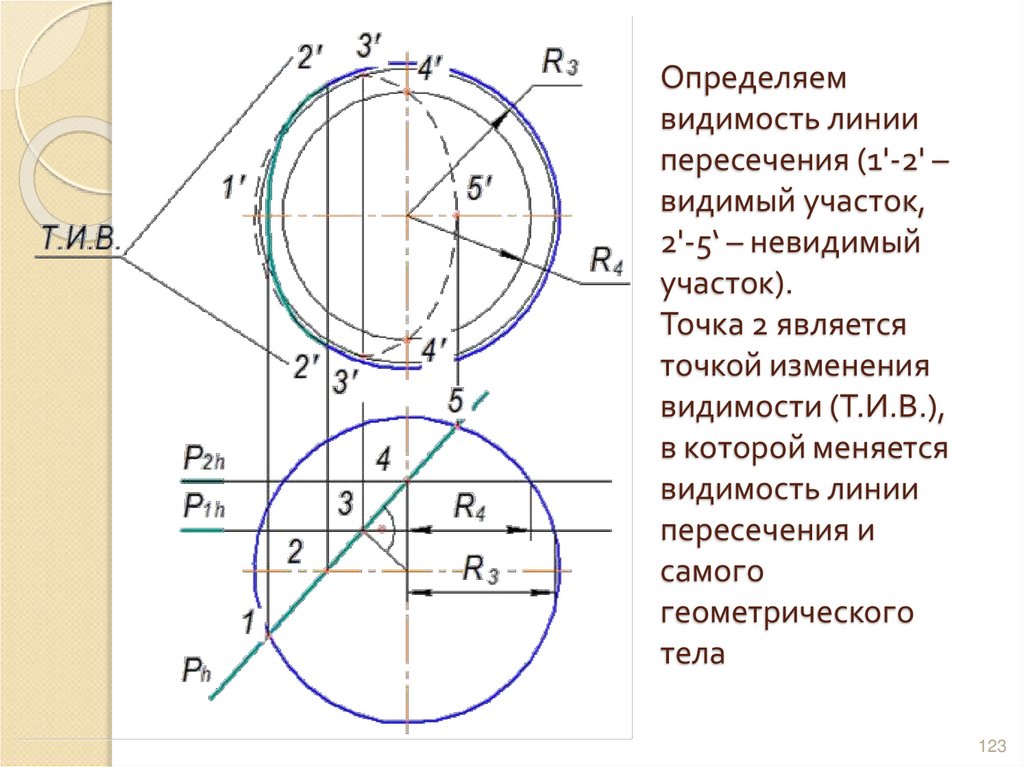
123. Определяем видимость линии пересечения (1'-2' – видимый участок, 2'-5‘ – невидимый участок). Точка 2 является точкой изменения

видимости (Т.И.В.),
в которой меняется
видимость линии
пересечения и
самого
геометрического
тела
123

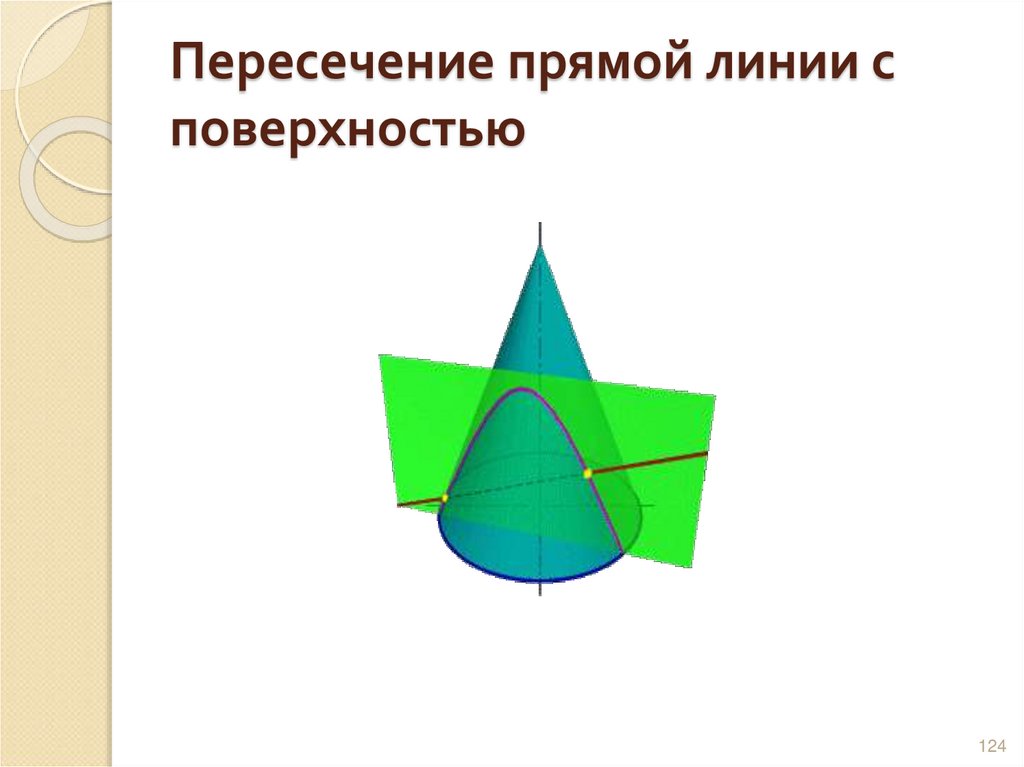
124. Пересечение прямой линии с поверхностью

124

125. Взаимное пересечение поверхностей геометрических тел

Способы построения линии пересечения
поверхностей:
- cпособ сечений вспомогательными
секущими плоскостями;
- способ сечений вспомогательными
секущими сферами.
125

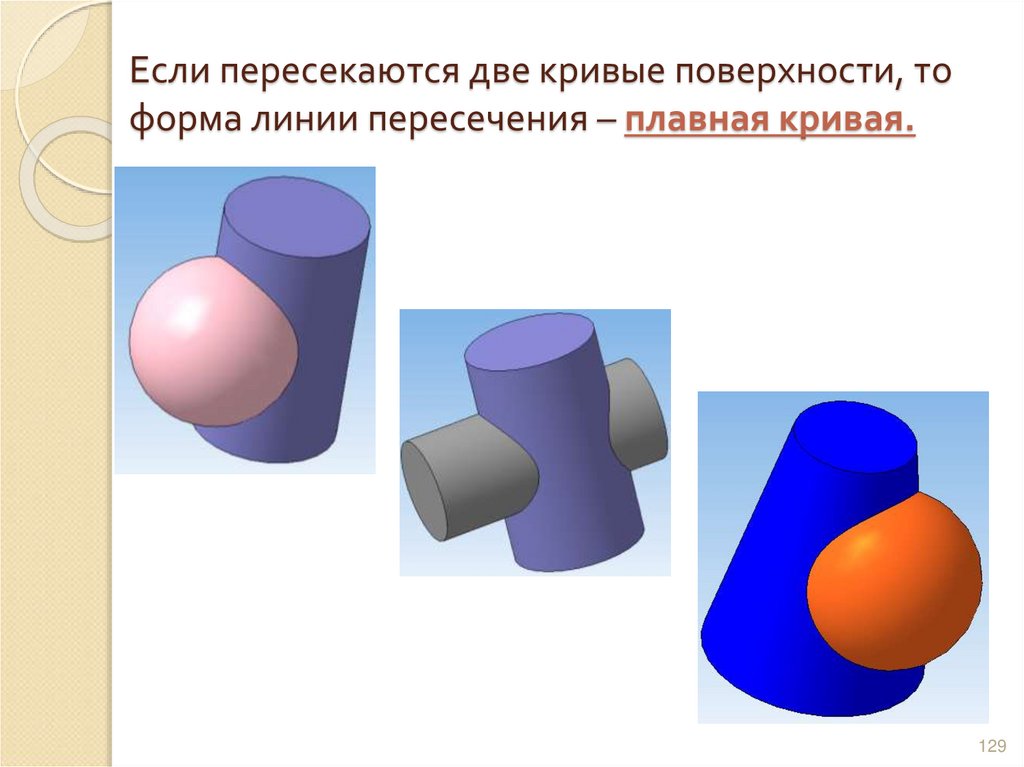
126. Форма линии пересечения зависит от пересекающихся поверхностей:

Если пересекаются две многогранные
поверхности, то форма линии
пересечения – ломаная прямая.
Если пересекаются многогранная и
кривая поверхности, то форма линии
пересечения – плавная кривая с точками
излома на ребрах многогранника.
Если пересекаются две кривые
поверхности, то форма линии
пересечения – плавная кривая.
126

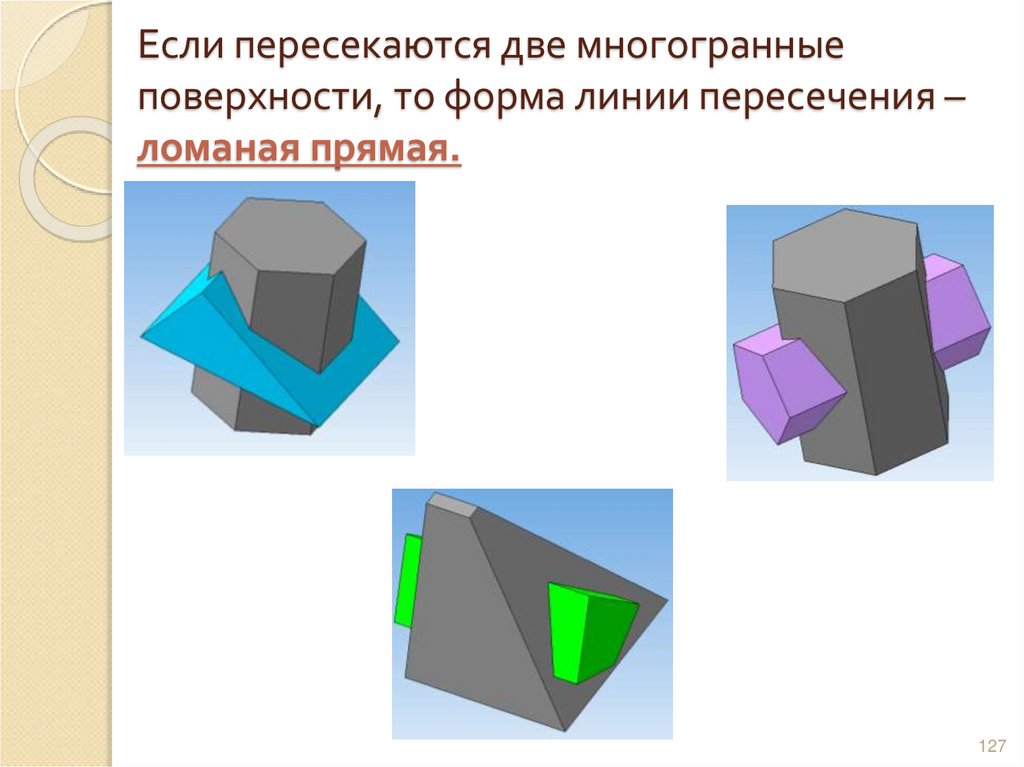
127. Если пересекаются две многогранные поверхности, то форма линии пересечения – ломаная прямая.

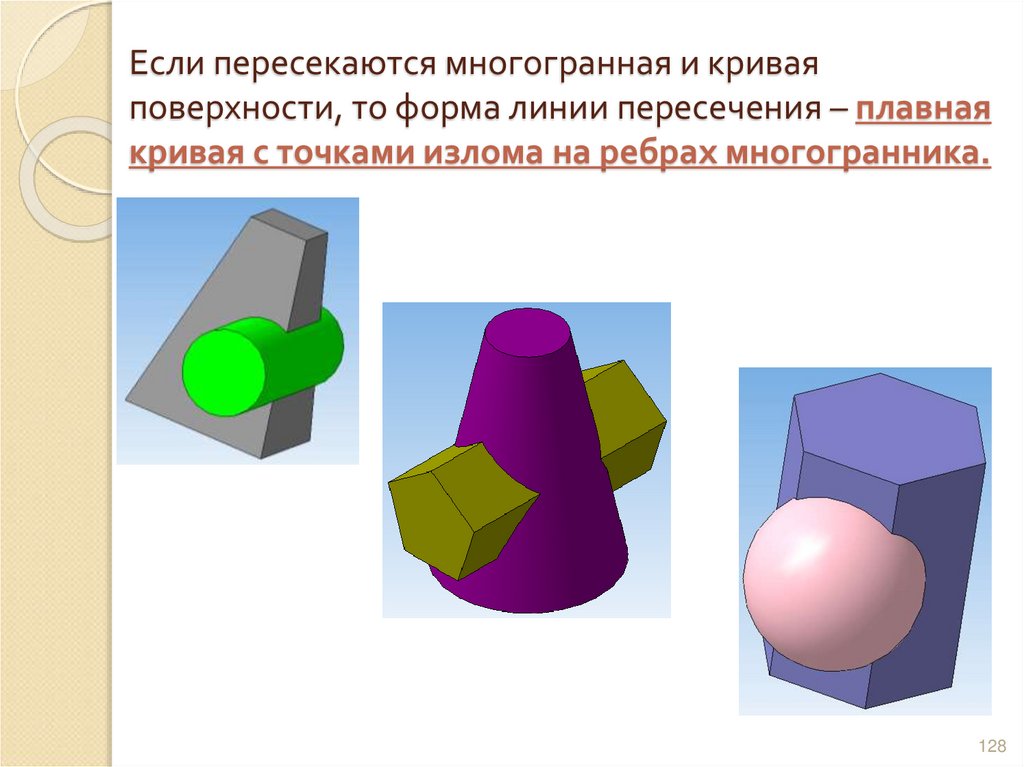
127

128. Если пересекаются многогранная и кривая поверхности, то форма линии пересечения – плавная кривая с точками излома на ребрах

многогранника.
128

129. Если пересекаются две кривые поверхности, то форма линии пересечения – плавная кривая.

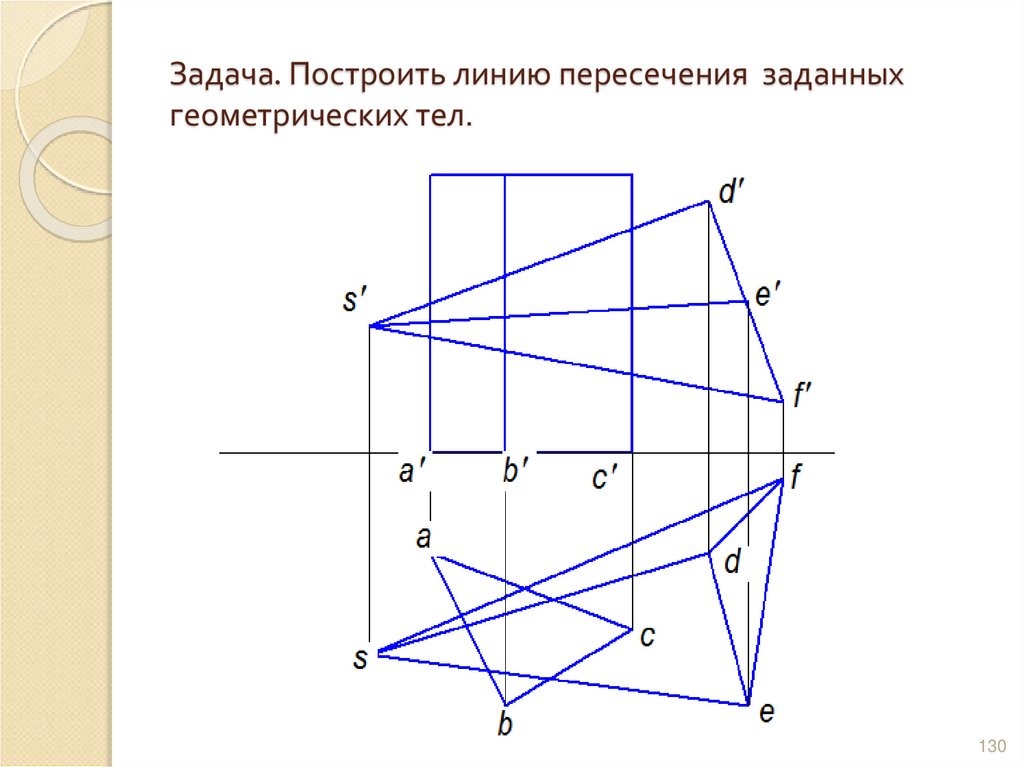
129

130. Задача. Построить линию пересечения заданных геометрических тел.

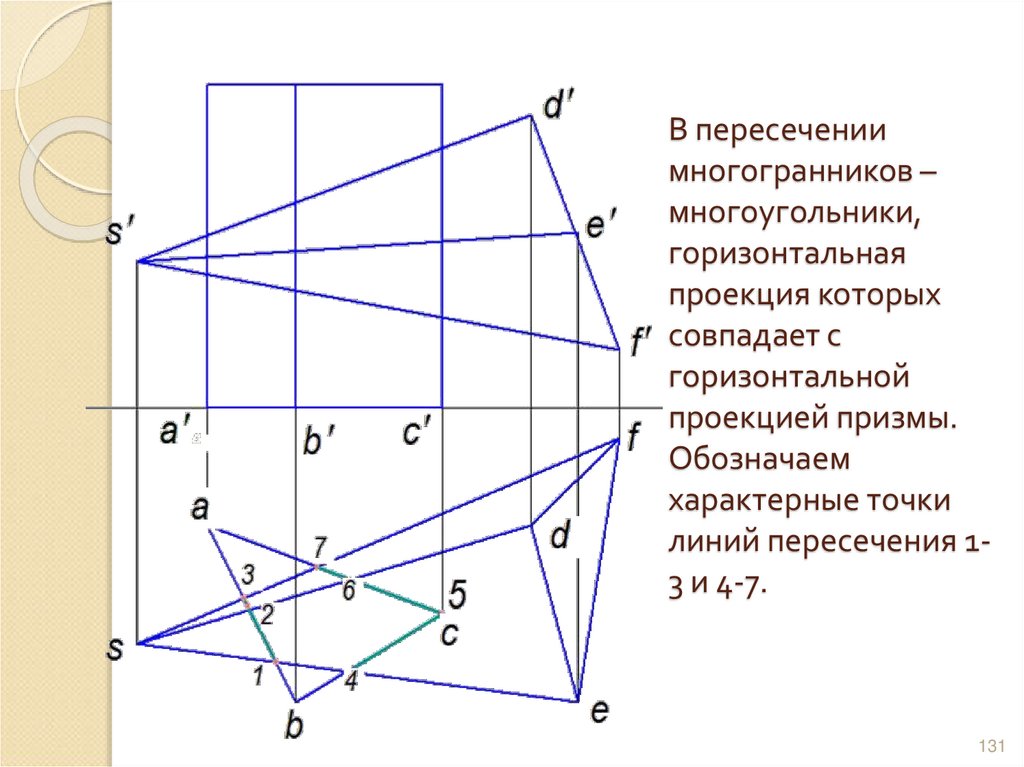
130

131. В пересечении многогранников – многоугольники, горизонтальная проекция которых совпадает с горизонтальной проекцией призмы.

Обозначаем
характерные точки
линий пересечения 13 и 4-7.
131

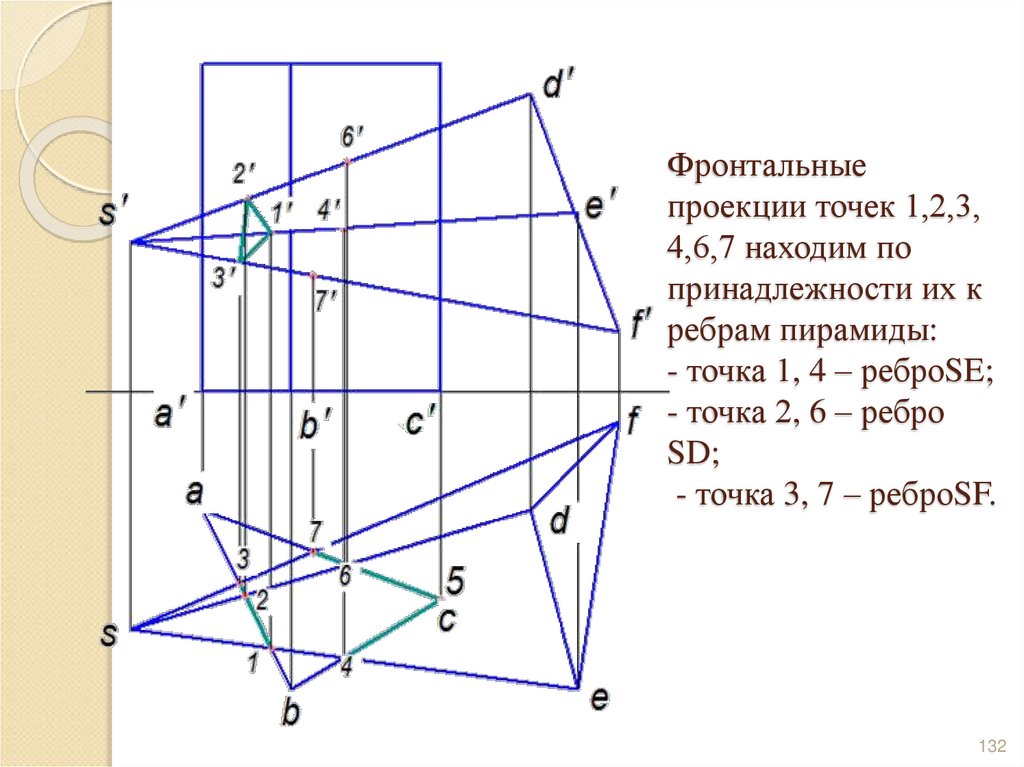
132. Фронтальные проекции точек 1,2,3, 4,6,7 находим по принадлежности их к ребрам пирамиды: - точка 1, 4 – реброSE; - точка 2, 6 –

ребро
SD;
- точка 3, 7 – реброSF.
132

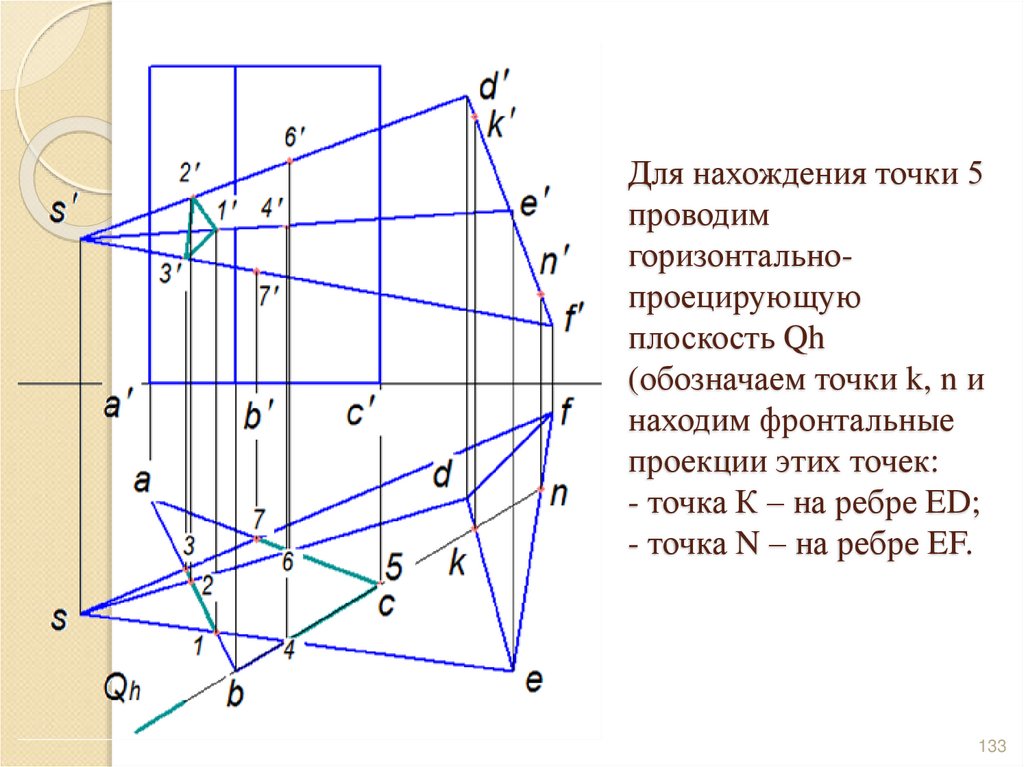
133. Для нахождения точки 5 проводим горизонтально-проецирующую плоскость Qh (обозначаем точки k, n и находим фронтальные проекции

Для нахождения точки 5
проводим
горизонтальнопроецирующую
плоскость Qh
(обозначаем точки k, n и
находим фронтальные
проекции этих точек:
- точка К – на ребре ED;
- точка N – на ребре EF.
133

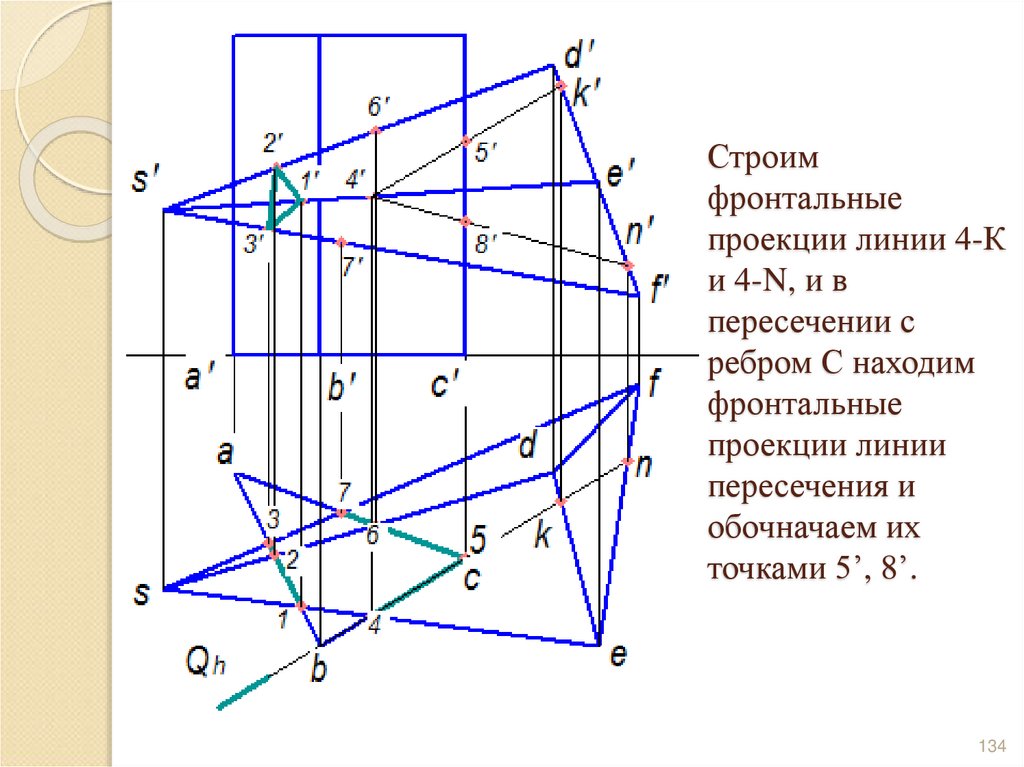
134. Строим фронтальные проекции линии 4-К и 4-N, и в пересечении с ребром С находим фронтальные проекции линии пересечения и

обочначаем их
точками 5’, 8’.
134

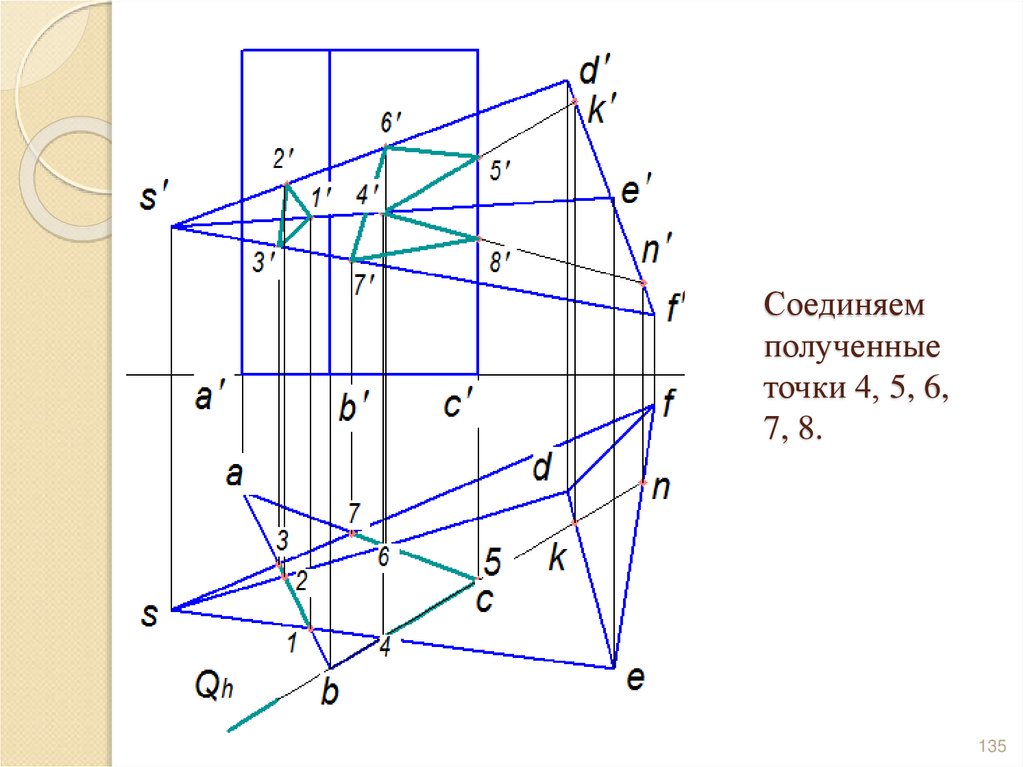
135. Соединяем полученные точки 4, 5, 6, 7, 8.

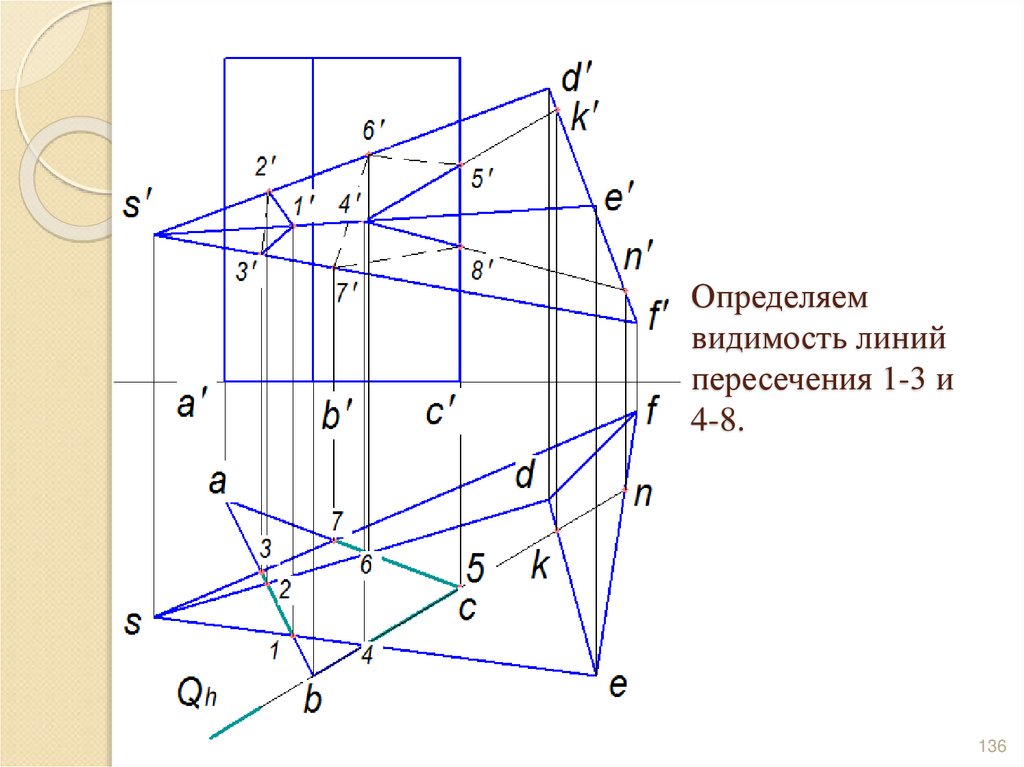
135

136. Определяем видимость линий пересечения 1-3 и 4-8.

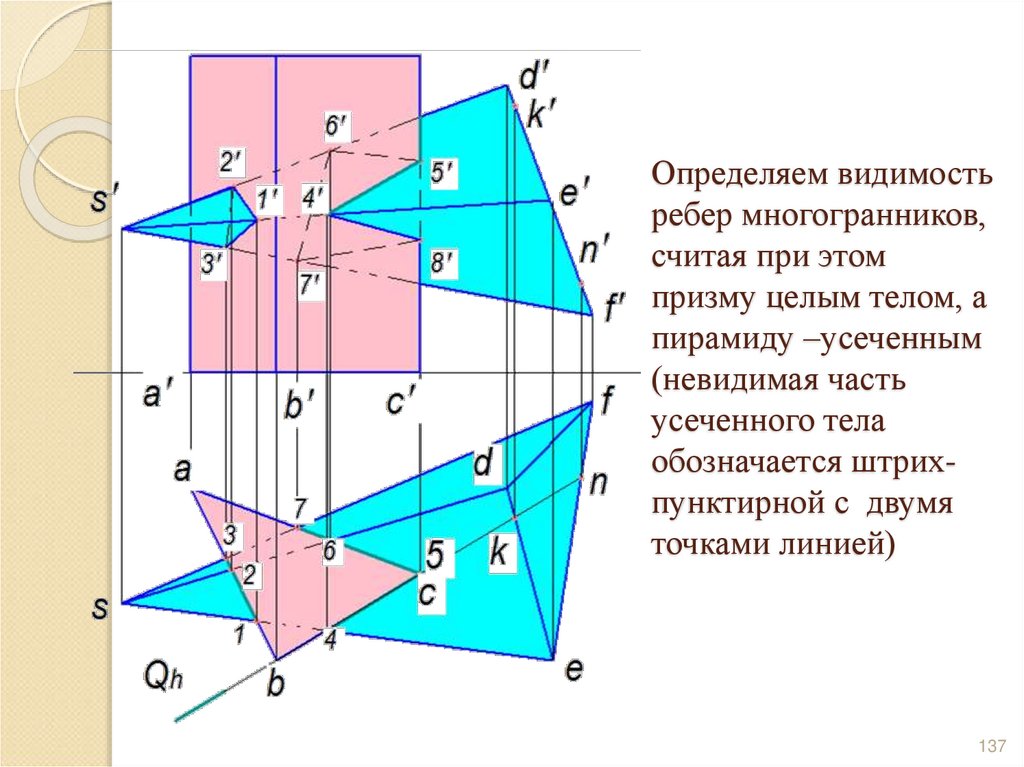
136

137. Определяем видимость ребер многогранников, считая при этом призму целым телом, а пирамиду –усеченным (невидимая часть

усеченного тела
обозначается штрихпунктирной с двумя
точками линией)
137

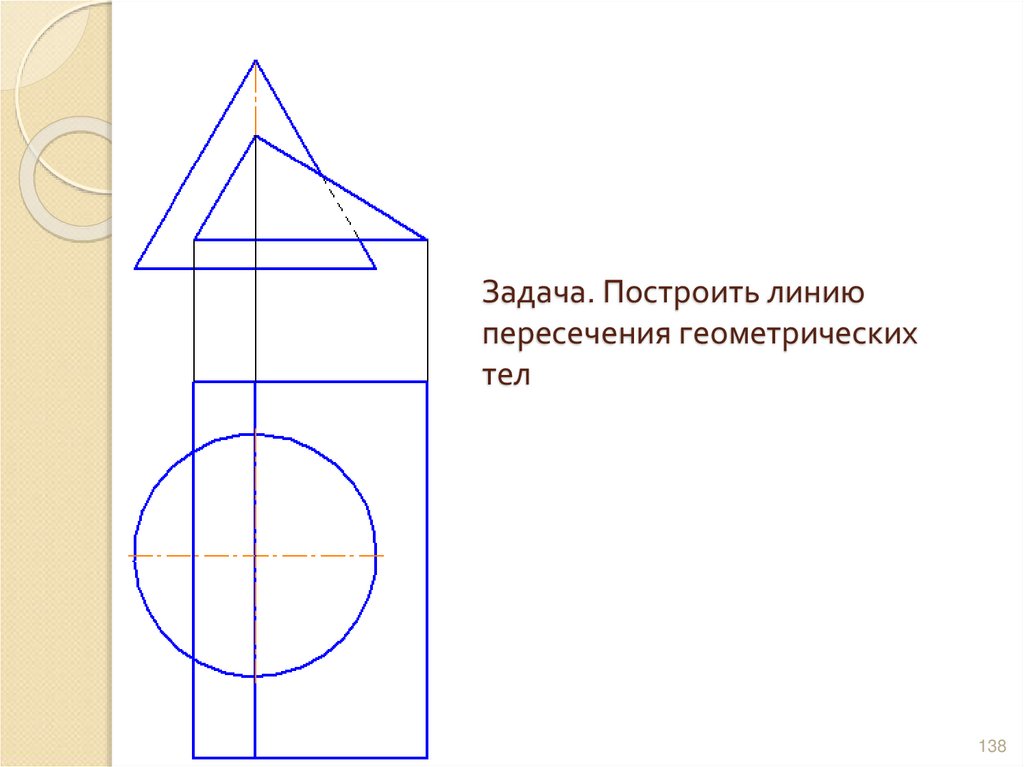
138. Задача. Построить линию пересечения геометрических тел

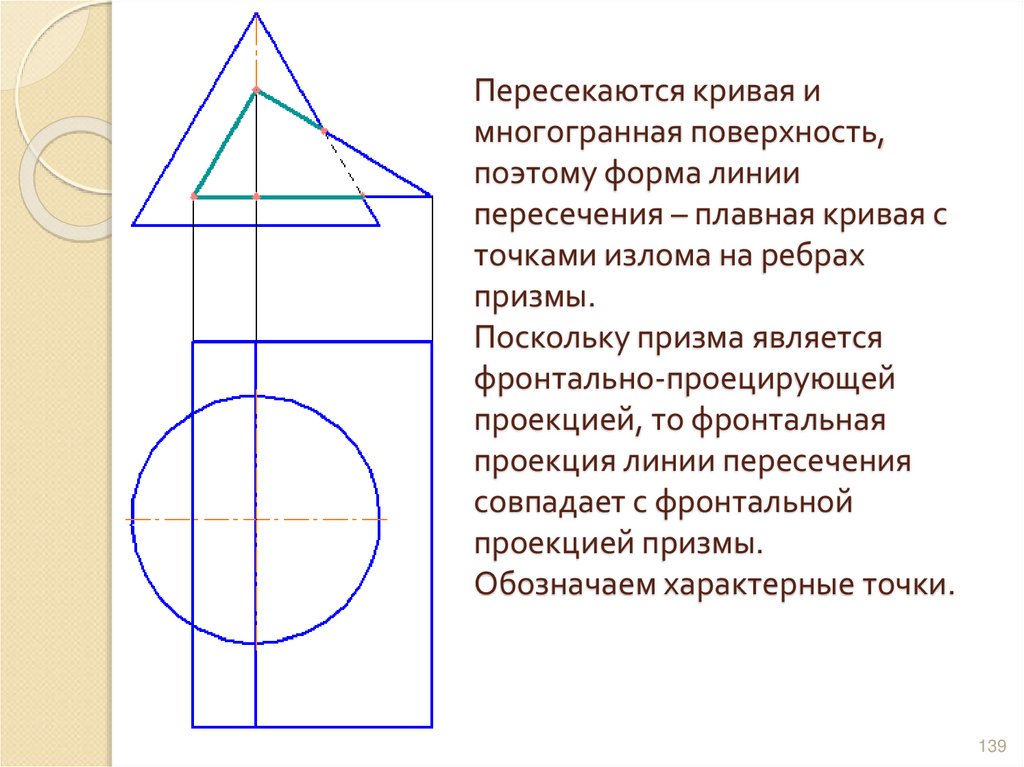
138

139. Пересекаются кривая и многогранная поверхность, поэтому форма линии пересечения – плавная кривая с точками излома на ребрах

призмы.
Поскольку призма является
фронтально-проецирующей
проекцией, то фронтальная
проекция линии пересечения
совпадает с фронтальной
проекцией призмы.
Обозначаем характерные точки.
139

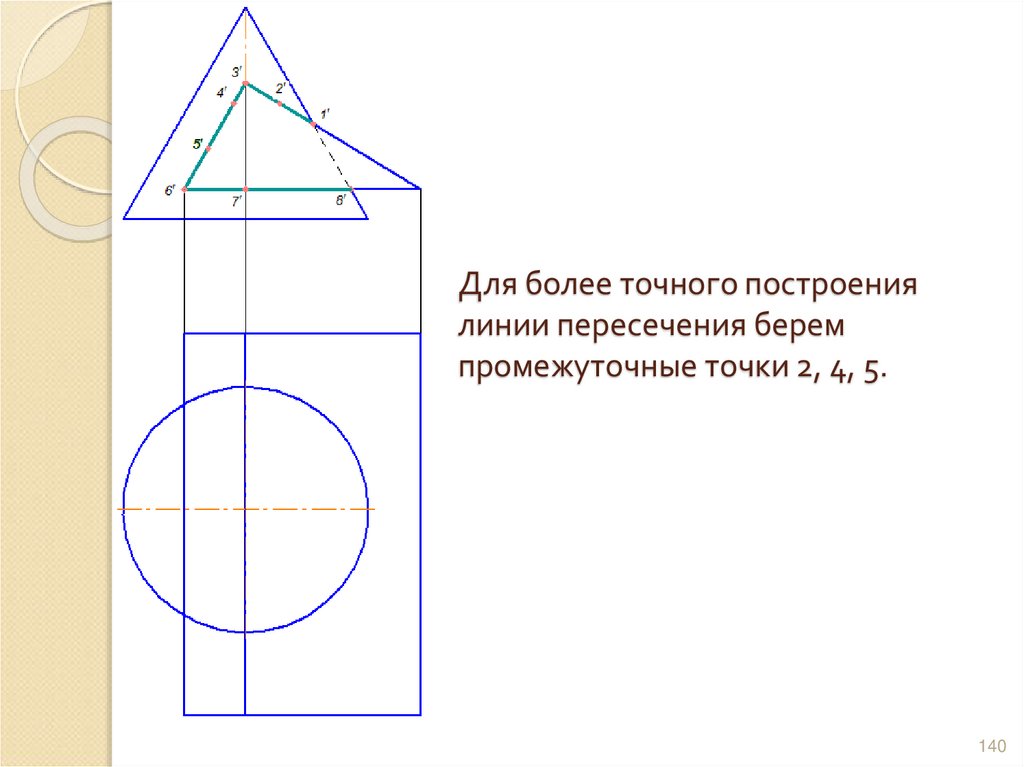
140. Для более точного построения линии пересечения берем промежуточные точки 2, 4, 5.

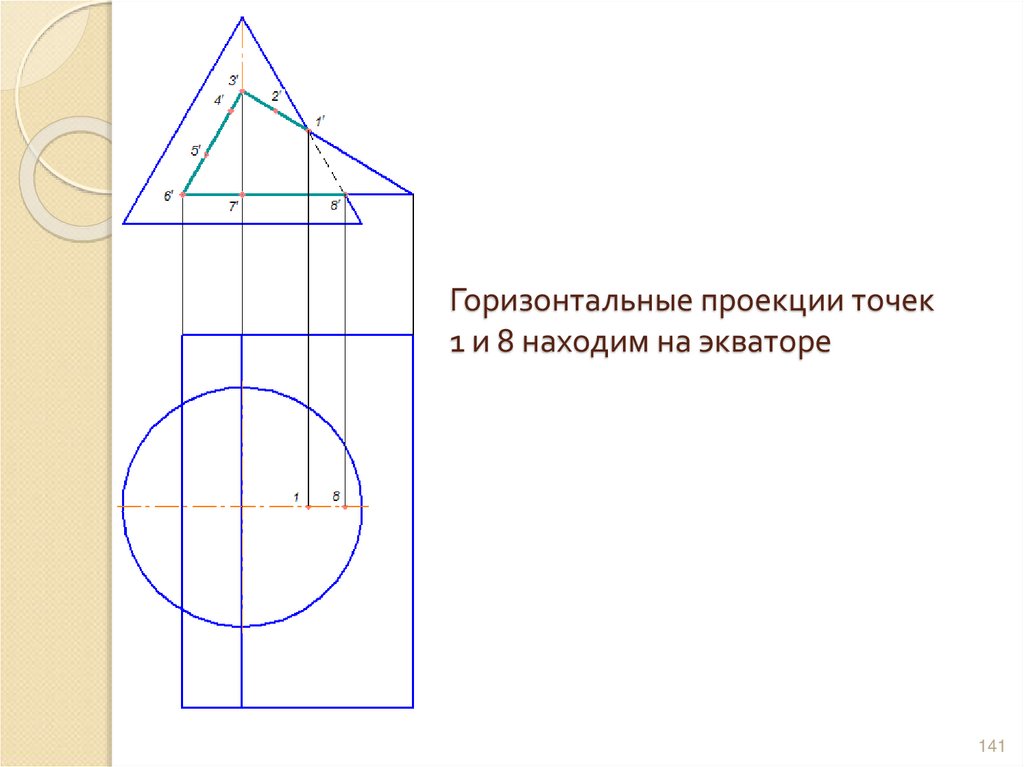
140

141. Горизонтальные проекции точек 1 и 8 находим на экваторе

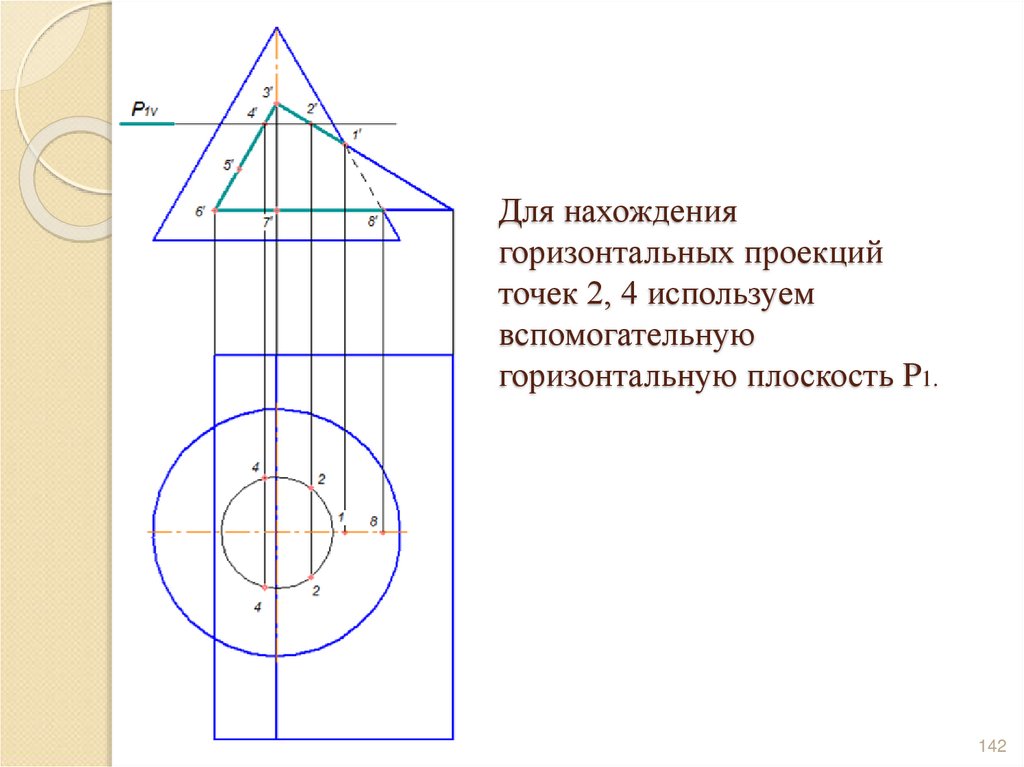
141

142. Для нахождения горизонтальных проекций точек 2, 4 используем вспомогательную горизонтальную плоскость P1.

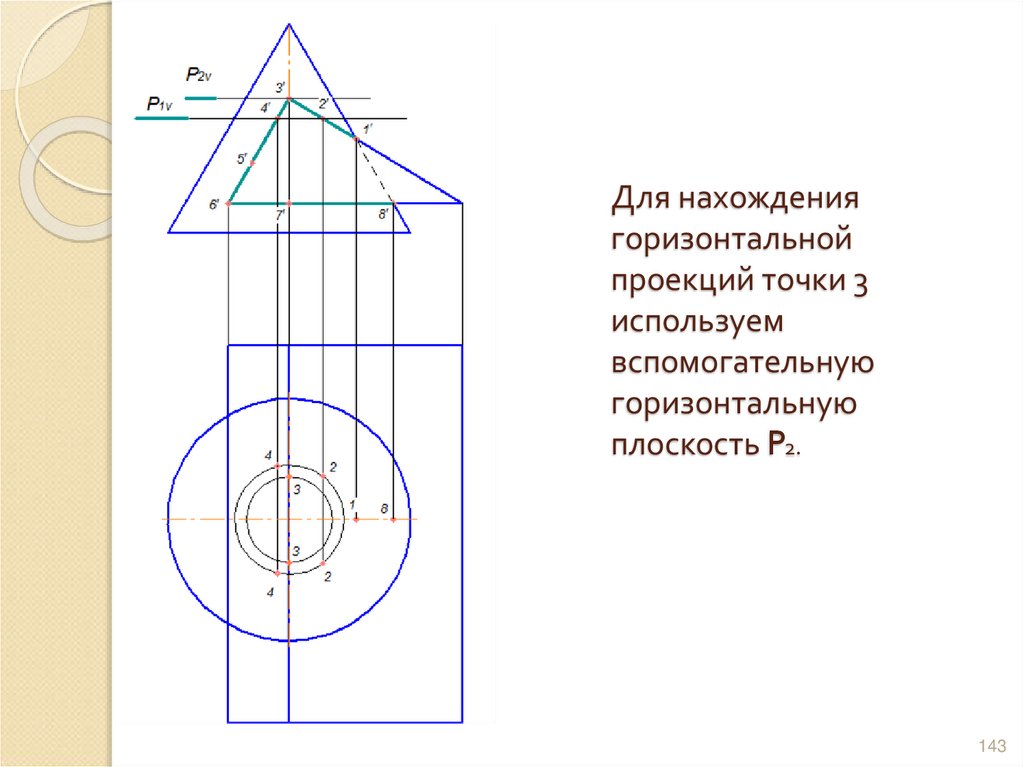
142

143. Для нахождения горизонтальной проекций точки 3 используем вспомогательную горизонтальную плоскость P2.

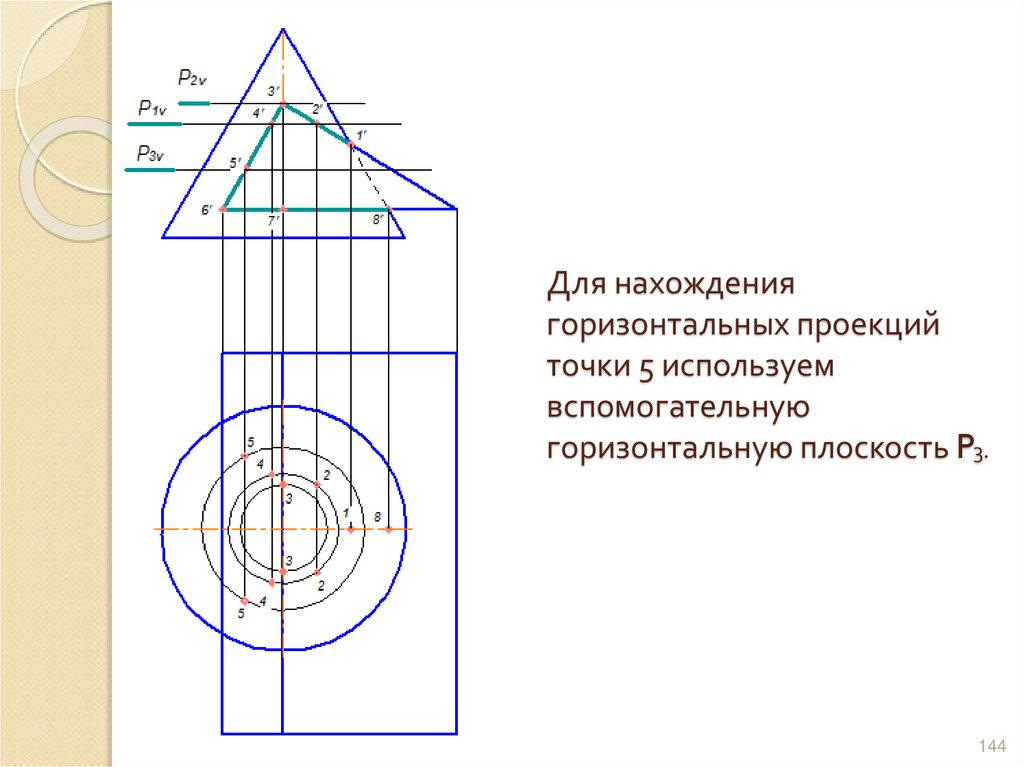
143

144. Для нахождения горизонтальных проекций точки 5 используем вспомогательную горизонтальную плоскость P3.

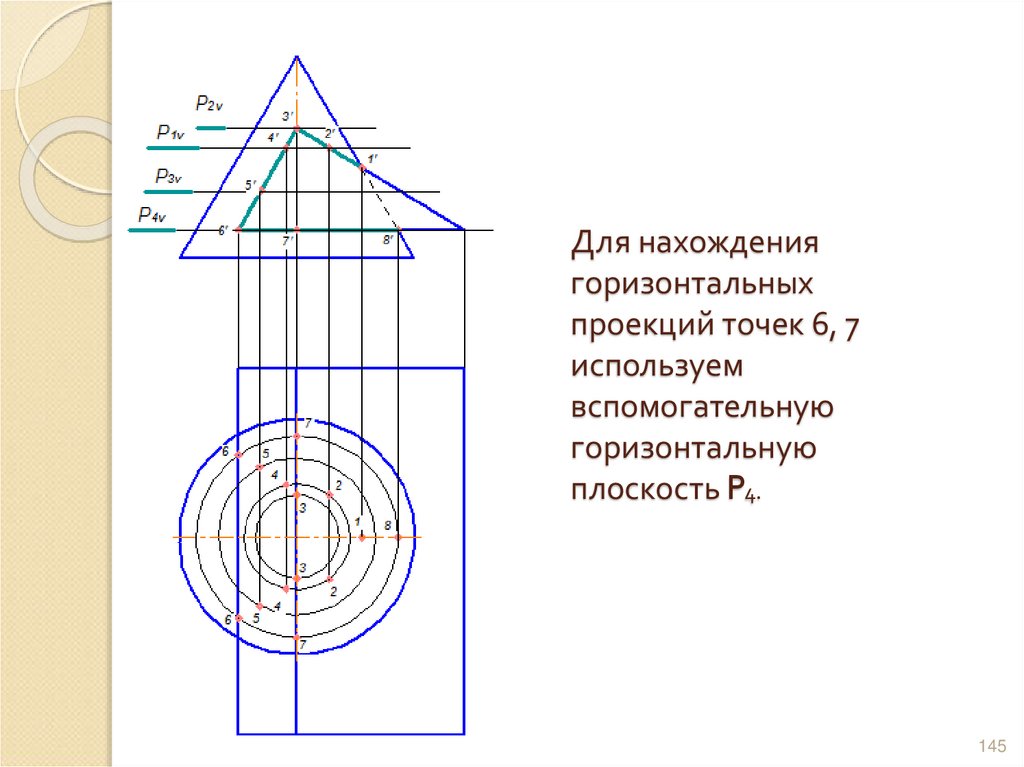
144

145. Для нахождения горизонтальных проекций точек 6, 7 используем вспомогательную горизонтальную плоскость P4.

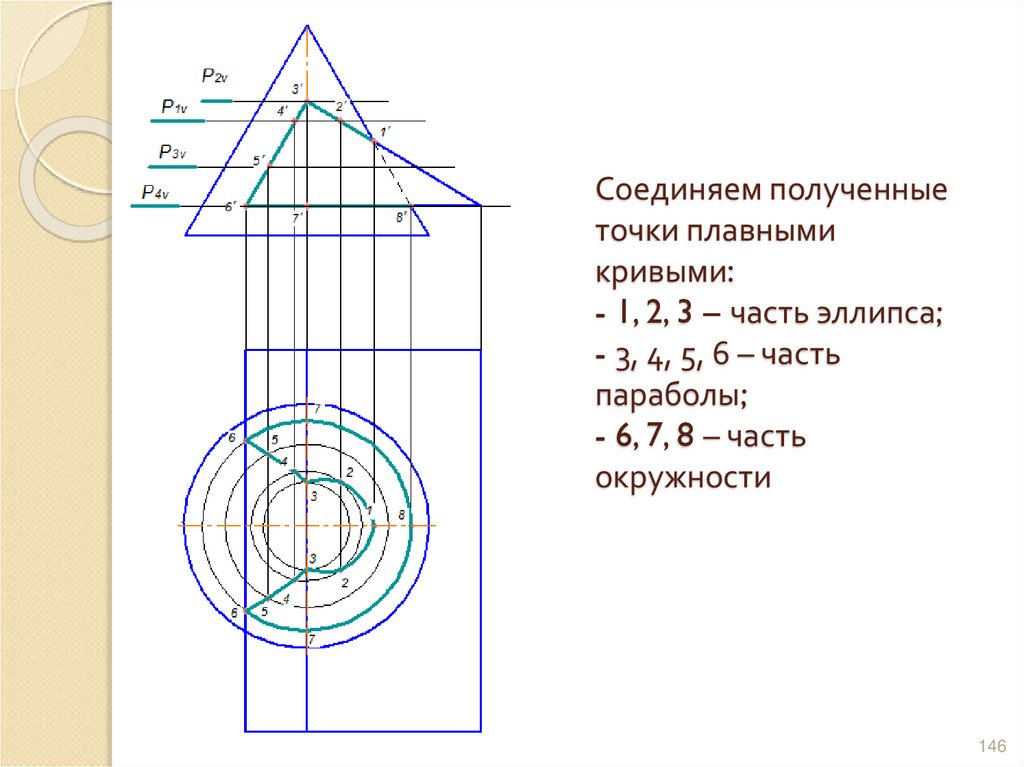
145

146. Соединяем полученные точки плавными кривыми: - 1, 2, 3 – часть эллипса; - 3, 4, 5, 6 – часть параболы; - 6, 7, 8 – часть

окружности
146

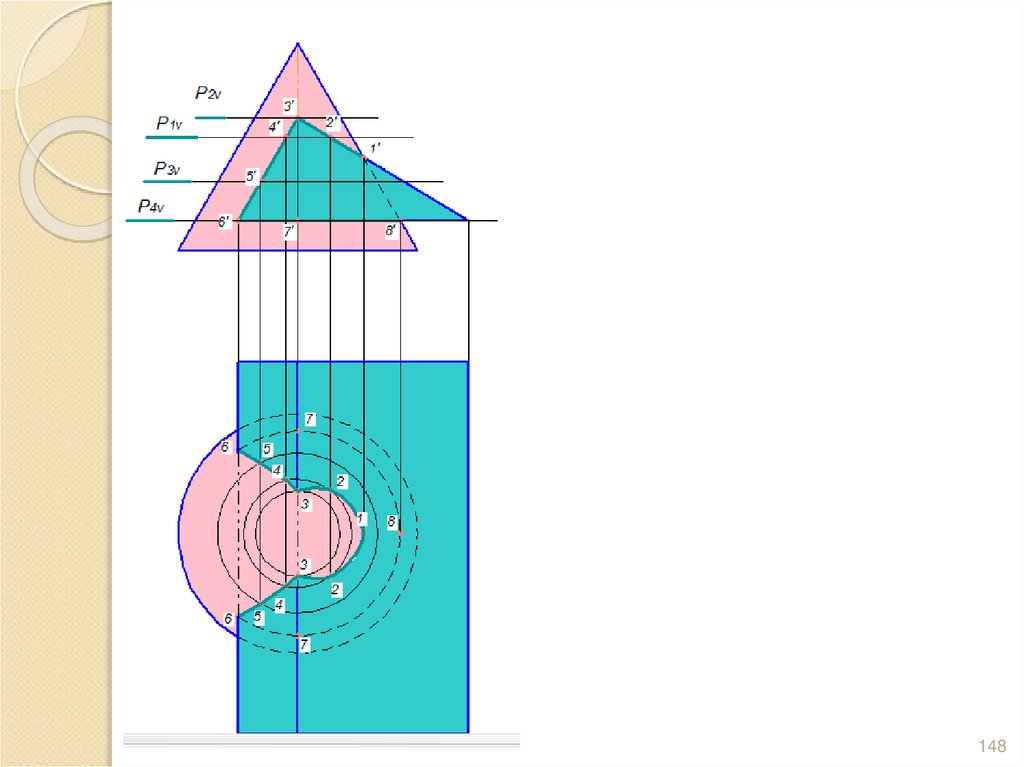
147. Определяем видимость линии пересечения и самих поверхностей, считая при этом конус целым телом, а призму – усеченным.

147

148.

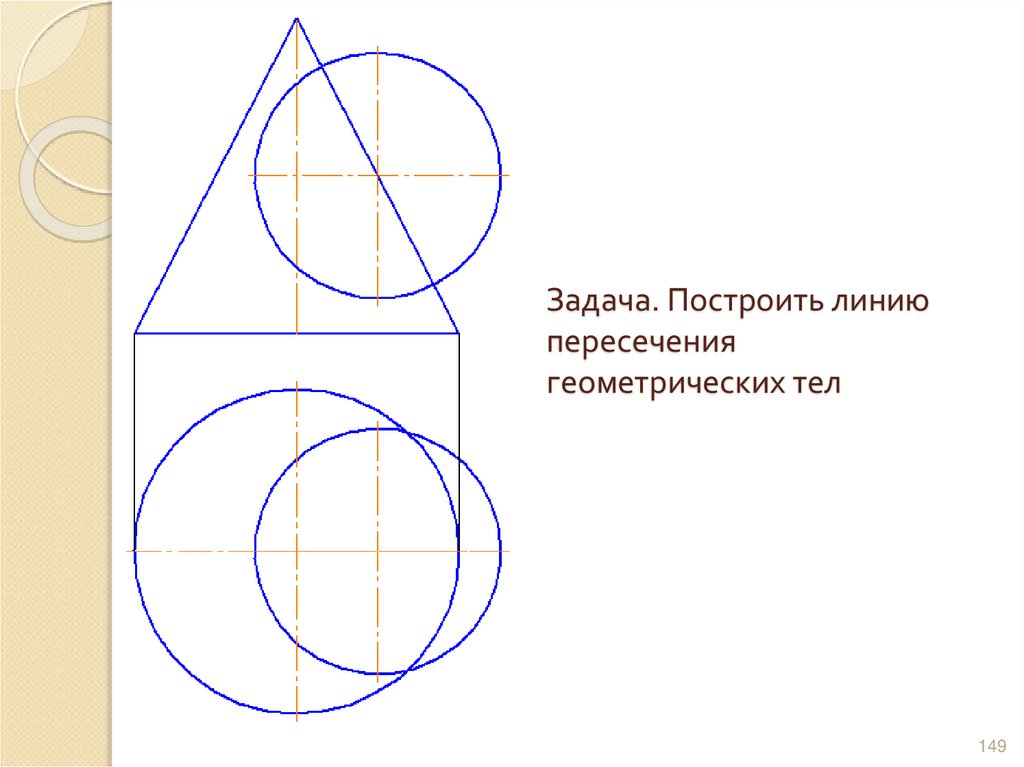
148

149. Задача. Построить линию пересечения геометрических тел

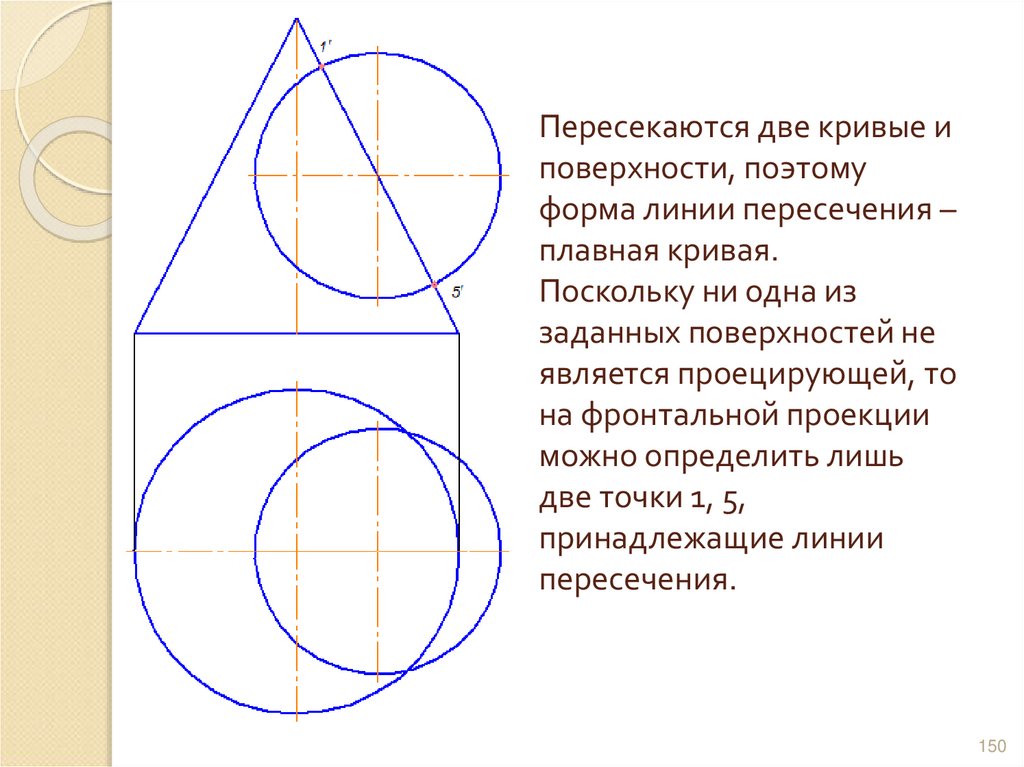
149

150. Пересекаются две кривые и поверхности, поэтому форма линии пересечения – плавная кривая. Поскольку ни одна из заданных

поверхностей не
является проецирующей, то
на фронтальной проекции
можно определить лишь
две точки 1, 5,
принадлежащие линии
пересечения.
150

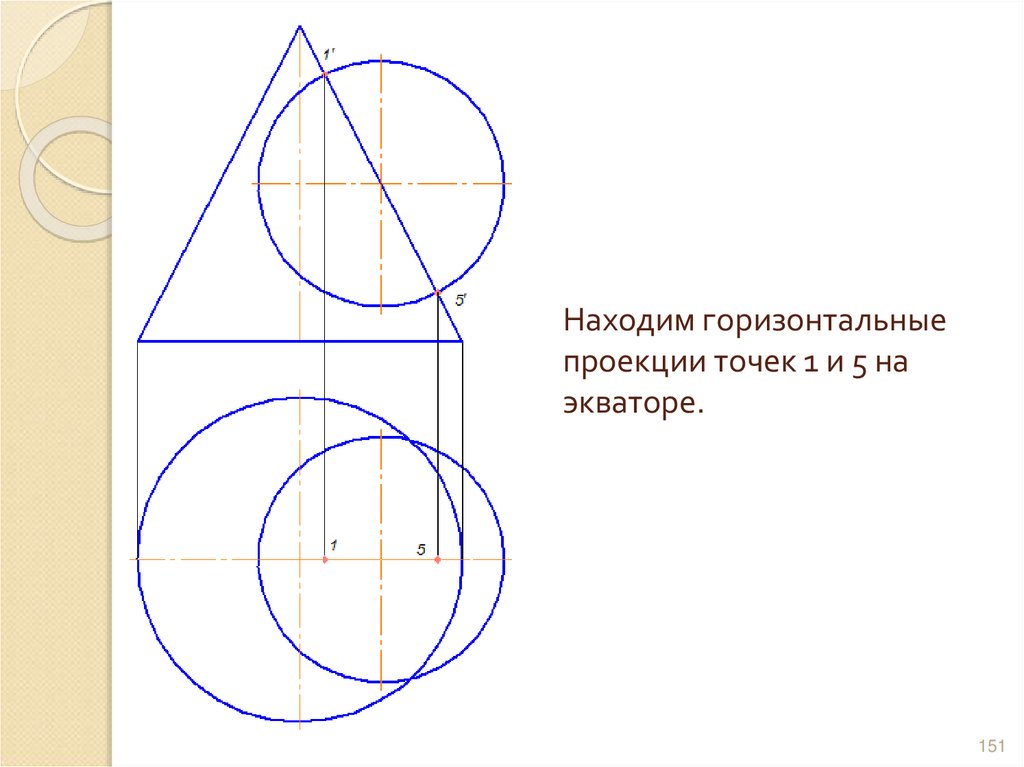
151. Находим горизонтальные проекции точек 1 и 5 на экваторе.

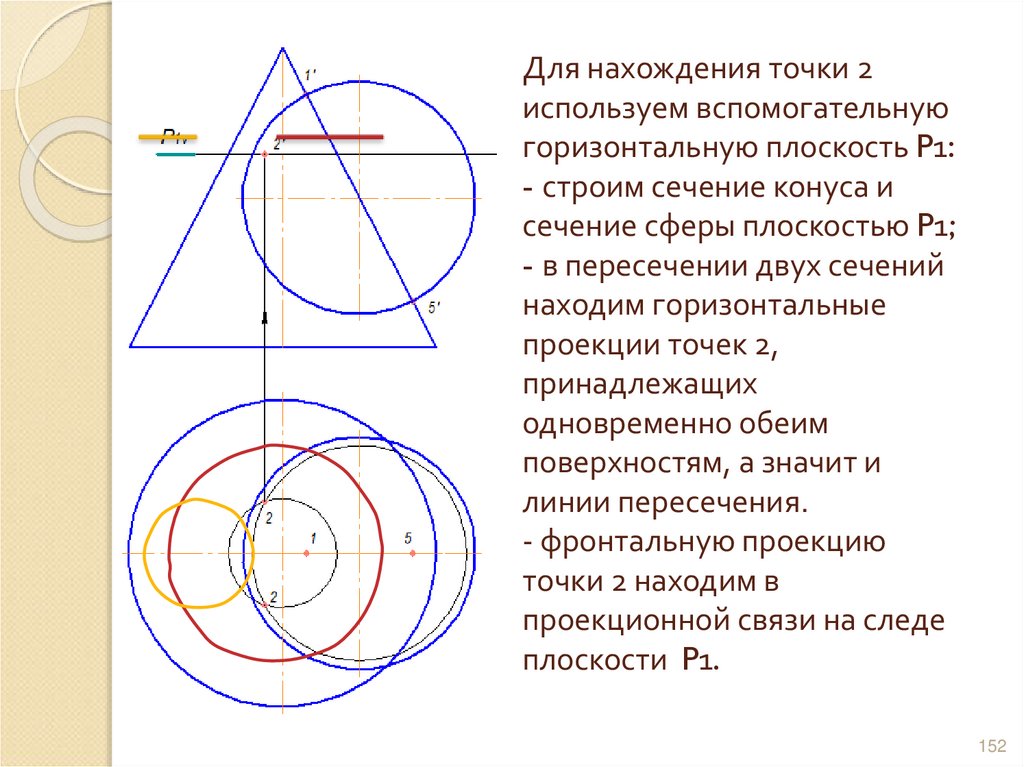
151

152. Для нахождения точки 2 используем вспомогательную горизонтальную плоскость P1: - строим сечение конуса и сечение сферы

плоскостью P1;
- в пересечении двух сечений
находим горизонтальные
проекции точек 2,
принадлежащих
одновременно обеим
поверхностям, а значит и
линии пересечения.
- фронтальную проекцию
точки 2 находим в
проекционной связи на следе
плоскости P1.
152

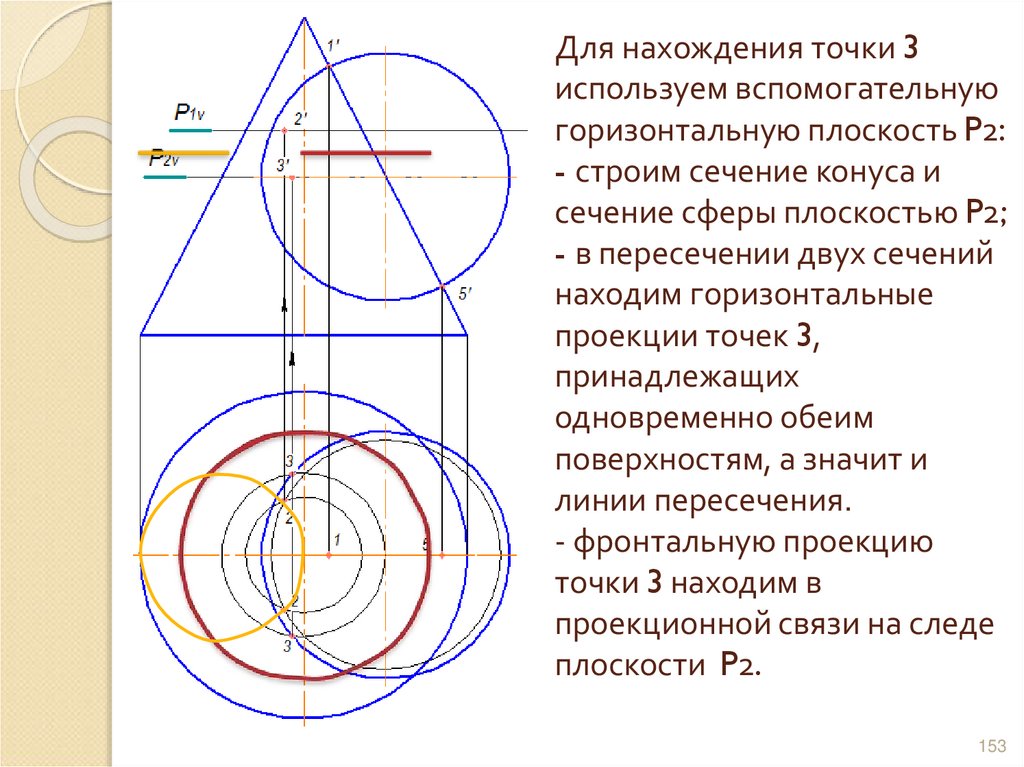
153. Для нахождения точки 3 используем вспомогательную горизонтальную плоскость P2: - строим сечение конуса и сечение сферы

плоскостью P2;
- в пересечении двух сечений
находим горизонтальные
проекции точек 3,
принадлежащих
одновременно обеим
поверхностям, а значит и
линии пересечения.
- фронтальную проекцию
точки 3 находим в
проекционной связи на следе
плоскости P2.
153

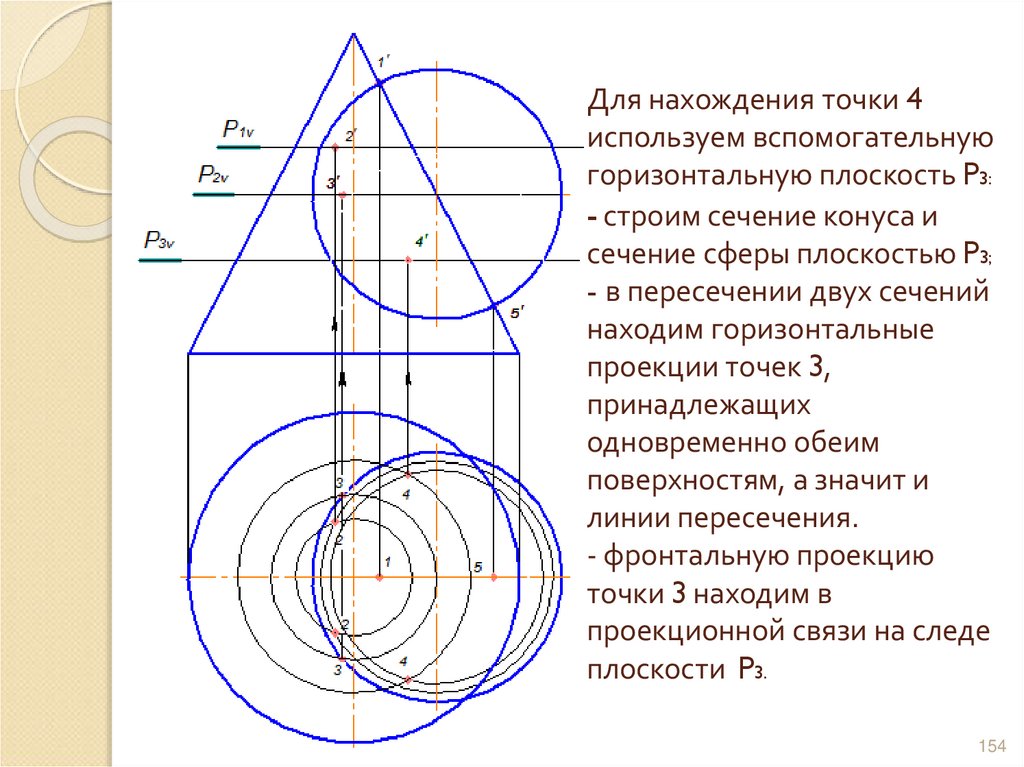
154. Для нахождения точки 4 используем вспомогательную горизонтальную плоскость P3: - строим сечение конуса и сечение сферы

плоскостью P3;
- в пересечении двух сечений
находим горизонтальные
проекции точек 3,
принадлежащих
одновременно обеим
поверхностям, а значит и
линии пересечения.
- фронтальную проекцию
точки 3 находим в
проекционной связи на следе
плоскости P3.
154

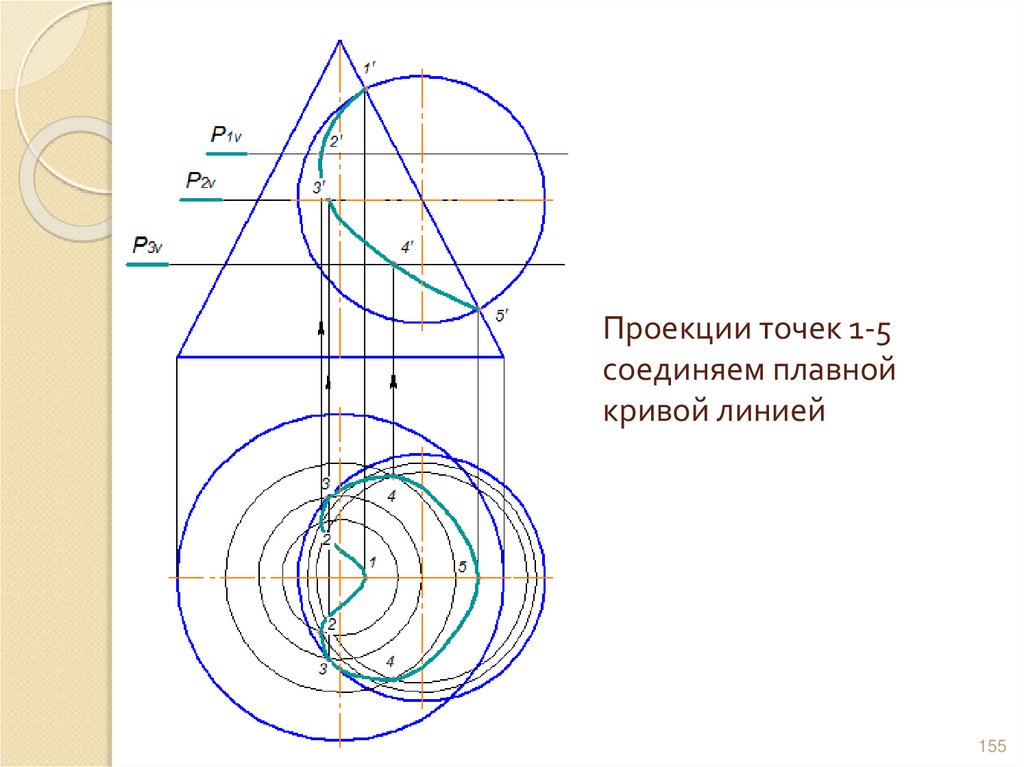
155. Проекции точек 1-5 соединяем плавной кривой линией

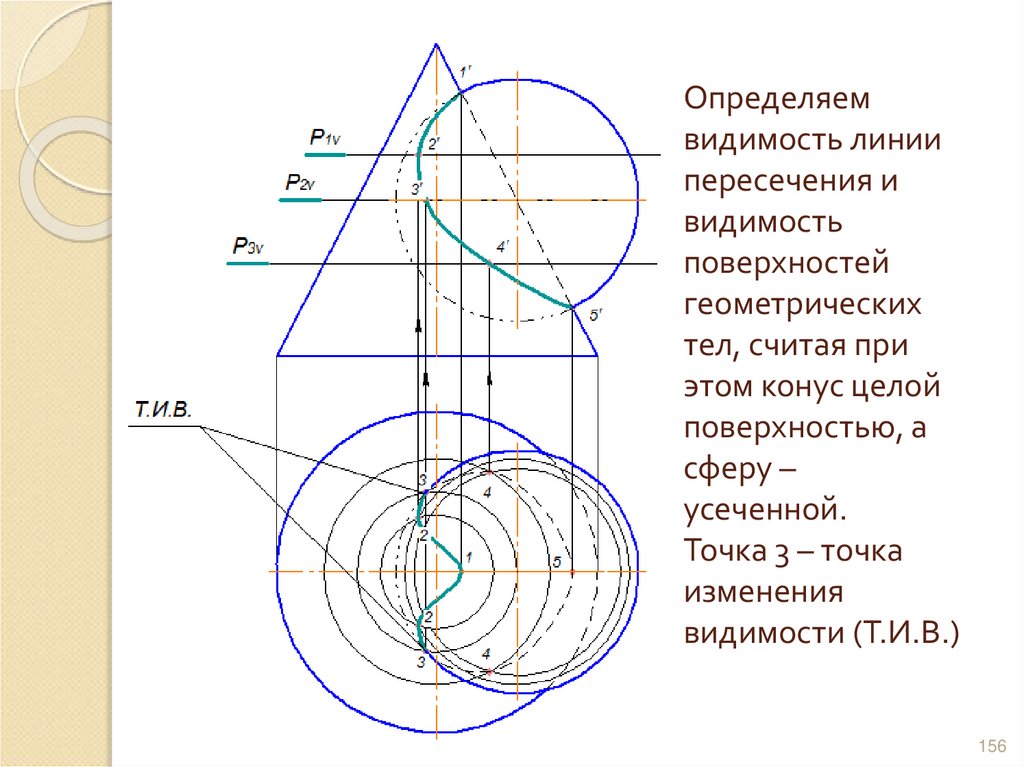
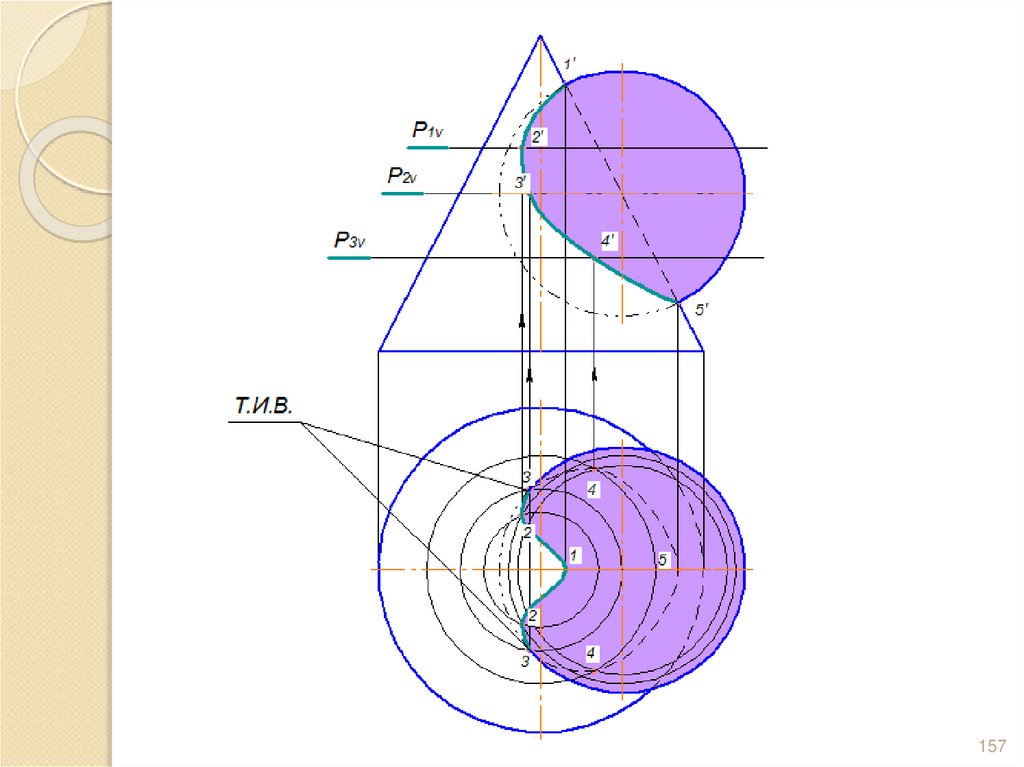
155

156. Определяем видимость линии пересечения и видимость поверхностей геометрических тел, считая при этом конус целой поверхностью, а

сферу –
усеченной.
Точка 3 – точка
изменения
видимости (Т.И.В.)
156

157.

157

158.

СПАСИБО ЗА ВНИМАНИЕ!
158