Похожие презентации:
Начертательная геометрия
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Для студентовФБФО
2.
• Чертеж – международный язык общениятехников.
• Начертательная геометрия – грамматика
этого языка (чертежа).
• Начертательная геометрия изучает
методы построения изображений
пространственных объектов на
плоскости, а также способы
преобразования полученных
изображений для упрощения решения
различных инженерных задач.
2
3. Базовые геометрические элементы начертательной геометрии
4.
• Точка – абстрактное математическое понятие.Нульмерный объект (не имеет измерений).
• Линия – непрерывное одномерное множество
точек ( цепочка точек). Непрерывная последовательность положений точки, перемещающейся в пространстве по определенному
закону (траектории). Измерение : только длина.
Толщины нет.
• Поверхность – непрерывное двумерное множество точек. Непрерывная последовательность положений линии, перемещающейся в
пространстве по определенному закону.
Измерения : длина, ширина, площадь. Толщины
и объема нет.
4
5. Проективное пространство
56.
Для устранения неоднородности Евклидовапространства
условно принято параллельные между собой прямые
пересекаются
в бесконечно удаленной точке F несобственной точке пространства.
(a b c…) (a ∩ b ∩ c… =
F
)
Евклидово
пространство,
дополненное
несобственными элементами, называют
проективным.
6
7. Метод проецирования
78. Метод проецирования
Пк – плоскость проекцийS – центр проецирования
- Аппарат проецирования
А – объект (точка)
SA – проецирующая
прямая
SA ∩ ПК = АК
АК – проекция объекта (точки) А на плоскости
проекций Пк
8
9.
Для любой точки пространстваSA ∩ Пк = Aк SВ ∩ Пк = Bк SС ∩ Пк = Cк
SA ∩ SВ ∩ SС ∩ …= S
9
10. Варианты метода проецирования
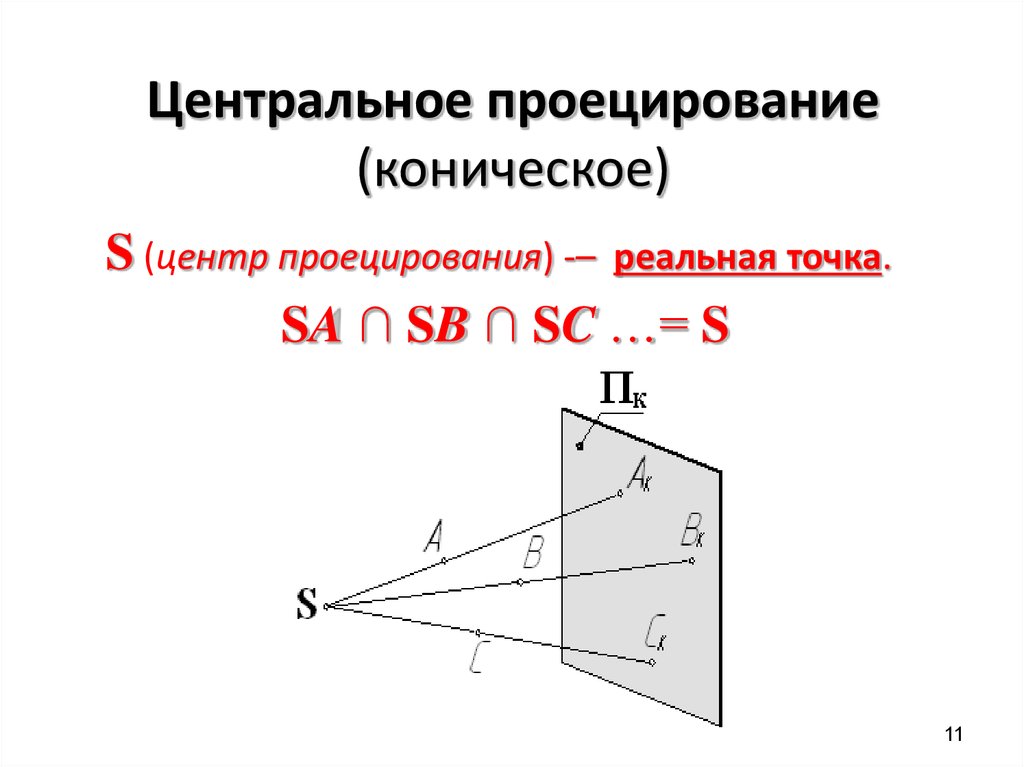
1011. Центральное проецирование (коническое)
S (центр проецирования) -– реальная точка.SA ∩ SB ∩ SC …= S
11
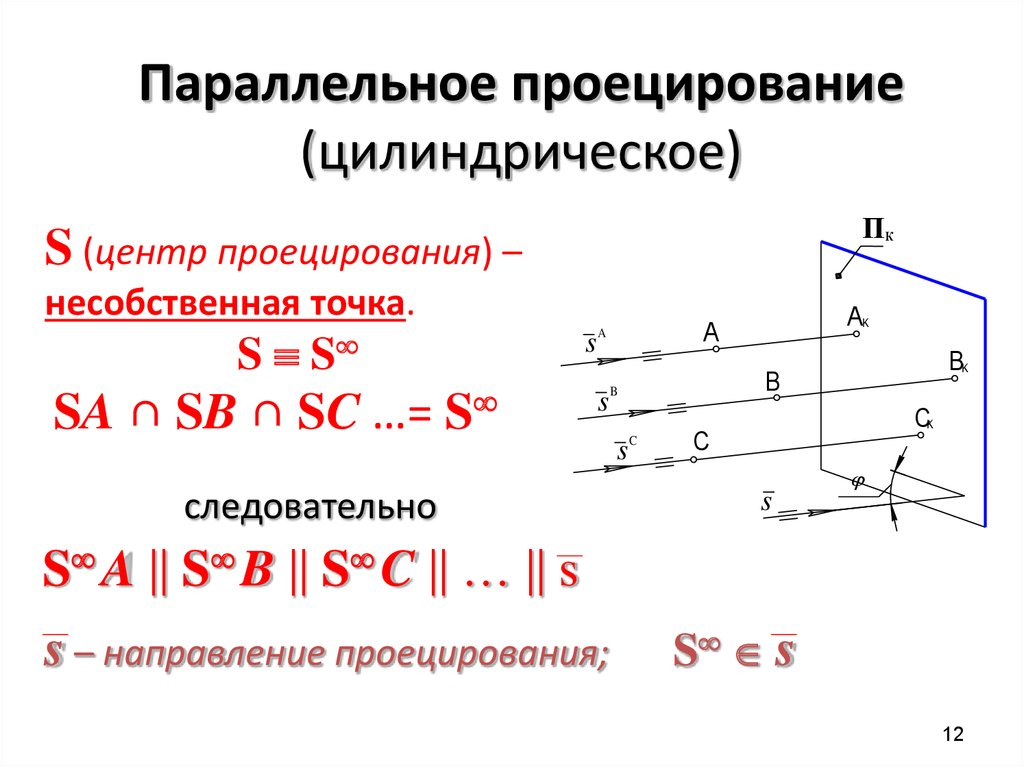
12. Параллельное проецирование (цилиндрическое)
ПКS (центр проецирования) –
несобственная точка.
S S
SA ∩ SB ∩ SC …=
s
S
s
BK
B
sB
следовательно
AK
A
A
C
CK
C
s
S A S B S C … s
s – направление проецирования;
S s
12
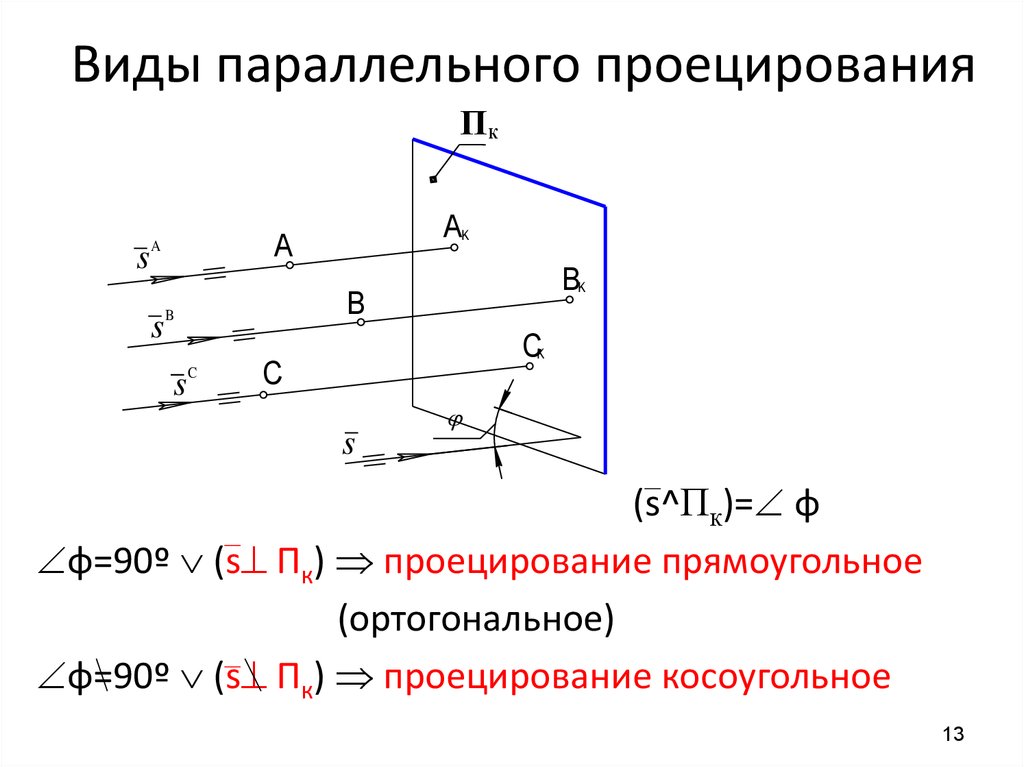
13. Виды параллельного проецирования
ПКs
s
AK
A
A
B
B
sC
BK
CK
C
s
(s^Пк)= φ
φ=90º (s Пк) проецирование прямоугольное
(ортогональное)
φ=90º (s Пк) проецирование косоугольное
13
14.
ПроецированиеЦентральное
Параллельное
Косоугольное
Прямоугольное
14
15.
Ортогональные проекции точки надве взаимно перпендикулярные
плоскости однозначно определяют
положение точки в пространстве и
делают изображения обратимыми.
16. Метод Монжа
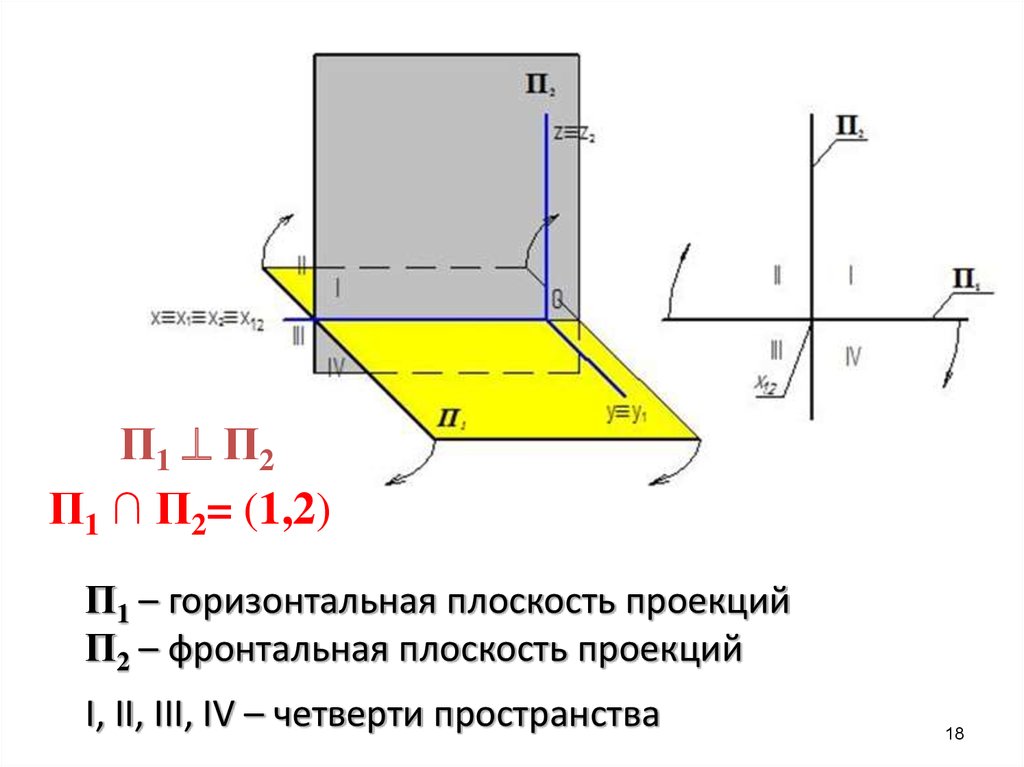
1617. Ортогональная система двух плоскостей проекций
18.
П1 П2П1 ∩ П2= (1,2)
П1 – горизонтальная плоскость проекций
П2 – фронтальная плоскость проекций
I, II, III, IV – четверти пространства
18
19.
Плоскости проекцийП1 и П2 совмещены в
одну общую
плоскость.
19
20. Проецирование точки
2021.
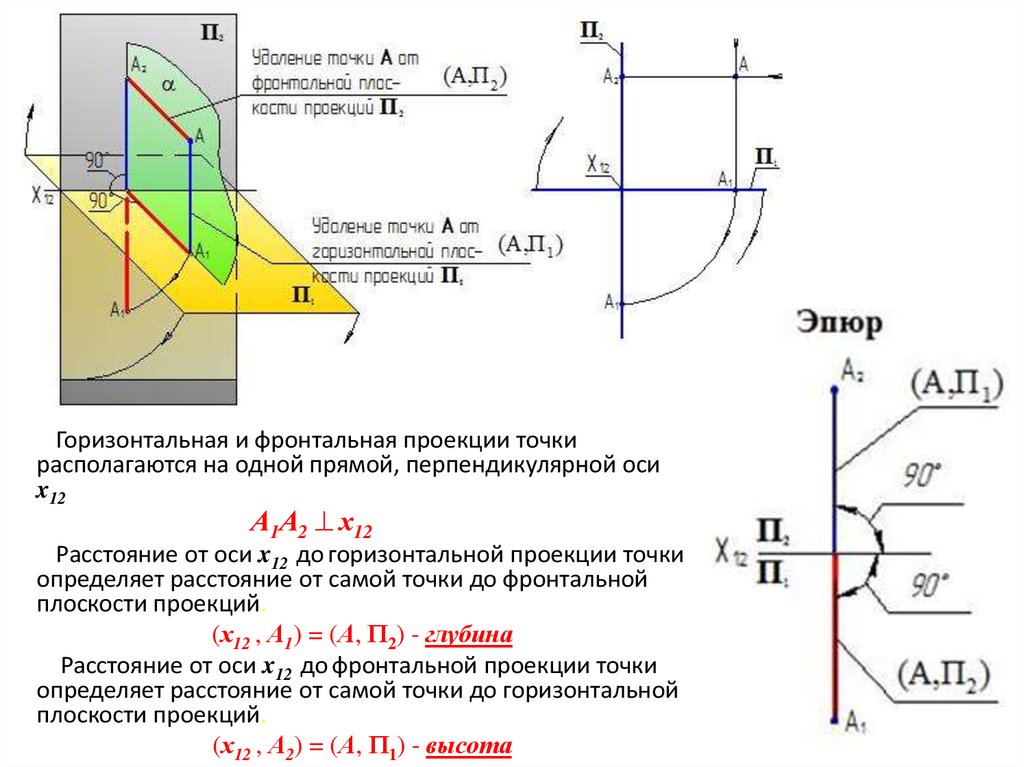
Горизонтальная и фронтальная проекции точкирасполагаются на одной прямой, перпендикулярной оси
x12
А1А2 х12
Расстояние от оси x12 до горизонтальной проекции точки
определяет расстояние от самой точки до фронтальной
плоскости проекций.
(х12 , А1) = (А, П2) - глубина
Расстояние от оси x12 до фронтальной проекции точки
определяет расстояние от самой точки до горизонтальной
плоскости проекций.
(х12 , А2) = (А, П1) - высота
22. Проецирование прямой линии
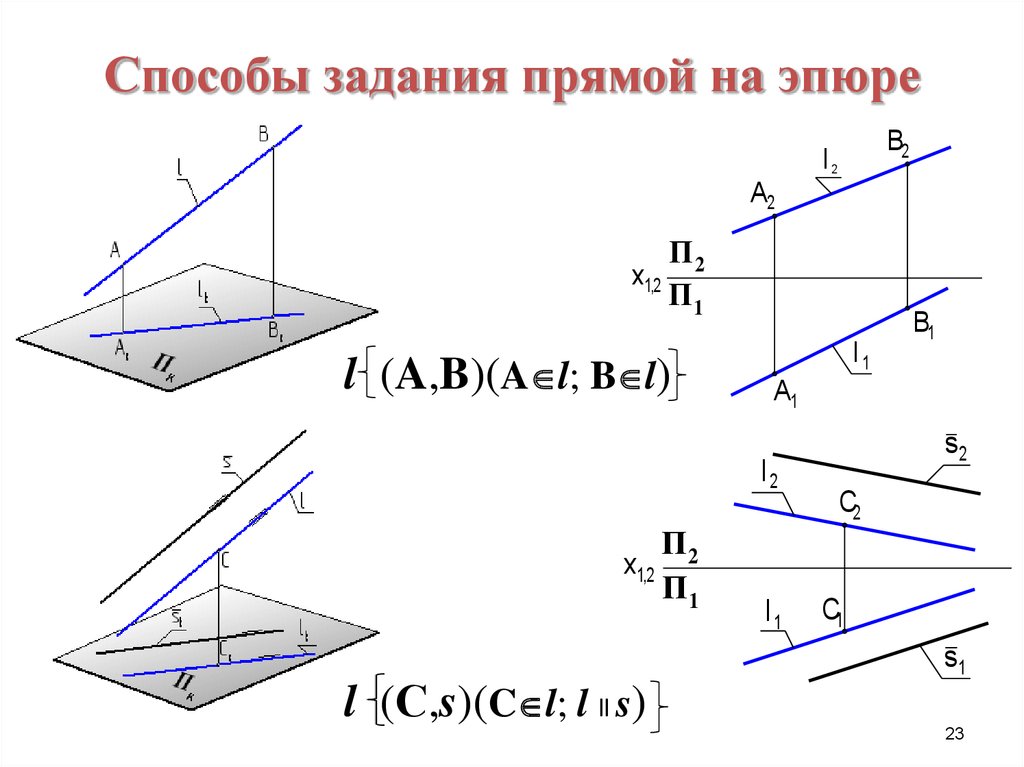
2223. Способы задания прямой на эпюре
В2l2
Способы задания прямой наА эпюре
2
П2
х1,2
П1
П2
х1,2
П1
l (A,B)(A l; B l)
А2
l1
П2
П1
П2
х1,2
П1
l (С,s)(C l; l ll s)
В1
А1
l1
В1
А1
l2
х1,2
В2
l2
l2
l1
s2
С2
s2
С1С2
s1
l1
С1
23
s
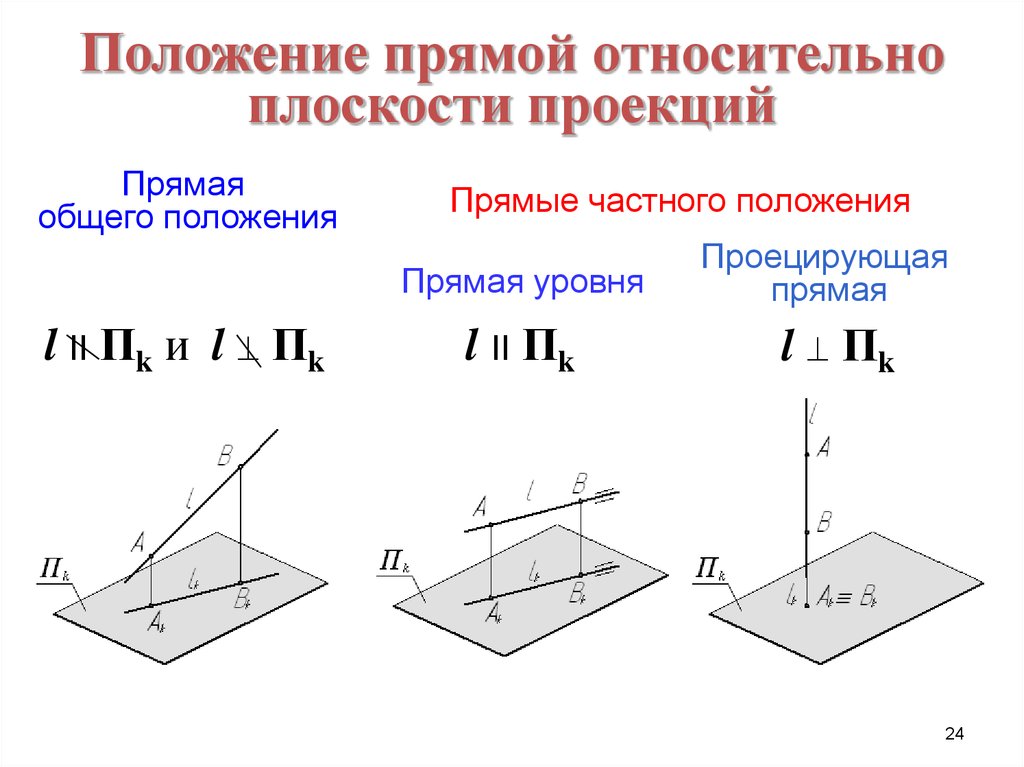
24. Положение прямой относительно плоскости проекций
Прямаяобщего положения
Прямые частного положения
Прямая уровня
l II Пk и l Пk
l II Пk
Проецирующая
прямая
l Пk
24
25.
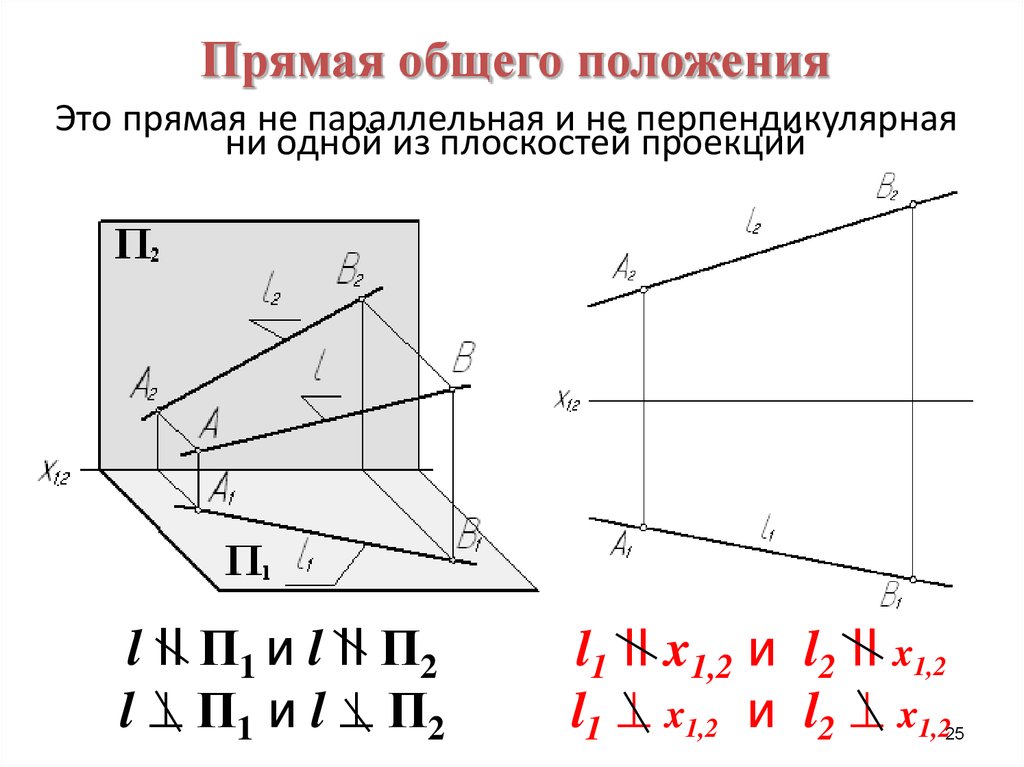
Прямая общего положенияЭто прямая не параллельная и не перпендикулярная
ни одной из плоскостей проекций
l II П1 и l II П2
l П1 и l П2
l1 II x1,2 и l2 II x1,2
l1 x1,2 и l2 x1,2
25
26. Характерная особенность эпюра прямой общего положения – горизонтальная и фронтальная проекции прямой не параллельны и не перпендикулярн
Характерная особенность эпюрапрямой общего положения –
горизонтальная и фронтальная
проекции прямой не
параллельны и не
перпендикулярны
координатной оси х12
26
27. Прямые уровня
Это прямые параллельныекакой-либо одной
плоскости проекций
l II Пк
27
28. Горизонталь – h Это прямая параллельная горизонтальной плоскости проекций
h II П1h2 II x1,2
AB h AB II П1 А1В1 IABI
h(AB)^П2 h1(А1В1) ^ x1,2
28
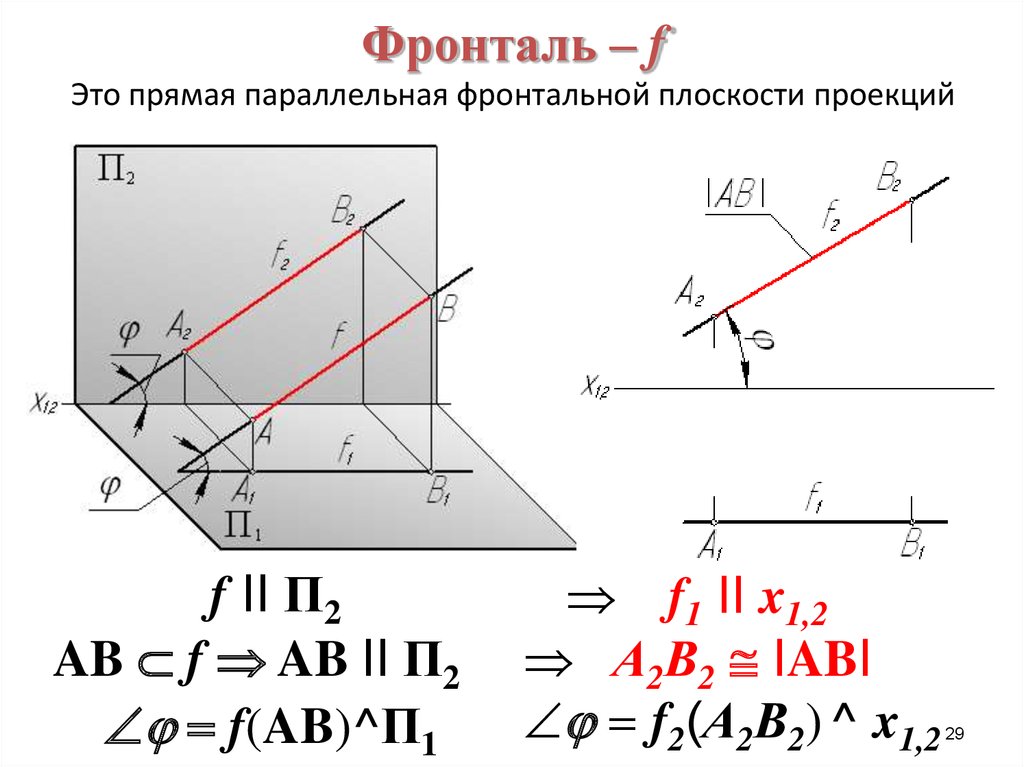
29. Фронталь – f Это прямая параллельная фронтальной плоскости проекций
f II П2AB f AB II П2
f(AB)^П1
f1 II x1,2
А2В2 IABI
f2(А2В2) ^ x1,2
29
30. Характерная особенность эпюра горизонтали и фронтали – одна из проекций параллельна координатной оси х1,2
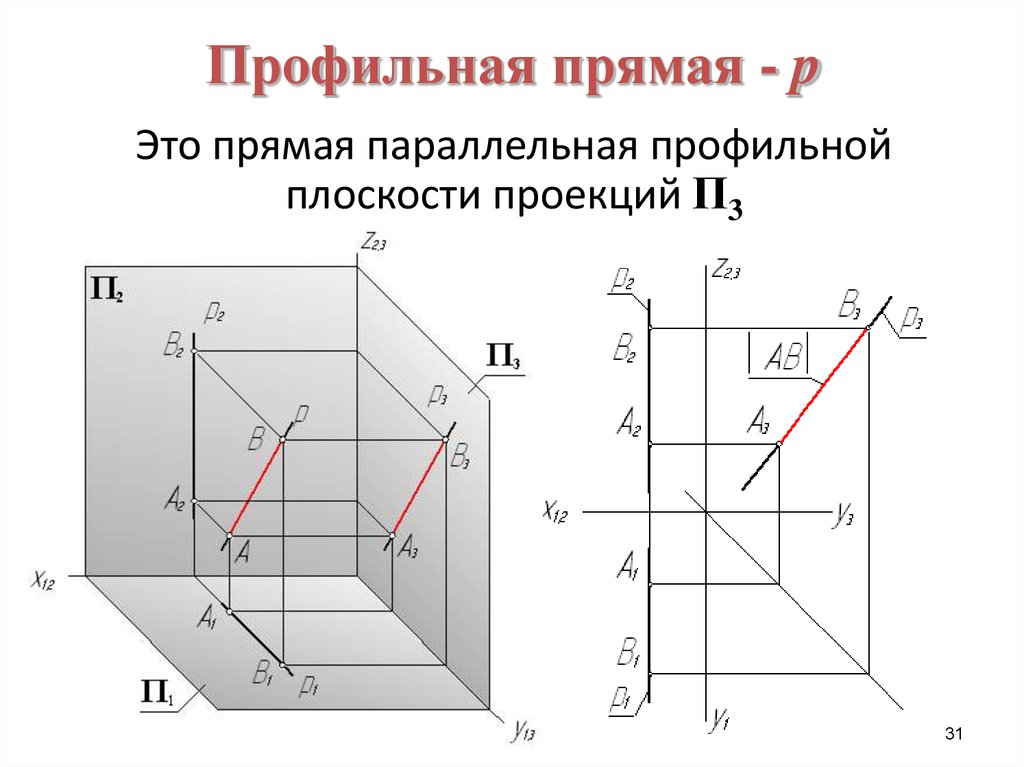
3031. Профильная прямая - p
Это прямая параллельная профильнойплоскости проекций П3
31
32. Проецирующие прямые
Это прямые перпендикулярныекакой-либо одной
плоскости проекций
l Пк
32
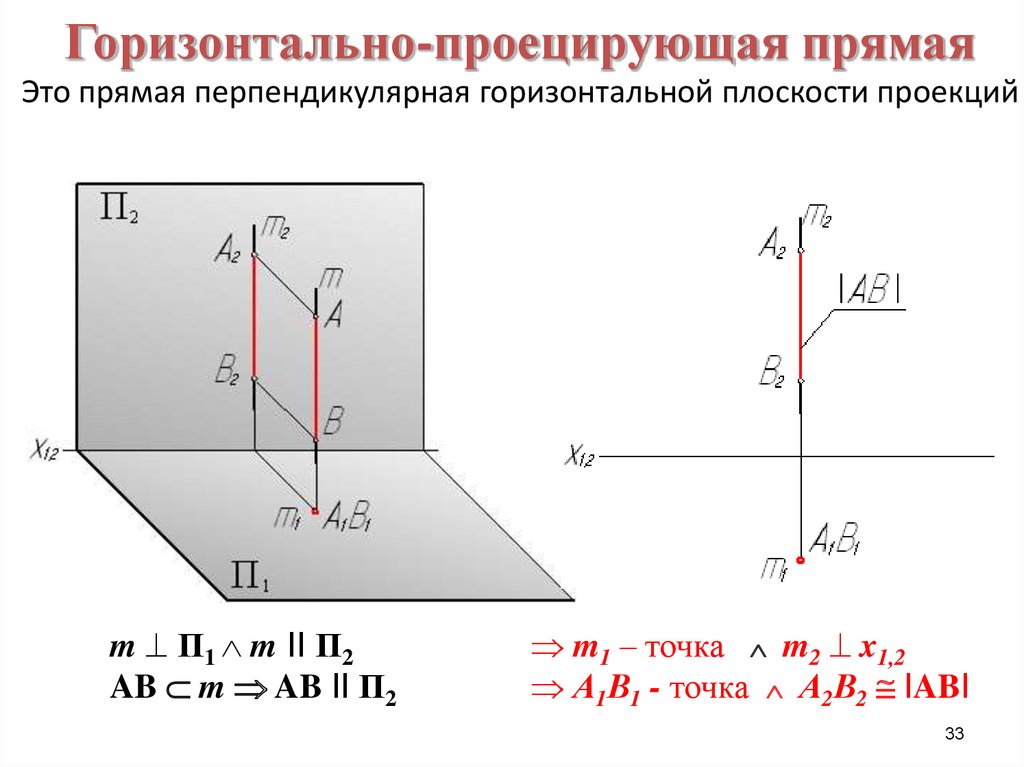
33. Горизонтально-проецирующая прямая Это прямая перпендикулярная горизонтальной плоскости проекций
m П1 m II П2AB m AB II П2
m1 – точка m2 x1,2
А1В1 - точка А2В2 IABI
33
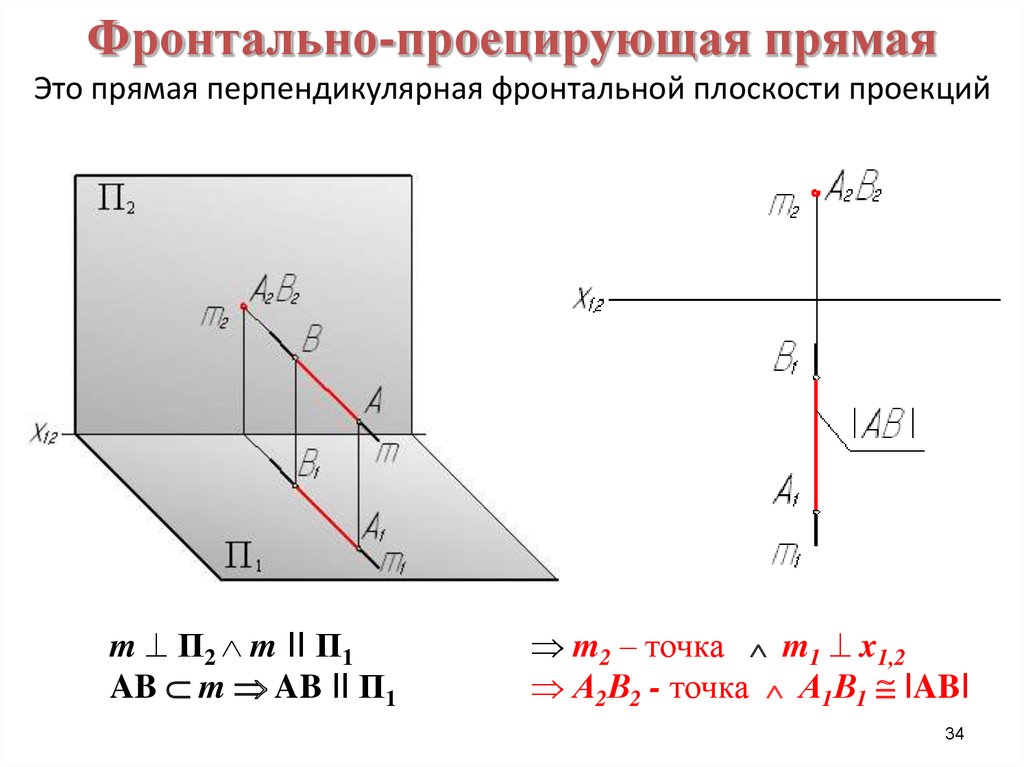
34. Фронтально-проецирующая прямая Это прямая перпендикулярная фронтальной плоскости проекций
m П2 m II П1AB m AB II П1
m2 – точка m1 x1,2
А2В2 - точка А1В1 IABI
34
35. Характерная особенность эпюра проецирующей прямой – одна из проекций прямой точка
3536. Взаимное положение двух прямых
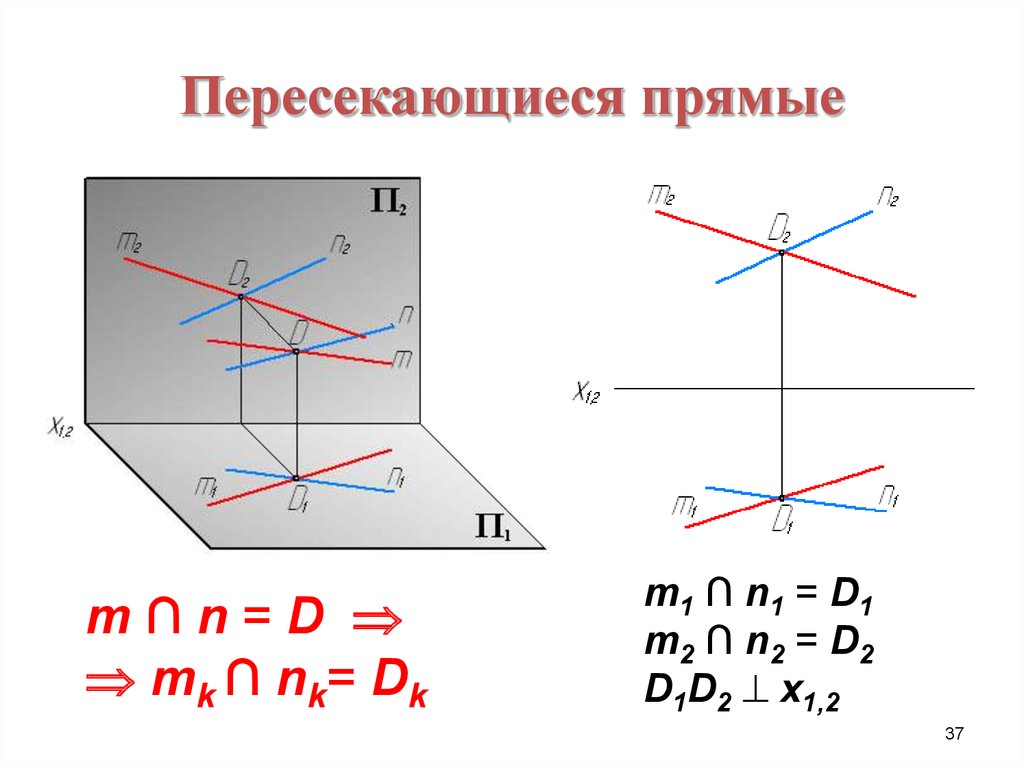
3637. Пересекающиеся прямые
m∩n=Dmk ∩ nk= Dk
m1 ∩ n1 = D1
m2 ∩ n2 = D2
D1D2 x1,2
37
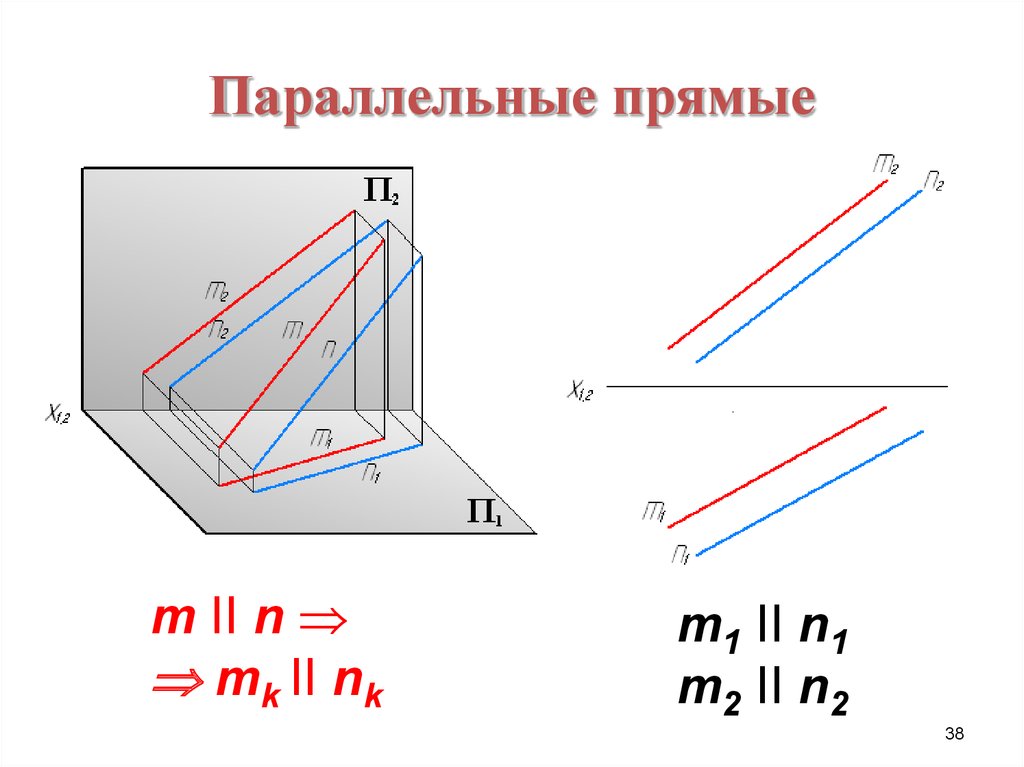
38. Параллельные прямые
m II nmk II nk
m1 II n1
m2 II n2
38
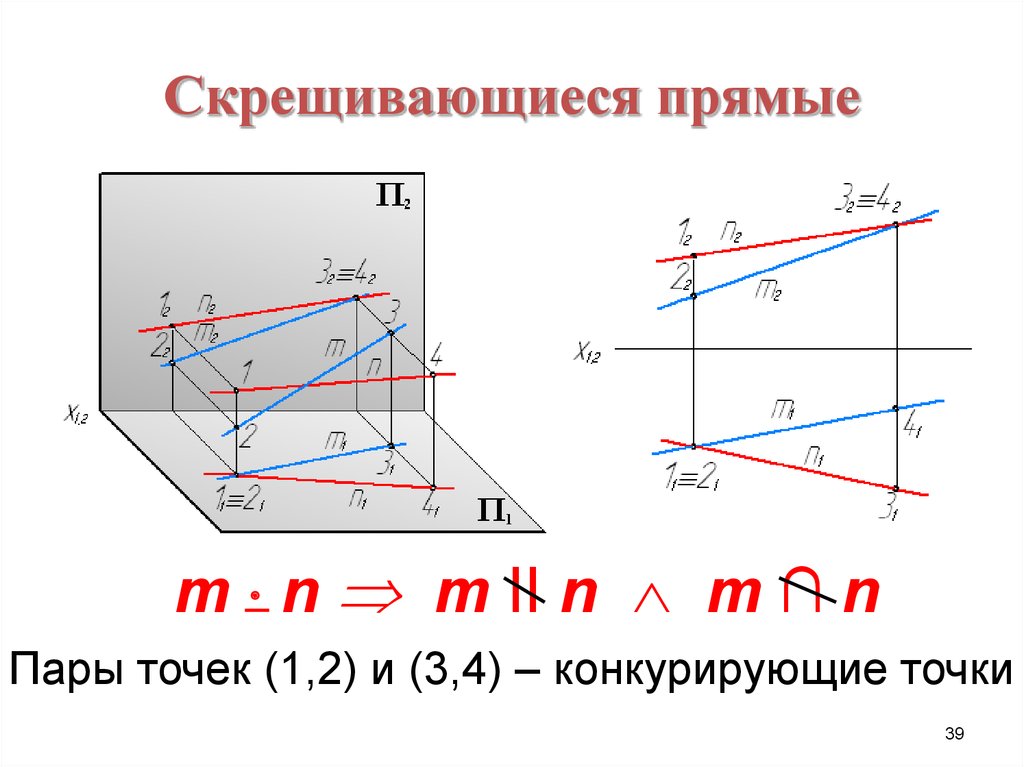
39. Скрещивающиеся прямые
m n m II n m ∩ nПары точек (1,2) и (3,4) – конкурирующие точки
39
40. Плоскость
4041.
Плоскость - это один из видов поверхности(плоская поверхность).
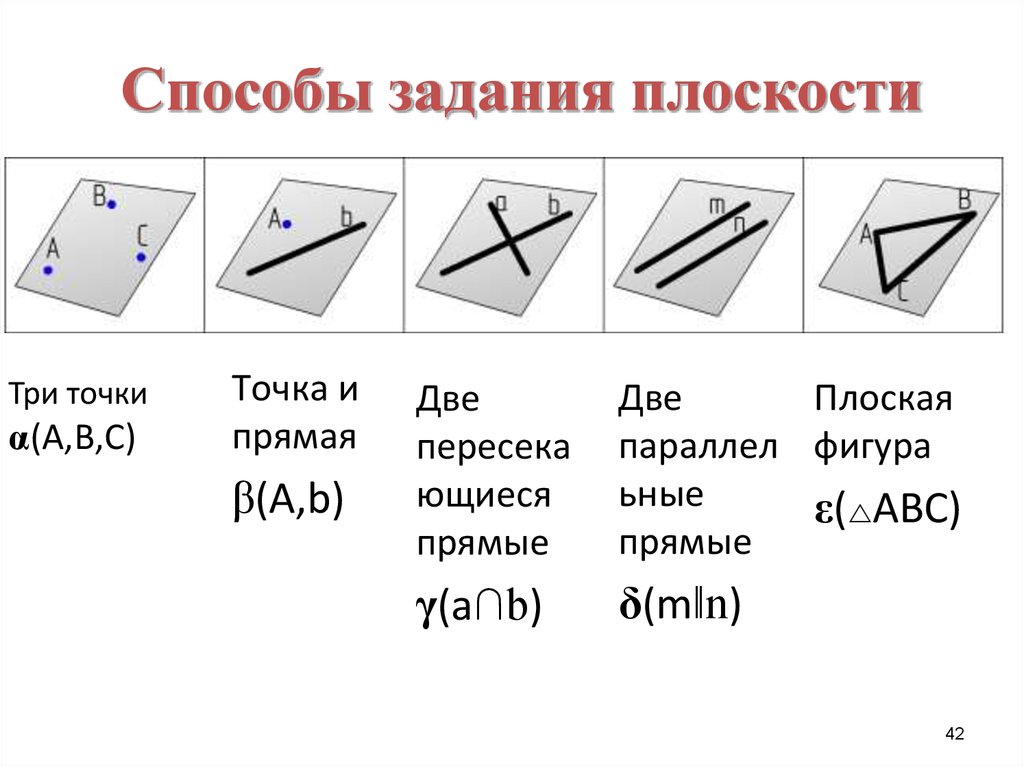
42. Способы задания плоскости
Три точкиα(А,В,С)
Точка и
прямая
β(А,b)
Две
пересека
ющиеся
прямые
Две
Плоская
параллел фигура
ьные
ε( АВС)
прямые
γ(a∩b)
δ(m‖n)
42
43. Положение плоскости относительно плоскостей проекций
ПЛОСКОСТИОБЩЕГО
ПОЛОЖЕНИЯ
ЧАСТНОГО
ПОЛОЖЕНИЯ
УРОВНЯ
ПРОЕЦИРУЮЩИЕ
43
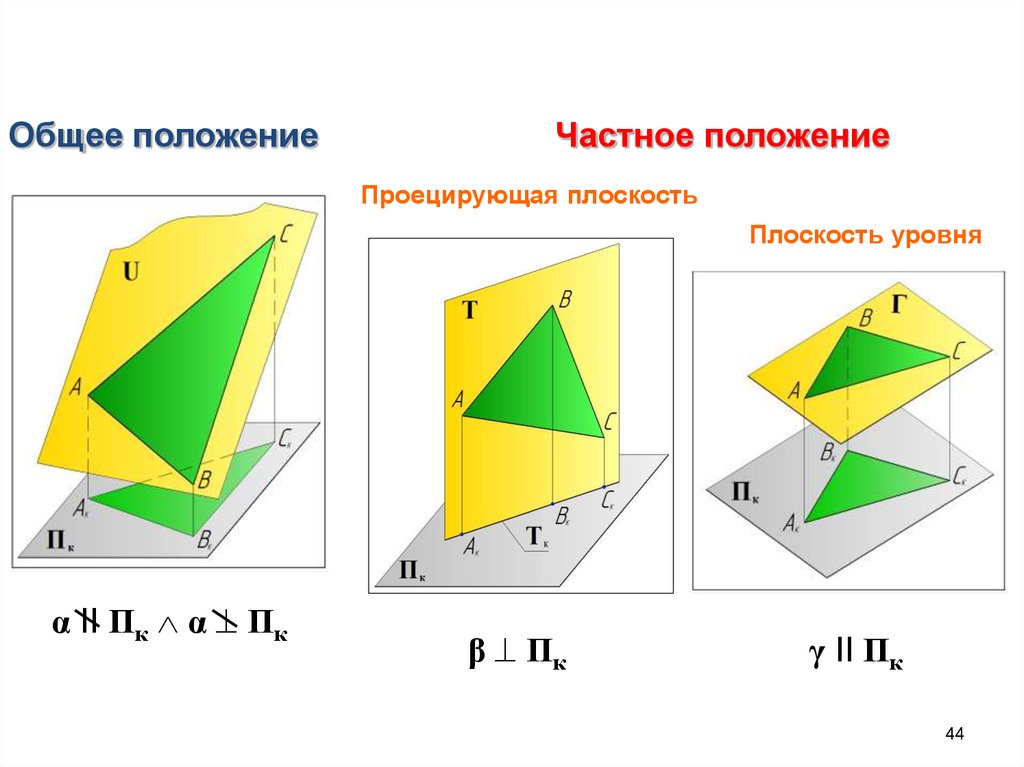
44.
Общее положениеЧастное положение
Проецирующая плоскость
Плоскость уровня
α II Пк α Пк
β Пк
γ II Пк
44
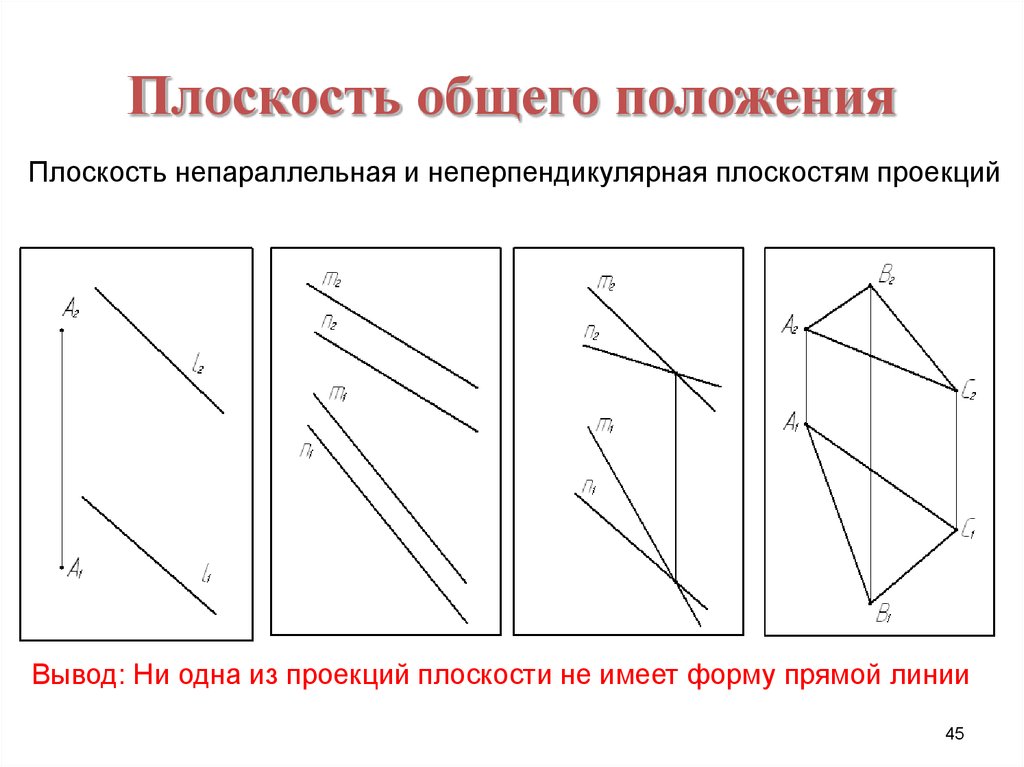
45. Плоскость общего положения
Плоскость непараллельная и неперпендикулярная плоскостям проекцийВывод: Ни одна из проекций плоскости не имеет форму прямой линии
45
46. Плоскости частного положения
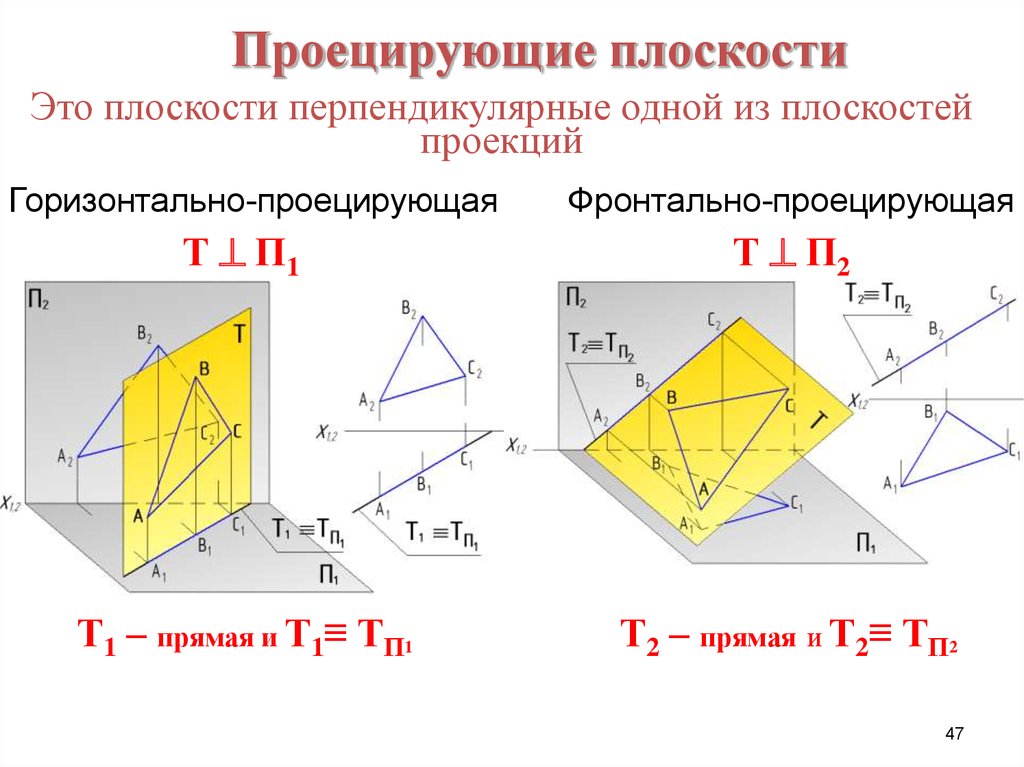
47. Это плоскости перпендикулярные одной из плоскостей проекций
Проецирующие плоскостиЭто плоскости перпендикулярные одной из плоскостей
проекций
Горизонтально-проецирующая
Фронтально-проецирующая
Т П1
Т П2
Т1 – прямая и Т1≡ ТП1
Т2 – прямая и Т2≡ ТП2
47
48. Это плоскости параллельные одной из плоскостей проекций
Плоскости уровняЭто плоскости параллельные одной из плоскостей
проекций
Горизонтальная плоскость
Фронтальная плоскость
α II П1
β II П2
α 2 – прямая и α 2≡ α П2
и α 2II x1,2
АВС
α АВС II П1 А1В1С1 АВС
β 1 – прямая и β 1≡ β П1
и β 1 II x1,2
АВС
β АВС II П2 А2В2С2 АВС
48
49.
Вывод:У плоскости частного положения одна из
проекций обязательно имеет форму прямой
линии.
49
50. Прямая линия в плоскости
ПРЯМАЯ ЛИНИЯВ ПЛОСКОСТИ
51.
В222
12
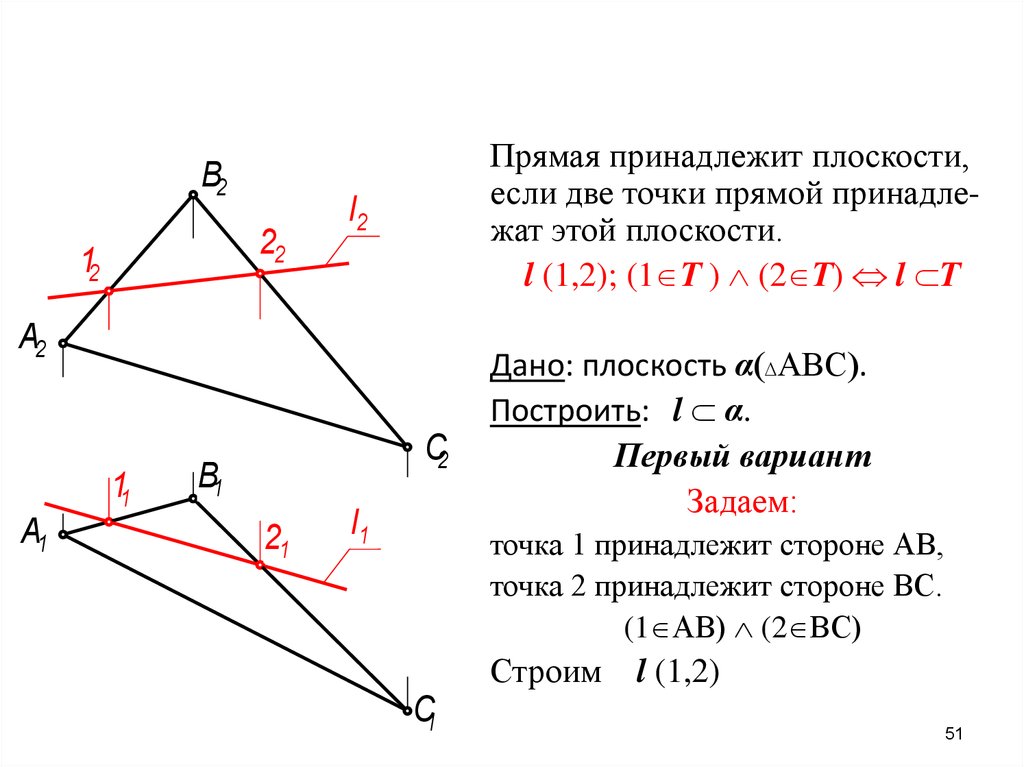
Прямая принадлежит плоскости,
если две точки прямой принадлежат этой плоскости.
l (1,2); (1 Т ) (2 Т) l Т
l2
А2
А1
11
С2
В1
21
l1
Дано: плоскость α АВС .
Построить: l α.
Первый вариант
Задаем:
точка 1 принадлежит стороне АВ,
точка 2 принадлежит стороне ВС.
(1 АВ) (2 ВС)
С1
Строим
l (1,2)
51
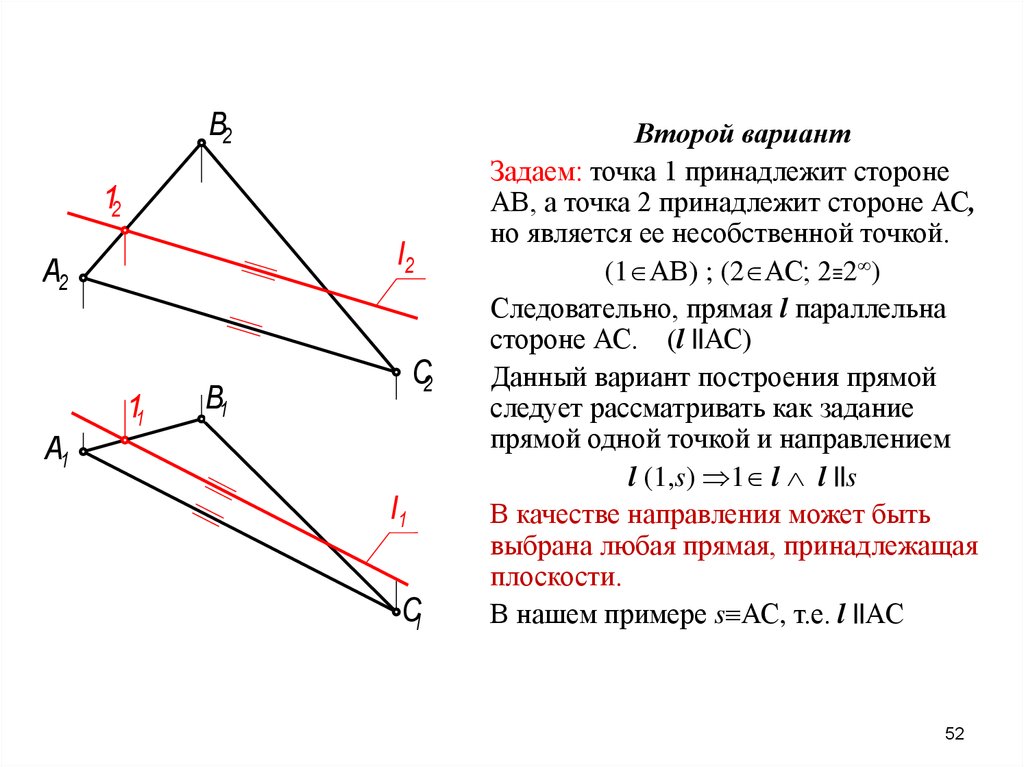
52.
В212
l2
А2
А1
11
С2
В1
l1
С1
Второй вариант
Задаем: точка 1 принадлежит стороне
АВ, а точка 2 принадлежит стороне АС,
но является ее несобственной точкой.
(1 АВ) ; (2 АС; 2≡2∞)
Следовательно, прямая l параллельна
стороне АС. (l ||АС)
Данный вариант построения прямой
следует рассматривать как задание
прямой одной точкой и направлением
l (1,s) 1 l l ||s
В качестве направления может быть
выбрана любая прямая, принадлежащая
плоскости.
В нашем примере s АС, т.е. l ||АС
52
53. Прямые уровня плоскости
5354. Горизонталь плоскости
Это прямая, принадлежащая плоскости,и параллельная горизонтальной плоскости
проекций
В2
А2
12
С2
В1
А1
h2
11
Дано: Плоскость α АВС
Построить: h α
Задаем h (А,1); 1 ВС
h 1 h2 x1,2
h1
С1
54
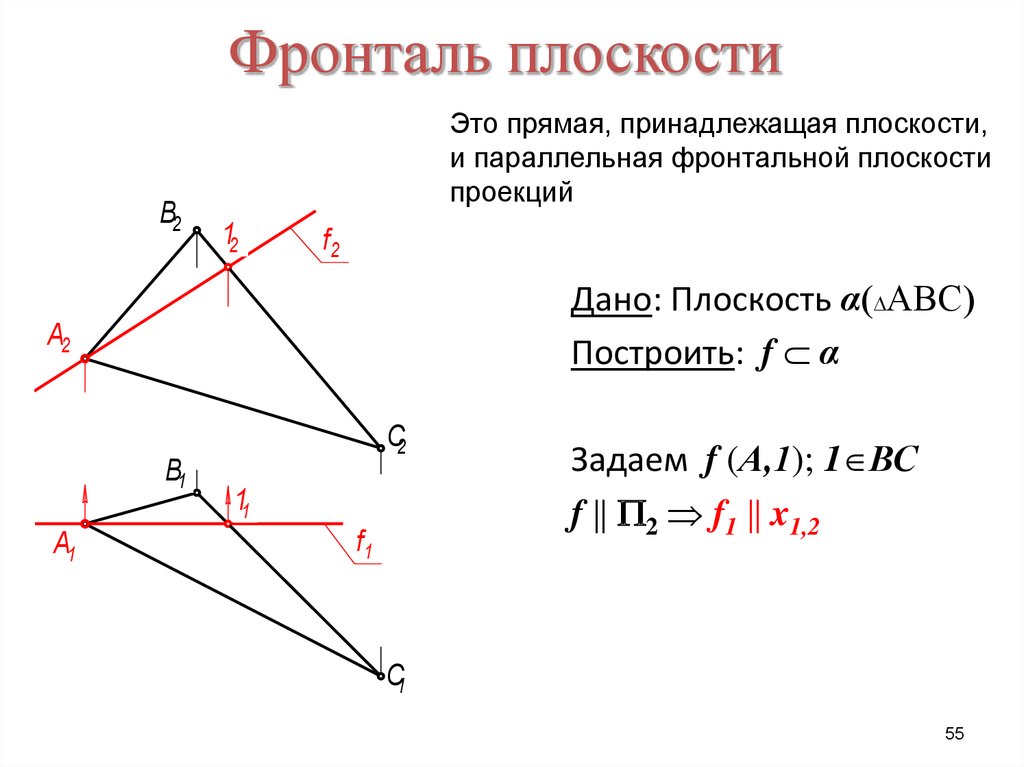
55. Фронталь плоскости
В2Это прямая, принадлежащая плоскости,
и параллельная фронтальной плоскости
проекций
12
f2
Дано: Плоскость α АВС
Построить: f α
А2
В1
А1
С2
11
f1
Задаем f (А,1); 1 ВС
f 2 f1 x1,2
С1
55
56. ТОЧКА В ПЛОСКОСТИ
5657.
Точка принадлежит плоскости, еслиона принадлежит прямой,
принадлежащей этой плоскости
А α А l,l α
57
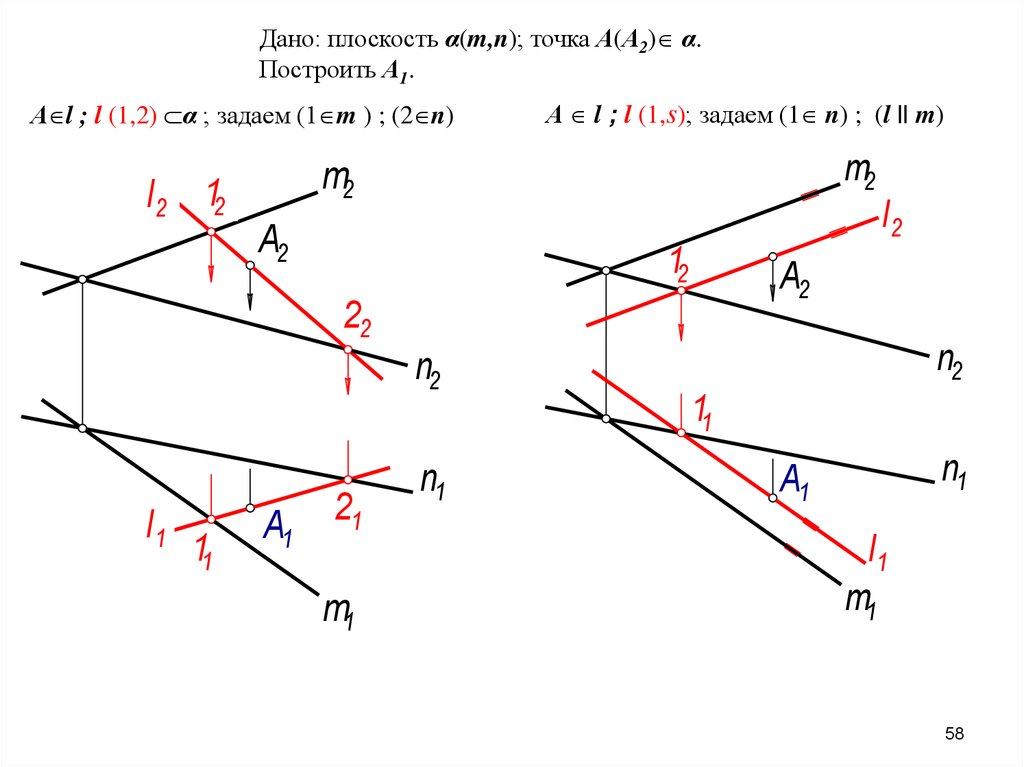
58.
Дано: плоскость α(m,n); точка А(А2) α.Построить А1.
А l ; l (1,2) α ; задаем (1 m ) ; (2 n)
А l ; l (1,s); задаем (1 n) ; (l || m)
m2
m2
l2 12
l2
A2
12
A2
22
n2
l1
11
A1
21
m1
n1
n2
11
n1
A1
l1
m1
58
59. Взаимное положение двух плоскостей
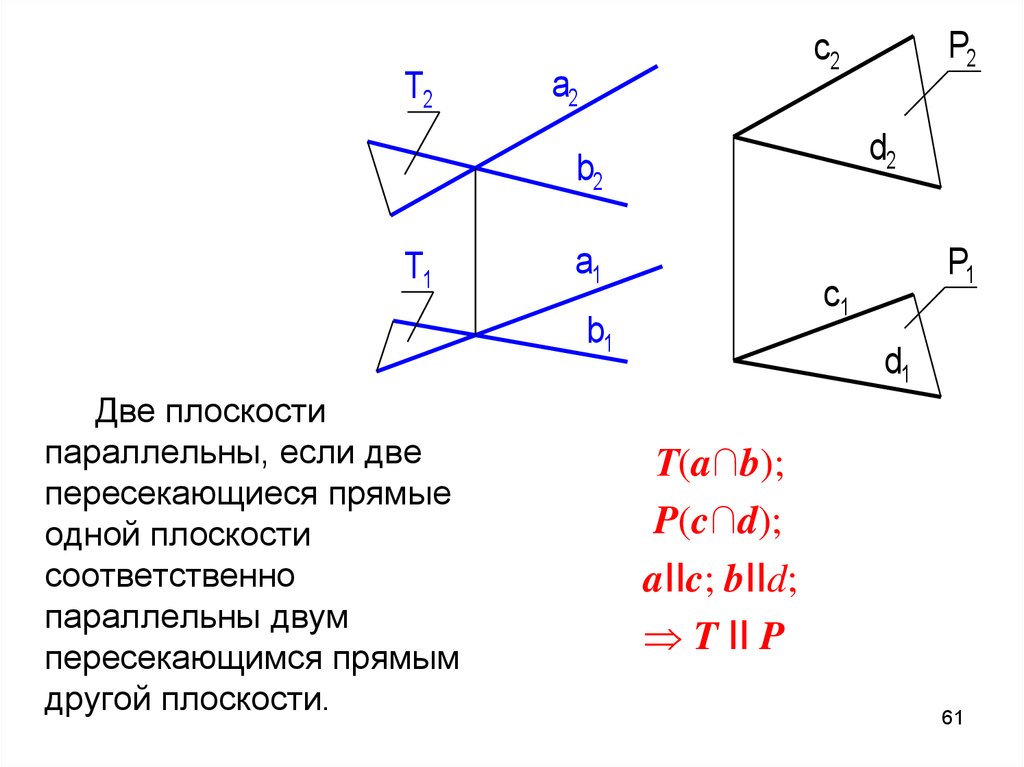
5960. Параллельные плоскости
6061.
T2T2a2a2
d2d2
b2b2
T1T1
a1a1
P1P1
c1c1
b1b1
Две плоскости
параллельны, если две
пересекающиеся прямые
одной плоскости
соответственно
параллельны двум
пересекающимся прямым
другой плоскости.
P2P2
c2c2
d1d1
Т(a∩b);
P(c∩d);
aIIc; bIId;
T II P
61
62. Пересечение двух плоскостей
6263.
Линией пересечения плоскостей является прямая,которая должна быть задана двумя точками.
Любая из этих двух точек может быть получена:
• пересечением двух прямых (в каждой из двух
заданных плоскостей выбирается по одной прямой и
находится точка их пересечения);
• пересечением прямой с плоскостью (в одной из двух
заданных плоскостей выбирается прямая и
определяется точка ее пересечения с другой
плоскостью);
• пересечением трех плоскостей (вводится
дополнительная третья плоскость, и строится точка
пересечения двух заданных плоскостей и
дополнительной).
64.
В первом варианте для выполнения пересечениядвух прямых должно быть обеспечено условие:
обе прямые должны лежать в одной плоскости.
Т.е. должна быть введена третья дополнительная
плоскость, которая при пересечении с исходными
плоскостями и создает эти прямые. Тем самым мы
переходим к третьему варианту.
При определении точки пересечения прямой линии
с плоскостью также должна быть введена
дополнительная секущая плоскость.
Следовательно, реально используются третий
вариант.
65. Способ вспомогательных секущих плоскостей
66.
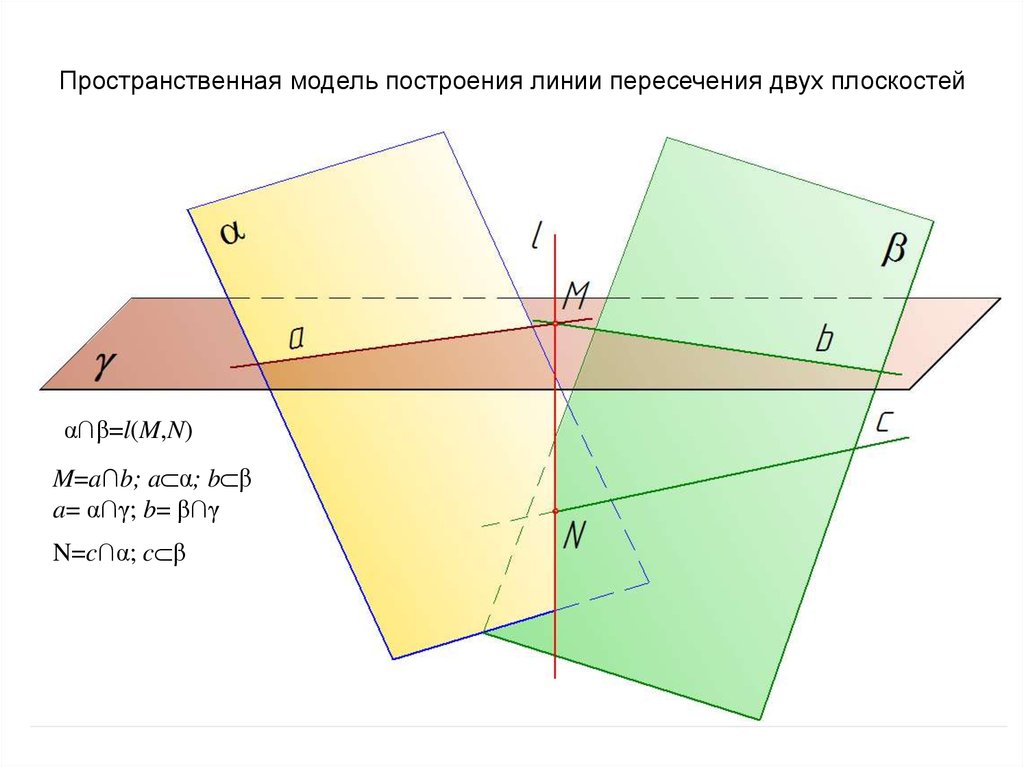
Пространственная модель построения линии пересечения двух плоскостейα∩β=l(M,N)
M=a∩b; a α; b β
a= α∩γ; b= β∩γ
N=c∩α; c β
67.
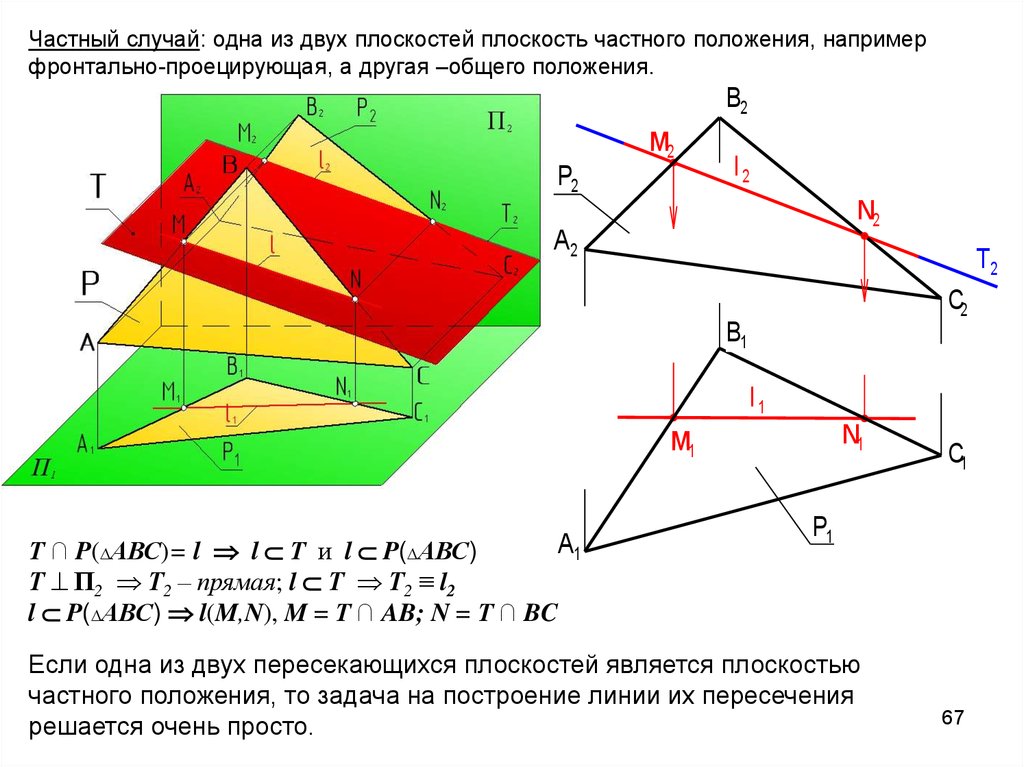
Частный случай: одна из двух плоскостей плоскость частного положения, напримерфронтально-проецирующая, а другая –общего положения.
B2
M2
P2
l2
N2
A2
T2
C2
B1
l1
N1
M1
A1
Т ∩ P(∆АВС)= l l Т и l P(∆АВС)
Т П2 Т2 – прямая; l Т Т2 ≡ l2
l P(∆АВС) l(M,N), M = Т ∩ AB; N = Т ∩ BC
C1
P1
Если одна из двух пересекающихся плоскостей является плоскостью
частного положения, то задача на построение линии их пересечения
решается очень просто.
67
68.
Следовательно, при построении линиипересечения двух плоскостей, для
упрощения построений вспомогательные
секущие плоскости должны быть только
плоскостями частного положения –
проецирующими или уровня.
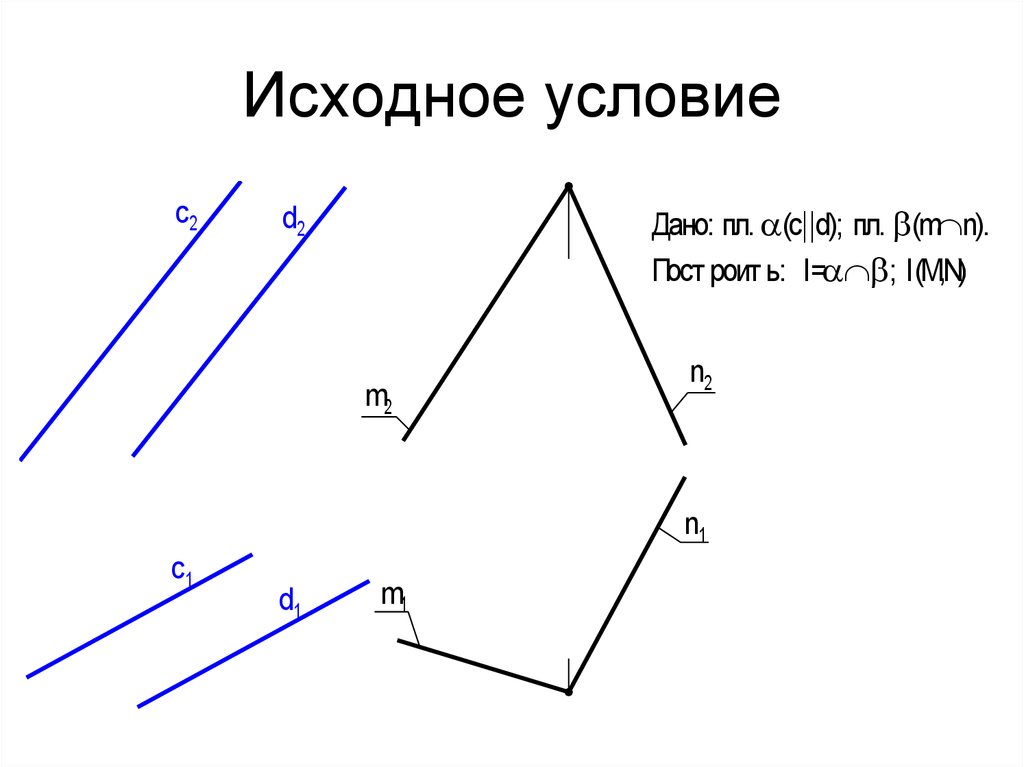
69. Исходное условие
c2Дано: пл. (с d); пл. (m n).
Пост роит ь: l= ; l(M,N)
d2
m2
n2
n1
c1
d1
m1
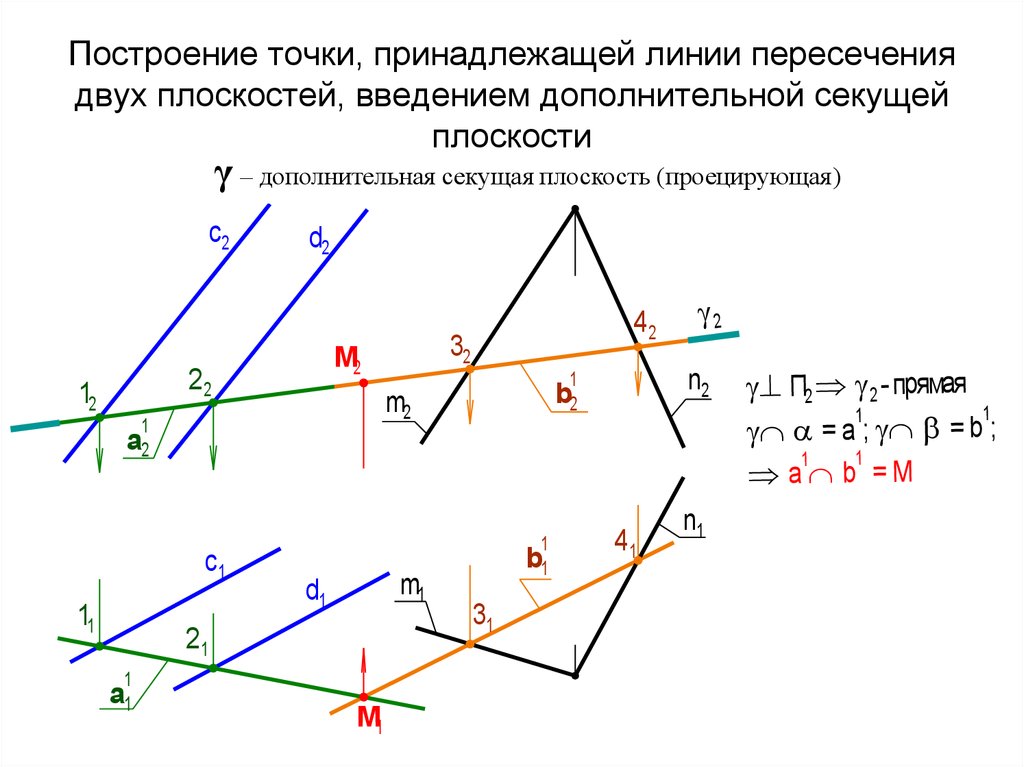
70. Построение точки, принадлежащей линии пересечения двух плоскостей, введением дополнительной секущей плоскости
γ – дополнительная секущая плоскость (проецирующая)c2
d2
32
M2
22
12
42
1
n2
1
b2
m2
2
a2
c1
11
m1
d1
21
1
a1
M1
1
b1
31
41
n1
П2 2 - прямая
1
1
b
= a ; = ;
1
1
=M
b
a
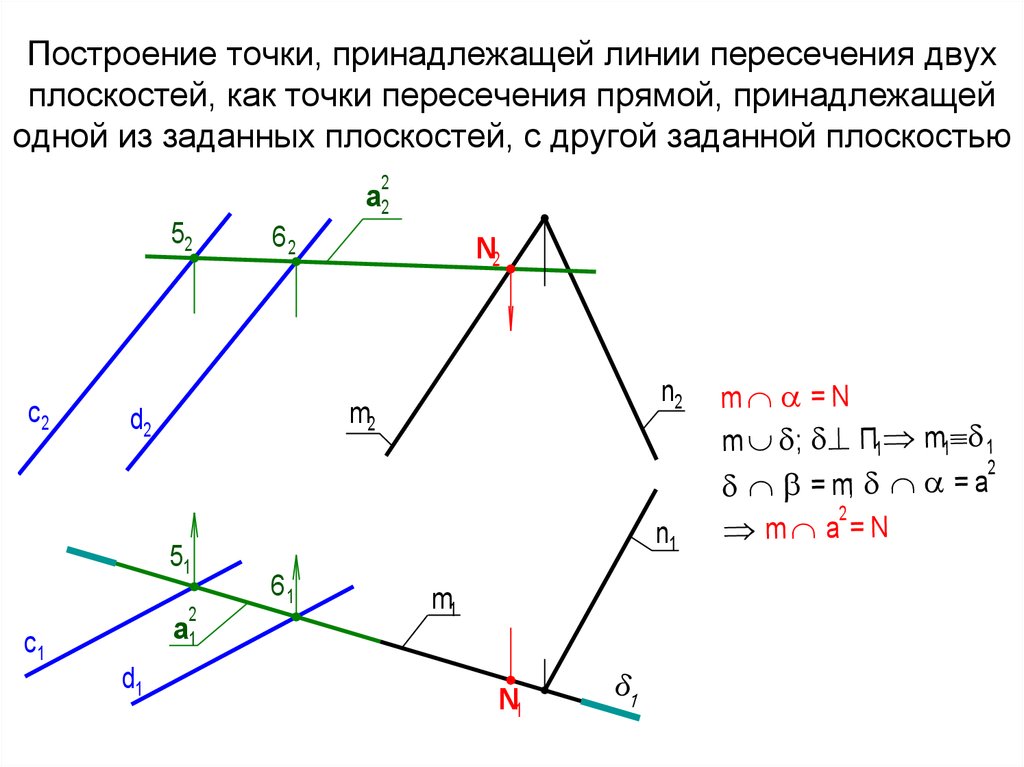
71. Построение точки, принадлежащей линии пересечения двух плоскостей, как точки пересечения прямой, принадлежащей одной из заданных плоскос
Построение точки, принадлежащей линии пересечения двухплоскостей, как точки пересечения прямой, принадлежащей
одной из заданных плоскостей, с другой заданной плоскостью
2
a2
52
c2
62
51
2
a1
d1
n2
m2
d2
c1
N2
n1
61
m1
N1
1
m =N
m ; П1 m1 1
2
a
=
m;
=
2
m a =N
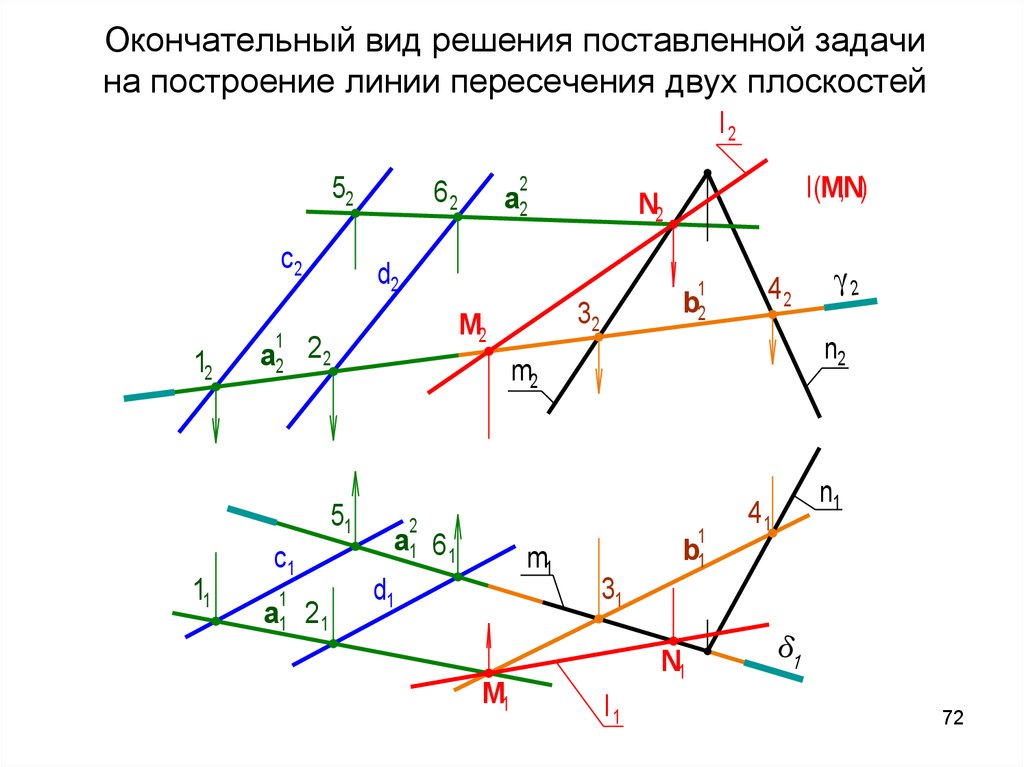
72. Окончательный вид решения поставленной задачи на построение линии пересечения двух плоскостей
l252
c2
12
c1
21
l(M,N)
N2
1
b2
32
M2
1
a2 22
1
a1
a2
d2
51
11
2
62
42
n2
m2
2
a1 6 1
m1
d1
M1
2
1
n1
41
b1
31
N1
l1
1
72
73. Взаимное положение прямой линии и плоскости
7374.
Прямая по отношению к плоскостиможет занимать следующие положения:
• Принадлежать;
• Быть параллельной;
• Пересекать;
• Быть перпендикулярной.
74
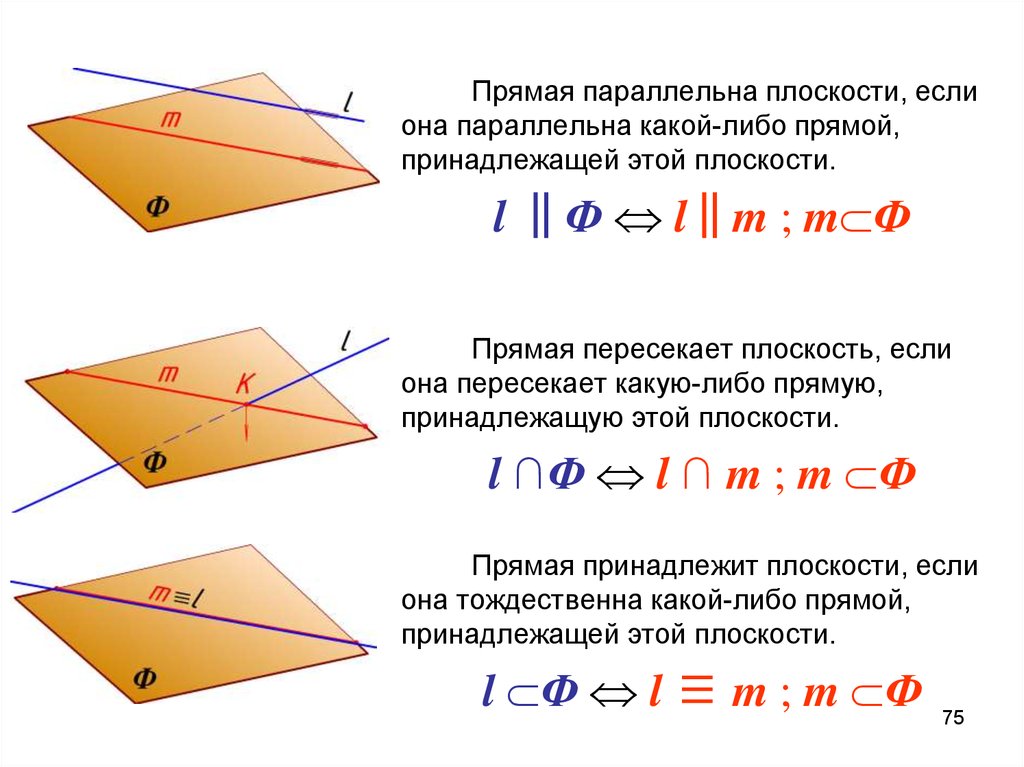
75.
Прямая параллельна плоскости, еслиона параллельна какой-либо прямой,
принадлежащей этой плоскости.
l ‖Ф l‖m ; m Ф
Прямая пересекает плоскость, если
она пересекает какую-либо прямую,
принадлежащую этой плоскости.
l ∩Ф l ∩ m ; m Ф
Прямая принадлежит плоскости, если
она тождественна какой-либо прямой,
принадлежащей этой плоскости.
l Ф l ≡ m ; m Ф
75
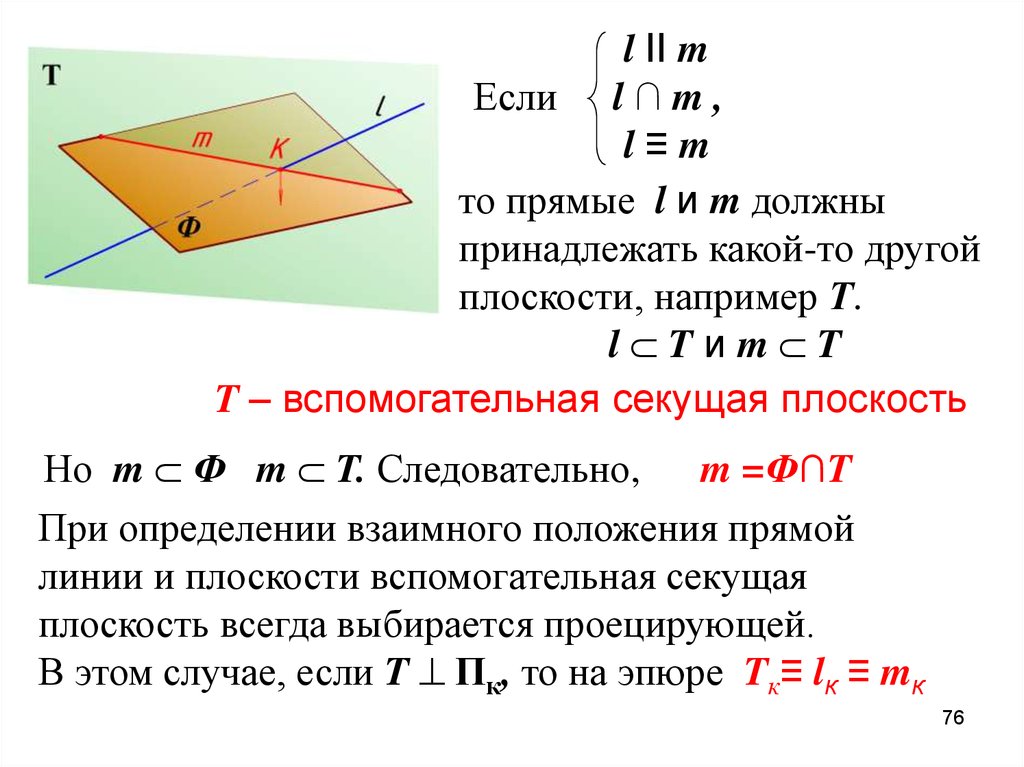
76.
l II mЕсли l ∩ m ,
l≡m
то прямые l и m должны
принадлежать какой-то другой
плоскости, например Т.
l Tиm T
T – вспомогательная секущая плоскость
Но m Ф m T. Следовательно,
m =Ф∩T
При определении взаимного положения прямой
линии и плоскости вспомогательная секущая
плоскость всегда выбирается проецирующей.
В этом случае, если T Пк, то на эпюре Tк≡ lк ≡ mк
76
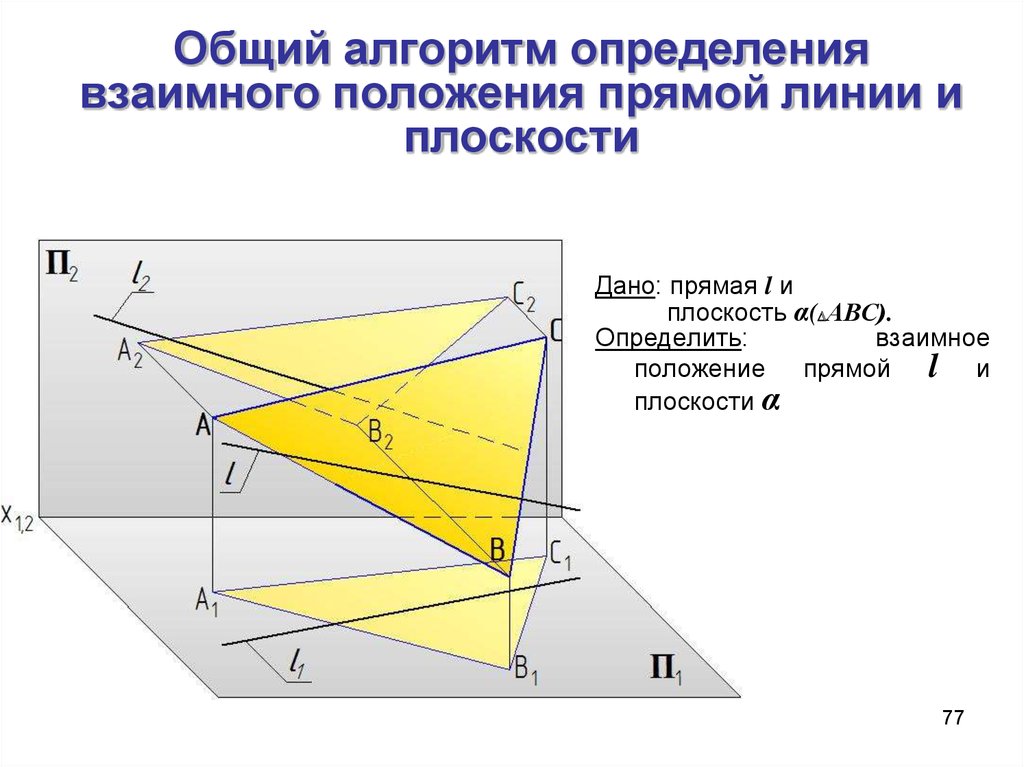
77. Общий алгоритм определения взаимного положения прямой линии и плоскости
Дано: прямая l иплоскость α( АВС).
Определить:
взаимное
положение прямой l и
плоскости α
77
78.
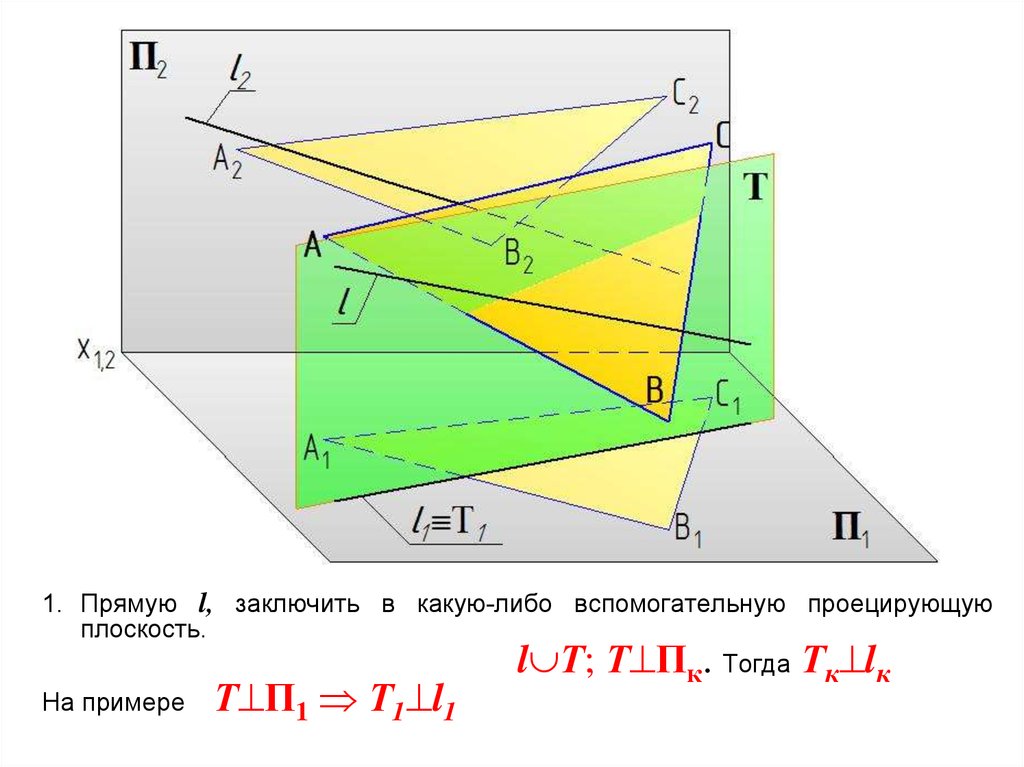
1. Прямую l, заключить в какую-либо вспомогательную проецирующуюплоскость.
l Т; Т Пк. Тогда Тк lк
На примере Т П1 Т1 l1
79.
2. Построить линию пересечения заданной плоскости α и вспомогательной Т.m =α∩T
m T mk Tk ; m α m (1,2)
На примере. m1 T1 ; m α m (1,2), 1=m∩AB, 2=m∩CB
3. Определить взаимное положение прямой l и плоскости α.
80.
Решение рассмотреннойзадачи на эпюре
81.
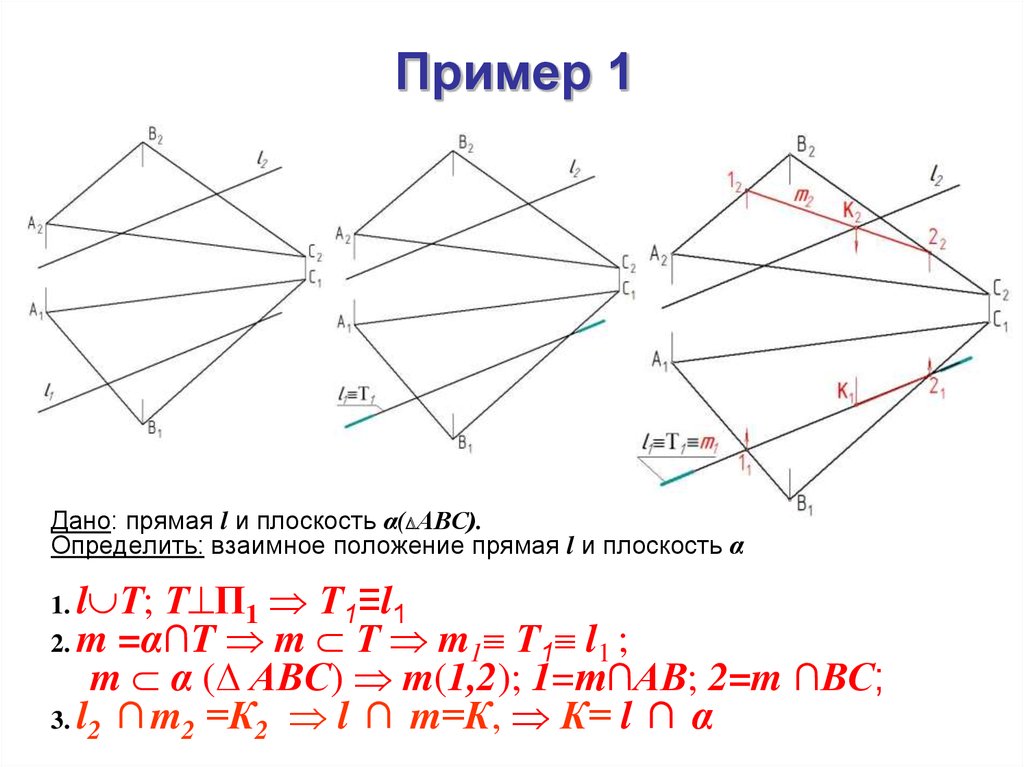
Пример 1Дано: прямая l и плоскость α( АВС).
Определить: взаимное положение прямая l и плоскость α
1. l Т; Т П1
2. m =α∩T m
Т1≡l1
Т m1 Т1 l1 ;
m α ( АВС) m(1,2); 1=m∩АВ; 2=m ∩ВС;
3. l2 ∩m2 =К2 l ∩ m=К, К= l ∩ α
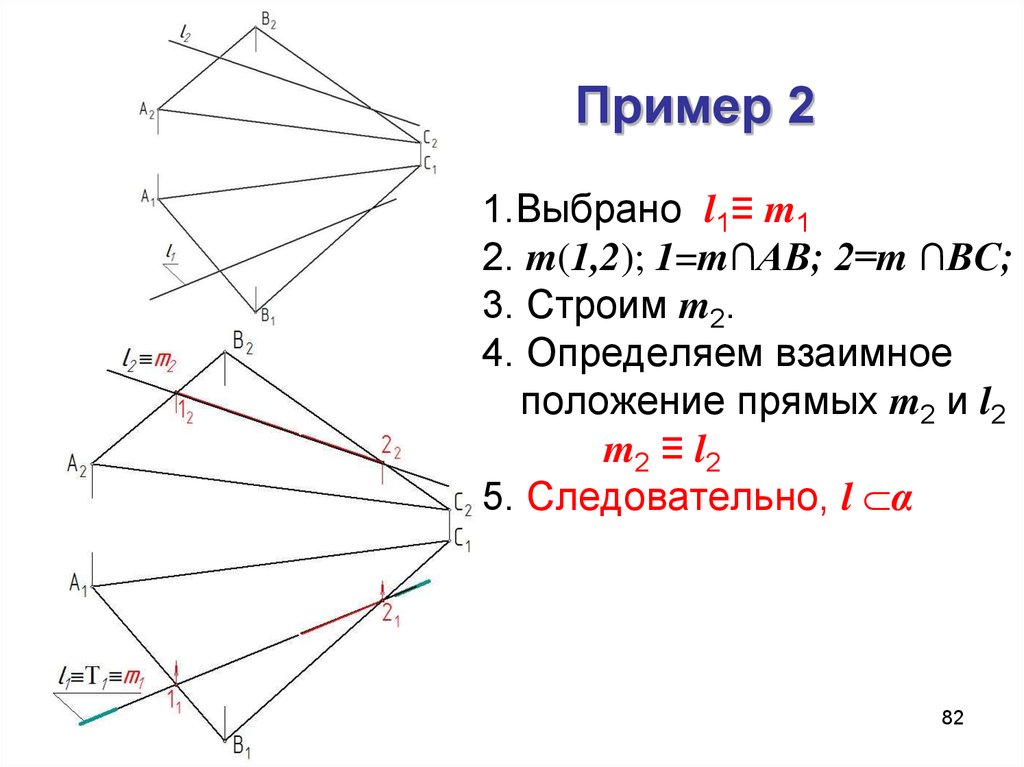
82. Пример 2
1.Выбрано l1≡ m12. m(1,2); 1=m∩АВ; 2=m ∩ВС;
3. Строим m2.
4. Определяем взаимное
положение прямых m2 и l2
m2 ≡ l2
5. Следовательно, l α
82
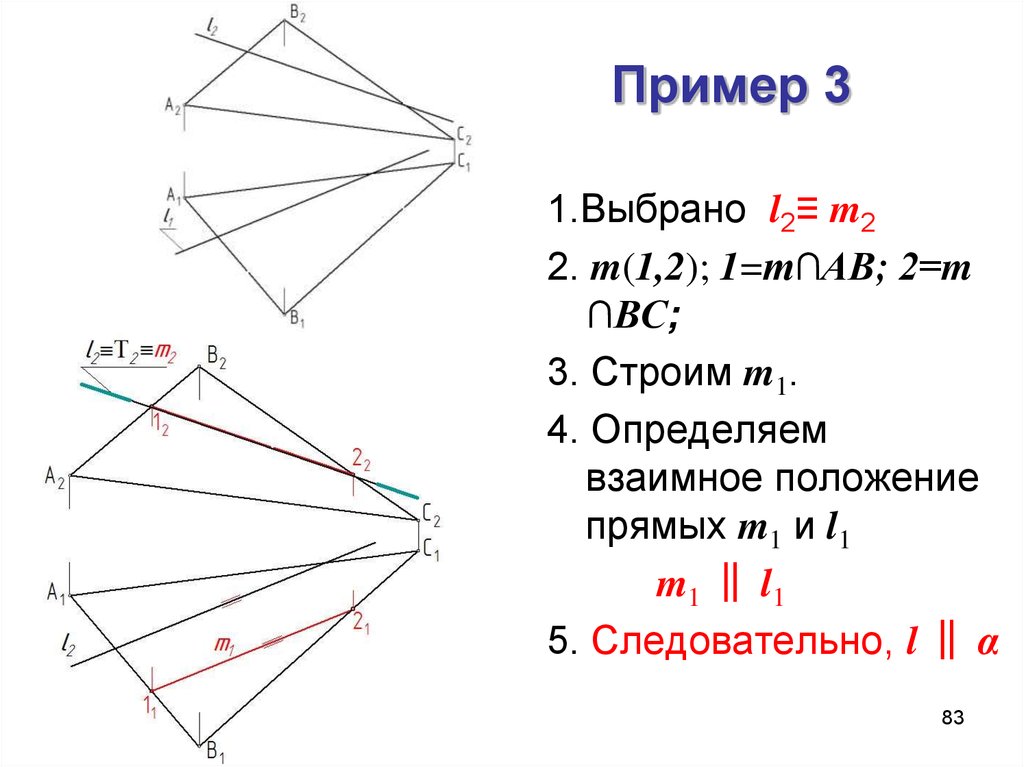
83. Пример 3
1.Выбрано l2≡ m22. m(1,2); 1=m∩АВ; 2=m
∩ВС;
3. Строим m1.
4. Определяем
взаимное положение
прямых m1 и l1
m1 ‖ l1
5. Следовательно, l ‖ α
83
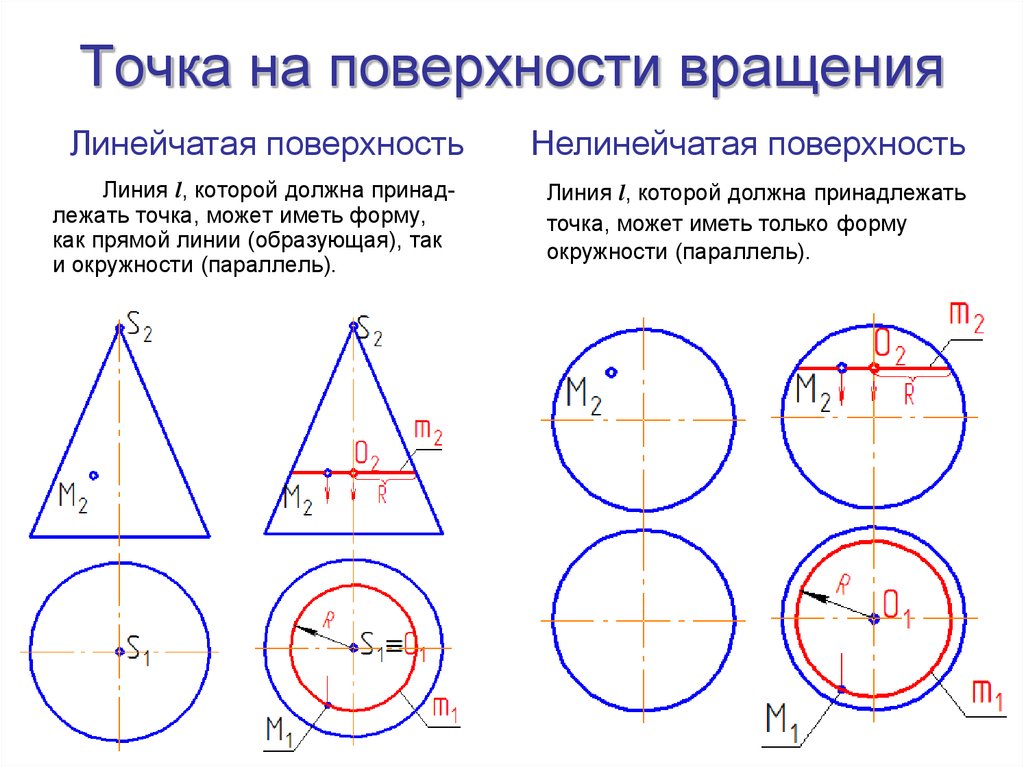
84. Точка на поверхности
8485.
Точка принадлежит поверхности,если она принадлежит линии,
принадлежащей этой поверхности
А Ф А l , l Ф
Линия l должна на проекциях иметь наиболее
простую геометрическую форму: прямая
или окружность (по возможности)
85
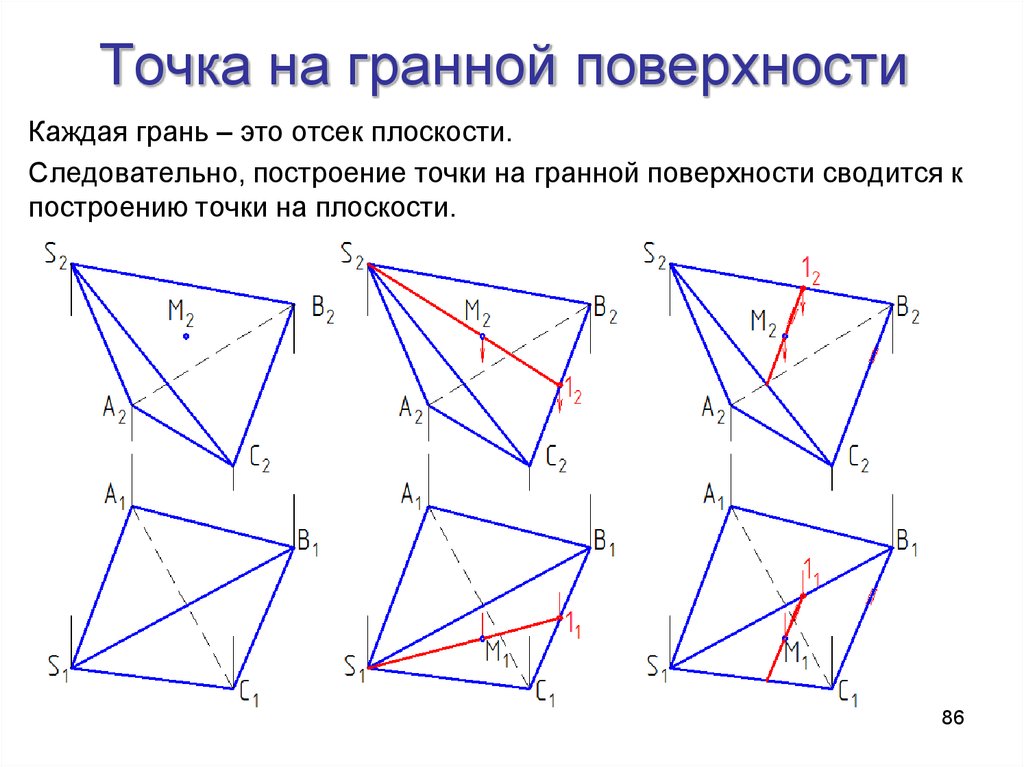
86. Точка на гранной поверхности
Каждая грань – это отсек плоскости.Следовательно, построение точки на гранной поверхности сводится к
построению точки на плоскости.
86
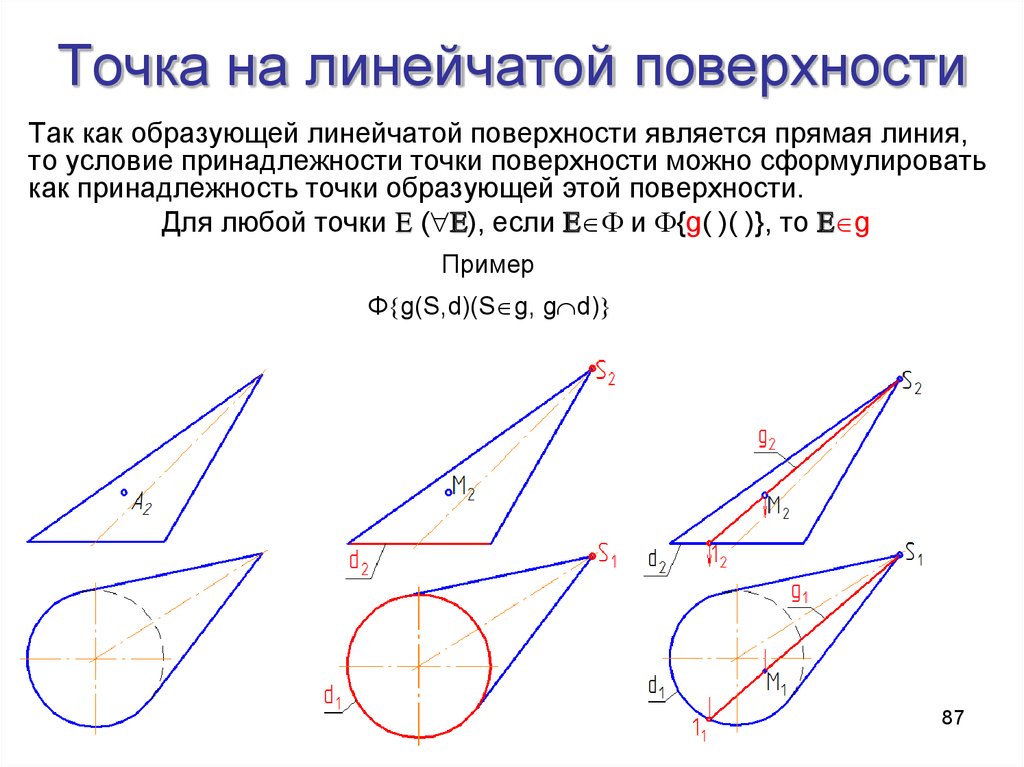
87. Точка на линейчатой поверхности
Так как образующей линейчатой поверхности является прямая линия,то условие принадлежности точки поверхности можно сформулировать
как принадлежность точки образующей этой поверхности.
Для любой точки ( ), если и {g( )( )}, то g
Пример
Ф g(S,d)(S g, g d)
87
88.
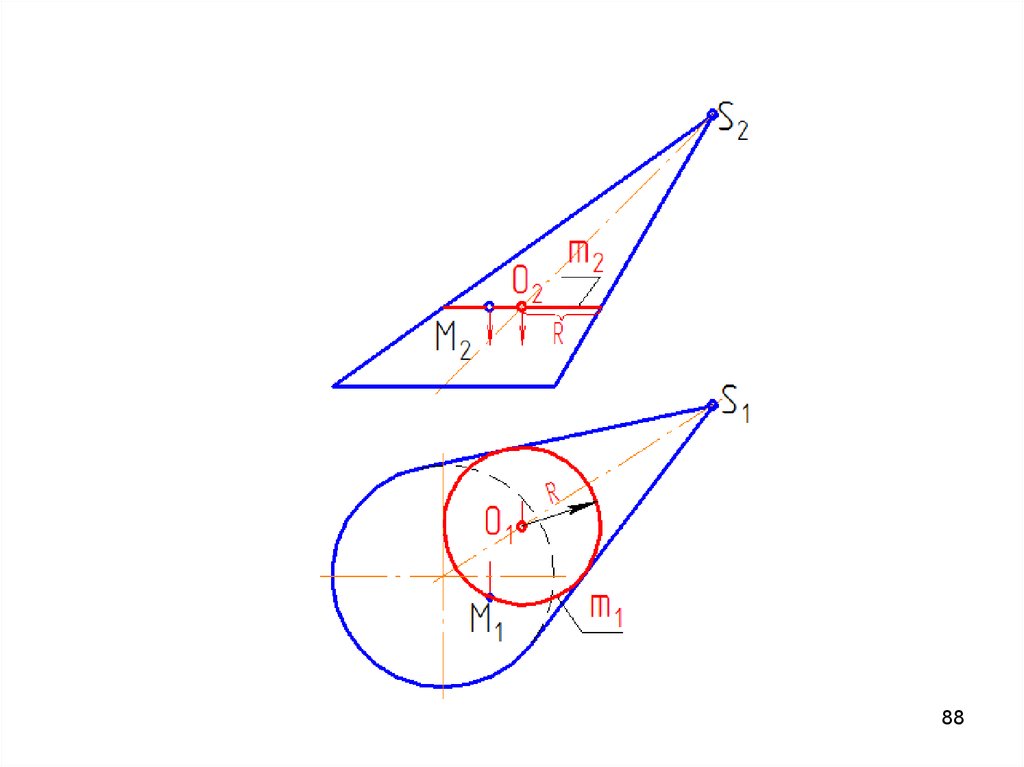
8889. Точка на поверхности вращения
Линейчатая поверхностьЛиния l, которой должна принадлежать точка, может иметь форму,
как прямой линии (образующая), так
и окружности (параллель).
Нелинейчатая поверхность
Линия l, которой должна принадлежать
точка, может иметь только форму
окружности (параллель).
89
90. Линия на поверхности
91.
• Линия принадлежит поверхности, есливсе множество ее точек принадлежит
этой поверхности.
• Следовательно, чтобы построить
линию на поверхности, необходимо
представить эту линию, как множество
точек, и построить каждую из точек
этого множества, используя условие
принадлежности точки поверхности.
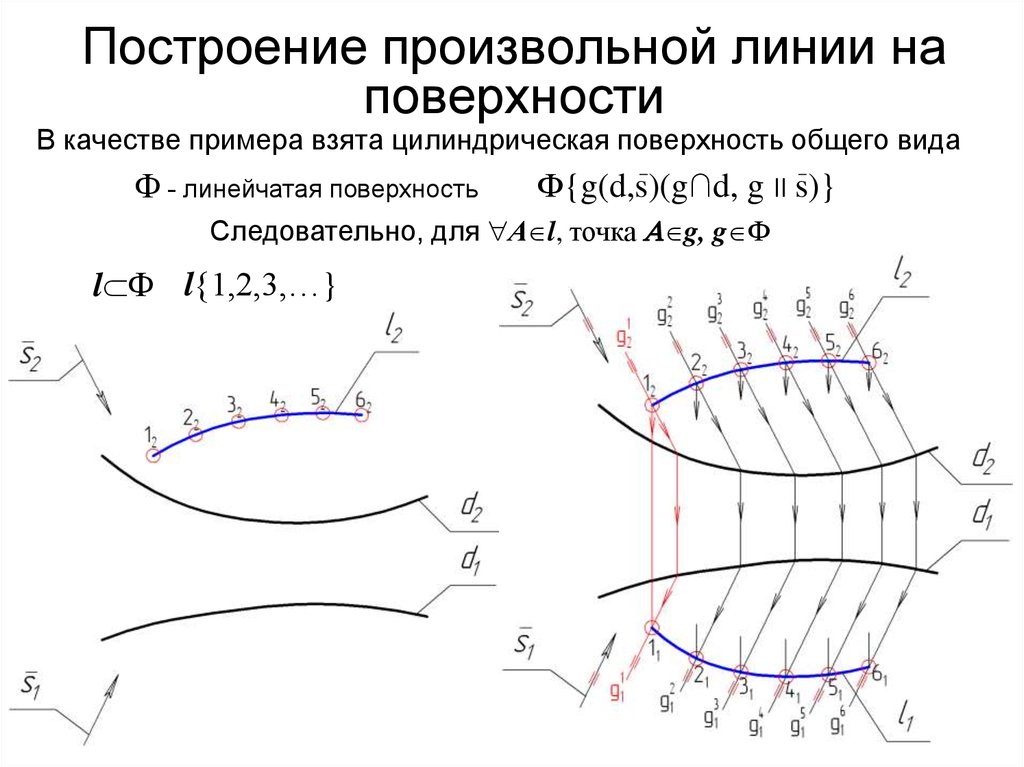
92. Построение произвольной линии на поверхности
В качестве примера взята цилиндрическая поверхность общего вида- линейчатая поверхность
Ф{g(d,s)(g∩d, g II s)}
Следовательно, для А l, точка g, g Ф
l l{1,2,3,…}
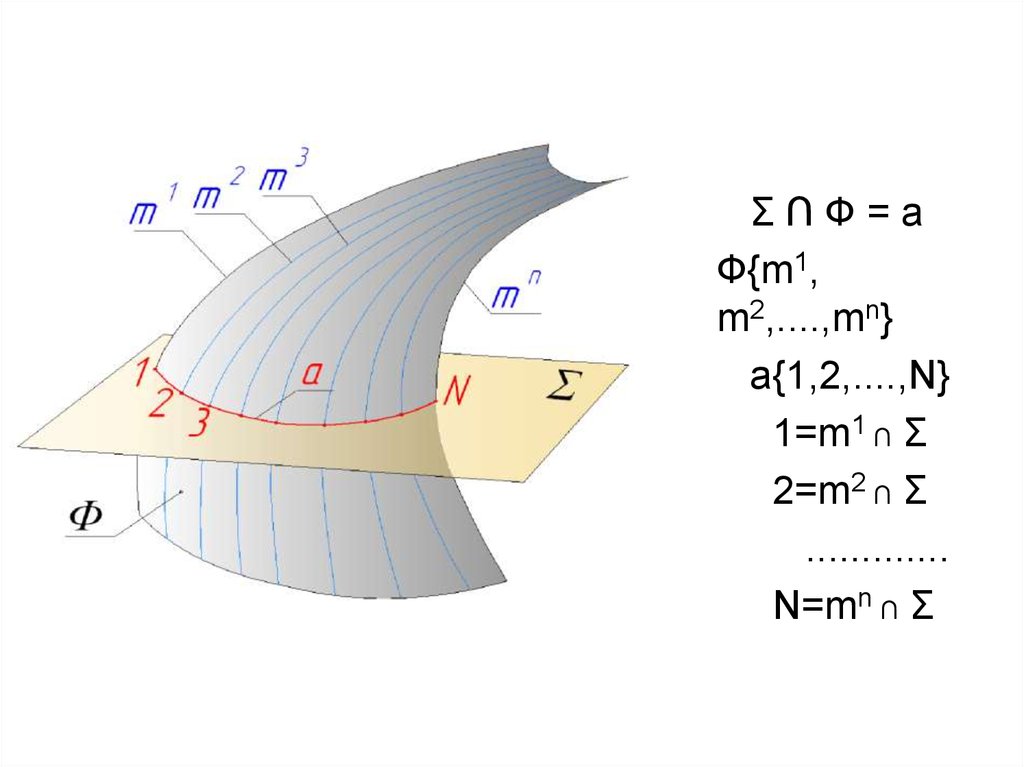
93. Пересечение поверхности плоскостью
94.
Σ∩Ф=aФ{m1,
m2,....,mn}
a{1,2,....,N}
1=m1 ∩ Σ
2=m2 ∩ Σ
.............
N=mn ∩ Σ
95.
• Линию пересечения поверхности плоскостьюследует рассматривать как множество точек
пересечения секущей плоскости с линиями,
принадлежащими поверхности.
• Форма линии пересечения поверхности
плоскостью определяется формой заданной
поверхности и положением плоскости
относительно этой поверхности.
• Для кривой поверхности, в общем случае, линия
пересечения - это плоская кривая линия.
96.
Из всего множества точек линии пересечениядолжны быть обязательно построены
следующие точки:
• точки, определяющие габариты формы
фигуру сечения;
• точки, определяющие габариты фигуры
сечения по высоте, глубине и длине;
• точки, определяющие видимость фигуры
сечения на проекциях.
97. Пересечение гранной поверхности плоскостью
98.
При пересечении граннойповерхности плоскостью
линия пересечения – это
ломаная линия, каждый
участок которой – отрезок
прямой, представляющий
собой линию пересечения
грани поверхности (отсека
плоскости) с секущей
плоскостью, а точки излома –
точки пересечения ребер
гранной поверхности
(отрезков прямых) с той же
секущей плоскостью.
99.
Следовательно, решение задачи напостроение линии пересечения гранной
поверхности плоскостью сводится к
определению точек пересечения ребер
гранной поверхности с принятой секущей
плоскостью (пересечение прямой с
плоскостью).
99
100.
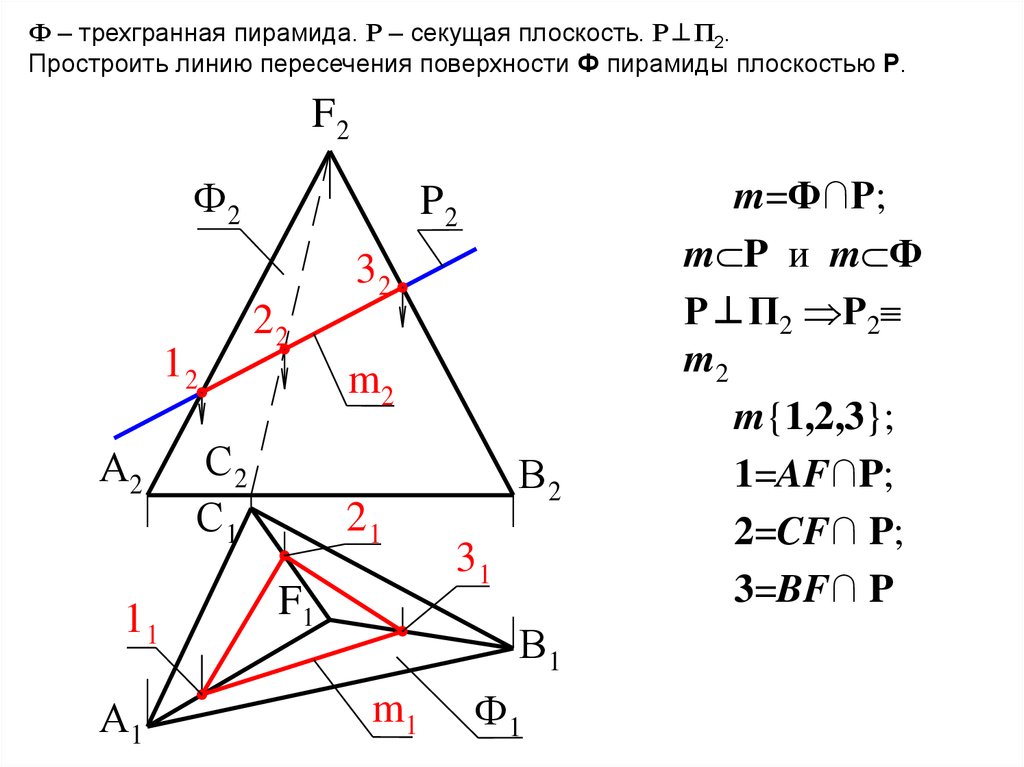
Ф – трехгранная пирамида. Р – секущая плоскость. Р⊥П2.Простроить линию пересечения поверхности Ф пирамиды плоскостью Р.
F2
Ф2
P2
32
12
А2
11
А1
22
m2
С2
С1
21
F1
В2
31
В1
m1
Ф1
m=Ф∩Р;
m P и m Ф
Р⊥П2 Р2
m2
m{1,2,3};
1=AF∩P;
2=CF∩ P;
3=BF∩ P
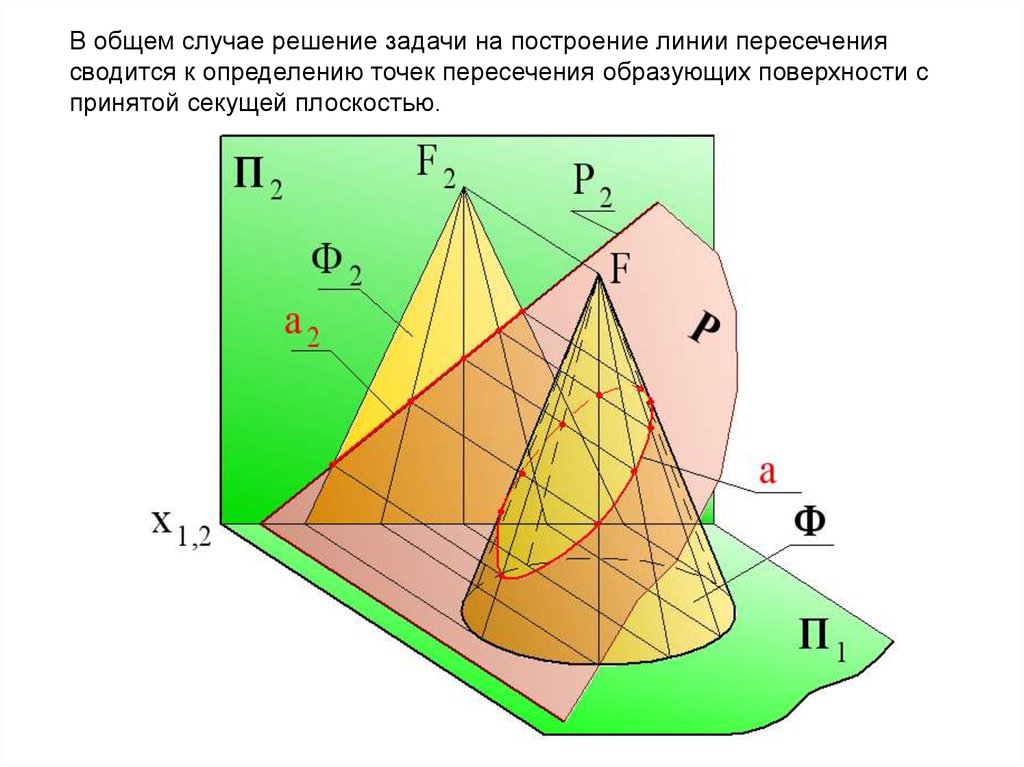
101. Пересечение конической поверхности плоскостью
102.
В общем случае решение задачи на построение линии пересечениясводится к определению точек пересечения образующих поверхности с
принятой секущей плоскостью.
103.
F2Ф2
g2 g2
1
Р2
2
72
a2
22
12
32
122
52
42
112
102
62
92
1
2
82
R
m2
4
m2
3
m2
m2
4
А2 В2
В1
m2
121 111 101 91
81
2
g1
F1
1
71
g1
11
a1
m2
21
А1
Ф1
31
41
51
61
m2
R
3
4
m2
4
2
1
Данная коническая
поверхность относится к
классу линейчатых и
подклассу поверхностей
вращения.
Следовательно, для
построения точки на
поверхности можно
использовать, как
прямую линия
(образующую), так и
окружность (параллель).
104. Пересечение прямой линии с поверхностью
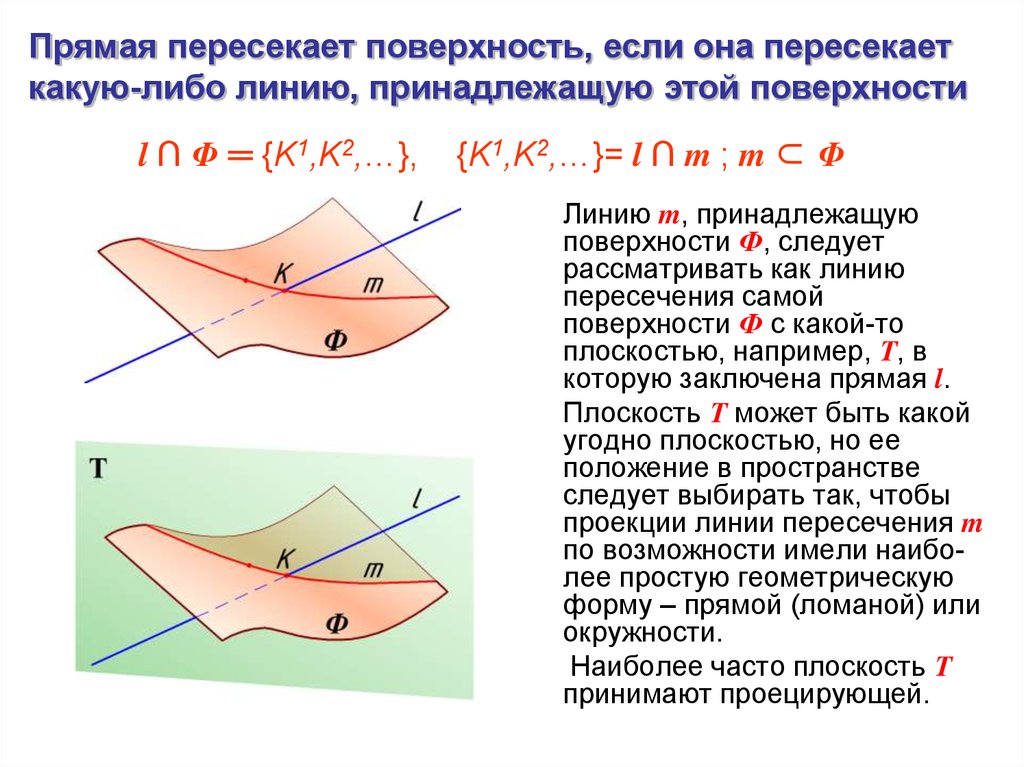
105.
Прямая пересекает поверхность, если она пересекаеткакую-либо линию, принадлежащую этой поверхности
l ∩ Φ ═ {K1,K2,…},
{K1,K2,…}= l ∩ m ; m ⊂ Φ
Линию m, принадлежащую
поверхности Ф, следует
рассматривать как линию
пересечения самой
поверхности Ф с какой-то
плоскостью, например, Т, в
которую заключена прямая l.
Плоскость Т может быть какой
угодно плоскостью, но ее
положение в пространстве
следует выбирать так, чтобы
проекции линии пересечения m
по возможности имели наиболее простую геометрическую
форму – прямой (ломаной) или
окружности.
Наиболее часто плоскость Т
принимают проецирующей.
106.
Общий (краткий) алгоритм построенияточки пересечения прямой с поверхностью
1. l Т с условием, что
Т ∩ Φ = m – линия на проекциях возможности
наиболее простой геометрической формы.
Если Т Пк, то mк ≡ Тк ≡ lк )
2. Строим проекции линии m.
3. Так как (l Т) (m Т)
l ∩ m = {К1, К2, …}
{К1, К2, …} m; m Φ
{К1, К2, …} Φ
{К1, К2, …} = l ∩Φ
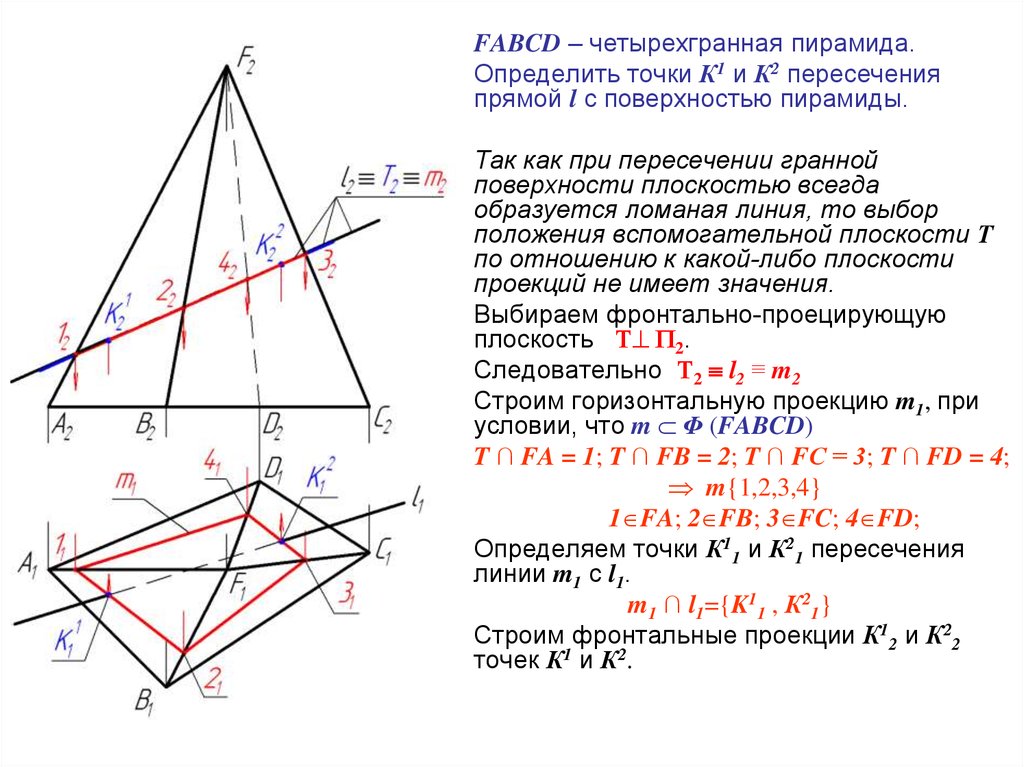
107. Пересечение прямой линии с гранной поверхностью (на примере пирамидальной поверхности)
108.
FABCD – четырехгранная пирамида.Определить точки К1 и К2 пересечения
прямой l с поверхностью пирамиды.
Так как при пересечении гранной
поверхности плоскостью всегда
образуется ломаная линия, то выбор
положения вспомогательной плоскости Т
по отношению к какой-либо плоскости
проекций не имеет значения.
Выбираем фронтально-проецирующую
плоскость Т П2.
Следовательно Т2 l2 ≡ m2
Строим горизонтальную проекцию m1, при
условии, что m Φ (FABCD)
T ∩ FA = 1; T ∩ FB = 2; T ∩ FС = 3; T ∩ FD = 4;
m{1,2,3,4}
1 FA; 2 FB; 3 FC; 4 FD;
Определяем точки К11 и К21 пересечения
линии m1 с l1.
m1 ∩ l1={K11 , К21}
Строим фронтальные проекции К12 и К22
точек К1 и К2.
109. Пересечение прямой линии с конической поверхностью
110.
Задана прямая круговая коническаяповерхность Ф и прямая l.
Определить точки К1 и К2
пересечения прямой l с конической
поверхностью Ф.
Так как коническая поверхность
является прямой круговой с
вертикальной осью вращения, то
все параллели этой поверхности
являются горизонталями.
Заданная прямая также является
горизонталью.
Следовательно, если прямую l
заключить в горизонтальную
плоскость уровня, например, Т, то
линией пересечения плоскости Т с
поверхностью Ф будет одна из
параллелей поверхности Ф.
111.
Совмещаем m2 ≡ l2Строим горизонтальную проекцию
m1-окружность линии m.
На горизонтальной проекции определяем точки К1 и К2 пересечения
прямой l и линии m.
Строим фронтальные проекции
точек К1 и К2.
Определяем видимость участков
прямой l.
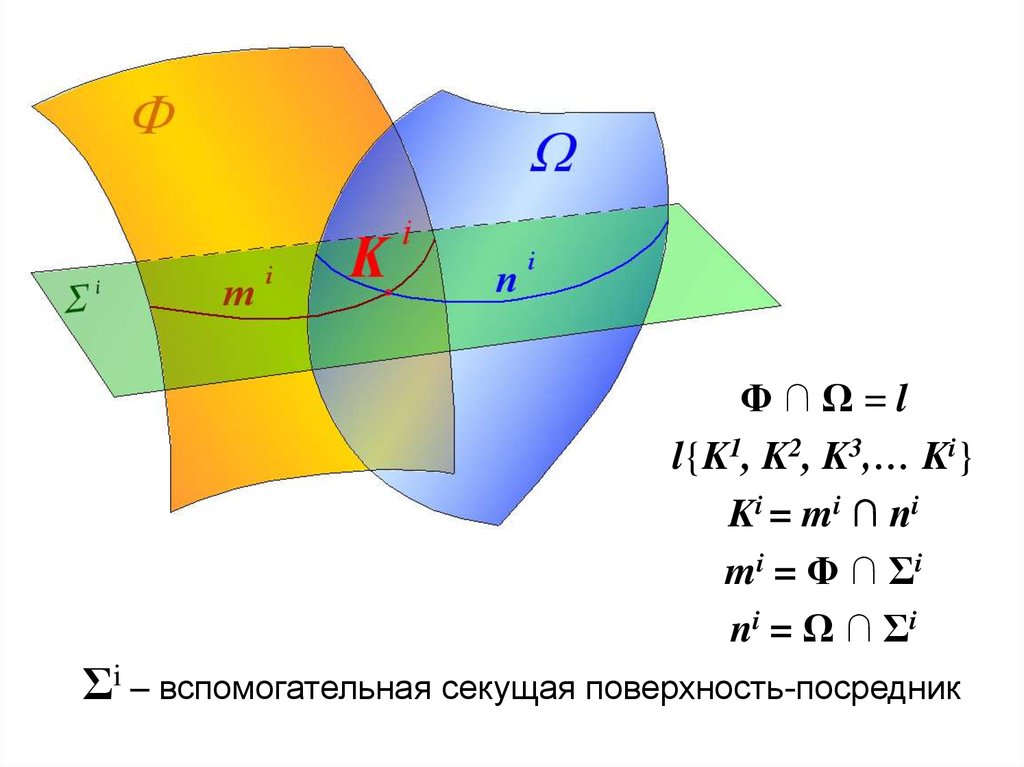
112. Взаимное пересечение поверхностей
113.
Линией пересечения двух поверхностей , вобщем случае, является пространственная
кривая линия, каждая точка которой может быть
представлена как точка пересечения двух линий,
принадлежащих каждой из заданных поверхностей
и принадлежащих вспомогательным секущим
поверхностям-посредникам, как плоским, так и
кривым.
Обязательные требования, предъявляемые к
секущим поверхностям-посредникам:
• каждая из секущих поверхностей-посредников
должна пересекать обе заданные поверхности;
• линии, получаемые в результате пересечения
должны пересекаться между собой и иметь, по
возможности, наиболее простую геометрическую
форму.
114.
Φ∩Ω=ll{K1, K2, K3,… Ki}
Ki = mi ∩ ni
mi = Φ ∩ Σi
ni = Ω ∩ Σi
Σi – вспомогательная секущая поверхность-посредник
115.
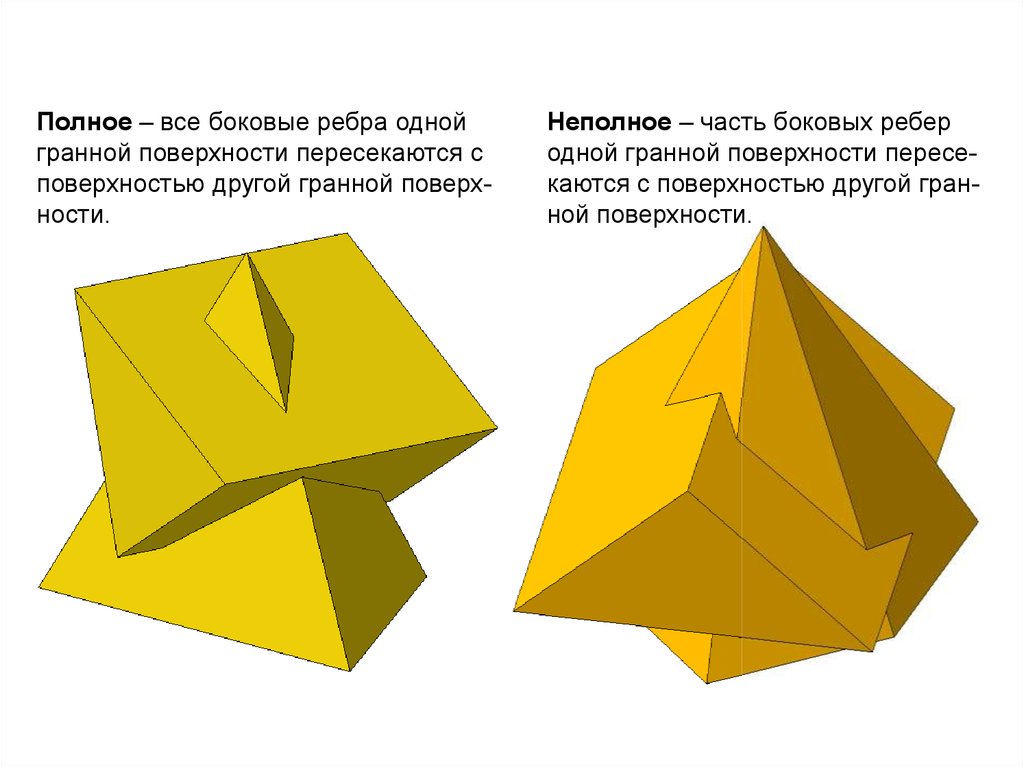
Пересечение двух поверхностей можетбыть полным и неполным (частичным).
Пересечение поверхностей считается
полным, если все образующие одной
поверхности пересекаются с другой
поверхностью. В общем случае образуются две замкнутые линии пересечения.
В противном случае пересечение считается неполным (частичным). В этом
случае формируется только одна замкнутая линия пересечения.
116.
Полное – все боковые ребра однойгранной поверхности пересекаются с
поверхностью другой гранной поверхности.
Неполное – часть боковых ребер
одной гранной поверхности пересекаются с поверхностью другой гранной поверхности.
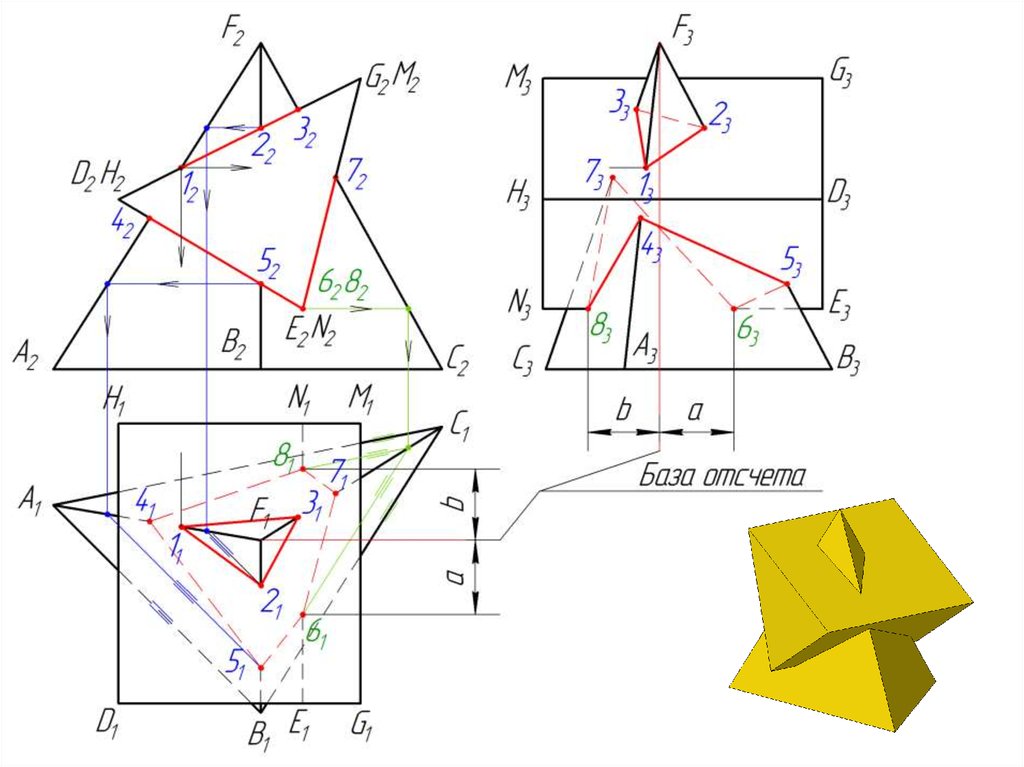
117. Взаимное пересечение двух гранных поверхностей
Линией пересечения двух гранных поверхностейявляется ломаная прямая линия, точками излома
которой являются точки пересечения ребер одной
гранной поверхности с гранями другой, а линиями,
соединяющими эти точки, – отрезки прямых
взаимного пересечения граней обеих поверхностей.
Т.е. вся задача на построение линии пересечения двух гранных поверхностей сводится к многократному решению задачи на определение точки
пересечения прямой с плоскостью.
118.
119.
120. Взаимное пересечение гранной поверхности с кривой поверхностью
Линия пересечения гранной поверхности с кривойповерхностью представляет собой ломаную кривую
линию, точками излома которой являются точки
пересечения ребер гранной поверхности с кривой
поверхностью, а линиями, соединяющими эти точки –
плоские кривые, получаемые при пересечении граней
гранной поверхности (отсеков плоскостей) с кривой
поверхностью.
Т.е. задача на построение линии пересечения
гранной поверхности с кривой поверхностью сводится к
многократному решению двух задач:
• определение точек пересечения прямой линии с
кривой поверхностью;
• построение линии пересечения кривой поверхности
плоскостью.
121.
12 22152 162
172 182
52 62
92 102
23
163
63
112 122
123
32 42
72 82
183
101
121
61
161
181
a
21
b
141
11
151
31
91
51
171
111
71
131
53
93
33
133
143
Выбранная база отсчета
41
b
43
132
81
a
153
173
103
83
142
13
113
73






































































 Математика
Математика








