Лекция 4 Способы преобразования_Строительство

1. Лекция 4 Тема: Способы преобразования чертежа

ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
Лекция 4
Тема: Способы преобразования чертежа
РАЗРАБОТАЛИ: ст. преп. кафедры Н Г и Г – Крамаровская В.И.
ст. преп. кафедры Н Г и Г – Стаселько О.Л.
ст. преп. кафедры Н Г и Г – Шушарина И.В.

2.

• Способы преобразования проекций предназначены для
решения метрических задач, связанных с определением
действительных размеров и формы изображенных на
эпюре объектов, а также для определения расстояния
между объектами

3.

• Решение многих задач начертательной геометрии значительно
упрощается, если заданные геометрические элементы занимают в
пространстве частное положение. Поэтому в основе способов
преобразования проекций лежит переход от общего положения к
частному, когда величина и форма объекта проецируются без
искажения
• Рассмотрим способы преобразования проекций на примере задач

4. Способ замены плоскостей проекций

5.

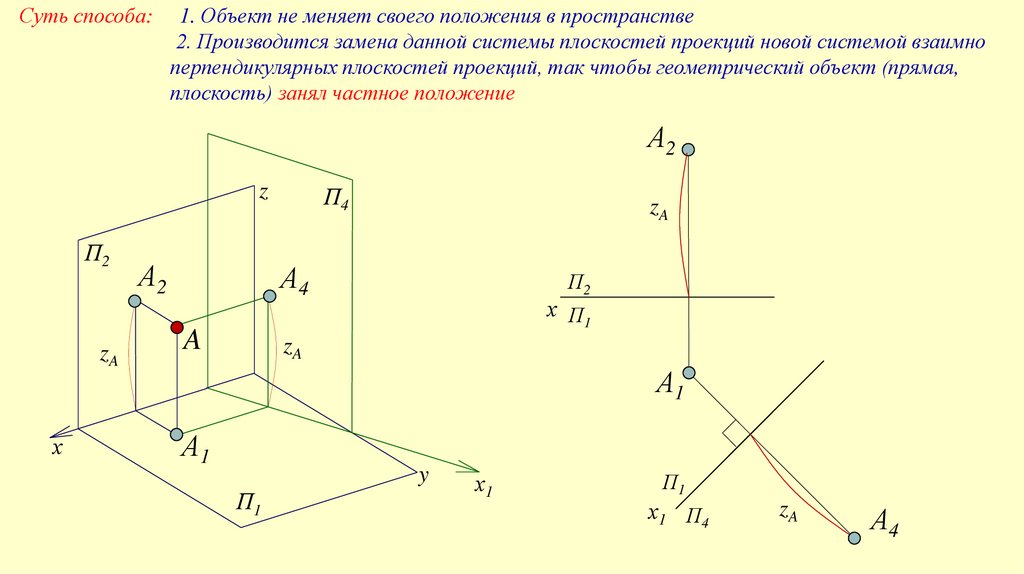
Суть способа:
1. Объект не меняет своего положения в пространстве
2. Производится замена данной системы плоскостей проекций новой системой взаимно
перпендикулярных плоскостей проекций, так чтобы геометрический объект (прямая,
плоскость) занял частное положение
А2
z
П2
zA
х
А2
П4
zA
А4
A
П2
х П1
zA
А1
А1
y
П1
х1
П1
х1 П4
zA
А4

6. Решение четырех основных задач способом замены плоскостей проекций:

7.

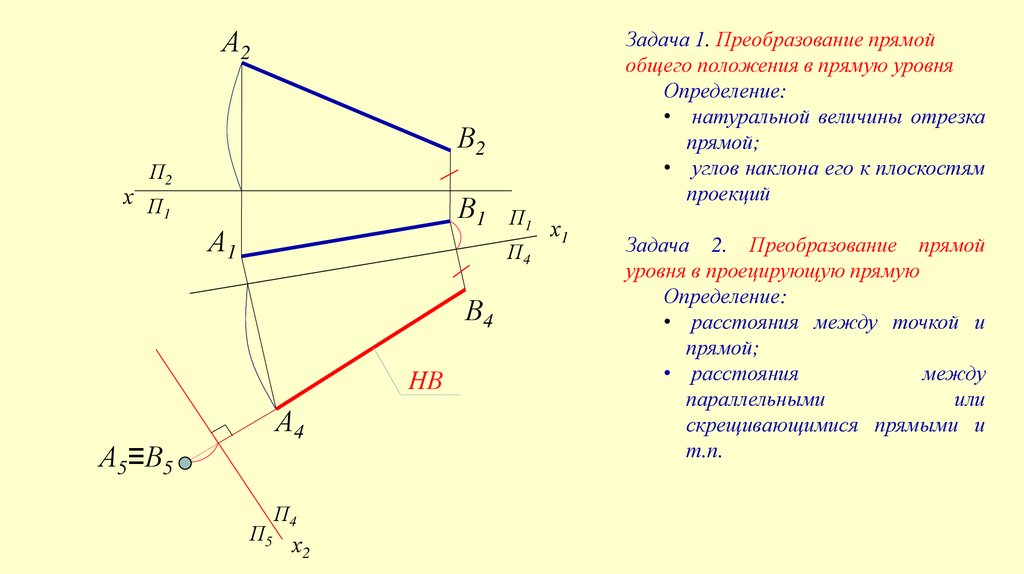
А2
Задача 1. Преобразование прямой
общего положения в прямую уровня
Определение:
• натуральной величины отрезка
прямой;
• углов наклона его к плоскостям
проекций
В2
П2
х П
В1
1
А1
П1
П4
В4
НВ
А4
А5≡В5
П5
П4
х2
х1
Задача 2. Преобразование прямой
уровня в проецирующую прямую
Определение:
• расстояния между точкой и
прямой;
• расстояния
между
параллельными
или
скрещивающимися прямыми и
т.п.

8.

А5
x1 h1
х2 C4A4B4
В2
Н.В.
А2
h2
С5
С2
П2
х П
В5
1
С1
С4
α
А4
В4
h1
А1
П1 П4
В1
х1
П5
П4 х2
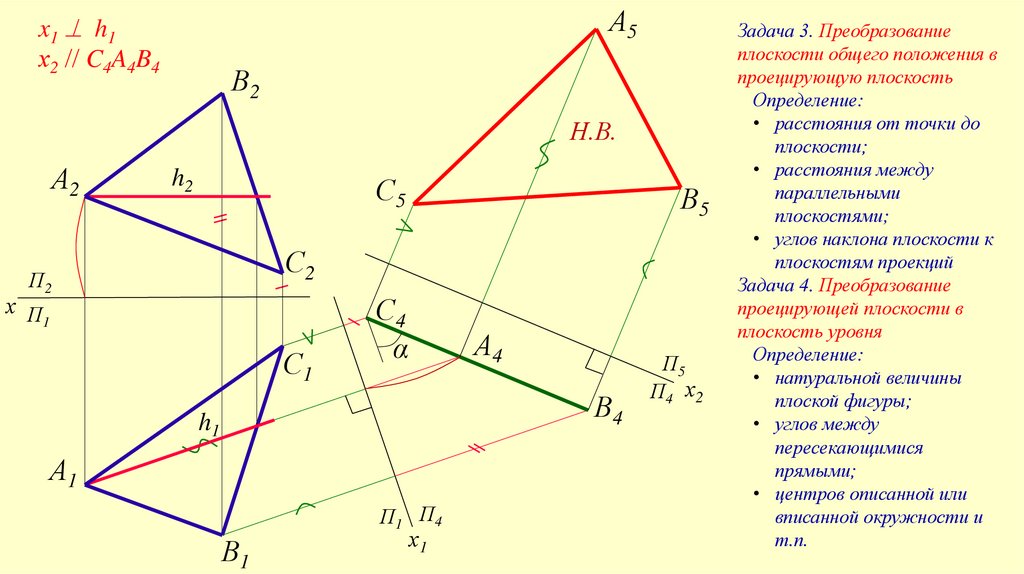
Задача 3. Преобразование
плоскости общего положения в
проецирующую плоскость
Определение:
• расстояния от точки до
плоскости;
• расстояния между
параллельными
плоскостями;
• углов наклона плоскости к
плоскостям проекций
Задача 4. Преобразование
проецирующей плоскости в
плоскость уровня
Определение:
• натуральной величины
плоской фигуры;
• углов между
пересекающимися
прямыми;
• центров описанной или
вписанной окружности и
т.п.

9.

В2
S2
К2 h
2
А2
х
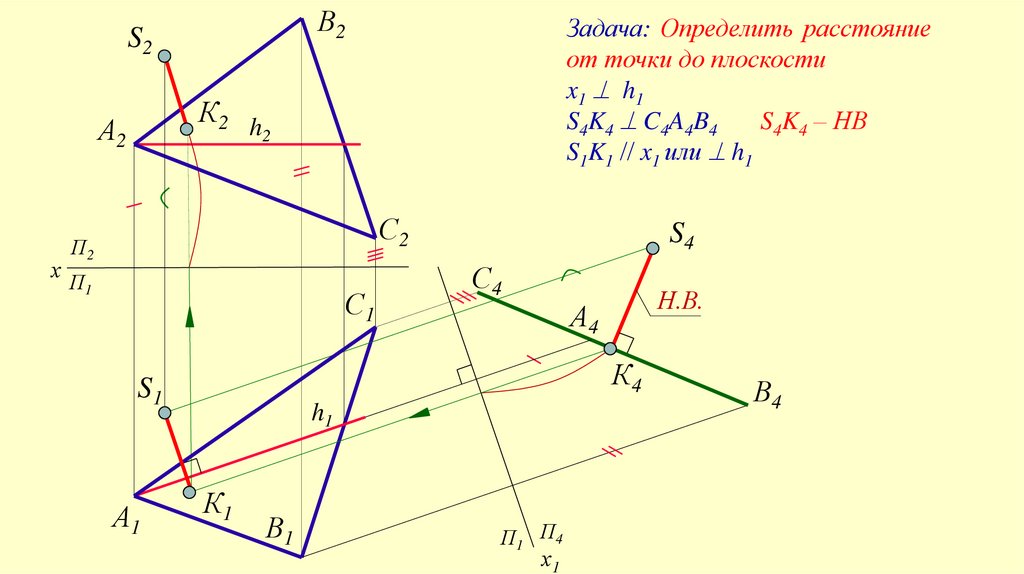
Задача: Определить расстояние
от точки до плоскости
x1 h1
S4K4 C4A4B4
S4K4 – НВ
S1K1 x1 или h1
С2
П2
П1
С1
С4
Н.В.
А4
К4
S1
А1
S4
h1
К1
В1
П 1 П4
х1
В4

10. Способ вращения

11.

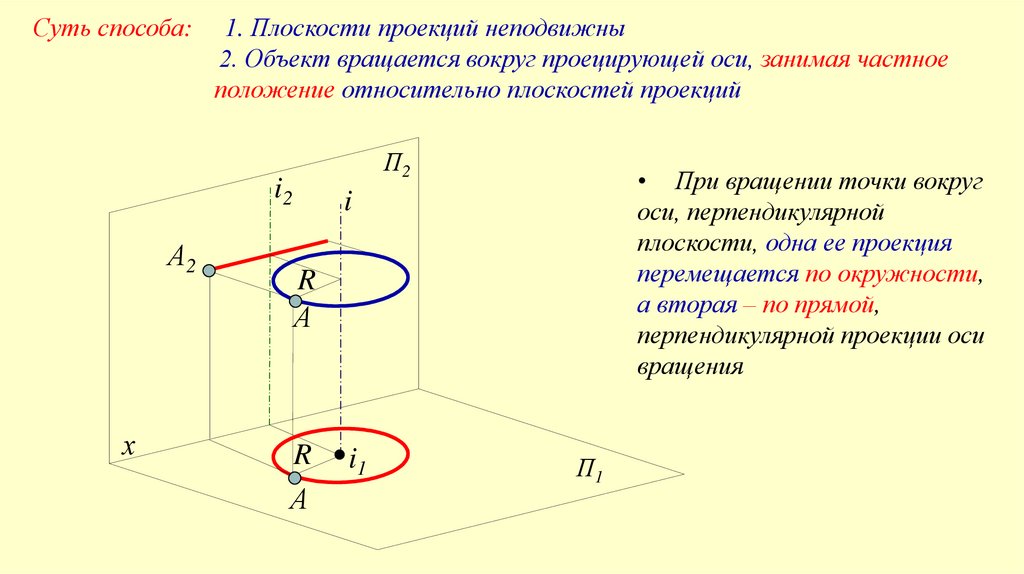
Суть способа:
1. Плоскости проекций неподвижны
2. Объект вращается вокруг проецирующей оси, занимая частное
положение относительно плоскостей проекций
П2
i2
А2
х
• При вращении точки вокруг
оси, перпендикулярной
плоскости, одна ее проекция
перемещается по окружности,
а вторая – по прямой,
перпендикулярной проекции оси
вращения
i
R
А
R
А
i1
П1

12.

Задача: Повернуть точку А вокруг оси i на 90°.
i2
А2
A2’
х
i1
R
А1
90⁰
А1’

13.

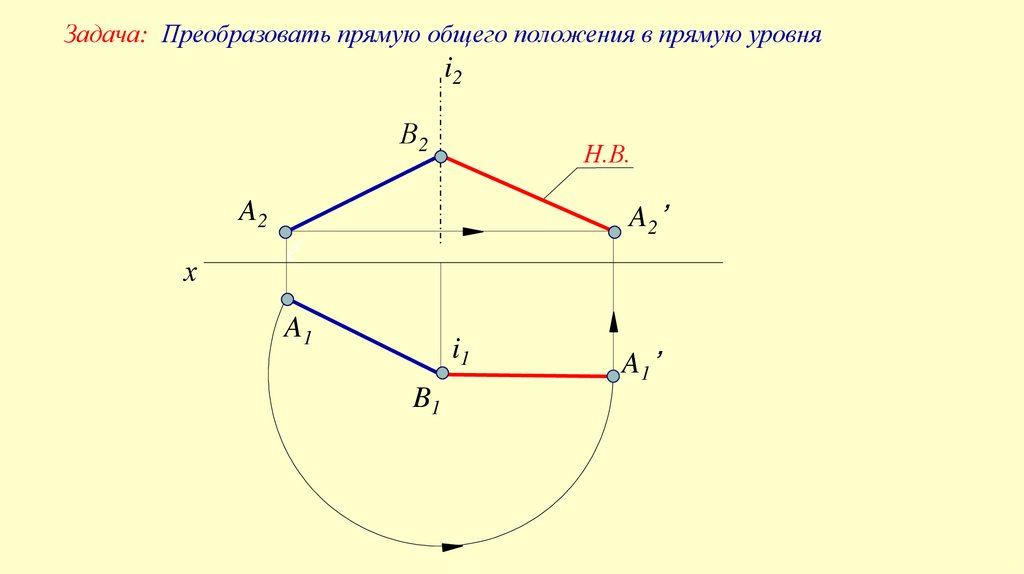
Задача: Преобразовать прямую общего положения в прямую уровня
i2
В2
Н.В.
A2’
A2
х
ё
A1
i1
B1
A1’

14. Способ плоскопараллельного перемещения

15.

Суть способа: 1. Плоскости проекций неподвижны
2. Одна из проекций объекта перемещается и поворачивается на свободном месте
чертежа так, чтобы относительно плоскостей проекций занять частное положение.
При этом форма и размер проекций сохраняется
3. При перемещении точки параллельно горизонтальной плоскости проекции, ее
фронтальная проекция движется по прямой, параллельной оси х, и наоборот
A2’’
А2
А2’
В2
Н.В.
α
х
B2’
B2’’
А1
A1’
В1
B1’
A1’’ B1’’

16.

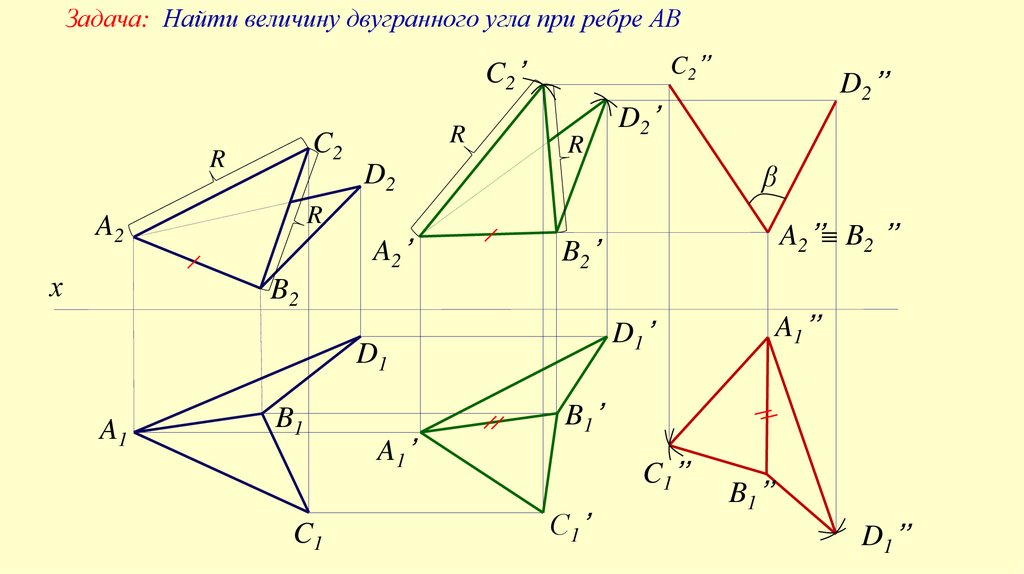
Задача: Найти величину двугранного угла при ребре АВ
C2’’
C2’
C2
R
R
D2’
β
D2
R
A2
х
R
D2’’
A2’
A2’’ B2 ’’
B2’
B2
D1
A1
B1
C1
A1’
A1’’
D1’
B1’
C1’’
С1’
B1’’
D1’’

17.

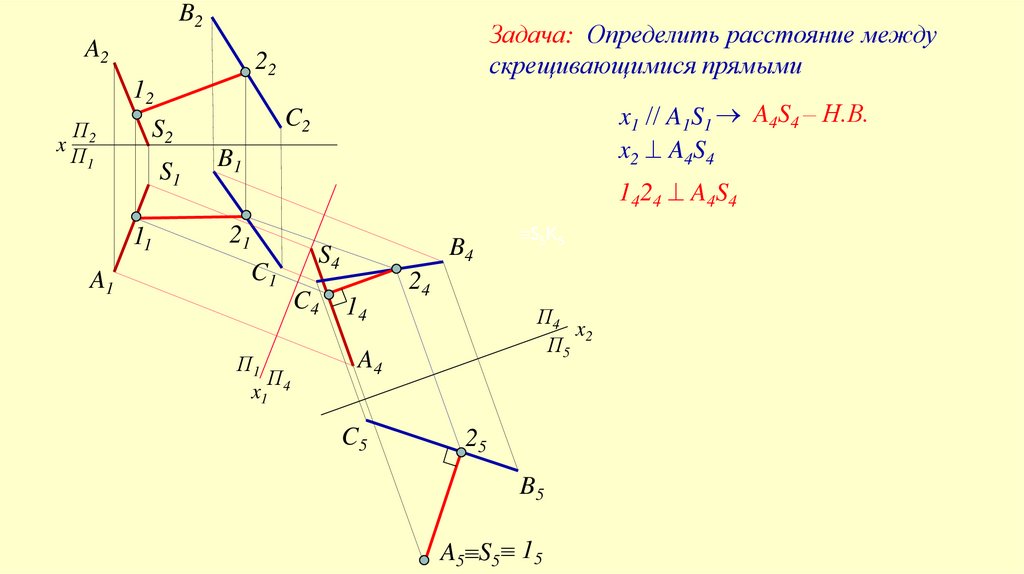
B2
A2
Задача: Определить расстояние между
скрещивающимися прямыми
22
12
x
П2
П1
S2
S1
11
A1
x1 A1S1 A4S4 – Н.В.
x2 A4S4
C2
B1
1424 A4S4
21
C1
S4
C4
П1
П
x1 4
B4
14
24
П4
x2
П5
A4
C5
S5K5
25
B5
A5 S5 15