Похожие презентации:
Основы образования чертежа. Проецирование плоскости. Метрические задачи. (Лекция 2)
1. Кафедра Инженерной графики Раздел1. Основы образования чертежа Лекция №2 Проецирование плоскости Метрические задачи
Материал создан на базе кура лекций поНачертательной геометрии,
разработанного доцентом кафедры
Инженерной графики МИСиС
Мокрецовой Л.О.- mok@misis.ru
Автор:
доцент Головкина Валерия Борисовна
2008
1
2.
Способы задания плоскости начертеже
А2
m2
С2
М2
K2
f2
n2
e2
В2
e1
n1
В1
K1
f1
m1
А1
С1
М1
2
3. Фронтально-проецирующая плоскость, П2
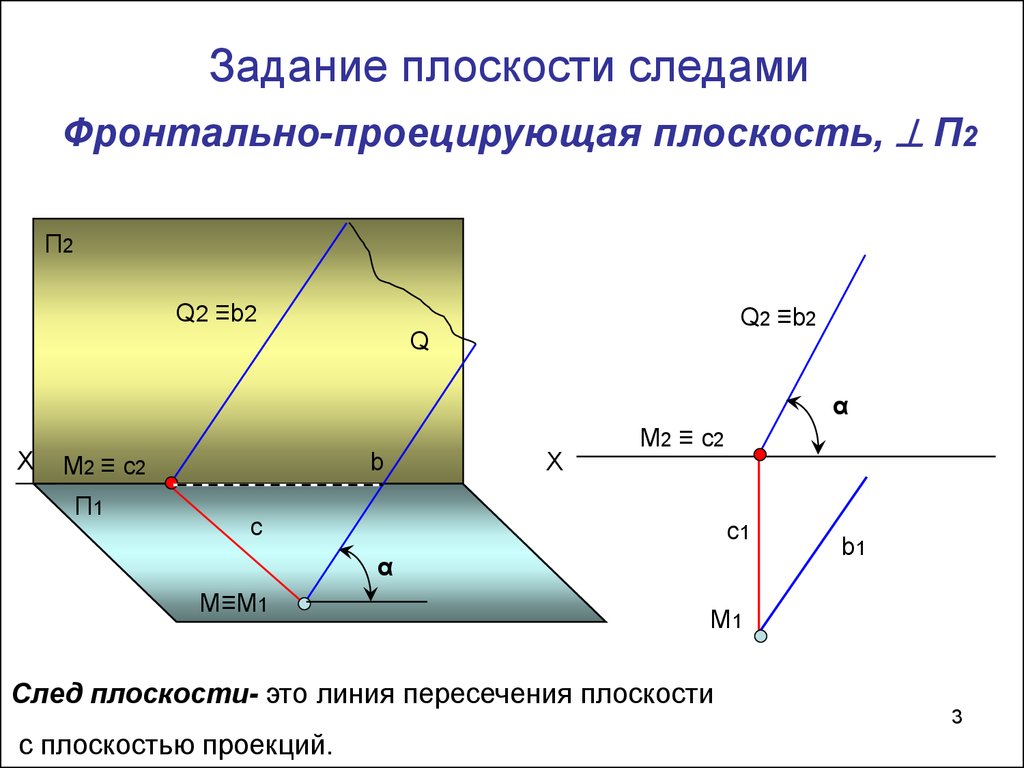
Задание плоскости следамиФронтально-проецирующая плоскость, П2
П2
Q2 ≡b2
Q2 ≡b2
Q
α
Х
M2 ≡ с2
П1
b
Х
M2 ≡ c 2
с
c1
α
M≡M1
b1
M1
След плоскости- это линия пересечения плоскости
3
с плоскостью проекций.
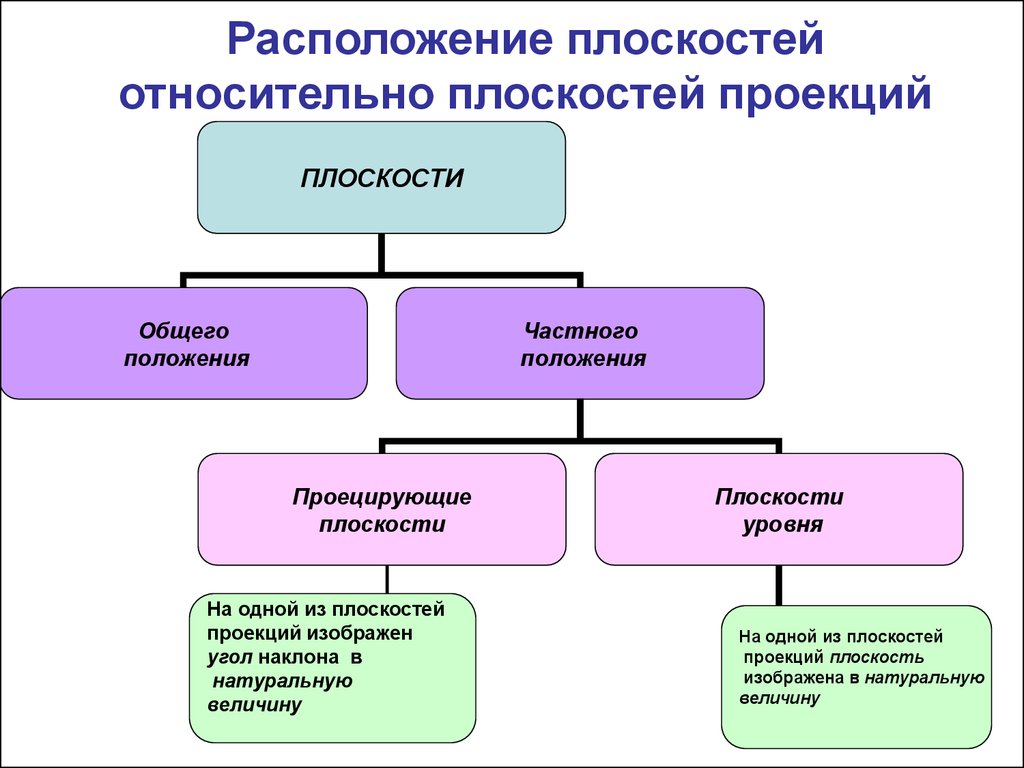
4. Расположение плоскостей относительно плоскостей проекций
ПЛОСКОСТИОбщего
положения
Частного
положения
Проецирующие
плоскости
На одной из плоскостей
проекций изображен
угол наклона в
натуральную
величину
Плоскости
уровня
На одной из плоскостей
проекций плоскость
изображена в натуральную
величину
4
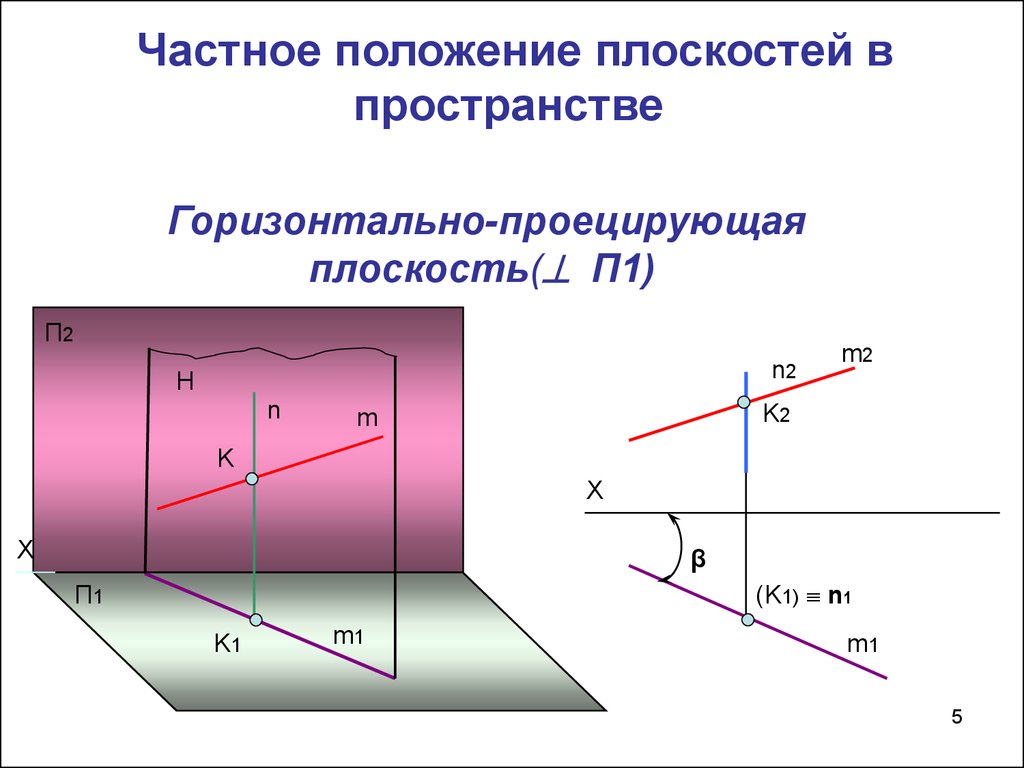
5. Частное положение плоскостей в пространстве
Горизонтально-проецирующаяплоскость( П1)
П2
n2
H
n
m2
K2
m
K
Х
Х
β
(K1) n1
П1
K1
m1
m1
5
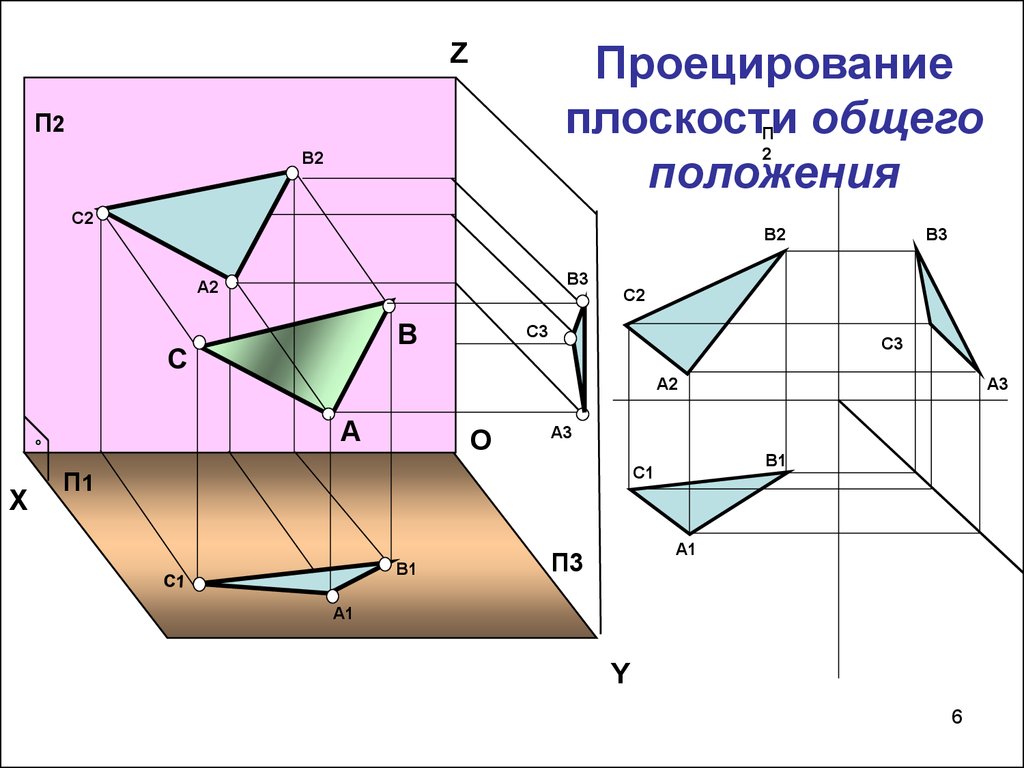
6. Проецирование плоскости общего положения
ZП2
П
2
В2
С2
В2
В3
А2
В
С
С2
С3
С3
А2
А
X
В3
0
П1
В1
О
А3
А3
В1
С1
А1
П3
А1
Y
6
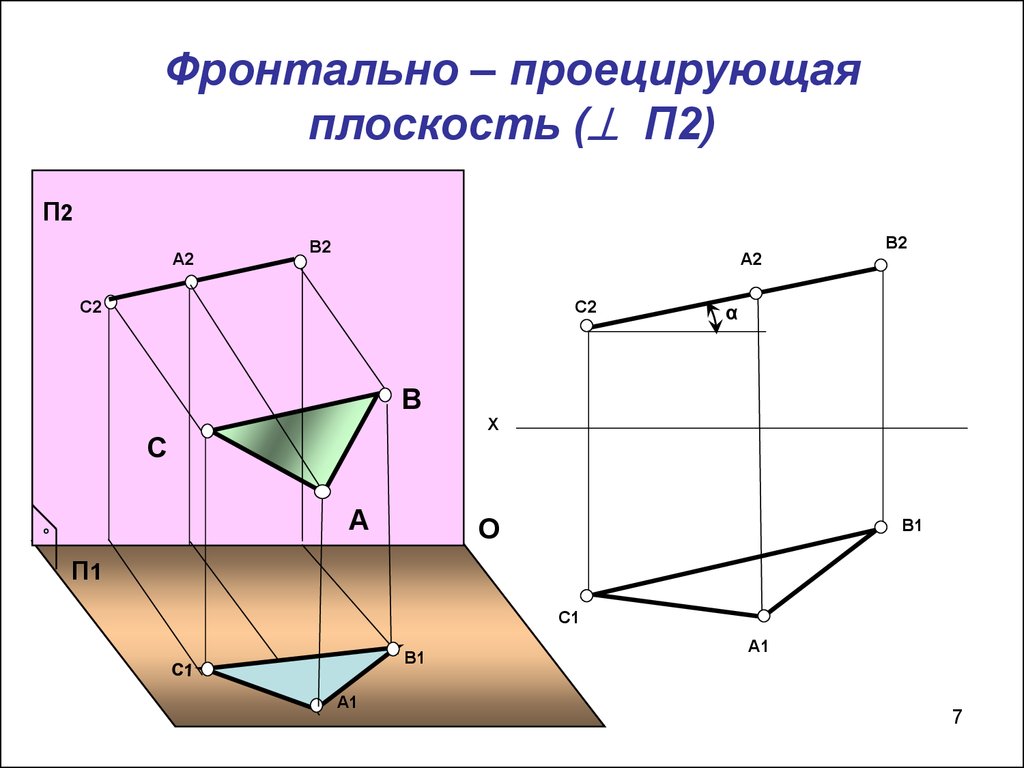
7. Фронтально – проецирующая плоскость ( П2)
Фронтально – проецирующаяплоскость ( П2)
П2
А2
В2
А2
С2
С2
В2
α
В
X
С
А
0
П1
О
В1
С1
В1
А1
А1
7
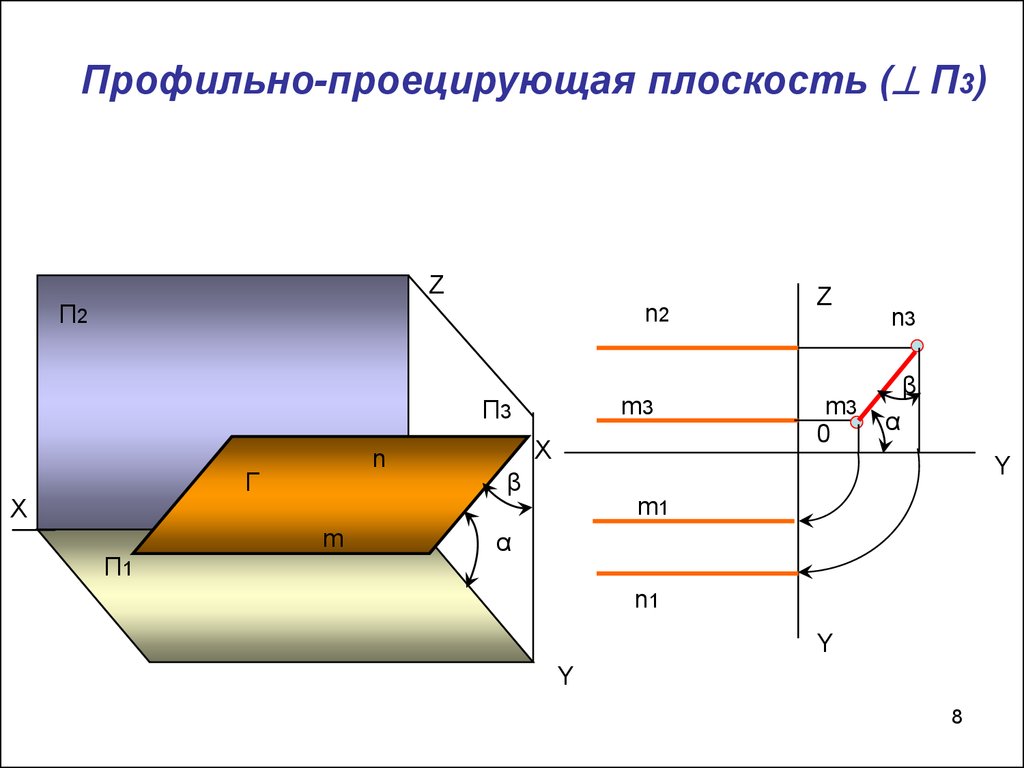
8. Профильно-проецирующая плоскость ( П3)
Профильно-проецирующая плоскость ( П3)Z
П2
n2
П3
n
Г
Х
m3
Х
Z
m3
0
n3
β
α
Y
β
m1
П1
m
α
n1
Y
Y
8
9. Плоскости уровня
Горизонтальная плоскость уровняП2
Q2 ≡(l2) ≡k2
Q2 ≡(l2) ≡k2
l
Х
П1
Х
l1
l1
k1
k1
9
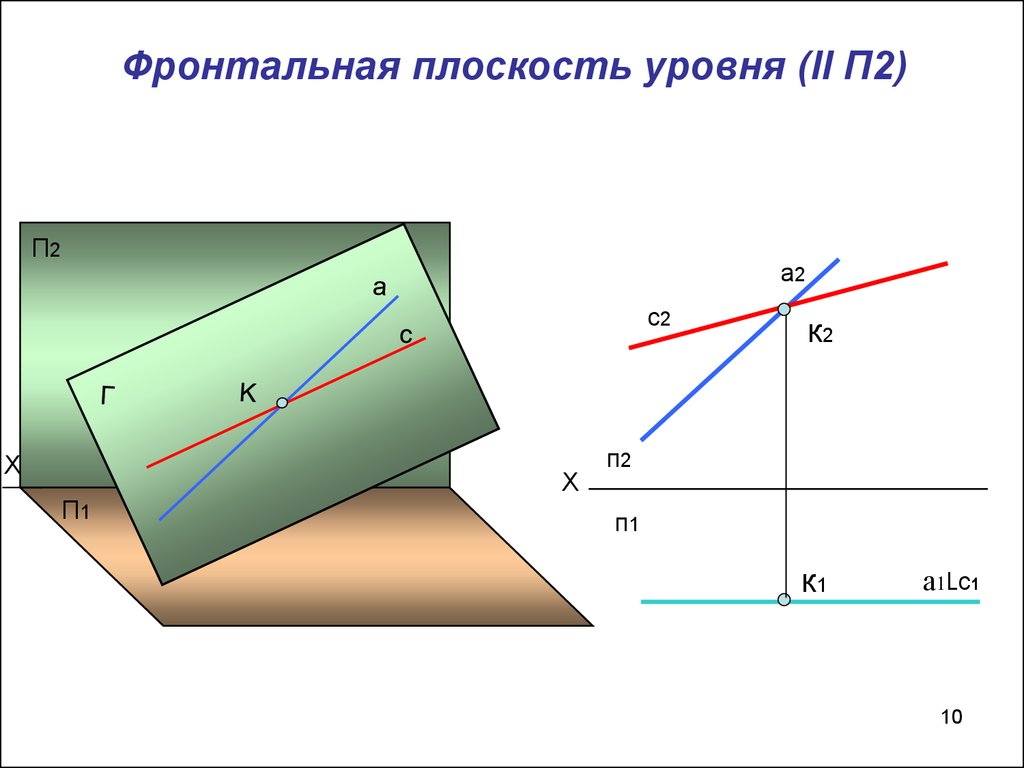
10. Фронтальная плоскость уровня (ll П2)
П2а2
с2
Х
П1
Х
к2
п2
п1
к1
а1Lс1
10
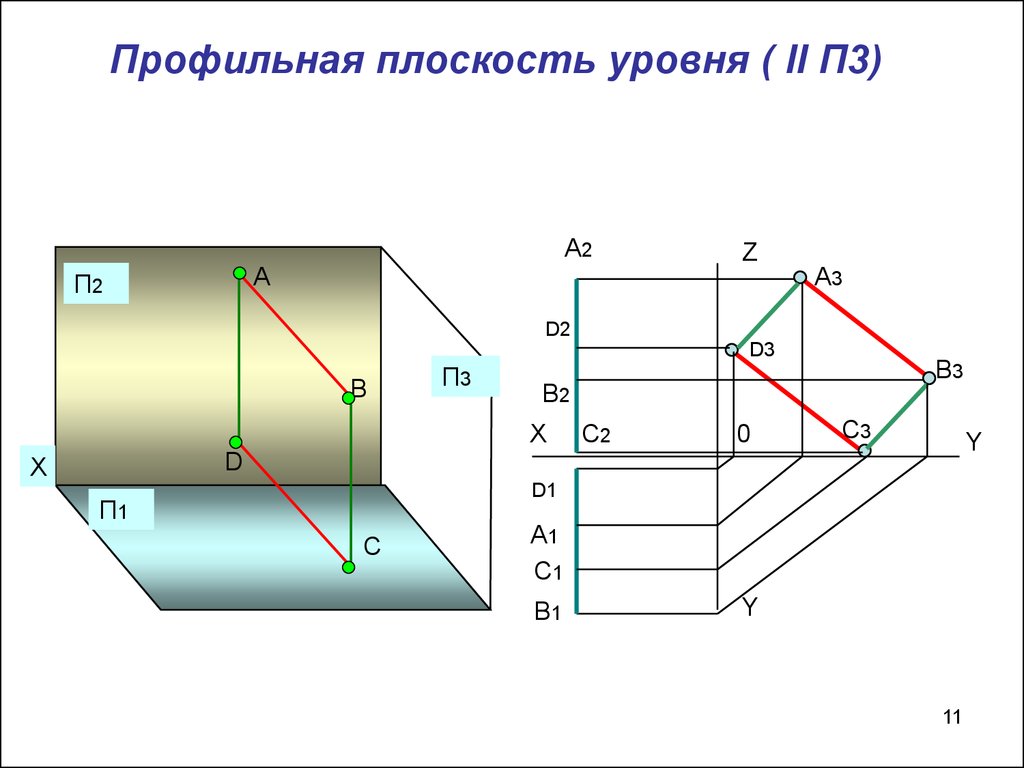
11.
Профильная плоскость уровня ( ll П3)А2
А
П2
Z
А3
D2
D3
В
П3
В3
В2
Х
С2
0
С3
Y
D
Х
D1
П1
С
А1
С1
В1
Y
11
12. Принадлежность точки и линии плоскости
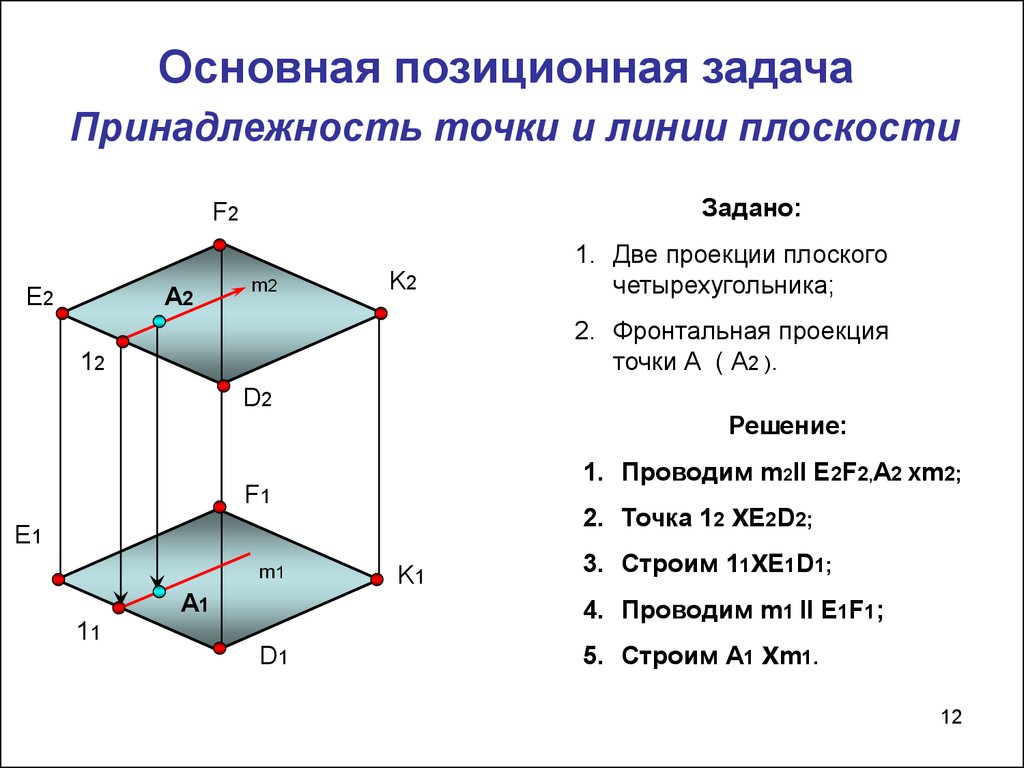
Основная позиционная задачаПринадлежность точки и линии плоскости
Задано:
F2
Е2
А2
m2
K2
1. Две проекции плоского
четырехугольника;
2. Фронтальная проекция
точки А ( А2 ).
12
D2
Решение:
1. Проводим m2ll E2F2,A2 Xm2;
F1
2. Точка 12 XE2D2;
Е1
m1
А1
K1
3. Строим 11XE1D1;
4. Проводим m1 ll E1F1;
11
D1
5. Строим А1 Xm1.
12
13. Линии частного положения в плоскости (главные линии плоскости)
К2f2
D2
22 h2
12
а2
М2
а2
b2
b2
b1
X
h1
М1
а1
а1
f1
21
11
b1
D1
К1
h - горизонталь
f - фронталь
13
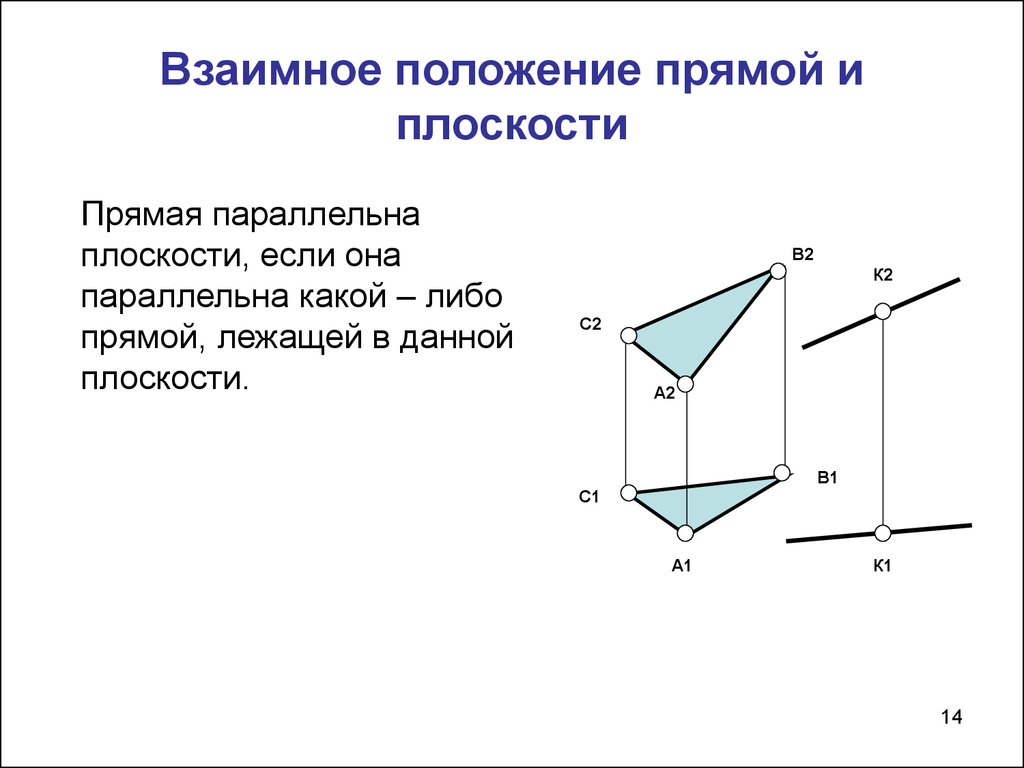
14. Взаимное положение прямой и плоскости
Прямая параллельнаплоскости, если она
параллельна какой – либо
прямой, лежащей в данной
плоскости.
В2
К2
С2
А2
В1
С1
А1
К1
14
15. Взаимное расположение плоскостей
1. Параллельность плоскостей: если плоскости параллельны, тодве пересекающиеся прямые одной плоскости параллельны двум
пересекающимся прямым другой плоскости
2. Пересечение плоскостей: результатом пересечения двух
плоскостей является прямая линия, для построения которой
достаточно найти две точки общие для пересекающихся плоскостей.
3. Перпендикулярность плоскостей: две плоскости взаимно
перпендикулярны, если одна из них содержит перпендикуляр к
другой. Прямая перпендикулярная плоскости называется нормаль
плоскости и перпендикулярна двум пересекающимся прямым,
лежащим в этой плоскости.
15
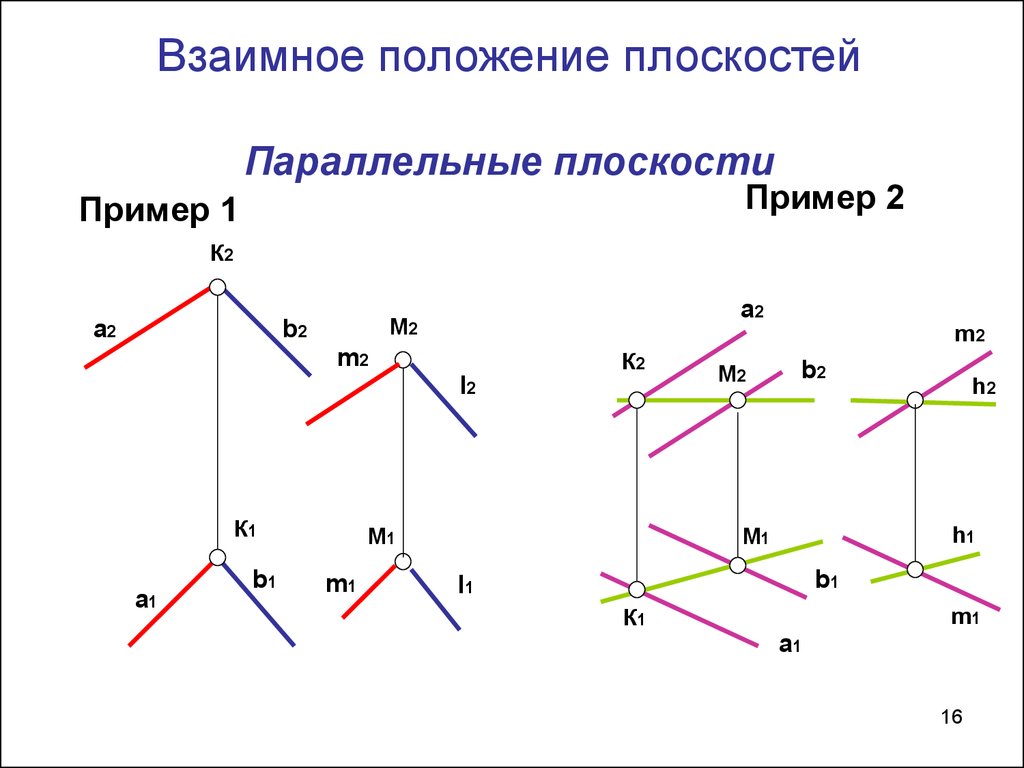
16. Взаимное положение плоскостей Параллельные плоскости
Пример 2Пример 1
К2
а2
а2
М2
b2
m2
m2
К2
l2
К1
а1
b1
М1
m1
М2
b2
М1
h2
h1
b1
l1
К1
m1
а1
16
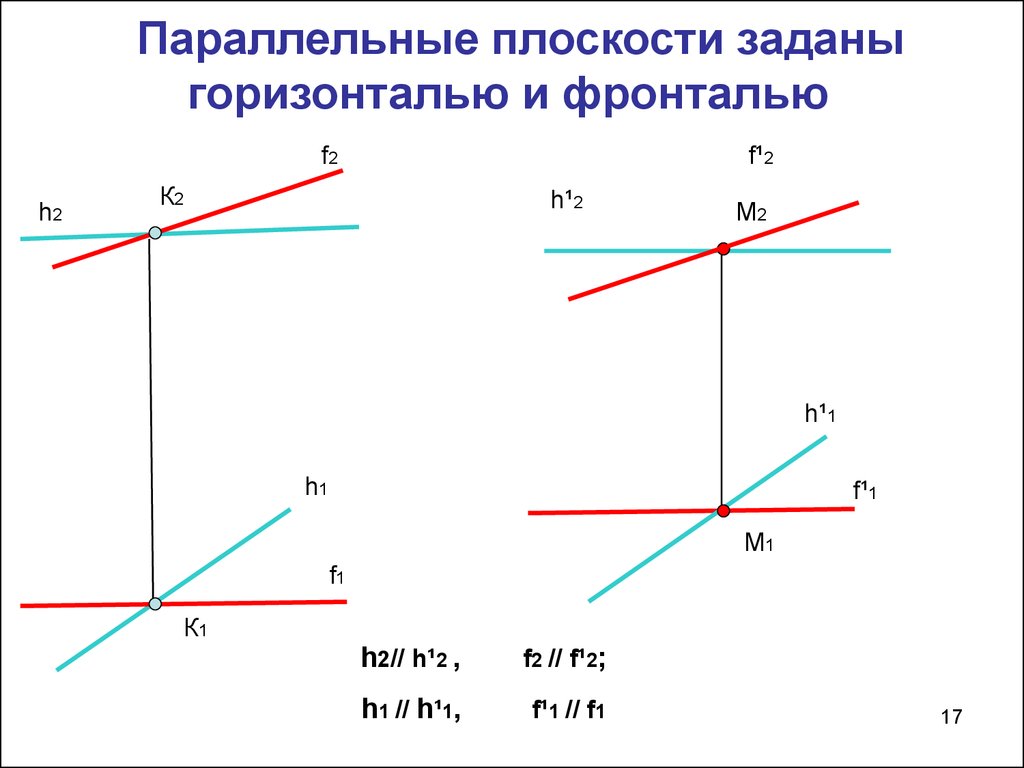
17. Параллельные плоскости заданы горизонталью и фронталью
f2h2
f¹2
К2
h¹2
M2
h¹1
h1
f¹1
M1
f1
К1
h2// h¹2 ,
f2 // f¹2;
h1 // h¹1,
f¹1 // f1
17
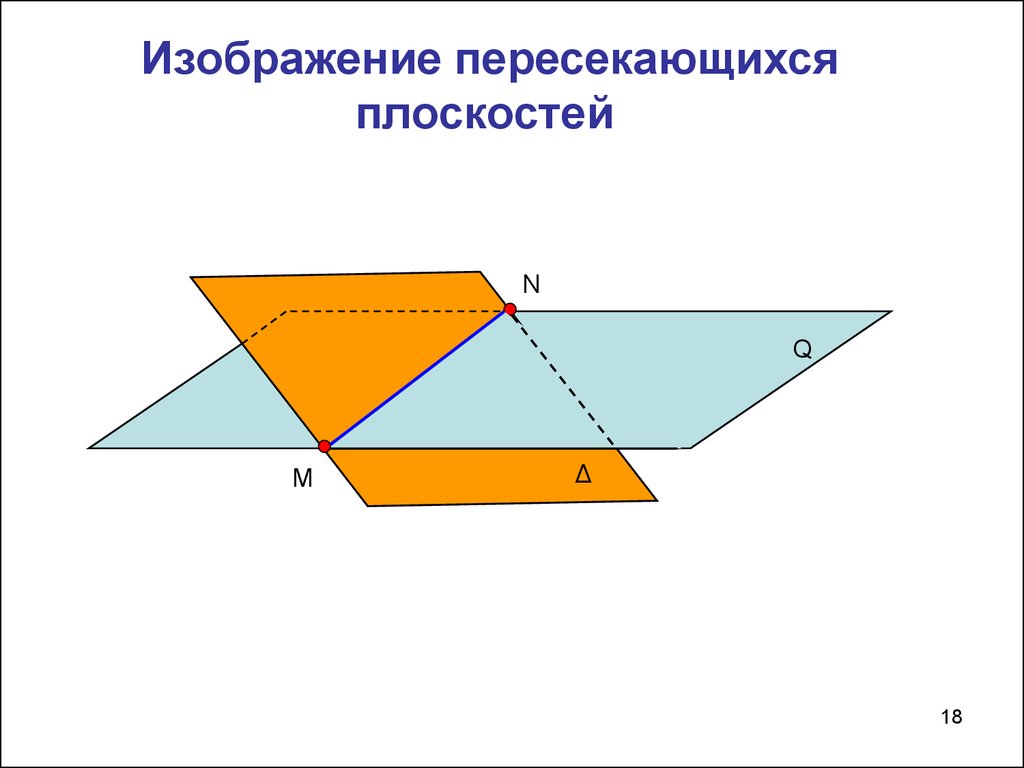
18. Изображение пересекающихся плоскостей
NQ
M
Δ
18
19.
Изображение перпендикулярныхплоскостей
n2
N
f2
Q
h2
A2
А
h
Δ
Х
f
h1
A1
Δ( h∩f) Q ( N h, N f )
f1
n1
19
20.
Метрические задачиК метрическим задачам относятся :
•Задачи на определение натуральной величины отрезка,
прямой или плоской фигуры;
•Задачи на определение углов наклона отрезка прямой
линии и плоской фигуры к плоскостям проекций;
•Задачи на определение расстояний между объектами
проецирования ( точкой и прямой, двумя прямыми,
прямой и плоскостью, двумя плоскостями)
20
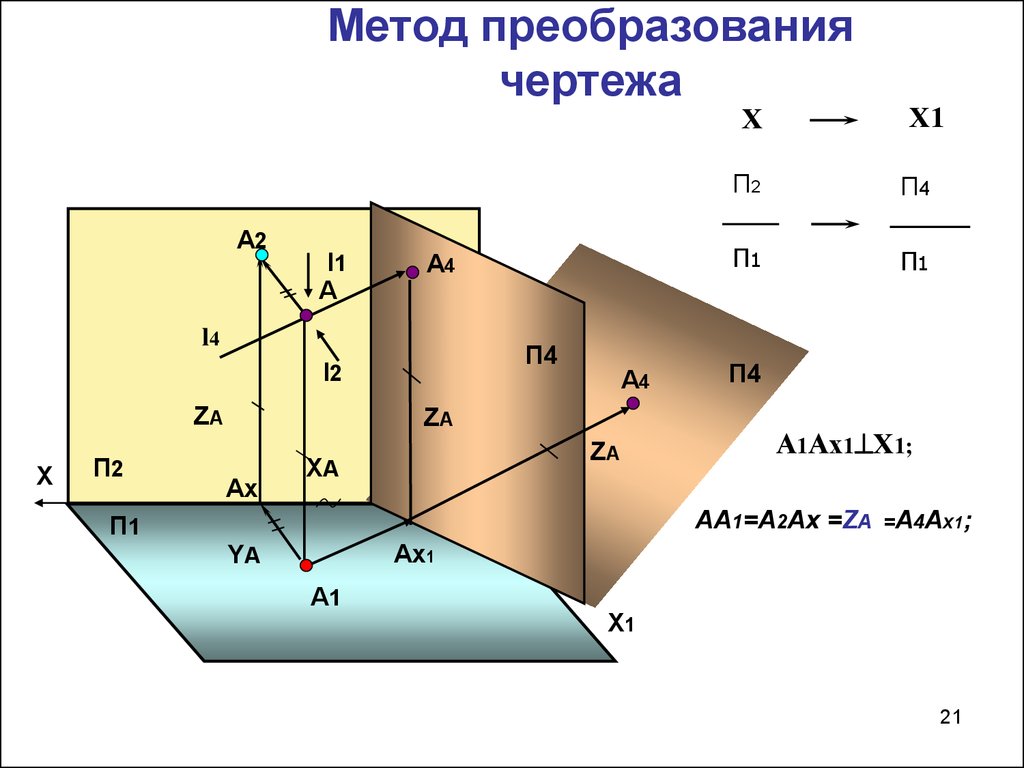
21.
Метод преобразованиячертежа
Х
А2
l1
А
А4
l4
П4
l2
ZА
Х
П2
А4
ZА
Ах
ZА
ХА
Х1
П2
П4
П1
П1
П4
А1Ах1 Х1;
0
АА1=А2Ах =ZА =А4Ах1;
П1
Ах1
YА
А1
Х1
21
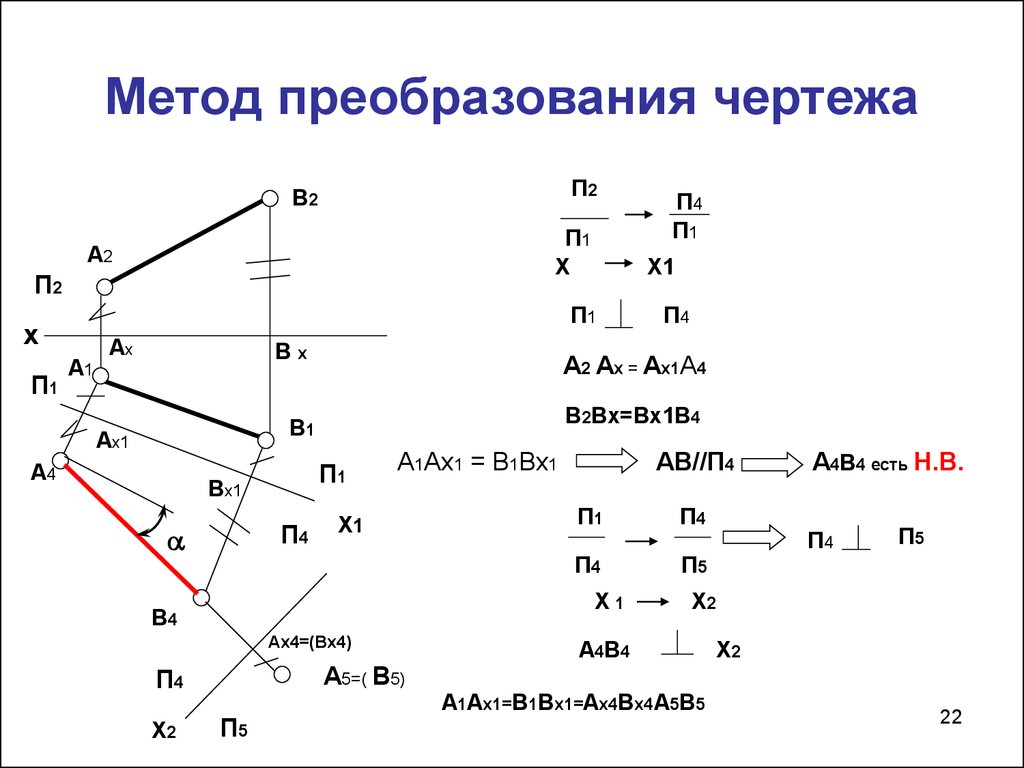
22. Метод преобразования чертежа
П2В2
П1
Х
А2
П2
П1
Х1
П1
х
А1
Ах
Вх
А4
В2Вх=Вх1В4
П1
Вх1
П4
А1Ах1 = В1Вх1
Х1
Ах4=(Вх4)
Х2
АВ//П4
П1
П4
П4
П5
Х1
В4
А5=( В5)
П4
П5
П4
А2 Ах = Ах1А4
В1
Ах1
П4
П1
А4В4 есть Н.В.
П4
П5
Х2
А4В4
А1Ах1=В1Вх1=Ах4Вх4А5В5
Х2
22
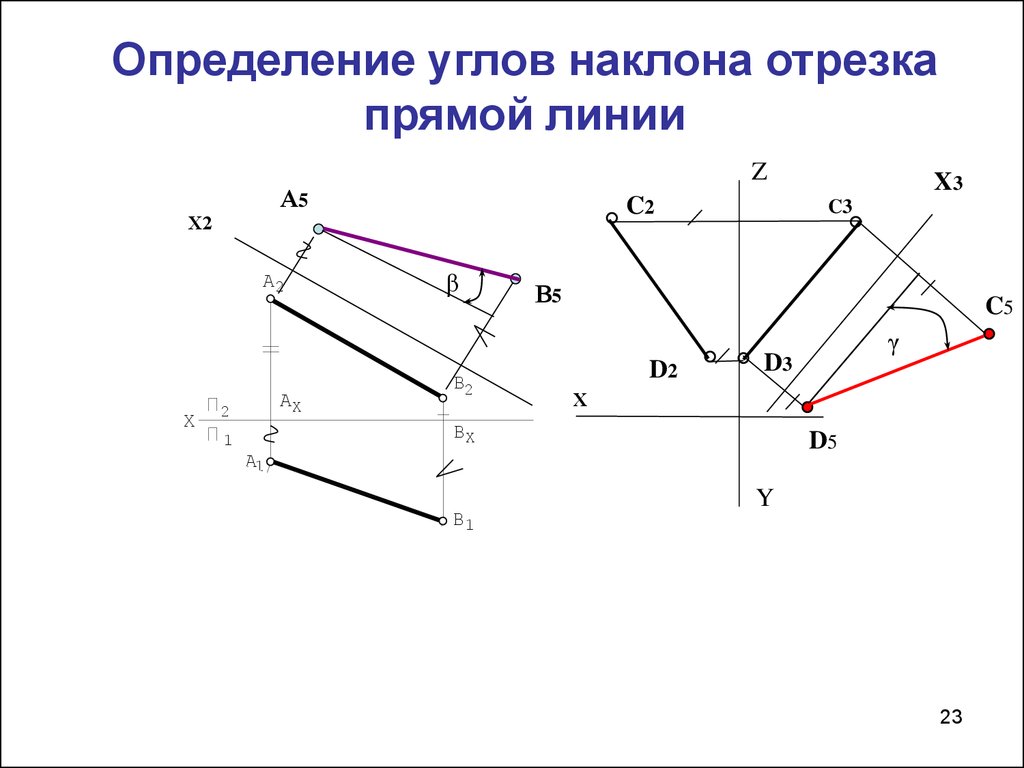
23. Определение углов наклона отрезка прямой линии
ZА5
Х2
C2
β
A2
X
C3
В5
B2
AX
2
C5
х
D2
D5
A1
BX 1
A4
Y
B1
AX 1
γ
D3
BX
1
X3
1
B4
HB
4
X1
23
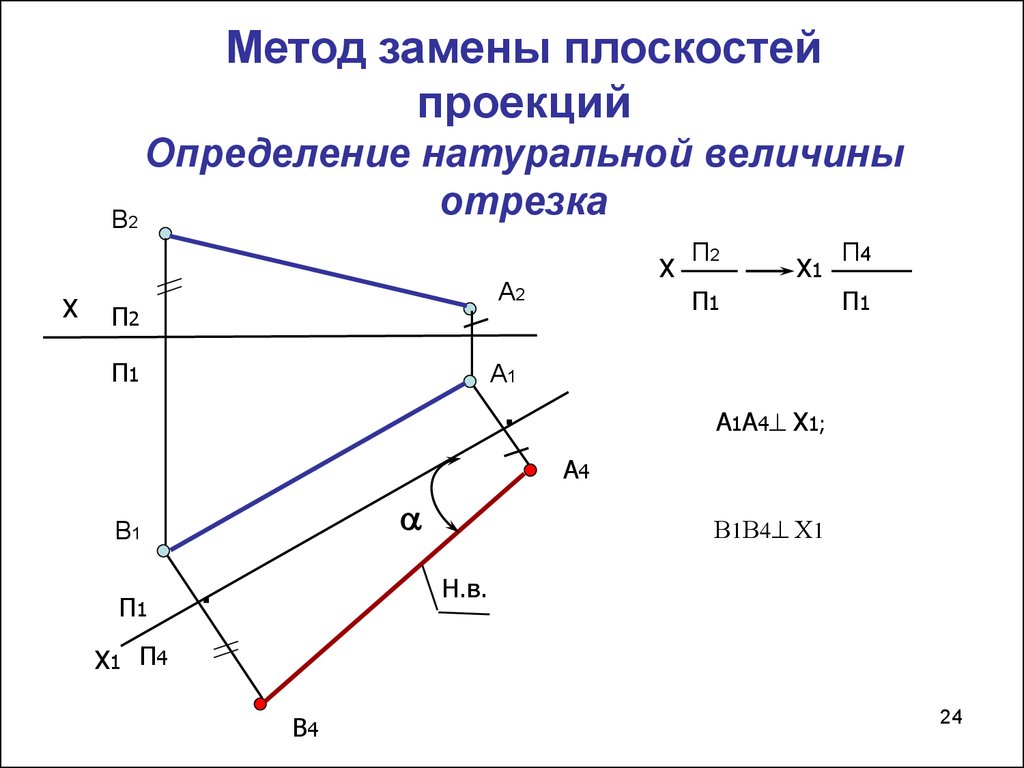
24. Метод замены плоскостей проекций Определение натуральной величины отрезка
В2Х
Х
А2
П2
П1
П2
Х1
П1
П4
П1
А1
А1А4 Х1;
▪
А4
В1
П1
В1В4 Х1
Н.в.
▪
Х1 П4
В4
24
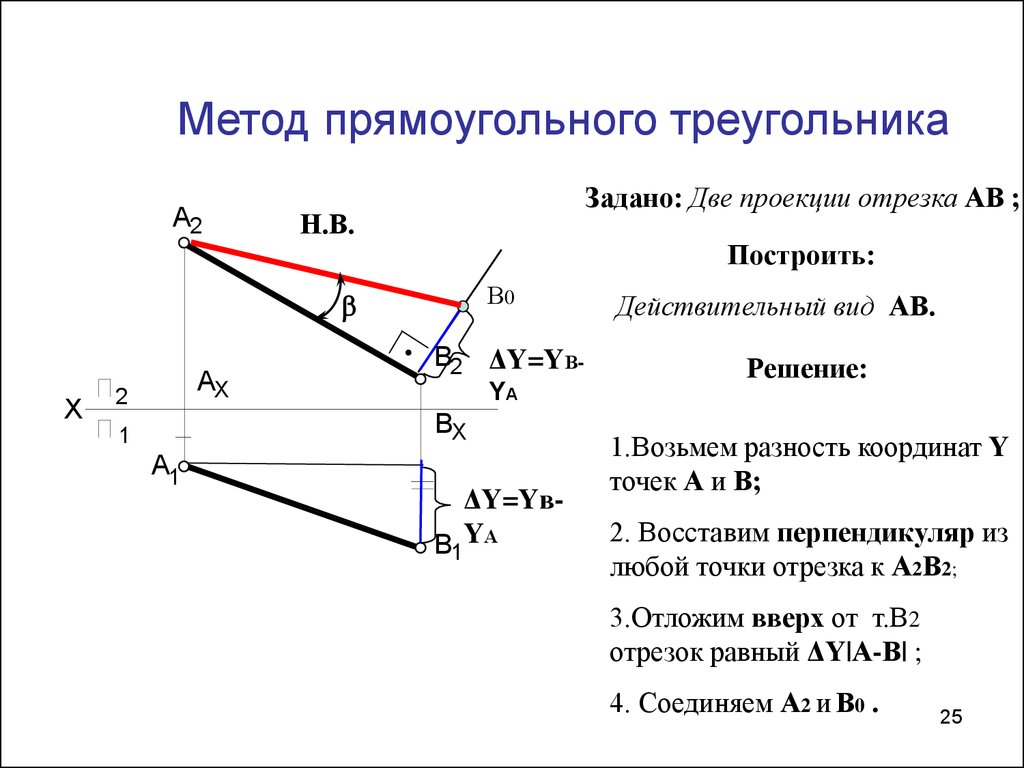
25. Метод прямоугольного треугольника
A2Задано: Две проекции отрезка АВ ;
Н.В.
Построить:
В0
X
AX
2
B2 ΔY=YВYА
BX
1
A1
ΔY=YвB1YА
Действительный вид АВ.
Решение:
1.Возьмем разность координат Y
точек А и В;
2. Восставим перпендикуляр из
любой точки отрезка к А2В2;
3.Отложим вверх от т.В2
отрезок равный ΔY|А-В| ;
4. Соединяем А2 и В0 .
25
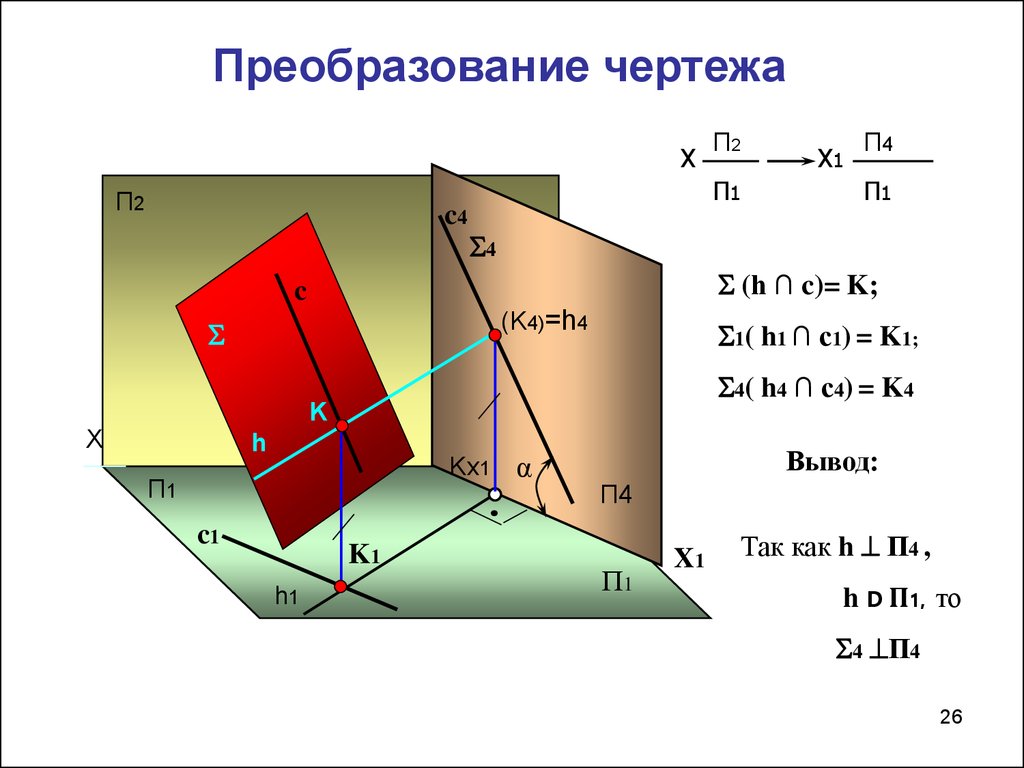
26. Преобразование чертежа
ХП2
c4
П1
4
(K4)=h4
1( h1 ∩ c1) = K1;
4 ( h 4 ∩ c4 ) = K 4
K
h
Kx1 α
П1
K1
h1
П4
(h ∩ c)= K;
c1
Х1
П1
c
Х
П2
Вывод:
П4
П1
X1
Так как h П4 ,
h D П1, то
4 П4
26
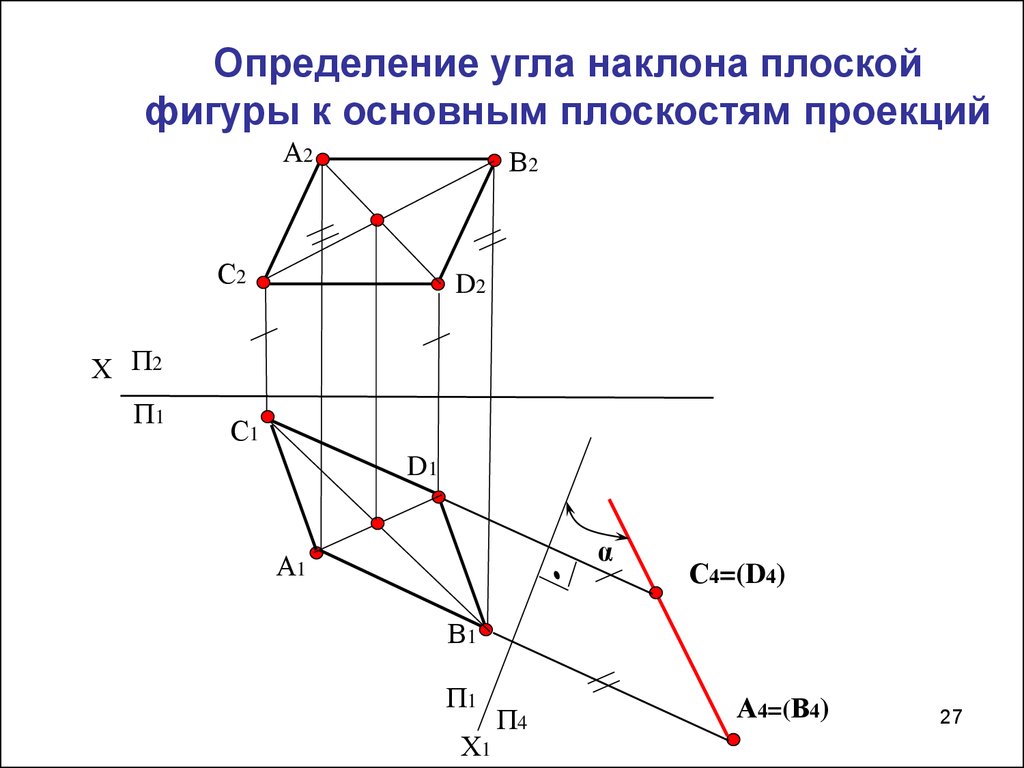
27. Определение угла наклона плоской фигуры к основным плоскостям проекций
А2В2
С2
D2
Х П2
П1
С1
D1
α
А1
С4=(D4)
В1
П1
Х1
П4
А4=(В4)
27
28. Определение натуральной величины плоской фигуры
С4А4
В4
28
29.
СПАСИБО ЗА ВНИМАНИЕ!29









 Математика
Математика Инженерная графика
Инженерная графика








