КУРСОВАЯ ПНК

1.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА
ИРКУТСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО
ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ» (МГТУ ГА)
Кафедра авиационных электросистем и пилотажно-навигационных комплексов
В. Ф. Диль, В. Н. Сизых
ПИЛОТАЖНО-НАВИГАЦИОННЫЕ
КОМПЛЕКСЫ
Учебно-методическое пособие
по выполнению курсовой работы
для обучающихся
по направлению подготовки 2.25.03.02
4 курса очной формы обучения
Иркутск – 2018 г

2.

ББК 0571.55
Д-46
Рецензент: доцент кафедры АЭС и ПНК Иркутского филиала МГТУ ГА, к.т.н,
доцент С. П. Назаров
В. Ф. Диль, В. Н. Сизых
Д-46 Пилотажно-навигационные комплексы: учебно-методическое пособие по
выполнению курсовой работы . Иркутск: Иркутский филиал МГТУ ГА, 2018.
– 44 с.
Учебно-методическое пособие по выполнению курсовой работе
предназначено для обучающихся 4 курса по направлению подготовки
2.25.03.02. очной формы обучения. Содержание пособия соответствует
государственному образовательному стандарту и учебной программе
«Пилотажно-навигационные комплексы», читаемой на кафедре «Авиационные
электросистемы и пилотажно-навигационные комплексы».
Пособие содержит общие положения по изучению дисциплины, варианты
заданий и порядок выбора варианта курсовой работы, исходные данные для
выполнения расчетов, порядок выполнения расчетов курсовой работы и пример
расчета передаточных чисел автопилота. В приложении приведен образец
титульного листа для оформления курсовой работы.
Рассмотрено и рекомендовано к изданию на заседании кафедры АЭС и
ПНК Иркутского филиала МГТУ ГА. Протокол № 8 от 16.02.2018 г.
Рассмотрено и рекомендовано к использованию в учебном процессе
Методическим советом по направлению подготовки 2.25.03.02 Иркутского
филиала МГТУ ГА. Протокол № 41 от 22.03.2018 г.
Тех. редактор Е. Л. Андреянова
Подписано в печать 18.05.2018.
Печать трафаретная
Формат 60х84/16
1,0 уч.-изд.л.
2,75 печ.л.
Тираж 25 экз.
Заказ № 667
Иркутский филиал Московского государственного технического
университета гражданской авиации
664047, г. Иркутск ул. Коммунаров, д. 3
Отдел редакционно-издательской и научной работы
664009, г. Иркутск ул. Советская, д. 139
© Иркутский филиал МГТУ ГА, 2018
2

3.

СОДЕРЖАНИЕ
Введение……………………………………………………………………….. 4
1. Общие положения по изучению дисциплины………………………….
5
2. Порядок выполнения курсовой работы……………………………………. 7
2.1. Выбор варианта курсовой работы……………………………………. 7
2.2. Порядок подготовки расчетной части курсовой работы…………… 9
2.3. Задание на выполнение курсовой работы…………………………… 13
3. Пример расчета передаточных чисел автопилота………………………… 16
3.1. Исходные данные для расчета.………………………………….......... 16
3.2. Содержание задания курсовой работы………………………………. 17
3.3. Выполнение курсовой работы………………………………………... 18
Заключение……………………………………………………………………. 27
Приложение № 1. Содержание отчета курсовой работы……………………. 28
Приложение № 2. Графические изображения параметров математической
модели ВС …………………………………………………………………….. 30
Приложение № 3. Метод стандартных переходных характеристик (СПХ)… 40
Список использованной литературы……………………………………........ 44
3

4.

ВВЕДЕНИЕ
Задача синтеза закона управления объектом состоит из трех этапов.
На первом этапе определяется структура закона управления, отвечающего
заданным условиям регулирования. Аппарат теории автоматического
управления линейных объектов развит настолько широко, что позволяет
выбрать структуру закона управления, отвечающую поставленной задаче.
На втором этапе синтеза закона управления определяются количественные
параметры составляющих выбранного закона управления, и определяются
численные значения коэффициентов передачи, обеспечивающих требуемое
качество регулирования объекта. На третьем этапе проверяется
работоспособность контура регулирования с рассчитанными составляющими
закона управления и уточняются, при необходимости, численные значения
расчетных коэффициентов передачи.
Данное пособие является руководством для студентов по выполнению
синтеза законов управления самолетов в режимах стабилизации углового
положения. При этом задаются исходная структура закона управления и
показатели качества управления. Задачей студентов является определение
численных значений коэффициентов передачи автопилота, отвечающих
заданным показателям качества управления самолетом. Исходными моделями
самолета следует принять линейные модели продольного или бокового
движения самолета, полученные в процессе выполнения лабораторных работ
№ 1 и № 2 по дисциплине САУП, в которых выполнялись исследования
неуправляемого продольного и бокового движения самолета. Для объяснения
результатов работы студенту потребуется восстановить некоторые знания и
понятия, полученные при изучении дисциплин в предыдущем семестре, в
частности: свойства самолета, как объекта управления, контур управления,
управляемость и устойчивость движения самолета, их качественные и
количественные характеристики, передаточные функции и переходные
процессы, частотный метод анализа контуров управления. Особое внимание
следует уделить пониманию физических процессов, происходящих в контуре
управления под воздействием управляющих и возмущающих факторов.
Приведенный пример выполнения расчета может облегчить выполнение
студентом его персонального задания, однако следует помнить, что это всего
лишь пример и не следует его копировать. Совершенно не обязательно точно
повторять все действия примера, проявление самостоятельности желательно.
4

5.

1. ОБЩИЕ ПОЛОЖЕНИЯ ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ
Цель изучения дисциплины
Целью дисциплины является изучение студентами теории и практики
автоматизированного и автоматического управления полетом воздушных
судов, принципа действия, устройства и особенностей автоматических средств
управления воздушных судов.
Данная дисциплина является одной из дисциплин специальности,
служащих основой для формирования специалиста по технической
эксплуатации авиационных электросистем и пилотажно-навигационных
комплексов, квалификации бакалавр, профиля подготовки «Техническое
обслуживание и ремонт авиационных электросистем и пилотажнонавигационных комплексов».
Курсовая работа является составной частью процесса изучения
дисциплины и формирует у студента такие свойства, как техническая
грамотность при выполнении расчетов, умение обосновывать принятие
решений, самостоятельность в реализации принятых решений, ответственность
за качество выполненной работы.
Требования к уровню освоения дисциплины
В результате изучения дисциплины обучающие должны:
знать:
– основные понятия аэродинамики самолета и вертолета;
– основы конструкции летательных аппаратов и авиационных
двигателей, самолетных систем;
– основы автоматики и управления;
– принцип действия и устройство бортовых цифровых вычислительных
устройств;
– принцип действия и устройство авиационных приборов;
– принцип действия и устройство систем автоматического управления
полетом;
– принцип действия и устройство авиационных информационноизмерительных систем,
– принцип действия и устройство бортовых радиоэлектронных систем;
уметь:
– исследовать замкнутые системы автоматического управления;
– подготовить самолет и смежные функциональные системы к проверке
пилотажно-навигационного комплекса;
5

6.

владеть:
– аппаратом и методами теории автоматического управления;
– аппаратом и методами моделирования систем и процессов.
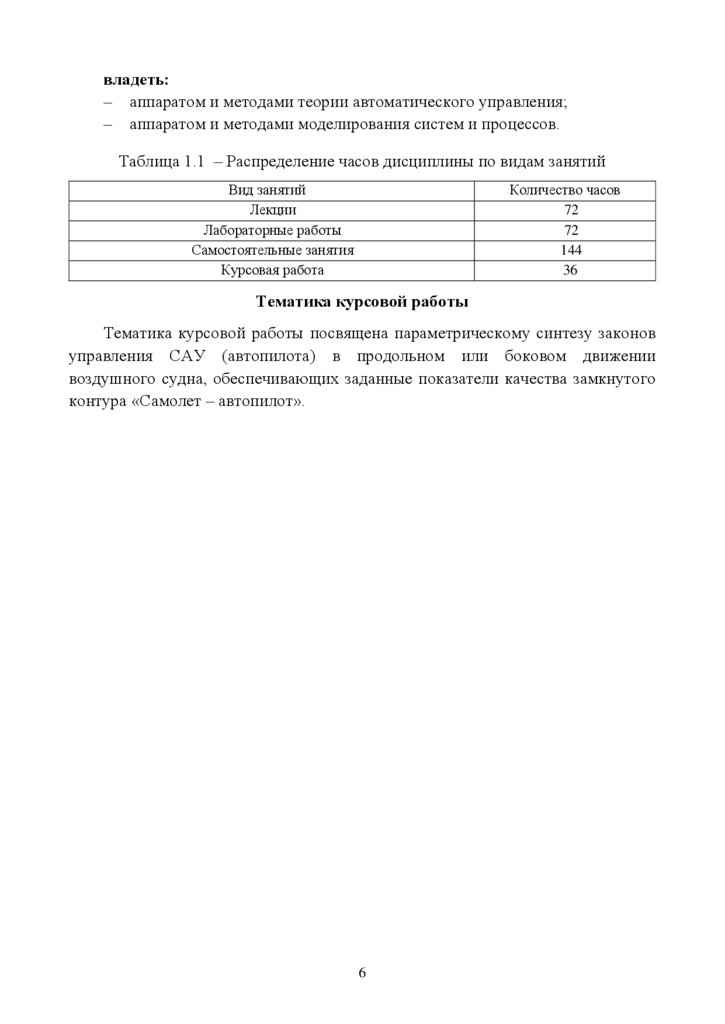
Таблица 1.1 – Распределение часов дисциплины по видам занятий
Вид занятий
Лекции
Лабораторные работы
Самостоятельные занятия
Курсовая работа
Количество часов
72
72
144
36
Тематика курсовой работы
Тематика курсовой работы посвящена параметрическому синтезу законов
управления САУ (автопилота) в продольном или боковом движении
воздушного судна, обеспечивающих заданные показатели качества замкнутого
контура «Самолет – автопилот».
6

7.

2. ПОРЯДОК ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ
2.1. Выбор варианта курсовой работы
Курсовая работа выполняется студентами 4 курса по дисциплине
«Пилотажно-навигационные комплексы». Вариант задания назначается
преподавателем дисциплины по своему усмотрению. В случае отсутствия
такового, студент самостоятельно выбирает вариант курсовой работы в
соответствии с критерием, указанном ниже.
По первой букве фамилии студента определяется канал синтезируемой
системы управления – продольный или боковой. Студенты, фамилии которых
начинаются с букв от А до О, рассматривают синтез параметров автопилота
угловой стабилизации продольного движения самолета, а студенты, фамилии
которых начинаются с букв от П до Я – синтез параметров автопилота угловой
стабилизации бокового движения самолета.
Номер и содержание задания в выбранном канале соответствует последней
цифре номера студенческого билета и определяется из таблиц 2.1, 2.3, 2.4.
Так студент Иванов В.В., имеющий номер студенческого билета АК –
68035, выполняет синтез закона управления автопилота угловой стабилизации в
продольном движении самолета, задание номер пять. В ходе выполнения
курсовой работы по дисциплине «Пилотажно-навигационные комплексы»
необходимо использовать математические модели движения самолета,
изучаемые по дисциплине САУП.
В качестве исходных математических моделей следует принять системы
линейных дифференциальных уравнений, записанные в символической форме
при нулевых начальных условиях, описывающих полные продольное (2.1) и
боковое (2.2) возмущенные движения самолета в связанной системе
координат.*
(2.1)
(2.2)
7

8.

*) Примечание: здесь и в дальнейшем знак вариации «Δ» опущен.
В системах уравнений (2.1) и (2.2) приняты следующие обозначения:
– оператор Лапласа − символ дифференцирования;
– приращение воздушной скорости − м/с;
– приращение угла атаки − град;
– приращение угла тангажа − град;
– приращение угла отклонения руля высоты − град;
– приращение угла рыскания − град;
– приращение угла крена − град;
– приращение угла скольжения − град;
– приращение угла отклонения руля направления − град;
– приращение угла отклонения элеронов − град;
– приращение угла отклонения рукоятки управления двигателем − град;
– приращение угла между вектором воздушной скорости и вектором
путевой скорости, обусловленное действием вертикальной и боковой
составляющими ветра - град;
– приращение угла между вектором воздушной скорости и вектором
путевой скорости, обусловленное действием горизонтальной составляющей
ветра – град;
М М М – приращение возмущающих моментов соответственно
относительно осей ОХ, ОУ, ОZ связанной системы координат - кГ м;
–коэффициенты линеаризованных уравнений систем (2.1) и
(2.2) продольного и бокового движений ВС.
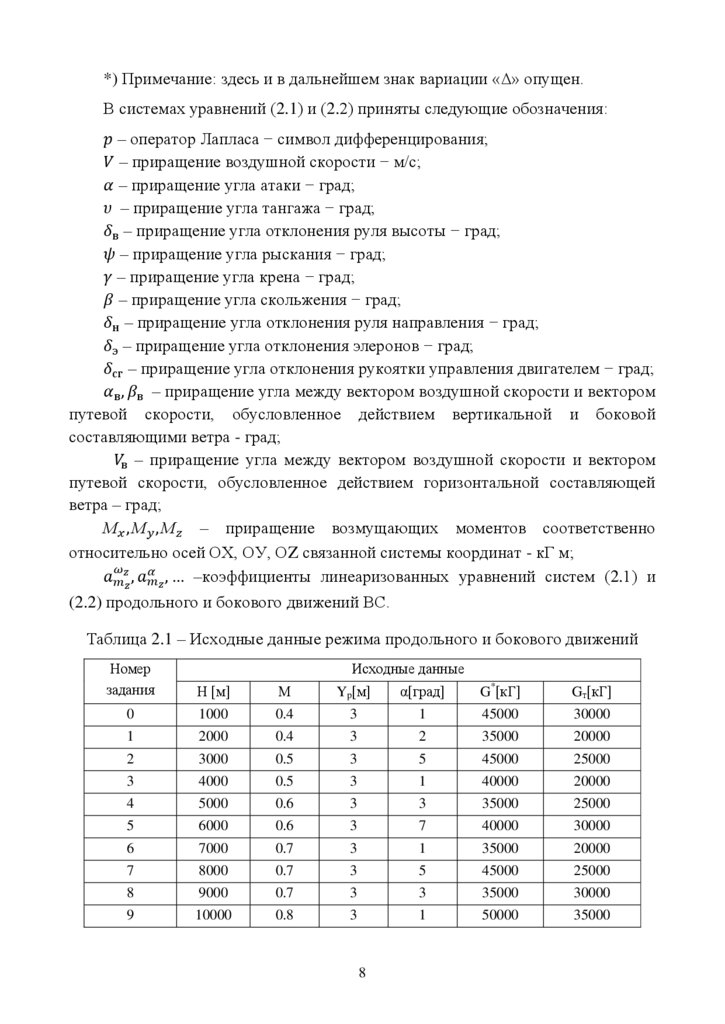
Таблица 2.1 – Исходные данные режима продольного и бокового движений
Номер
задания
Исходные данные
Н [м]
М
Yp[м]
α[град]
G*[кГ]
Gт[кГ]
0
1000
0.4
3
1
45000
30000
1
2000
0.4
3
2
35000
20000
2
3000
0.5
3
5
45000
25000
3
4000
0.5
3
1
40000
20000
4
5000
0.6
3
3
35000
25000
5
6000
0.6
3
7
40000
30000
6
7000
0.7
3
1
35000
20000
7
8000
0.7
3
5
45000
25000
8
9000
0.7
3
3
35000
30000
9
10000
0.8
3
1
50000
35000
8

9.

Исходные сведения для выполнения курсовой работы:
– g = 9.8 м/с2 – ускорение свободного падения;
– ρ – массовая плотность воздуха, заданная графически ρ=ρ(Н), кГс2/м4;
– Н – высота полета является исходным данным, м;
– а – скорость звука, заданная графически а=а(Н), м/с;
– V – воздушная скорость самолета, определяется через заданное
значение числа Маха (М), м/с;
– S = 180 м2 – площадь крыла самолета;
– l=38 м – размах крыла;
– ba= 5 м – средняя аэродинамическая хорда (САХ);
– G= G*+ Gт – полетный вес самолета, кГ;
– G*– вес пустого самолета, является исходным данным, кГ;
– Gт – вес топлива, является исходным данным, кГ;
– m – полетная масса самолета, кг;( для системы МКГСС масса численно
равна весу);
– Jx, Jy, Jz, Jxy – моменты инерции самолета, заданные графически
зависимостями Jx(Gт), Jy(Gт), Jz(Gт), Jxy(Gт), кГмс2;
– Cyгп = Су = 2G/SρV2 – безразмерный коэффициент подъемной силы;
– Сх – безразмерный коэффициент лобового сопротивления,
определяется из графической зависимости Сх=f(Cy) ;
–
mzM mxM myM 0,002
частные
производные
продольного,
поперечного и путевого моментов от соответствующих возмущающих
моментов.
2.2. Порядок подготовки расчетной части курсовой работы
1. Из приведенных математических моделей (2.1) и (2.2) выделить
математические
модели
своего
варианта
задания
(продольное
короткопериодическое движение, изолированные боковые движения «Рыскание
– скольжение» и «Чистый крен»).
2. Задаваемые исходные сведения (Н, М, Yp, G*, Gт, α, S, l, ba), входящие в
выражения коэффициентов, соответствуют значениям по варианту задания и
указаны в таблице 2.1
3. Численные значения коэффициентов моделей продольного или
бокового движений самолета определяются согласно выражений таблицы 2.2. с
учетом варианта задания.
9

10.

Таблица 2.2 – Коэффициенты линеаризованной математической модели ВС
Коэффициенты продольного движения
m z z V 2
аmz
Sba
Jz 2
1
с
m z& V 2
аmz
Sba
Jz 2
1
с
m z V 2
аmz
Sba
Jz 2
1
с2
57.3 mzM 2 Cx C y sin 0 Yp V 2
V
а
Sb
P
Y
a
p
J z a
Vba
2
град
с м
m z B V 2
аmz
Sba
Jz 2
1
с2
z
&
V
mz
B
аmMz z
аy
град
с 2 кг м
57.3
Jz
C y Cx V
m
S
2
M
57.3 S C y M
а
C y 1
m
2
C
y
V
y
а x
аx
g
cos 0
57.3
Сx C y V 2
57.3m
2
S
1
с
град
м
м
с 2 град
м
с 2 град
SV CxM M
PV
а
Cx 1
m
2
C
SVCx
x
1
c
м
аxP kСГ 1.5, 2
.
с град
м
с 2 град
V
x
10

11.

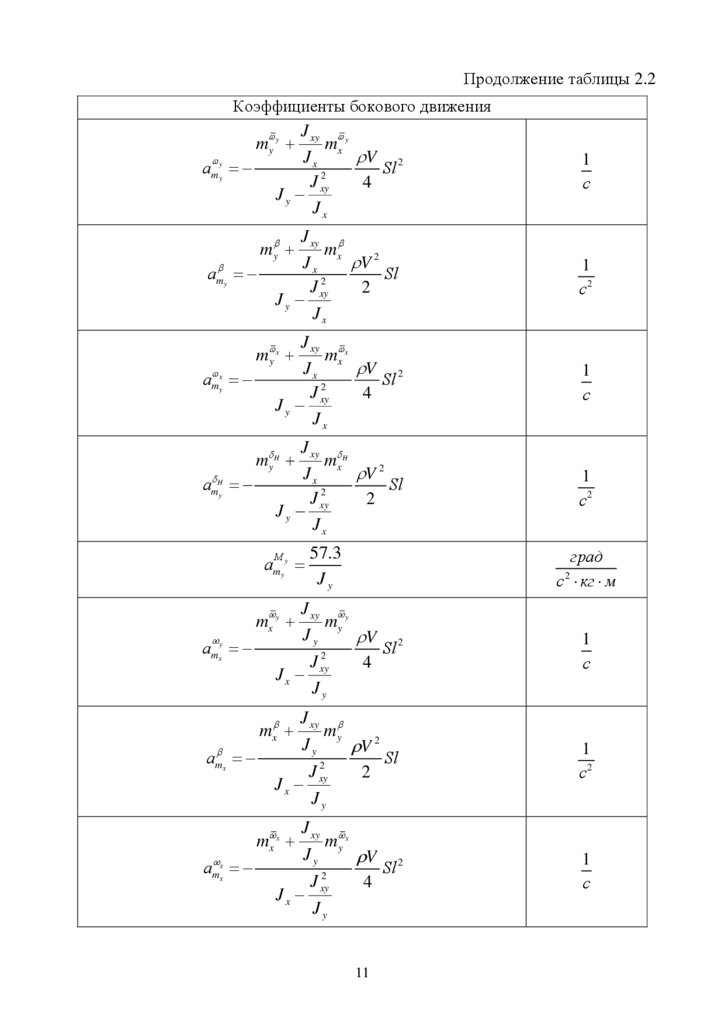
Продолжение таблицы 2.2
Коэффициенты бокового движения
J
my y xy mx y
Jx
V 2
аmyy
Sl
2
J xy
4
Jy
Jx
аm y
аm xy
аm Hy
J xy
mx
Jx
V 2
Sl
J xy2
2
Jy
Jx
1
с2
J xy x
mx
Jx
V 2
Sl
J xy2
4
Jy
Jx
1
с
J xy H
mx
Jx
V 2
Sl
J xy2
2
Jy
Jx
1
с2
my
m y x
m y H
М
аmyy
57.3
Jy
град
с кг м
2
J xy y
my
Jy
V 2
Sl
2
J xy
4
Jx
Jy
1
с
J xy
my
Jy
V 2
Sl
J xy2
2
Jx
Jy
1
с2
J xy x
my
Jy
V 2
Sl
2
J xy
4
Jx
Jy
1
с
mx y
аmxy
mx
аm x
m x x
аm xx
1
с
11

12.

Продолжение таблицы 2.2
Коэффициенты бокового движения
J xy Э
my
Jy
V 2
Sl
J xy2
2
Jx
Jy
m x Э
аm Эx
аmМxx
1
с2
град
с кг м
57.3
Jx
2
Cz V
а
S
m 2
g
аz cos
V
z
1
с
1
с
4. Частные производные Ci j , mij , моменты инерции J i и параметры среды
а, V, ρ, входящие в выражения коэффициентов aij
определяются по
графическим зависимостям соответствующих параметров, представленных в
приложении №2.
5. Передаточные функции упрощенных моделей продольного и бокового
движений самолета, связывающие операторные изображения выходных
параметров ВС с операторными изображениями входных воздействий
определяются правилом Крамера. Согласно этого правила, передаточная
функция представляет собой отношение определителей двух матриц,
составленных из коэффициентов исследуемой математической модели ВС. В
знаменателе располагается матрица, составленная из коэффициентов левой
части математической модели ВС. Матрица числителя получается из матрицы
знаменателя, путем замены столбца коэффициентов, стоящих при выбранном
выходном параметре на столбец коэффициентов, стоящих при выбранном
входном параметре. После раскрытия матриц в числителе и знаменателе и
приведения подобных относительно степени оператора p, получаем
передаточную функцию в виде отношения полиномов. Вариант определения
передаточной функции рассмотрен в разделе 3 методички.
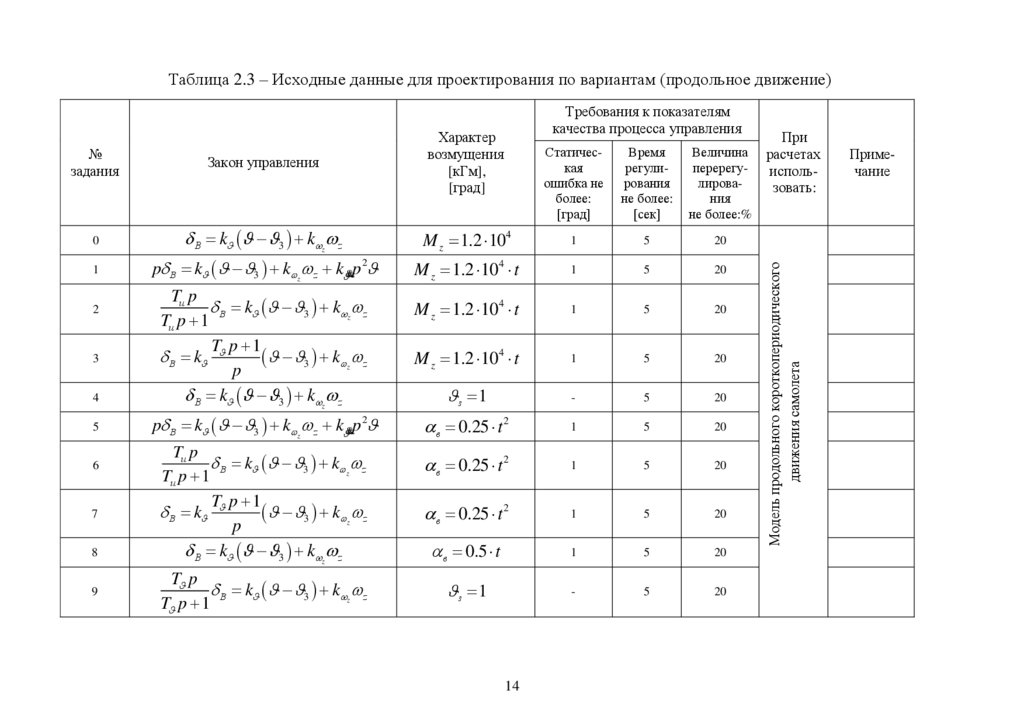
6. В таблицах 2.3 и 2.4 заданы исходные данные для проектирования по
вариантам задания: законы управления автопилота воздушного судна, характер
входного (возмущающего или управляющего) воздействия, приложенного к
системе «Самолет – автопилот», и показатели качества процесса управления,
необходимые для расчета передаточных чисел автопилота.
12

13.

2.3. Задание на выполнение курсовой работы
1. Составить структурную схему замкнутого контура управления системы
«Самолет – автопилот». При этом моделью самолета должна быть конкретная
модель, соответствующая заданию варианта курсовой работы.
2. По заданным показателям качества процесса управления системы
«Самолет – автопилот» рассчитать передаточные числа автопилота.
3. Выполнить проверку на устойчивость системы «Самолет – автопилот»
с рассчитанными передаточными числами автопилота, для чего построить
ЛАЧХ и ЛФЧХ разомкнутого контура управления и определить запасы
устойчивости по фазе и амплитуде.
4. Построить график переходного процесса системы «Самолет –
автопилот» по стабилизируемому автопилотом параметру при заданном
входном возмущающем или управляющему воздействии, приложенным к
системе «Самолет – автопилот».
5. Построить графики переходных процессов основного параметра
стабилизации при отказах датчиков измеряемых параметров (угла, угловой
скорости, углового ускорения) и проанализировать влияние отказов на
динамические свойства системы «Самолет – автопилот».
6. По результатам выполненной работы сделать обоснованные выводы.
7. Оформить выполненную работу в письменном виде, соблюдая
требования по оформлению курсовой работы (Приложение № 1).
13

14.

Таблица 2.3 – Исходные данные для проектирования по вариантам (продольное движение)
Статическая
ошибка не
более:
[град]
Время
регулирования
не более:
[сек]
Величина
перерегулирования
не более:%
1
5
20
p В k 3 k z z k &&p 2
M z 1.2 104
M z 1.2 104 t
1
5
20
Tи p
В k 3 k z z
Tи p 1
T p 1
В k
3 k z z
p
В k 3 k z z
M z 1.2 104 t
1
5
20
M z 1.2 104 t
1
5
20
з 1
-
5
20
p В k 3 k z z k &&p 2
в 0.25 t 2
1
5
20
Tи p
В k 3 k z z
Tи p 1
T p 1
В k
3 k z z
p
в 0.25 t 2
1
5
20
в 0.25 t 2
1
5
20
Закон управления
0
В k 3 k z
1
3
4
5
6
7
z
8
В k 3 k z
в 0.5 t
1
5
20
9
T p
В k 3 k z z
T p 1
з 1
-
5
20
z
14
При
расчетах
использовать:
Модель продольного короткопериодического
движения самолета
Характер
возмущения
[кГм],
[град]
№
задания
2
Требования к показателям
качества процесса управления
Примечание

15.

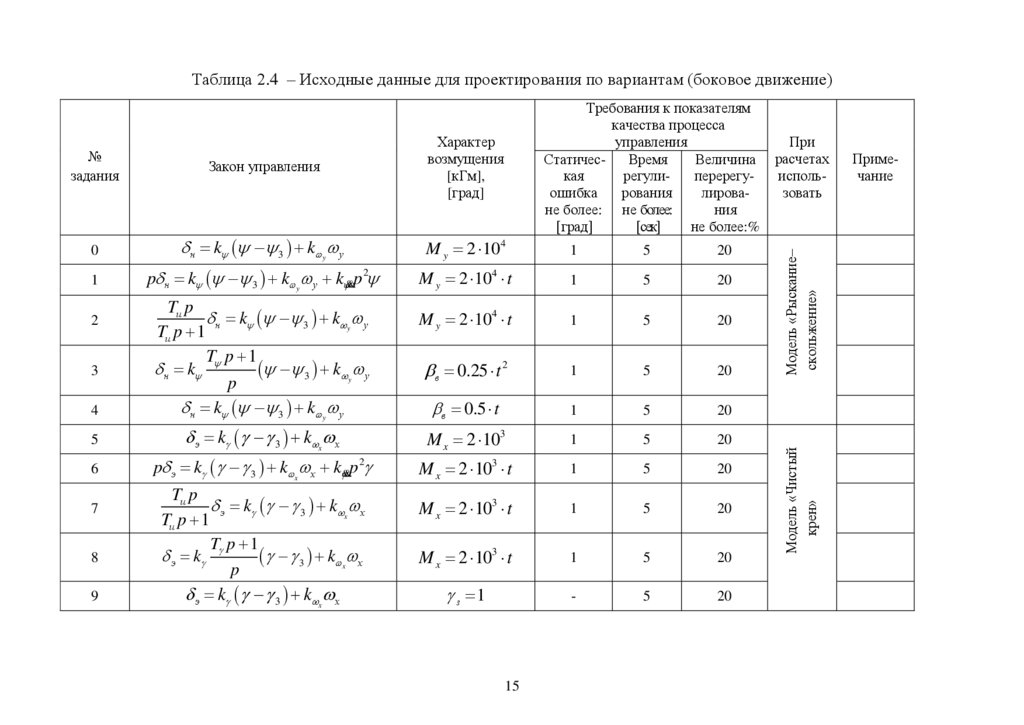
Таблица 2.4 – Исходные данные для проектирования по вариантам (боковое движение)
Закон управления
0
н k 3 k y
M y 2 104
1
5
20
1
p н k 3 k y y k &&p 2
M y 2 104 t
1
5
20
Tи p
н k 3 k y y
Tи p 1
T p 1
н k
3 k y y
p
н k 3 k y y
M y 2 104 t
1
5
20
в 0.25 t 2
1
5
20
в 0.5 t
1
5
20
M x 2 103
1
5
20
2
3
4
y
5
э k 3 k x
6
p э k 3 k x x k &&p 2
M x 2 103 t
1
5
20
Tи p
э k 3 k x x
Tи p 1
T p 1
э k
3 k x x
p
э k 3 k x x
M x 2 103 t
1
5
20
M x 2 103 t
1
5
20
з 1
-
5
20
7
8
9
x
15
При
расчетах
использовать
Модель «Рыскание–
скольжение»
Характер
возмущения
[кГм],
[град]
№
задания
Модель «Чистый
крен»
Требования к показателям
качества процесса
управления
СтатичесВремя
Величина
кая
регулиперерегуошибка
рования
лироване более: не более:
ния
[град]
[сек]
не более:%
Примечание

16.

3. ПРИМЕР РАСЧЕТА ПЕРЕДАТОЧНЫХ ЧИСЕЛ АВТОПИЛОТА
3.1. Исходные данные для расчета
Исходными данными для расчета являются:
1. Система линеаризованных дифференциальных уравнений продольного
движения самолета, записанных в символической форме при нулевых
начальных условиях, описывающих продольное движение самолета (2.1).
В соответствии с вариантом задания из уравнения полного продольного
движения выделено короткопериодическое продольное движение, имеющее
следующий вид:
(3.1)
2. Значения коэффициентов линеаризованных уравнений системы
определены из таблицы 2.2, заданных исходных данных и графиков
приложения №2. Для данного варианта задания их значения равны (здесь взят
произвольный вариант режима полета):
(3.2)
16

17.

3. Коэффициенты
характеристического
уравнения
короткопериодического продольного движения самолета определяются из
системы уравнений (3.1), для чего составляется матрица коэффициентов левых
частей системы уравнений (3.1) и определяется определитель полученной
матрицы:
(3.3)
Положительное значение коэффициентов указывает на устойчивость
короткопериодического продольного движения.
4. Заданный закон управления имеет вид:
(3.4)
5. Характер ветрового возмущения, действующего на систему «Самолет –
автопилот»:
(3.5)
где B ( p) – преобразование Лапласа входного ветрового возмущения.
6. Показатели качества процесса управления, необходимые для расчета
передаточных чисел автопилота:
– установившаяся ошибка по углу тангажа уст при действии
возмущающего нормального ветра (3.5) не должна превышать 1 град;
– время регулирования не должно превышать 5 с;
– величина перерегулирования не должна превышать 20 %.
3.2.
Содержание задания курсовой работы
1. Составить структурную схему системы «Самолет – автопилот».
2. По заданным показателям качества процесса управления системы
«Самолет – автопилот» рассчитать передаточные числа автопилота.
3. Провести проверку на устойчивость системы «Самолет – автопилот» с
рассчитанными передаточными числами автопилота и определить запасы
устойчивости по фазе и амплитуде.
17

18.

4. Построить переходный процесс системы «Самолет – автопилот» по
стабилизируемому автопилотом параметру при заданном входном
возмущающем или управляющему воздействии, приложенным к системе
«Самолет – автопилот».
5. Проанализировать по переходным процессам влияние отказов датчиков
(угла, угловой скорости, углового ускорения) на динамические свойства
системы «Самолет – автопилот».
3.3. Выполнение курсовой работы
3.3.1. Построение структурной схемы контура «Самолет – автопилот»
Структурная схема системы «Самолет – автопилот» для заданного закона
управления (3.4) и модели короткопериодического продольного движения (3.1)
строится по известным из курса «Автоматика и управление» правилам, и ее вид
представлен на рисунке 3.1.
При построении структурной схемы были использованы передаточные
функции короткопериодического продольного движения (3.6 и 3.7) [1, 2].
(3.6)
(3.7)
Ветровое возмущение приводится к точке ввода управляющего
воздействия в виде эквивалентного ветровому возмущению отклонения руля
высоты ЭB p .
Передаточная функция W B p , обеспечивающая эквивалентность угла
B
отклонения руля высоты ЭB p ветровому возмущению B p определяется
как отношение передаточных функций 3.7 к 3.6:
(3.8)
18

19.

Структурная схема замкнутого контура управления представлена на рис.
3.1. Все параметры на схеме являются преобразованиями Лапласа. Операторы
Лапласа p при параметрах опущены для упрощения изображения схемы и
уменьшения ее загромождения.
Например, на схеме ЭB ЭB p и т.д.
Рисунок 3.1 − Структурная схема замкнутой системы «Самолет-автопилот»
3.3.2. Определение передаточных чисел в законе управления автопилота
Преобразуем закон управления (3.4) таким образом, чтобы разделить
изменяемые собственные параметры и задаваемые величины и добавим
преобразованный закон управления к системе (3.1). В результате получим
систему уравнений (3.9) соответствующую структурной схеме замкнутого
контура «Самолет – автопилот», изображенной на рис. 3.1.
(3.9)
Из системы уравнений (3.9), по правилу Крамера определим
передаточную функцию замкнутой системы по ветровому возмущающему
воздействию B ( p) :
19

20.

(3.10)
В выражении 3.10 в знаменателе матрица коэффициентов левых частей
системы уравнений 3.9, из которой находится главный определитель
передаточной функции, в числителе матрица коэффициентов, составленная
путем замены коэффициентов столбца выходного параметра в матрице
знаменателя на коэффициенты входного воздействия. Из матрицы числителя
определяется дополнительный определитель передаточной функции.
После преобразований получим передаточную функцию Ф p , в виде
B
отношений полиномов по степени оператора Лапласа p:
(3.11)
где
Определим минимально возможную величину коэффициента k ,
обеспечивающего заданную статическую ошибку, при действии возмущения
(3.5).
20

21.

Согласно заданию, установившаяся ошибка по углу тангажа уст при
2
2
действии возмущения B t B 0 t 0.25 t не должна превышать 1 град.
По теореме о предельных значениях, получим:
(3.12)
B0
2
3
где p – преобразование по Лапласу функции B t B 0 t .
Подставляя в (3.12) выражение (3.11), получим:
(3.13)
Откуда определим минимально возможную величину коэффициента
обеспечивающего требуемую точность в установившемся режиме:
k ,
(3.14)
Числитель дроби в выражении отрицательный, что свидетельствует о том,
что положительное приращение B 0 приводит к отрицательному приращению
угла тангажа. Поэтому целесообразно рассматривать реакцию автопилота на
отрицательное приращение B 0 . При этом значение коэффициента ,
обеспечивающее требуемую точность в установившемся режиме, будет
положительным.
Далее, исходя из заданных показателей качества процесса стабилизации,
k
k
определим все передаточные числа и уточним значение коэффициента .
Для этого будем использовать метод стандартных переходных характеристик
(приложение №3).
В приложении №3
приведены стандартные характеристики
передаточных функций до третьего порядка включительно, что позволяет
определить требуемые значения передаточных коэффициентов для полученных
в процессе решения неизвестных передаточных функций.
21

22.

В нашем примере приходится применить «обходное», нестандартное
решение. Синтез закона управления по полученной ранее передаточной
функции (3.11) замкнутой системы по возмущающему воздействию B
потребует использования стандартной передаточной функции 4-го порядка, что
приведет к некоторым затруднениям в расчетах коэффициентов. Считая, что
основные характеристики контура управления сохраняются при различных
видах внешнего воздействия на контур, выполним синтез автопилота на основе
свойств контура стабилизации заданного угла тангажа зад .
С этой целью, используя систему уравнений (3.9) определим передаточную
функцию замкнутого контура по задающему воздействию
зад :
(3.15)
После преобразований получим:
(3.16)
Передаточная функция 3.16 имеет один ненулевой корень. Поэтому в
соответствии с методом стандартных переходных характеристик, приравняем
полученную передаточную функцию (3.16) с неизвестными пока
передаточными числами k , k z , k && к стандартной передаточной функции Ф0 ( p) ,
параметры которой известны, а показатели качества переходного процесса
удовлетворяют требованиям задания. Стандартная передаточная функция,
удовлетворяющая вышеназванным условиям, в общем виде выглядит
следующим образом (приложение №3):
22

23.

(3.17)
Параметры стандартной передаточной функции (3.17), соответствующие
требуемому качеству переходного процесса, определены по графику №3
таблицы П.3.1, приложения № 3, для которого:
(3.18)
где
– безразмерное время переходного процесса, соответствующее графику
№3, таблицы П.3.1; приложения№ 3.
t 5 – время переходного процесса, заданное в задании.
В развернутом виде равенство Ф p Ф0 p примет вид:
З
(3.19)
После преобразования равенства (3.19) к виду
(3.20)
приравняем коэффициенты характеристических полиномов при одинаковых
степенях р и, учитывая соотношение (3.16), получим систему уравнений (3.21):
(3.21)
Разрешая ее относительно неизвестных передаточных чисел k , k z , k &&,
получим численное значение искомых коэффициентов:
(3.22)
23

24.

3.3.3. Проверка на устойчивость и определение запасов
устойчивости системы
Для проверки системы на устойчивость и определения запасов
устойчивости по фазе и амплитуде необходимо построить логарифмические
амплитудную и фазовую частотные характеристики разомкнутой системы.
Определим передаточную функцию разомкнутой системы по структурной
схеме замкнутого контура, представленной на рис. 3.1. Порядок определения
структурной схемы разомкнутого контура по исходной структурной схеме
замкнутого контура определен в [5].
В итоге получим следующий вид передаточной функции разомкнутого
контура:
(3.23)
Определим полюса разомкнутой системы (3.23)
и представим передаточную функцию (3.23) в стандартной форме
(3.24)
24

25.

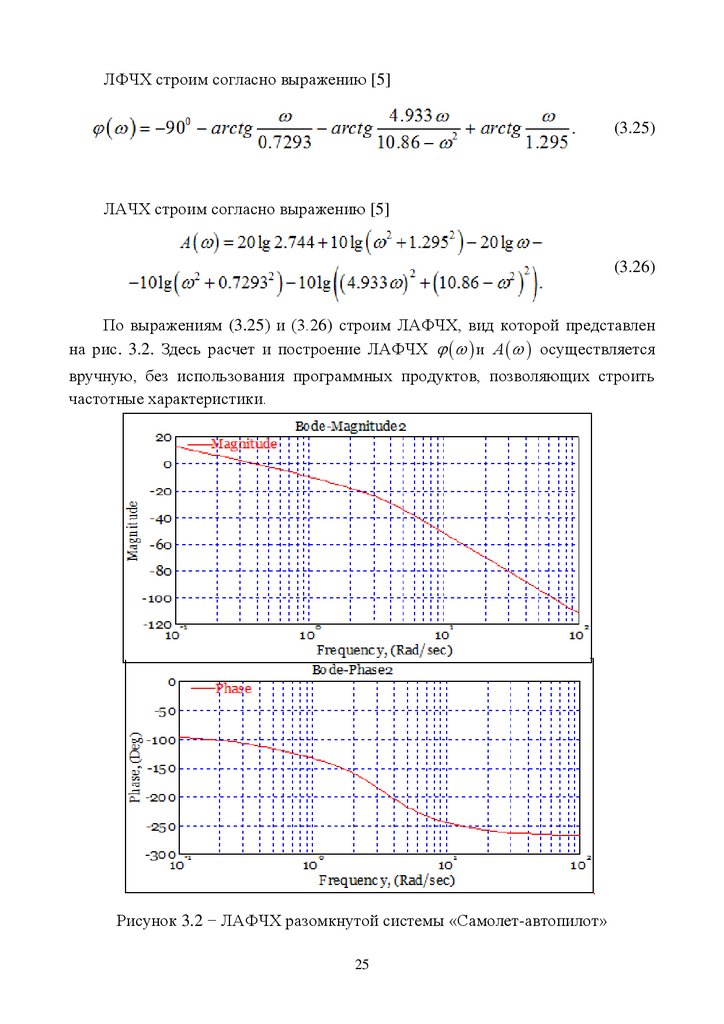
ЛФЧХ строим согласно выражению [5]
(3.25)
ЛАЧХ строим согласно выражению [5]
(3.26)
По выражениям (3.25) и (3.26) строим ЛАФЧХ, вид которой представлен
на рис. 3.2. Здесь расчет и построение ЛАФЧХ и А осуществляется
вручную, без использования программных продуктов, позволяющих строить
частотные характеристики.
Рисунок 3.2 − ЛАФЧХ разомкнутой системы «Самолет-автопилот»
25

26.

Построенные ЛАФЧХ позволяют сделать вывод об устойчивости системы.
Из графиков на рис.3.2 следует, что запас устойчивости по фазе равен 700 , а по
амплитуде 23дБ [5].
В курсовой работе для построения ЛАФЧХ может использоваться любой
программный продукт, в котором возможно графическое построение частотных
характеристик и которым владеет студент (VisSim, MathLab, MathCad и др).
3.3.4. Построение переходного процесса для системы
«Самолет – автопилот» и оценка влияния отказов датчиков
на характер переходного процесса
Построение переходных процессов контура «Самолет – автопилот» и
оценка влияния отказов датчиков на характер переходного процесса
осуществляется по передаточной функции замкнутой системы при воздействии
на самолет возмущающего воздействия (3.5). Для этих целей использован
программный продукт VisSim.
В общем виде передаточная функция исправной системы описывается
выражением (3.11). После подстановки в выражение (3.11) численных значений
найденных коэффициентов закона управления, передаточная функция по
ветровому возмущению будет иметь вид:
(3.27)
Оценим влияние отказов датчиков на характер переходного процесса
приравниванием к нулю соответствующих передаточных чисел в
коэффициентах характеристического полинома передаточной функции (3.27).
Переходные процессы для рассматриваемого варианта задания, построенные с
использованием программы VisSim, представлены на рис 3.3.
26

27.

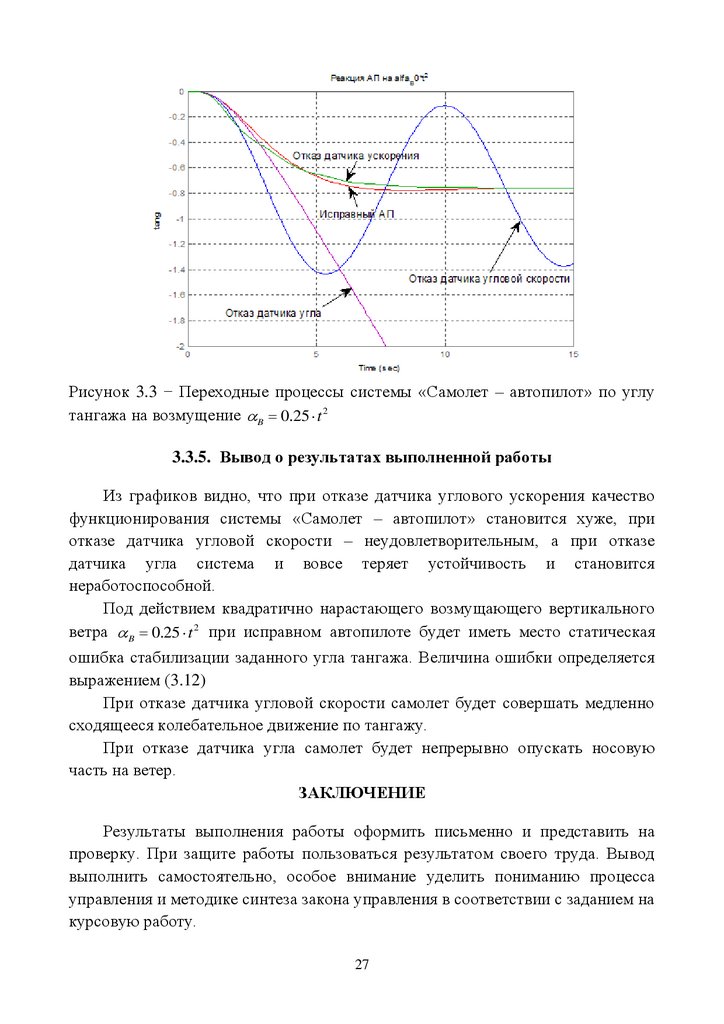
Рисунок 3.3 − Переходные процессы системы «Самолет – автопилот» по углу
тангажа на возмущение B 0.25 t 2
3.3.5. Вывод о результатах выполненной работы
Из графиков видно, что при отказе датчика углового ускорения качество
функционирования системы «Самолет – автопилот» становится хуже, при
отказе датчика угловой скорости – неудовлетворительным, а при отказе
датчика угла система и вовсе теряет устойчивость и становится
неработоспособной.
Под действием квадратично нарастающего возмущающего вертикального
ветра B 0.25 t 2 при исправном автопилоте будет иметь место статическая
ошибка стабилизации заданного угла тангажа. Величина ошибки определяется
выражением (3.12)
При отказе датчика угловой скорости самолет будет совершать медленно
сходящееся колебательное движение по тангажу.
При отказе датчика угла самолет будет непрерывно опускать носовую
часть на ветер.
ЗАКЛЮЧЕНИЕ
Результаты выполнения работы оформить письменно и представить на
проверку. При защите работы пользоваться результатом своего труда. Вывод
выполнить самостоятельно, особое внимание уделить пониманию процесса
управления и методике синтеза закона управления в соответствии с заданием на
курсовую работу.
27

28.

ПРИЛОЖЕНИЕ № 1
Содержание отчета курсовой работы
В отчете выполненной курсовой работы необходимо представить:
1. Титульный лист курсовой работы (образец представлен ниже).
2. Исходные данные для выполнения курсовой работы.
3. Задание на курсовую работу.
4. Выполненные расчеты в курсовой работе.
5. Графические материалы.
6. Выводы по проведенным расчетам и экспериментам.
7. Используемые источники.
Расчеты и преобразования алгоритмов выполняются в общем виде с
подстановкой численных значений в конечные выражения, без промежуточных
численных расчетов.
Выводы делаются обоснованными, конкретными и содержательными.
28

29.

Образец оформления титульного листа курсовой работы
ИРКУТСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО
ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ»
Кафедра авиационных электросистем и пилотажно-навигационных комплексов
КУРСОВАЯ РАБОТА
по дисциплине
Пилотажно-навигационные комплексы
Тема: «Параметрический синтез законов управления САУ
(автопилота)»
Выполнил: студент специальности
2.25. 03.02 (бакалавр)
________________________
«______»___________2018 г
Принял:_________________________
«______»___________2018 г
Иркутск 2018 г.
29

30.

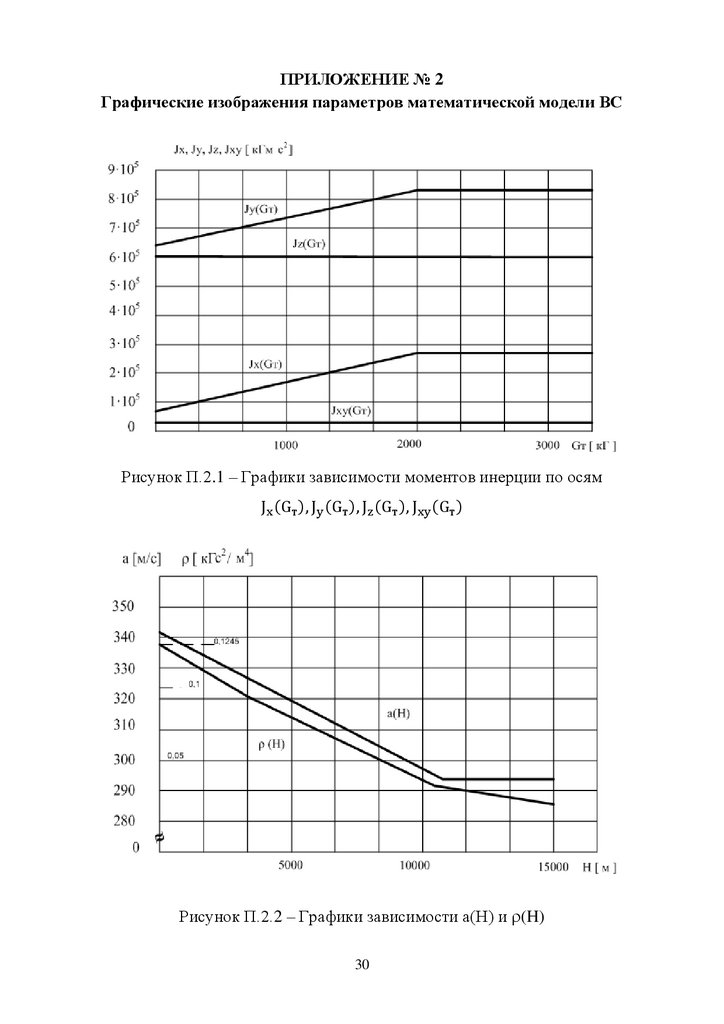
ПРИЛОЖЕНИЕ № 2
Графические изображения параметров математической модели ВС
Рисунок П.2.1 – Графики зависимости моментов инерции по осям
Рисунок П.2.2 – Графики зависимости а(Н) и (H)
30

31.

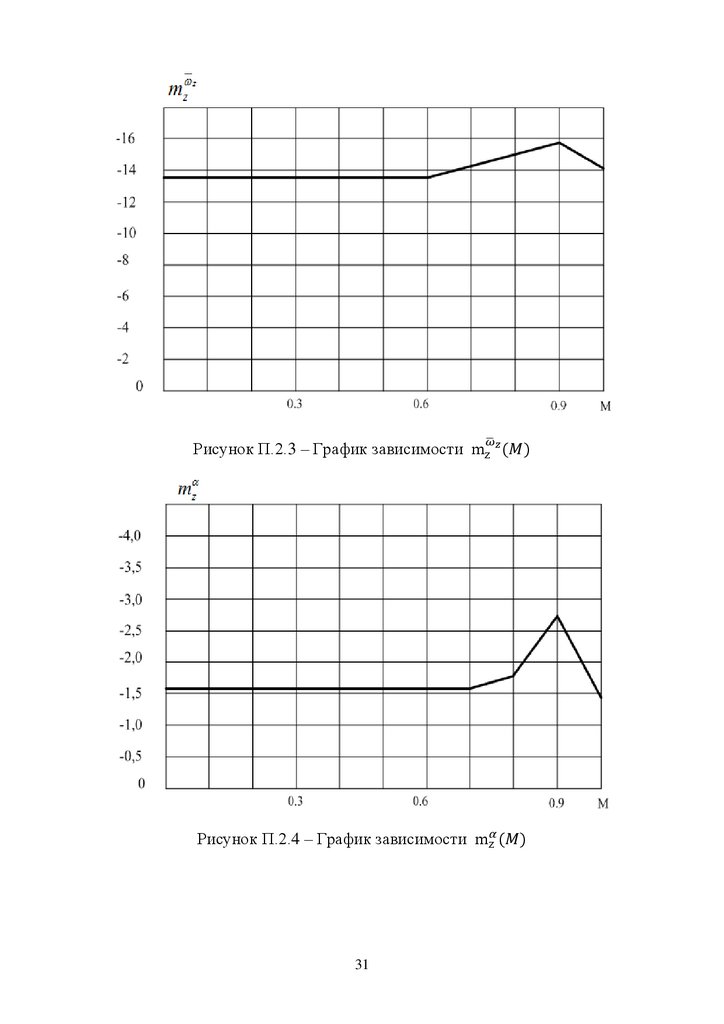
Рисунок П.2.3 – График зависимости
Рисунок П.2.4 – График зависимости
31

32.

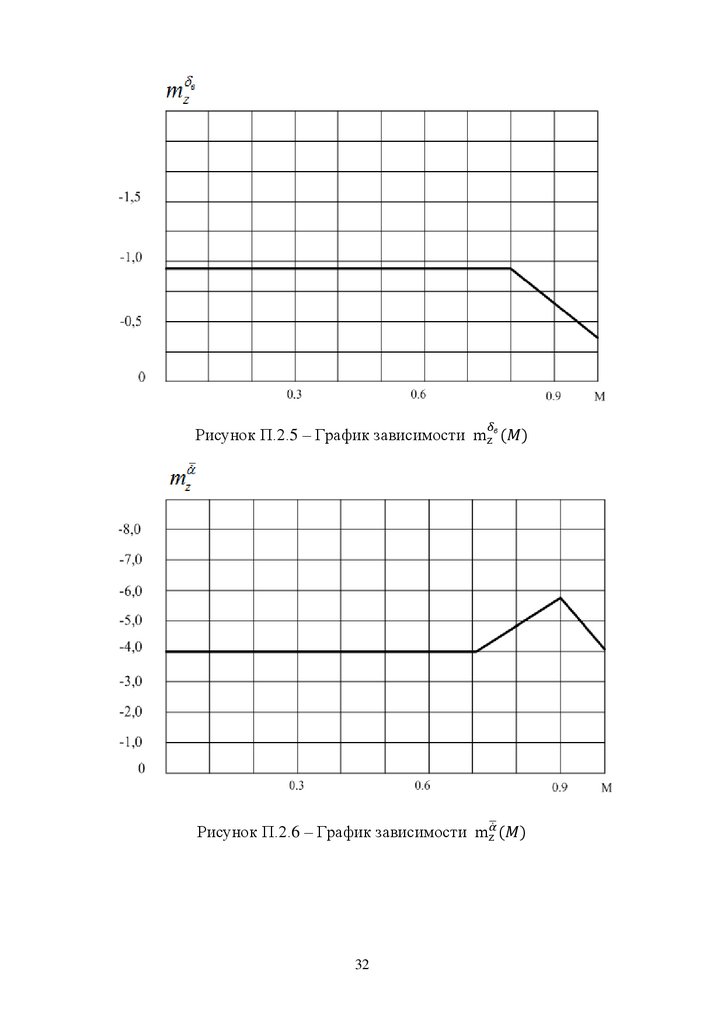
Рисунок П.2.5 – График зависимости
Рисунок П.2.6 – График зависимости
32
в

33.

Рисунок П.2.7 – График зависимости
Рисунок П.2.8 – График зависимости
33

34.

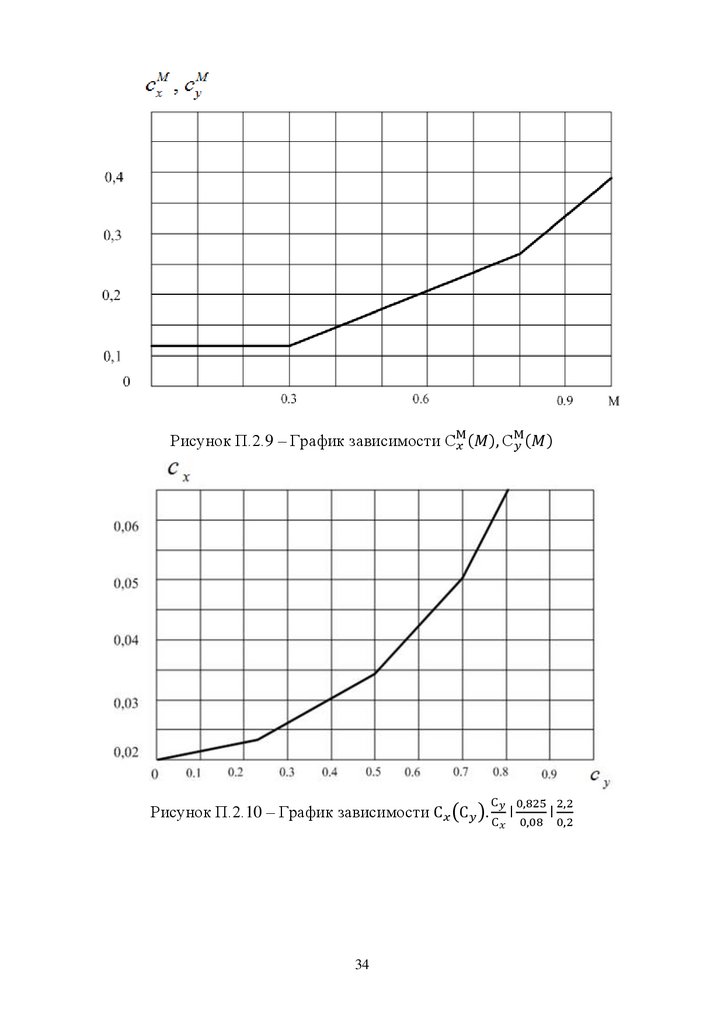
Рисунок П.2.9 – График зависимости
Рисунок П.2.10 – График зависимости
34

35.

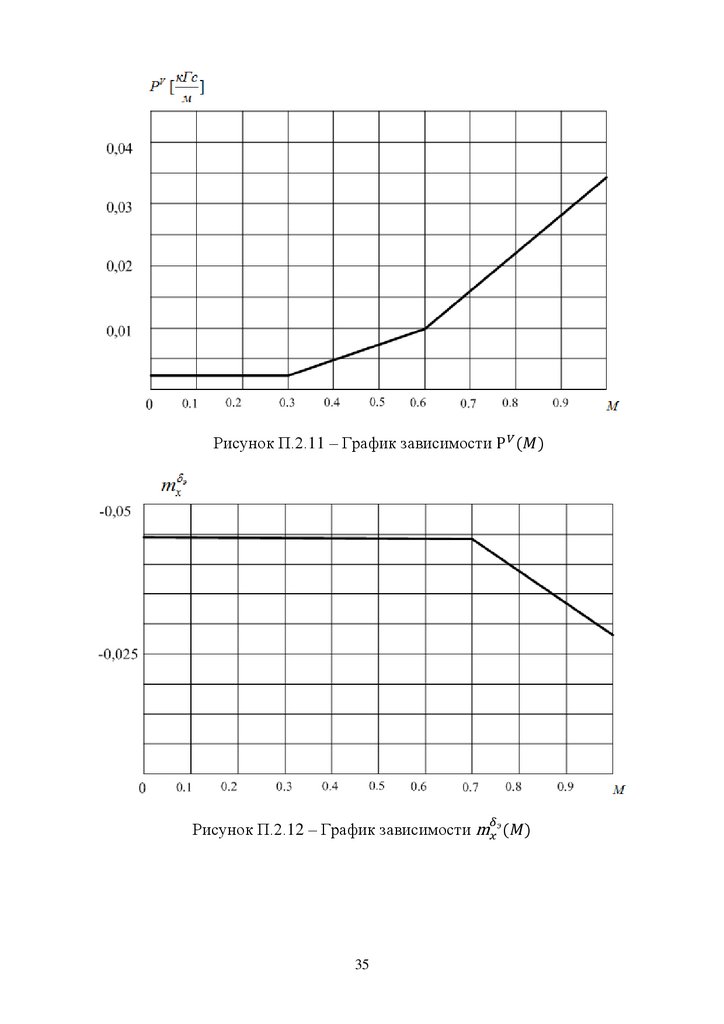
Рисунок П.2.11 – График зависимости
Рисунок П.2.12 – График зависимости
35
э

36.

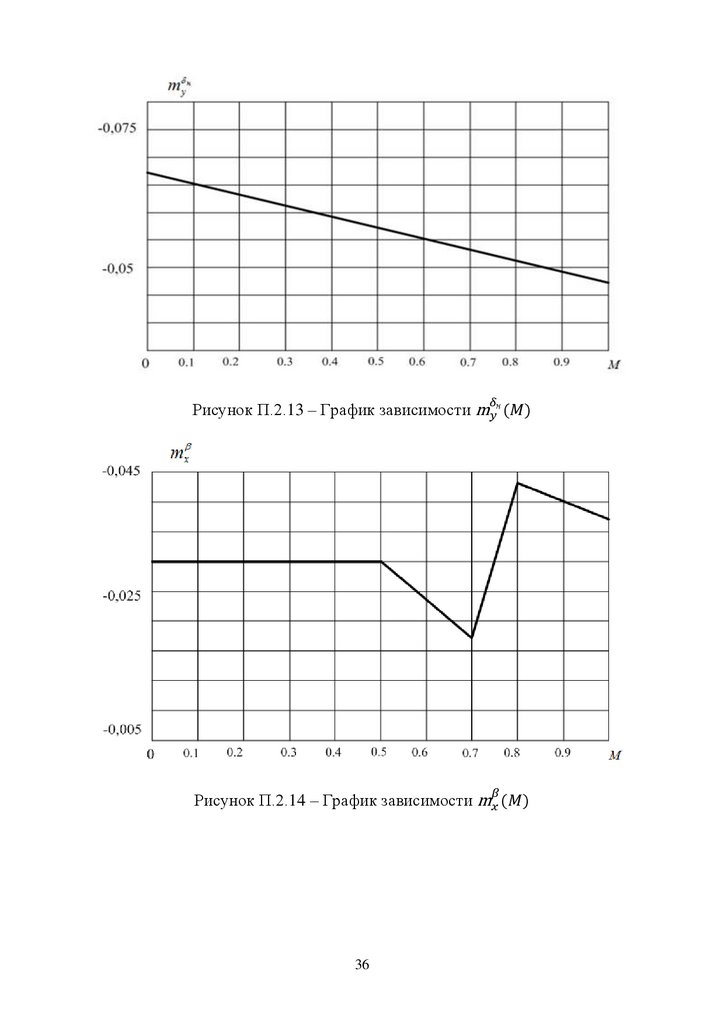
Рисунок П.2.13 – График зависимости
Рисунок П.2.14 – График зависимости
36
н

37.

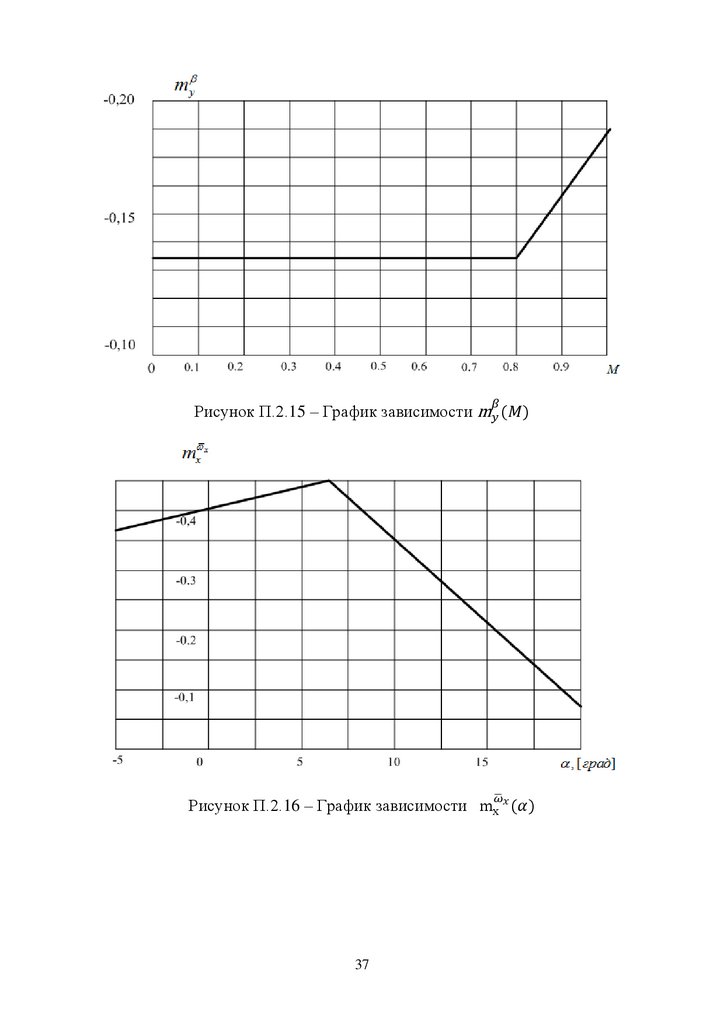
Рисунок П.2.15 – График зависимости
Рисунок П.2.16 – График зависимости
37

38.

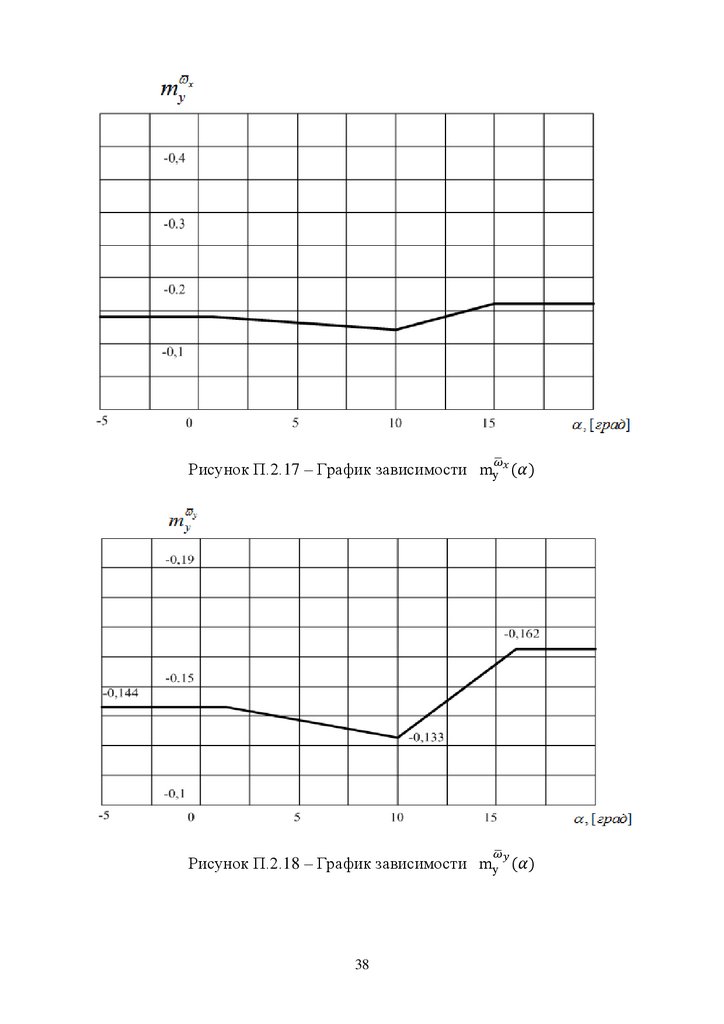
Рисунок П.2.17 – График зависимости
Рисунок П.2.18 – График зависимости
38

39.

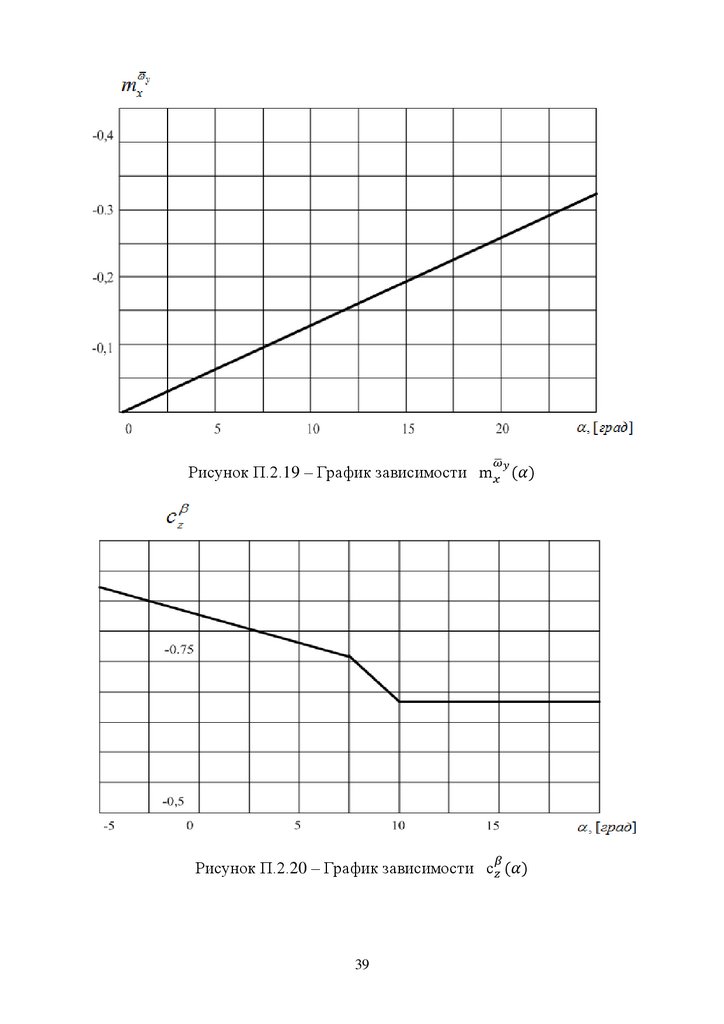
Рисунок П.2.19 – График зависимости
Рисунок П.2.20 – График зависимости
39

40.

ПРИЛОЖЕНИЕ № 3
Метод стандартных переходных характеристик (СПХ)
Одним из методов синтеза структур САУ, получивший широкое
распространение в практике инженерных расчетов, является метод стандартных
переходных характеристик (СПХ).
Суть метода СПХ, заключается в том, что для принятой структурной
схемы проектируемой (с неизвестными параметрами) системы автоматического
регулирования (САР) выбирают приемлемый вид переходного процесса.
Выбранному переходному процессу ставят в соответствие передаточную
функцию с уже известными параметрами.
Приравнивая передаточную функцию с неизвестными параметрами к
передаточной функции, вид переходного процесса которой удовлетворяет
поставленным в задании требованиям, определяют неизвестные значения
параметров в структуре проектируемой САР.
Не рассматривая здесь теоретические аспекты метода СПХ, представим
необходимый справочный материал для его практического использования.
При расчетах в курсовой работе возможны два вида передаточных
функций замкнутой системы «Самолет – автопилот», параметры которых
необходимо определять.
1. Если передаточная функция замкнутой системы в общем виде
определена выражением П.3.1:
(П.3.1)
то передаточная функция с известным качеством переходного процесса будет
иметь вид П.3.2:
(П.3.2)
где k = n – m.
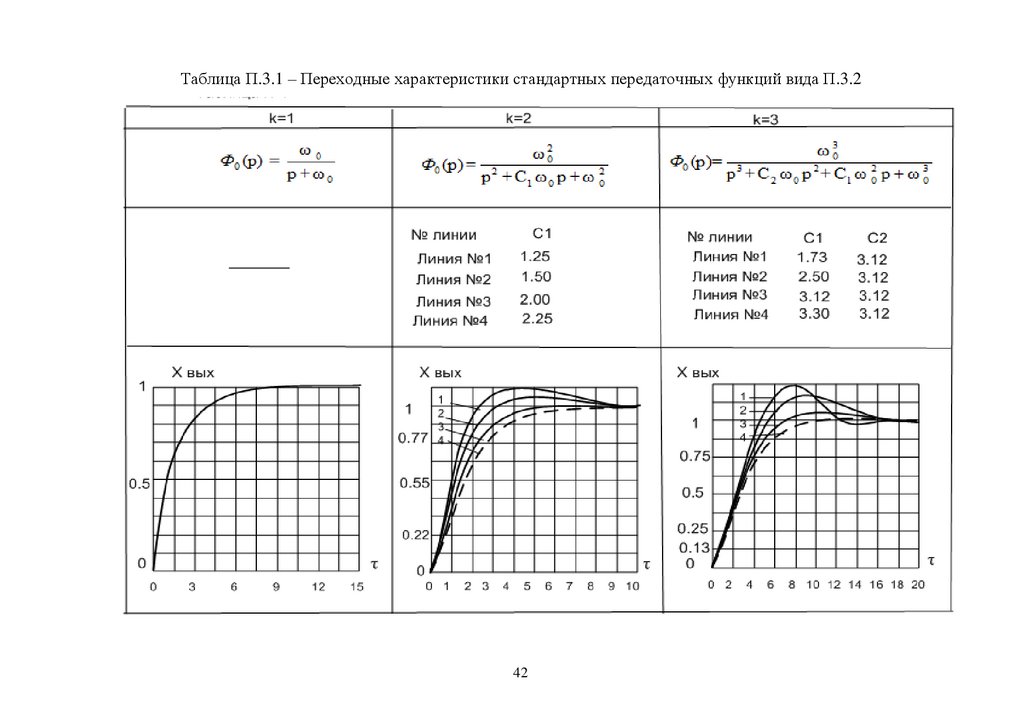
Переходные характеристики для систем первого, второго и третьего
порядка, т.е. для k=1, 2, 3, а также значения коэффициентов Ci (i = 1…k–1)
представлены в таблице П.3.1 приложения №3.
2. Если передаточная функция замкнутой системы в общем виде
определена выражением П.3.3:
40

41.

(П.3.3)
то передаточная функция с известным качеством переходного процесса будет
иметь вид П.3.4:
(П.3.4)
где k = n – m.
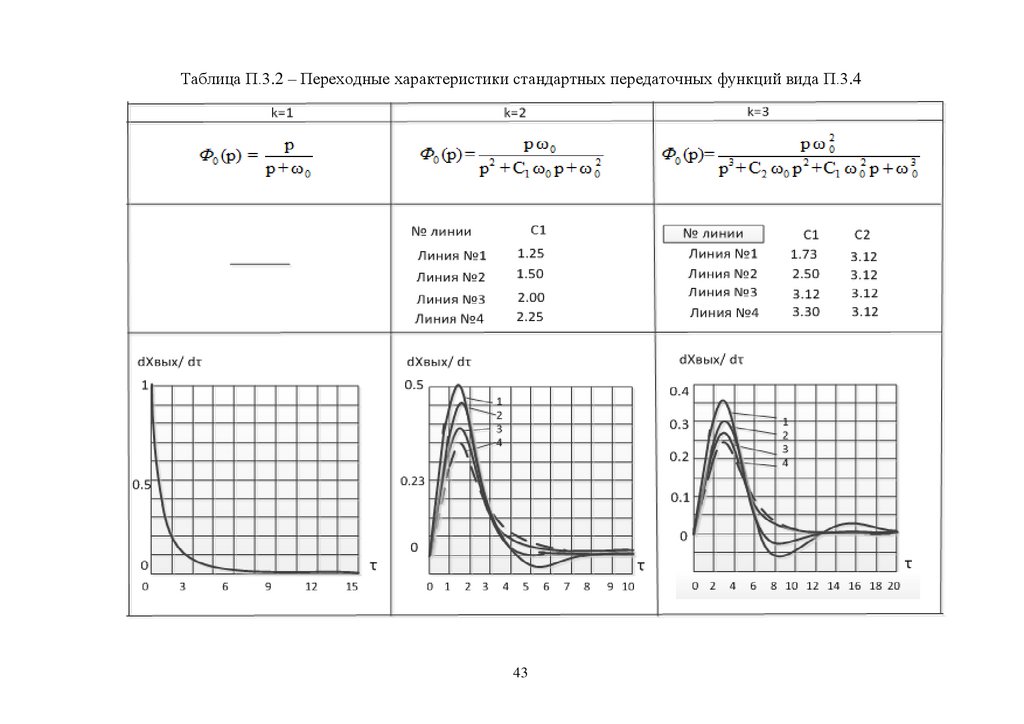
Переходные характеристики для систем первого, второго и третьего
порядка, т.е. для k=1,2,3, а также значения коэффициентов Ci (i=1…k–1)
представлены в таблице П.3.2 приложения №3.
Все графики, представленные в таблицах П.3.1 и П.3.2 соответствуют
значению 0 1 . По оси абсцисс отложено безразмерное время . Для перехода
к размерному времени используется соотношение:
(П.3.5)
41

42.

Таблица П.3.1 – Переходные характеристики стандартных передаточных функций вида П.3.2
42

43.

Таблица П.3.2 – Переходные характеристики стандартных передаточных функций вида П.3.4
43

44.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1.
2.
3.
4.
5.
6.
7.
8.
9.
Воробьев В.Г, Кузнецов С.В. Автоматическое управление полетом
самолетов. – М.: Транспорт, 1995. – 448 с.
Вавилов Ю.А. Системы автоматического управления полетом. – М.: ВВИА
им. проф. Н.Е. Жуковского, 2009. – 403 с.
Михалев И.А., Окоемов Б.Н., Павлина И.Г., Чекулаев М.С., Киселев Ю.Ф.
Системы автоматического и директорного управления самолетом. – М.:
«Машиностроение», 1974. – 230 с.
Шумилов И.С. Системы управления рулями самолета. – М.: Изд. МГТУ
им. Н.Э. Баумана, 2009. – 481 с.
Лайков М.И. Автоматика и управление. – Иркутск: ИФ МГТУ ГА, 2010 .–
305 с
Диль В.Ф. Системы автоматического управления полетом. Методическое
пособие по выполнению лабораторных работ по САУП, часть I. – Иркутск:
ИФ МГТУ ГА, 2013. – 34 с.
Кузнецов С.В., Гусев А.А. Системы автоматического управления полетом.
Пособие по изучению дисциплины и контрольные задания для студентов
5 курса специальности 131000 заочного обучения. − М: МГТУ ГА, 2004. –
48 с.
Кузнецов С.В., Гусев А.А. Пилотажно-навигационные комплексы.
Пособие по изучению дисциплины и выполнению контрольной работы.
Для студентов 5 курса специальности 131000 заочного обучения. – М.:
МГТУ ГА, 2004. – 36 с.
Голованов И.Г. Пилотажно-навигационные комплексы. Конспект лекций.
− Иркутск, РИО ИФ МГТУ ГА. 2014. − 140 с.
44