10 рабочее тело и теплопроводность Microsoft Office PowerPoint

1. Состояние рабочего тела

2.

Цель урока:
1. Повторить пройденный материал по
основным параметрам физических тел
2. Понять физический смысл характеристик
рабочего тела
3. Проверить усвоение понятия идеального
газа
4. Закрепить полученные знания на решении
практических задач

3.

Процессы преобразования энергии в различных
тепловых машинах осуществляется с помощью
вещества, называемого рабочим телом. В качестве
рабочих тел могут выступать вещества в жидком,
газообразном и твердом состояниях. Они являются
«посредниками» в процессе обмена энергией между
системой и окружающей средой. Так, например,
нагреваемый газ расширяется и совершает
механическую работу. В результате происходит
преобразование тепловой энергии в механическую.
Рабочее тело характеризуют различные параметры
состояния – давление, объем, температура,
внутренняя энергия, энтальпия, т.д. В качестве
основных параметров состояния принимают:
удельный объём, абсолютное давление и
абсолютную температуру

4.

Удельным
вещества:
.
объёмом
называется
объём
единицы
массы
V / m , м3/кг.
Масса единицы объёма, т.е. величина обратная удельному
объему, называется плотностью:
m / V , кг/м3.
Очевидно соотношение:
1 .

5.

Абсолютным давлением называется давление газа,
обусловленное
совокупностью
ударов
беспорядочно
движущихся молекул о стенки сосуда, в котором заключен
газ, и представляет собой нормальную силу F, действующую
на единицу площади А поверхности стенки:
F
P
A , кг/м = Па.
2
В системе СИ давление измеряется в паскалях (Па).

6.

Для
измерения
давления
используют
приборы:
атмосферного – барометры, выше
атмосферного –
манометры, ниже атмосферного – вакуумметры. Барометр –
единственный прибор, измеряющий абсолютное давление
атмосферы (ратм). Давление, которое регистрирует манометр
или вакуумметр, называют избыточным (ризб). Оно не
является параметром состояния рабочего тела, а лишь
показывает на сколько давление в сосуде выше или ниже
атмосферного. Действительное давление (р) в сосуде
(абсолютное) является параметром состояния и равно
сумме:
p pатм. pизб. .
Давление на шкале вакуумметра обычно указывают со знаком
минус.

7.

Величина, характеризующая степень нагретости
тела, называется температурой.
Степень
нагретости
тел
связана
со
среднеквадратичной скоростью движения молекул
выражением:
2 (m )
kT
3 2 ,
2
где m = масса молекулы,
k – постоянная Больцмана,
Т – абсолютная температура.

8.

Абсолютная температура измеряется в кельвинах (К) и всегда
положительна. Абсолютный нуль – это температура, при которой
прекращается тепловое движение молекул, т.е. начало отсчета
температуры по шкале Кельвина. Температура
по
шкале
Кельвина
связана
с
температурой
по шкале
Цельсия
соотношением:
T t C 273,16 .
o
В шкалах Кельвина и Цельсия различно лишь начало отсчета, а
линейные размеры, соответствующие одному градусу, одинаковы.
Поэтому разность температур в 1 оС равна 1 К.
В технике для измерения температур используют различные
свойства тел: расширение при нагревании в жидкостных
термометрах, изменение давления при постоянном объеме в
газовых термометрах, изменение электрического сопротивления
проводника при нагревании, изменение термоЭДС в цепи
термопары и т. д.

9. Модель идеального газа. Уравнение состояния идеального газа. Удельная и универсальная газовые постоянные

10.

Идеальным газом называется газ, молекулы
которого имеют пренебрежимо малые размеры
по сравнению с расстоянием между ними (такой
газ можно сжать до нулевого объёма) и между
которыми отсутствуют силы взаимодействия.
Опыт показывает, что реальные газы при
низком давлении и высокой температуре ведут
себя как идеальные. Отличие в поведении
реальных и идеальных газов проявляется при
высоких давлениях и низких температурах.
Поведение многих технически важных газов и их
смесей в условиях работы ряда тепловых машин
незначительно отличается от поведения
идеальных газов. Поэтому, термодинамические
расчёты тепловых машин, в которых рабочим
телом является реальный газ, базируются на
теории идеального газа.

11.

В равновесном состоянии основные
термодинамические
параметры системы р, ,Т связаны между собой зависимостью,
называемой уравнением состояния газа. В общем виде уравнение
состояния имеет вид:
f p, ,T 0.
Таким образом, независимо могут бать заданы только два
параметра системы, третий определяется уравнением состояния.
Построение уравнений состояния конкретных систем
(реальных газов) есть задача не только термодинамики, но
молекулярной и статистической физики. Для каждого вещества
характер
функциональной
связи
индивидуален
и
термодинамические свойства описываются своим уравнением
состояния. Даже для газов, свойства которых изучены наиболее
полно, вопрос построения уравнения состояния окончательно не
решен.

12.

Наиболее простой вид имеет уравнение состояния идеального газа. Это
уравнение впервые получено в 1834 г. французским физиком Д. Клапейроном
путем объединения газовых законов Бойля-Мариотта и Гей-Люссака:
P R T , Дж/кг.
(1)
Уравнение записано для 1 кг газа и называют его уравнением Клапейрона.
Умножая обе части уравнения на массу газа m, получим уравнение состояния в
другой размерности:
PV m R T , Дж.
(2)
Через R в уравнениях (1) и (2) обозначена так называемая удельная газовая
постоянная, отнесенная к массе газа 1 кг. В соответствии с уравнением ее
размерность
Дж
R
кг К .

13.

Смысл газовой постоянной можно установить, рассматривая процесс
расширения газа в процессе при р =const . Пусть газ массой m кг в этом
процессе перешел из состояния с параметрами р, 1,T1 в новое состояние с
параметрами р, 2,T2. Пользуясь уравнением (2), для каждого состояния можно
записать:
pV1 mRT1 ,
pV2 mRT2 .
Вычитая из второго уравнения первое, получим:
p V2 V1
R
m T2 T1 .
Числитель представляет собой работу m кг газа в изобарном процессе
расширения. При условиях, что в процессе участвует газ массой m = 1 кг, а
изменение температуры при расширении равно ΔТ = Т2 – Т1 = 1 К, можно
утверждать, что газовая постоянная численно равна работе 1 кг газа в
изобарном процессе расширения при изменении температуры газа на 1 К.

14.

Умножая обе части уравнения (1) на молярную массу газа μ,
кг/кмоль, получим уравнение состояния, записанное в
размерности Дж/кмоль:
P R T .
(3)
Обозначим произведение μ = Vμ, м3/кмоль. Величина Vμ
представляет собой объем 1 киломоля газа и называется
мольным (или молярным) объемом.

15.

На основании закона Авогадро киломоль любого газа при одинаковых давлении и
температуре занимает один и тот же объем. Следовательно, величина
R R , Дж/(кмоль К)
имеет одинаковое постоянное значение
физическими условиями считаются:
для
всех
газов.
Нормальными
Т0 = 273,15 К,
р0 = 101332 Па.
При этих условиях объем одного киломоля газа равен Vμ = 22,4146 м3. Тогда
101332 22,4146
R
8314,3
273,15
Дж/(кмоль К).

16.

Эту величину, впервые введенную в уравнение состояния Д.И. Менделеевым,
называют универсальной газовой постоянной. Таким образом:
PV R T , Дж/кмоль,
(4)
а умножая обе части уравнения (4) на количество киломолей газа
m
, кмоль,
получаем еще одну форму записи уравнения состояния:
PV R T
, Дж.
Уравнения (4) и (5) называют уравнениями Клапейрона - Менделеева.
(5)

17.

Газовой смесью понимается смесь отдельных
газов, вступающих между собой ни в какие
химические реакции. Каждый газ (компонент) в
смеси независимо от других газов полностью
сохраняет все свои свойства и ведет себя так, как
если бы он один занимал весь объем смеси.
Парциальное давление – это давление, которое
имел бы каждый газ, входящий в состав смеси,
если бы этот газ находился один в том же
количестве, в том же объеме и при той же
температуре, что и в смеси.

18.

Газовая смесь подчиняется закону Дальтона:
Общее давление смеси газов равно сумме
парциальных давлений отдельных газов,
составляющих смесь.
Р = Р1 + Р2 + Р3 + . . .Рn = ∑ Рi ,
где Р1 , Р2 , Р3 . . .Рn – парциальные давления.

19.

Состав смеси задается объемными, массовыми и
мольными долями, которые определяются
соответственно по следующим формулам:
r1 = V1 / Vсм ; r2 = V2 / Vсм ; … rn = Vn / Vсм ,
g1 = m1 / mсм ; g2 = m2 / mсм ; … gn = mn / mсм ,
r1′ = ν1 / νсм ; r2′ = ν2 / νсм ; … rn′ = νn / νсм ,
где V1 ; V2 ; … Vn ; Vсм –объемы компонентов и смеси;
m1 ; m2 ; … mn ; mсм – массы компонентов и смеси;
ν1 ; ν2 ; … νn ; νсм – количество вещества (киломолей)
компонентов и смеси.

20.

Для идеального газа по закону Дальтона:
r1 = r1′ ; r2 = r2′ ; … rn = rn′ .
Так как V1 +V2 + … + Vn = Vсм
и
m1 + m2 + … + mn = mсм ,
то r1 + r2 + … + rn = 1 ,
g1 + g2 + … + gn = 1.
Связь между объемными и массовыми долями
следующее:
g1 = r1∙μ1/μсм ; g2 = r2∙μ2 /μсм ; … gn = rn∙μn /μсм ,
где: μ1 , μ2 , … μn , μсм – молекулярные массы
компонентов и смеси.

21.

• Молекулярная масса смеси:
• μсм = μ1 r1 + r2 μ2+ … + rn μn .
• Газовая постоянная смеси:
• Rсм = g1 R1 + g2 R2 + … + gn Rn = Rμ (g1/μ1 + g2/μ2+
… + gn/μn ) = 1 / (r1/R1 + r2/R2+ … + rn/Rn) .
• Удельные массовые теплоемкости смеси:
• ср см. = g1 ср 1 + g2 ср 2 + … + gnср n .
сv см. = g1ср 1 + g2сv 2 + … + gnсv n .
• Удельные молярные (молекулярные)
теплоемкости смеси:
• срμ см. = r1 срμ 1 + r2 срμ 2 + … + rnсрμ n .
сvμсм. = r1сvμ 1 + r2сvμ 2 + … + rnсvμ n .

22. ТЕПЛОЁМКОСТЬ ГАЗОВ

23.

Массовая, объёмная и мольная удельные теплоёмкости
Известно, что подвод теплоты к рабочему телу или
отвод теплоты от него в каком-либо процессе приводит
к изменению его температуры. Отношение количества
теплоты, подведенной (или отведенной) в данном
процессе,
к
изменению
температуры
называется
теплоемкостью
тела
(системы тел):
,
где
— элементарное количество теплоты;
элементарное изменение температуры.
—

24. Теплоемкость численно равна количеству теплоты, которое необходимо подвести к системе, чтобы при заданных условиях повысить ее

температуру на 1 градус. Так как единицей
количества теплоты в СИ является джоуль, а температуры —
градус К, то единицей теплоемкости будет Дж/К.
В зависимости от внешних условий и характера
термодинамического процесса теплота может либо подводиться к
рабочему телу, либо отводиться от него. Учитывая, что система
участвует в бесчисленном множестве процессов,
сопровождающихся теплообменом, величина для одного и того же
тела может иметь различные значения. В общем случае значение
теплоёмкости лежит в интервале от -∞ до +∞, то есть она может
быть любой положительной или отрицательной величиной.

25.

Поэтому обычно в выражении
при теплоёмкости
указывается
индекс
"x",
который
характеризует
вид
процесса теплообмена
.
Индекс "x" означает, что процесс подвода (или отвода)
теплоты идет при постоянном значении какого-либо из
параметров,
других.
например,
давления
,
объема
или
Теплоемкость
является величиной, относящейся к
системе,
которая
находится
в
состоянии
термодинамического
равновесия.
Таким
образом,
теплоемкости
являются
функциями
параметров
термодинамической системы. Для простых систем — это
функции каких-либо двух из трех параметров:
,
,
.

26.

Опыты показывают, что количество теплоты,
подведенное к рабочему телу системы или
отведенное от него, всегда пропорционально
количеству рабочего тела. Для возможности
сравнения вводят, как известно, удельные
величины теплоемкости, относя
подведенную (или отведенную) теплоту
количественно к единице рабочего тела.
В зависимости от количественной единицы
тела, к которому подводится теплота в
термодинамике, различают массовую,
объемную и мольную теплоемкости.

27.

Массовая теплоемкость — это теплоемкость, отнесенная к
единице массы рабочего тела,
.
Единицей измерения массовой теплоемкости является
Дж/(кг • К). Массовую теплоемкость называют также
удельной теплоемкостью.
Объемная теплоемкость — теплоемкость, отнесенная к
единице объема рабочего тела,
,
где и — объем и плотность тела при нормальных
физических условиях.
Объемная теплоемкость измеряется в Дж/(м3 • К).

28.

Мольная теплоемкость —
количеству рабочего тела
(газа) в молях,
теплоемкость,
отнесенная к
,
где
— количество газа в молях.
Мольную теплоемкость измеряют в Дж/(моль • К).
Массовая и мольная теплоемкости связаны следующим
соотношением:
или
,
где
- молекулярная масса.

29.

Объемная
мольную как
теплоемкость
газов
выражается
или
,
где
м3/моль — мольный объем газа при
нормальных условиях
через

30.

• Средняя и истинная теплоёмкости
• Учитывая, что теплоемкость непостоянна, а зависит от
температуры и других термических параметров,
различают истинную и среднюю теплоемкости. Истинная
теплоемкость выражается уравнением при определенных
параметрах термодинамического процесса, то есть в
данном состоянии рабочего тела. В частности, если хотят
подчеркнуть зависимость теплоёмкости рабочего тела от
температуры, то записывают её как , а удельную – как .
Обычно под истинной теплоёмкостью понимают
отношение элементарного количества теплоты, которое
сообщается термодинамической системе в каком-либо
процессе к бесконечно малому приращению температуры
этой системы, вызванному сообщенной теплотой. Будем
считать истинной теплоёмкостью термодинамической
системы при температуре системы равной , а - истинной
удельной теплоёмкостью рабочего тела при его
температуре равной . Тогда среднюю удельную
теплоёмкость рабочего тела при изменении его
температуры от до можно определить как

31.

Обычно
в
теплоемкости
таблицах
для
начинающихся с
термодинамический
приводятся
различных
средние
интервалов
значения
температур,
. Поэтому во всех случаях, когда
процесс
проходит
в
интервале
температур от до , в котором
, количество удельной
теплоты
процесса
определяется
с
использованием
табличных
образом:
значений
средних
теплоемкостей
следующим
.
Значения средних теплоемкостей
таблицам.
и
, находят по

32.

Теплоёмкости при постоянном объёме и давлении
Особый
интерес
представляют
средние
и
истинные
теплоемкости
в
процессах
при
постоянном
объеме
(изохорная
теплоемкость,
равная
отношению
удельного
количества теплоты в изохорном процессе к изменению
температуры рабочего тела dT) и при постоянном давлении
(изобарная
теплоемкость,
равная
отношению
удельного
количества теплоты в изобарном процессе к изменению
температуры рабочего тела dT).
Для идеальных газов связь между изобарной и изохорной
теплоёмкостями и устанавливается известным уравнением
Майера
.

33.

Из
уравнения
Майера
следует,
что
изобарная
теплоемкость
больше
изохорной
на
значение
удельной
характеристической
постоянной
идеального
газа.
Это
объясняется тем, что в изохорном процессе (
) внешняя
работа не выполняется и теплота расходуется только на
изменение внутренней энергии рабочего тела, тогда как в
изобарном процессе (
) теплота расходуется не только
на изменение внутренней энергии рабочего тела, зависящей
от его температуры, но и на совершение им внешней работы.
Для реальных газов
, так как при их
расширении и
совершается работа не только против
внешних
сил,
но
и
внутренняя
работа
против
сил
взаимодействия между молекулами газа, на что дополнительно
расходуется теплота.
В
теплотехнике
широко
применяется
отношение
теплоемкостей
, которое носит название коэффициента
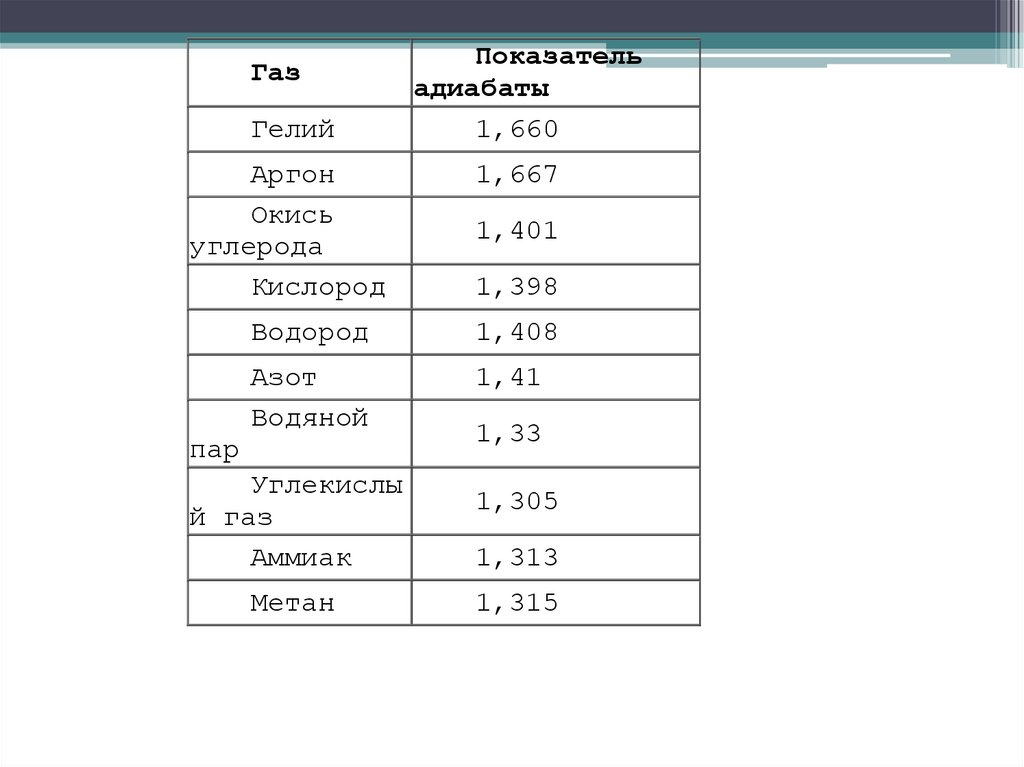
Пуассона (показателя адиабаты). В табл. 2.1 приведены
значения
некоторых газов, полученные экспериментально
при температуре 15 °С.

34.

Газ
Гелий
Показатель
адиабаты
1,660
Аргон
Окись
углерода
Кислород
1,667
Водород
1,408
Азот
Водяной
1,41
пар
Углекислы
й газ
Аммиак
Метан
1,401
1,398
1,33
1,305
1,313
1,315

35.

Теплоемкости
и
зависят от температуры,
следовательно, и показатель адиабаты
должен
зависеть от температуры.
Известно,
что
с
повышением
температуры
теплоёмкость
увеличивается. Поэтому с ростом
температуры
уменьшается, приближаясь к единице.
Однако всегда остается больше единицы. Обычно
зависимость показателя адиабаты от температуры
выражается формулой вида
,
где
- значение коэффициента при 00 С; коэффициент, принимающий для каждого газа своё
постоянное значение.

36.

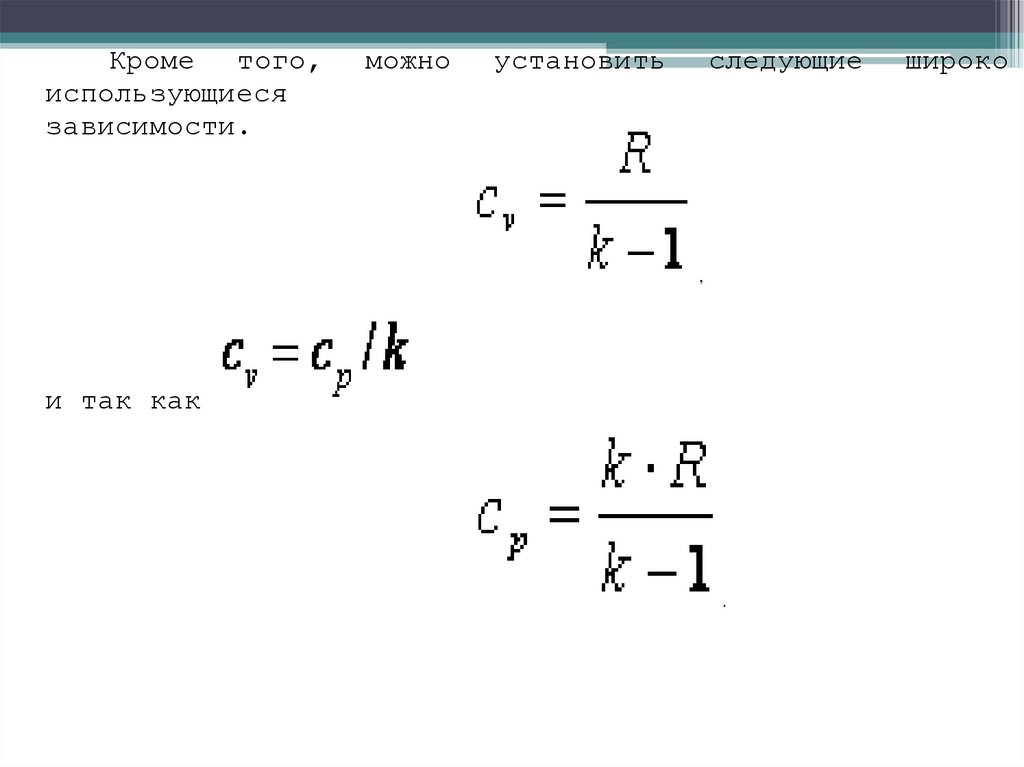
Кроме того,
использующиеся
зависимости.
можно
установить
следующие
,
и так как
.
широко

37.

Данные о теплоёмкостях различных газов приводятся в
табличной форме. Обычно в таблицах приводят для
различных температур значения мольной истинной и
средней теплоёмкости при постоянном давлении и
постоянном объёме. Указывают также средние массовые
и объёмные теплоёмкости при постоянном объёме и
постоянном давлении.
Мольная теплоёмкость указывается в кДж/(кмоль · 0С),
массовая – в кДж/(кг · 0С), объёмная – в кДж/(м3 · 0С).
При этом значения объёмной теплоёмкости относят к
массе газа, заключённой 1 м3 его при нормальных
физических условиях.
Для газов, массовая теплоёмкость которых зависит как от
температуры, так и от давления, приводят значения
удельного объёма и энтальпии 1 кг газа при различных
давлениях и температурах. С такого рода зависимостями
приходится иметь дело при изучении свойств водяного
пара.

38.

Теплоёмкость смеси рабочих тел (газовой смеси)
Теплоемкость газовой смеси вычисляется по составу
газовой смеси и теплоемкостям отдельных газов, входящих
в данную газовую смесь. Газовая смесь может быть задана
массовым, объемным и молярным составом. Пусть смесь
газов
задана
массовым
составом,
тогда
масса
смеси
.
где
— масса i-го компонента, входящего в смесь.

39.

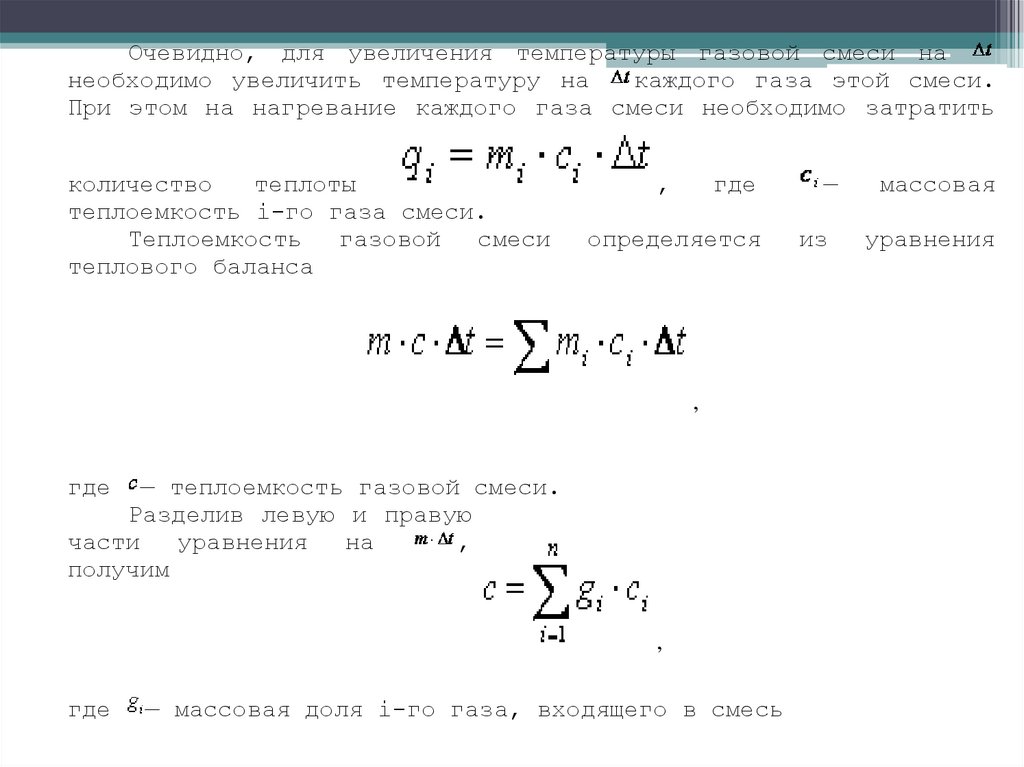
Очевидно, для увеличения температуры газовой смеси на
необходимо увеличить температуру на
каждого газа этой смеси.
При этом на нагревание каждого газа смеси необходимо затратить
количество
теплоты
теплоемкость i-го газа смеси.
Теплоемкость
газовой
смеси
теплового баланса
,
где
—
массовая
определяется
из
уравнения
,
где
— теплоемкость газовой смеси.
Разделив левую и правую
части
уравнения
на
,
получим
,
где
— массовая доля i-го газа, входящего в смесь

40.

Из выражения видно, что теплоемкость смеси
газов, заданной массовыми долями (массовая
теплоемкость смеси), равна сумме
произведений массовых долей на массовую
теплоемкость каждого газа.
С помощью аналогичных рассуждений можно
найти сходные по структуре с полученным
выражением выражения для объёмной и
мольной теплоёмкостей газовой смеси.