Lektsia_3_4_5_O

1. 2. Математическое описание линейных объектов и систем автоматического управления

2.1 Моделирование как метод исследования САУ
2. 2 Декомпозиция САУ/САР
2.3 Свойство однонаправленности САУ
2.4 Типизация воздействий и сигналов в САУ
2.5 Режимы работы САУ.
2.6 Статическая характеристика САУ.
2.7 Динамические характеристики САУ
2.8 Дифференциальные уравнения
2.9 Передаточные функции
2.10 Структурные преобразования линейных САР
2.11 Передаточные функции одноконтурной системы
2.12 Виды временных и частотных характеристик
2.13 Временные характеристики
2.14 Частотные характеристики
2.15 Логарифмические частотные характеристики

2. 2.1 Моделирование как метод исследования САУ

Для анализа и синтеза системы управления требуется ее
математическое описание, которое бы связывало поведение координат
системы - ее переменных величин в процессе работы, то есть во времени.
Поведение координат системы во времени называется динамикой
системы.
Так как система состоит из взаимосвязанных функциональных
элементов, то для получения ее математического описания необходимо
получить математические описания отдельных элементов.
Большинство задач, связанных с исследованием САУ/САР,
решается на основе детерминированной, одномерной или
многомерной, линейной, стационарной математической
модели с сосредоточенными параметрами.
2

3. 2.2 Декомпозиция САУ/САР

Каждая входная величина системы создает свою составляющую
выходной величины.
Реакция системы на несколько одновременно действующих входных
воздействий равна сумме реакций на каждое воздействие в
отдельности.
Функционирование САУ/САР можно рассматривать отдельно по
каждому каналу прохождения того или иного сигнала от его входа к
выходу.
Для упрощения математического описания САУ разбивают на
отдельные элементы (динамические звенья), но не по
функциональному
или
конструктивному
признаку,
а
по
динамическим свойствам.
Динамическое звено – это математическая модель САУ/САР или любого ее элемента,
отражающая определенные динамические свойства элемента вне зависимости от
физической природы протекающих в нем процессов.
3

4. 2.3 Свойство однонаправленности САУ

В процессе функционирования САУ осуществляется преобразование энергии одного
вида в энергию другого вида. Процессы преобразования и перераспределения энергии
в САУ, в отличие от многих других физических систем, строго ориентированы.
Полученные в результате декомпозиции САУ динамические звенья должны
быть направленного действия: сигнал в звене идет в одном направлении –
только от входа к выходу; сигнал на выходе звена не оказывает никакого
воздействия на сигнал на его входе.
Направленность передачи воздействий в САУ обеспечивается благодаря наличию у
одного или нескольких конструктивных элементов системы так называемого
детектирующего свойства, т.е. рассматриваемый элемент не оказывает обратного
действия на предыдущий элемент. Свойством однонаправленности обладают те
элементы САУ, которые передают информационные воздействия. К таким элементам
относятся в первую очередь измерители и преобразователи сигналов.
Электрический
четырехполюсник
обладает
однонаправленностью передачи воздействий, если он не
нагружает предшествующий четырехполюсник, т. е.
если выходное сопротивление предшествующего
элемента существенно меньше входного сопротивления
рассматриваемого четырехполюсника.
Без
элементов
направленного
действия САУ были
бы неработоспособны
4

5. 2.4 Типизация воздействий и сигналов в САУ

При исследовании САУ и их элементов используют ряд стандартных
сигналов, называемых типовыми воздействиями. Эти воздействия
описываются
простыми
математическими
функциями
и
легко
воспроизводятся при исследовании САУ.
Использование типовых воздействий позволяет унифицировать анализ
различных систем и облегчает сравнение их передаточных свойств
Типовые возмущения в САР:
1. Единичная ступенчатая функция;
2. Единичная импульсная функция;
3. Единичная линейная функция;
4. Единичное гармоническое колебание.
5

6. 2.4 Типизация воздействий и сигналов САУ

1. Единичная ступенчатая функция h(t) (функция Хевисайда)– это
функция следующего вида:
h(t )
1 при t 0,
h (t )
0 при t 0.
Ступенчатое воздействие – воздействие, которое
мгновенно возрастает от нуля до некоторого
значения и далее остается постоянным.
1
t
0
Ступенчатое воздействие чаще всего используют
при
исследованиях
систем
стабилизации
параметров, так как эти воздействия наиболее
близки к реальным входным (задающим и
возмущающим) воздействиям систем стабилизации.
6

7. 2.4 Типизация воздействий и сигналов САУ

2.Единичное импульсное воздействие (единичная дельта – функция,
функция (игла) Дирака) задается выражением:
(t )
0 при t 0,
(t )
при t 0.
(t ) 1
t 0
Можно рассматривать дельта-функцию, как
импульс, имеющий бесконечно большую
высоту, бесконечно малую длительность и
единичную площадь.
t
0
Единичную дельта – функцию δ(t) можно рассматривать также, как
производную от h(t):
dh t d1 t
t
dt
dt
7

8. 2.4 Типизация воздействий и сигналов САУ

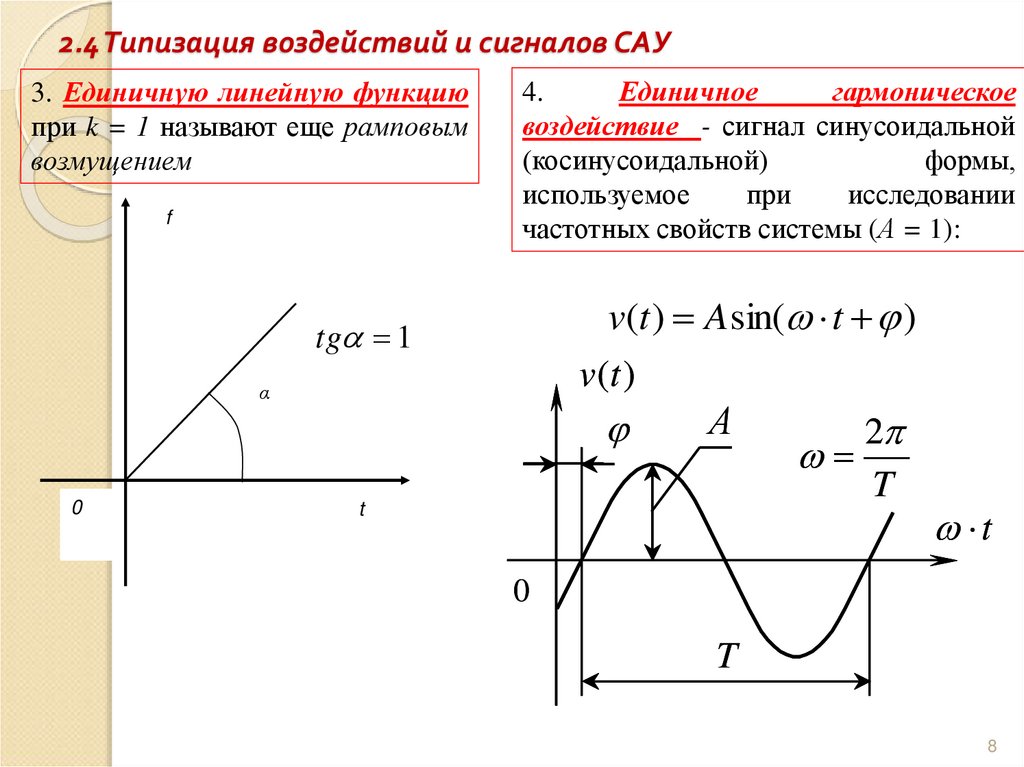
3. Единичную линейную функцию
при k = 1 называют еще рамповым
возмущением
f
4.
Единичное
гармоническое
воздействие - сигнал синусоидальной
(косинусоидальной)
формы,
используемое
при
исследовании
частотных свойств системы (А = 1):
v(t ) Asin( t )
v(t )
A
2
T
tg 1
α
0
t
t
0
T
8

9. 2.5 Режимы работы САУ

Статический режим – состояние элемента САУ, при котором выходная
величина не изменяется во времени, т. е. y(t) = const. Очевидно, что
статический режим (или состояние равновесия) может иметь место лишь
тогда, когда входные воздействия постоянны во времени. Связь между
входными и выходными величинами в статическом режиме описывают
алгебраическими уравнениями.
Динамический режим – состояние элемента САУ, при котором выходная
величина непрерывно изменяется во времени, т. е. y(t) = var. Динамический
режим имеет место, когда в элементе после приложения входного
воздействия происходят процессы установления заданного состояния или
заданного изменения выходной величины. Эти процессы описываются в
общем случае дифференциальными уравнениями.
Переходной
режим
–
режим,
существующий от момента начала
изменения входного воздействия до
момента, когда выходная величина
начинает изменяться по закону этого
воздействия.
Установившийся режим – режим,
наступающий после того, когда выходная
величина начинает изменяться по такому
же закону, что и входное воздействие, т. е.
наступающий
после
окончания
переходного процесса.
9

10. 2.6 Статическая характеристика САУ

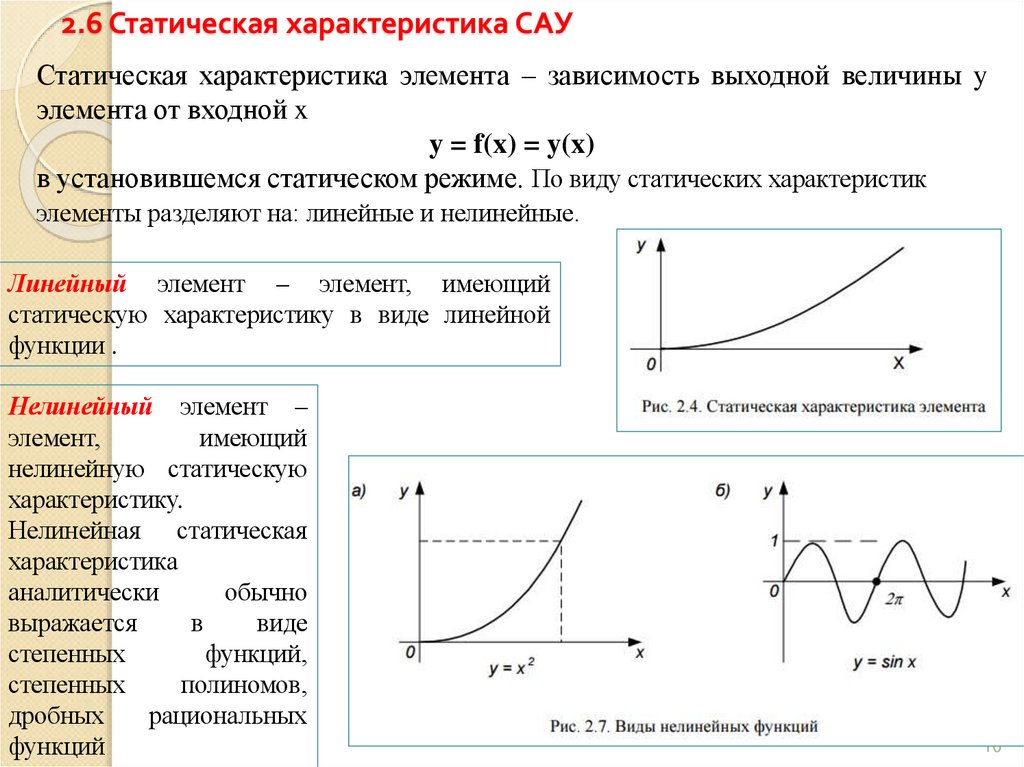
Статическая характеристика элемента – зависимость выходной величины y
элемента от входной x
y = f(x) = y(x)
в установившемся статическом режиме. По виду статических характеристик
элементы разделяют на: линейные и нелинейные.
Линейный элемент – элемент, имеющий
статическую характеристику в виде линейной
функции .
Нелинейный элемент –
элемент,
имеющий
нелинейную статическую
характеристику.
Нелинейная статическая
характеристика
аналитически
обычно
выражается
в
виде
степенных
функций,
степенных
полиномов,
дробных
рациональных
функций
10

11. 2.7 Динамические характеристики САУ

Передаточные свойства элементов АСУ в динамическом режиме описывают
с помощью динамических характеристик. Различают следующие формы
динамических характеристик:
• обыкновенное дифференциальное уравнение;
• передаточная функция;
Нелинейное дифференциальное уравнение
•временные характеристики;
– уравнение, в котором функция
• частотные характеристики.
Линейное
дифференциальное
уравнение – уравнение, в
котором функция Ф линейна по
отношению
ко
всем
ее
аргументам
содержит
произведения,
частные,
степени и т. д. переменных y(t), x(t) и их
производных
Дифференциальное уравнение
второго порядка:
dx1
d2y
dy
a0 2 a1 a2 y b0
b1 x1 c0 x2
dt
dt
dt
Большинство
реальных
элементов
описываются
нелинейными
дифференциальными уравнениями, что значительно усложняет последующий
анализ САУ. Поэтому стремятся перейти от нелинейных к линейным.
11

12. Линеаризация нелинейной функции

Линеаризацию
гладких
(несущественно
нелинейных)
статических характеристик можно
осуществлять по методу касательной.
Для
линеаризации
нелинейную
функцию
раскладывают
в
ряд
Тейлора в окрестности расчетного
статического режима и затем
«отбрасывают» нелинейные члены –
остаток этого ряда ввиду его малости.
Линеаризованная функция равна линейной части ряда Тейлора:
2
dF x
1 d F x
2
F x F x0
x
x
x
x
0
0
2
2! dx
dx 0
0
dF x
F x F x0
x
dx 0
12

13. 2.8 Порядок составления уравнений динамических систем/звеньев

1.
Установление
физического
закона
протекания
процессов.
Математическое выражение этого закона образует дифференциальное
уравнение.
2. Анализ факторов для определения зависимостей переменных, входящих в
исходное уравнение. Нахождение математических зависимостей. Эти
зависимости, как правило, нелинейные функции.
3. Линеаризация (если она допустима) полученных уравнений (это
приближенная замена нелинейной функции (уравнения) соответствующей
линейной функцией (уравнением).
4. Приведение дифференциальных уравнений к безразмерному виду.
Ток i (в амперах), проходящий
по цепи с конденсатором,
пропорционален производной
от разности потенциалов u (в
вольтах) на его пластинах:
Падение напряжения u на
катушке
индуктивности
пропорционально производной
от проходящего тока i :
13

14. 2.8 Порядок составления уравнений динамических систем/звеньев

5. Составленные уравнения решаются совместно относительно выходной
величины.
Совместное решение ДУ упрощается за счет их алгебраизации,
выполняемой двумя путями:
переходом к операторной форме, когда символ дифференцирования по
времени
обозначается
«р»
и
рассматривается,
как
оператор
дифференцирования, с которым можно производить все алгебраические
действия за исключением перестановки, т.е.
py yp
переходом к уравнениям в изображениях по Лапласу.
6. Полученное уравнение звена приводится к стандартному виду,
принятому в ТАУ.
14

15. Формы записи дифференциальных уравнений, характеризующих функционирование звеньев/ САР/САУ

1. В левой части уравнения записывают выходную величину и ее
производные по убыванию их порядков.
2. В правой части в аналогичной последовательности записывают входные
величины и их производные.
3. Все члены уравнения делятся на некоторые постоянные значения
переменной имеющей размерность членов уравнения.
4. Переход к относительным единицам (выбирают некоторое постоянное
значение каждой переменной и определяют соотношения приращений и
выбранных постоянных значений).
5. Вводят обозначение относительных единиц и коэффициентов.
Дифференциальное уравнение второго порядка:
dx1
d2y
dy
a0 2 a1
a2 y b0
b1 x1 c0 x2
dt
dt
dt
15

16. Формы записи дифференциальных уравнений, характеризующих функционирование звеньев/ САР/САУ

Стандартный вид уравнения в операторной форме:
a p a p a y b p b x c x
2
0
1
2
0
1
1
0 2
Операторная форма дифференциального уравнения:
a0 2 a1
c0
b1 b0
p p 1 y p 1 x1 x2
a2
a2 b1
a2
a2
Преобразованное ДУ в операторной форме:
T p T p 1 y k T p 1 x k x
2
0
2
1
1
2
1
2 2
Коэффициенты передачи определяют статические свойства звена
в соответствии с его уравнением статики.
c0
b
1
a2
k1 ,
a2
k2
Постоянные времени определяют масштаб времени динамических
процессов, в частности, переходных.
b0
a
T2 , 1 T1
b1
a2
16

17. Преобразование Лапласа

Для решения дифференциальных уравнений широкое распространение получил
операторный метод, при использовании которого задача нахождения решения
дифференциального уравнения сводится к алгебраическим действиям. Чтобы перейти
от исходного дифференциального уравнения элемента при нулевых начальных
условиях к операторному, необходимо в дифференциальном уравнении вместо
реальных функций времени записать их изображения по Лапласу, а в полиномах символ
дифференцирования p заменить на оператор Лапласа s.
Преобразование Лапласа – функциональное преобразование, при
котором функция вещественного переменного y(t) преобразуется в
функцию комплексного переменного Y(s):
Здесь s - комплексная переменная преобразования Лапласа.
L y t Y s y t exp st dt,s j , j 1
0
Операции прямого и обратного преобразований Лапласа будем
обозначать через L{} и L-1{} соответственно.
Функцию y(t) называют
оригиналом.
Функцию Y(s) называют изображением
(по Лапласу).
17

18. Преобразование Лапласа

Определение. Преобразование оригинала в изображение называют
прямым преобразованием Лапласа и осуществляют с помощью
интеграла:
Y( s ) y( t )e st dt
0
Определение. Преобразование изображения в оригинал называют
обратным преобразованием Лапласа и осуществляют с помощью
интеграла:
Связь между оригиналом
c j
y( t )
1
Y( s )e ds
2 j
st
c j
и
изображением
записывается в виде:
y( t ) L 1 Y( s )
2 2
T
0 s T1s 1 Y s k1 T2 s 1 X 1 s k2 X 2 s
T p T p 1 y k T p 1 x k x
2
0
2
1
1
2
1
2 2
Уравнения формально совпадают между
собой. Но одно уравнение является
дифференциальным,
а
другое
уравнение
алгебраическим
18
относительно изображений по Лапласу.

19. 2.9 Передаточные функции

Передаточные функции могут быть определены двумя
способами:
в операторной форме;
в изображениях Лапласа.
Передаточная функция в операторной форме равна отношению
оператора входного воздействия к собственному оператору звена
Количество передаточных функций равно количеству входных величин звена при
одной выходной.
Передаточная функция имеет важное основополагающее значение в классической
теории управления. Она устанавливает связь в динамическом режиме между
выходной и входной величинами элемента и полностью характеризует его
динамические свойства.
19

20. 2.9 Передаточная функция в операторной форме

Рассмотрим нахождение передаточной функции в операторной форме
применительно к дифференциальному уравнению второго порядка (звено
второго порядка):
T p T p 1 y k T p 1 x k x
2
0
2
1
1
2
1
2 2
Для рассматриваемого случая можно записать две передаточные функции:
передаточная функция по х1 относительно у:
W1 p
k1 T2 p 1
T02 p 2 T1 p 1
передаточная функция по х2 относительно у:
W2 p
k2
T02 p 2 T1 p 1
Уравнение звена в операторной форме с применением передаточных
функций имеет вид:
y W1 p x1 W2 p x2
20

21. 2.9 Передаточная функция в изображениях по Лапласу

Определение. Передаточная функция в изображениях по Лапласу
равна отношению изображения по Лапласу выходной величины к
изображению Лапласа входной величины при нулевых начальных
условиях и равенстве «0» всех остальных входных величин.
2 2
T
0 s T1s 1 Y s k1 T2 s 1 X 1 s k2 X 2 s
21

22. 2.8 Передаточная функция в изображениях по Лапласу

Согласно данному определению получаем передаточные функции в
изображениях по Лапласу:
W1 s
Y s
k T s 1
21 2 2
X 1 s T0 s T1 s 1
Y s
k
W2 s
2 2 2
X 2 s T0 s T1 s 1
Уравнение звена в изображениях по Лапласу имеет вид:
Y s W1 s X 1 s W2 s X 2 s
Знаменатель передаточных функций W1(s) и W2(s) одинаков и называется
характеристическим полиномом:
D s T02 s 2 T1s 1
Приравнивая
к
«0»
характеристический
полином,
получаем
характеристическое уравнение, количество корней которого равно
порядку уравнения.
Степень характеристического полинома – полинома знаменателя
передаточной функции определяет порядок системы.
22

23. 2.9 Передаточная функция в изображениях по Лапласу

В реальных системах степень полинома числителя передаточной
функции не превышает степени характеристического полинома –
полинома знаменателя.
Это условие называют физической реализуемостью САР - оно
означает, что нельзя создать систему, передаточная функция которой
не удовлетворяла бы этому условию.
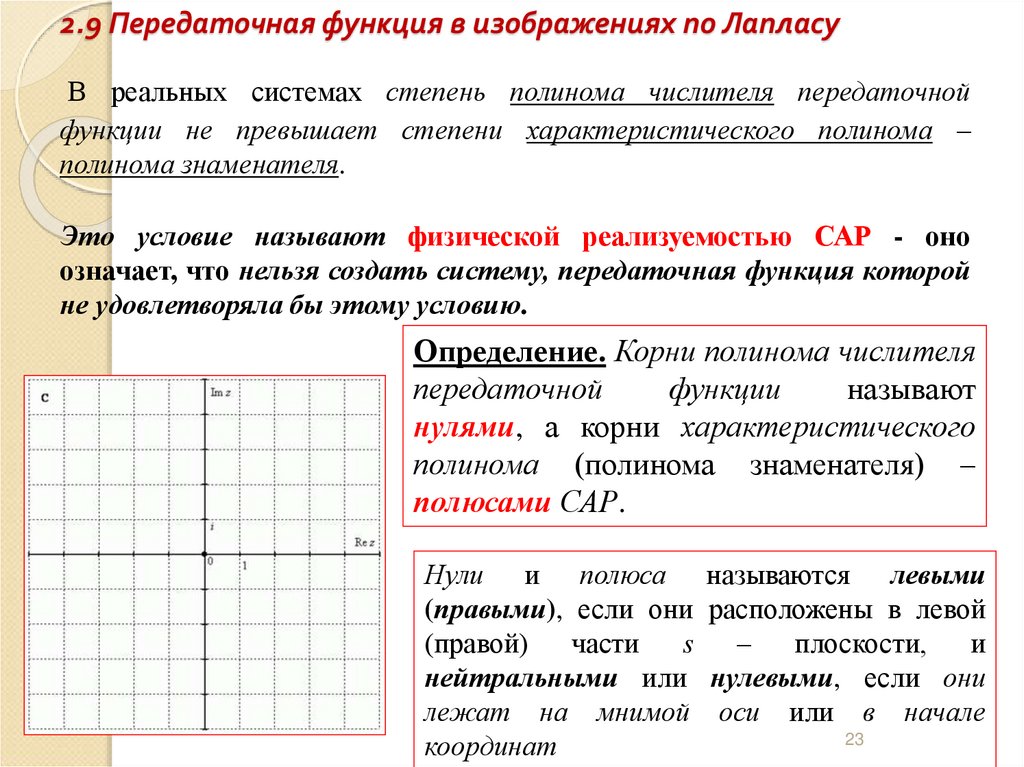
Определение. Корни полинома числителя
передаточной
функции
называют
нулями, а корни характеристического
полинома (полинома знаменателя) –
полюсами САР.
Нули и полюса называются левыми
(правыми), если они расположены в левой
(правой)
части
s
–
плоскости,
и
нейтральными или нулевыми, если они
лежат на мнимой оси или в начале
23
координат

24. 2.9. Структура САУ

Под структурой САР принято понимать совокупность частей (элементов) системы,
на которые ее можно разбить по определенным признакам, и путей передачи
сигналов между ними.
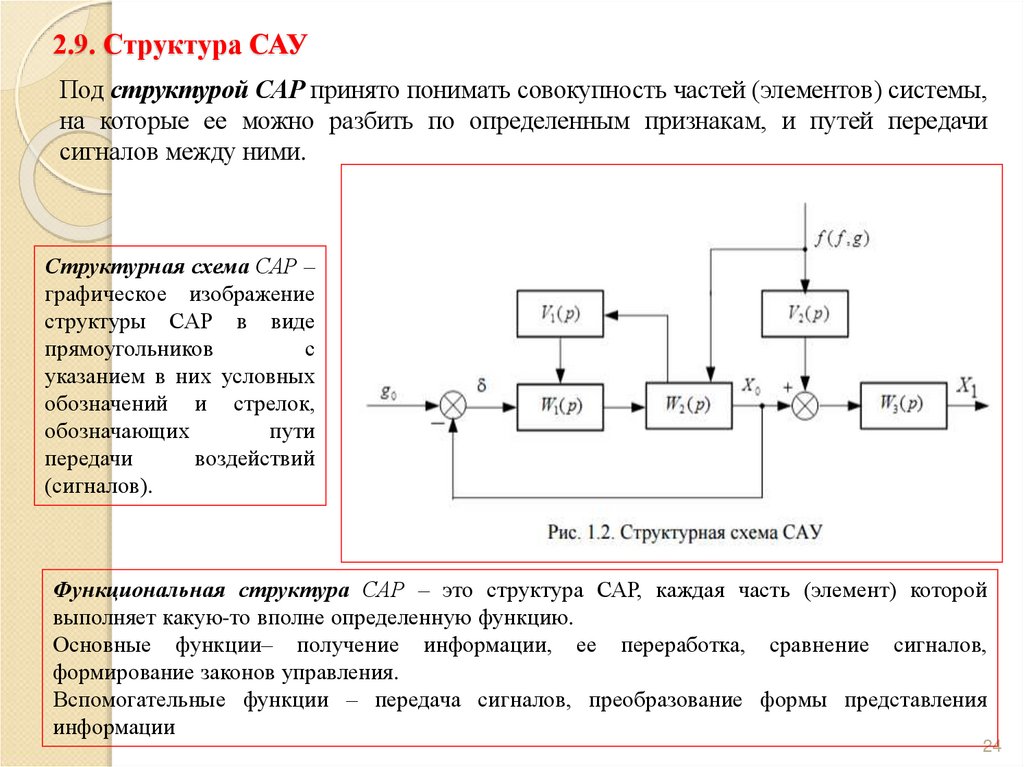
Структурная схема САР –
графическое изображение
структуры САР в виде
прямоугольников
с
указанием в них условных
обозначений и стрелок,
обозначающих
пути
передачи
воздействий
(сигналов).
Функциональная структура САР – это структура САР, каждая часть (элемент) которой
выполняет какую-то вполне определенную функцию.
Основные функции– получение информации, ее переработка, сравнение сигналов,
формирование законов управления.
Вспомогательные функции – передача сигналов, преобразование формы представления
информации
24

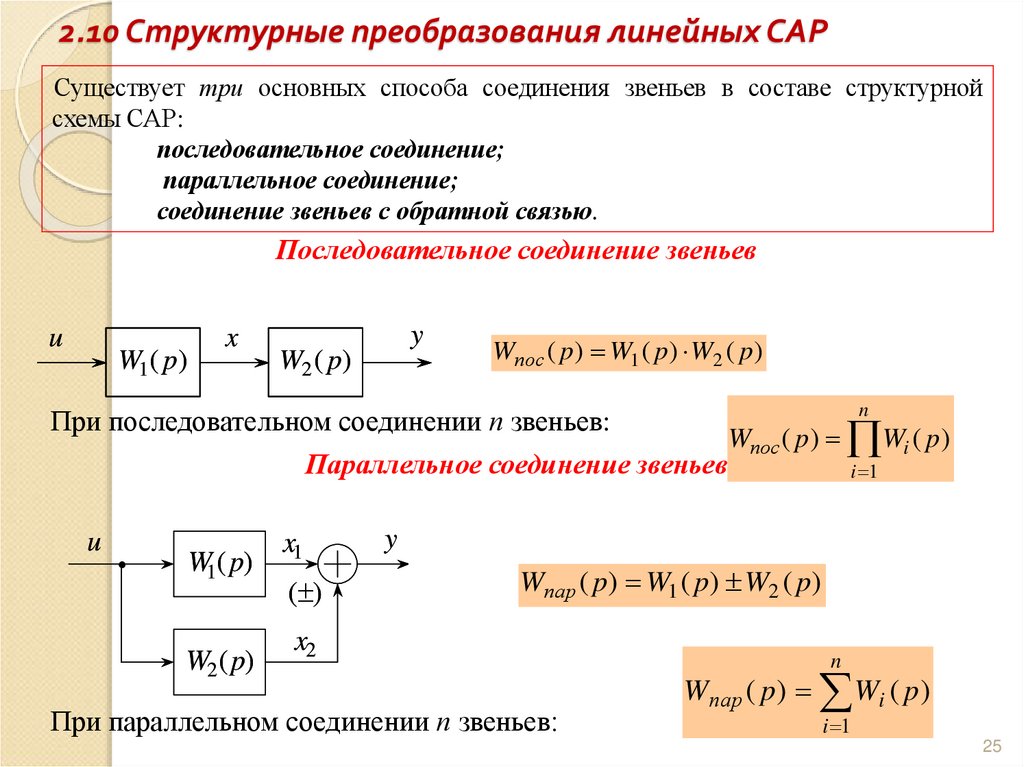
25. 2.10 Структурные преобразования линейных САР

Существует три основных способа соединения звеньев в составе структурной
схемы САР:
последовательное соединение;
параллельное соединение;
соединение звеньев с обратной связью.
Последовательное соединение звеньев
u
W1( p)
x
y
W2 ( p)
Wпос ( p) W1 ( p) W2 ( p)
n
При последовательном соединении п звеньев:
Wпос ( p ) Wi ( p )
Параллельное соединение звеньев
i 1
u
W1( p)
W2 ( p)
x1
( )
y
Wпар ( p) W1 ( p) W2 ( p)
x2
При параллельном соединении п звеньев:
n
Wпар ( p ) Wi ( p )
i 1
25

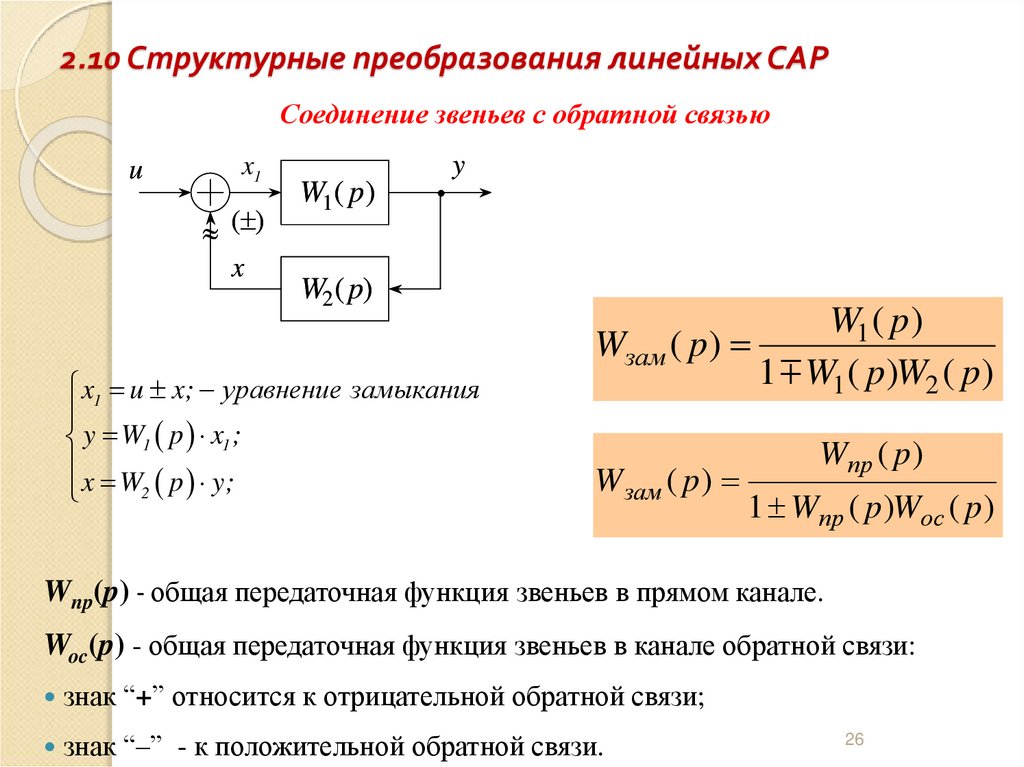
26. 2.10 Структурные преобразования линейных САР

Соединение звеньев с обратной связью
u
x1
( )
x
y
W1 ( p)
W2 ( p)
x1 u x; уравнение замыкания
y W1 p x1 ;
x W2 p y;
W1 ( p )
Wзам ( p)
1 W1 ( p)W2 ( p)
W зам ( p )
Wпр ( p )
1 Wпр ( p )Wос ( p )
Wnp(p) - общая передаточная функция звеньев в прямом канале.
Woc(p) - общая передаточная функция звеньев в канале обратной связи:
знак “+” относится к отрицательной обратной связи;
знак “–” - к положительной обратной связи.
26

27. 2.10 Структурные преобразования линейных САР

Передаточной функцией САР в разомкнутом состоянии называют
произведение передаточных функций всех динамических звеньев,
получаемых путем обрыва обратной связи в месте суммирования.
Wраз(p) = W1(p)W2(p) = Wnp(p)Woc(p)
При обратной связи с Woc(p) ≠ 1 верно:
Wзам ( p )
Wпр ( p )
1 W раз ( p )
При единичной обратной связи Woc(p) = 1 :
Wзам ( p )
Wпр ( p )
1 Wпр ( p )
27

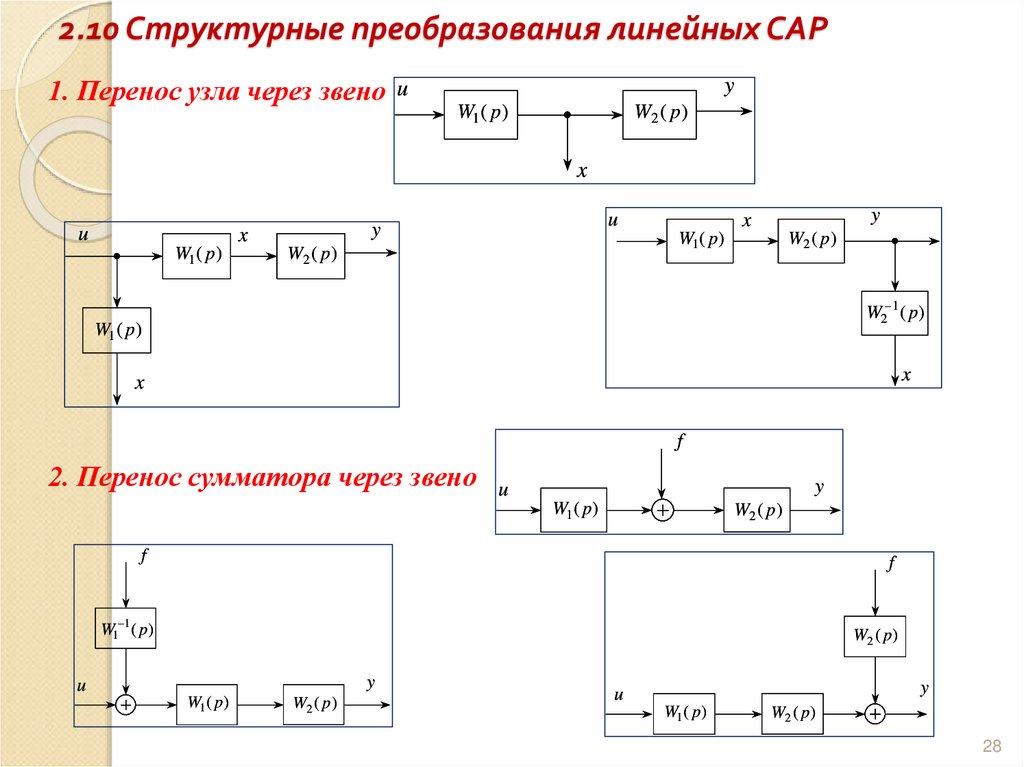
28. 2.10 Структурные преобразования линейных САР

1. Перенос узла через звено u
y
W1 ( p )
W2 ( p )
x
u
W1 ( p )
u
y
x
y
x
W1 ( p )
W2 ( p )
W2 ( p )
W2 1 ( p )
W1 ( p )
x
x
f
2. Перенос сумматора через звено
y
u
W1 ( p )
W2 ( p )
f
f
W1 1 ( p )
W2 ( p )
y
u
W1 ( p )
W2 ( p )
y
u
W1 ( p )
W2 ( p )
28

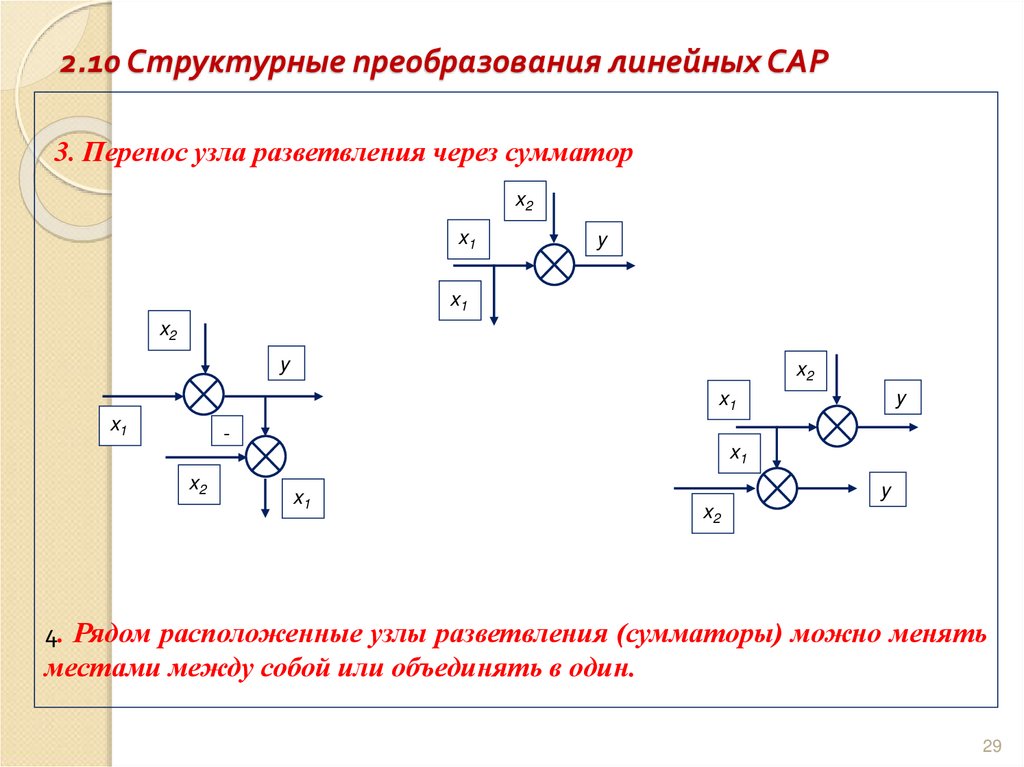
29. 2.10 Структурные преобразования линейных САР

3. Перенос узла разветвления через сумматор
x2
x1
y
x1
x2
y
x2
y
x1
x1
x2
x1
x1
y
x2
4. Рядом расположенные узлы разветвления (сумматоры) можно менять
местами между собой или объединять в один.
29

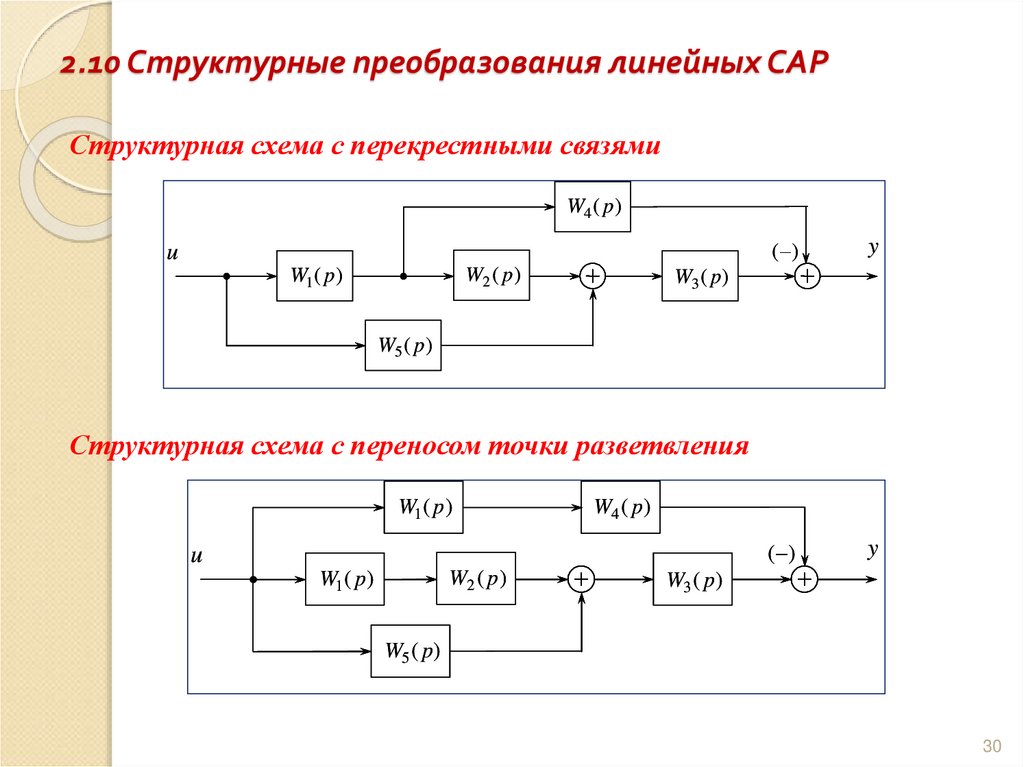
30. 2.10 Структурные преобразования линейных САР

Структурная схема с перекрестными связями
W4 ( p )
u
W2 ( p )
W1 ( p )
( )
y
( )
y
W3 ( p )
W5 ( p)
Структурная схема с переносом точки разветвления
W1 ( p )
W4 ( p )
u
W2 ( p )
W1 ( p )
W3 ( p )
W5 ( p)
30

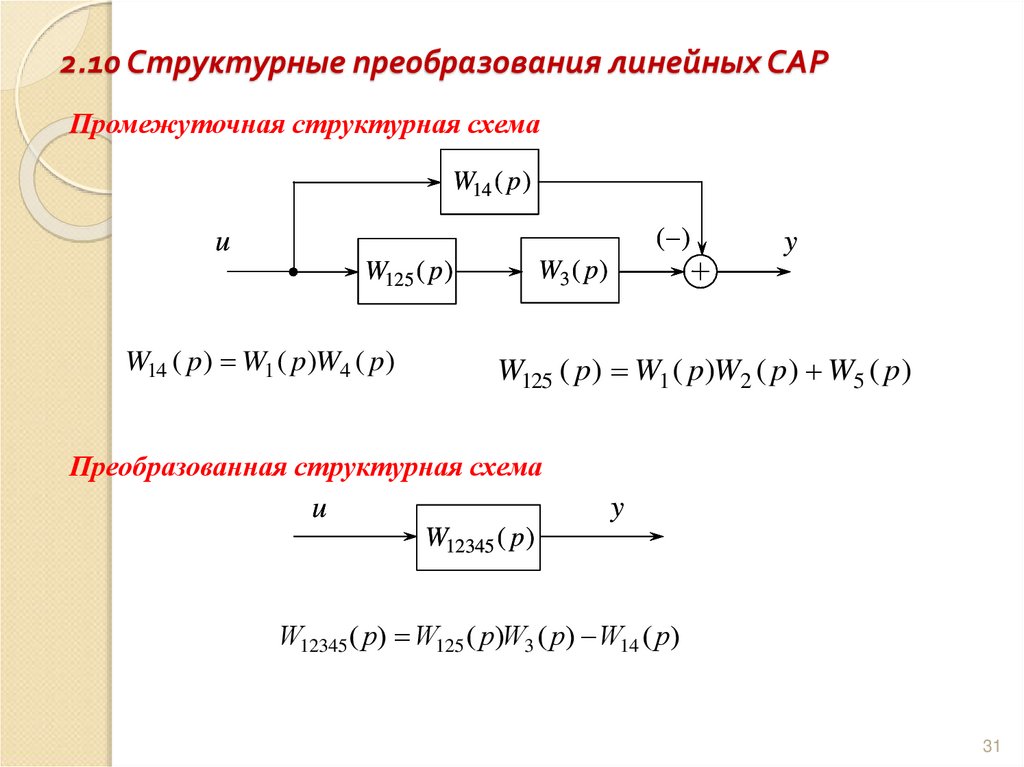
31. 2.10 Структурные преобразования линейных САР

Промежуточная структурная схема
W14 ( p )
( )
u
W125 ( p )
W14 ( p) W1 ( p)W4 ( p)
y
W3 ( p)
W125 ( p) W1 ( p)W2 ( p) W5 ( p)
Преобразованная структурная схема
u
W12345 ( p )
y
W12345 ( p) W125 ( p)W3 ( p) W14 ( p)
31

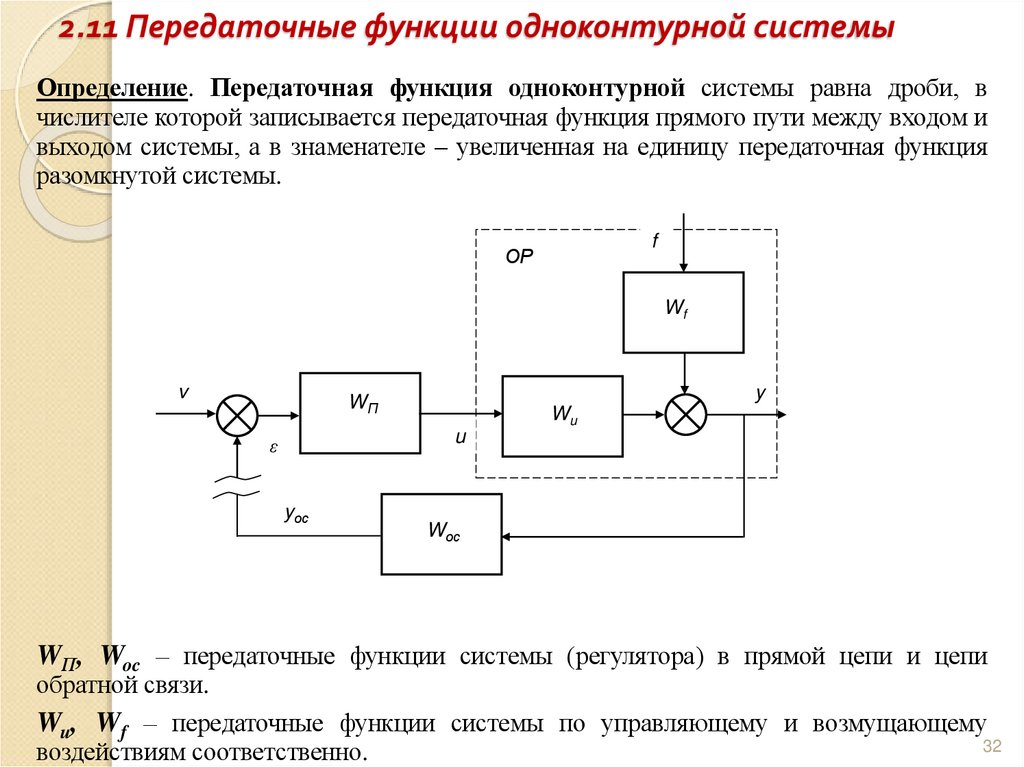
32. 2.11 Передаточные функции одноконтурной системы

Определение. Передаточная функция одноконтурной системы равна дроби, в
числителе которой записывается передаточная функция прямого пути между входом и
выходом системы, а в знаменателе – увеличенная на единицу передаточная функция
разомкнутой системы.
f
ОР
Wf
v
y
WП
Wu
u
ε
yос
Wос
WП, Woc – передаточные функции системы (регулятора) в прямой цепи и цепи
обратной связи.
Wu, Wf – передаточные функции системы по управляющему и возмущающему
воздействиям соответственно.
32

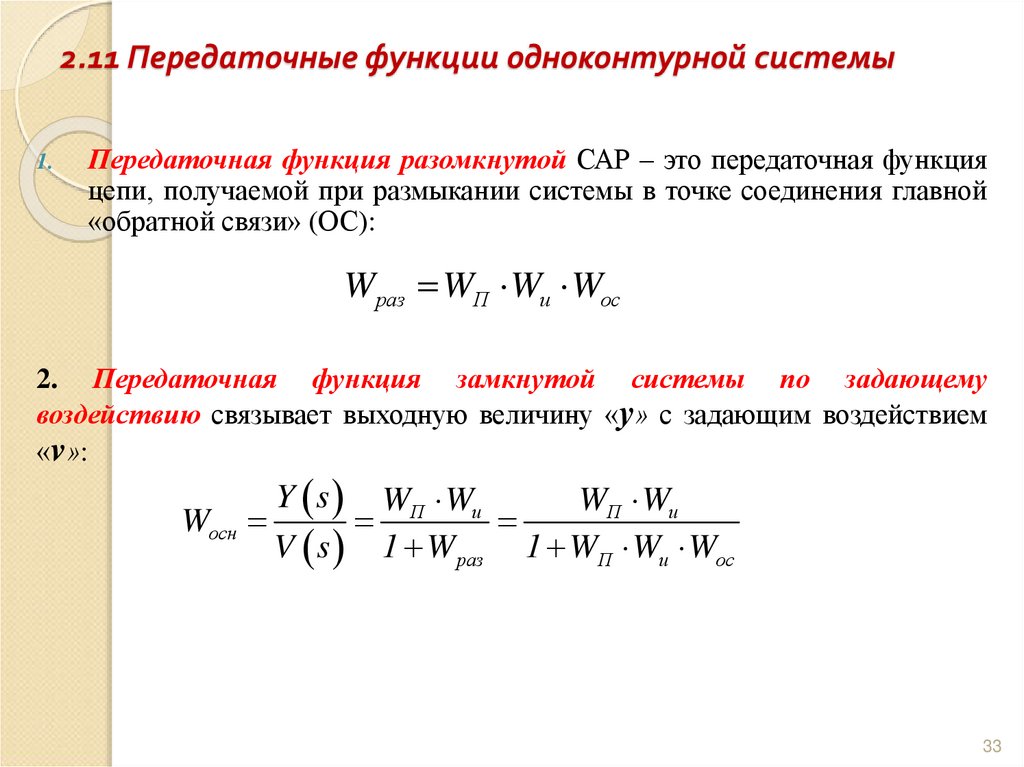
33. 2.11 Передаточные функции одноконтурной системы

1.
Передаточная функция разомкнутой САР – это передаточная функция
цепи, получаемой при размыкании системы в точке соединения главной
«обратной связи» (ОС):
Wраз WП Wи Wос
2. Передаточная функция замкнутой системы по задающему
воздействию связывает выходную величину «у» с задающим воздействием
«v»:
Y s WП Wи
WП Wи
Wосн
V s 1 W раз 1 WП Wи Wос
33

34. 2.11 Передаточные функции одноконтурной системы

3. Передаточная функция по возмущению относительно регулируемой
величины:
4. Передаточная функция по задающему воздействию относительно
рассогласования:
34

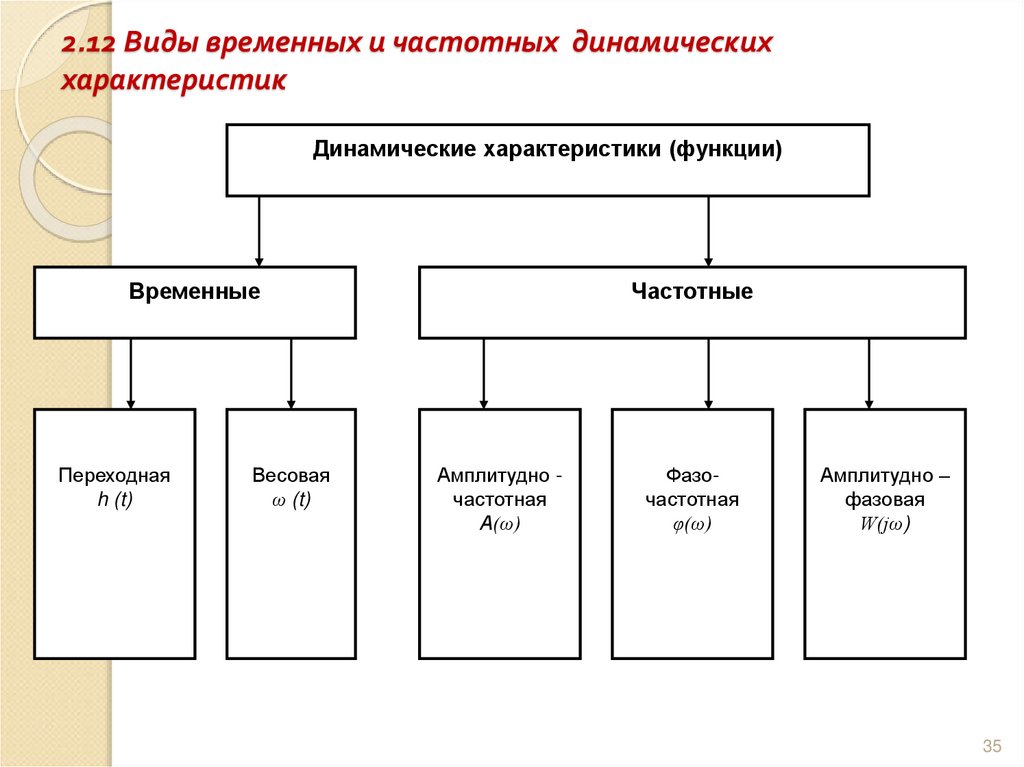
35. 2.12 Виды временных и частотных динамических характеристик

Динамические характеристики (функции)
Временные
Переходная
h (t)
Весовая
ω (t)
Частотные
Амплитудно частотная
А(ω)
Фазочастотная
φ(ω)
Амплитудно –
фазовая
W(jω)
35

36. 2.13 Временные характеристики

Определение. Временные характеристики это реакция звена или системы
на типовые воздействия при нулевых начальных условиях.
Определение. Переходная характеристика (функция) h(t) – это переходный
процесс изменения выходной величины при единичном ступенчатом
воздействии на входе и нулевых начальных условиях.
Изображение переходной функции h(t) по Лапласу имеет вид:
L h t H s W s 1
Другое название
«Кривая разгона»
s
36

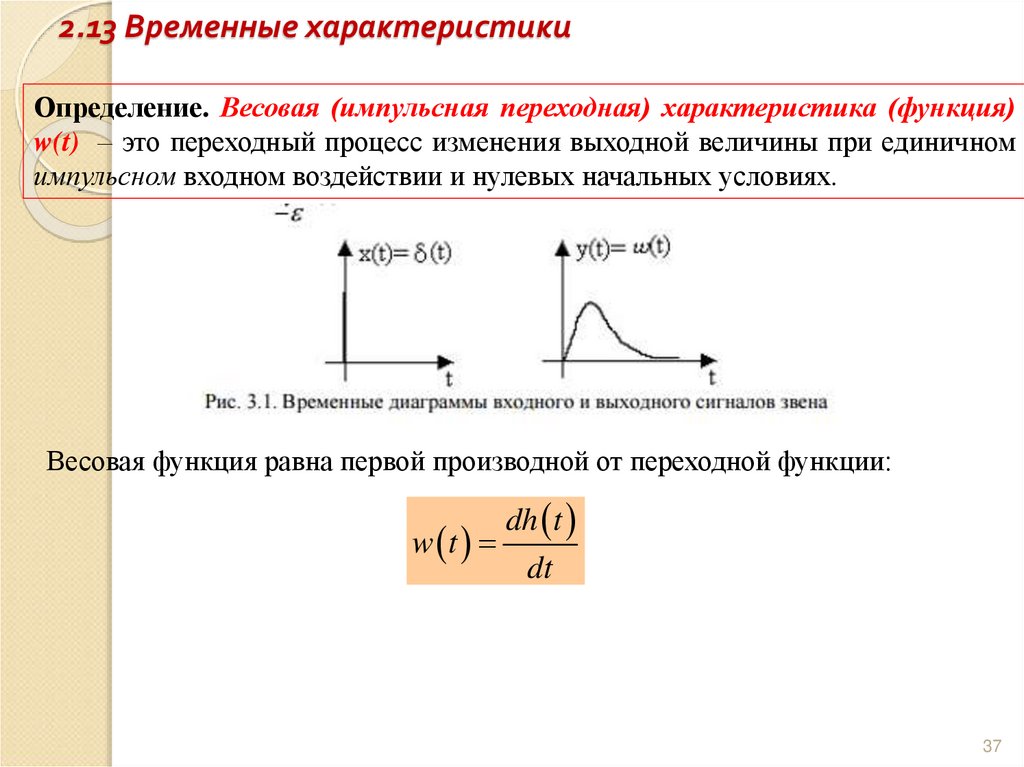
37. 2.13 Временные характеристики

Определение. Весовая (импульсная переходная) характеристика (функция)
w(t) – это переходный процесс изменения выходной величины при единичном
импульсном входном воздействии и нулевых начальных условиях.
Весовая функция равна первой производной от переходной функции:
dh t
w t
dt
37

38. 2.14 Частотные характеристики

Укрупненная структурная схема САУ/САР, иллюстрирующая частотные
характеристики
u (t ) Aвх sin( t вх )
Линейная
стационарная
одномерная САУ
y(t ) Aвых sin( t вых )
Символическая форма записи синусоидальных колебаний с использованием
функции комплексного переменного:
u(t ) Aвхe
y(t ) Aвыхe
j t вх
j t вых
Aвхe
j вх
Aвыхe
e
j вых
j t
e j t
38

39. 2.14 Частотные характеристики

По аналогии с передаточной функцией в изображениях Лапласа, введем в
анализ частотную передаточную функцию, или иначе комплексный
коэффициент передачи W(jω):
W ( j )
Aвых e j вых
Aвх e j вх
Aвых j вых вх
e
Aвх
Определение. Амплитудно-частотная характеристика (АЧХ) – это
зависимость отношения амплитуды выходного сигнала к амплитуде входного
сигнала от частоты w:
Aвых ( )
A( )
Aвх ( )
АЧХ показывает, как элемент пропускает сигналы
различной частоты.
Определение. Фазо-частотная характеристика (ФЧХ) – это
зависимость разности (сдвига) фаз выходного и входного колебаний от
частоты w :
( ) вых ( ) вх ( )
ФЧХ показывает, какое отставание или опережение
выходного сигнала по фазе создает элемент39при различных
частотах

40. 2.14 Частотные характеристики

Амплитудную и фазовую характеристики можно объединить в одну общую –
амплитудно- фазовую частотную характеристику (АФЧХ).
АФЧХ представляет собой функцию комплексного переменного jω :
(показательная форма),
где A(ω ) – модуль функции; ϕ (ω) – аргумент функции.
Если на комплексной плоскости отложить
вектор W(j ) , длина которого равна
модулю
W ( j ) A( )
а
пространственное
положение
определяется аргументом arg W(j ) = φ( )
(угол между вектором и положительной
вещественной
полуосью),
то
при
изменении частоты от 0 до ∞ конец W(j )
будет описывать в двумерном пространстве
кривую, которая называется амплитуднофазо-частотной
характеристикой
(АФЧХ).
j
W ( j )
P( i )
0
Q( i ) A( i )
( i )
0
i
40

41. 2.14 Частотные характеристики

При использовании алгебраической формы записи функции комплексной
переменной:
W ( j ) A( )e j ( ) P( ) jQ( )
можно также выделить вещественную частотную характеристику (ВЧХ):
P( ) ReW ( j ) A( ) cos ( )
и мнимую частотную характеристику (МЧХ):
Q( ) ImW ( j ) A( ) sin ( )
ВЧХ и МЧХ связаны с АЧХ и ФЧХ следующими зависимостями:
A( ) W ( j ) P 2 ( ) Q 2 ( )
( ) arg W ( j ) arctg
Q( )
P( )
41

42. 2.15 Логарифмические частотные характеристики

Логарифмические частотные характеристики (ЛЧХ) позволяют
упростить построение и расчеты частотных характеристик системы и
делятся на три вида:
логарифмические амплитудно-частотные характеристики (ЛАЧХ);
логарифмические фазо-частотные характеристики (ЛФЧХ);
логарифмические амплитудно-фазовые характеристики (ЛАФХ).
ЛАЧХ и ЛФЧХ строятся в прямоугольных координатах, причем на оси
абсцисс используется логарифмический масштаб частоты.
От произвольно выбранной точки, соответствующей ω = 1 рад/сек., влево
и вправо откладываются отрезки, пропорциональные lg .
Единицей измерения при этом является декада, которая по физическому
смыслу соответствует диапазону частот, крайние значения которого
отличаются в 10 раз, т.к.
lg 10 i lg i 1 дек
42

43. 2.15 Логарифмические частотные характеристики

Логарифмические частотные характеристики
При построении ЛАЧХ по оси ординат также применяется
логарифмическая шкала, по которой откладываются значения
в
децибеллах (0,1 бела), (дБ):
L 20lg A
Бел – единица измерения отношения мощности двух сигналов. Если мощность
одного сигнала больше мощности другого в 10 раз, то эти мощности
отличаются на 1 Б (lg10 = 1).
Т.к. мощность сигнала пропорциональна квадрату амплитуды ,то
В верхней полуплоскости
ЛАЧХ (А(ω) > 1) происходит
усиление
амплитуды
входного
гармонического
сигнала, а в нижней при
А(ω) < 1 - ослабление.
43

44. 2.15 Логарифмические частотные характеристики

Логарифмические частотные характеристики
При построении ЛФЧХ по вертикали используется обычный натуральный масштаб, т.е.
откладываются отрезки, пропорциональные сдвигу фаз в угловых градусах или радианах.
ЛАФХ L тоже строится в прямоугольных координатах по L и , а частота является
параметром как и для АФХ.
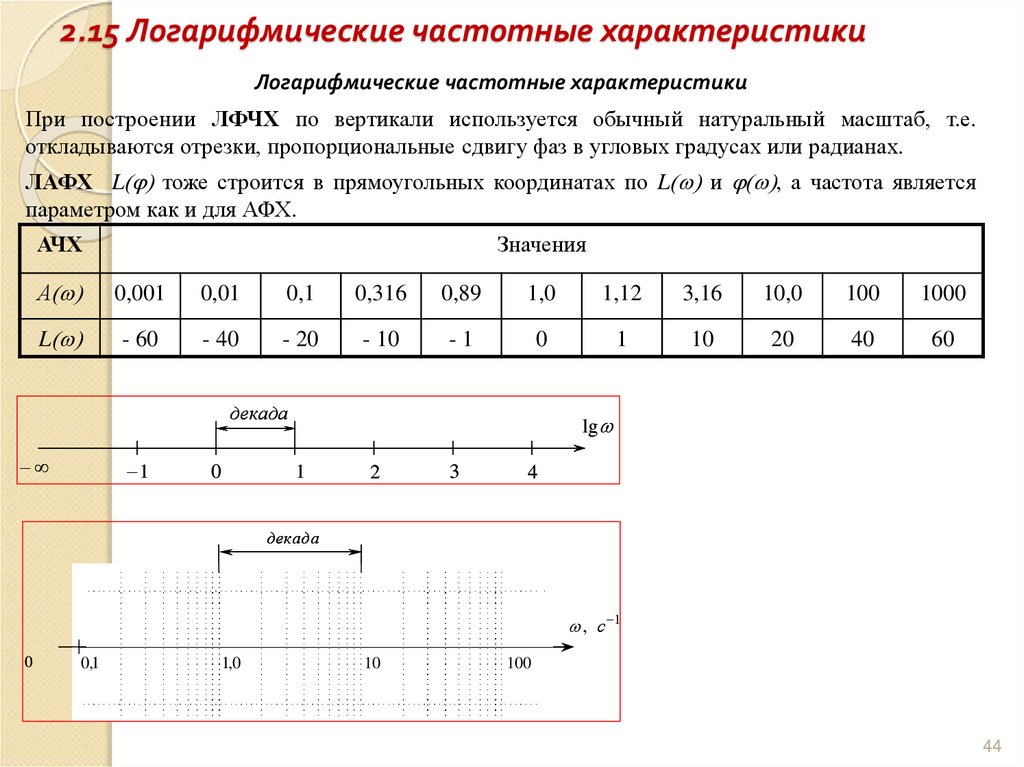
АЧХ
Значения
А
0,001
0,01
0,1
0,316
0,89
1,0
1,12
3,16
10,0
100
1000
L
- 60
- 40
- 20
- 10
-1
0
1
10
20
40
60
декада
1
lg
1
0
2
3
4
декада
, с 1
0
0,1
1,0
10
100
44

45. 2.15 Логарифмические частотные характеристики

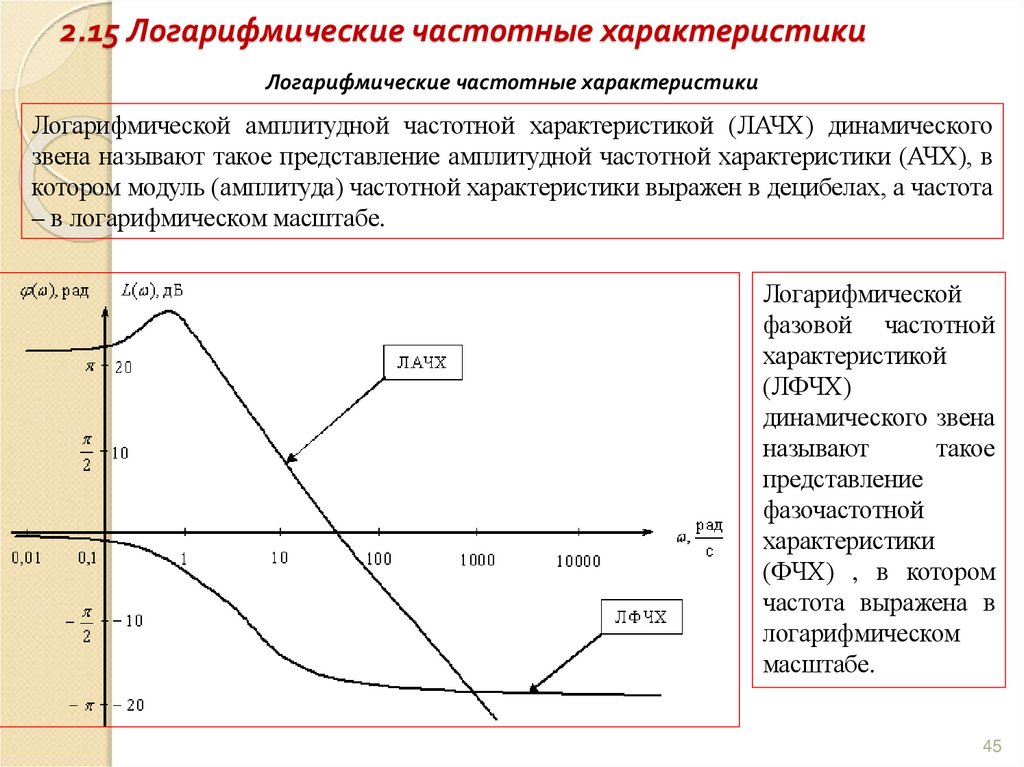
Логарифмические частотные характеристики
Логарифмической амплитудной частотной характеристикой (ЛАЧХ) динамического
звена называют такое представление амплитудной частотной характеристики (АЧХ), в
котором модуль (амплитуда) частотной характеристики выражен в децибелах, а частота
– в логарифмическом масштабе.
Логарифмической
фазовой частотной
характеристикой
(ЛФЧХ)
динамического звена
называют
такое
представление
фазочастотной
характеристики
(ФЧХ) , в котором
частота выражена в
логарифмическом
масштабе.
45