выступ_Байрахтарова_П_+_Сероокая_А_

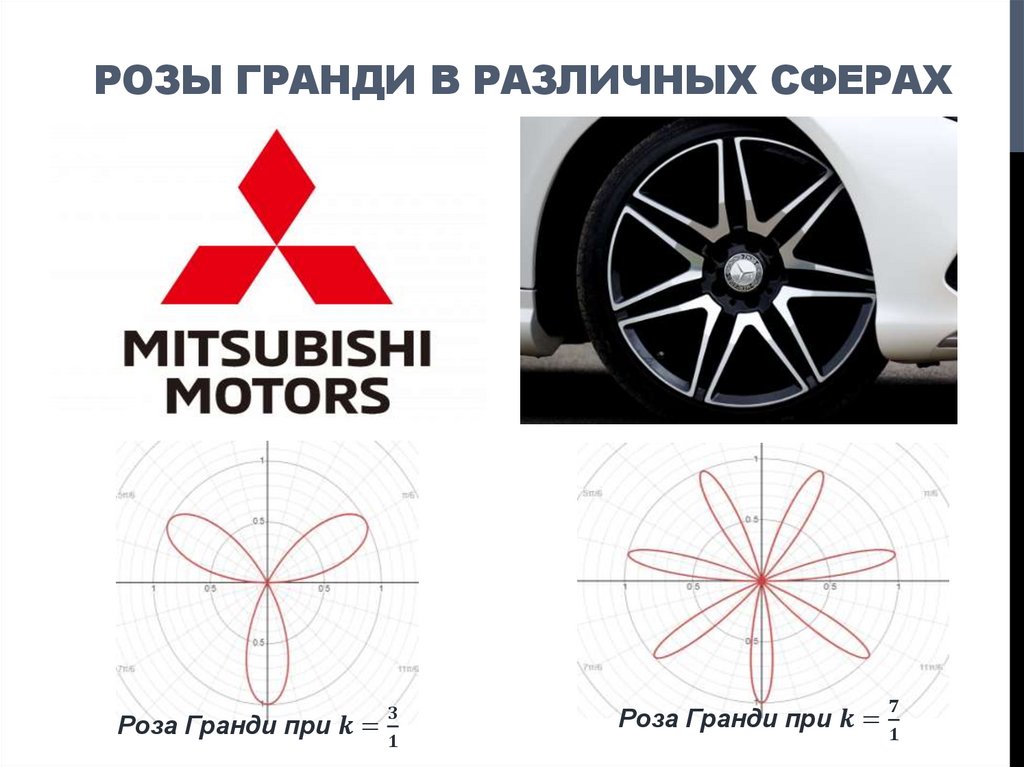
1. РОЗОВИДНЫЕ КРИВЫЕ ГВИдо Гранди

Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа № 27
г.о. Люберцы Московской области
РОЗОВИДНЫЕ КРИВЫЕ
ГВИДО ГРАНДИ
Работу выполнили:
Байрахтарова Полина,
Сероокая Анастасия,
учащиеся 10 «А» класса
Руководитель:
Терещенкова Е. В.,
к.п.н.,проф. преподаватель
математики

2.

Актуальность
заключается в демонстрации и
применении
математических
знаний
в
практической
деятельности человека. Люди различают окружающие их
вещи по форме. Интерес к форме предмета может быть
вызван какой-либо потребностью у человека, а может и
красотой самой формы. В проекте изучен вопрос применения
кривых - математических роз и спиралей в природе и жизни
человека.
ОБЪЕКТ
ИССЛЕДОВАНИЯ:
функция,
описывающая
кривые «розы
Гранди»
ПРЕДМЕТ
ИССЛЕДОВАНИЯ:
зависимость очертаний и форм
лепестков от изменения
коэффициентов в функции,
задающей кривую Гранди

3. ГИПОТЕЗА ИССЛЕДОВАНИЯ

Мы предполагаем, что задавая параметр функции Гвидо
Гранди отношением натуральных чисел можно получить
множество
различных
замкнутых
кривых,
при
определенных
условиях
превращающиеся
в
лепестковые цветы или в ажурные розетки, которые
могут служить элементами декора или орнамента.

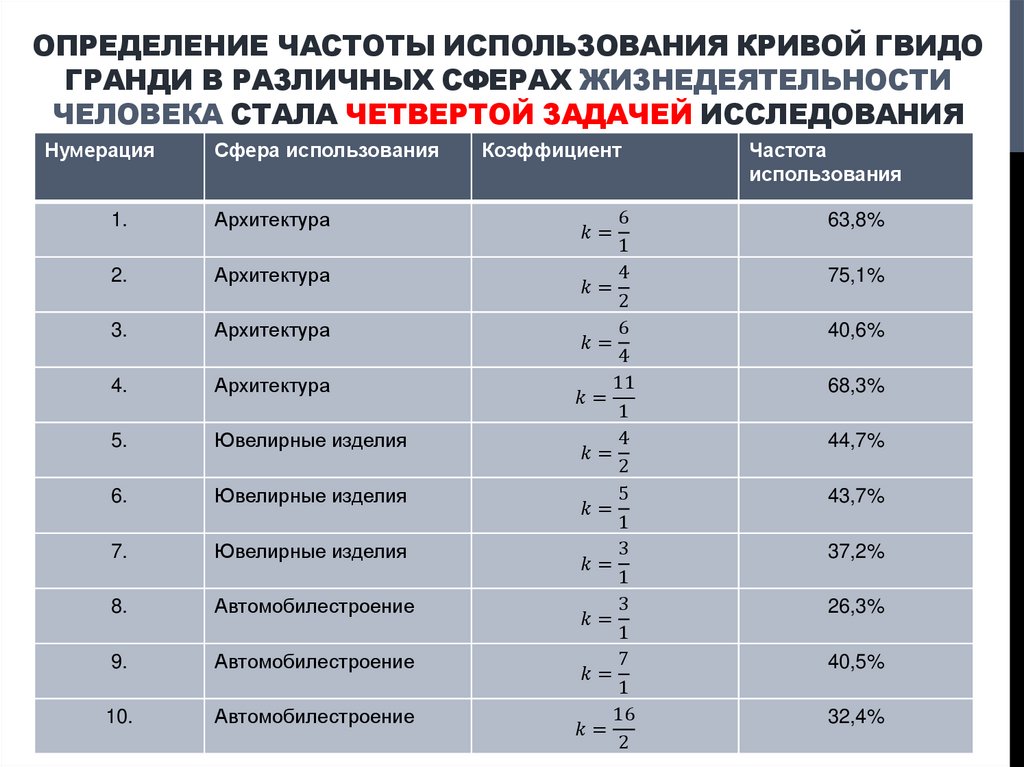
4. ЦЕЛЬ ИССЛЕДОВАНИЯ

разработать классификатор (систематизированный перечень
множества кривых Гвидо Гранди), который позволяет
определить количество лепестков и форму цветка кривой, в
заданной полярной системе координат, в зависимости от
различных значений параметра k.
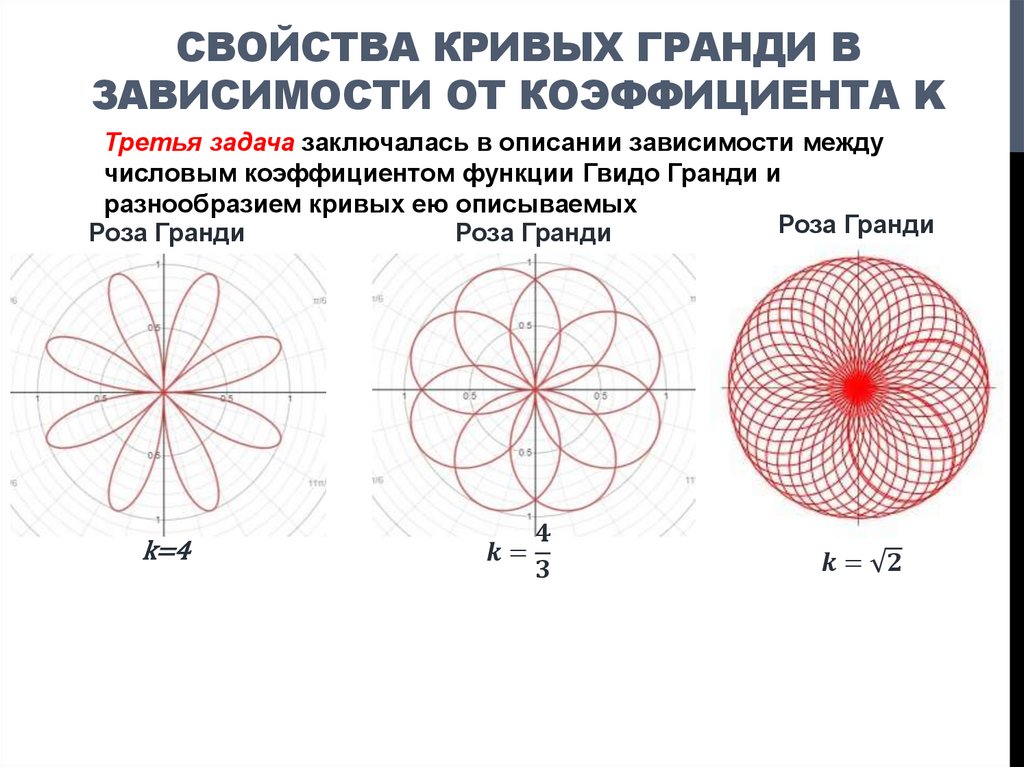
ОСТАНОВИМСЯ НА ПОЛУЧЕННЫХ РЕЗУЛЬТАТАХ

5. Сущность «замечательных» кривых: их виды и характеристики

СУЩНОСТЬ «ЗАМЕЧАТЕЛЬНЫХ» КРИВЫХ: ИХ
ВИДЫ И ХАРАКТЕРИСТИКИ
Согласно первой задаче, мы
уточнили сущность, виды
кривых. Кривая - есть след
движущейся линии. Они могут
быть
плоскими
и
пространственными,
замкнутыми и открытыми.
Также кривых различают по
их
порядку.
Многие
выдающиеся
математики
изучали кривые, и даже
открыли некоторые из них:
улитка
Паскаля,
спираль
Архимеда, циссоида и др.
Спираль Архимеда
Улитка Паскаля

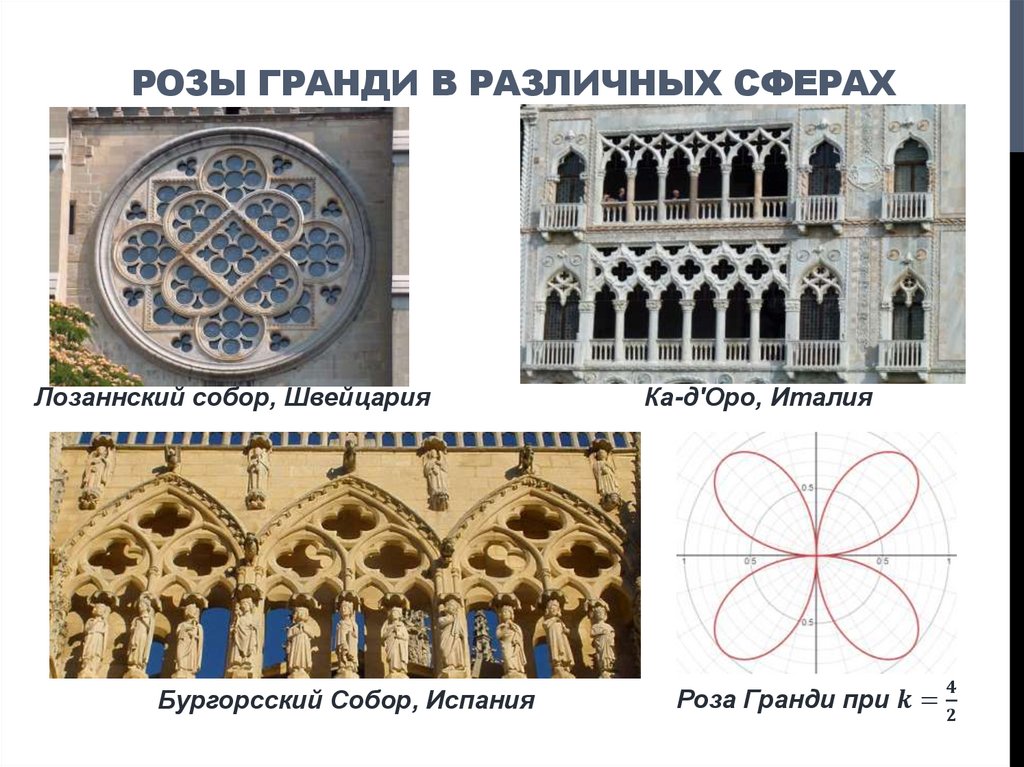
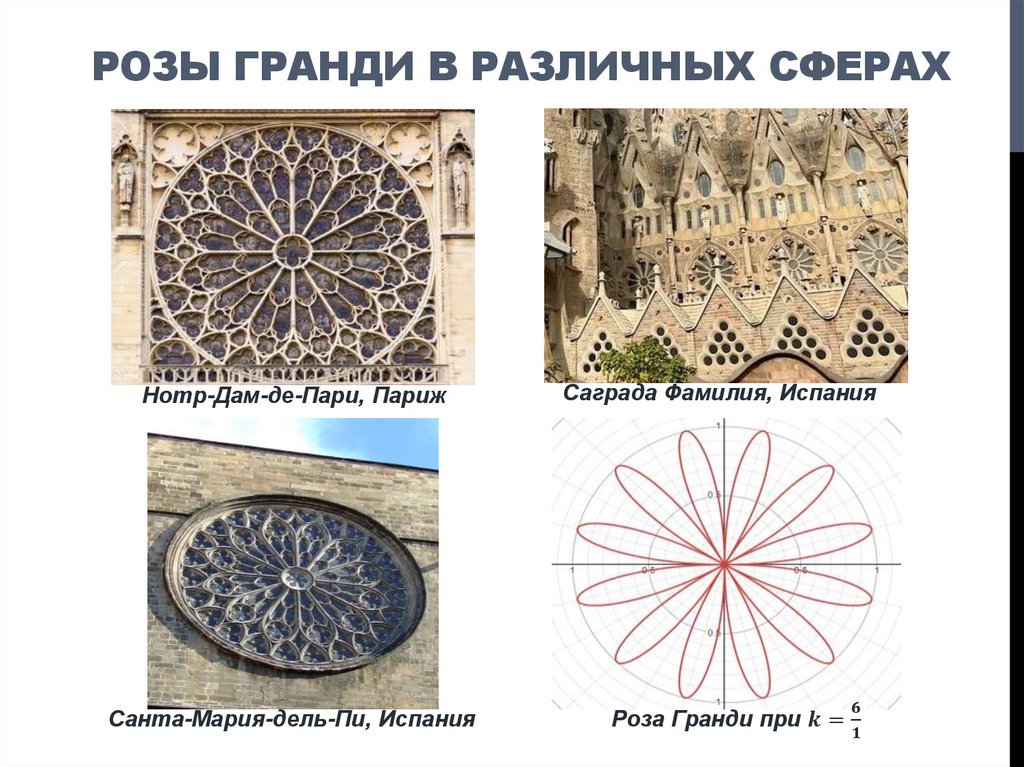
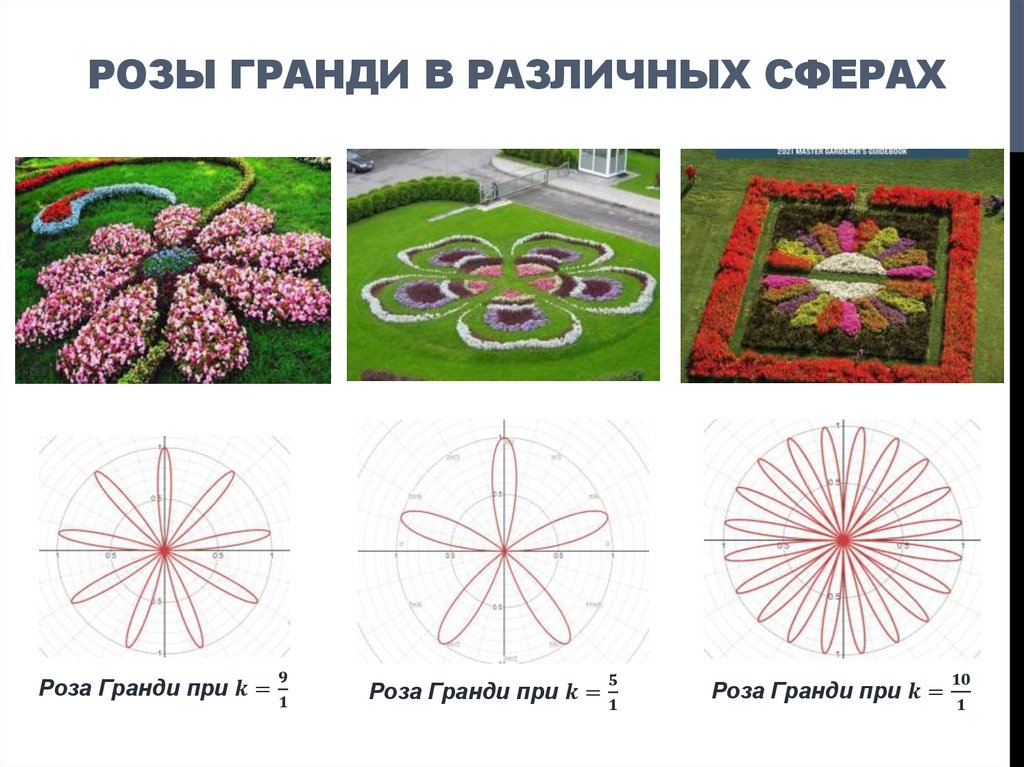
6. Специфика «замечательной» кривой: розы Гвидо Гранди

СПЕЦИФИКА «ЗАМЕЧАТЕЛЬНОЙ» КРИВОЙ:
РОЗЫ ГВИДО ГРАНДИ
Решая
вторую
задачу
исследования,
мы
выявили
специфику
«замечательной»
кривой
Итальянский
геометр
Гвидо
Гранди (1671–1742), работая с
полярной системой координат,
решил воссоздать с помощью
линий эти прекрасные растения.
Полярное уравнение роз Гранди
выглядит следующим образом: