системы_счисления[1]

1.

Системы
счисления

2.

Системы счисления: от наскальных
рисунков до цифровой эры.
Система счисления — это способ записи чисел с
помощью специальных символов (цифр) по
определённым правилам.
Это фундаментальный язык математики,
техники и науки. История развития систем
счисления отражает эволюцию человеческого
мышления — от конкретного счета предметов до
абстрактных понятий, лежащих в основе
современных компьютеров и глобальных
коммуникаций.

3.

Происхождение систем счисления.
Старейшие свидетельства использования чисел – кости
с отметками, найденные в археологических раскопках.
Древнейшая из подобных находок – кость бабуина,
найденная в Африке в 1973 г., возраст которой
оценивается в 35 000 лет. На этой кости нанесено 29
отметок. Считается, что она использовалась для
подсчета фаз Луны.
Первый вычислительный
инструмент человека - пальцы.
Генри Мортон Стэнли (1841–1904)
— британский журналист и
исследователь Африки
задокументировал, что некоторые
африканские племена
использовали пятеричную
систему счисления.

4.

Древнейшие системы счисления:
единичная (унарная) и непозиционные.
Единичная система
является самой древней.
В единичной системе число
обозначалось повторением
одного символа (черточки,
зарубки, узелки, камни).
Например, число 5 — это
пять палочек |||||. В
единичной системе была
прямая связь между
количеством предметов и
Узелковое
письмо
«кипу»
инков.

5.

Древнейшие системы счисления:
единичная (унарная) и непозиционные.
Непозиционной
системой счисления
называется система, в
которой значение цифры
или знака не зависит от
её положения в записи
числа. Каждая цифра
имеет фиксированное
значение, которое
определяется её
символом, а не местом,
которое она занимает.
Древнеегипетская
система счисления
представляла
иероглифы-символы для
записи степеней
десятков (1, 10, 100, 1000
и т.д). Значение числа
определялось суммой
значений всех символов,
а не их позицией, при
этом каждый символ мог
повторяться до девяти
раз. Порядок записи мог
быть справа налево,
слева направо или

6.

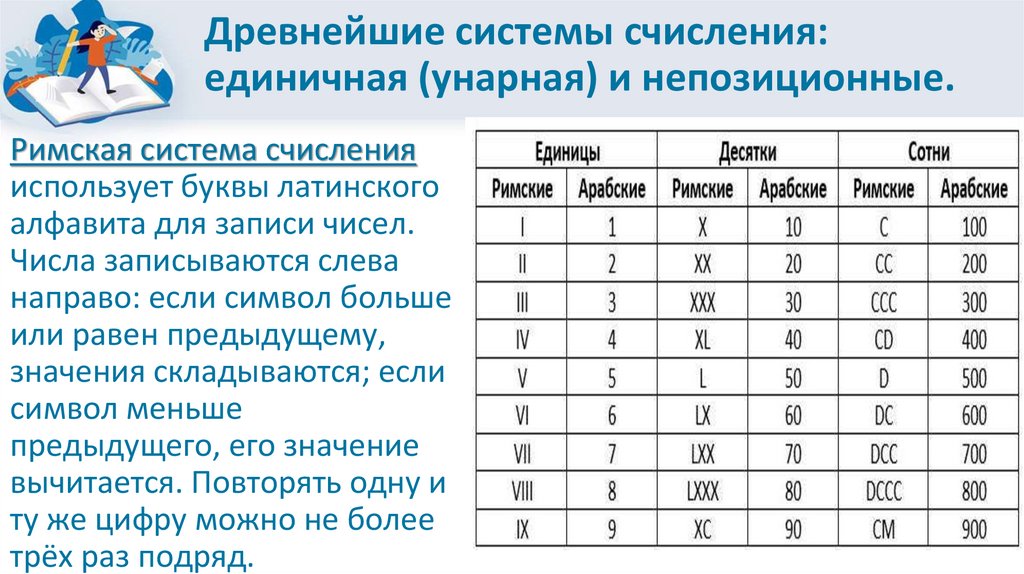
Древнейшие системы счисления:
единичная (унарная) и непозиционные.
Римская система счисления
использует буквы латинского
алфавита для записи чисел.
Числа записываются слева
направо: если символ больше
или равен предыдущему,
значения складываются; если
символ меньше
предыдущего, его значение
вычитается. Повторять одну и
ту же цифру можно не более
трёх раз подряд.

7.

Позиционный принцип в системах
счисления.
Позиционная
система
счисления
подразумевает,
что запись
числа
производится,
исходя из
положения
цифры (её
разряда) в
Вавилонская
шестидесятеричная система
счисления (3000 лет до н.э.)
является первой известной
позиционной системой.
Основание было равно 60,
использовали два знака:
прямой клин для единиц,
лежачий клин для десятков
внутри каждого разряда.
Несмотря на отсутствие нуля в
начале, система стала
основной для современной
записи времени, углов и
георгафических координат.
Например, 60 минут в часе, 360
градусов в круге.

8.

Позиционный принцип в системах
счисления.
Система счисления майя —
это двадцатеричная
позиционная система,
которая использовала три
символа: точку (1), черту (5) и
ракушку (0). Числа до 19
составлялись из комбинаций
этих символов, а для записи
чисел от 20 и выше
использовался позиционный
принцип, где разряды
располагались снизу вверх.
Система была очень
развитой и применялась, в
частности, для
астрономических расчётов в

9.

Позиционный принцип в системах
счисления.
Индийские математики (V-VII вв.) создали
позиционный десятичный принцип счисления.
Ввели цифры от 0 (шунья) до 9. Ноль перестал
быть просто пустым местом, а стал
полноценным числом, обозначающим
отсутсвие единиц в разряде.
Учёный аль-Хорезми, живший в Арабском
халифате (IX в.), в своём трактате «Книга об
индийском счёте» подробно описал эту
систему. Благодаря арабским торговцам и
учёным система счисления попала в Европу.
Новая система счисления пришла в Европу (XIIXVI вв.) с арабскими торговцами, поэтому ее
стали называть «арабской». Внедрение новой
системы счисления шло медленно. Решающую
роль сыграла книга Леонардо Пизанского
(Фибоначчи) «Книга абака» (1202 г.), где он
показал огромное преимущество новой
системы в вычислениях перед римскими
цифрами и абаком. К XVI веку десятичная
Готфрид Вильгельм Лейбниц (1646-1716).
Немецкий философ и математик.
Разработал двоичную систему счисления
(основание 2), в которой используются
только цифры 0 и 1. Он вкладывал в неё
философский смысл (сотворение мира из
ничто и единицы). Его работы заложили
теоретическую основу для будущих
компьютеров.

10.

Современные системы счисления.
Двоичная (бинарная) система счисления — это позиционная система с
основанием 2, использующая всего две цифры: 0 и 1. Она широко
применяется в компьютерах, поскольку позволяет представить два состояния
электрического сигнала (есть напряжение или нет) и логические значения
(истина и ложь).
Принцип работы двоичной системы счисления:
1. Каждый разряд числа имеет свой вес, который является степенью двойки.
2. Для перевода двоичного числа в десятичную систему необходимо сложить
произведения каждой цифры на вес соответствующего разряда (степень
двойки).
Двоичная система счисления используется для внутренней работы
компьютеров, процессоров и других электронных устройств; так же в
программировании: все данные компьютеоа представлены в двоичном коде.
Недостаток системы заключается в длинной записи чисел, затрудняющей их
восприятие человеком.

11.

Современные системы счисления.
Для перевода десятичного
числа в двоичную систему
нужно последовательно делить
его на 2, записывая остатки от
деления, и затем собрать их в
обратном порядке.
Пример: перевести число 43 10 в
двоичную систему.
43/2=21 (остаток 1)
21/2=10 (остаток 1)
10/2=5 (остаток 0)
5/2=2 (остаток 1)
2/2=1 (остаток 0)
1/2=0 (остаток 1)
Собираем остатки в обратном
Чтобы перевести число из
двоичной в десятичную систему,
нужно умножить каждую цифру на
степень двойки, соответствующую
её позиции (справа налево,
начиная с 0), и сложить
полученный результат.
Пример: перевести число 11012 в
десятичную систему.
1*20=1
0*21=0
1*22=4
1*23=8
8+4+0+1=13

12.

Современные системы счисления.
Восьмеричная система счисления — это позиционная система с основанием 8, использующая
цифры от 0 до 7. Её основное применение связано с цифровыми устройствами, поскольку
восьмеричные числа легко переводятся в двоичные (и наоборот) путём группировки
двоичных разрядов в триады (тройки).
Восьмеричную систему счисления использовали в старых компьютерных системах
(например, сериях ДВК, СМ ЭВМ, БЭСМ) для кодирования команд и записи содержимого
памяти. В настоящее время она в основном применяется в Linux и других Unix-системах для
установки прав доступа к файлам.
Десятичная система — это позиционная система счисления с основанием 10, использующая
цифры от 0 до 9 для записи чисел. Её основная особенность заключается в том, что значение
цифры зависит от её позиции в числе, например, 2345, цифра 2 означает 2000, 3 — 300, 4 —
40 и 5 — 5. Эта система является наиболее распространённой в мире, так как её основание,
предположительно, связано с количеством пальцев на руках человека.

13.

Современные системы счисления.
Шестнадцатеричная система счисления
— это позиционная система с
основанием 16, использующая цифры
от 0 до 9 и буквы латинского алфавита
A–F для обозначения чисел от 10 до 15.
Она широко применяется в
программировании для работы с
цветами и двоичными данными, так
как позволяет компактно записывать
большие числа и облегчает их чтение и
запись по сравнению с двоичной
системой.

14.

Специализированные системы счисления.
Двенадцатеричная система счисления — это позиционная система счисления с
основанием 12. Она использует двенадцать различных символов для
представления чисел.
В отличие от привычной нам десятичной системы, в двенадцатеричной системе
требуются два дополнительных символа для обозначения значений 10 и 11.
Обычно для этого используют латинские буквы A (для 10) и B (для 11).
Двенадцатеричная система до сих пор широко встречается в быту и культуре:
-измерение времени - сутки делятся на два периода по 12 часов;
-календарь - в году 12 месяцев;
-торговля и счет - многие товары исторически продавались и считались дюжинами
(12 штук), гроссами (12 дюжин, или 144). Так считали столовые приборы, бутылки
или канцелярские товары;
-языки - в некоторых редких языках в Африке и Непале до сих пор используются
двенадцатеричные числительные.

15.

Специализированные системы счисления.
Шестидесятеричная система счисления — это позиционная система
счисления с основанием 60. Она является одной из древнейших известных
систем счисления, изобретенной шумерами в III тысячелетии до н. э..
В современном миры мы ее используем в следующих случаях:
-измерение времени - деление часа на 60 минут, а минуты — на 60 секунд;
-измерение углов и географических координат - деление окружности на
360 градусов, градуса — на 60 угловых минут, а минуты — на 60 угловых
секунд.
Преимущества шестидесятеричной системы счисления заключается в том,
что число 60, имея большое количество делителей (1, 2, 3, 4, 5, 6, 10, 12,
15, 20, 30, 60), позволяет легко делить целые числа на множество равных
частей и упрощает работу с дробями.

16.

СПАСИБО ЗА
ВНИМАНИЕ!