Похожие презентации:
2 Определители_ПИЭ
1. Лекция 2 Определитель матрицы. Обратная матрица. Матричные уравнения
Любой квадратной матрице Аn-го порядка можно поставить в
соответствие выражение,
которое называется
определителем (детерминантом)
матрицы А – det A или |A| или Δ
2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
О п р е д е л е н и е 1. Определителемквадратной матрицы А второго порядка
или определителем второго порядка
называется число, обозначаемое:
a11
a12
a21
a22
(или |A|)
и вычисляемое по формуле:
a11
a12
a 21
a 22
а11 а 22 а12 а 21
(1)
3. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
О п р е д е л е н и е 2. Определителем квадратнойматрицы А третьего порядка (или
определителем третьего порядка) называется
число, обозначаемое:
a11
a21
a31
a12
a22
a32
a13
a23
a33
(или |A|)
и вычисляемое по формуле:
a11 a12
a 21 a 22
a31 a32
a13
a 22
a 23 a11
a32
a33
a 23
a 21 a 23
a 21 a 22
(2)
a12
a13
a33
a31 a33
a31 a32
4. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
З а м е ч а н и е 1. Определитель третьего порядка можетбыть вычислен не только по формуле (2), называемой
разложением определителя по элементам первой
строки.
1) Для вычисления определителя третьего порядка можно
воспользоваться правилом разложения определителя по
элементам л ю б о й строки (столбца) матрицы А.
При этом элементы выбранной строки (столбца) берут со
знаками, указанными в следующей схеме:
то есть знак «+» ставят у тех элементов аij , для которых сумма
индексов i+j есть число четное, «–» – сумма индексов i+j есть
число нечетное.
5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
Например, выбрав для разложения вторую строкуопределителя, получим формулу разложения
определителя третьего порядка по элементам
второй строки:
a11 a12 a13
a12 a13
a11 a13
a11 a12
a 21 a 22 a 23 a 21
a 22
a 23
.
a32 a33
a31 a33
a31 a32
a31 a32 a33
6. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
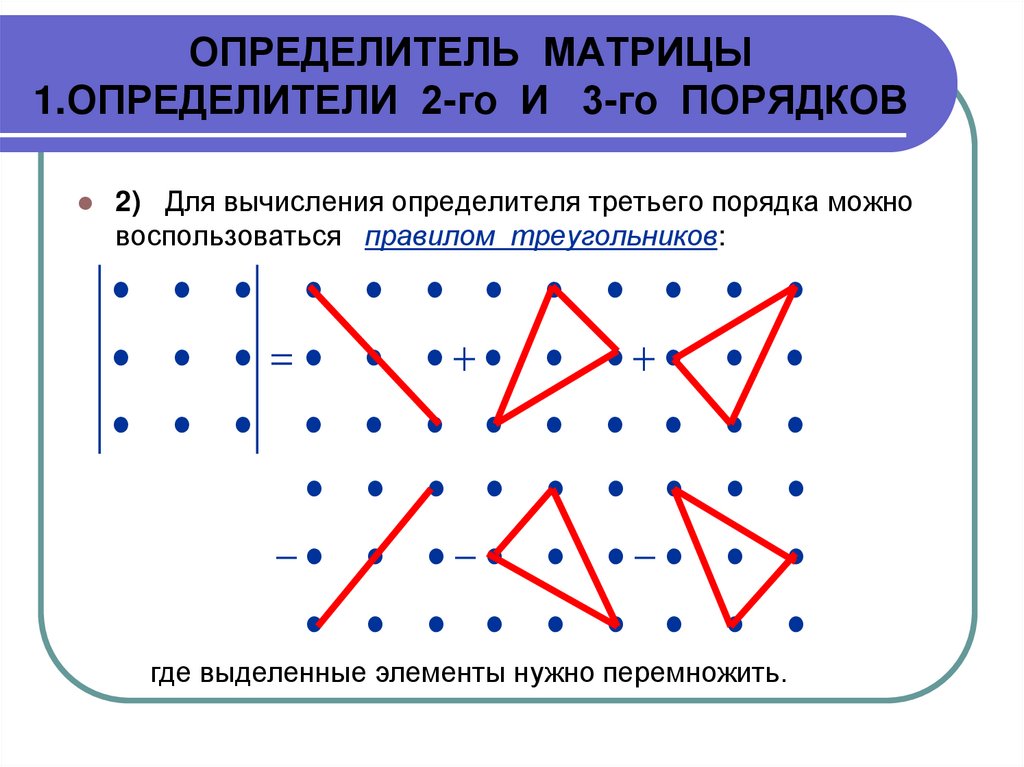
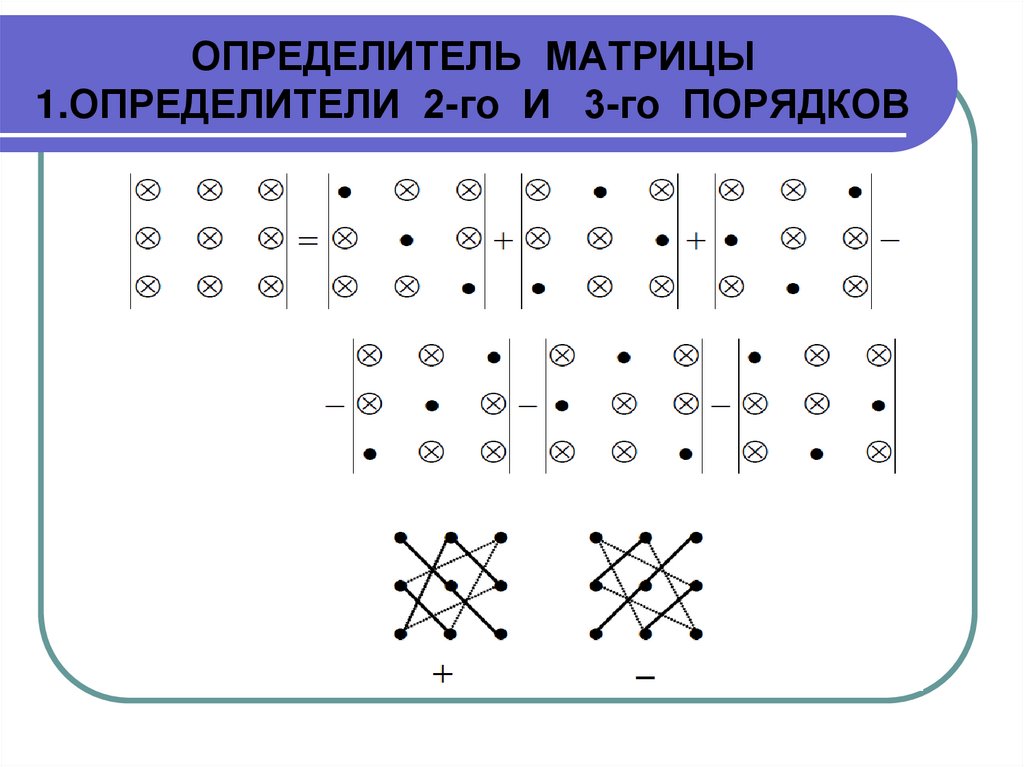
2) Для вычисления определителя третьего порядка можновоспользоваться правилом треугольников:
где выделенные элементы нужно перемножить.
7.
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
8. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2. Свойства определителя
1. Определитель не меняется притранспонировании матрицы;
2. Если все элементы некоторой строки
(столбца) равны нулю, то определитель
также равен нулю;
3. Определитель с двумя одинаковыми
строками (столбцами) равен нулю;
4. Общий множитель элементов какойлибо строки (столбца) определителя
можно выносить за знак определителя;
9. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2. Свойства определителя
5. При перестановке строк (столбцов)определитель меняет знак;
6. Если к элементам некоторой строки
(столбца) прибавить соответствующие
элементы другой строки (столбца),
умноженные на одно и то же число, то
определитель не изменится;
7. Определитель, в котором все элементы
одной из строк являются суммами двух
слагаемых, равен сумме двух
определителей.
10. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Примеры
Вычислить определитель:1 2
6
4 3 1
2 2 5
Р е ш е н и е.
Способ I (разложение по элементам первой строки):
1 2
6
3 1
4 1
4 3
4 3 1 1
2
6
2 5
2 5
2 2
2 2 5
3 5 2 1 2 4 5 2 1 6 4 2 2 3
1 5 2 2 2 0 2 6 8 6 1 3 4 4 8 4 1 1 5 .
11. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Примеры
П р и м е р . Вычислить определитель1 2 3
0 7
4
5 3 3
Р е ш е н и е. Способ I (правило треугольников):
1 2 3
0 7
4 1 7 3 2 4 5 0 3 3 5 7 3
5 3 3
3 4 1 0 2 3 2 1 4 0 1 0 5 1 2 1 7 8
12. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 3. Определитель матрицы n-го порядка
Определение. Минором некоторого элементаa ij матрицы A порядка n называется
определитель n 1 порядка,
соответствующий матрице, которая
получается из исходной матрицы A в
результате вычеркивания той строки и того
столбца, на пересечении которых стоит
элемент a ij, т.е. i строки и j го столбца.
Минор элемента a ij обозначается M ij.
13. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 3. Определитель матрицы n-го порядка
n -го порядка,Определение. Определителем
соответствующим матрице
а11 а12
a21 a22
A
an1 an 2
называется число, равное
a11 M 11 a12 M 12 ... ( 1)
и обозначаемое
n 1
а1n
a2 n
ann
n
a1 n M 1 n 1
j 1
det A , либо A
1 j
a1 j M 1 j
14.
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ3. Определитель матрицы n-го порядка
det A A
а11
a21
а12
a22
а1n
a2 n
n
1
j 1
a n1
an 2
1 j
a1 j M 1 j .
ann
Эта формула называется разложением определителя
го порядка по первой строке.
n
15.
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ3. Определитель матрицы n-го порядка
Теорема 1. Каков бы ни был номер строки
i
i 1, 2,...n для определителя матрицы
справедлива формула
A 1 a i1 M i1 1
i 1
n
1
j 1
i j
i 2
ai 2 M i 2 ... ( 1) i n ain M in
aij M ij .
Эта формула называется разложением определителя
го порядка по i ой строке.
n
16.
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ3. Определитель матрицы n-го порядка
Теорема 2. Каков бы ни был номер столбца
j 1, 2,...n для определителя матрицы
j
справедлива формула
A 1
1 j
n
1
i 1
i j
a1 j M 1 j 1
2 j
a 2 j M 2 j ... ( 1) n j a nj M nj
aij M ij .
Эта формула называется разложением определителя
го порядка по j му столбцу.
n
17. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 3. Определитель матрицы n-го порядка
Определительможет
быть
вычислен
разложением по элементам его
л ю б о й
строки или столбца.
Замечание. Для определителя используют те
же термины (элементы, строки, столбцы,
главная и побочная диагонали), что и для
соответствующей квадратной матрицы, чей
определитель вычисляется.
18. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 4. Свойства определителя
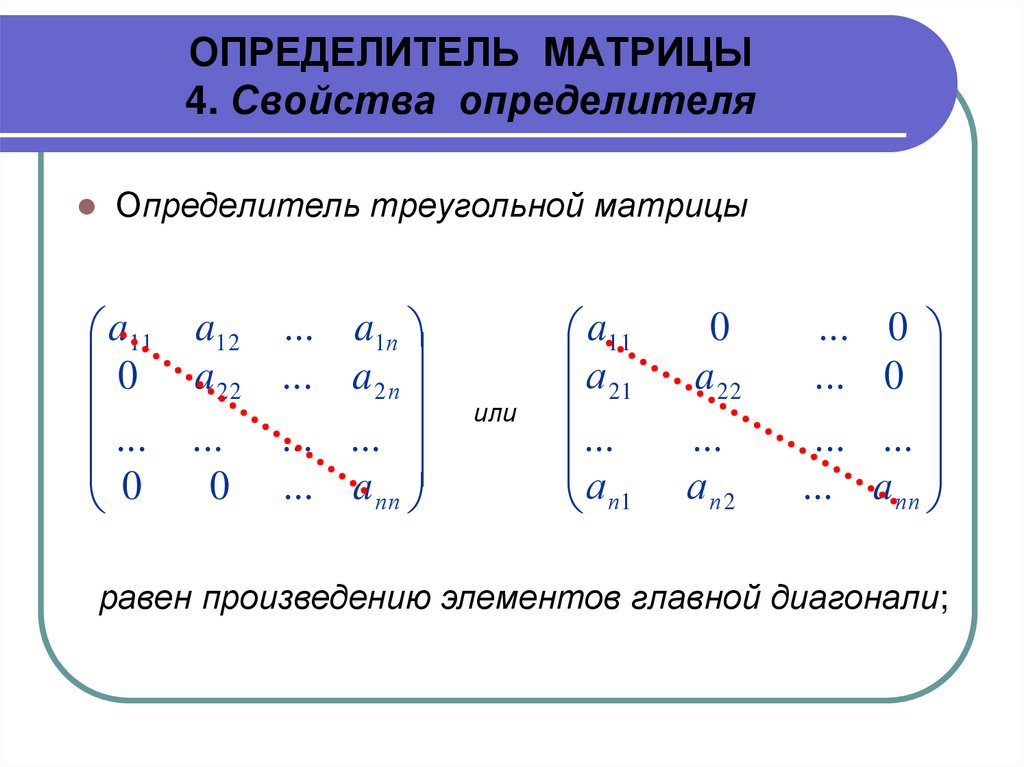
Определитель треугольной матрицыa11 a12 ... a1п
0 a
...
a
2п
22
... ... ... ...
0
0
...
a
пп
или
a11
а
21
...
а
п1
0
a 22
...
ап2
... 0
... 0
... ...
... a пп
равен произведению элементов главной диагонали;
19. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 4. Свойства определителя
Определитель произведения квадратных матрицравен произведению определителей сомножителей.
т.е.
AB A B .
Определение. Алгебраическим дополнением
элемента a ij матрицы A порядка
число, равное Aij 1
i j
n называется
M ij , (i 1, 2,...n,
j 1, 2,...n).
Используя алгебраическое дополнение, имеем
n
A aij Aij .
j 1
20. 5. Обратная матрица
ПустьA квадратная матрица n го, E
единичная матрица того же порядка.
Определение. Матрица
B
называется обратной
для квадратной матрицы , если
AB BA E.
Замечание. Обратная матрица B такого же порядка,
что и матрица
A
.
Обратная матрица для матрицы A обозначается A
AA 1 A 1 A E.
1
.
21. 5. Обратная матрица
Определение. Матрица называется невырожденной,если определитель этой матрицы отличен от нуля:
A 0,
в противном случае матрица называется
вырожденной.
Теорема. Если матрица
A имеет обратную, то эта
матрица является невырожденной:
1
A
A
1
A 0.
22. 5. Обратная матрица
Теорема. Всякая невырожденная матрица имеетобратную, причем
A11
A12
1
1
A
A
A1n
A21
A22
A2 n
An1
An 2
,
Ann
где Aij алгебраическое дополнения элемента
матрицы A.
a ij
23. 5. Обратная матрица
Обратную матрицу можно вычислить последующей формуле
T
ij
где A
A
,
алгебраическое дополнения элемента a ij
в определителе
A.
A 1
AijT
T
A , транспонированной к матрице
24. Примеры
Пример 1. Найти матрицу, обратную данной:3 1 0
A 2 1 1
2 1 4
Решение. Найдем определитель матрицы.
3
A 2
2
1 0
1
0
1 1
1 4
1 0
1
1 1
1 1 4
1 2
( 1)
1
1
1 4
5
25. Примеры
3 2 2 Найдем алгебраические дополненияT
AT 1 1 1
матрицы A .
0 1 4
1 1
1 2
A11 ( 1) (4 1) 5; A12 ( 1) ( 4 0) 4;
1 3
2 1
2 2
2 3
A13 ( 1) ( 1 0) 1; A21 ( 1) ( 8 2) 10;
A22 ( 1)
(12 0) 12; A23 ( 1) (3 0) 3;
3 1
3 2
A31 ( 1) (2 2) 0; A32 ( 1) ( 3 2) 1;
A33 ( 1)3 3 (3 2) 1.
26. Примеры
Составляем обратную матрицуA11 5; A12 4; A13 1; A21 10;
A22 12; A23 3; A31 0; A32 1;
A33 1.
5 4 1
1 4 / 5 1/ 5
1
1
1
A 10 12 3 ; A 2 12 / 5 3/ 5 .
5
0 1/ 5 1/ 5
0
1
1
27. Примеры
Проведем проверку, умножив3 1 0
A 2 1 1
2 1 4
A на
A 1.
1 4 / 5 1/ 5
1
A 2 12 / 5 3/ 5 .
0 1/ 5 1/ 5
1 0 0
A A 1 0 1 0 E.
0 0 1
28. 6. Решение матричных уравнений
Теорема. ЕслиA 0 и A, B матрицы порядка, n
то решение матричных уравнений
A X B и
X A B,
где X квадратная матрица порядка n , находится
по соответствующей из формул:
X A 1 B и
X B A 1.
29. 6. Решение матричных уравнений
С 0 ,где A, B, Сматрицы размерностью n n, n m, m m
Теорема. Если
A 0и
соответственно ,то решение матричного уравнения
A X С B,
где X матрица размерности n m, находится по
формуле:
X A 1 B С 1.
30. Примеры
Пример. Решить матричное уравнение1 2
3 5
, B
.
A
3 4
5 9
A X B, где
Решение. Найдем A 1 .
1 3
1 4 2
1
, A
A 4 6 2; A
2 3 1
2 4
T
1
X A B,
1
1 4 2 2
A
2 3 1 1,5 0,5
1
1 3 5 1 1
2
X
1,5 0,5 5 9 2 3



























 Математика
Математика








