Похожие презентации:
Определители. Обратная матрица. Ранг матрицы
1.
§5. Определители. Обратнаяматрица. Ранг матрицы
п.1. Определители.
Каждой квадратной матрице A можно
поставить в соответствие некоторое число,
которое называется определителем и
обозначается
det A | A |
a11
a12 a1n
a21
a22 a2 n
an1
an 2 ann
2.
Определителем первого порядканазывается число, которое определяется по
правилу
a11 a11
3.
Определителем второго порядканазывается число, которое определяется по
правилу
a11 a12
a11a22 a21a12
a21 a22
Пример.
1
2
3
4
1 4 ( 2) 3 4 6 10.
4.
Определителем третьего порядканазывается число, которое определяется по
правилу
a11
a12
a21 a22
a31 a32
a13
a23
a33
a11a22a33 a12a23a31 a21a32a13
a31a22a13 a12a21a33 a23a32a11
5.
a11a12
a21 a22
a31
a32
a13
a23 a11a22a33 a12a23a31 a21a32a13
a33 a31a22a13 a12a21a33 a23a32a11
Правило треугольников
(+)
(-)
6.
(+)(-)
Пример.
2 1
0
3 4 2 2 4 2 ( 1) ( 2) ( 1) 3 1 0
1 1
2
0 4 ( 1) ( 1) 3 2 ( 2) 1 2
16 2 0 0 6 4 24.
7.
(-)(+)
Пример.
2 1
3
1
0 2 1
4 2 3
1
2 1
0
4 2
1
2
2 4 2 ( 1) ( 2) ( 1) 0 3 1 0 4 ( 1) ( 1) 3 2
2 ( 2) 1 16 2 0 0 6 4 24.
8.
Свойства определителей1. Если определитель транспонировать, то его
значение не изменится.
Пример.
2 1
3
1
0
2
4 2 1
1
2
Проверить самостоятельно.
3 1
4
0 2
1.
2
9.
2. Если в определителе поменять местамилюбые две строки или столбца, то он изменит
знак.
Пример.
2 1
3
1
0
3
4 2
4 2 2 1
1
2
1
Проверить самостоятельно.
1
0.
2
10.
3. Если любую строку (столбец) определителяумножить на число, то получим определитель
равный исходному, умноженному на это число.
Другими словами, общий множитель
элементов любой строки (столбца) можно
вынести за знак определителя.
Пример.
2 4
6
1 2
3
3 4 2 2 3 4 2.
1 1
2
1 1
Проверить самостоятельно.
2
11.
4. Если все элементы какой-либо строки(столбца) определителя равны нулю, то
определитель равен нулю.
Пример.
2 1 5
0
1
0 0 0.
1 2
Проверить самостоятельно.
12.
5. Если соответствующие элементы какихлибо двух строк (столбцов) равны междусобой, то определитель равен нулю.
Пример.
2 4
2
3 4
3 0.
1 1 1
Проверить самостоятельно.
13.
Замечание 1.Если элементы какой-либо строки (столбца)
пропорциональны соответствующим
элементам другой строки (столбца), то
определитель равен нулю.
Доказательство.
a11
a12
k a11 k a12
a31
a32
a13
a11
a12
a13
k a13 k a11
a12
a13 k 0 0.
a33
a31 a32
Свойство 3
a33
Свойство 5
14.
6. Если элементы какой-либо строки (столбца)являются суммой двух слагаемых, то
определитель можно разложить на сумму двух
соответствующих определителей.
a11
a12
a13 b
a11
a12
a13
a11
a12
b
a21 a22
a23 c a21 a22
a23 a21 a22
c.
a31 a32
a33 d
a33
d
a31 a32
a31 a32
15.
7. Если к элементам какой-либо строки(столбца) определителя прибавить элементы
другой строки (столбца) этого же
определителя, умноженные на любое число,
то значение определителя не изменится.
Доказательство. Св. 6
a11
a12
a13 k a12
a11
Зам. 1
a12
a13
a11
a12
k a12
a21 a22
a23 k a22 a21 a22
a23 a21 a22
k a22
a31 a32
a33 k a32
a33
k a32
a31 a32
a11
a12
a21 a22
a31 a32
a13
a31 a32
a11
a12
a13
a23 0 a21 a22
a23 .
a33
a33
a31 a32
16.
Пример.1
2 3
2 1 1.
1
1 2
Первую строку домножим на (-2) и сложим
со второй.
Первую строку сложим с третьей.
11
22
33
0 5 5
0
3
5
Проверить самостоятельно.
17.
Минором элемента aij определителяназывается определитель, получаемый
из исходного вычеркиванием i-той
строки и j-того столбца.
Обозначается:
M ij .
Пример.
1
2 3
2 1 1.
1
1 2
M 21
2 3
1 2
1.
18.
Алгебраическим дополнением элементаaij определителя называется число, которое
обозначается Aij и равное
Aij ( 1)i j M ij .
Пример.
1
2 3
2 1 1.
1
1 2
A21 ( 1)
2 1
M 21 1.
19.
Теорема 1 (Лапласа).Определитель равен сумме произведений
элементов любой строки (столбца) на их
алгебраические дополнения.
Доказательство. Покажем, что
a11
a12
a13
a21 a22
a23 a11 A11 a12 A12 a13 A13.
a31 a32
a33
Преобразуем правую часть
20.
a11 A11 a12 A12 a13 A13 a11a22 a23
a32
a33
a12
a21 a23
a31 a33
a13
a21 a22
a31 a32
a11 (a22a33 a23a32 ) a12 (a21a33 a23a31 ) a13 (a21a32 a22a31 )
a11a22a33 a11a23a32 a12a21a33 a12a23a31
a13a21a32 a13a22a31 .
Пример.
1 2 1 3
2 0
2 3
1 2
1 1
0
1
0 4
.
21.
1 2 1 32 0
2 3
1 2
1 1
0
1
.
0 4
Выберем ту строку (столбец), которая
содержит наибольшее количество нулей.
1 A13 1 A23 0 A33 0 A43.
2 0
1
A13 ( 1)1 3 2 3 1 13;
1 2 4
1 ( 13) 1 ( 13) 0.
1 2 3
A23 ( 1) 2 3 2 3 1 13;
1 2 4
22.
Теорема 2 (аннулирования).Сумма произведений элементов какой-либо
строки (столбца) определителя на
алгебраические дополнения соответствующих
элементов другой строки (столбца) равна
нулю.
a11 A21 a12 A22 a13 A23 0.
23.
п.2. Обратная матрицаКвадратная матрица называется
(не)вырожденной, если ее определитель
(не) равен нулю.
Матрица A 1называется обратной к
матрице A, если выполняются равенства:
1
1
A A A A E.
24.
Нахождение обратной матрицыA11
1 A21
1
A
det A
A
n1
A12 A1n
A22 A2 n
An 2 Ann
det A ─ определитель матрицы A
Aij ─ алгебраическое дополнение
T
25.
Доказательство. Рассмотрим матрицуA11
*
A A21
A
31
T
A13 A11 A21 A31
A22 A23 A12 A22 A32 .
A32 A33 A13 A23 A33
Найдем произведение
a11 a12 a13 A11 A21 A31
*
A A a21 a22 a23 A12 A22 A32
a
A
a
a
A
A
33 13
23
33
31 32
A12
a11 A11 a12 A12 a13 A13 a11 A21 a12 A22 a13 A23 a11 A31 a12 A32 a13 A33
a21 A11 a22 A12 a23 A13 a21 A21 a22 A22 a23 A23 a21 A31 a22 A32 a23 A33
a A a A a A
a
A
a
A
a
A
a
A
a
A
a
A
31 21
32 22
33 23
31 31
32 32
33 33
31 11 32 12 33 13
26.
Применяем теоремы Лапласа ианнулирования
0
0
1 0 0
det A
0 det A 0 1 0 det A E.
det A
0
0 0 1
0
A
det
0
*
Значит,
A A det A E
или
*
A
A
E.
det A
Аналогично,
A*
A E.
det A
*
A
1
По определению
A
.
det A
27.
1 2 1A 0 3 1
4 0 2
Пример.
1 2
1
A 0 3 1 2 0
матрица A невырождена,
1
существует
1
3 2 1 0 6
0 2
A21 4
A31 1
0 1
(0 2 1 4) 4
4 2
A22 2
A32 1
A23 8
A33 3
4 0 2
A
1 1 3
A11 ( 1)
1 2
A12 ( 1)
A13 12
28.
A111 A21
1
A
det A
A
n1
T
A12 A1n
A22 A2 n
An 2 Ann
4 12
6
1 1
1
A 4 2
6
2
1
1
3
6 4 1 3 2 0,5
1
4 2 1 2 1 0,5
2
6
12
6
3
3
1
,
5
T
29.
Свойства обратной матрицы1
1) det( A )
.
det A
1
2) ( AB) 1 B 1 A 1.
1 T
T 1
3) ( A ) ( A ) .
30.
п.3. Ранг матрицыРассмотрим матрицу
Am n
a11 a12
a21 a22
a
m1 am 2
a1n
a2 n
.
amn
Пусть k min( m, n).
Выделим в матрице k строк и k столбцов.
Из элементов, стоящих на пересечении,
составим определитель порядка k.
Составленные таким образом определители
называются минорами матрицы.
31.
Пример.1
3
A
1
2
1
5
2 1
4 1
.
4 2 3 5
2 3
0 0
2
0
Составим минор 3-го порядка.
2 1 5
2
1
1.
2
3
0
32.
Рангом матрицы называется наибольшийпорядок отличного от нуля минора этой
матрицы.
Обозначается r ( A), rang A.
Замечание 2. r ( Am n ) min( m, n).
Пример.
1 2 1
A 0 3 1
1 5 3
1 2 1
A 0 3 1 0
1 5 3
M11
1 2
0 3
r ( A) 2
3 0
33.
Свойства ранга матрицы1) Ранг матрицы не меняется при
транспонировании.
2) Ранг матрицы не меняется при умножении
строки (столбца) на число, не равное нулю.
3) Ранг матрицы не меняется при
вычеркивании нулевой строки (столбца).
4) Ранг матрицы не меняется при сложении
элементов какой-либо строки (столбца) с
соответствующими элементами другой строки
(столбца), умноженными на некоторое число.
34.
Пример. Найти ранг матрицы1 2 1 3
A 2 1 1 0 .
4 3 1 6
Решение.
1 2 1 3 1 2 1 3 1 2 1 3
2 1 1 0 ~ 0 5 3 6 ~ 0 5 3 6 ~
4 3 1 6 0 5 3 6 0 0
0
0
1 2 1 3
.
~
0 5 3 6
Значит,
r ( A) 2.





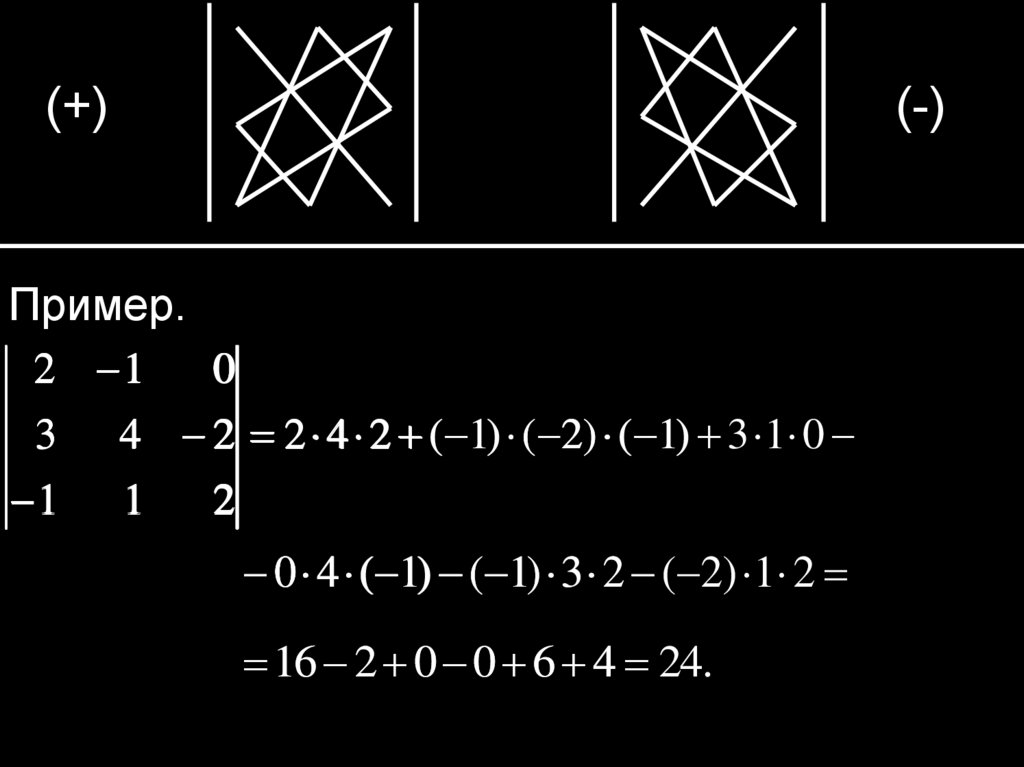













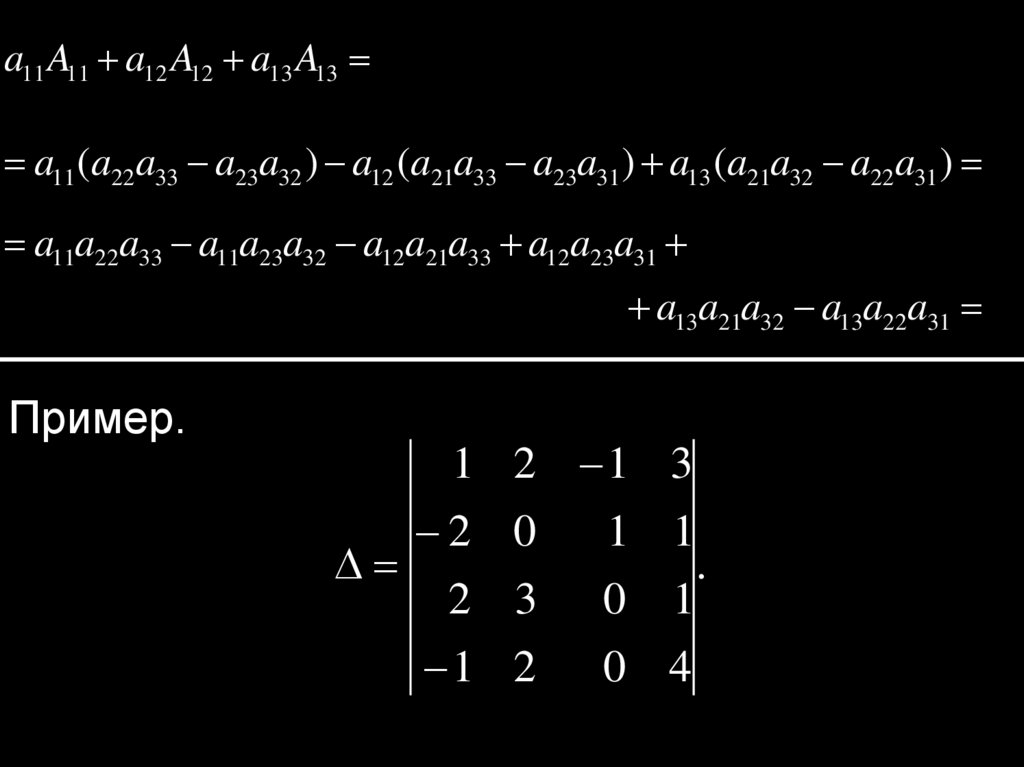














 Математика
Математика








