Обратимые_и_необратимые_процессы

1. Обратимые и необратимые процессы. Энтропия. Циклические процессы. Цикл Карно. Коэффициент полезного действия тепловых машин.

Второе
начало термодинамики. Энтропия
как функция состояния системы.
Третье начало термодинамики.

2.

• Обратимые и необратимые процессы, пути изменения
состояния термодинамической системы.
• Процесс называют обратимым, если он допускает
возвращение рассматриваемой системы из конечного
состояния в исходное через ту же последовательность
промежуточных состояний, что и в прямом процессе, но
проходимую в обратном порядке.
• Свойство обратимого процесса: протекание обратимого
процесса в одном и обратном направлении и возвращение
системы в первоначальное состояние не должно вносить
никаких изменений в окружающую среду.
• Обратимый процесс
должен протекать настолько
медленно, чтобы его можно было рассматривать как
непрерывный ряд равновесных состояний.
• Обратимый процесс - идеализированный случай,
достижим лишь при бесконечно медленном изменении
термодинамических параметров.

3.

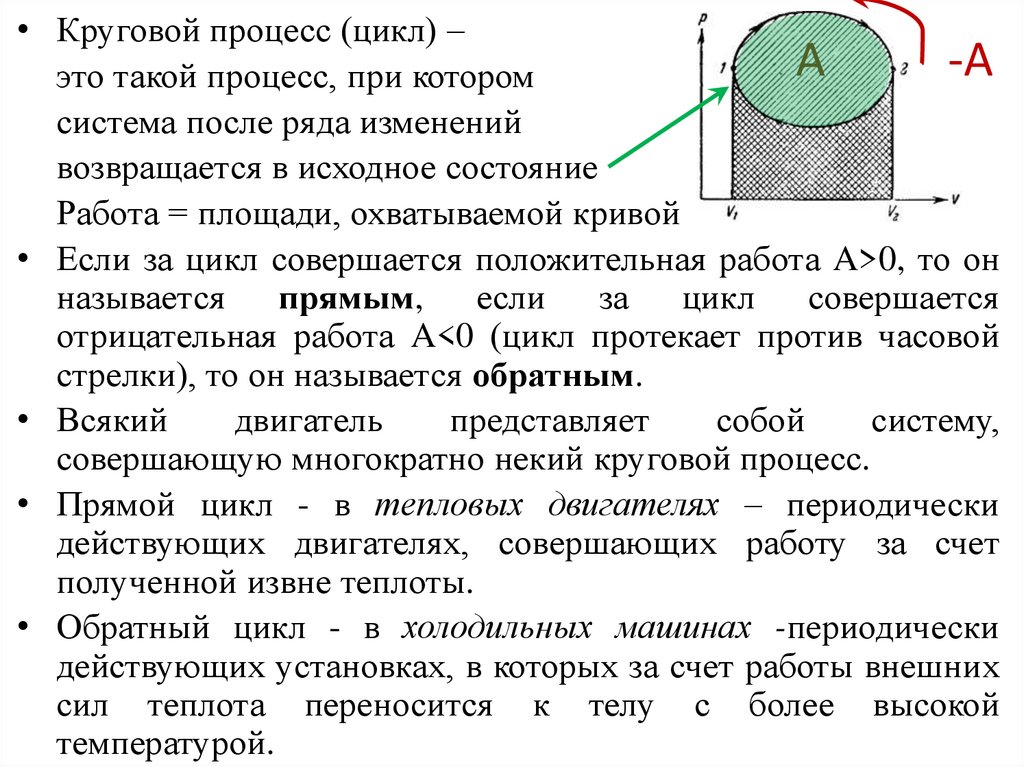
• Круговой процесс (цикл) –
А
-А
это такой процесс, при котором
система после ряда изменений
возвращается в исходное состояние
Работа = площади, охватываемой кривой
• Если за цикл совершается положительная работа A>0, то он
называется прямым, если за цикл совершается
отрицательная работа A<0 (цикл протекает против часовой
стрелки), то он называется обратным.
• Всякий
двигатель
представляет
собой
систему,
совершающую многократно некий круговой процесс.
• Прямой цикл - в тепловых двигателях – периодически
действующих двигателях, совершающих работу за счет
полученной извне теплоты.
• Обратный цикл - в холодильных машинах -периодически
действующих установках, в которых за счет работы внешних
сил теплота переносится к телу с более высокой
температурой.

4.

• Газ – рабочее веществорасширяется от V1 до V2
затем сжимается от V2 до V1
• A>0, т.к. Pрасширения>Pсжатия
• При расширении – сообщают тепло
• При сжатии – отнимают тепло
• Первое начало термодинамики при
расширении:
• Первое начало термодинамики при сжатии:
• Сложим и получим:
работа за весь цикл
• При цикле ΔU=0
• Тепловая машина – периодически действующий двигатель,
совершающий работу за счёт получаемого извне тепла.
• Работа A за цикл = полученному за цикл количеству теплоты Q.
Отношение работы A к количеству теплоты Q1, полученному
рабочим телом за цикл от нагревателя, называется
коэффициентом полезного действия η тепловой машины:
• К.п.д. ≤1

5.

• Необратимые процессы могут протекать самопроизвольно
только в одном направлении (диффузия, теплопроводность,
вязкое течение и другое)
• Теплота всегда переходит от горячего тела к холодному, а
механическая энергий макроскопических тел – во внутреннюю.
• Второй закон термодинамики определяет условия превращения
видов энергии и направления протекания процессов:
• Клаузиус (1850): Невозможен самопроизвольный переход тепла
от менее к более нагретому телу, или невозможны процессы,
единственным результатом которых был бы переход тепла от
менее к более нагретому телу
• Кельвин (1851): невозможны процессы, единственным
конечным результатом, которых было бы превращение тепла
целиком в работу
• Например, изотермическое расширение газа – не единственный
конечный результат:
• все тепло превращается в работу
• происходит изменение объема газа

6.

• Рассмотрим тепловой двигатель состоит из: нагревателя с
температурой T1, холодильника T2 и рабочего тела (устройства
способного получать тепло и совершать работу) – идеальный
газ в цилиндре с поршнем
• Цикл Карно: две изотермы+
две адиабаты
• 1-2 : изотермическое расширение при T1,
получает тепло Q1
• 3-4:изотермическое сжатие при T2,
отдаёт тепло Q2
• К.п.д. двигателя:
• Если его проводить бесконечно медленно,
то цикл можно рассмотреть как обратимый
• К.п.д. всех обратимых машин, работающих с одним и тем же
нагревателем и холодильником, должен быть одинаков
• Теорема Карно: к.п.д. обратимой машины зависит только от
температуры нагревателя и холодильника, и не зависит от рода
рабочего вещества.

7.

• Необратимая тепловая машина - цикл в обратном направлении: А
газа < 0, Q1-тепло к нагревателю, Q2’ – тепло от холодильника к
газу.
• К.п.д. необратимой машины может быть больше обратимой
машины? η необр > η обр?
• Сравним обратимы и необратимый циклы расширения и сжатия
газа:
• Обратимый цикл - протекает медленно
давление газа по
объему выравнивается: А обрат= А+расшир+А-сжатия
• Необратимый цикл – давление не выравнивается
• Расширение:
Р под поршнем < Р под поршнем при обратимом цикле
• Сжатие:
Р под поршнем > Р под поршнем при обратимом цикле
• Полная работа в необратимом цикле: А необрат= А’+расшир+ А’-сжатия
• При этом А+расшир >А’+расшир , А-сжатия < А’-сжатия , А необрат < А обрат
• Значит всегда: η необр > η обр

8.

• Рассмотрим к.п.д. цикла Карно для идеального газа:
• Найдём зависимость к.п.д. от T1 и T2
• По определению:
где Q1- тепло, получаемое за цикл
от нагревателя, Q2’ – тепло,
отдаваемое за цикл холодильнику
T=const ΔU=0 Q1=A12 – работа газа при переходе из 1 в 2
Для изотермического процесса:
• где m- масса идеального газа в машине
• Тогда Q2’=A’34- работа на сжатие газа:
• Цикл замкнутый состояния 1 и 4 и состояния 2 и 3 должны
лежать на определенных адиабатах:
• Условие замкнутости цикла:

9.

• Тогда к.п.д.:
• - к.п.д. любой обратимой машины
• Т.к. к.п.д. необратимой машины
обратимой машины:
всегда меньше к.п.д.
• Равенство – обратимая машина, неравенство- необратимая
машина
• Пусть получаемое Q положительно, если тепло передаётся от
какого- то внешнего тела системе, и Q принимает
отрицательное значение, если система отдает тепло внешнему
телу, тогда:
- неравенство Клаузиуса

10.

• Приведенное количество теплоты - отношение количества
тепла, полученного системой от какого-либо тела,
к температуре этого тела.
• Если система вступает
в теплообмен с N телами:
• Сумма элементарных приведенных количеств
тепла, получаемых системой в ходе цикла
извне, равна нулю, если цикл обратим, и меньше нуля, если
цикл необратим.
• Сумма
для любого некругового обратимого (возможен
переход из 2 в 1) процесса при переходе из состояния 1 в 2 не
зависит от пути
• Термодинамическая величина –
• энтропия S:
• Приращение энтропии равно элементарному количества тепла,
получаемому обратимо системой извне, отнесенному к
температуре, при которой тепло получается.

11.

• Энтропия в интегральной форме:
• Свойства энтропии:
1. Энтропия – функция состояния , то приращение энтропии есть
разность значений энтропии в конечном и начальном
состояниях.
2. Энтропия аддитивна- равна сумме энтропий отдельных её
частей.
3. Энтропия замкнутой макросистемы не уменьшается – она или
возрастает, или остается постоянной
Для цикла Карно: площадь прямоугольника
равна количеству тепла, получаемому
системой за цикл:
- площадь цикла

12.

Изменение энтропии при обратимом изотермическом процессе:
где Q12 - количество теплота, полученное системой при
обратимом изотермическом процессе при переходе из 1 в 2.
• Если Q12< 0, то S2 < S1
• Величина возрастания энтропии может служить мерой
необратимости процессов, протекающих в системе.
4. Теорема Нернста: при приближении температуры к
абсолютному нулю энтропия макросистемы также стремится к
нулю:
- третье начало термодинамики
5. Связь энтропии и вероятности состояния системы:
где k- постоянная Больцмана, W- термодинамическая
вероятность состояния системы – число различных способов,
которыми может быть осуществлено данное состояние
Любой необратимый процесс – это процесс, обратный которому
маловероятен.

13.

• Рассмотрим систему- теплоизолированный сосуд объемом V
заполненный двумя идеальными газами 1 и 2 , разделенных
перегородкой.
• T1=T2=T, P1=P2=P, ν1=ν2=ν
• Удалили перегородку – газы смешиваются
• Система переходи в равновесное состояние, где газы
равномерно перемешаны.
• Т – не изменится, т.к. система теплоизолирована, газы идеальны
• При V1=V2 и T= const:
Приращение энтропии каждого газа:
Приращение энтропии всей системы:
ΔS>0 – процесс необратимый
Парадокс Гиббса: пусть газы тождественны; после удаления
перегородки энтропия увеличится, хотя конечное состояние
системы ничем не отличается от начального.